Significance
Many applications in engineering require stretchable materials that dissipate little energy during normal operation of cyclic loads (low hysteresis), but dissipate much energy to resist rupture (high toughness), and survive prolonged cyclic loads (fatigue resistant). However, existing stretchable materials cannot meet these requirements simultaneously. Here we present a principle to achieve this goal, and demonstrate the principle by a composite of two stretchable materials of low hysteresis, with large modulus contrast and strong adhesion. The composite retains the low hysteresis, but is much tougher and more fatigue resistant than the constituents. The same principle applies to elastomers, gels, and elastomer–gel hybrids. This class of materials provides opportunities to create high-cycle and low-dissipation soft robots and soft human–machine interfaces.
Keywords: elastomer, stretchable materials, toughness, hysteresis, fatigue
Abstract
In materials of all types, hysteresis and toughness are usually correlated. For example, a highly stretchable elastomer or hydrogel of a single polymer network has low hysteresis and low toughness. The single network is commonly toughened by introducing sacrificial bonds, but breaking and possibly reforming the sacrificial bonds causes pronounced hysteresis. In this paper, we describe a principle of stretchable materials that disrupt the toughness–hysteresis correlation, achieving both high toughness and low hysteresis. We demonstrate the principle by fabricating a composite of two constituents: a matrix of low elastic modulus, and fibers of high elastic modulus, with strong adhesion between the matrix and the fibers, but with no sacrificial bonds. Both constituents have low hysteresis (5%) and low toughness (300 J/m2), whereas the composite retains the low hysteresis but achieves high toughness (10,000 J/m2). Both constituents are prone to fatigue fracture, whereas the composite is highly fatigue resistant. We conduct experiment and computation to ascertain that the large modulus contrast alleviates stress concentration at the crack front, and that strong adhesion binds the fibers and the matrix and suppresses sliding between them. Stretchable materials of high toughness and low hysteresis provide opportunities to the creation of high-cycle and low-dissipation soft robots and soft human–machine interfaces.
Stretchable materials such as elastomers and gels enable the fast-moving field of soft (and possibly biocompatible) systems. Examples include stretchable electronics (1–4), soft robots (5, 6), ionotronics (7–9), drug delivery (10, 11), and tissue regeneration (12). Many systems require that the stretchable materials have high toughness (i.e., dissipate much energy to resist the extension of cracks), but have low hysteresis (i.e., dissipate little energy during normal operation of load and unload). These two requirements, however, usually conflict: Toughness and hysteresis are often correlated. Toughness and hysteresis both result from energy dissipation, just under different conditions. A stretchable material of a single polymer network usually has low hysteresis and low toughness—that is, the stress–stretch curves for load and unload almost coincide, and the material ruptures at a much-reduced stretch when containing a crack (13).
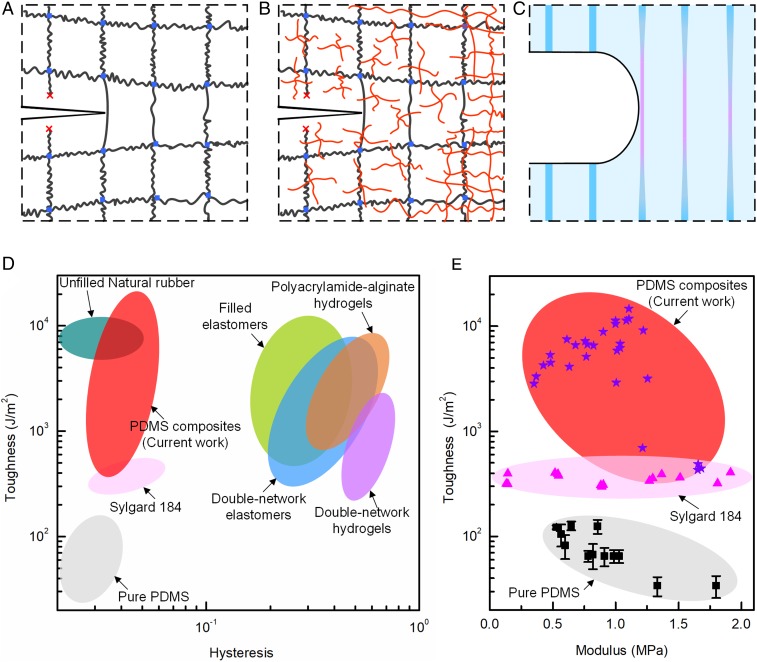
The toughness–hysteresis correlation has a molecular origin (Fig. 1A). A stretchable material such as an elastomer or a gel has a molecular architecture that mixes strong and weak bonds, enabling the hybrid behavior of solid and liquid. Strong bonds (e.g., covalent bonds) link monomer units into polymer chains, and cross-link the polymer chains into a network. Weak bonds (e.g., hydrogen bonds and van der Waals interaction) aggregate the monomer units of different polymer chains, as well as solvent molecules, into a condensed phase, but allow them to change neighbors constantly, transmit force negligibly, and act like a liquid of low viscosity. The weak interchain bonds enable the network to be an entropic spring of low hysteresis. A crack concentrates stretch and breaks the polymer chains ahead, while the network off the crack plane remains elastic. This concentration of stretch causes a low toughness between 10 and 100 J/m2, estimated by the bond energy of a single layer of polymer chains per unit area (14).
Fig. 1.
Toughness and hysteresis. (A) An unfilled polymer network typically has low toughness and low hysteresis. At the front of a crack, a polymer chain is highly stretched, and its scission dissipates the energy stored in the entire chain. (B) A primary network added with sacrificial bonds has high toughness and high hysteresis. The primary network transmits the stress from the front of a crack into the bulk of the network, breaking many sacrificial bonds off the crack plane, and dissipating a large amount of energy. (C) A composite of a soft matrix and hard fibers has high toughness and low hysteresis. At the front of a crack, the soft matrix shears greatly to spread large stretch over a long segment of each fiber, and the rupture of a fiber dissipates the energy in the segment. (D) Toughness–hysteresis diagram. Many existing elastomers and gels occupy the diagonal region, but natural rubber and our composite PDMS occupy the upper-left quadrant. (E) Toughness–modulus diagram. The toughness of the pure PDMS is collected from the literature (27). The toughness of Sylgard PDMS and composite PDMS is measured in this work. The few composites have low toughness because they have low fiber/matrix modulus contrast. The hysteresis of the composite PDMS and homogeneous Sylgard PDMS is measured in this work for stretch between 1.5 and 1.8. The hysteresis of other materials is obtained from the literature (17–19, 28–30, 38, 39) for stretch between 1.5 and 3. (The other materials shown here are all much more stretchable than PDMS. The hysteresis for natural rubber can be very small at a stretch below 3.)
The single network is commonly toughened by introducing sacrificial bonds, through fillers (15, 16) or a secondary polymer network (17–19). A crack breaks not only a layer of polymer chains of the primary network, but also many sacrificial bonds off the crack plane (Fig. 1B). The synergy of the scission of the primary network and the dissipation of the sacrificial bonds amplifies toughness to 103–105 J/m2. Double-network hydrogels (17) and elastomers (19) are elastic under small stretch. The elastic range can be tuned, e.g., by prestretch (20). These approaches trade off toughness and hysteresis. Some types of broken sacrificial bonds do not reform, but other types do. If the sacrificial bonds break progressively and do not reform, the stress–stretch curve changes cycle by cycle, and the material is said to fatigue damage. If the broken sacrificial bonds reform, the stress–stretch curve forms a stable loop in subsequent cycles of load and unload, and the material is said to heal. In a material containing sacrificial bonds, either healable or not, a crack extends cycle by cycle when the magnitude of the load exceeds a threshold, much below the toughness (21–23). Even for a material that heals after fatigue damage, the hysteresis associated with the sacrificial bonds consumes energy, complicates the stress–stretch behavior, and is extremely undesirable in many applications, such as in robots, sensors, and actuators.
We are inspired by materials that achieve high toughness without using sacrificial bonds. Bones and nacre shells have “brick-mortar” microstructures, which resist fracture by inducing tortuous crack (24). Combination of dissimilar materials has long enabled composites such as fiber-reinforced plastics (25) and elastomers (26). These materials, although not stretchable, have high toughness and low hysteresis.
Here we show that the principle of composites can also enable stretchable materials that disrupt the toughness–hysteresis correlation, achieving both high toughness and low hysteresis (Fig. 1C). We illustrate this principle using a composite of two constituents: a matrix of low elastic modulus, and fibers of high elastic modulus. The matrix and fibers form strong adhesion. At a crack front, the soft matrix shears greatly, spreading large stretch in a long segment of each fiber. When a fiber ruptures, all of the elastic energy stored in the highly stretched segment is released. This deconcentration of stress is analogous to that in a single polymer network, but rupture releases energy in a fiber segment, rather than that in a polymer chain. The former has a much larger volume than the latter. The composite achieves high toughness through large fiber/modulus contrast, with no sacrificial bonds. The composite achieves low hysteresis so long as the fibers and matrix have low hysteresis and strong adhesion.
Results and Discussion
We demonstrate this principle by making a model composite of polydimethylsiloxane (PDMS) (SI Appendix, Fig. S1). The precursor (Sylgard 184 from Dow Corning) has two liquids: a base (part A) and a curing agent (part B). We call the PDMS of weight ratio A:B = 10:1 suggested by the supplier the “hard PDMS,” and call the ones of smaller fractions of the curing agent the “soft PDMS.” We make a thin film of the hard PDMS using a mold, cut the film into fibers using a paper cutter, align the fibers in the precursor of a soft PDMS, and cure the composite. The composite is transparent; we color the matrix in translucent red to see the fibers and the crack profile in a sample.
We measure the toughness and hysteresis of homogeneous PDMS of various A:B ratios, as well as composites of the hard fibers and matrices of various A:B ratios (SI Appendix, Fig. S2). We then plot the data, along with those of representative existing stretchable materials, on the toughness–hysteresis diagram (Fig. 1D). Hysteresis depends on the maximum applied stretch; here we choose maximum stretch between 1.5 and 1.8 for PDMS, and between 1.5 and 3 for other materials, representative values in applications. In the diagram, the toughness–hysteresis correlation corresponds to the diagonal region, and the conflicting requirements of high toughness and low hysteresis correspond to the upper-left quadrant. Of the existing stretchable materials, many occupy the diagonal region, but natural rubber occupies the upper-left quadrant. Natural rubber disrupts the toughness–hysteresis correlation by an unusual mechanism. Natural rubber is a single-network elastomer, has low hysteresis when the stretch is small, and has high toughness because polymer chains undergo strain-induced crystallization at large stretch. However, natural rubber is prone to fatigue fracture, as the high stretch at the front of a crack causes repeated crystallization and melting (14). Our composite PDMS also disrupts the toughness–hysteresis correlation, achieving simultaneously the high toughness of networks containing sacrificial bonds, and the low hysteresis of single networks. The composite is highly fatigue resistant because the constituents are elastic up to limiting stretches.
We compare several kinds of PDMS in the toughness–modulus diagram (Fig. 1E). For pure PDMS without silica fillers, toughness decreases from 100 to 10 J/m2 as the elastic modulus increases (27). This toughness–modulus conflict is common among single-network elastomers and gels containing no sacrificial bonds. The Sylgard PDMS reconciles the toughness–modulus conflict, but has a relatively low toughness around 300 J/m2. We can easily tune the toughness of the composite PDMS between the order of 100 and 10,000 J/m2 by varying the contrast of the moduli and the concentration of the fibers. The composites reconcile the toughness–modulus conflict and increase both modulus and toughness.
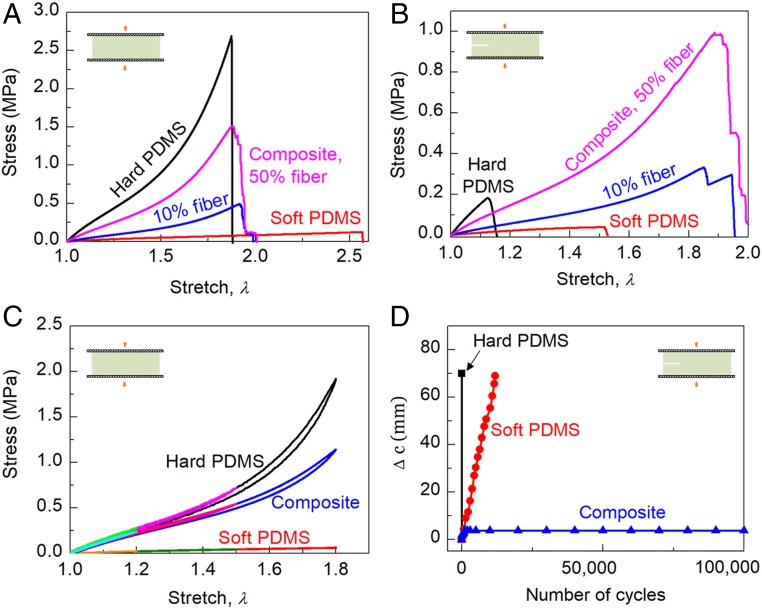
We stretch samples with precut cracks and watch the cracks run (Fig. 2). When a homogeneous hard PDMS is stretched to 1.12 times its original height, the crack runs rapidly through the entire sample (Fig. 2A and Movie S1). When a composite PDMS is stretched to 1.5 its original height, the crack blunts and remains stable. Upon further stretch, the crack branches near the interface between the matrix and fiber (Fig. 2B). At a stretch of 1.9, the fibers start to break at a random location far ahead of the crack front, and the whole composite PDMS ruptures (Movie S2). When a homogeneous hard PDMS is under cyclic load of maximum stretch of 1.2, the crack extends rapidly before reaching the maximum stretch in the first cycle (Fig. 2C). When a composite is under the same cyclic load, the crack in the composite propagates to the fiber/matrix interface within 1,000 cycles, and then arrests without any further extension for 100,000 cycles (Fig. 2D). This experiment gives a fatigue threshold above 160 J/m2 for the composite PDMS. By comparison, the fatigue threshold is about 50 J/m2 for natural rubber (14).
Fig. 2.
Fracture and fatigue of homogeneous PDMS and composite PDMS. Each sample is glued to two rigid clamps, and precut with a crack using a razor blade. (A) A homogeneous hard PDMS ruptures at a monotonic stretch of 1.12. (B) A composite PDMS does not rupture at a monotonic stretch of 1.85. (C) When a homogeneous hard PDMS is subjected to cycles of load and unload of maximum stretch of 1.2, the crack extends rapidly before reaching the maximum stretch in the first cycle. (D) When a composite PDMS is subjected to cycles of load and unload of maximum stretch of 1.2, the crack extends to the first fiber in front within 1,000 cycles, but then arrests without any further extension over 100,000 cycles. A:B = 10:1 for the homogeneous hard PDMS. For the composite, A:B = 10:1 for the fibers, and 30:1 for the matrix.
Each constituent is flaw sensitive, but the composite is not. When the samples without precut crack are pulled, the homogeneous hard PDMS ruptures at a stretch of 1.9, the homogeneous soft PDMS ruptures at stretch of 2.5, and the composite PDMS ruptures at almost the same stretch of the homogeneous hard PDMS (Fig. 3A). However, when the samples with precut cracks are pulled, both the hard and the soft PDMS rupture at much reduced stretches, whereas the composite ruptures at about the same stretch as that of the sample without precut crack (Fig. 3B).
Fig. 3.
Flaw insensitivity, low hysteresis, and fatigue resistance. (A) Stress–stretch curves of samples without precut cracks stretched monotonically to rupture. The stress is defined as the force applied on the deformed sample divided by the cross-sectional area of the undeformed sample. (B) Stress–stretch curves of samples with precut cracks stretched monotonically to rupture. (C) Stress–stretch curves of samples without precut cracks subjected to loading and unloading to measure hysteresis. (D) Samples with precut cracks are cycled between stretches 1 and 1.2. The extension of the crack, , is recorded as a function of the number of cycles. A:B = 10:1 for the hard PDMS and for the fibers of composite PDMS. A:B = 30:1 for the soft PDMS and the matrix of the composite PDMS.
The hysteresis of the composite is low, comparable to that of the hard and the soft PDMS (Fig. 3C), but much lower than that of stretchable materials toughened by sacrificial bonds (17–19) and fillers (28–30) (Fig. 1D). [The Sylgard 184 PDMS does contain small amount of silica filler to modify the rheology of the precursor and mechanical properties of the elastomer (31), but still has low hysteresis and low toughness, as confirmed by our measurements.]
Each constituent is susceptible to fatigue fracture, but the composite is not (Fig. 3D). We cycle precracked samples between stretch of 1 and 1.2, and record the extension of the crack, , as a function of the number of cycles. The crack extends substantially cycle by cycle in the hard and in the soft PDMS, but negligibly in the composite.
Our principle of stretchable materials of high toughness and low hysteresis requires that (i) the fibers should be stiffer than the matrix, and (ii) the fibers and the matrix should be adherent. We next ascertain these requirements by a combination of experiment and computation. We test homogeneous samples with various A:B ratios (SI Appendix, Fig. S3), as well as composites of the hard fibers and matrices of various A:B ratios (SI Appendix, Fig. S4). When the matrix is also made of the hard PDMS, the toughness of the composite is almost the same as that of the homogeneous hard PDMS. As the fraction of the curing agent in the matrix decreases, the toughness of the composite increases and then plateaus. The crack tends to cut the fibers when the modulus contrast is small (Movie S3), but bifurcates near the fiber/matrix interface when the modulus contrast is large.
Toughness is defined as the energy dissipated when a crack extends by a unit area (SI Appendix, Fig. S2). For a homogeneous PDMS and a PDMS composite of small fiber/matrix modulus contrast, the crack extends forward and the measured toughness is the steady-state toughness. For a PDMS composite of large fiber/matrix modulus contrast, the fracture process is more complicated: The crack may bifurcate into the soft PDMS, and a hard PDMS fiber far away from precut crack tip may break first. In experiment, the critical stretch is defined as the stretch when a fiber breaks. The measured toughness is not a material constant and increases with sample height (SI Appendix, Fig. S4F). The sample size is limited in our experiment, and the toughness reported here is a lower bound of the steady-state toughness. If the sample is large enough, the crack will extend forward with a large process zone. Such a large-scale fracture process zone is common in tough materials. For tough hydrogels and elastomers toughened by sacrificial bonds, a great deal of energy is dissipated off the defined crack plane by breaking sacrificial bonds. For nacre shells, tortuous crack path is created to toughen the material.
To appreciate the significance of strong adhesion, we make a composite of weak adhesion by distributing spandex fibers (Dorlastan made by Asahi Kasei) in the soft PDMS matrix (SI Appendix, Fig. S5). When a sample with a precut crack is pulled to a stretch around 1.4, the crack grows in the matrix, and the fibers remain intact and slide against the matrix (Movie S4). The stress–stretch curves show larger hysteresis than that of the composites with strong adhesion, and degrade cycle by cycle, corresponding to debonding and sliding between the fibers and matrix (Movie S5). Eventually, the debonded interface turns into a running crack and ruptures the whole sample.
Strong adhesion between sequentially cured PDMS pieces is perhaps unremarkable due to covalent bonds and topological entanglements (Fig. 4A). Partially cured PDMS has been used to glue layers of PDMS (32), but no study on PDMS adhesion exists in the literature. To study the adhesion resembling that in the composite PDMS, we cure two layers of the hard PDMS, sandwich a thin layer of the precursor of PDMS, cure the laminate, and double peel the laminate (SI Appendix, Fig. S6). We observe three peeling modes (Fig. 4B), corresponding to different values of peeling toughness (Fig. 4C). When the middle layer is the hard PDMS, the peeling toughness is around 50 J/m2, and the sample peels along an interface between the middle layer and an arm, leaving the red middle layer on one peeled arm, but not on the other (Movie S6). For the middle layer of A:B = 12:1 and 15:1, the sample peels either along an interface or through the middle layer. When the sample peels along an interface, the peeling toughness is low. When the sample peels through the middle layer, the peeling toughness is almost the same as the bulk toughness (over 300 J/m2), and the middle layer leaves residuals on both peeled arms (Movie S7). As the middle layer becomes softer (A:B = 20:1 and 30:1), the peeling toughness is around 200 J/m2, and the sample peels through the middle layer with a wavy peeling front (Movie S8). Such a wavy peeling front is commonly observed in soft adhesives (33).
Fig. 4.
Peeling sequentially cured PDMS. (A) A hard PDMS and a soft PDMS adhere through covalent bonds and topological entanglements. (B) Photos of three peeling modes. A middle layer is cured between two precured hard PDMS. The middle layer is colored in red, and its A:B ratio varies from 10:1 to 30:1. (C) Peeling toughness depends on the A:B ratio of the middle layer. Four identical samples are tested for each A:B ratio of the middle layer.
We further ascertain the significance of large fiber/matrix modulus contrast by finite-element calculation (SI Appendix, Fig. S7). The soft matrix shears greatly and makes stretch much less concentrated in the composite than in the homogeneous PDMS. A fiber ahead of the crack front is highly stretched in a segment of a macroscopic length Y (SI Appendix, Fig. S8). When the fiber ruptures, the elastic energy stored in this large length scale is released, leading to high toughness. This model predicts the measured toughness remarkably well.
Hysteresis can be low in materials of constituents of any size and geometry, but toughness increases with the size of the constituents (SI Appendix, Fig. S9). A composite of uniaxial fibers resists fracture in one direction, but ruptures readily in other directions. A laminate with multidirectional fibers resists fracture in many directions, but can still delaminate easily. A composite of a 3D lattice of one material in a matrix of a much softer material will resist cracks in all directions. A composite of randomly distributed short fibers may also achieve high toughness and low hysteresis, while easing fabrication. Recent advances in technologies like additive manufacture (34), electric spinning (35), and stress-guided assembly (36) enable the fabrication of 3D structures that integrate different material at various length scales. The same principle applies to elastomers, gels, and elastomer–gel hybrids. One can also make stretchable materials of high toughness and low hysteresis by embedding fringed fibers of a nonstretchable material in a matrix of a stretchable material.
Our requirement for strong fiber/matrix adhesion is perhaps surprising to researchers familiar with tough composites of ceramic fibers and ceramic matrices, where the fiber–matrix interfaces are designed to have weak adhesion (37). In such a ceramic composite, the fiber/matrix modulus contrast is negligible. During fracture, after the matrix cracks, the weak adhesion enables the fibers to remain intact, slide relative to the matrix, and distribute high stress over long segments of the fibers. By contrast, to minimize hysteresis in the stretchable composite, here we require strong adhesion between the fibers and the matrix, and rely on large fiber/matrix modulus contrast to distribute high stretch to long segments of the fibers. Incidentally, composites of glass or carbon fibers and plastic matrices have large fiber/matrix modulus contrast and strong adhesion. Indeed, the deconcentration of stress is a unifying principle to achieve high toughness, for both stretchable and nonstretchable materials.
Conclusion
In summary, we have demonstrated a principle of stretchable materials of high toughness and low hysteresis. Such a material is a composite of two materials of low hysteresis, with large modulus contrast and strong adhesion, but with no sacrificial bonds. The composite retains the low hysteresis of its constituents, but is much tougher and much more fatigue resistant than the constituents. It is hoped that this class of materials will soon translate to high-cycle and low-dissipation soft robots and soft human–machine interfaces.
Materials and Methods
Material Fabrication.
We use Sylgard 184 from Dow Corning as the precursor to make the composite PDMS. The precursor comes with two liquids: a base (part A) and a curing agent (part B). We pour the precursor at a ratio of A:B = 10:1 into a cup, mix them in a mixer (ARE-250; Thinky) at 2,000 r/min for 1 min, and degas at 2,200 r/min for 1 min. We pour the mixture into a rectangular acrylic mold, thickness of 0.5 mm, degas the mixture again in a desiccator driven by a vacuum pump until all of the air bubbles are removed, and cure the mixture in an oven at 65 °C for 4 h. We cut the cured PDMS film into fibers of 1 mm in width by a paper cutter, align the fibers in an acrylic mold, thickness of 0.8 mm, pour the PDMS precursor at some ratio of A:B (varying from 10:1 to 30:1), and degas and cure again. The composite is fully transparent; we add 1 vol % red dye (Createx airbrush colors) into the precursor of matrix to see the crack profile and the fibers. For comparison, homogeneous PDMS samples of various A:B ratios are also prepared.
Hysteresis.
All of the mechanical tests are carried out on the Instron 5966 dual-column testing system. Samples of length mm, thickness mm, and height between two grippers mm are prepared. The samples are subjected to cyclic load of some maximum stretch, at a strain rate of 0.5/min (Fig. 3C).
Toughness.
We measure the toughness using a two-sample method described before (18). For a material of the same composition, we prepare two samples of the same dimensions. One sample does not contain precrack, and the other one has a precrack (SI Appendix, Fig. S2B, Insets). The samples are glued between two rigid plastic grippers by using 3M Super Silicone Sealant 8661 (purchased from McMaster-Carr). In the undeformed state, each sample is of length mm, thickness mm, and the height between two grippers is mm. The uncracked sample is used to measure the stress–stretch curve. All of the samples are stretched at a strain rate of 0.5/min. When the sample is pulled to a stretch of , the area beneath the stress–stretch curve is the elastic energy density in the gel, . The precracked sample is prepared by cutting a crack with mm by a razor blade. The precracked sample is used to measure the critical rupture stretch, . For homogeneous PDMS and composite PDMS of small fiber/matrix modulus contrast, the precut crack extends throughout the entire sample at a low stretch, and is defined as the stretch when the precut crack starts to grow. For composite PDMS of large fiber/matrix modulus ratio, the precut crack branches near the interface between the matrix and fiber as stretch increases. To a critical stretch, the fibers start to break at a random location far ahead of the crack front, and is defined as the stretch when the first fiber breaks. In all cases, the toughness is given by .
Elastic Modulus.
The initial slope of the stress–stretch curve measured using an uncracked sample is the plane-strain modulus, . The elastomer is an incompressible material, so that the elastic modulus under uniaxial tension is given by .
Fatigue Fracture.
Samples of dimensions mm, mm, mm, and mm are prepared. The samples are subjected to cyclic load of maximum stretch , with a fixed frequency of 0.5 Hz. A digital camera is used to record the extension of the crack.
Peeling Toughness.
We cure two layers of the hard PDMS of thickness a = 3 mm, width w = 20 mm, and length l = 100 mm, sandwich a thin layer of the precursor of PDMS of thickness t = 0.5 mm, length lm = 40 mm, and then cure the laminate. The two arms of the hard PDMS are attached with flexible but nonstretchable films (Polyester film of 50 μm in thickness, from McMaster-Carr) using the silicone adhesive (3M Super Silicone Sealant 8661, from McMaster-Carr). The thin middle layer is colored in translucent red and its composition varies from 10:1 to 30:1. We stretch the two arms by Instron at a constant rate of 10 mm/min, and record the force-extension curve (SI Appendix, Fig. S6). A plateau of Pc is recorded as the crack extends steadily. The peeling toughness is calculated by . Four identical samples are tested for each composition.
Work to Fracture of Fibers.
Uncracked hard PDMS samples of length mm, thickness mm, and height mm are stretched to rupture at a strain rate of 0.5/min (SI Appendix, Fig. S8C). The work to rupture is the area under the stress–stretch curve.
Finite-Element Simulation.
We use a commercial finite-element software, ABAQUS, to calculate the stress distribution and energy release rate. We measure the stress–stretch curves of hard and soft PDMS and fit them to the Gent model. Two parameters––shear modulus, and the limit of first invariant of the left Cauchy–Green deformation tensor, ––are identified (SI Appendix, Fig. S7 A and B). ABAQUS does not support the Gent model directly, and we use the UHYPER subroutine to implement the Gent model. We use the CPS8R element in ABAQUS. The geometry is a thin sheet with mm, mm. A cut exists at the middle of one edge with length mm. We assume the thin sheet in plane stress condition. Because of the symmetry of the geometry, we model a half of the sheet with a symmetric boundary in the crack plane. To avoid the singularity at the crack tip in calculations, we model a blunt tip with a small radius ρ = 0.001 mm before stretching. We stretch the sample to and calculate the stress distribution (SI Appendix, Fig. S7 C and D).
Supplementary Material
Acknowledgments
This work was supported by NSF Materials Research Science and Engineering Centers (Grant DMR-14-20570), and performed in part at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Infrastructure Network which is supported by the National Science Foundation under NSF Award ECS-0335765. CNS is part of Harvard University. C.X. was supported by China Scholarship Council as a visiting scholar for 2 y at Harvard University.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1821420116/-/DCSupplemental.
References
- 1.Kim D-H, et al. Epidermal electronics. Science. 2011;333:838–843. doi: 10.1126/science.1206157. [DOI] [PubMed] [Google Scholar]
- 2.Lipomi DJ, Tee BCK, Vosgueritchian M, Bao Z. Stretchable organic solar cells. Adv Mater. 2011;23:1771–1775. doi: 10.1002/adma.201004426. [DOI] [PubMed] [Google Scholar]
- 3.Minev IR, et al. Biomaterials. Electronic dura mater for long-term multimodal neural interfaces. Science. 2015;347:159–163. doi: 10.1126/science.1260318. [DOI] [PubMed] [Google Scholar]
- 4.Park S, et al. Self-powered ultra-flexible electronics via nano-grating-patterned organic photovoltaics. Nature. 2018;561:516–521. doi: 10.1038/s41586-018-0536-x. [DOI] [PubMed] [Google Scholar]
- 5.Whitesides GM. Soft robotics. Angew Chem Int Ed Engl. 2018;57:4258–4273. doi: 10.1002/anie.201800907. [DOI] [PubMed] [Google Scholar]
- 6.Wallin TJ, Pikul J, Shepherd RF. 3D printing of soft robotic systems. Nat Rev Mater. 2018;3:84–100. [Google Scholar]
- 7.Keplinger C, et al. Stretchable, transparent, ionic conductors. Science. 2013;341:984–987. doi: 10.1126/science.1240228. [DOI] [PubMed] [Google Scholar]
- 8.Yang C, Suo Z. Hydrogel ionotronics. Nat Rev Mater. 2018;3:125–142. [Google Scholar]
- 9.Schroeder TBH, et al. An electric-eel-inspired soft power source from stacked hydrogels. Nature. 2017;552:214–218. doi: 10.1038/nature24670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li J, Mooney DJ. Designing hydrogels for controlled drug delivery. Nat Rev Mater. 2016;1:16071. doi: 10.1038/natrevmats.2016.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu J, et al. Triggerable tough hydrogels for gastric resident dosage forms. Nat Commun. 2017;8:124. doi: 10.1038/s41467-017-00144-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Annabi N, et al. 25th anniversary article: Rational design and applications of hydrogels in regenerative medicine. Adv Mater. 2014;26:85–123. doi: 10.1002/adma.201303233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen C, Wang Z, Suo Z. Flaw sensitivity of highly stretchable materials. Extreme Mech Lett. 2017;10:50–57. [Google Scholar]
- 14.Lake G, Thomas A. The strength of highly elastic materials. Proc R Soc London Ser A. 1967;300:108–119. [Google Scholar]
- 15.Bueche AM. Filler reinforcement of silicone rubber. J Polym Sci Polym Phys Ed. 1957;25:139–149. [Google Scholar]
- 16.Lin W-C, Fan W, Marcellan A, Hourdet D, Creton C. Large strain and fracture properties of poly(dimethylacrylamide)/silica hybrid hydrogels. Macromolecules. 2010;43:2554–2563. [Google Scholar]
- 17.Gong JP, Katsuyama Y, Kurokawa T, Osada Y. Double-network hydrogels with extremely high mechanical strength. Adv Mater. 2003;15:1155–1158. [Google Scholar]
- 18.Sun J-Y, et al. Highly stretchable and tough hydrogels. Nature. 2012;489:133–136. doi: 10.1038/nature11409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ducrot E, Chen Y, Bulters M, Sijbesma RP, Creton C. Toughening elastomers with sacrificial bonds and watching them break. Science. 2014;344:186–189. doi: 10.1126/science.1248494. [DOI] [PubMed] [Google Scholar]
- 20.Lin S, Zhou Y, Zhao X. Designing extremely resilient and tough hydrogels via delayed dissipation. Extreme Mech Lett. 2014;1:70–75. [Google Scholar]
- 21.Bai R, et al. Fatigue fracture of tough hydrogels. Extreme Mech Lett. 2017;15:91–96. [Google Scholar]
- 22.Zhang W, et al. Fatigue of double-network hydrogels. Eng Fract Mech. 2018;187:74–93. [Google Scholar]
- 23.Bai R, Yang J, Morelle XP, Yang C, Suo Z. Fatigue fracture of self-recovery hydrogels. ACS Macro Lett. 2018;7:312–317. doi: 10.1021/acsmacrolett.8b00045. [DOI] [PubMed] [Google Scholar]
- 24.Wegst UGK, Bai H, Saiz E, Tomsia AP, Ritchie RO. Bioinspired structural materials. Nat Mater. 2015;14:23–36. doi: 10.1038/nmat4089. [DOI] [PubMed] [Google Scholar]
- 25.Mallick PK. Fiber-Reinforced Composites: Materials, Manufacturing, and Design. CRC Press; Boca Raton, FL: 2007. [Google Scholar]
- 26.Goettler LA, Shen KS. Short fiber reinforced elastomers. Rubber Chem Technol. 1983;56:619–638. [Google Scholar]
- 27.Genesky GD, Cohen C. Toughness and fracture energy of PDMS bimodal and trimodal networks with widely separated precursor molar masses. Polymer (Guildf) 2010;51:4152–4159. [Google Scholar]
- 28.Mullins L, Tobin NR. Theoretical model for the elastic behavior of filler-reinforced vulcanized rubbers. Rubber Chem Technol. 1957;30:555–571. [Google Scholar]
- 29.Harwood JAC, Mullins L, Payne AR. Stress softening in natural rubber vulcanizates. Part II. Stress softening effects in pure gum and filler loaded rubbers. Rubber Chem Technol. 1966;39:814–822. [Google Scholar]
- 30.Diani J, Fayolle B, Gilormini P. A review on the Mullins effect. Eur Polym J. 2009;45:601–612. [Google Scholar]
- 31.Lee JN, Jiang X, Ryan D, Whitesides GM. Compatibility of mammalian cells on surfaces of poly(dimethylsiloxane) Langmuir. 2004;20:11684–11691. doi: 10.1021/la048562+. [DOI] [PubMed] [Google Scholar]
- 32.Shiroma LS, et al. Self-regenerating and hybrid irreversible/reversible PDMS microfluidic devices. Sci Rep. 2016;6:26032. doi: 10.1038/srep26032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shull KR, Flanigan CM, Crosby AJ. Fingering instabilities of confined elastic layers in tension. Phys Rev Lett. 2000;84:3057–3060. doi: 10.1103/PhysRevLett.84.3057. [DOI] [PubMed] [Google Scholar]
- 34.Muth JT, et al. Embedded 3D printing of strain sensors within highly stretchable elastomers. Adv Mater. 2014;26:6307–6312. doi: 10.1002/adma.201400334. [DOI] [PubMed] [Google Scholar]
- 35.Niu H, Wang H, Zhou H, Lin T. Ultrafine PDMS fibers: Preparation from in situ curing-electrospinning and mechanical characterization. RSC Adv. 2014;4:11782–11787. [Google Scholar]
- 36.Xu S, et al. Materials science. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science. 2015;347:154–159. doi: 10.1126/science.1260960. [DOI] [PubMed] [Google Scholar]
- 37.Evans AG. Perspective on the development of high-toughness ceramics. J Am Ceram Soc. 1990;73:187–206. [Google Scholar]
- 38.Rey T, Chagnon G, Le Cam JB, Favier D. Influence of the temperature on the mechanical behaviour of filled and unfilled silicone rubbers. Polym Test. 2013;32:492–501. [Google Scholar]
- 39.Kaltseis R, et al. Natural rubber for sustainable high-power electrical energy generation. RSC Adv. 2014;4:27905–27913. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.