Quantitative Ranking of Ligand Binding Kinetics with a Multiscale Milestoning Simulation Approach

Abstract

Efficient prediction and ranking of small molecule binders by their kinetic (k_on and k_off) and thermodynamic (∆tt) properties can be a valuable metric for drug lead optimization, as these quantities are often indicators of in vivo efficacy. We have previously described a hybrid molecular dynamics, Brownian dynamics, and milestoning model, Simulation Enabled Estimation of Kinetic Rates (SEEKR), that can predict k_on’s, k_off’s, and ∆tt’s. Here we demonstrate the effectiveness of this approach for ranking a series of seven small molecule compounds for the model system, β-cyclodextrin, based on predicted k_on’s and k_off’s. We compare our results using SEEKR to experimentally determined rates as well as rates calculated using long-timescale molecular dynamics simulations and show that SEEKR can effectively rank the compounds by k_off and ∆tt with reduced computational cost. We also provide a discussion of convergence properties and sensitivities of calculations with SEEKR to establish “best practices” for its future use.

Graphical Abstract

Molecular binding processes are ubiquitous in biology and serve as the fundamental basis for biological complexity. For the drug discovery community, engineering pharmacologically active small molecules is of particular importance. Traditionally, the paradigm for lead optimization is to select for leads with the greatest affinity for a protein, or other, target of interest. However, recent evidence suggests that the kinetics of binding may also be a useful metric for lead selection. It is now thought that both residence times and association rates are key determinants of in vivo efficacy for many drugs.^1–5 Similar to computational predictions of binding thermodynamics, molecular simulations can be used to compute binding kinetics.^6–8 Methods such as Brownian Dynamics (BD) have been used effectively for estimating molecular association rates.^9–12 Molecular dynamics (MD) simulations which explicitly represent all atoms and forces, can also be used to predict binding kinetics. Due to significantly increased model complexity, MD is limited by sampling. Nevertheless, owing to software improvements and the development of commodity hardware such as GPUs and specialty hardware such as Anton,^13,14 “brute force” calculation of binding kinetics with MD is now a possibility.^15–19 To improve upon “brute force” sampling statistics, many sampling strategies employ force biases or other statistical mechanical techniques to predict both association and dissociation rates of many systems. This includes methods such as: Markov State Models,^20–23 metadynamics,^24–26 milestoning,^{27,28,28–32} and other techniques.^33–39

Our previous work uses a multiscale MD, BD, and Milestoning approach for the calculation of both association and dissociation rates of receptor-ligand complexes.^40,41 Our implementation, “Simulation Enabled Estimation of Kinetic Rates” (SEEKR) is a freely available software package¹ that automates the preparation, simulation, and analysis of these multiscale milestoning calculations using existing softwares: NAMD⁴² for MD simulations and BrownDye¹² for BD simulations. Milestoning theory provides the glue for the multiscale scheme by providing a strategy to subdivide, simulate, and subsequently statistically reconnect small regions of simulation space called “milestones”^{27,40,41,43–52} This approach reduces the compute time required to simulate transition events, is embarrassingly parallel, and is agnostic to the simulation modality used. This allows us to use atomically detailed, yet computationally expensive, fully flexible MD simulations in milestones near the binding site where these interactions are critical for understanding the binding and unbinding, and BD simulations far from the binding site where rigid body dynamics provides a sufficient description at significantly reduced computational cost. For a more thorough description of milestoning theory and the calculation of kinetic quantities, such as k_on and k_off, we refer the reader to the existing literature.^{27,40,41,43–52}

The effectiveness of the SEEKR scheme for the calculation of k_on and k_off values has been demonstrated for multiple protein-ligand systems.^40,41 However, it has not yet been used for rank ordering sets of compounds by kinetic (k_on and k_off) and thermodynamic (∆G) values, as would be done in pharmaceutical discovery settings. Here we use SEEKR to estimate k_on, k_off, and ∆G for a model host-guest system, β-cyclodextrin with seven ligands representing diverse chemical groups (Fig. 1), using two forcefields for β-cyclodextrin GAFF^53,54 and Q4MD.⁵⁵ We compare the SEEKR estimates with previously published “brute force” (long-timescale) MD predictions¹⁹ and experimental results.^56–61 Using this model system we examine both the accuracy and efficiency of SEEKR compared to long-timescale MD. We further explore the reduction in computational effort required for SEEKR estimates as well as discuss the convergence properties and sensitivity of SEEKR calculations to establish “best practices” for its future use.

Figure 1:

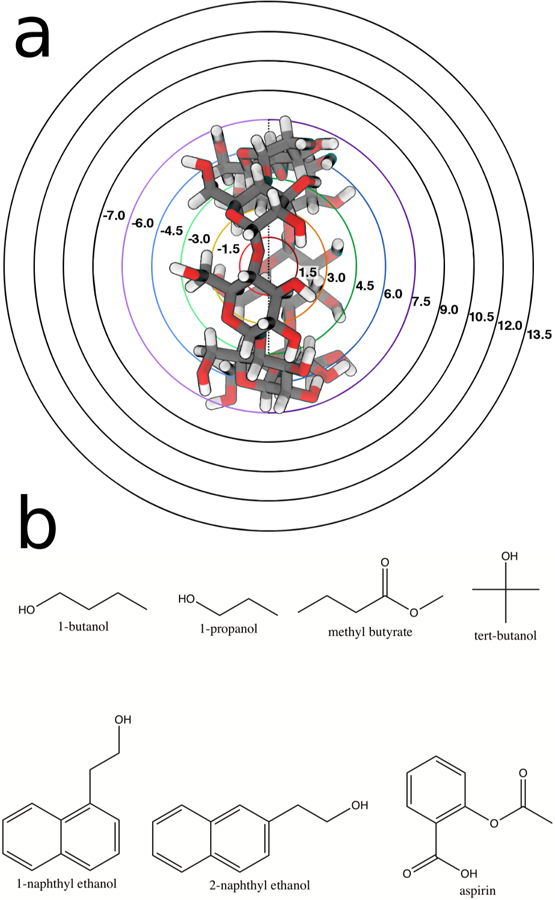
a) β-cyclodextrin with milestones spaced at 1.5 Å increments and b) the seven ligands used in this study. The top four ligands are known to bind more weakly while the bottom three are known to bind more tightly.

SEEKR calculations and the long timescale MD simulations struggle to reproduce both the values and rank ordering of the experimentally determined k_on’s (Fig. 2). However, similar qualitative results are seen with the SEEKR calculations and long timescale MD calculations using the same forcefield. On rates calculated using Q4MD are approximately one order of magnitude faster than experimental rates, while the GAFF forcefield produces rates closer to the experimental values, differing by approximately a factor of 3 or less.

Figure 2:

a) Experimental and calculated on rates for SEEKR GAFF and Q4MD forcefields as well as long timescale MD with both forcefields. b) Calculated rank correlation coefficients. Errors are determined with a bootstrapping analysis.

Both methods fail to effectively order the ligands by increasing k_on, as demonstrated by low or negative Kendall and Spearman rank correlation coefficients. As the values of all the experimental rates have limited variability (all within half an order of magnitude), the sensitivity of the methods as well as the errors associated with the calculations and experiments makes differentiation and ordering challenging.

Unlike the experimental k_on’s, k_off’s for the seven guest molecules span multiple orders of magnitude, making them a better target for ranking the compounds with SEEKR. Again, off rates calculated with SEEKR are in good agreement with the long timescale MD simulations using the same forcefield (Fig. 3). Rates calculated using the GAFF forcefield are consistently faster than experiment by approximately one order of magnitude. This trend is seen in both the long timescale MD and SEEKR, but is more pronounced in the SEEKR calculations. The Q4MD forcefield, however, more accurately reproduces the magnitude of the experimental values with both SEEKR and long timescale MD. SEEKR calculations with both Q4MD and GAFF forcefields were effective for ranking the compounds by increasing off rates, as evidenced by high rank correlation values. The smaller magnitudes of the Q4MD values potentially contribute to this forcefield’s difficulty to differentiate between compounds with similar rates, where the larger values associated with the GAFF forcefield allow for more variability in the rate value without changing the overall ordering. Both the GAFF and Q4MD forcefields successfully differentiate the three tighter binding compounds from the four weaker binding, with the tighter binding compounds all having slower off rates and a difference of one order of magnitude between the fastest tightly binding compound and the slowest weakly binding compound. This suggests that SEEKR could be useful for identifying and separating long residence time ligands from shorter residence time ligands and then further discriminating the compounds through ranking by k_off.

Figure 3:

a) Experimental and calculated off rates for SEEKR GAFF and Q4MD forcefields as well as long timescale MD with both forcefields. b) Calculated rank correlation coefficients. Errors are determined with a bootstrapping analysis.

An additional benefit of kinetics calculations with SEEKR is that binding free energies can also be obtained from the same simulations (Fig. 4). Binding free energies calculated using the rate constants are most heavily influenced by the k_off for these ligands, as this value is more variable, where the k_on’s for all ligands are more similar. Therefore, similar trends are observed for the calculated binding free energies as were observed for the off rates. Binding free energies can also be calculated using the stationary probabilities for each milestone, rather than the rate constants, and produce similar results. The GAFF forcefield consistently underestimates the binding free energies in both SEEKR and the long timescale MD, resulting from the consistent underestimation of the magnitudes of the k_off’s. The magnitudes of the binding free energies calculated using Q4MD are in much better agreement with the experimental values, differing by 1 kcal or less. SEEKR with both Q4MD and GAFF successfully differentiates the three known tighter binding compounds from the four weaker binding compounds. SEEKR can also further discriminate ligands by its effective ranking by binding free energies, demonstrated by high rank correlation values.

Figure 4:

a) Experimental and calculated binding free energies for SEEKR GAFF and Q4MD forcefields as well as long timescale MD with both forcefields. b) Calculated rank correlation coefficients. Errors are determined with a bootstrapping analysis.

A key aspect of future development of the SEEKR software is the systematic development of methodological best-practices as well as the elucidation of the sensitivity of calculated kinetic parameters to various SEEKR input conditions.

While it is possible to determine the kinetics for small systems like β-cyclodextrin using conventional long timescale MD simulations, increasing system size soon makes this inefficient or even impossible. The convergence of k_on and k_off were assessed by calculating the rate constants as a function of the reversal trajectory number at increasing intervals of 50 reversal numbers (with 10 trajectories initiated for each reversal number). The reversal number is a direct measure of the equilibrium simulation length, as reversals are initiated from evenly spaced configurations of the equilibrium distribution. In general, both the on and off rates appear converged in less than the maximum number of reversals available. Approximately half the total reversals (4000 of 8000) were sufficient for obtaining reasonably converged rate constants. This suggests that the total simulation cost to obtain a similar result could be as little as 2 µs per ligand, rather than 3.8 µs.

Convergence of the rate constant is a highly complicated quantity dependent on the transition probabilities as well as the incubation times obtained from each milestone. Therefore, a more detailed analysis of the convergence of these quantities on a per milestone level can provide further insight into the overall convergence of a rate calculation within SEEKR. Fig. 5a,b shows the convergence of k_on and k_off, respectively, as a function of the number of reversals launched for the representative system of Q4MD β-cyclodextrin with aspirin. Reversal number is directly related to the length of equilibrium sampling, the current bottleneck of a SEEKR calculation. While both values appear to converge in fewer than the maximum number of reversals, the dramatic change in k_off after reversal number 400 is of note. Further analysis of the per-milestone transition counts (Fig. 5c) and incubation times (Fig. 5d) revealed that this change in k_off was due to poor initial sampling of the −1.5 Å milestone, which once sampled decreased the overall k_off.

Figure 5.

: Convergence analysis for a representative ligand, aspirin, and β-cyclodextrin with the Q4MD forcefield. Convergence of a) k_on, b) k_off, c) transition counts, and d) incubation times for each milestone are plotted as a function of the number of reversals launched. Reversal number is directly related to the length of equilibrium sampling, as reversals were launched at 2 ns intervals from the equilibrium trajectory.

This was only observed for the aspirin ligand, one of the bulkiest ligands, where it was extremely unlikely to observe transitions outward from the primary face due to steric effects. Evaluation of these convergence properties on a per milestone basis is a valuable diagnostic tool; identifying which milestones contribute most to the mean first passage time (and therefore k_on and k_off) and milestones where the ligand spends only a short time, providing detailed molecular insight into the binding and unbinding processes. Furthermore, this analysis is also useful during the simulation process, as the convergence of each milestone can be assessed “on the fly” and individual simulations can be terminated or extended accordingly for each milestone.

We also explore the sensitivity of the calculated rate constants to the milestoning model construction. In particular, the appropriate spacing of milestones is critical for the calculation. Milestones must not be spaced so close such that the velocity of the system cannot decorrelate between transitions.^45,46 This assumption is typically valid for molecular dynamics simulations, as velocities typically decorrelate on the subpicosecond timescale.⁴⁶ However, if milestones are spaced far apart, transitions will require much longer simulations and milestioning sampling efficiency is lost.

For our systems, the incubation times of all milestones are on the order of multiple picoseconds or greater, which is longer than the sub-picosecond timescale typically necessary for decorrelation.⁴⁶ When the milestone spacing was doubled to 3 Å, simulation efficiency was dramatically reduced, such that few to no transitions between milestones were observed, precluding the calculation of rate constants. These observations suggest that the 1.5 Å spacing used in our simulations was appropriate for the calculation of the desired kinetic parameters.

Our milestoning model differentiates the two faces of the cyclodextrin ring and therefore defines two bound states, corresponding to each face. Investigation into the effect of this on the resulting rate constants revealed that it had only minimal effects. When the two bound states were combined into a single milestone, only small changes to the rate were observed, within the error of both calculations. Furthermore, when the the two faces were not differentiated with unique milestones, minimal change in the calculated rate constants was observed.

It is also important to note that our milestoning model did not explicitly resolve the ligand orientation in any way, and therefore any ligand orientational sampling was achieved entirely through simulation. This resulted in some ligand orientations being unsampled in the deepest milestones where the orientation was sterically restricted to the starting conformation on that milestone. While this is a limitation that will be addressed in future developments of SEEKR, it also highlights that a relatively simplistic model was able effectively calculate kinetic parameters with good agreement to experimental values.

The simplicity of this model has many advantages. The bound state is defined naturally as the innermost milestone and all other milestones can be defined at the same time, including what defines the unbound state. The long timescale MD employed a more empirical definition of the bound state where the ligand was only considered bound when the COM of the ligand was within 7.5 Å of the COM of the β-cyclodextrin for at least 1.0 ns. Similarly the ligand was considered unbound when it left this 7.5 Å bound state for at least 1.0 ns. With the SEEKR approach, minimal prior knowledge of the system is required, as binding and unbinding are determined only from the milestone surfaces. No time cutoff is required, as short excursions that do not result in full binding and unbinding events are captured naturally in the milestoning model. The simplicity of SEEKR milestoning calculation setup, in conjunction with the ability to monitor convergence for each milestone and terminate simulations accordingly, makes this approach well-suited for calculations with multiple ligands as would be necessary in a drug discovery setting.

We present the first successful ranking of a set of seven guest molecules with the β-cyclodextrin host using the SEEKR hybrid MD/BD/Milestoning approach. SEEKR effectively reproduces both the magnitudes and rankings of the experimental off rates^56–61 and binding free energies, two quantities of interest in typical drug discovery campaigns.^1–4 SEEKR also successfully differentiates the known longer residence time and tighter binding compounds from the weaker binding compounds. Our results are also in good agreement with previously conducted long timescale MD simulations for the same set of ligands.¹⁹ In particular SEEKR and long timescale MD simulations using the same forcefield (GAFF or Q4MD) exhibited similar deviations from the experimental values, with GAFF producing consistently faster off rates than experiment and Q4MD producing consistently faster on rates. In general both methods and both forcefields struggled to reproduce the experimental on rate ranking, as all ligands had very similar k_on’s. The SEEKR method requires less simulation time (3.8 µs per ligand) than the long timescale MD approach (4.5 – 11 µs per ligand). Furthermore, convergence analysis of the SEEKR calculations suggests that comparable results could be achieved with as little as 2 µs per ligand. In addition, SEEKR’s milestoning approach makes these calculations highly parallel, as the simulations on each milestone are completely independent from all other milestones. We also provide an analysis of the sensitivity of the SEEKR calculations to various factors such as sampling, milestone spacing, and the construction of the milestoning model with the intention of putting forth “best practices” for the use of SEEKR. SEEKR’s effectiveness at ranking compounds for this small model system suggest that it is well suited for ranking compounds of more complex protein-ligand and protein-drug systems, where the efficiency and enhanced sampling advantages of our multiscale MD/BD/milestoning approach will be more apparent.

Computational Methods

GAFF^53,54 forcefield parameters for the seven guest molecule along with both GAFF and Q4MD-CD⁵⁵ parameterizations of β-cyclodextrin were obtained from Tang and Chang.¹⁹ For comparison we use identical structures and parameterizations as those used in their study. These initial structures were used by the SEEKR software for preparation of the milestoning simulations. The preparation procedure was the same for each of the seven guest molecules and followed standard SEEKR protocols.⁴¹ All systems were solvated with TIP3P waters.⁶² All BD simulations were performed using the BrownDye software package.¹² Electrostatic potentials of the host and guest molecules used as inputs for the BD simulation were calculated with APBS version 1.4.⁶³ A modified version of NAMD 2.12 was used for all MD simulations.⁴² For all 13 milestones in the MD region, the standard SEEKR procedure for minimization, equilibration and simulation was followed. In total, 2.6 µs of equilibrium sampling (160 ns for 16 milestones) were used and approximately 570 ns of FHPD sampling for a total of 3.2 µs of simulation used in the milestoning model. The total cost per ligand (including simulation discarded for equilibration) was therefore ∼3.8 µs.