Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Feb 25;123(11):6831–6838. doi: 10.1021/acs.jpcc.8b11709

Interplay between Intra- and Intermolecular Charge Transfer in the Optical Excitations of J-Aggregates

Michele Guerrini †,‡,§, Caterina Cocchi §,*, Arrigo Calzolari ‡, Daniele Varsano ‡,*, Stefano Corni ‡,∥
PMCID: PMC6443228  PMID: 30949274

Abstract

graphic file with name jp-2018-117096_0006.jpg

In a first-principles study based on density functional theory and many-body perturbation theory, we address the interplay between intra- and intermolecular interactions in a J-aggregate formed by push–pull organic dyes by investigating its electronic and optical properties. We find that the most intense excitation dominating the spectral onset of the aggregate, i.e., the J-band, exhibits a combination of intramolecular charge transfer, coming from the push–pull character of the constituting dyes, and intermolecular charge transfer, due to the dense molecular packing. We also show the presence of a pure intermolecular charge-transfer excitation within the J-band, which is expected to play a relevant role in the emission properties of the J-aggregate. Our results shed light on the microscopic character of optical excitations of J-aggregates and offer new perspectives to further understand the nature of collective excitations in organic semiconductors.

Introduction

J-aggregates are a special class of molecular crystals with enhanced light–matter interaction properties.1−5 Their optical spectra are dominated by a very strong and narrow peak at the onset—the so-called J-band—which appears at lower energy with respect to the isolated molecular constituents.6−10 This peculiar feature emerges as a collective effect of the monomers in the aggregated phase and is typically explained in terms of coherent intermolecular dipole coupling.6,8,9,11,12 The microscopic nature and the fundamental mechanisms that give rise to the J-band are still debated.6 The situation is even more complex in the case of J-aggregates formed by polar molecules like push–pull organic dyes. In this case, intramolecular charge-transfer (CT) adds up to the aforementioned intermolecular interactions that are responsible for the formation of the J-band. An example of this kind of system is the J-aggregate formed by the organic chromophore 4-(N,N-dimethyl-amino)-4-(2,3,5,6-tetra-fluorostyryl)-stilbene (C24H19F4N), which has been recently proposed and synthesized by Botta et al.13 Some of the authors have recently investigated this J-aggregate by means of time-dependent density functional theory (TDDFT) showing that its optical behavior cannot be deduced by considering only its isolated components due to the intrinsically supramolecular nature of its optical response.14 On the other hand, the character of the excitations forming the J-band and the interplay between inter- and intramolecular interactions still need to be addressed. This issue is relevant in the broader context of the electronic structure characterization of molecular crystals. Even in the case of nonpolar molecules, the discussion regarding the nature of optical excitations in organic semiconductors15−19 is still ongoing. Both localized Frenkel excitons and delocalized intermolecular excitations can appear at the spectral onset of organic semiconductors: Their relative energetic position has been rationalized in terms of intermolecular interactions and wave-function overlap.19 Identifying the character of the lowest-energy excitations in molecular crystals is particularly relevant to interpret phenomena like multiple exciton generation and singlet fission that have been recently observed in these systems20−32 and that promise a breakthrough in view of optoelectronic applications. Addressing this question from a theoretical perspective requires a high-level methodology that incorporates a reliable description of the electronic structure and excitations including electron–electron and electron–hole (e–h) correlation effects.

Many-body perturbation theory (MBPT), based on the GW approximation and the solution of the Bethe–Salpeter equation (BSE), is the state-of-the-art approach to investigate optical excitations in crystalline materials. In the last two decades, it has been successfully applied also to molecular systems, providing unprecedented understanding on the character of the excitations therein.15−19,33−39 Many of these studies are focused on oligoacenes,15,16,19,35 which have drawn particular attention since the last years of the past century for their appealing optoelectronic and transport properties.40−47 The first-principles works cited above have revealed that the low-energy excitations in these materials exhibit a remarkable excitonic character, with binding energies of the order of a few hundreds of milli-electron volts and an intermixed Frenkel-like and intermolecular charge-transfer character. Intermolecular interactions generally play a decisive role in the optical properties of a variety of molecular aggregates.48,49 For example, in azobenzene-functionalized self-assembled monolayers, intermolecular interactions impact strongly on light absorption and excitonic coupling, and hence critically influence the photoisomerization process.50−53 In these systems, intermolecular coupling and packing effects have been shown to be crucial also in core excitations.54

In this work, we adopt the formalism of MBPT to investigate the nature of the excitations in a J-aggregate formed by C24H19F4N dyes (Figure 1), devoting specific attention to the interplay between intra- and intermolecular charge transfer. MBPT calculations are carried out on top of density functional theory (DFT) on the J-aggregate and, for comparison, also on its isolated molecular unit. With the analysis of the quasi-particle (QP) electronic structure and the optical absorption spectra including excitonic effects, we characterize the excited states of this J-aggregate with unprecedented insight. Specifically, we focus on two excited states with different characters appearing within the J-band: the first one gives rise to the main peak of the J-band and manifests a mixed intra- and intermolecular charge-transfer nature; the second one is a very weak excited state possessing a dominant intermolecular CT behavior. This analysis demonstrates how the interplay between intra and intermolecular charge transfer determines the optical properties in a molecular J-aggregate and contributes to the more general understanding of the nature of collective excitations in molecular crystals.

Figure 1.

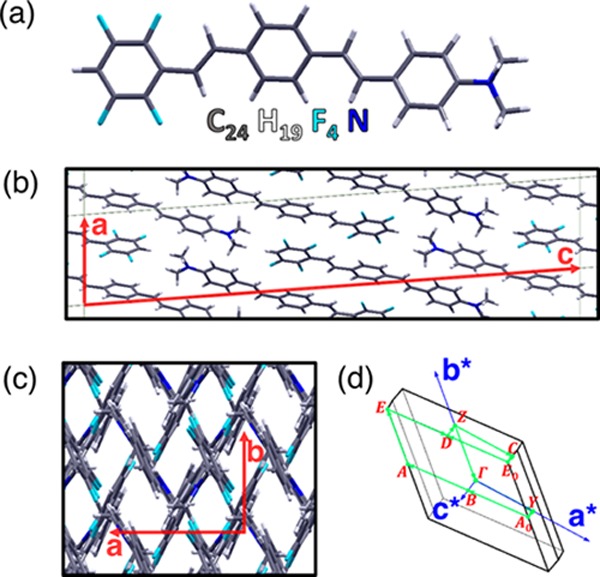
Figure 1

Open in a new tab

(a) Push–pull organic dye 4-(N,N-dimethyl-amino)-4-(2,3,5,6-tetra-fluorostyryl)-stilbene (C24H19F4N) and its J-aggregate viewed (b) from the a–c plane and (c) from the a–b plane, with the lattice vectors marked in red; crystallographic structure from CCDC no. 961738 and ref (13). (d) Brillouin zone (BZ) associated with the unit cell of the J-aggregate with the reciprocal lattice vectors indicated in blue, the high-symmetry points highlighted in red, and the path chosen for the band structure plot marked in green.

Methods

Theoretical Background

This study is based on DFT55,56 and MBPT (the GW approximation and the Bethe–Salpeter equation).57−59 The workflow adopted to calculate the electronic and optical properties proceeds through three steps: First, a DFT calculation is performed to compute Kohn–Sham (KS) single-particle energies and wave functions as a basis in the successive steps; next, the quasi-particle correction to the KS energies is calculated through a single-shot GW calculation;57,58,60 the Bethe–Salpeter equation is solved to obtain optical absorption spectra together with excitonic eigenfunctions and eigenenergies.57 This approach ensures state-of-the-art accuracy methods in the calculation of excited-state properties and, concomitantly, a quantitative insight into the character of the excitations.

In solving the BSE, we adopt the Tamm–Dancoff approximation (TDA)57 consisting in diagonalizing an effective excitonic Hamiltonian

graphic file with name jp-2018-117096_m001.jpg 1

where the index v(c) indicates valence (conduction) bands, k and k′ are wave vectors in the Brillouin zone (BZ), and a†(a) and b†(b) are creation (annihilation) operators for electrons and holes, respectively. The quasi-particle energies ϵck and ϵvk are obtained from the GW calculation. The matrix elements of v̅, which is the short-range unscreened Coulomb interaction, and of W, the statically screened Coulomb interaction, represent the exchange and direct part of the BSE Hamiltonian of eq 1 and are expressed as v̅v′c′k′vck = ⟨ck, v′k′|v̅|vk, c′k′⟩ and Wv′c′k′ = ⟨ck, v′k′|W|c′k′, vk⟩, respectively. The latter takes into account the screened electron–hole interaction (i.e., excitonic effects), while the former is responsible for crystal local-field effects (the factor 2 derives from spin summation in the singlet channel). Note that the potential v̅ is a modified Coulomb interaction defined as the bare Coulomb interaction without the long-range (i.e., macroscopic) contribution (i.e., limq→0v̅G=0(q) = 0 in reciprocal space).61 To quantify local field effects (LFEs) for a certain excited eigenstate |λ⟩ of the excitonic Hamiltonian (eq 1) with excitation energy Eλ, we define the e–h exchange energy Inline graphic, where Avckλ are the BSE coefficients of the eigenstate |λ⟩. When the total excitation energy Eλ is below the QP gap, i.e., Eλ – EGW < 0, the excited state |λ> is considered a bound exciton with a binding energy defined as Eb = EGWgap – Eλ, which physically represents the energy required to separate a bound electron–hole pair into a free electron and a free hole.

Computational Details

The unit cell of the bulk J-aggregate crystal, composed of 192 atoms, corresponding to 4 nonequivalent push–pull molecules, has been taken from the experimental X-ray structure available in the CCDC no. 961738 (for more details, see also the Supporting Information (SI) of ref (13)) without any further relaxation. As previously shown in the case of the pentacene crystal,16 the optical properties of organic semiconductors are rather insensitive to the optimization of the internal geometry. Moreover, the experimental X-ray structure already takes into account all of the supramolecular effects (e.g., van der Waals, π-stacking, hydrogen bonds, etc.), which determine the relative orientation and the packing of the molecules, is a reliable starting point for our calculations.

DFT calculations of the J-aggregate were performed with the plane-wave code Quantum Espresso62 by using the semilocal Perdew–Burke–Ernzerhof (PBE)63 exchange–correlation (xc) functional and treating core electrons with a norm conserving pseudopotential.64 The plane-wave cutoff for the Kohn–Sham (KS) wave functions (density) was fixed to 40 Ry (160 Ry), and the convergence criterion on the total energy was fixed to 10–8 Ry. The mean residual force per atom is 0.01 Ry/bohr due to nonequilibrium C–H bond lengths, which are however not expected to alter the electronic structure of the system and the essence of our results. GW and BSE calculations were performed using the plane-wave code Yambo.65 QP corrections were calculated by single-shot GW (i.e., perturbative G0W0) and adopting the Godby–Needs plasmon pole approximation (GN-PPA) model66 to approximate the frequency dependency of the inverse dielectric function. The GN-PPA is considered a reliable approach for different kinds of bulk systems for which it yields results comparable to the more computationally demanding contour deformation approach.67−69 Since the QP corrections obtained from G0W0 were almost constant for all of the KS states around the gap, in building the BSE Hamiltonian (eq 1), we applied a scissors plus stretching correction for all of the energies within the irreducible BZ by linear fitting of the QP-corrected values from G0W0 (scissors operator of 1.73 eV and stretching factors Sv = 1.258 and Sc = 1.216 for the occupied and unoccupied states, respectively). The QP gap of the J-aggregate obtained from G0W0 was checked against the one obtained with eigenvalue-only self-consistent GW calculations. The difference between the band gaps obtained with these two methods turned out to be in the order of 160 meV (see Section 2 of the Supporting Information (SI)). The BSE Hamiltonian of the J-aggregate was evaluated and diagonalized within the Tamm–Dancoff approximation using an e–h basis composed of 27 occupied and 34 unoccupied states and a 5 × 3 × 2 k-point grid to sample the BZ. The final absorption spectrum of the bulk crystal was obtained by averaging the spectra computed for three orthogonal electric field polarizations (i.e., along a, b axes and along the component of the c axis perpendicular to the a–b plane in Figure 1).

To treat the gas-phase push–pull molecule at the same level of theory as the J-aggregate, we computed the electronic and optical properties for the monomer as extracted from the J-aggregate without any further relaxation. In Section 1 of the SI, we show for the isolated gas-phase monomer that the main effect of the minimization of interatomic forces is to blue-shift the main absorption peak by a few hundreds of milli-electron volts without changing its character. To investigate the electronic and optical properties of the gas-phase push–pull dye, we used MOLGW,70 a code that implements DFT and MBPT using localized basis orbitals, which are computationally more suited and efficient for isolated systems compared to plane waves. These DFT calculations were carried out using the PBE functional, cc-PVTZ basis set, and a full-electron treatment with frozen-core approximation and total energy convergence precision fixed to 10–8 Ry. The QP correction was computed by an eigenvalue-only self-consistent GW calculation to minimize the dependence on the approximation for the xc functional used in the DFT starting point.71 To calculate the correlation part of the self-energy, the MOLGW code adopts an analytical expression exploiting the spectral decomposition of the screened Coulomb potential and the residue theorem.72 The following BSE step was solved in the TDA over a transition space of 50 occupied and 100 unoccupied orbitals. Additional information about the effects of different approximations and codes adopted in these calculations is reported in the SI.

Results and Discussion

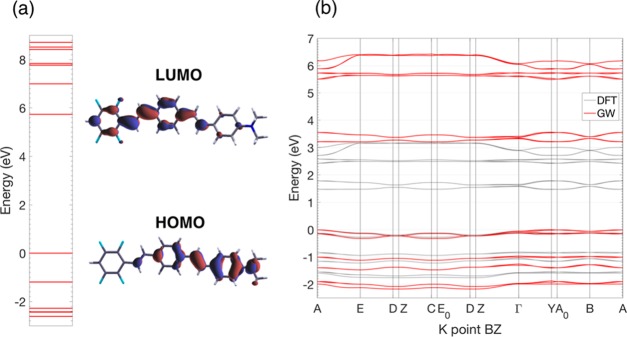
We start our analysis by inspecting the electronic structure of the isolated push–pull dye (Figure 1a) and of its J-aggregate (Figure 1b–d). In Figure 2a, the quasi-particle energy levels of the isolated organic dye are shown, together with the isosurface plots of the frontier molecular orbitals (MOs). The dimethylamino (push) and fluorinated ring (pull) groups at the opposite ends of the π-conjugated chromophore are responsible for the polarization on the frontier orbitals and the intrinsic dipole. The highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) are mostly localized on the electron-donating (push) and electron-withdrawing (pull) sides of the molecule, respectively. The QP band structure shown in Figure 2b exhibits a direct gap of 3.2 eV at the Y point, which is more than twice as large as the corresponding DFT (PBE) value of 1.48 eV and is half the QP gap of the isolated molecule, which is 5.66 eV in Figure 2a. The QP correction manifests itself as an almost rigid shift of 1.7 eV for all the conduction bands. This behavior is consistent with that of other organic crystals like pentacene and polythiophene.18,73 As expected for molecular crystals,15,16,39,74 the band dispersion is very limited and quite anisotropic: bands are almost flat along those directions in which intermolecular interactions are negligible and the wave-function overlap is hence minimized.

Figure 2.

Figure 2

Open in a new tab

(a) GW energy levels (HOMO level set to zero) and frontier molecular orbitals of the isolated push–pull dye. The isovalues are fixed at 0.04 bohr–3/2. (b) Band structure of the J-aggregate computed from DFT (gray) and one-shot GW (red), where in the latter, a scissors plus stretching has been applied to the DFT energy levels. The Fermi energy is set to zero at the GW valence band maximum (VBM).

Conversely, along the π-stacking directions (e.g., along the Z−Γ−Y path in the BZ), intermolecular interactions are enhanced. As a result, bands are slightly more dispersive and band splitting is observed. Due to the presence of four inequivalent molecules in the unit cell, the bands close to the gap, which exhibit π–π* character, are almost degenerate. In Figure 3, the square moduli of the wave functions at the valence band maximum (VBM) and at the conduction band minimum (CBM) at the high-symmetry point Y are reported. The localized character of the frontier MOs found in the isolated push–pull dye is preserved also in the J-aggregate: The KS states corresponding to the VBM and CBM are mostly localized on the push and pull ends of each monomer, respectively. Figure 4 displays the optical absorption spectra of the isolated push–pull dye in the gas phase (Figure 3a) and of its J-aggregate (Figure 3b). In these plots, the red bars mark the analyzed excited-states. In Tables 1 and 2, we report information about the analyzed excited states for the monomer and the J-aggregate, respectively. The red shift of the principal peak of the J-aggregate with respect to the one of the single molecule amounts to 0.39 eV. This result is in better agreement with the experimental value of 0.48 eV,13 compared to the outcome of TDDFT calculations with a semilocal xc-functional14 (0.11 eV). The BSE results reveal also a rich excitonic structure underneath the J-band, which turns out to be composed of several transitions not shown in Figure 4b. Most of these excitations appear below the QP gap at 3.2 eV, and their binding energies do not exceed 0.4 eV, in line with the values reported for conjugated polymers17,75−78 and slightly smaller than those of crystalline pentacene (0.5 eV),16,19 picene (0.7 eV),19 and antracene (0.8 eV).15

Figure 3.

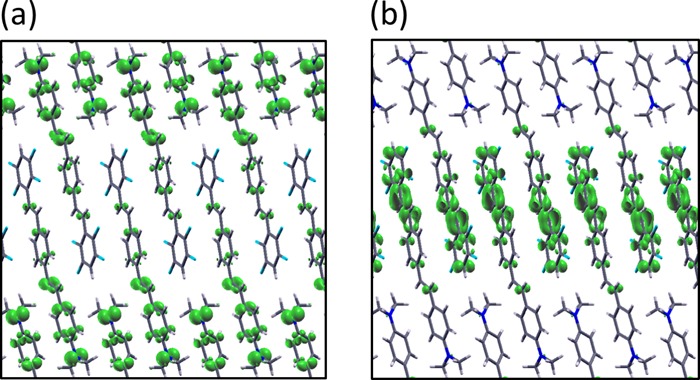
Figure 3

Open in a new tab

Isosurfaces of the squared modulus of the KS wave functions of the (a) valence band maximum and (b) conduction band minimum of the J-aggregate computed at the high-symmetry point Y. Isovalues fixed at 0.001 bohr–3.

Figure 4.

Figure 4

Open in a new tab

Absorption spectra of (a) the push–pull dye in the gas phase and (b) in the J-aggregate. The excited states analyzed in the text (M, J, JCT) are marked by red bars with height representative of the relative oscillator strengths. The absorption in both BSE spectra is normalized with respect to the maximum value in the examined energy window. In (b), the absorption spectrum calculated from the independent quasi-particle approximation is also shown (gray-shaded area). All absorption spectra include a Lorentzian line width of 200 meV.

Table 1. Energy and Composition of the First Excited State of the Push–Pull Monomer C24H19F4N, Including the Associated Transition Energy and Weight Given by the Square of the BSE Coefficient.

excited state energy (eV) occupied level unoccupied level ϵcQP – ϵv (eV) weight |Acvλ|2
EM = 3.39 HOMO LUMO 5.73 0.83
Open in a new tab

Table 2. Energy and Composition of the J and JCT Excitations of the J-Aggregate, Including the Associated Transition Energy, the Associated k-Point in the Brillouin Zone Expressed in Reciprocal Crystal Units (RCUs), and the Weight Given by the Square of the BSE Coefficienta.

excited state energy (eV) occupied band unoccupied band k-point (RCU) ϵckQP – ϵvk (eV) weight |Acvkλ|2 × 10
EJ = 3 VBM – 2 CBM + 1 (0.4, 0, −0.5) 3.34 0.59
VBM – 2 CBM + 1 (−0.4, 0, 0.5) 3.34 0.56
VBM – 3 CBM (0.4, 0, 0) 3.35 0.54
VBM – 3 CBM (−0.4, 0, 0) 3.35 0.52
VBM – 2 CBM + 1 (0.4, 0, 0) 3.33 0.29
VBM – 3 CBM (0.4, 0, −0.5) 3.34 0.29
VBM – 3 CBM (−0.4, 0, 0.5) 3.34 0.26
VBM – 2 CBM + 1 (−0.4, 0, 0) 3.33 0.26
ECTJ = 2.89 VBM CBM + 1 (−0.2, 0, 0.5) 3.29 0.47
VBM CBM + 1 (−0.2, 0, 0) 3.28 0.41
VBM CBM + 1 (0.2, 0, −0.5) 3.29 0.40
VBM – 1 CBM (−0.2, 0, 0) 3.31 0.37
VBM CBM + 1 (0.2, 0, 0) 3.28 0.36
VBM – 1 CBM (0.2, 0, 0) 3.31 0.32
VBM – 1 CBM (−0.2, 0, 0.5) 3.29 0.26
VBM – 1 CBM (−0.4, 0, 0.5) 3.23 0.24
VBM CBM + 1 (−0.4, 0, 0) 3.22 0.23
VBM – 1 CBM (0.2, 0, −0.5) 3.29 0.23
Open in a new tab
a

Only weights larger than 2% are reported.

In the following, we focus on two representative excited states within the J-band: the first one labeled as J, at 3 eV, corresponding to the J-band peak; the second one labeled as JCT, at 2.89 eV, which has a very low oscillator strength and represents a paradigmatic example of several intermolecular charge-transfer excited states within the J-band. Both excitations are analyzed in Figure 5 in terms of their excitonic wave functions and transition densities. Information about additional excited states of interest for the J-aggregate is reported in Section 2 of the SI. In Table 2, the composition of the J excitation is reported, showing that it is mainly formed by transitions between (quasi-)degenerate bands at the valence band top and conduction band bottom, which carry π and π* characters like the HOMO and LUMO of the isolated dye (see Figures 2a and 3). The excitonic probability density of the excitation J (Figure 5a,b) reveals its intermixed intramolecular charge transfer as well as intermolecular charge transfer between nearest-neighboring molecules. Having fixed the position of the hole on the push side (i.e., the dimethylamino group) of one molecule in the unit cell, the electron is found on the pull part (i.e., the fluorinated ring) of the same molecule and of its nearest neighbors. By inspecting Figure 5a,b, the electron distribution is also delocalized around neighboring molecules along the π-stacking direction (i.e., the a–b plane), where the dispersion is more pronounced because of the enhanced wave-function overlap. The intermolecular character of this excitation is therefore due to the π-interactions in the molecular packing direction, in analogy with the excitons of organic crystals formed by nonpolar molecules.16,17,79,80 On the other hand, the intramolecular CT nature of the J excitation is inherited from the polarized character of contributing electronic states, in analogy with the MOs of the push–pull molecules constituting the J-aggregate. The transition density of J shown in Figure 5c offers complementary information to the exciton wave function in terms of the spatial distribution of the excitation and the orientation of the molecular transition dipole moments. Since they are coherently aligned and in phase with respect to each other, the excitation J is associated with an induced charge density mainly displaced along the long crystal axis within the a–c plane (see Figure 1b). It is also worth noting that, by visual inspection, the transition density shown in Figure 5c does not completely sum to zero within a single monomer unit, as the positive (red) and negative (blue) charge blocks are not present in equal amount. This suggests that there could be a partial intermolecular CT mechanism that has been highlighted above in the analysis of the exciton wave function of Figure 1b. This result has similarities with that obtained for pentacene molecular crystals,16,19 where exciton delocalization on neighboring molecules also appears. However, as opposed to pentacene, the J-aggregate considered here is composed of polar push–pull molecules: the intrinsic dipole strongly polarizes the frontier MOs and thus reduces the spatial overlap between electron and hole.

Figure 5.

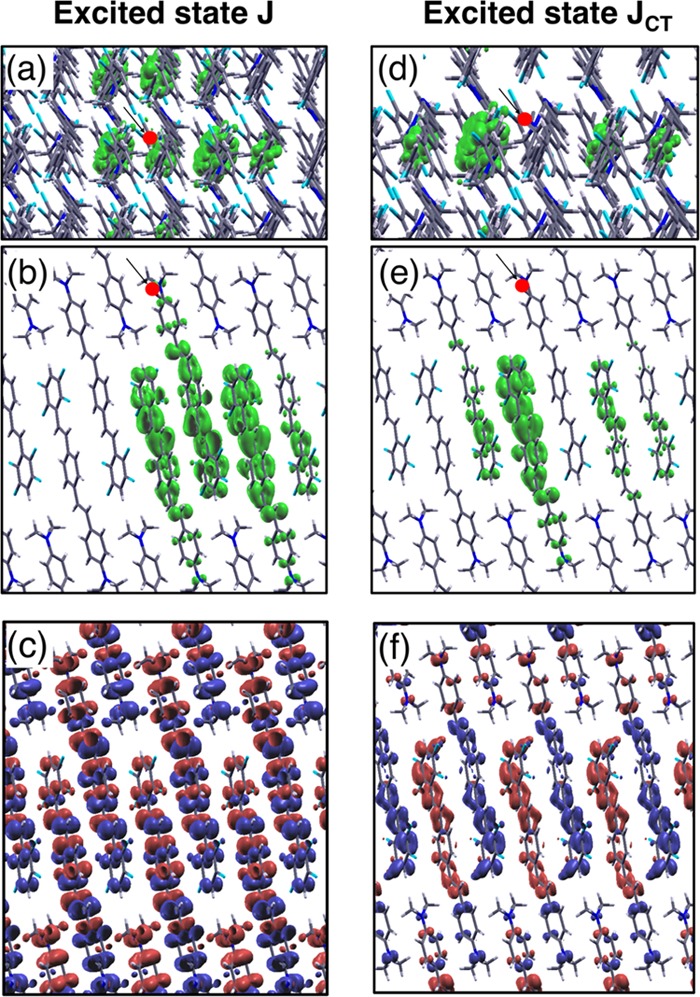
Figure 5

Open in a new tab

(a, b, d, e) Exciton probability density with fixed hole position (red dot), defined as |Ψλ(re, r̅h)|2 = |⟨λ|Ψ†(re)Ψ(r̅h)|0⟩|2 = |∑cvkAvckλφck(re)φvk(r̅h)|2, where Ψλ(re, r̅h) is the exciton two-body wave function, r̅h (re) is the hole (electron) position, Avckλ is the BSE coefficient for the excited states λ = J, JCT of the J-aggregate, and φvk(ϕck) is the occupied (unoccupied) KS electronic state with wavevector k in the BZ; views from the a–b plane (a, d) and from a–c plane (b, e). The exciton plot gives the probability to find the electron at position re with the hole fixed at r̅h. (c, f) Transition density, defined as ρλ(r) = ⟨λ|Ψ†(r)Ψ(r)|0⟩ = ∑cvkAvckφck(r)φvk*(r), for the excited states λ = J, JCT of the J-aggregate; views from the a–c plane. The transition density provides information about the charge spatial displacement associated with the specific excited state λ. Isosurfaces of the exciton wave functions (transition densities) fixed at 10% of their maximum value.

The very weak excitation JCT, at slightly lower energy compared to J (see Figure 4b), has a different nature. As shown in Figure 5d–f by the exciton wave function and the transition density, this excitation has a pure intermolecular CT character, with the electron and the hole localized on different neighboring molecules. The slightly larger binding energy of JCT (Eb = 0.32 eV) compared to J (Eb = 0.21 eV) is consistent with its enhanced spatial localization (Figure 5d,e), while the reduced wave-function overlap between the hole and the electron components is consistent with the very weak oscillator strength. Such a CT excitation is associated with lower electron–hole recombination rates and enhanced electron–hole dissociation probability compared to excitons with more pronounced intramolecular character.81 The transition density associated with JCT (Figure 5c) confirms and complements this picture: neighboring monomers are almost completely depleted of positive and negative charges, respectively, meaning that intermolecular CT is the dominant mechanism here. It is worth mentioning that the character and the microscopic features of excited states, such as JCT, cannot be captured by simple models based on transition dipoles coupling (e.g., the Kasha’s model11) but need an advanced first-principles description as provided in this work.

The intra- and intermolecular character of singlet excitations in organic crystals is determined by a competition between the e–h exchange interaction, which is responsible for the LFE, and the screened e–h attraction.19 While the exchange interaction is quite sensitive to the spatial overlap between occupied and unoccupied electronic states involved in the transition, the direct e–h attraction can be nonvanishing even upon a negligible spatial overlap between occupied and unoccupied states.19 Here, due to the push–pull character of the constituting dyes, the gap states of the J-aggregate are quite polarized and hence only slightly overlap (see Figures 2a and 3), as opposed, for instance, to pentacene.19 Hence, we should expect a reduced influence from the LFE to the low-lying excited states of the J-aggregate. To quantify the contribution of the LFE on a given excited state |λ⟩, we use the e–h exchange energy Exλ and its ratio with respect to the total excitation energy Ẽx = Exλ/Eλ. In the isolated monomer, Ex = 0.76 eV (ẼxM = 0.22), while in the J-aggregate, Ex = 0.07 eV (ẼxJ = 0.023) and Ex = 0.01 eV (ẼxJCT = 0.003). From these values, it is apparent that LFE contribute ∼20% to the first excitation energy of the isolated monomer while they are almost negligible in the J-aggregate (2% for J and 0.3% for JCT). The predominant intermolecular CT character of JCT is related to a weaker e–h exchange interaction with respect to J, where in the latter, the spatial overlap between the electron and the hole is larger (see also Figure 5a,b). The intermolecular CT that characterizes both J and JCT is favored by the close molecular packing82−84 of the aggregate, which enhances the electron delocalization between neighboring molecules as generally observed in optical excitations of organic crystals.17,50,53,54,85,86 The reduction of LFE in the J-aggregate compared to the isolated monomer is due to the more homogeneous electron distribution in the crystal.

Conclusions

To summarize, in the framework of MBPT, we have investigated the electronic and optical properties of a J-aggregate formed by the push–pull organic dye C24H19F4N, specifically addressing the interplay between intra- and intermolecular interactions. We have found that the intense J-band dominating the absorption onset is formed by a number of excitations stemming from transitions between the highest occupied and lowest unoccupied bands. The most intense of these excitations exhibits a combination of inter- and intramolecular charge transfers, resulting from the competing effects of dense molecular packing and the push–pull nature of the constituting molecules. The other excitations within the J-band have very weak intensity. Among them, JCT has pronounced intermolecular charge-transfer character. Being at lower energy compared to the most intense excitation in the J-band, this state is expected to play a relevant role in the emission properties of the J-aggregate.

Our analysis demonstrates that the complex mechanisms ruling the optical properties of organic crystalline aggregates cannot be unveiled based solely on simple models, but require a high level of theory that is able to quantitatively address all of the facets of the problem. Many-body perturbation theory is capable of thoroughly capturing the collective effects and providing a robust insight into the excitations of the system. As such, our results offer unprecedented insight into the nature of the excitations of J-aggregates formed by push–pull chromophores and contribute to the further understanding of these materials that are relevant for optoelectronic applications.

Acknowledgments

This work was partially funded by the European Union under the ERC grant TAME Plasmons (ERC-CoG-681285), by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Projektnummer 182087777—SFB 951 and HE 5866/2-1, and by the EU Centre of Excellence “MaX - Materials Design at the Exascale” (Horizon 2020 EINFRA-5, Grant No. 676598). M.G. acknowledges support from the German Academic Exchange Service (DAAD) and HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme. Computational resources were partly provided by PRACE on the Marconi machine at CINECA and by the High-Performance Computing Center Stuttgart (HLRS).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.8b11709.

  • Electronic and optical properties of the isolated push–pull monomer and the J-aggregate (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp8b11709_si_001.pdf (927.4KB, pdf)

References

  1. Bricks J. L.; Slominskii Y. L.; Panas I. D.; Demchenko A. P. Fluorescent J-Aggregates of Cyanine Dyes: Basic Research and Applications Review. Methods Appl. Fluoresc. 2017, 6, 012001 10.1088/2050-6120/aa8d0d. [DOI] [PubMed] [Google Scholar]
  2. Melnikau D.; Savateeva D.; Susha A. S.; Rogach A. L.; Rakovich Y. P. Strong Plasmon-Exciton Coupling in a Hybrid System of Gold Nanostars and J-Aggregates. Nanoscale Res. Lett. 2013, 8, 134 10.1186/1556-276X-8-134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ferdele S.; Jose B.; Foster R.; Keyes T. E.; Rice J. H. Strong Coupling in Porphyrin J-Aggregate Excitons and Plasmons in Nano-Void Arrays. Opt. Mater. 2017, 72, 680–684. 10.1016/j.optmat.2017.07.018. [DOI] [Google Scholar]
  4. Wurtz G. A.; Evans P. R.; Hendren W.; Atkinson R.; Dickson W.; Pollard R. J.; Zayats A. V.; Harrison W.; Bower C. Molecular Plasmonics with Tunable Exciton–Plasmon Coupling Strength in J-Aggregate Hybridized Au Nanorod Assemblies. Nano Lett. 2007, 7, 1297–1303. 10.1021/nl070284m. [DOI] [PubMed] [Google Scholar]
  5. Fofang N. T.; Park T.-H.; Neumann O.; Mirin N. A.; Nordlander P.; Halas N. J. Plexcitonic Nanoparticles: Plasmon–Exciton Coupling in Nanoshell–J-Aggregate Complexes. Nano Lett. 2008, 8, 3481–3487. 10.1021/nl8024278. [DOI] [PubMed] [Google Scholar]
  6. Egorov V. V. Theory of the J-Band: From the Frenkel Exciton to Charge Transfer. Phys. Procedia 2009, 2, 223–326. 10.1016/j.phpro.2009.07.014. [DOI] [Google Scholar]
  7. Jelley E. E. Spectral Absorption and Fluorescence of Dyes in the Molecular State. Nature 1936, 138, 1009. 10.1038/1381009a0. [DOI] [Google Scholar]
  8. Eisfeld A.; Briggs J. S. The J-Band of Organic Dyes: Lineshape and Coherence Length. Chem. Phys. 2002, 281, 61–70. 10.1016/S0301-0104(02)00594-3. [DOI] [Google Scholar]
  9. Eisfeld A.; Briggs J. S. The J- and H-Bands of Organic Dye Aggregates. Chem. Phys. 2006, 324, 376–384. 10.1016/j.chemphys.2005.11.015. [DOI] [Google Scholar]
  10. Walczak P. B.; Eisfeld A.; Briggs J. S. Exchange Narrowing of the J Band of Molecular Dye Aggregates. J. Chem. Phys. 2008, 128, 044505 10.1063/1.2823730. [DOI] [PubMed] [Google Scholar]
  11. Kasha M. Energy Transfer Mechanisms and the Molecular Exciton Model for Molecular Aggregates. Radiat. Res. 1963, 20, 55–70. 10.2307/3571331. [DOI] [PubMed] [Google Scholar]
  12. Kasha M.; Rawls H. R.; Ashraf El-Bayoumi M. The Exciton Model in Molecular Spectroscopy. Pure Appl. Chem. 1965, 11, 371–392. 10.1351/pac196511030371. [DOI] [Google Scholar]
  13. Botta C.; Cariati E.; Cavallo G.; Dichiarante V.; Forni A.; Metrangolo P.; Pilati T.; Resnati G.; Righetto S.; Terraneo G.; et al. Fluorine-Induced J-Aggregation Enhances Emissive Properties of a New NLO Push-Pull Chromophore. J. Mater. Chem. C 2014, 2, 5275–5279. 10.1039/c4tc00665h. [DOI] [Google Scholar]
  14. Guerrini M.; Calzolari A.; Corni S. Solid-State Effects on the Optical Excitation of Push–Pull Molecular J-Aggregates by First-Principles Simulations. ACS Omega 2018, 3, 10481–10486. 10.1021/acsomega.8b01457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hummer K.; Puschnig P.; Ambrosch-Draxl C. Lowest Optical Excitations in Molecular Crystals: Bound Excitons versus Free Electron-Hole Pairs in Anthracene. Phys. Rev. Lett. 2004, 92, 147402 10.1103/PhysRevLett.92.147402. [DOI] [PubMed] [Google Scholar]
  16. Cocchi C.; Breuer T.; Witte G.; Draxl C. Polarized Absorbance and Davydov Splitting in Bulk and Thin-Film Pentacene Polymorphs. Phys. Chem. Chem. Phys. 2018, 20, 29724–29736. 10.1039/C8CP06384B. [DOI] [PubMed] [Google Scholar]
  17. Ruini A.; Caldas M. J.; Bussi G.; Molinari E. Solid State Effects on Exciton States and Optical Properties of PPV. Phys. Rev. Lett. 2002, 88, 206403 10.1103/PhysRevLett.88.206403. [DOI] [PubMed] [Google Scholar]
  18. Tiago M. L.; Northrup J. E.; Louie S. G. Ab Initio Calculation of the Electronic and Optical Properties of Solid Pentacene. Phys. Rev. B 2003, 67, 115212 10.1103/PhysRevB.67.115212. [DOI] [Google Scholar]
  19. Cudazzo P.; Gatti M.; Rubio A. Excitons in Molecular Crystals from First-Principles Many-Body Perturbation Theory: Picene versus Pentacene. Phys. Rev. B 2012, 86, 195307 10.1103/PhysRevB.86.195307. [DOI] [Google Scholar]
  20. Broch K.; Dieterle J.; Branchi F.; Hestand N. J.; Olivier Y.; Tamura H.; Cruz C.; Nichols V. M.; Hinderhofer A.; Beljonne D.; et al. Robust Singlet Fission in Pentacene Thin Films with Tuned Charge Transfer Interactions. Nat. Commun. 2018, 9, 954 10.1038/s41467-018-03300-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Zeng T.; Hoffmann R.; Ananth N. The Low-Lying Electronic States of Pentacene and Their Roles in Singlet Fission. J. Am. Chem. Soc. 2014, 136, 5755–5764. 10.1021/ja500887a. [DOI] [PubMed] [Google Scholar]
  22. Refaely-Abramson S.; da Jornada F. H.; Louie S. G.; Neaton J. B. Origins of Singlet Fission in Solid Pentacene from an Ab Initio Green’s Function Approach. Phys. Rev. Lett. 2017, 119, 267401 10.1103/PhysRevLett.119.267401. [DOI] [PubMed] [Google Scholar]
  23. Coto P. B.; Sharifzadeh S.; Neaton J. B.; Thoss M. Low-Lying Electronic Excited States of Pentacene Oligomers: A Comparative Electronic Structure Study in the Context of Singlet Fission. J. Chem. Theory Comput. 2015, 11, 147–156. 10.1021/ct500510k. [DOI] [PubMed] [Google Scholar]
  24. Beljonne D.; Yamagata H.; Brédas J. L.; Spano F. C.; Olivier Y. Charge-Transfer Excitations Steer the Davydov Splitting and Mediate Singlet Exciton Fission in Pentacene. Phys. Rev. Lett. 2013, 110, 226402 10.1103/PhysRevLett.110.226402. [DOI] [PubMed] [Google Scholar]
  25. Kolata K.; Breuer T.; Witte G.; Chatterjee S. Molecular Packing Determines Singlet Exciton Fission in Organic Semiconductors. ACS Nano 2014, 8, 7377–7383. 10.1021/nn502544d. [DOI] [PubMed] [Google Scholar]
  26. Berkelbach T. C.; Hybertsen M. S.; Reichman D. R. Microscopic Theory of Singlet Exciton Fission. III. Crystalline Pentacene. J. Chem. Phys. 2014, 141, 074705 10.1063/1.4892793. [DOI] [PubMed] [Google Scholar]
  27. Berkelbach T. C.; Hybertsen M. S.; Reichman D. R. Microscopic Theory of Singlet Exciton Fission. II. Application to Pentacene Dimers and the Role of Superexchange. J. Chem. Phys. 2013, 138, 114103 10.1063/1.4794427. [DOI] [PubMed] [Google Scholar]
  28. Sharifzadeh S.; Darancet P.; Kronik L.; Neaton J. B. Low-Energy Charge-Transfer Excitons in Organic Solids from First-Principles: The Case of Pentacene. J. Phys. Chem. Lett. 2013, 4, 2197–2201. 10.1021/jz401069f. [DOI] [Google Scholar]
  29. Wilson M. W. B.; Rao A.; Ehrler B.; Friend R. H. Singlet Exciton Fission in Polycrystalline Pentacene: From Photophysics toward Devices. Acc. Chem. Res. 2013, 46, 1330–1338. 10.1021/ar300345h. [DOI] [PubMed] [Google Scholar]
  30. Wilson M. W. B.; Rao A.; Clark J.; Kumar R. S. S.; Brida D.; Cerullo G.; Friend R. H. Ultrafast Dynamics of Exciton Fission in Polycrystalline Pentacene. J. Am. Chem. Soc. 2011, 133, 11830–11833. 10.1021/ja201688h. [DOI] [PubMed] [Google Scholar]
  31. Zimmerman P. M.; Bell F.; Casanova D.; Head-Gordon M. Mechanism for Singlet Fission in Pentacene and Tetracene: From Single Exciton to Two Triplets. J. Am. Chem. Soc. 2011, 133, 19944–19952. 10.1021/ja208431r. [DOI] [PubMed] [Google Scholar]
  32. Zimmerman P. M.; Zhang Z.; Musgrave C. B. Singlet Fission in Pentacene through Multi-Exciton Quantum States. Nat. Chem. 2010, 2, 648. 10.1038/nchem.694. [DOI] [PubMed] [Google Scholar]
  33. Schuster R.; Knupfer M.; Berger H. Exciton Band Structure of Pentacene Molecular Solids: Breakdown of the Frenkel Exciton Model. Phys. Rev. Lett. 2007, 98, 037402 10.1103/PhysRevLett.98.037402. [DOI] [PubMed] [Google Scholar]
  34. Cudazzo P.; Sottile F.; Rubio A.; Gatti M. Exciton Dispersion in Molecular Solids. J. Phys.: Condens. Matter 2015, 27, 113204 10.1088/0953-8984/27/11/113204. [DOI] [PubMed] [Google Scholar]
  35. Hummer K.; Ambrosch-Draxl C. Oligoacene Exciton Binding Energies: Their Dependence on Molecular Size. Phys. Rev. B 2005, 71, 081202 10.1103/PhysRevB.71.081202. [DOI] [Google Scholar]
  36. Bussi G.; Ruini A.; Molinari E.; Caldas M. J.; Puschnig P.; Ambrosch-Draxl C. Interchain Interaction and Davydov Splitting in Polythiophene Crystals: An Ab Initio Approach. Appl. Phys. Lett. 2002, 80, 4118–4120. 10.1063/1.1483905. [DOI] [Google Scholar]
  37. Rangel T.; Berland K.; Sharifzadeh S.; Brown-Altvater F.; Lee K.; Hyldgaard P.; Kronik L.; Neaton J. B. Structural and Excited-State Properties of Oligoacene Crystals from First Principles. Phys. Rev. B 2016, 93, 115206 10.1103/PhysRevB.93.115206. [DOI] [Google Scholar]
  38. Sharifzadeh S.; Biller A.; Kronik L.; Neaton J. B. Quasiparticle and Optical Spectroscopy of the Organic Semiconductors Pentacene and PTCDA from First Principles. Phys. Rev. B 2012, 85, 125307 10.1103/PhysRevB.85.125307. [DOI] [Google Scholar]
  39. Ambrosch-Draxl C.; Nabok D.; Puschnig P.; Meisenbichler C. The Role of Polymorphism in Organic Thin Films: Oligoacenes Investigated from First Principles. New J. Phys. 2009, 11, 125010 10.1088/1367-2630/11/12/125010. [DOI] [Google Scholar]
  40. Nelson S. F.; Lin Y.-Y.; Gundlach D. J.; Jackson T. N. Temperature-Independent Transport in High-Mobility Pentacene Transistors. Appl. Phys. Lett. 1998, 72, 1854–1856. 10.1063/1.121205. [DOI] [Google Scholar]
  41. Lee J. Y.; Roth S.; Park Y. W. Anisotropic Field Effect Mobility in Single Crystal Pentacene. Appl. Phys. Lett. 2006, 88, 252106 10.1063/1.2216400. [DOI] [Google Scholar]
  42. Takeya J.; Yamagishi M.; Tominari Y.; Hirahara R.; Nakazawa Y.; Nishikawa T.; Kawase T.; Shimoda T.; Ogawa S. Very High-Mobility Organic Single-Crystal Transistors with in-Crystal Conduction Channels. Appl. Phys. Lett. 2007, 90, 102120 10.1063/1.2711393. [DOI] [Google Scholar]
  43. Dimitrakopoulos C. D.; Brown A. R.; Pomp A. Molecular Beam Deposited Thin Films of Pentacene for Organic Field Effect Transistor Applications. J. Appl. Phys. 1996, 80, 2501–2508. 10.1063/1.363032. [DOI] [Google Scholar]
  44. Lin Y.-Y.; Gundlach D. I.; Nelson S. F.; Jackson T. N. Pentacene-Based Organic Thin-Film Transistors. IEEE Trans. Electron Devices 1997, 44, 1325–1331. 10.1109/16.605476. [DOI] [Google Scholar]
  45. Jin Y.; Rang Z.; Nathan M. I.; Ruden P. P.; Newman C. R.; Frisbie C. D. Pentacene Organic Field-Effect Transistor on Metal Substrate with Spin-Coated Smoothing Layer. Appl. Phys. Lett. 2004, 85, 4406–4408. 10.1063/1.1814802. [DOI] [Google Scholar]
  46. Yang S. Y.; Shin K.; Park C. E. The Effect of Gate-Dielectric Surface Energy on Pentacene Morphology and Organic Field-Effect Transistor Characteristics. Adv. Funct. Mater. 2005, 15, 1806–1814. 10.1002/adfm.200400486. [DOI] [Google Scholar]
  47. Graz I. M.; Lacour S. P. Flexible Pentacene Organic Thin Film Transistor Circuits Fabricated Directly onto Elastic Silicone Membranes. Appl. Phys. Lett. 2009, 95, 243305 10.1063/1.3265737. [DOI] [Google Scholar]
  48. Varghese S.; Das S. Role of Molecular Packing in Determining Solid-State Optical Properties of π-Conjugated Materials. J. Phys. Chem. Lett. 2011, 2, 863–873. 10.1021/jz200099p. [DOI] [PubMed] [Google Scholar]
  49. Köhler A.; Wilson J. S.; Friend R. H. Fluorescence and Phosphorescence in Organic Materials. Adv. Mater. 2002, 14, 701–707. . [DOI] [Google Scholar]
  50. Benassi E.; Corni S. Exciton Transfer of Azobenzene Derivatives in Self-Assembled Monolayers. J. Phys. Chem. C 2013, 117, 25026–25041. 10.1021/jp405077w. [DOI] [Google Scholar]
  51. Utecht M.; Klamroth T.; Saalfrank P. Optical Absorption and Excitonic Coupling in Azobenzenes Forming Self-Assembled Monolayers: A Study Based on Density Functional Theory. Phys. Chem. Chem. Phys. 2011, 13, 21608–21614. 10.1039/c1cp22793a. [DOI] [PubMed] [Google Scholar]
  52. Cocchi C.; Moldt T.; Gahl C.; Weinelt M.; Draxl C. Optical Properties of Azobenzene-Functionalized Self-Assembled Monolayers: Intermolecular Coupling and Many-Body Interactions. J. Chem. Phys. 2016, 145, 234701 10.1063/1.4971436. [DOI] [PubMed] [Google Scholar]
  53. Cocchi C.; Draxl C. Understanding the Effects of Packing and Chemical Terminations on the Optical Excitations of Azobenzene-Functionalized Self-Assembled Monolayers. J. Phys.: Condens. Matter 2017, 29, 394005 10.1088/1361-648X/aa7ca7. [DOI] [PubMed] [Google Scholar]
  54. Cocchi C.; Draxl C. Bound Excitons and Many-Body Effects in x-Ray Absorption Spectra of Azobenzene-Functionalized Self-Assembled Monolayers. Phys. Rev. B 2015, 92, 205105 10.1103/PhysRevB.92.205105. [DOI] [Google Scholar]
  55. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  56. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  57. Onida G.; Reining L.; Rubio A. Electronic Excitations: Density-Functional versus Many-Body Green’s-Function Approaches. Rev. Mod. Phys. 2002, 74, 601–659. 10.1103/RevModPhys.74.601. [DOI] [Google Scholar]
  58. Hedin L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas-Problem. Phys. Rev. 1965, 139, A796. 10.1103/PhysRev.139.A796. [DOI] [Google Scholar]
  59. Strinati G. Application of the Green’s Functions Method to the Study of the Optical Properties of Semiconductors. La Riv. Nuovo Cimento 1988, 11, 1–86. 10.1007/BF02725962. [DOI] [Google Scholar]
  60. Hybertsen M. S.; Louie S. G. Electron Correlation in Semiconductors and Insulators: Band Gaps and Quasiparticle Energies. Phys. Rev. B 1986, 34, 5390–5413. 10.1103/PhysRevB.34.5390. [DOI] [PubMed] [Google Scholar]
  61. Hanke W. Dielectric Theory of Elementary Excitations in Crystals. Adv. Phys. 1978, 27, 287–341. 10.1080/00018737800101384. [DOI] [Google Scholar]
  62. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21, 395502 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  63. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  64. Hamann D. R. Optimized Norm-Conserving Vanderbilt Pseudopotentials. Phys. Rev. B 2013, 88, 085117 10.1103/PhysRevB.88.085117. [DOI] [Google Scholar]
  65. Marini A.; Hogan C.; Grüning M.; Varsano D. Yambo: An Ab Initio Tool for Excited State Calculations. Comput. Phys. Commun. 2009, 180, 1392–1403. 10.1016/j.cpc.2009.02.003. [DOI] [Google Scholar]
  66. Godby R. W.; Needs R. J. Metal-Insulator Transition in Kohn-Sham Theory and Quasiparticle Theory. Phys. Rev. Lett. 1989, 62, 1169–1172. 10.1103/PhysRevLett.62.1169. [DOI] [PubMed] [Google Scholar]
  67. Larson P.; Dvorak M.; Wu Z. Role of the Plasmon-Pole Model in the GW Approximation. Phys. Rev. B 2013, 88, 125205 10.1103/PhysRevB.88.125205. [DOI] [Google Scholar]
  68. Stankovski M.; Antonius G.; Waroquiers D.; Miglio A.; Dixit H.; Sankaran K.; Giantomassi M.; Gonze X.; Côté M.; Rignanese G.-M. G0W0 Band Gap of ZnO: Effects of Plasmon-Pole Models. Phys. Rev. B 2011, 84, 241201 10.1103/PhysRevB.84.241201. [DOI] [Google Scholar]
  69. Lebègue S.; Arnaud B.; Alouani M.; Bloechl P. E. Implementation of an All-Electron GW Approximation Based on the Projector Augmented Wave Method without Plasmon Pole Approximation: Application to Si, SiC, AlAs, InAs, NaH, and KH. Phys. Rev. B 2003, 67, 155208 10.1103/PhysRevB.67.155208. [DOI] [Google Scholar]
  70. Bruneval F.; Rangel T.; Hamed S. M.; Shao M.; Yang C.; Neaton J. B. MOLGW 1: Many-Body Perturbation Theory Software for Atoms, Molecules, and Clusters. Comput. Phys. Commun. 2016, 208, 149–161. 10.1016/j.cpc.2016.06.019. [DOI] [Google Scholar]
  71. Bruneval F.; Marques M. A. L. Benchmarking the Starting Points of the GW Approximation for Molecules. J. Chem. Theory Comput. 2013, 9, 324–329. 10.1021/ct300835h. [DOI] [PubMed] [Google Scholar]
  72. Bruneval F.; Rangel T.; Hamed S. M.; Shao M.; Yang C.; Neaton J. B. MOLGW 1: Many-Body Perturbation Theory Software for Atoms, Molecules, and Clusters. Comput. Phys. Commun. 2016, 208, 149–161. 10.1016/j.cpc.2016.06.019. [DOI] [Google Scholar]
  73. van der Horst J.; Bobbert P.; de Jong P.; Michels M.; Brocks G.; Kelly P. Ab Initio Prediction of the Electronic and Optical Excitations in Polythiophene: Isolated Chains versus Bulk Polymer. Phys. Rev. B 2000, 61, 15817–15826. 10.1103/PhysRevB.61.15817. [DOI] [Google Scholar]
  74. Cocchi C.; Draxl C. Optical Spectra from Molecules to Crystals: Insight from Many-Body Perturbation Theory. Phys. Rev. B 2015, 92, 5126. 10.1103/PhysRevB.92.205126. [DOI] [Google Scholar]
  75. Alvarado S. F.; Seidler P. F.; Lidzey D. G.; Bradley D. D. C. Direct Determination of the Exciton Binding Energy of Conjugated Polymers Using a Scanning Tunneling Microscope. Phys. Rev. Lett. 1998, 81, 1082–1085. 10.1103/PhysRevLett.81.1082. [DOI] [Google Scholar]
  76. Campbell I. H.; Hagler T. W.; Smith D. L.; Ferraris J. P. Direct Measurement of Conjugated Polymer Electronic Excitation Energies Using Metal/Polymer/Metal Structures. Phys. Rev. Lett. 1996, 76, 1900–1903. 10.1103/PhysRevLett.76.1900. [DOI] [PubMed] [Google Scholar]
  77. Barth S.; Bässler H. Intrinsic Photoconduction in PPV-Type Conjugated Polymers. Phys. Rev. Lett. 1997, 79, 4445–4448. 10.1103/PhysRevLett.79.4445. [DOI] [Google Scholar]
  78. Varsano D.; Marini A.; Rubio A. Optical Saturation Driven by Exciton Confinement in Molecular Chains: A Time-Dependent Density-Functional Theory Approach. Phys. Rev. Lett. 2008, 101, 133002 10.1103/PhysRevLett.101.133002. [DOI] [PubMed] [Google Scholar]
  79. Cocchi C.; Prezzi D.; Ruini A.; Caldas M. J.; Molinari E. Optical Properties and Charge-Transfer Excitations in Edge-Functionalized All-Graphene Nanojunctions. J. Phys. Chem. Lett. 2011, 2, 1315–1319. 10.1021/jz200472a. [DOI] [PubMed] [Google Scholar]
  80. Ruini A. Ab Initio Optical Absorption in Conjugated Polymers: The Role of Dimensionality. Phys. Scr. 2004, T109, 121. 10.1238/Physica.Topical.109a00121. [DOI] [Google Scholar]
  81. Barford W.Electronic and Optical Properties of Conjugated Polymers; International Series of Monographs on Physics; OUP: Oxford, 2005. [Google Scholar]
  82. Dreuw A.; Head-Gordon M. Single-Reference Ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009–4037. 10.1021/cr0505627. [DOI] [PubMed] [Google Scholar]
  83. Dreuw A.; Weisman J. L.; Head-gordon M. Long-Range Charge-Transfer Excited States in Time-Dependent Density Functional Theory Require non-local Exchange. J. Chem. Phys. 2003, 119, 2943. 10.1063/1.1590951. [DOI] [Google Scholar]
  84. Dreuw A.; Head-Gordon M. Failure of Time-Dependent Density Functional Theory for Long-Range Charge-Transfer Excited States: The Zincbacteriochlorin–Bacteriochlorin and Bacteriochlorophyll–Spheroidene Complexes. J. Am. Chem. Soc. 2004, 126, 4007–4016. 10.1021/ja039556n. [DOI] [PubMed] [Google Scholar]
  85. Hummer K.; Puschnig P.; Ambrosch-Draxl C. Ab Initio Study of Anthracene under High Pressure. Phys. Rev. B 2003, 67, 184105 10.1103/PhysRevB.67.184105. [DOI] [Google Scholar]
  86. Puschnig P.; Hummer K.; Ambrosch-Draxl C.; Heimel G.; Oehzelt M.; Resel R. Electronic, Optical, and Structural Properties of Oligophenylene Molecular Crystals under High Pressure: An Ab Initio Investigation. Phys. Rev. B 2003, 67, 235321 10.1103/PhysRevB.67.235321. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp8b11709_si_001.pdf (927.4KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES