Multi-Label Nonlinear Matrix Completion With Transductive Multi-Task Feature Selection for Joint MGMT and IDH1 Status Prediction of Patient With High-Grade Gliomas

Abstract

The O⁶-methylguanine-DNA methyltransferase (MGMT) promoter methylation and isocitrate dehydrogenase 1 (IDH1) mutation in high-grade gliomas (HGG) have proven to be the two important molecular indicators associated with better prognosis. Traditionally, the statuses of MGMT and IDH1 are obtained via surgical biopsy, which has limited their wider clinical implementation. Accurate presurgical prediction of their statuses based on preoperative multimodal neuroimaging is of great clinical value for a better treatment plan. Currently, the available data set associated with this study has several challenges, such as small sample size and complex, nonlinear (image) feature-to-(molecular) label relationship. To address these issues, we propose a novel multi-label non linear matrix completion (MNMC) model to jointly predict both MGMT and IDH1 statuses in a multi-task framework. Specifically, we first employ a nonlinear random Fourier feature mapping to improve the linear separability of the data, and then use transductive multi-task feature selection (performed in a nonlinearly transformed feature space) to refine the imputed soft labels, thus alleviating the overfitting problem caused by small sample size. We further design an optimization algorithm with a guaranteed convergence ability based on a block prox-linear method to solve the proposed MNMC model. Finally, by using a single-center, multimodal brain imaging and molecular pathology data set of HGG, we derive brain functional and structural connectomics features to jointly predict MGMT and IDH1 statuses. Results demonstrate that our proposed method outperforms the previously widely used single- and multi-task machine learning methods. This paper also shows the promise of utilizing brain connectomics for HGG prognosis in a non-invasive manner.

I. Introduction

Gliomas account for approximately 45% of primary brain tumors. The most deadly gliomas are classified by World Health Organization (WHO) as Grades III and IV using histopathological criteria, which are referred to as high-grade gliomas (HGG) and account for about 75% of all gliomas [1], [2]. Related clinical studies have shown that the O⁶-methylguanine-DNA methyltransferase promoter methylation (MGMT-m) and isocitrate dehydrogenase 1 mutation (IDH1-m) are the two strong molecular indicators associated with better prognosis for HGG compared to their counterparts, MGMT promoter unmethylation (MGMT-u) and IDH1 wild-type (IDH1-w) [3], [4]. Specifically, MGMT methylation can reduce the deoxyribonucleic acid (DNA) repair activity of glioma cells, overcoming their resistance to alkylating agents, thus is a strong predictor of response to temozolomide-based therapy [5]. With such an increased sensitivity to the therapy, MGMT-m is associated with a longer survival time for HGG [3]. IDH1-m is another important molecular biomarker for gliomas. It has been suggested that the patients with IDH1-m have significantly longer survival time when compared with those with IDH1-w [6], [7]. To date, the identification of MGMT and IDH1 statuses (i.e., MGMT-m vs. MGMT-u, and IDH1-m vs. IDH1-w) is becoming a clinical routine and is mainly derived from molecular pathological analysis based on invasively acquired tumor tissue specimen, which may sometimes cause severe brain injury, and increase the risk of infection and even severe complications (e.g., neurological deficits). Moreover, obtaining such molecular information is expensive, requiring special examination devices and taking a long waiting time. All these shortcomings have limited the extensive clinical applications of these molecular biomarkers, especially in the hospitals without cutting-edge testing devices. Non-invasive and preoperative prediction of MGMT and IDH1 statuses is convenient and time-saving, thus highly desired.

A few studies have been carried out to predict either MGMT or IDH1 status based on the tumor characteristics from preoperative brain images. For example, Drabycz et al. extracted tumor texture features from T1- and T2-weighted Magnetic Resonance Images (MRIs), and employed simple linear discriminant analysis to predict MGMT status [8]. Korfiatis et al. also extracted tumor texture features from a single T2-weighted MRI (T2-MRI) modality and trained a linear support vector machine (SVM) to predict MGMT status [9]. Yamashita et al. extracted both functional features (i.e., cerebral blood flow) based on perfusion MRI and morphometric features based on T1-weighted MRI (T1-MRI) from the tumor regions, and employed a group-level statistical approach to examine each feature’s association with the IDH1 status [10]. Zhang et al. extracted more voxelwise and histogram-based features from the tumor areas using T1-/T2-MRI and diffusion-weighted images (DWI), and employed a more sophisticated Random Forest (RF) classifier to predict IDH1 status [11]. It is worth noting that all the above studies are based predominantly on local appearance/morphometric features by extracting features from structural MRI, ignoring that the brain is actually an integrated system and its organization and connections could also be associated with genes and molecular indicators. Abundant evidence has indicated that neurological and psychiatric diseases could alter brain functional connectivity (FC) and structural connectivity (SC), as measured by resting-state functional MRI (RS-fMRI) and diffusion tensor imaging (DTI), respectively [12], [13]. High-grade gliomas, as fast-growing, highly invasive neoplasms with diffusive infiltration along the white matter, has been recently found to significantly affect largescale brain connectomics [14]‒[21]. In our previous works, we have found that the glioma’s influence on the brain connectomics could be informative for outcome prediction [21]. Therefore, it is worth investigating whether such macro-scale, systems-level changes could also be associated with microscale information such as genotype or molecular pathology. Moreover, the local “radiomics” features could bear large variability due to highly heterogeneous tumor characteristics; however, the “connectomics” features extracted based on large-scale network analysis could more consistently and sensitively reflect individual differences in different MGMT and IDH1 statuses. Thus, how to design an effective classification framework based on the connectomics features is non-trivial. We found that all the previous studies are limited to predict either MGMT or IDH1 status by using a simple, single-task inductive machine learning method, ignoring the potential relationship between the two molecular indicators which could help each other in achieving more accurate prediction results [22]. It is desirable to use a multi-task learning approach to jointly predict MGMT and IDH1 statuses to improve the overall accuracy. In our case, if we treat the MGMT statuses (i.e., ‘MGMT-m vs. MGMT-u’) and the IDH1 statuses (i.e., ‘IDH1-m vs. IDH1-w’) as two groups of binary molecular labels, then the MGMG and IDH1 status prediction problem can be regarded as a multi-task binary classification problem, with one task to predict the molecular labels ‘MGMT-m vs. MGMT-u’ and another task to predict other molecular labels (‘IDH1-m vs. IDH1-w’). However, such a study still faces at least two challenges for the currently available dataset. First, since the molecular pathology testing was not included as clinical routine during the data collection a few years ago, the available data used in this paper has limited sample size. Second, in clinical practice, complete molecular pathological tests may not always be conducted; in some cases, only one biopsy-proven MGMT or IDH1 status is available, making the prediction become an incomplete annotation or missing data problem. Traditional methods usually simply discarded the subjects with missing labels, which, however, further reduced the number of training samples. The recently proposed Multi-label Transductive Matrix Completion (MTMC) [23] model is a suitable transductive multi-task classification approach, which simultaneously explores feature distributions of both the training samples with (partially) known labels and the testing samples with unknown labels in the training stage, thus producing good performance in many previous computational vision or medical imaging analysis problems [23]‒[26]. However, such a model is difficult to be generalized if a study has a limited sample size due to the increasing overfitting concern that many phenotypegenotype association studies may suffer. In order to address this challenge, in our preliminary work [27], we introduced an online inductive learning strategy into the conventional MTMC model, which resulted in a Multi-label Inductive Matrix Completion (MIMC) model for joint prediction of MGMT and IDH1 statuses. However, the MIMC model conducts transductive multi-task feature selection in a noisy feature space, rather than in a more ideal, noise-free feature space. Moreover, the MIMC model is essentially a linear model that heavily assumes a linear relationship between features and labels; however, this is not always guaranteed for real applications. In the current study, the relationship could be much more complex and probably nonlinear.

To address these limitations, in this study, we employ nonlinear feature transformation in conjunction with transductive multi-task feature selection in the denoised feature space, which is substantially different from the MIMC model. We thus propose a novel Multi-label Nonlinear Matrix Completion (MNMC) model. Specifically, we first conduct explicit random Fourier feature mapping to improve the linear separability of the data, and then conduct transductive multi-task feature selection in the denoised nonlinear feature space, which leverages the unlabeled testing subjects together with the (partially) labeled training subjects to make them simultaneously participate in the denoised nonlinear feature selection. We step further to learn a shared representation across the related tasks, hence selecting important nonlinear features from all subjects and alleviating the overfitting problem. Unlike the previous MIMC model, which is jointly convex and can be easily solved by a standard Block Coordinate Descent method, the proposed MNMC framework in this paper is a non-convex model, which makes its solution non-trivial. Therefore, we turn to employ a recently proposed Block Prox-Linear (BPL) method [28] to design an efficient algorithm for solving the non-convex MNMC model, and also demonstrate that the designed algorithm is guaranteed to be convergent. Finally, by using a 10-fold cross-validation strategy on a single-center, multi-modality brain imaging and molecular pathology dataset from HGG patients, we perform two experiments based on the single modality and multiple modalities, separately. We show our new method has significant performance improvement for both experiments, compared with several state-of-the-art methods for MGMT and IDH1 status prediction.

Our proposed MNMC model is significantly different from the existing multi-task learning models used in medical image analysis [29]–[31]. Specifically, the existing multi-task learning models are usually the inductive learning models, while our proposed MNMC model is a transductive multi-task learning model and can simultaneously explore feature distributions of both training and testing samples in the training stage. Therefore, the MNMC model could help improve the generalization performance of the testing samples. In addition, although our MNMC model is proposed just for predicting MGMT and IDH1 statuses, it is actually a generic multi-task binary classification model that is also applicable for other small-sample-size applications such as heart rate estimation from face videos [25], multi-atlas patch-based label fusion [26], emotion recognition from abstract paintings [32], cancer survival prediction [33], and neurodegenerative disease diagnosis [34], to name a few.

II. Materials

A. Summary

In this study, we use T1-MRI, RS-fMRI and DTI data from a glioma brain imaging database collected by Huashan Hospital, Shanghai, during 2010–2015. Informed written consents were acquired from all the participants before imaging. The imaging study was also approved by the local ethical committee at Huashan hospital. A total of 54 HGG patients who had all three imaging modalities were originally included in this study. We excluded 2 subjects with significant imaging artifacts based on T1-MRI, 1 subjects with severe tumor mass effect and normal brain tissue distortion (which could severely affect the spatial registration), and 4 subjects with excessive head motion during RS-fMRI. The subject exclusion was based on the consensus of three raters (HZ, JL and LL). Finally, 47 HGG subjects with at least one biopsy-proven MGMT or IDH1 status were included in this study. That is, among 47 subjects, 45 subjects have both known MGMT and IDH1 status, one subject has only known IDH1 status, and another subject has only known MGMT status. Table I summarizes the demographic and clinical information of these 47 subjects. In addition, we also check statistical significance of the demographic and clinical information by conducting the statistical comparison at 95% significance level between the age (with two-sample t-test), gender (with chi-square test), and WHO grade (with chi-square test) of the patients with MGMT-m (IDH1-m) and those with MGMT-u (IDH1-w), with the corresponding p-values shown in Table I. The results indicate that (1) gender and WHO grade of the patients with MGMT-m (or IDH1-m) are not statistically different from those of the patients with MGMT-u (or IDH1-w), and (2) IDH1-m matches IDH1-w with respect to age on a trend level, i.e., close to be statistically significant (with p = 0.074). To the best of our knowledge, there is no paper clearly showing that age is a contributing factor to different MGMT statuses. According to all the existing MGMT-related tumor studies, we found that MGMT promoter methylation seems to be randomly distributed among different age groups of glioma patients [35]. Specifically, previous studies have been separately focusing on young patients and old patients (>70 years old), but with few studies on the elderly group. The current studies have suggested that MGMT-m is also a beneficial biomarker for the elderly group [36]. In addition, although some literature indicated that the patients with IDH1-m have both younger age and longer survival time [37], the IDH1-m has been found as independent predictor for better outcome [38]. Taken together, we think that age difference might not act as a sole contributing factor to successful genomic classification results.

TABLE I.

Demographic AND Clinical Information OF THE Patients Used

	MGMT				IDH1
	MGMT-m	MGMT-u	Unlabeled	p-value	IDH1-m	IDH1-w	Unlabeled	p-value
Number	26	20	1	-	13	33	1	-
Age (mean/range)	47.0/24–68	49.9/23–68	39/39–39	0.287	45.9/23–67	49.2/24–68	41/41–41	0.074
Gender (M/F)	16/10	10/10	0/1	0.434	8/5	18/15	0/1	0.667
WHO III/IV	14/12	8/12	1/0	0.351	9/4	14/19	0/1	0.102
Total number	47				47

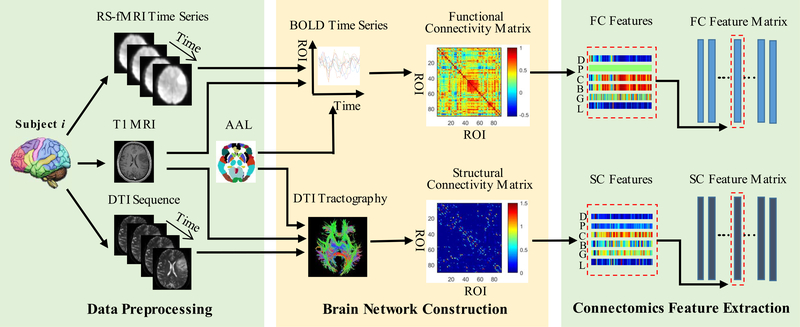
All the T1-MRI, RS-MRI and DTI data were collected preoperatively with a 3.0-Tesla scanner (MAGNETOM Verio, Siemens Healthcare, Siemens AG, Germany) with the following parameters: (1) T1-MRI: TR (repetition time) = 1900 ms, TE (echo time) = 2.3 ms, FA (flip angle) = 9°, FOV (field of view) = 240 × 240 mm², matrix size = 256 × 215, slice thickness = 1 mm; (2) RS-fMRI: TR = 2000 ms, TE = 35 ms, FA = 90°, number of slices = 33, slice thickness = 4 mm, inter-slice gap = 0; FOV = 210 × 210 mm², matrix size = 64×64, number of acquisitions = 240, voxel size = 3.4×3.4×4 mm³. (3) DTI: 20 diffusion-weighted directions, voxel size = 2 × 2 × 2 mm³, b = 1000 s/mm², and multiple acquisition factor = 2. The T1-MRI was used to guide spatial registration of all subject’s images (see Section B), and RS-fMRI and DTI were used to extract functional and structural connectomics information, respectively. Fig. 1 illustrates the pipeline of imaging data preprocessing (as detailed in Section B), brain structural and functional network construction (as detailed in Section C), and connectomics feature extraction based on graph theory (as detailed in Section D).

Fig. 1.

The pipeline of data (i.e., RS-fMRI and DTI data) preprocessing, brain network construction, and connectomics feature extraction. (D: degree; P: shortest path length; C: clustering coefficient; B: betweenness centrality; G: global efficiency; L: local efficiency; FC: functional connectivity; SC: structural connectivity).

B. Data Preprocessing

For RS-fMRI, data preprocessing was conducted similarly as for our previous works [21], [39] by widely-used fMRI data analysis software: SPM8 (http://www.fil.ion.ucl.ac.uk/spm/), Data Processing Assistant for Resting-State fMRI (DPARSF) [40], and REsting-State fMRI data analysis Toolkit (REST) [41]. Specifically, it includes discarding the first 5 volumes for scanner calibration, correction for slice acquisition timing and head motion, spatial registration to the standard Montreal Neurological Institute (MNI) space by using the deformation field obtained from “New Segmentation” (an extension of unified segmentation which obtains more robust brain tissue segmentation result) [42] and DARTEL (a fast diffeomorphic registration algorithm which achieves better performance on lesion brain group-wise registration) [43] to the co-registered T1-MRI, spatial smoothing using an isotropic Gaussian kernel with FWHM (full-width-athalf-maximum) of 6 mm³, removal of temporal linear trend, temporal band-pass filtering (0.01–0.08 Hz), and regressing out nuisance signals including the head motion profiles (Friston-24 model) and other physiological noise (averaged white-matter signals and averaged cerebrospinal-fluid signals).

For each subject, T1 MRI is used to guide spatial normalization of RS-fMRI. Specifically, individual T1 MRI is first registered to each patient’s averaged RS-fMRI data after head motion correction and then spatially normalized to the MNI standard space based on tissue segmentation and group-wise registration as implemented in SPM (New Segment + DAR-TEL). As different subjects have different tumor locations, and the group-wise registration iteratively registers each subject to a group-averaged template gradually, the tumor effect (spatial misregistration) could be minimized. The registration quality was visually inspected by experts on MRI analysis (HZ, JL, and LL) with consensus [21], [27], [44]. One subject who have visible tumor-induced distortion in the registered T1 MRI were excluded from further study. The processed RS-fMRI data with good registration are used for FC network construction, which will be described in detail in Section C.

For DTI, we use a pipeline toolbox for analyzing brain diffusion images (PANDA) [45] based on the FMRIB Software Library (FSL, https://fsl.fmrib.ox.ac.uk/fsl/), as detailed before [46]. The procedures include brain tissue extraction using bet command, eddy-current correction, diffusion tensor calculation using dtifit command, and deterministic tractography using fact command in FSL, which generates all possible fibers within the putative white matter tissue (fractional anisotropy (FA) > 0.2) with angle threshold = 45° and two seeds for each voxel. All above processing steps are carried out in each subject’s native space. To construct SC networks, each subject’s T1 image is first co-registered to its respective b = 0 s/mm² (T2-weighted) image based on flirt in FSL and then spatially registered to the standard MNI space with the same method as used for RS-fMRI registration. The resultant deformation field is then applied to map the brain parcellation atlas from the MNI space to each individual’s native space, which is used to construct SC networks described in Section C.

Note that the same T1 image is used to guide both the RS-fMRI and DTI registrations, so that multimodal imaging data can be registered in a consistent manner.

C. Brain Network Construction

To construct brain functional networks based on RS-fMRI, we use the Automated Anatomical Labeling (AAL) atlas, which defines 90 regions of interest (ROIs) in the cerebral gray matter area in a standard MNI space [47]. For each subject, we first extract the ROI mean blood oxygenation level-dependent (BOLD) time series s_i(i ∈ N) based on the AAL atlas; then, we construct the functional network N _f by defining the FC strength between nodes i and j as:

$$w_{ij}^f=Corr\left(s_i,s_j\right),$$ (1)

where i, j ∈ N ≡ {1,2, · · ·, 90} and i ≠ j, and Corr(s_i, s_j) denotes the Pearson’s correlation between the two BOLD time series from any ROI pair (i, j) of the 90 brain regions.

For construction of DTI-based SC network, N_s, we apply a warped individual AAL template in each subject’s native space to each subject’s DTI tractography results, and calculate the SC between the ROIs i and j using PANDA as the normalized total number of fibers connecting the ROI pair (i, j):

$$w_{ij}^s={\sum }_{i,j\in N,i\ne j}n(f)/(\frac{a_i+a_j}{2}),$$ (2)

where n( f ) is the total number of fibers (i.e., the mainstreams generated by tractography) linking ROIs i and j, and a_i is the surface area of the ROI i in its interface between gray matter and white matter. Dividing the fiber counts with $\frac{a_i+a_j}{2}$ corrects the bias in the SC-strength estimation caused by different ROI sizes.

For both FC and SC networks of each subject, there are the same 90 “nodes”. The “edges” connecting every pair of the nodes form two weighted networks (N_f and N_s), namely, functional and structural brain “connectomics”.

D. Connectomics Feature Extraction

After construction of the brain connectomics (i.e., N _f and N_s), we use a graph theoretical network analysis (GRETNA) toolbox [48] to extract various network properties, including nodal degree, small-world properties (shortest path length and clustering coefficient), network efficiency properties (global and local efficiency), and betweenness centrality [49]. These network properties are extracted as connectomics features for each node from each network of each subject.

Specifically, we extract 540 (6 metrics × 90 regions) FC features and the same number of SC features for each subject. In addition, we also use 12 clinical features (CL for short) from each subject as they have been extensively used in prognosis evaluation in the clinical practice, including patient’s age, gender, tumor size, WHO grade, tumor’s main and specific locations (in each of the five brain lobes), epilepsy or not, and the involved hemisphere.

III. Method

We first introduce the notations used in this section. X = [x₁, · · ·, x_m] ∈ ℝ^d×m denotes the feature matrix with m samples and d features (for each sample). Each sample (i.e., a column in X) represents one subject with SC, FC or/and CL features. Y = [y₁, · · ·, y_m] ∈ {−1, 1,?}^t×m denotes the corresponding label matrix with t labels (here t = 2, i.e., MGMT status and IDH1 status; 1 for MGMT-m and IDH1-m, −1 for MGMT-u and IDH1-w; and ‘?’ for unknown status). Furthermore, X is divided into X_train and X_test, where X_train is for training and X_test is for testing samples. Correspondingly, Y is also divided into Y_train and Y_test, where Y_train may be partially unknown. Our purpose is to predict Y_test for the testing samples. We also let X_last denotes the last row of matrix X. X_ij denotes the element in the i-th row and j-th column of matrix X. 1 denotes the all-ones row vector. Id×d denotes the d × d identity matrix. X^T denotes the transpose of matrix X. In addition, we denote the Frobenius norm, ℓ_2,1-norm, and nuclear norm of matrix X as $\Vert \mathbf{X}{\Vert }_{\text{F}}={({\sum }_i{\sum }_j{\text{X}}_{ij}^2)}^{1/2}$, $\Vert \mathbf{X}{\Vert }_{\text{2,1}}={\sum }_i{({\sum }_j{\text{X}}_{ij}^2)}^{1/2}$, and $\Vert \mathbf{X}{\Vert }_{*}={\sum }_i{\sigma }_i(\mathbf{X})$ respectively, where σ_i(X) denotes the i-th largest singular value of matrix X. Finally, we let X⁰ ∈ ℝ^d×m denote the true underlying feature matrix corresponding to X. Let Y⁰ ∈ ℝ^t×m and sign Y⁰ respectively denote the true underlying soft label (i.e., the continuous value in ℝ) matrix, and the true underlying hard label (i.e., the discrete value 1 or −1) matrix, where sign (·) is the element-wise sign function.

A. Multi-Label Transductive Matrix Completion (MTMC)

The MTMC is a well-known multi-label matrix completion model, which is developed with two assumptions. First, linear dependence relationship is assumed between X⁰ and Y⁰, i.e., Y⁰ = W^T [X⁰; 1], where W ∈ ℝ^(d+1)×t is an implicit weight matrix. Second, X⁰ is also assumed to be low-rank, i.e., rows (columns) of X⁰ could be represented by other rows (columns). Letting M⁰ = [Y⁰;X⁰; 1] denote the true underlying feature-label matrix corresponding to the observed feature-label matrix M = [Y;X; 1], then, from rank (M⁰) ≤ rank (X⁰)+1, we can infer that M⁰ is also low-rank. The goal of MTMC is to impute M⁰ given M. In real applications, M is usually contaminated by noise, so the MTMC is formulated as:

$$\underset{{}_{\mathbf{Z}}}{\min }\mu \Vert \mathbf{Z}{\Vert }_{*}+\frac{1}{2}{\Vert {\mathbf{Z}}_{\mathbf{X}}-\mathbf{X}\Vert }_F^2+\gamma \mathcal{L}\left({\mathbf{Z}}_{\mathbf{Y}},\mathbf{Y}\right)\text{s.t.}{\mathbf{Z}}_{\text{last}}=\mathbf{1}$$ (3)

where Z= [Z_Y; Z_X; Z_last] ∈ ℝ^(t+d+1)×m denotes the objective matrix to be optimized, Z_X denotes the feature submatrix, and Z_Y denotes the soft label submatrix. $\mathcal{L}\left({\mathbf{Z}}_{\mathbf{Y}},\mathbf{Y}\right)={\sum }_{(i,j)\in {\mathrm{\Omega }}_{\mathbf{Y}}}l\left({\left({\mathbf{Z}}_{\mathbf{Y}}\right)}_{ij},{\mathbf{Y}}_{ij}\right)$, where Ω_Y denotes the index set of known labels in Y, and l (·,·) denotes the element-wise logistic loss function:

$$l(u,v)=\log (1+\exp (-uv)).$$ (4)

Once the optimal objective matrix Z^opt is determined, the labels Y_test of the testing subjects can then be imputed by $sign\left({\mathbf{Z}}_{{\mathbf{Y}}_{test}}^{opt}\right)$, where ${\mathbf{Z}}_{{\mathbf{Y}}_{test}}^{opt}$ is the submatrix of Z^opt and denotes the optimal soft labels for the testing subjects. Based on the formulation of MTMC, we know that ${\mathbf{Z}}_{{\mathbf{Y}}_{test}}^{opt}$ is implicitly obtained from ${\mathbf{Z}}_{{\mathbf{Y}}_{test}}^{opt}={\left({\mathbf{W}}^{opt}\right)}^{\text{T}}\left[{\mathbf{X}}_{test}^{opt};\mathbf{1}\right]$, where ${\mathbf{X}}_{test}^{opt}$ is the optimal denoised counterpart of X_test, and W^opt is the optimal estimation of the weight matrix W. Although W^opt is not explicitly computed, it is implicitly determined by the training subjects and their known labels via low-rank approximation in Eq. (3). Therefore, for multi-label classification tasks with insufficient training subjects, as in our case, the MTMC will have the inherent overfitting problem.

Moreover, as mentioned before, the formulation of the MTMC greatly relies on the assumptions of low rank and linear setting. Though the low-rank assumption is relatively solid and widely accepted, as real data usually lie on low-dimensional manifolds, the linear feature-to-label relationship assumption implying all subjects to be linearly separable in the original feature space is too ideal for the complex nonlinear classification problems, as in this study.

In order to address the limitation of linear classification setting of MTMC, Alameda et al. employed a popular kernel-based approach and proposed the first kernel-based Nonlinear Transductive Matrix Completion (NTMC) model [32]. The primary theoretical motivation for the use of kernel tricks is the famous Cover’s Theorem [50], which states that, given a set of data that is not linearly separable on the original feature space, one can, with high probability, transform it to a new dataset that is linearly separable, by projecting it to a higher-dimensional space via nonlinear feature transformation. However, though NTMC benefits from possible linear separability of the data in the mapped kernel feature space, it also suffers the increased overfitting risk caused by lifting the original features to a higher dimensional Reproducing Kernel Hilbert Space. Moreover, since the NTMC employs the kernel trick to conduct the implicit nonlinear feature transformation, it is difficult to further adopt any overfitting-resistant technique to alleviate the overfitting deficiency.

B. Multi-Label Nonlinear Matrix Completion (MNMC)

The alternative method of making linear models work for nonlinear classification is using kernel approximation [51], which explicitly maps the original data to a finite dimensional feature transformation space:

$$\mathrm{\Phi }\left({\mathbf{x}}_{\mathbf{i}}\right):{ℝ}^d\to {ℝ}^h,$$ (5)

and assures that the expectation of the inner product of any two points in the transformed feature space is an unbiased estimation of the corresponding kernel function, i.e.,

$$\text{K}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\text{E}\left[\langle \mathrm{\Phi }\left({\mathbf{x}}_i\right),\mathrm{\Phi }\left({\mathbf{x}}_j\right)\rangle \right].$$ (6)

The random Fourier feature mapping is a widely used kernel approximation technique [51], which can help revealing nonlinear features of data when used in conjunction with linear algorithms and, for basic tasks such as regression or classification, using nonlinear random Fourier features incurs little or no loss in performance compared with the exact kernel methods [52], [53].

Theoretically, for shift-invariant kernels, Bochner’s theorem [54] implies that the random Fourier feature mapping Φ(·) can be written as:

$$\mathrm{\Phi }\left({\mathbf{x}}_i\right)=(1/\sqrt{h})\left[\cos \left({\mathbf{u}}_1^{\text{T}}{\mathbf{x}}_i+b_1\right),\cdots ,\cos \left({\mathbf{u}}_h^{\text{T}}{\mathbf{x}}_i+b_h\right)\right],$$ (7)

where {u₁, · · ·, u_h} are the projection directions sampled according to the distribution from the Fourier transform of the kernel function using Monte Carlo method, and {b₁, · · ·, b_h} are drawn uniformly from [0, 2π]. For instance, for the popularly used Radial Basis Function (RBF) kernel with δ representing the kernel width,

$$\text{K}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=exp\left(-\delta {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2\right),$$ (8)

its sampling distribution is a Gaussian distribution $\mathcal{N}\left(0,2\delta {\mathbf{I}}_{d\times d}\right)$.

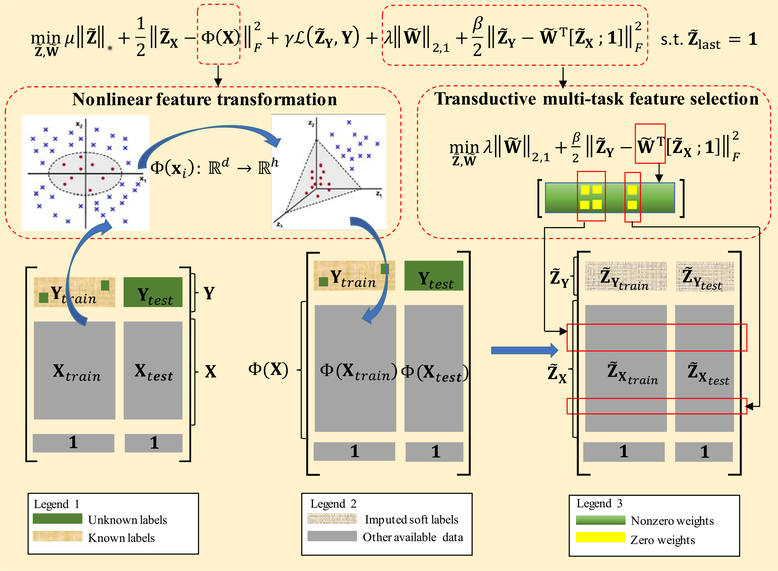
In this study, we propose a Multi-label Nonlinear Matrix Completion (MNMC) model, which is a modification of the conventional MTMC model by introducing random Fourier feature mapping and transductive multi-task feature selection, to jointly predict MGMT and IDH1 statuses. Fig. 2 illustrates our MNMC model. As shown in Fig. 2, we first conduct nonlinear feature transformation, i.e., random Fourier feature mapping, for all subjects X, and get the mapped nonlinear feature matrix:

$$\mathrm{\Phi }(\mathbf{X})=\left[\mathrm{\Phi }\left({\mathbf{x}}_1\right),\cdots ,\mathrm{\Phi }\left({\mathbf{x}}_m\right)\right].$$ (9)

Fig. 2.

The illustration of Multi-label Nonlinear Matrix Completion (MNMC) model.

Then the corresponding MTMC model in the transformed nonlinear feature space can be formulated as:

$$\begin{gathered} \underset{{}_{\mathbf{z}}}{\min }\mu \Vert \tilde{\mathbf{Z}}{\Vert }_{*}+\frac{1}{2}\Vert {\tilde{\mathbf{Z}}}_{\mathbf{X}}-\mathrm{\Phi }(\mathbf{X}){\Vert }_F^2+\gamma \mathcal{L}\left({\tilde{\mathbf{Z}}}_{\mathbf{Y}},\mathbf{Y}\right) \\ \text{s.t.}{\tilde{\mathbf{Z}}}_{\text{last}}=\mathbf{1}, \end{gathered}$$ (10)

where $\tilde{\mathbf{Z}}=\left[{\tilde{\mathbf{Z}}}_{\mathbf{Y}};{\tilde{\mathbf{Z}}}_{\mathbf{X}};{\tilde{\mathbf{Z}}}_{\text{last}}\right]$ denotes the objective matrix to be optimized in the mapped nonlinear feature space, ${\tilde{\mathbf{Z}}}_{\mathbf{Y}}$ denotes the soft label submatrix, and ${\tilde{\mathbf{Z}}}_{\mathbf{X}}$ denotes the feature submatrix.

As previously stated, by mapping the original features to a relatively higher-dimensional nonlinear feature space, the subjects may be linearly separated with higher probability. However, this advantage comes at the expense of exacerbating the overfitting issue. To address this issue, we further employ the transductive multi-task feature selection technique to refine the imputed soft labels ${\tilde{\mathbf{Z}}}_{\mathbf{Y}}$ by introducing a following regularization term into the Eq. (10):

$$\underset{{}_{\tilde{\mathbf{Z}},\tilde{\mathbf{W}}}}{\min }\lambda \Vert \tilde{\mathbf{W}}{\Vert }_{2,1}+\frac{\beta }{2}\Vert {\tilde{\mathbf{Z}}}_{\mathbf{Y}}-{\tilde{\mathbf{W}}}^{\text{T}}\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}};\mathbf{1}\right]{\Vert }_F^2,$$ (11)

where $\tilde{\mathbf{W}}\in {ℝ}^{(h+1)\times t}$ denotes the explicit predictor matrix (with each column of $\tilde{\mathbf{W}}$ corresponding to a predictor for each task), and the ℓ₂,₁-norm imposes the row sparsity on $\tilde{\mathbf{W}}$ to learn the shared representations across all related tasks by selecting the common discriminative features. In addition, please note that, in the second term of Eq. (11), we use all subjects, including the training and testing samples, to simultaneously conduct feature selection. In other words, we leverage the testing subjects as an effective supplement to the limited training subjects to alleviate the over-fitting issue caused by limited training data. Finally, by combining Eq. (10) and Eq. (11), our proposed MNMC model is formulated as:

$$\begin{gathered} \underset{{}_{\tilde{\mathbf{Z}},\tilde{\mathbf{W}}}}{\min }\{\mu \Vert \tilde{\mathbf{Z}}{\Vert }_{*}+\frac{1}{2}{\Vert {\tilde{\mathbf{Z}}}_{\mathbf{X}}-\mathrm{\Phi }(\mathbf{X})\Vert }_F^2+\gamma \mathcal{L}\left({\tilde{\mathbf{Z}}}_{\mathbf{Y}},\mathbf{Y}\right)+\lambda \Vert \tilde{\mathbf{W}}{\Vert }_{2,1} \\ +\frac{\beta }{2}{\Vert {\tilde{\mathbf{Z}}}_{\mathbf{Y}}-{\tilde{\mathbf{W}}}^{\text{T}}\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}};\mathbf{1}\right]\Vert }_F^2\}\text{s.t.}{\tilde{\mathbf{Z}}}_{\text{last}}=\mathbf{1}. \end{gathered}$$ (12)

Obviously, from Eq. (12), we can see that the conventional MTMC model is the special case of our proposed MNMC model if set Φ(X) to the identity function and set the parameters λ and β to zeroes.

C. Optimizing MNMC via Block Prox-Linear Method

The optimization of the MNMC model is not trivial, as it contains the two coupled variables $\left({\tilde{\mathbf{Z}}}_{\mathbf{X}}\text{and}\tilde{\mathbf{W}}\right)$ and one all1-row constraint $\left({\tilde{\mathbf{Z}}}_{\mathrm{last}}=\mathbf{1}\right)$, along with the fact that the ℓ₂,₁-norm and nuclear norm are non-smooth penalties. Here, we employ BPL method [28] to design an algorithm for solving the optimization problem in the MNMC model. The BPL method is a recently proposed Block Coordinate Descent method, which can efficiently solve the following standard unconstrained optimization problems in the form of [28]:

$$\underset{{\mathbf{X}}_1,\cdots ,{\mathbf{X}}_s}{\min }\text{F}\left({\mathbf{X}}_1,\cdots ,{\mathbf{X}}_s\right)+{\sum }_{i=1}^s{\text{R}}_i\left({\mathbf{X}}_i\right),$$ (13)

where X₁, · · ·, X_s ∈ ℝ^m×n, F (X₁, · · ·, X_s) is continuously differentiable nonconvex function, and R_i (X_i), i = 1, · · ·, s, are proximable non-smooth functions (‘proximable’ means that it is easy to obtain the minimizer of $\frac{1}{2\tau }{\Vert {\mathbf{X}}_i-\mathbf{A}\Vert }_F^2$ for any A ∈ ℝ^m×n and τ > 0). The BPL method cyclically updates each block of variables in Gauss-Seidel style by minimizing a prox-linear surrogate function. Specifically, at each iteration k, X_i, i = 1, · · ·, s, are updated as follows:

$$\begin{gathered} {\mathbf{X}}_{\mathbf{i}}^{\mathbf{k}}=\arg \underset{{}_{{\mathbf{x}}_i}}{\min }\{{\text{R}}_i\left({\mathbf{X}}_i\right)+\frac{1}{2{\tau }_{{\mathbf{X}}_i}^{\mathbf{k}}}\Vert {\mathbf{X}}_i-({\mathbf{X}}_{\mathbf{i}}^{\mathbf{k}-\mathbf{1}} \\ -{\tau }_{{\mathbf{X}}_i}^{\mathbf{k}}{\nabla }_{{\mathbf{X}}_i}\mathrm{F}\left({\mathbf{X}}_{<i}^{\mathbf{k}},{\mathbf{X}}_{\mathbf{i}}^{\mathbf{k}-\mathbf{1}},{\mathbf{X}}_{>i}^{\mathbf{k}-\mathbf{1}}\right)){\Vert }_F^2\}, \end{gathered}$$ (14)

where $\left({\mathbf{X}}_{<i}^{\mathbf{k}},{\mathbf{X}}_{\mathbf{i}}^{\mathbf{k}-\mathbf{1}},{\mathbf{X}}_{>i}^{\mathbf{k}-\mathbf{1}}\right)$ denotes the point $({\mathbf{X}}_1^{\mathbf{k}},\cdots ,{\mathbf{X}}_{\mathbf{i}-\mathbf{1}}^{\mathbf{k}},{\mathbf{X}}_{\mathbf{i}}^{\mathbf{k}-\mathbf{1}},{\mathbf{X}}_{\mathbf{i}+\mathbf{1}}^{\mathbf{k}-\mathbf{1}},\cdots ,{\mathbf{X}}_s^{\mathbf{k}-\mathbf{1}})$, ${\nabla }_{{\mathbf{X}}_i}\text{F}\left({\mathbf{X}}_{<i}^{\mathbf{k}},{\mathbf{X}}_{\mathbf{i}}^{\mathbf{k}-\mathbf{1}},{\mathbf{X}}_{>i}^{\mathbf{k}-1}\right)$ denotes the gradient of F (X₁, · · ·, X_s) with respect to X_i at the point $\left({\mathbf{X}}_{<i}^{\mathbf{k}},{\mathbf{X}}_{\mathbf{i}}^{\mathbf{k}-\mathbf{1}},{\mathbf{X}}_{>i}^{\mathbf{k}-\mathbf{1}}\right)$, and ${\tau }_{{\mathbf{X}}_i}^{\mathbf{k}}$ is a step size which can be determined by the line search according to the Armijo-Goldstein rule.

For our proposed MNMC model, if let $\text{G}(\tilde{\mathbf{Z}})$ be an indicator function defined as:

$$\text{G}(\tilde{\mathbf{Z}})=\{\begin{array}{ll}0,\hfill & {\tilde{\mathbf{Z}}}_{\text{last}}=\mathbf{1}\hfill \\ \infty ,\hfill & \text{otherwise,}\hfill \end{array}$$ (15)

and let:

$${\text{R}}_1(\tilde{\mathbf{Z}})=\mu \Vert \tilde{\mathbf{Z}}{\Vert }_{*}+\text{G}(\tilde{\mathbf{Z}}),$$ (16)

$${\text{R}}_2(\tilde{\mathbf{W}})=\lambda \Vert \tilde{\mathbf{W}}{\Vert }_{2,1},$$ (17)

$$\begin{gathered} \text{F}(\tilde{\mathbf{Z}},\tilde{\mathbf{W}})=\frac{\beta }{2}{\Vert {\tilde{\mathbf{Z}}}_{\mathbf{Y}}-{\tilde{\mathbf{W}}}^{\text{T}}\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}};\mathbf{1}\right]\Vert }_F^2+\gamma \mathcal{L}\left({\tilde{\mathbf{Z}}}_{\mathbf{Y}},\mathbf{Y}\right) \\ +\frac{1}{2}{\Vert {\tilde{\mathbf{Z}}}_{\mathbf{X}}-\mathrm{\Phi }(\mathbf{X})\Vert }_F^2, \end{gathered}$$ (18)

the proposed MNMC model can be reformulated as the following unconstrained form:

$$\underset{\tilde{\mathbf{Z}},\tilde{\mathbf{W}}}{\min }\text{F}(\tilde{\mathbf{Z}},\tilde{\mathbf{W}})+{\text{R}}_1(\tilde{\mathbf{Z}})+{\text{R}}_2(\tilde{\mathbf{W}}).$$ (19)

Therefore, according to the BPL method, the variables $\tilde{\mathbf{Z}}$ and $\tilde{\mathbf{W}}$ can be iteratively updated as follows:

$$\{\begin{array}{l}{\tilde{\mathbf{Z}}}^k=\arg \underset{\tilde{\mathbf{Z}}}{\min }\{{\text{R}}_1(\tilde{\mathbf{Z}})+\frac{1}{2{\tau }_{\tilde{\mathbf{Z}}}^{\mathbf{k}}}\hfill \\ {\Vert \tilde{\mathbf{Z}}-({\tilde{\mathbf{Z}}}^{k-1}-{\tau }_{\tilde{\mathbf{Z}}}^{\mathbf{k}}{\nabla }_{\tilde{\mathbf{Z}}}\text{F}({\tilde{\mathbf{Z}}}^{k-1},{\tilde{\mathbf{W}}}^{k-1}))\Vert }_F^2\}\hfill \\ {\tilde{\mathbf{W}}}^k=\mathrm{argarg}\underset{\tilde{\mathbf{W}}}{\min }\{{\text{R}}_2(\tilde{\mathbf{W}})+\frac{1}{2{\tau }_{\tilde{\mathbf{W}}}^{\mathbf{k}}}\\ {\Vert \tilde{\mathbf{W}}-({\tilde{\mathbf{W}}}^{k-1}-{\tau }_{\tilde{\mathbf{W}}}^{\mathbf{k}}{\nabla }_{\tilde{\mathbf{W}}}\text{F}({\tilde{\mathbf{Z}}}^k,{\tilde{\mathbf{W}}}^{k-1}))\Vert }_F^2\}.(20b)\end{array}$$ (20a)

Specifically, the variables ${\tilde{\mathbf{Z}}}^k$ in Eq. (20a) can be analytically solved by the following steps:

$$\{\begin{array}{l}{\tilde{\mathbf{Z}}}^k={\mathcal{D}}_{\mu {\tau }_{\tilde{\mathbf{Z}}}^{\mathbf{k}}}\left({\tilde{\mathbf{Z}}}^{k-1}-{\tau }_{\tilde{\mathbf{Z}}}^{\mathbf{k}}{\nabla }_{\tilde{\mathbf{Z}}}\text{F}\left({\tilde{\mathbf{Z}}}^{k-1},{\tilde{\mathbf{W}}}^{k-1}\right)\right)\hfill \\ {\left({\tilde{\mathbf{Z}}}^k\right)}_{\text{last}}=\mathbf{1},\hfill \end{array}$$ (21)

where ${\mathcal{D}}_{\mu {\tau }_{\tilde{\mathbf{Z}}}^{\mathbf{k}}}(\cdot )$ denotes the proximal operator of the nuclear norm (with the details provided in the online Supplementary Materials) [55], and ${\nabla }_{\tilde{\mathbf{Z}}}\text{F}(\cdot ,\cdot )$ can be calculated as:

$$\begin{gathered} {\nabla }_{\tilde{\mathbf{Z}}}\text{F}\left(\tilde{\mathbf{Z}},{\tilde{\mathbf{W}}}^{k-1}\right) \\ =\{\begin{array}{ll}\{\left({\tilde{\mathbf{Z}}}_{\mathbf{X}}-\mathrm{\Phi }(\mathbf{X})\right)& \\ +\beta {\widehat{\mathbf{W}}}^{k-1}\left({\left({\tilde{\mathbf{W}}}^{k-1}\right)}^{\text{T}}\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}};\mathbf{1}\right]-{\tilde{\mathbf{Z}}}_{\mathbf{Y}}\right)\},& (i,j)\in \mathrm{\Delta }\mathbf{X}\\ \{-\gamma {\mathbf{Y}}_{ij}/\left(\exp \left({\tilde{\mathbf{Z}}}_{ij}\cdot {\mathbf{Y}}_{ij}\right)+1\right)& \\ +\beta \left({\tilde{\mathbf{Z}}}_{ij}-{\left({\left({\tilde{\mathbf{W}}}^{k-1}\right)}^{\text{T}}\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}};\mathbf{1}\right]\right)}_{ij}\right)\},& (i,j)\in {\mathbf{\Omega }}_{\mathbf{Y}}\\ \beta \left({\tilde{\mathbf{Z}}}_{ij}-{\left({\left({\tilde{\mathbf{W}}}^{k-1}\right)}^{\text{T}}\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}};1\right]\right)}_{ij}\right),& (i,j)\in {\mathbf{\Omega }}_{\mathbf{Y}}^C\\ 0,& \text{otherwise}\end{array} \end{gathered}$$ (22)

where ΔX denotes the index set of elements in ${\tilde{\mathbf{Z}}}_{\mathbf{X}}$, ${\widehat{\mathbf{W}}}^{k-1}$ denotes the first h rows of ${\widehat{\mathbf{W}}}^{k-1}$, and ${\mathbf{\Omega }}_{\mathbf{Y}}^C$ denotes the index set of unknown labels in Y. Also, the variables ${\widehat{\mathbf{W}}}^k$ in Eq. (20b) can be analytically solved by:

$${\tilde{\mathbf{W}}}^k={\mathcal{J}}_{\lambda {\tau }_{\tilde{\mathbf{W}}}^{\mathbf{k}}}\left({\tilde{\mathbf{W}}}^{k-1}-{\tau }_{\tilde{\mathbf{W}}}^{\mathbf{k}}{\nabla }_{\tilde{\mathbf{W}}}\text{F}\left({\tilde{\mathbf{Z}}}^k,{\tilde{\mathbf{W}}}^{k-1}\right)\right)$$ (23)

Algorithm 1.

Proposed MNMC Algorithm

Input: Matrices X, Y, and parameters h, δ, λ,μ, γ, β.

Output: ${\tilde{\mathbf{W}}}^{opt}$, ${\tilde{\mathbf{Z}}}^{opt}$

1 Compute Φ(X) according to Eq. (9);

2 Initialize ${\tilde{\mathbf{W}}}^0$ as the zeroes matrix, and ${\tilde{\mathbf{Z}}}^0$ as the rank 1 approximation of [Y;Φ(X);1] with the unobserved entries set to 0;

3 While not converged do

4  Update ${\tilde{\mathbf{Z}}}^k$ according to Eq. (21);

5   Update ${\tilde{\mathbf{W}}}^k$ according to Eq. (23);

6 End while;

7 Return ${\tilde{\mathbf{W}}}^{opt}\leftarrow {\tilde{\mathbf{W}}}^k$, ${\tilde{\mathbf{Z}}}^{opt}\leftarrow {\tilde{\mathbf{Z}}}^k$.

where ${\mathcal{J}}_{\lambda {\tau }_{\tilde{\mathbf{W}}}^{\mathbf{k}}(\cdot )}$ denotes the proximal operator of l_2,1-norm (with the details provided in the online Supplementary Materials) [56], and ${\nabla }_{\tilde{\mathbf{W}}}\text{F(}\cdot \text{,}\cdot \text{)}$ can be calculated as:

$${\nabla }_{\tilde{\mathbf{W}}}\text{F}\left({\tilde{\mathbf{Z}}}^k,\tilde{\mathbf{W}}\right)=\beta \left[{\tilde{\mathbf{Z}}}_{\mathbf{X}}^k;\mathbf{1}\right]\left({\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}}^k;\mathbf{1}\right]}^{\text{T}}\tilde{\mathbf{W}}-{\left({\tilde{\mathbf{Z}}}_{\mathbf{Y}}^k\right)}^{\text{T}}\right)$$ (24)

Based on the aforementioned analysis, the proposed algorithm can be summarized as in Algorithm 1.

Theoretically, for nonconvex non-smooth problems with the separable non-smooth terms, Xu and Yin [28] have demonstrated that the BPL method is guaranteed to converge to a critical point, as long as ${\nabla }_{{\mathbf{X}}_i}\text{F}\left({\mathbf{X}}_{<i}^{\mathbf{k}},{\mathbf{X}}_i,{\mathbf{X}}_{>i}^{\mathbf{k}-\mathbf{1}}\right)$, i = 1, · · ·, s, has Lipschitz continuity constant $L_{{\mathbf{X}}_i}^{\mathbf{k}}$ with respect to variable X_i, i.e.,

$$\begin{gathered} {\Vert {\nabla }_{{\mathbf{X}}_i}\text{F}\left({\mathbf{X}}_{<i}^{\mathbf{k}},\mathbf{U},{\mathbf{X}}_{>i}^{\mathbf{k}-\mathbf{1}}\right)-{\nabla }_{{\mathbf{X}}_i}\text{F}\left({\mathbf{X}}_{<i}^{\mathbf{k}},\mathbf{V},{\mathbf{X}}_{>i}^{\mathbf{k}-\mathbf{1}}\right)\Vert }_F \\ \le L_{{\mathbf{X}}_i}^{\mathbf{k}}\Vert \mathbf{U}-\mathbf{V}{\Vert }_F,\forall \mathbf{U},\mathbf{V}\in {\mathbf{R}}^{m\times n}. \end{gathered}$$ (25)

For our MNMC model, we can easily see that the objective function in Eq. (19) has the two separable non-smooth terms, i.e., ${\text{R}}_1{(\tilde{\mathbf{Z}})}^1$ and ${\text{R}}_2(\tilde{\mathbf{W}})$, and it is easy to verify that ${\nabla }_{\tilde{\mathbf{Z}}}\text{F}\left(\tilde{\mathbf{Z}},{\tilde{\mathbf{W}}}^{k-1}\right)$ and ${\nabla }_{\tilde{\mathbf{W}}}\text{F}\left(\tilde{\mathbf{Z}},\tilde{\mathbf{W}}\right)$ are Lipschitz continuous with constants $L_{\tilde{\mathbf{Z}}}^{\mathbf{k}}$ and $L_{\tilde{\mathbf{W}}}^{\mathbf{k}}$ (with the details provided in the online Supplementary Materials):

$$\begin{gathered} L_{\tilde{\mathbf{Z}}}^{\mathbf{k}}=max\{\sqrt{4{\sigma }_1^2\left(\beta {\widehat{\mathbf{W}}}^{k-1}\right)+4{\beta }^2+{\gamma }^2/8}, \\ \sqrt{2+4{\sigma }_1^2\left(\beta {\widehat{\mathbf{W}}}^{k-1}{\left({\widehat{\mathbf{W}}}^{k-1}\right)}^{\text{T}}\right)+4{\sigma }_1^2\left(\beta {\left({\widehat{\mathbf{W}}}^{k-1}\right)}^{\text{T}}\right)}\} \end{gathered}$$ (26)

$$L_{\tilde{\mathbf{W}}}^{\mathbf{k}}={\sigma }_1\left(\beta \left[{\tilde{\mathbf{Z}}}_{\mathbf{X}}^k;\mathbf{1}\right]{\left[{\tilde{\mathbf{Z}}}_{\mathbf{X}}^k;\mathbf{1}\right]}^{\text{T}}\right).$$ (27)

Based on this fact, our proposed optimization algorithm also has the provable convergence, and the concrete convergence analysis is the same as in [28].

IV. Results

A. Experimental Setting

Due to the limited number of samples, we use 10-fold cross validation to evaluate the performance of MGMT and IDH1 status prediction. Specifically, we randomly partition the whole dataset into 10 roughly equivalent subsets, and then successively select each subset as the testing data and assemble the remaining subsets as the training data. This process is independently repeated for 20 times, and the average accuracy (ACC), average sensitivity (SEN), average specificity (SPE) and the average area under receiver operating characteristic curve (AUC) are reported as the final performance measures. Specifically, the average ACC, SEN, and SPE are obtained by averaging all the 20 ACC, SEN, and SPE scores across the 20 trials, respectively, while the average AUC is obtained by computing AUC once based on all prediction scores of 20 trials. To this end, we label the subjects with MGMT-m and IDH1-m statuses as “positive” samples (favorable prognosis), and those with MGMT-u and IDH1-w as “negative” samples (unfavorable prognosis).

In our experiments, the proposed MNMC method involves 6 parameters (i.e., h, δ, μ, γ, λ and β) that need to be determined. To this end, we use a two-stage grid searching strategy to determine the optimal values of these parameters. Specifically, we start with conducting the first-stage hierarchical optimization-based coarse-grained grid searches on the training data with wide ranges (h ∈ {1000, 2000, 3000, 4000, 5000}, δ, μ, γ, λ, β ∈ {0.0001, 0.001, 0.01, 0.1, 1, 10, 20, 30, 50, 100}) to explore the bounds of the search spaces. For each parameter, we use 10-fold cross-validation with 20 repetitions to evaluate the average prediction performance (i.e., accuracy, ACC) by varying its value while fixing the other five parameters (i.e., h is fixed as 3000, and δ, μ, γ, λ, β are fixed as 1, respectively), so that we can select a narrowed parameter range with a relatively better ACC as the new search bounds in the second-stage fine-grained optimizations. Based on this principle, we can determine the search bounds of 5 parameters as follows: δ ∈ [0.01, 10], μ ∈ [0.001, 0.1], γ ∈ [0.1, 20], λ ∈ [0, 20] and β ∈ [1,30]. Exceptionally, for parameter h, we observed that, with its increase from 3000 to 5000, the ACC increased slightly; however, the computation cost increased significantly. Therefore, in order to balance the performance and computation complexity, we select its search bounds as [1000, 3000]. After that, to further determine the optimal parameter values, we conduct the second-stage global optimization-based fine-grained grid searches with the following ranges: h ∈ {1000, 1500, 2000, 2500, 3000}, δ ∈ {0.01, 0.05, 0.1, 0.5, 1, 10}, μ ∈ {0.001, 0.01, 0.02, 0.04, 0.06, 0.08, 0.1}, γ ∈ {0.1, 0.5, 1, 5, 10, 15, 20}, λ ∈ {0, 2, 4, 6, 8, 10, 20}, and β ∈ {1, 5, 10, 15, 20, 25, 30}. Specifically, we conduct another 10-fold cross validation with 20 repetitions on the training data to evaluate the average ACC with each combination of the above parameter values; those leading to the best ACC are used to construct the optimal MNMC model. Finally, the constructed optimal model is applied to the testing data.

B. Competing Methods

To validate the effectiveness of our proposed method, we have performed extensive experiments by also comparing with five different competing methods, including two widely-used classic methods (RF [57] and kernel Transductive SVM (TSVM) [58]) and three state-of-the-art matrix completion methods (MTMC [23], MIMC [27], and NTMC [32]). Table II summarizes the five competing methods and our proposed MNMC method with the characteristics of linear/nonlinear classification setting, inductive/transductive learning scheme, single-label/multi-label classification mode, and adaptive feature selection strategy. All the involved parameters in these competing methods are optimized by using the same nested 10-fold cross-validation procedure as in our MNMC model. Specially, for RF method, we conduct grid search for the number of decision trees from the range {10, 20, 50, 100, 200, 300, 400, 500}, the number of predictors from the range {2, 5, 10, 20, 50, 100, 150, 200}, and the minimum number of observations per tree leaf from the range {1, 2, 3}; For TSVM method, we conduct grid search for the regularization parameter from the range {0.00001, 0.0001, 0.001, 0.01, 0.1, 1, 10}, and the RBF kernel (variance) parameter from the range {0.01, 0.05, 0.1, 0.5, 1, 5}; For MTMC and MIMC methods, we conduct grid search for those counterpart parameters with the same ranges as our MNMC method. For NTMC model, we conduct a grid search for the regularization parameter and the RBF kernel (variance) parameter with the same range as TSVM, and the decomposition size with the range {2, 3, 4, 5}. In addition, since our proposed MNMC, MIMC and RF have the inline adaptive feature selection function, to make a fair comparison, for those methods without feature selection, we adopt the popular feature selection methods to help them remove irrelevant or redundant features. Specifically, the LASSO (Least Absolute Shrinkage and Selection Operator) [59] is employed to facilitate the single-task TSVM method. Also, the semi-supervised multi-task feature selection method proposed by Li et al. [33] is employed to facilitate multi-task MTMC and NTMC methods.

Table II.

Comparison of Characteristics for the Competing Methods

	RF	TSVM	MTMC	NTMC	MIMC	MNMC
Linear classification setting	⎷	×	⎷	×	⎷	×
Nonlinear classification setting	×	⎷	×	⎷	×	⎷
Inductive learning scheme	⎷	×	×	×	⎷	×
Transductive learning scheme	×	⎷	⎷	⎷	⎷	⎷
Single-label classification mode	⎷	⎷	×	×	×	×
Multi-label classification mode	×	×	⎷	⎷	⎷	⎷
Adaptive feature selection strategy	⎷	×	×	×	⎷	⎷

C. Prediction Results

First, we evaluate MGMT/IDH1 status prediction performance using features from single modality, i.e., based on CL, SC, and FC features, separately. Table III reports the experimental results of the five competing methods and our proposed method, where the best results are highlighted. From Table III, we can see that, except that the TSVM achieves higher SEN than our proposed MNMC method (i.e., 72.3% vs. 70.8%) in IDH1 status prediction using SC features, the MNMC consistently outperforms all other competing methods (i.e., RF, TSVM, MTMC, NTMC and MIMC) in almost all performance metrics. The results indicate that our proposed nonlinear feature transformation and transductive multi-task feature selection strategies can improve the performance of MGMT and IDH1 status prediction.

Table III.

Comparison of Prediction Performance for the Competing Methods Using Single Modality (std: Standard Deviation)

Feature	Method	MGMT-m vs. MGMT-u					IDHl-m vs. IDHl-w
		ACC (%)	SEN (%)	SPE (%)	AUC		ACC (%)	SEN (%)	SPE (%)	AUC
		Mean ± std	Mean ± std	Mean 1 std	Mean	p-value	Mean ± std	Mean ± std	Mean 1 std	Mean	p-value
CL	RF	60.4 ± 2.5	65.4±3.1	54.0 ± 3.5	0.685	<0.001	72.6 ± 1.9	60.8 ± 4.3	77.3 ± 2.1	0.795	<0.001
	TSVM	61.7 ± 2.4	66.5 ±2.5	55.5 ±3.9	0.641	<0.001	73.5 ± 1.8	52.3 ±3.2	81.9 ±2.0	0.741	<0.001
	MTMC	60.9 ± 2.0	61.2±1.7	60.5 ±3.9	0.624	<0.001	72.4± 1.6	48.5 ±3.6	81.8 ±2.2	0.739	<0.001
	NTMC	62.4 ± 2.1	66.5±3.1	57.0±3.0	0.644	<0.001	74.1 ± 1.9	54.6 ± 4.3	81.8 ±2.2	0.765	<0.001
	MIMC	61.2 ± 1.3	61.3±2.3	61.0±2.1	0.655	<0.001	72.7 ± 1.7	59.2 ± 3.6	78.0 ± 2.4	0.790	<0.001
	MNMC	65.7 ± 1.1	67.7±2.9	63.0±3.0	0.705	-	76.5 ± 1.5	61.5 ± 4.3	82.4 ± 1.9	0.822	-
SC	RF	61.512.2	60.0±4.5	63.5 ± 5.1	0.635	<0.001	72.8 ± 2.1	57.7 ±3.9	78.8 ± 2.9	0.783	<0.001
	TSVM	63.3 ± 1.9	68.1±2.5	57.0±2.5	0.648	<0.001	74.6 ± 2.0	72.3 ±3.9	75.5 ± 2.4	0.803	<0.001
	MTMC	62.8 ± 2.0	63.5±2.3	62.0±3.4	0.664	<0.001	74.8 ± 1.9	63.8 ±3.6	79.1 ± 2.6	0.805	<0.001
	NTMC	64.4 ± 1.8	68.9±2.5	58.5 ±2.9	0.638	<0.001	76.1 ± 1.7	66.9 ± 3.6	79.7 ± 2.4	0.820	<0.001
	MIMC	63.4 ± 1.3	64.0±1.9	62.5 ±3.0	0.671	<0.001	74.1 ± 1.4	61.5 ±4.3	79.1 ± 1.4	0.806	<0.001
	MNMC	68.3 ± 1.3	70.0±1.6	66.0±3.1	0.702	-	80.4 ± 1.2	70.8 ± 4.7	83.3 ± 1.6	0.864	-
FC	RF	64.1 ± 2.2	70.0 ± 3.0	56.5 ± 2.9	0.665	<0.001	73.5 ± 1.8	78.5 ±4.0	71.5 ± 1.9	0.835	<0.001
	TSVM	65.4 ± 2.0	72.7 ±2.8	56.0 ± 4.2	0.663	<0.001	76.1 ± 1.9	81.5 ±3.9	73.9 ± 2.9	0.852	<0.001
	MTMC	66.1 ± 1.6	76.9 ±2.5	52.0 ± 2.5	0.667	<0.001	75.4 ± 1.9	63.9 ±3.6	80.0 ± 2.1	0.808	<0.001
	NTMC	68.5 ± 1.8	77.7±2.7	56.5 ± 2.9	0.721	<0.001	77.6 ± 1.6	77.7 ±3.4	77.6 ± 2.3	0.857	<0.001
	MIMC	67.8 ± 1.5	76.7±2.0	56.3 ± 2.2	0.718	<0.001	75.5 ± 1.6	79.2 ±3.6	74.1 ± 2.7	0.825	<0.001
	MNMC	71.5 ± 1.2	80.8±2.2	59.5±1.5	0.755	-	83.3 ± 1.6	91.5 ± 2.4	80.0 ± 2.3	0.956	-

Second, considering that different modalities could provide complementary information and thus may enhance the prediction performance, we also perform experiments based on multiple modality fusion. We construct a new feature matrix with concatenated CL, FC and SC features at each column. Table IV summarizes the prediction results of the five competing methods and our proposed MNMC method. As expected, the modality fusion can help improve the prediction performance. Our proposed method not only achieves the highest ACC for MGMT (74.6%) and IDH1 (87.0%) prediction, but also consistently outperforms the single-task RF/TSVM and the multi-task MTMC/NTMC/MIMC in terms of SEN and AUC.

Table IV.

Comparison of Prediction Performance for the Competing Methods Using Multiple Modalities (std: Standard Deviation)

Method	MGMT-m vs. MGMT-u					IDHl-m vs. IDHl-w
	ACC (%)	SEN (%)	SPE (%)	AUC		ACC (%)	SEN (%)	SPE (%)	AUC
	Mean ± std	Mean ± std	Mean 1 std	Mean	p-value	Mean ± std	Mean ± std	Mean 1 std	Mean	p-value
RF	67.8 ± 2.1	71.5 ±4.6	63.0 ± 5.7	0.707	<0.001	73.7 ± 2.2	60.8 ± 4.9	78.8 ± 2.2	0.750	<0.001
TSVM	69.6 ± 2.0	78.1 ±3.1	58.5 ± 3.7	0.734	<0.001	80.4 ± 1.6	70.8 ± 4.0	84.2 ±2.1	0.864	<0.001
MTMC	68.9 ± 2.1	71.5 ±2.3	65.5 ± 3.6	0.732	<0.001	76.1 ±2.1	69.2 ± 5.6	78.8 ± 2.4	0.797	<0.001
NTMC	71.3 ± 1.8	78.9 ±2.3	61.5 ±3.3	0.732	<0.001	82.6 ± 1.6	84.6 ± 4.3	81.8 ± 1.7	0.874	<0.001
MIMC	71.7 ± 1.6	73.1 ±3.3	70.0 ±4.0	0.772	<0.001	83.3 ± 1.4	84.6 ± 4.3	82.7 ± 2.0	0.885	>0.05
MNMC	74.6 ± 1.4	79.2 ± 1.9	68.5 ± 2.9	0.787	-	87.0 ± 1.4	92.3 ± 4.3	84.9 ± 1.4	0.886	-

Third, we also investigate the prediction performance when applying the proposed MNMC method to the only 45 subjects with both known MGMT and IDH1 statuses (indicated by ‘MNMC(45)’), and applying it to the two binary classification tasks separately (indicated by ‘MNMC(S)’). Table V reports the experimental results of the MNMC method with the three different experimental settings, i.e., MNMC, MNMC(45), and MNMC(S). From Table V, we can observe (1) the MNMC(45) method consistently outperforms the classic methods (RF and TSVM) in all performance metrics, and it also obtains a comparable prediction performance with the MNMC method applied to all 47 subjects, and (2) the MNMC(S) method obtains a lower prediction performance than the MNMC method applied to the two binary classification tasks simultaneously, but outperforms the classic methods applied to the two binary classification tasks separately. The results further validated that our proposed MNMC model can effectively exploit the potential relationship between the two molecular indicators (i.e., MGMT and IDH1) to improve the overall prediction performance.

Table V.

Comparison of Prediction Performance for the Competing Methods and Our Proposed MNMC Method Under the Three Different Experimental Settings Using Multiple Modalities (std: Standard Deviation)

Method	MGMT-m vs. MGMT-u					IDHl-m vs. IDHl-w
	ACC (%)	SEN (%)	SPE (%)	AUC		ACC (%)	SEN (%)	SPE (%)	AUC
	Mean ± std	Mean ± std	Mean 1 std	Mean	p-value	Mean ± std	Mean ± std	Mean 1 std	Mean	p-value
RF	67.8 ± 2.1	71.5 ±4.6	63.0 ± 5.7	0.707	<0.001	73.7 ± 2.2	60.8 ± 4.9	78.8 ± 2.2	0.750	<0.001
TSVM	69.6 ± 2.0	78.1 ±3.1	58.5 ±3.7	0.734	<0.001	80.4 ± 1.6	70.8 ± 4.0	84.2 ±2.1	0.864	<0.001
MNMC(45)	74.4 ± 1.3	79.4 ± 1.9	67.6 ± 2.6	0.779	>0.05	86.8 ± 1.5	91.5 ±4.9	84.8 ± 1.8	0.882	>0.05
MNMC(S)	71.9 ± 1.8	75.2 ± 2.9	67.5 ± 3.0	0.753	<0.001	84.4 ± 1.5	85.8 ±2.8	83.8 ±1.8	0.875	<0.01
MNMC	74.6 ± 1.4	79.2 ± 1.9	68.5 ± 2.9	0.787	-	87.0 ± 1.4	92.3 ± 4.3	84.9 ± 1.4	0.886	-

MNMC is the proposed method applied to all 47 subjects; MNMC(45) is the proposed method applied to the 45 subjects who had the complete data; MNMC(S) is the proposed method applied to two binary genomic status classification tasks separately.

In addition, to check the statistical significance of our results, we further conduct Delong’s test [60] at 95% confidence level between AUC values of our proposed method and the competing methods, with the corresponding p-values shown in Table III, Table IV, and Table V. DeLong’s test is a widely-used nonparametric statistical approach to the analysis of areas under correlated ROC curves, which can be employed to assess statistical significance by using the theory on generalized U-statistics to generate an estimated covariance matrix [61]–[63]. The results indicate that, except that our method is marginally significantly better than MIMC (with p-value = 0.079) in IDH1 status prediction using multiple modalities, our method is statistically superior to all other competing methods in terms of AUC.

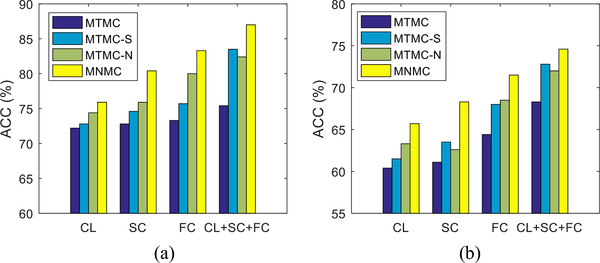
D. Effects of the Proposed Strategies

The main argument in our work is that the nonlinear feature transformation and the transductive multi-task feature selection strategies can advance the linear separability of the data and adaptively select a small set of crucial features across the related tasks, respectively, and thus reduce the prediction errors of MGMT/IDH1 statuses. To validate the effects of these two strategies, we further carry out some experiments to compare our proposed MNMC method that considers only one of the two strategies. Specifically, we use the “MTMC-S” to indicate the counterpart with only the transductive multi-task feature selection strategy, i.e., the MNMC model with Φ(·) being the identity function. On the other hand, we use “MTMCN” to indicate the counterpart with only the nonlinear feature transformation, i.e., the MNMC method with parameters λ = 0 and β = 0.

We present experimental results of the counterpart methods and our proposed method in Fig. 3. For better understanding, we also present the performance of MTMC as baseline method that does not consider any of the two strategies. From the two graphs in Fig. 3, we can observe (1) a method that utilizes any of the two strategies is still better than the MTMC baseline method, and (2) the inclusion of both strategies into the objective function is better than the inclusion of just one strategy.

Fig. 3.

Comparison of prediction performance (%) of the MNMC and its counterparts without nonlinear feature transformation (MTMC-S), multi-task feature selection (MTMC-N), and both (MTMC). (a) IDH1-m vs. IDH1-w (b) MGMT-m vs.MGMT-u.

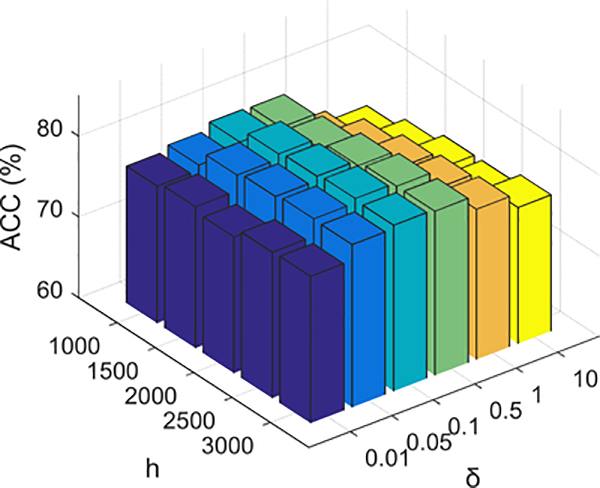
E. Sensitivity Analysis of Parameters

Next, we investigate the sensitivity of the proposed MNMC method to the parameter setting. There are six different parameters (i.e., h, δ, μ, γ, λ, β) that need to be determined in our method. Considering that parameters h and δ, which determine the nonlinear feature mapping in Eq. (7), are relatively independent to other four parameters, we design a set of experiments to investigate how these two parameters jointly affect the prediction performance of MNMC. Fig. 4 reports the average ACC of both the MGMT and IDH1 status predictions, with varying h and δ by fixing the other four parameters, i.e., μ = 0.04, γ = 10, λ = 8, β = 10. As shown in Fig. 4, the optimal working point of our proposed method is at h = 2500 and δ = 0.1. We also notice that the working point is on a relatively flat part of the performance surface, implying that our proposed method is not very sensitive to the variations of the parameters h and δ around the optimal working point.

Fig. 4.

Sensitivity analysis of parameters h and δ in our proposed MNMC method.

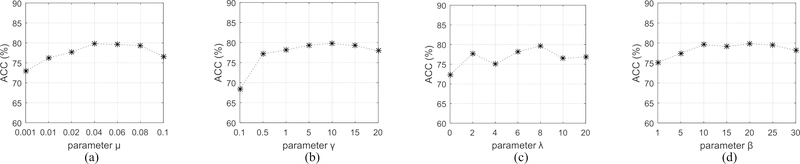
On the other hand, we also carry out four sets of experiments to explore the sensitivity of parameters μ, γ, λ and β, respectively. Fig. 5 reports the average ACC of both the MGMT and IDH1 status predictions, with varying μ, γ, λ and β, respectively, when fixing the other parameters. First, we can observe that the performance is relatively stable if the parameters μ, γ and β respectively falls in a certain range (i.e., μ ∈ [0.04, 0.08], γ ∈ [5, 15], β ∈ [10, 25]), and the performance deteriorates when they fall outside of the range. Second, we observe that the performance is largely affected by the value of λ, suggesting the importance of selecting the optimal λ value for MGMT and IDH1 status predictions. This is reasonable since the parameter λ controls the sparsity of the weight matrix and hence determines the scale of the optimal feature subset. Finally, Fig. 5(c) shows that the prediction accuracy with feature selection (i.e., λ > 0) is better than the counterpart without feature selection (i.e., λ = 0), demonstrating again the importance of feature selection.

Fig. 5.

Sensitivity analysis of the parameters μ, γ, λ and β in our proposed MNMC method. (a) ACC performance w.r.t.μ. (b) ACC performance w.r.t. γ. (c) ACC performance w.r.t. λ. (d) ACC performance w.r.t. β.

V. Conclusion

In this paper, we aim to predict MGMT and IDH1 statuses for HGG patients. Considering that the available imaging data are constrained in size and have a complex feature-to-label relationship, we propose a novel multi-label nonlinear classification model within a transductive learning framework, i.e., Multi-label Nonlinear Matrix Completion (MNMC) model, to address this task. Compared with the conventional MTMC model, the proposed MNMC not only addresses the limitation of linear classification setting by lifting the original features to a more possible linearly separable nonlinear feature space, but also conducts a transductive multi-task feature selection to refine the predictions of MGMT and IDH1 statuses for the testing subjects. Finally, in order to validate our proposed method, we conduct extensive experiments using 47 subjects with both the DTI and RS-fMRI imaging data and the incomplete MGMT/IDH1 statuses. The promising results verify the advantages of our proposed MNMC method over the widely-used single-task or multi-task classifiers. Also, for the first time, we show the feasibility of MGMT and IDH1 status prediction based on the preoperative multi-modality neuroimaging and connectomics analysis.

However, this study still has some limitations. First, larger patient populations with more heterogeneous data origins are needed to investigate the generalizability and robustness of our proposed method. Second, our proposed MNMC model is able to deal with the missing values in the label matrix, but cannot handle the missing values in the feature matrix. Future work will focus on extending our proposed MNMC model to handle the missing features, and integrate other useful sources of information for improving the prediction performance of MGMT and IDH1 statuses. Finally, based on RS-fMRI, other FC metrics such as partial correlation-based FC can be extracted as additional features. Note that partial correlation is also widely used in functional network construction and has been suggested to measure mainly the direct and effective connectivities [64], [65]. It could supplement the Pearson’s correlation-based FC to achieve better prediction, which will be our future work.