Pressure-induced spin transition and site-selective metallization in CoCl₂

Abstract

The interplay between spin states and metallization in compressed CoCl₂ is investigated by combining diffraction, resistivity and spectroscopy techniques under high-pressure conditions and ab-initio calculations. A pressure-induced metallization along with a Co²⁺ high-spin (S = 3/2) to low-spin (S = 1/2) crossover transition is observed at high pressure near 70 GPa. This metallization process, which is associated with the p-d charge-transfer band gap closure, maintains the localization of 3d electrons around Co²⁺, demonstrating that metallization and localized Co²⁺ -3d low-spin magnetism can coexist prior to the full 3d-electron delocalization (Mott-Hubbard d-d breakdown) at pressures greater than 180 GPa.

Introduction

Pressure-induced structural phenomena have received considerable attention in transition-metal (M) dihalides and oxides MX₂ (X: Cl, Br, F, O) due to their ample and subtle polymorphism^1–20 and their intriguing electronic properties associated with changes of metal coordination, spin state, and/or insulator-metal transition. Most MX₂ are antiferromagnetic Mott insulators²¹ that present strong d-d electron-electron correlation²². The breakdown of the Mott-Hubbard d-d or charge-transfer d-p electron correlation leading to a metallization, concurrent with a collapse of magnetism via electron delocalization, is the typical pressure-induced electronic/magnetic behavior. These phenomena involve external pressures that induce a large crystal-field strength at M, causing the high-spin to low-spin (HS-LS) transition^1,23–25. In fact, spin crossover (SCO) is often portrayed as a trigger for metallization either by volume collapse^22,25, or as a result of the ground-state change from HS to LS^22–24. Nevertheless, the coupling between structure, spin state, and electron delocalization (Mott-Hubbard metal-insulator transition) governing the electronic properties in MX₂ requires clarification. The access to both electronic ground and excited states via optical spectroscopy at high pressure, combined with the modelling of the electronic properties through ab initio calculations and precise crystal structure determination and resistivity measurements, can provide a definitive description of electronic phenomena in compressed MX₂ systems.

Pressure-induced transformations in MX₂ involve a large variety of energetically-equivalent dense structures, which are characterized either by an increase of the M coordination number^11,20, or by stacking up dense MX₂ layers keeping the metal coordination^14,26, depending on the metal/ligand ionic radii ratio. Due to their simple structure, phase diagrams of crystals in the MX₂ family show common features regarding the coordination polyhedra and the stacking sequence. This distinct structural behavior has important implications in their electronic properties, which are substantially modified upon compression. Besides, these studies of MX₂ under pressure are of importance in geophysics to understand polymorphism in the Earth’s interior, where SiO₂ plays an important role^27–29.

CoCl₂ is an attractive system for studying combined structural and electronic effects because the octahedral coordination of Co²⁺ (3d⁷) is thought to be stable in a wide pressure range^{13–15,26,30}, which enables us to exclude the physics coming from the coordination number changes. Besides, this system has a relatively small energy difference between its HS and LS phases³¹, and the SCO of the system can be observed in a very  accessible pressure regime. Furthermore, it is the member of the MCl₂ series (M: Cr, Mn, Fe, Co) where SCO is expected to take place at the lowest pressure. In addition, SCO phenomena involving transition-metal ions with 3d⁷ electronic configuration are very scarce. Thus, this system can be a good model system to explore the various origins of SCO and to give answer to questions such as whether the pressure-induced LS states (t⁶e¹ configuration) originate from large crystal-field effects enhanced by the Jahn-Teller effect associated with LS configuration, or from the metallization, which can be induced either by the p-d charge-transfer gap closure or breakdown of d-d Mott-Hubbard correlation.

Here we report on the stability of the Co²⁺ coordination under compression in CoCl₂, and the relationship between SCO, crystal structure, and metallization. In order to achieve these goals we perform a combined experimental and theoretical study using optical absorption, Raman spectroscopy, X-ray diffraction (XRD) and resistivity under pressure, and first-principles Density Functional Theory (DFT) calculations.

Results

The Co²⁺ (3d⁷) Tanabe-Sugano diagram describing the electronic states’ energy in terms of the octahedral crystal field (in Racah parameter B units, Fig. 1) shows that, for CoCl₂ (B ≈ 80 meV at 50 GPa^15,30), the HS-LS (⁴T₁, S = 3/2 → ²E, S = 1/2) transition should occur at Δ_SCO = 1.7 eV. Importantly, the LS state may be affected by a strong Jahn-Teller effect, providing an additional lattice relaxation energy which, in principle, could reduce the SCO crystal-field strength triggering metallization at unexpectedly low pressure^19,30. Alternatively, high pressure could, in turn, suppress the Jahn-Teller distortion causing the HS-LS to occur at higher pressures than expected, or even disappear if CoCl₂ transforms into a fluorite-type structure (d³-like Co²⁺)²⁰.

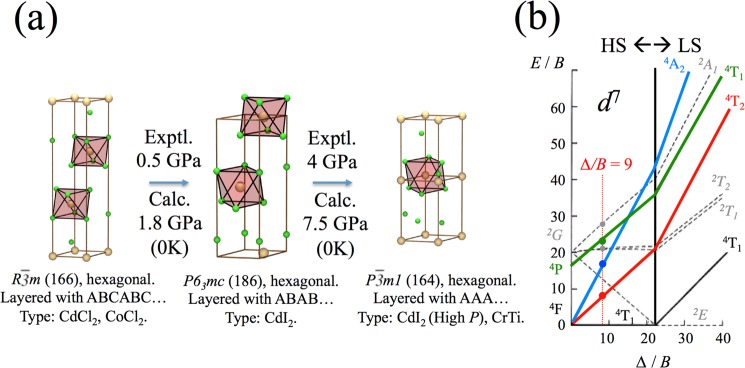
Figure 1.

(a) Structural phase-transition sequence in CoCl₂ under high-pressure conditions determined by density-functional-theory calculations and confirmed experimentally by x-ray diffraction. (b) Simplified Tanabe-Sugano diagram for octahedral Co²⁺ (3d⁷) showing the effect of pressure (i.e. Δ/B) on the excited state energies, and HS-LS crossover (Δ/B = 21). See also Supplementary Figs S1–S9.

XRD shows that CoCl₂ exhibits nearly-degenerate layered structures at ambient conditions. The CoCl₂ pressure-induced phase transition sequence as determined experimentally with support of DFT calculations is indicated in Fig. 1. The three represented layered structures are more stable than the rutile, cotunnite, and fluorite phases at all pressures up to 100 GPa. This result, which is confirmed by both single-crystal and powder XRD experiments at high pressure, demonstrates the stability of the hexagonal layered structure of CoCl₂ and thus the Co²⁺ sixfold coordination in a wide pressure range (0–60 GPa), in a way similar to FeCl₂¹⁴ and MgCl₂²⁶ and contrary to CoF₂^10,20. The stability of the given CoCl₂ structures, which involve the different packing sequence of layers of face-sharing CoCl₆ octahedra, is a consequence of the subtle competition of inter-layer van der Waals interactions. The CoCl₂ equation-of-state can be phenomenologically described by two Murnaghan’s equations: one above and one below 14 GPa (see Supplementary Figs S1–S3).

Figure 2 shows the pressure dependence of the optical absorption spectra of CoCl₂ around the charge-transfer band gap (a) and in the sub-gap Co²⁺ d-d crystal-field region (b). Besides the gap energy, these spectra allow us to determine the excited-state electronic structure in the transparency window of CoCl₂ (≈50 GPa). At ambient conditions, the main sub-gap absorption peaks within the D_3d (nearly O_h) CoCl₆⁴⁻ octahedron^7,8 correspond to crystal-field transitions ⁴T₁(F) → ⁴T₂(F), ⁴A₂(F), and ⁴T₁(P) and are located at 0.79, 1.66 and 2.10 eV, respectively. In terms of the Tanabe-Sugano diagram for d⁷ ions (Fig. 1b)^32,33, the transition energies at ambient pressure correspond to Δ = 0.87 eV and B = 97 meV with Δ/B = 9.0 (see Supplementary Table S1)^15,30,32. According to this diagram the crystal-field strength required to induce the SCO is (Δ/B)_SCO = 21. Interestingly, the SCO also involves crossing of the ⁴T₂(F) and ²T₁(G) excited states, hence these states, which are well observed by optical absorption, can be used to efficiently probe the HS-LS transition.

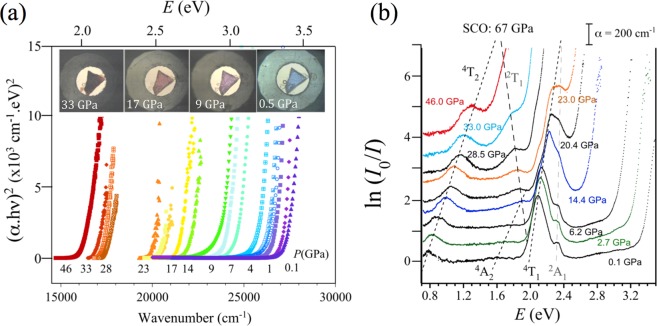
Figure 2.

Pressure dependence of the optical absorption spectrum of CoCl₂. (a) Variation of the charge-transfer absorption threshold in the 0–50 GPa transparency region. The pictures show the piezochromism of CoCl₂. (b) Pressure dependence of the Co²⁺ crystal-field absorption peaks. Peak labeling follows the Tanabe-Sugano diagram of Fig. 1.

The variation of the absorption spectra with pressure shows that the band gap energy decreases linearly with pressure at a rate of −43 meV/GPa (Fig. 3). Such a large shift is responsible for the intense piezochromism exhibited by CoCl₂ (Fig. 2a). The pressure-induced redshift of the bandgap follows a quadratic dependence with the crystal volume yielding gap closure at V = 17.5 ų/Co (V/V₀ = 0.56) – i.e. 80 GPa– (see Supplementary Fig. S5(c)). This redshift is produced by the hybridization enhancement of the Cl⁻-p and Co²⁺-d orbitals with pressure which in turn causes a broadening of the mainly 3p- and 3d-orbital valence band and an energy decrease of the mainly 3d-orbital intermediate band both reducing the p-d charge-transfer bandgap. DFT reproduces the decrease in the band gap of HS state (P < 67 GPa) reasonably well (see Supplementary Fig. 6(c)). The plots of the electron band and density of states certainly show a clear energy delocalization of the d-orbital manifolds with pressure yielding band broadening (see Supplementary Fig. S7(c,d)). Concurrently, the increasing crystal-field energy as obtained from the optical spectra, and the reduction of B from 97 to 82 meV in the 0–50 GPa range yield a Δ/B variation from 9.0 to 18.5, which implies an almost doubled splitting between e and t₂ orbitals, Δ, from 0.87 to 1.52 eV (see Supplementary Table S1 and Fig. S5).

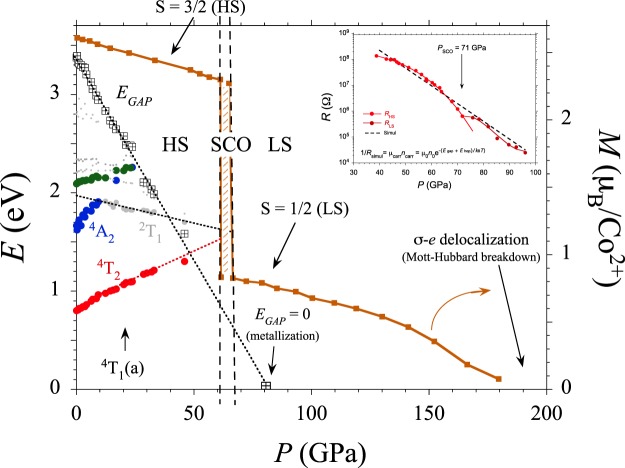
Figure 3.

Variations of the Co²⁺ crystal-field state energy of the ⁴T₁(a) → Γ_i transition and of the charge-transfer band gap energy of CoCl₂ (E_GAP) with pressure. The color of the experimental points (Γ_i) is the same one employed for representing the energy of Γ_i state in the Tanabe-Sugano diagram of Fig. 1. Note that the HS-LS crossover corresponds to the ⁴T₂(F) ↔ ²T₁(G) crossing point, and the p-d band gap closure to E_GAP = 0 (metallization). The continuous curves in brown color are the calculated Co²⁺ local moment within DFT + U method keeping the P$\overline{3}$ m1 phase in the whole pressure range. The HS-LS transition and p-d band gap closure take place at 67 and 80 GPa, respectively, whereas the Mott-transition (σ-electron delocalization) in LS is found for P > 180 GPa (detailed information in Supplementary Figs S4–S7). The inset shows the variation of the electrical resistance of CoCl₂ with pressure, R(P), in a semilog plot. It must be noted that R(P) behaves differently below and after 71 GPa indicating SCO transition. The change of slope above 80 GPa unveils the metallization onset. Linear dashed line corresponds to the least-square fit to R(P) taking the linear variation of p-d charge-transfer band gap, E_GAP, obtained by optical absorption, and a thermal activated hoping term, E_hop(P) associated to the carrier mobility (see also Supplementary Fig. S12).

As Figs 2 and 3 show, the variation of the absorption spectrum and its associated peak energies with pressure reveal that Co²⁺ has a HS state in the crystal transparency range. However, extrapolating the linear dependence of the transition energies with pressure we obtain a HS to LS [⁴T₁(F) ↔ ²E(G)] transition at 67 GPa. It is worth noting that the SCO is observed in the DFT + U results using a Coulomb correlation energy U = 3 eV (Figs 3 and 4). As indicated in the Methods section, this method cannot capture the evolution of the Coulomb correlation parameter upon volume changes and could underestimate the SCO pressure for high pressure regime^31,34,35. However, the essence of the electronic and magnetic properties before and after the transition is valid. The spectroscopic determination of the 3d-electron structure together with the DFT estimates make CoCl₂ a reference system to validate theories dealing with SCO phenomena and metallization processes in transition-metal systems^25,36–43.

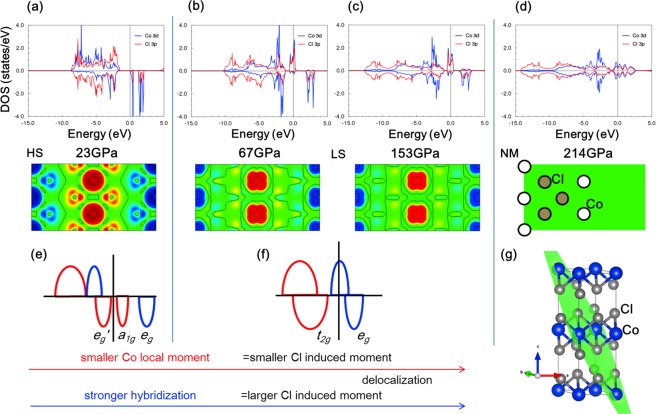
Figure 4.

Total energy DFT + U calculations performed on CoCl₂ (space group P$\overline{3}$ m1) using a Coulomb correlation energy, U = 3 eV. Top panels show the electron DOS projected on the Co²⁺ 3d (blue) and Cl⁻ 3p (red) orbitals at 23 (HS), 67 (LS), 153 (met) and 214 (deloc) GPa (a–d). The corresponding spin density around the Fermi level on the (111) plane is shown in panels below with red and blue denoting up and down spin density. A schematic Co²⁺ 3d bands associated with t_2g (e_e′, a_1g) + e_g in blue and red colors, respectively, illustrates the HS and LS states (e,f). It must be noted that spin density in LS is significantly localized around Co²⁺ whereas it is more delocalized around Cl⁻ in spite the electronic Fermi levels have about the same contributions from Cl⁻-p and Co²⁺-d orbitals (detailed information in Supplementary Figs S7–S10). Note that above 150 GPa, calculated pressures by DFT + U are overestimated as the Coulomb correlation energy was fixed to U = 3 eV. Indeed pressure should be corrected by about 20% in that range if U decreases by 20% due to ultra-high pressure effects. The lattice structure of CoCl₂ is depicted in (g). Note that the green plane is (111) plane for spin density plot.

Figure 3 plots the calculated magnetic moment as a function of pressure. According to DFT calculations, the Co²⁺ magnetic moment abruptly decreases from HS, μ_eff = 2.6 μ_B, to LS, μ_eff = 0.9 μ_B, at around 67 GPa with a hysteresis of 8 GPa. The experimental SCO pressure and the crystal and electronic structures demonstrate that the Jahn-Teller coupling is not involved in the stabilization of the LS ground state, ²E. This contrasts with one of the hypotheses given elsewhere^30,31, that the high-pressure conditions required for SCO could be relaxed by the strong Jahn-Teller effect in the LS ²E state down to 35 GPa if we consider a Jahn-Teller coupling similar to those measured in the CuCl₆ system⁴⁴. The lack of a HS-LS transition at ≈35 GPa in CoCl₂ indicates that the Jahn-Teller effect is unable to distort the Co²⁺ environment in the severe high-pressure conditions required for SCO.

The pressure dependence of the optical gap, E_GAP, allows us to infer that the p-d charge-transfer gap closure (metallization) takes place at 80 GPa. This result is confirmed by electrical resistance measurements under pressure (inset of Fig. 3 and Supplementary Fig. S12). Its pressure dependence R(P) unveils two distinct regions corresponding to HS and LS states. The associated SCO pressure, P_SCO = 70 GPa, is close to that derived from optical absorption. Interestingly, the progressive decrease of R(P) in LS shows a change of slope for P > 80 GPa indicating the metallization onset. Spin density- and DOS simulations indicate that the charges are mainly localized at the Co²⁺ site and small p-d hybridized ones can be observed at Cl⁻ sites for HS. For P > 67 GPa (LS) a progressive decrease of the localized charges at Co²⁺ occurs due to hybridization increase. However, the hybridized spin density spreads out over the entire crystal for P > 80 GPa (E_GAP = 0) in the Cl⁻ plane, while it is strongly localized at Co²⁺, indicating that metallization mainly involves Cl⁻ sublattices rather than the Co²⁺ ones. Furthermore, a full electron delocalization is completed for P > 180 GPa (Fig. 4). This result is noteworthy since it correlates two distinct electronic features: (1) the insulator-to-metal transition involves p-d charge-transfer states and can be induced under compression in close proximity right after the HS-LS transition; (2) Mott-Hubbard d-d electron breakdown should occur for P > 180 GPa. Thus, 3d(e)-electrons still keep their local character at the band-gap closure, albeit pressure-induced progressive delocalization occurs within LS ground state up to approximately 180 GPa, at which delocalization process is completed (Figs 3 and 4).

Conclusions

In summary, with various types of experimental and theoretical approaches, we have thoroughly analysed the physics of the pressure-induced spin-state transition and metallization phenomena in CoCl₂. We have shown that the layered structure of CoCl₂, and hence the Co²⁺ sixfold coordination, is stable in the 0–200 GPa range, in contrast to CoF₂, whose high-pressure phases involve increasing coordination numbers (6 → 8 → 9). We demonstrate that pressure-induced metallization is associated with p-d charge-transfer band gap, closing at about 80 GPa. Although the HS-to-LS transition (67 GPa) can trigger insulator-to-metal transition, DFT calculations also show that after the SCO metallization Co²⁺ preserves the local character of the 3d-electrons and that Mott-Hubbard-electron breakdown takes place for P > 180 GPa in LS. In consequence, this work demonstrates that metallization with involvement of Cl⁻ planes and localized Co²⁺-3d LS magnetism can coexist prior to Mott-Hubbard breakdown in CoCl₂. These results unveil the complex metallization mechanism of CoCl₂ under compression with Cl⁻ and Co²⁺ layers exhibiting site-dependent electrical and magnetic behaviours. Especially, the intermediate phase with metallic magnetism is rarely observed in a system with local moment such as transition metal complexes. We believe these findings provide new insight into unforeseen electronic properties of multilayer 2D systems and highlight the importance of high-pressure studies as a route to novel electronic and magnetic phases.

Methods

Crystal structure: X-ray diffraction

Both single-crystal plates (100 × 80 × 30 μm³) and powder of CoCl₂ (Merck) were used for high-pressure experiments. CoCl₂ crystallizes in the trigonal space group R3m at ambient conditions⁴⁵. The evolution of the crystal structure with pressure was studied by x-ray diffraction (XRD) using the I15 beam station at the DIAMOND synchrotron under proposals 832, 1655 and 6078. The pressure was applied by means of Almax-Boehler and MALTA-type Diamond Anvil Cell (DAC). DACs were loaded with several Ruby spheres (10 μm diameter) as pressure gauge⁴⁶ using helium, silicone oil and paraffin as pressure transmitting media for powder and single crystal XRD experiments (see Supplementary Figs S1–S3).

Optical absorption and Raman spectroscopy

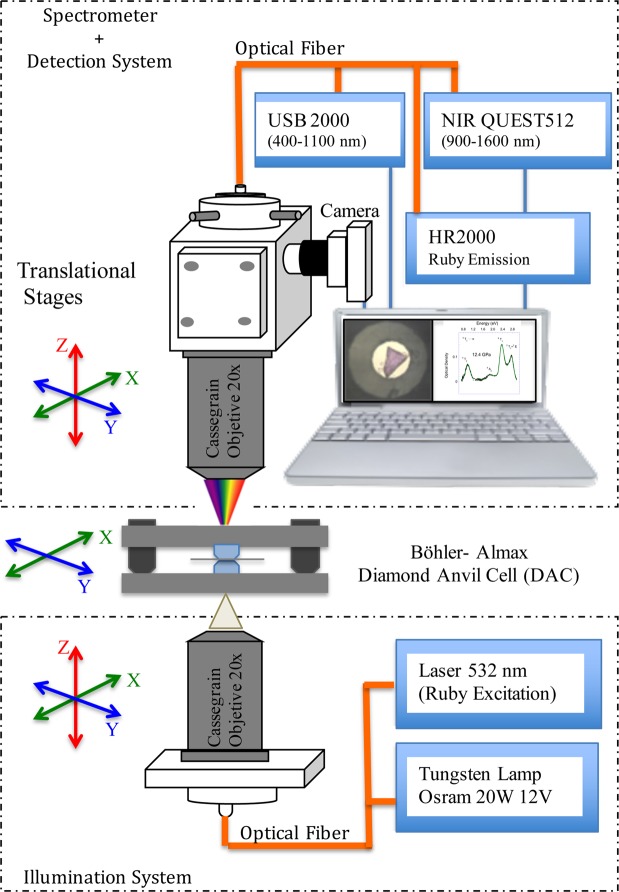
Optical absorption and Raman experiments were performed on single-crystal plates (100 × 80 × 35 μm³) of CoCl₂. The optical spectroscopy experiments were carried out in membrane and Almax-Boehler DACs. 200-μ m-thick Inconel 625 gaskets were preindented to 40 μm. 170-μ m-diameter holes were perforated with a BETSA motorized electrical discharge machine. The DAC was loaded with a CoCl₂ single crystal and ruby microspheres (10 μm diameter) as pressure probes⁴⁶ using silicone oil as pressure-transmitting medium in an argon atmosphere inside a globe box to avoid sample hydration. Optical absorption under high-pressure conditions was performed on a prototype fiber-optics microscope equipped with two 20× reflecting objectives mounted on two independent x -y -z translational stages for the microfocus beam, and the collector objective and a third independent x -y -z translational stage for the DAC holder (Fig. 5). Optical absorption data and images were obtained simultaneously with the same device. Spectra in the UV-VIS and NIR were recorded with Ocean Optics USB 2000 and NIRQUEST 512 monochromators using Si- and InGaAs-CCD detectors, respectively.

Figure 5.

Schematic setup of the microscope adapted for optical absorption with attached diamond anvil cell [Barreda-Argüeso, J. A. and Rodríguez, F. (Patent PCT/ES2014/000049)].

Unpolarized micro-Raman scattering measurements were performed with a triple monochromator Horiba-Jobin-Yvon T64000 spectrometer in subtractive mode backscattering configuration, equipped with a Horiba Symphony liquid-nitrogen-cooled CCD detector. The 514.5-nm and 647-nm lines of a Coherent Innova 70 Ar⁺-Kr⁺ laser were focused on the sample with a 20× objective for micro-Raman, and the laser power was kept below 4 mW in order to avoid heating effects. The laser spot was 20 μm in diameter and the spectral resolution was better than 1 cm⁻¹. The Raman technique was used to check the sample structure through the characteristic first-order modes (A_1g and E_g in the trigonal R$\overline{3}$m CdCl₂-type phase)³⁸ as well as to determine structural phase-transition pressures (see Supplementary Figs S10 and S11 and Table S3). The Raman high-pressure experiments were performed on the same CoCl₂ single crystals employed in the optical absorption measurements.

Electrical measurements at high pressure

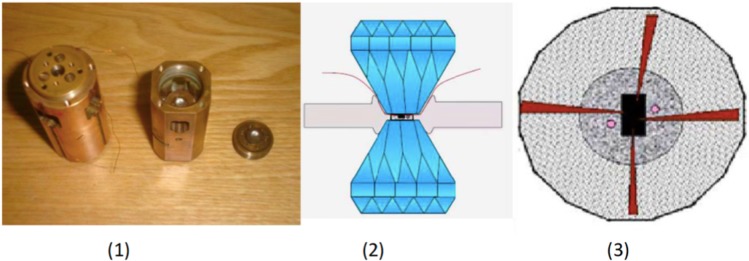
The electrical resistance measurement under pressure up to 96 GPa was performed using diamond anvil cell with solid transmitting medium NaCl (diamond’s culet diameter of 100 μm). Gasket consists of T301 and the insulate layer is cBN. Pressure was determined by ruby fluorescence method at low pressure and the shift of diamond’s Raman peaks. Figure 6 shows a schematic view of the DAC.

Figure 6.

Setup for electrical resistance measuremets under high pressure conditions. (1) Piston-cylinder diamond anvil cell, (2) schematic view of opposite anvils pressing the CoCl₂ sample, and (3) view of the four-points electrical contacts in the CoCl₂ single crystal.

First-principles theoretical calculations

Density functional theory: crystal structure and phase transition

For the description of an accurate phase transition, we have performed total-energy calculations within the framework of dispersion-corrected Density-Functional Theory in the Projector Augmented Wave (PAW) and plane-waves (PW) formulation. The Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional was employed coupled with the exchange-hole dipole moment (XDM) model dispersion correction (damping function parameters a₁ = 0.0000 and a₂ = 3.8036 Å) as implemented in Quantum ESPRESSO. The calculation parameters are: 6 × 6 × 6 Monkhorst-Pack k-point grid, 60 Ry plane-wave cutoff energy, 600 Ry density-cutoff energy and cold smearing with a smearing parameter of 0.05 Ry. Based on previous studies, we considered the following phases of CoCl₂: cotunnite (Pnma, orthorhombic, Z = 4), CaCl₂ (deformed rutile structure, Pnnm, orthorhombic, Z = 2), fluorite (Fm$\overline{3}$ m, cubic, Z = 1), CoCl₂ (R$\overline{3}$ m, rhombohedral, ABCABC stacking), CdI₂ (P6₃ mc, hexagonal, ABAB stacking), ω-phase (P$\overline{3}$ m1, hexagonal, AAA stacking). All CoCl₂ phases were calculated in a range of volumes encompassing the 0–100 GPa range and the internal degrees of freedom (atomic positions and cell shape) were relaxed at each volume.

Density functional theory: spin crossover and metallization

After clarifying structural phase transitions, we identified that the electronic and magnetic transitions occur in P$\overline{3}$ m1 phase. Thus, employing the same symmetry, we investigated the SCO behaviors in detail. We further performed electronic-structure calculations within DFT + U scheme as implemented in Vienna Ab Initio Simulation Package (VASP)⁴⁷. As for layered system, where the van der Waals interactions are important, frequently used generalized gradient approximation (GGA) functionals sometimes fails to predict the correct structural behaviors. We found van der Waals-corrected functions gives better description of the ground state volume such that the errors were 1.6% for many-body dispersion and 2.2% for Tkatchenko-Scheffler methods while D3 approach severely underestimates the volume by 8.2%^31,34,35). From GGA⁴⁸, we found that PBEsol overperforms PBE (3.8% vs. 8.1%) with accuracy similar to van der Waals approach, which enables us to choose PBEsol scheme with safety. Note that in our previous reports, PBEsol successfully explained the spin-state transition behaviors for CoCl₂³¹. We also carefully tested various U parameters and found that U_eff = 3.0 eV fits best in describing the experimental transition behaviors. To obtain the pressure evolution of the electronic structure and magnetic properties, we fully relaxed the atomic positions until the atomic forces are less than 0.001 eV/Å for each volume point. Once the transition volume is found, we have cross-checked the results employing full potential full relativistic code FPLO⁴⁹, and further analyzed its partial density of states (see Supplementary Figs S6–S9).

Author Contributions

All authors reviewed the manuscript. F.R. participated in all parts of the project. J.A.B.-A. and I.H. did the optical absorption and J.G. the Raman spectra as a function of pressure. L.N., I.H., W.H. and A.J. conducted the x-ray diffraction measurements and F.A. collected diffraction data and helped with structure refinement. A.O.R. and V.L. did the DFT calculations for structural refinement and phase transitions, and B.K., K.K. and B.I.M. performed the DFT + U electronic structure calculations for spin crossover and metallization processes. Y.J. and C.J. did the electrical measurements at high pressure. All authors participated in the analysis of data and revised the manuscript.

Data Availability

All data generated or analysed during this study are included in this published article (and its Supplementary Information files).

Competing Interests

The authors declare no competing interests.

Supplementary information

Supplementary information accompanies this paper at 10.1038/s41598-019-41337-4.