Performance of nanofiltration process during concentration of strawberry juice

Abstract

The aim of this study was to evaluate the microfiltration and nanofiltration of strawberry juice. Processes performance was evaluated in terms of resistances-in-series, flux decline modeling and extract quality (maintenance of the phenolic compounds). The results obtained showed that concentration polarization is the main resistance to permeate flux in nanofiltration process, representing around 95% of the total resistance. Microfiltration process suffered more influence of the concentration polarization and fouling, next to 47% for both resistances. For all the processes, Hermia’s pore blocking models presented good fitting, with R² over 0.85. The same behavior was observed for a conjugated model which provided a realistic description (R² > 0.76). Also, nanofiltration process allowed phenolic compounds maintenance, demonstrating the efficiency of this process for strawberry juice concentration.

Introduction

Strawberry is a worldwide consumed fruit because of its attractive color, flavor, high nutritional quality and biological activity against cardiovascular and neurological diseases, cancer and diabetes (Crecente-Campo et al. 2012). Besides of that, it presents great adaptability to climatic conditions, allowing it to be grown in different regions (Antunes and Peres 2013; Ornelas-paz et al. 2013). The worldwide production of strawberry according to FAO (2014) was approximately 4.2 million tons per year, being that only in Brazil the production was approximately 133 thousand tons (Portal do Agronegócio 2014).

This large production presents high perishability, making it necessary to process the in natura fruit to derivative products such as frozen pulps or jelly (Mota 2006). Another alternative is the production of concentrated juices or fruit drinks with high nutritional quality.

The traditional methods for producing fruit juices use high temperatures to inactivate the enzymes and to concentrate the juice (Sui et al. 2016). When using flash evaporation, even if the residence time is low, it is enough to affect the sensorial qualities, such as color, flavor and nutritional quality, such as phenolic and anthocyanin content, resulting in a qualitative decline (Cassano et al. 2007; Sui et al. 2016). Based on this context the study of new technologies that can improve juice quality, as membrane technology, is essential.

One alternative is the processing of the strawberry into concentrated juice by membranes. The main advantages of this process is the high selectivity, lower energy consumption and the use of moderate temperatures resulting in the conservation of thermolabile compounds (Cassano et al. 2007). Nonetheless, membrane incrustation is a major problem to the membrane process due to the reduction of permeate flux. This decline is occasioned by the accumulation of the species on the membrane surface, causing a sharp decline on the permeate flux at the beginning of the process, known as concentration polarization, and then followed by gradual decline; known as the cake layer formation (de Bruijn et al. 2002). The flux decline behavior can vary according to the membrane utilized and is influenced by a number of properties, such as membrane chemistry and morphology and the fluid-dynamic conditions (Riedl et al. 1998).

In order to scale up the systems used for juice concentration, the flux decline behavior must be completely understood. Also, it is important to emphasize that the maintenance of permeate flux and the quality of the concentrate requires periodic cleaning and maintenance, which increases the costs, process time and can damage the membrane (Said et al. 2015).

The flux decline behavior has been accurately predicted by mathematical models proposed by Hermia (1982) for dead-end filtration and modified by Field et al. (1995) for cross-flow filtration. These models describe how the solute particles block the membrane pore, relating four conditions: cake layer, standard pore blocking, complete pore blocking and intermediate pore blocking. According to Salahi et al. (2010) the use of this semi-empirical models can provide an accurate prediction and better understanding of the fouling phenomena.

However, according to Torkamanzadeh et al. (2016) these classical models mentioned above are not able to describe the behavior of the transition between different fouling mechanisms that can occur during membrane filtration, once they are based on a single fouling mechanism. In this sense, Ho and Zydney (2000) developed a model that consider the both pore blockage and cake filtration layer, which must be studied for a complete understanding of the process.

In this context, the objective of this work was to evaluate the membrane efficiency for phenolic compound maintenance and study the flux decline behavior on the processing of strawberry juice using different mathematical models. The mathematical models modified by Field et al. (1995) for cross-flow filtration was applied. Also the conjugated model proposed by Ho and Zydney (2000) was evaluated. The hydraulic permeability of the membrane was measured with regard to the influences of the membrane, polarization of concentration and cake layer resistances.

Materials and methods

Strawberry juice preparation

The juice was prepared with strawberry fruit (Fragaria X ananassa Duch cv. Oso Grande) at high ripeness. The fruits were washed with potable water with the removal of the calyx and sepals. A commercial juicer (Walita 700 W, model RI1855) was used for juice extraction, this product obtained was named in natura juice.

Microfiltration process

This step was performed as an alternative to increase the permeate flux by removing the suspended solids. The microfiltration (MF) was carried out with fixed conditions, which are 20 ± 2 °C and 300 kPa. A polyamide membrane (PAM Selective Membranes, Rio de Janeiro, RJ, Brazil) with pore diameter of 0.4 μm and filter area of 0.7 m² was used. The permeate obtained was named microfiltered juice and was used as feed solution for the nanofiltration step.

Nanofiltration Process

The nanofiltration (NF) process was performed with two different feed solution: (1) in natura juice (NF IN) and (2) microfiltered juice (NF MF). For both experiments a polyvinylidene fluoride (PVDF) membrane (GE Osmonics^®, Philadelphia, USA) with molar mass cut-off between 150 and 300 Da and filtration area of 1.2 m² was used. The assays were performed with operational conditions of 20 ± 2 °C and 600 kPa. The permeate flux (J) (L h⁻¹ m⁻²) was obtained every 5 min with Eq. 1 below:

$$J=V_P/\left(A\ast t\right)$$ 1

where V_p is the permeate volume collected on time t and A is the permeation area.

Total phenolic compounds (FT)

The FT were determined according to method suggested by Singleton and Rossi (1965), using the reaction of the sample with 20% sodium carbonate solution and Folin-Ciocalteu reagent. The solution was left in the dark for 2 h, and the absorbance measured on spectrophotometer (UV–Vis mini-1241) at 765 nm with distilled water as blank. The same procedure was performed for the gallic acid standard and the results were expressed in mg of gallic acid equivalent (GAE) per mL (mg GAE mL⁻¹). The analyses were performed in triplicates.

Determination of resistance-in-series to permeate flux

According to Cheryan (1998) the permeate flux can be related with the permeability coefficient of the membrane, the transmembrane pressure (P) and the fluid viscosity (μ). Considering that the membrane permeability is the inverse of the membrane resistance (R_m) and using filtered water as feed solution, Eq. 2 was obtained.

$$J=P/\left(\mu \ast R_m\right)$$ 2

However, other resistances can appear when a complex solution is used as feed solution, so the membrane resistance is replaced for a total resistance (R_t) as shown in Eq. 3. The total resistance is considered a sum of all the resistances of the system (Eq. 4).

$$J=P/\left(\mu \ast R_t\right)$$ 3

$$R_t=R_m+R_r+R_{\mathit{ir}}$$ 4

These resistances were obtained for MF, NF IN and NF MF. The physical cleaning was performed with filtered water at 45 ± 2 °C during 40 min. The chemical cleaning was performed with NaOH 0.1% circulation at 45 ± 2 °C and 100 kPa during 30 min. Before that, the membrane was left in this solution without circulation during 30 min and then cleaned with filtered water until it reached neutral pH.

Mathematical modelling

On porous membranes, the flux decline could be related to different pore blocking mechanisms that could happen individually or coexisting. In order to study the flux decline for this different pore blocking mechanisms, Hermia (1982) proposed a general equation for dead-end filtration that was modified for cross-flow filtration by Field et al. (1995) and is described on Eq. 5.

$$-dJ/dt\left(J^{n-2}\right)=k\left(J-J^{\ast }\right)$$ 5

where J* is the critical flux which should not be exceeded to avoid the fouling phenomena, being considered in this work as the limit value of the permeate flux on the steady-state condition, k is the phenomenological coefficient depending on the fouling mechanisms and n a general index that vary according the pore blocking which are studied (Field et al. 1995). The n values are defined as n = 0 for cake filtration layer, n = 1 for intermediate pore blocking, n = 1.5 for standard pore blocking and n = 2 for complete pore blocking. The goodness of fit (R²) was used as indicative of which fouling mechanism is dominant during the filtration.

Furthermore, a conjugated model suggested by Ho and Zydney (2000) described on Eq. 6 was used to evaluate the combined effect of the pore blockage and the cake filtration layer.

$$Q=Q_0\left[exp\left(-\frac{\alpha \mathrm{\Delta }PC}{\mu R_m}t\right)+\frac{R_m}{R_m+R_p}X\left(1-exp\left(-\frac{\alpha \mathrm{\Delta }PC}{\mu R_m}t\right)\right)\right]$$ 6

where Q₀ is the initial volumetric flow rate (m³ s⁻¹), α is the pore blockage parameter (m² kg⁻¹), ΔP is the transmembrane pressure (Pa), C is the feed carbohydrate concentration (g L⁻¹), which was considered of approximately 76 g L⁻¹ for the strawberry juice, µ is the permeate viscosity (Pa s), R_m is the membrane resistance (m⁻¹), t is the filtration time (s) and R_p is the maximum value of the resistance layer (m⁻¹).

This model shows the conjugated fouling mechanisms that occur during the filtration time. In fact, this model considers that the solutes with similar size to the membrane pore are the first to block the membrane and, subsequently other solutes deposit on the previously deposited particles, behavior related with the intermediate pore blocking. The continuous deposit of particles in the already blocked membrane results in the formation of an additional resistance, the cake layer.

A computer routine was developed for the software Matlab (R2013a, MathWorks Inc, MA,USA) by adjusting all the equations with the experimental data by the nonlinear regression method using the nlinfit function.

Statistical analyses

The data analysis was carried out using Statistica 7.0 software. The ANOVA and Tukey’s test (5% significance) were used to identify significant differences. The results were expressed as mean ± standard deviation (SD).

Results and discussion

Phenolic compounds maintenance

Although the membrane processes are performed at mild temperatures aiming to avoid the degradation of bioactive compounds present on feed solution, it is still necessary to evaluate the stability of this compounds during the process due to the turbulence generated and the oxygen incorporation (Castañeda-Ovando et al. 2009). Table 1 shows the values of FT on the interest fractions, i.e., the permeate obtained during microfiltration and the retentate obtained by nanofiltration.

Table 1.

Phenolic compounds content (FT) during MF and NF processes of strawberry juice

Sample	FT (mg GAE mL−1)
MF
Feed solution	14.8 ± 0.7a
Permeate 4 min	13.1 ± 0.3b
Permeate 14 min	13.1 ± 0.3b
Permeate 24 min	12.8 ± 0.0b
Final permeate (34 min)	12.8 ± 0.0b
NF
Feed solution	12.8 ± 0.0a
Concentrate 8 min	12.6 ± 0.3a
Concentrate 16 min	12.6 ± 0.3a
Final concentrate (22 min)	13.1 ± 0.3a

^{a, b}Means followed by the same letter on the vertical (column) didn’t differ statistically (5% of significance)

In the fractions obtained for microfiltration and nanofiltration processes it can be observed that both processes were efficient for the FT maintenance. Microfiltration process presented statistical difference (p < 0.05) between permeate fractions and the feed solution. Comparing the permeate fractions collected along the process it can be seen that, even with a progressive reduction in the FT content along the time, this reduction was not significant (p > 0.05). Then it is possible to say that no degradation of FT occurred along the process time. The small reduction visualized in the FT can be justified by the deposition of these compounds in the membrane surface and the development of the blocking models, and this behavior can be confirmed on topic below.

For the NF process the concentrates did not differ statistically (p > 0.05), evidencing that nanofiltration process is capable of maintaining the FT content along the time. The maintenance of the FT shows the viability of the membrane processes without large losses of bioactive compounds. On this way, the NF and MF processes, even on the presence of light and oxygen, are good alternative for the processing of strawberry juice.

Flux decline modelling

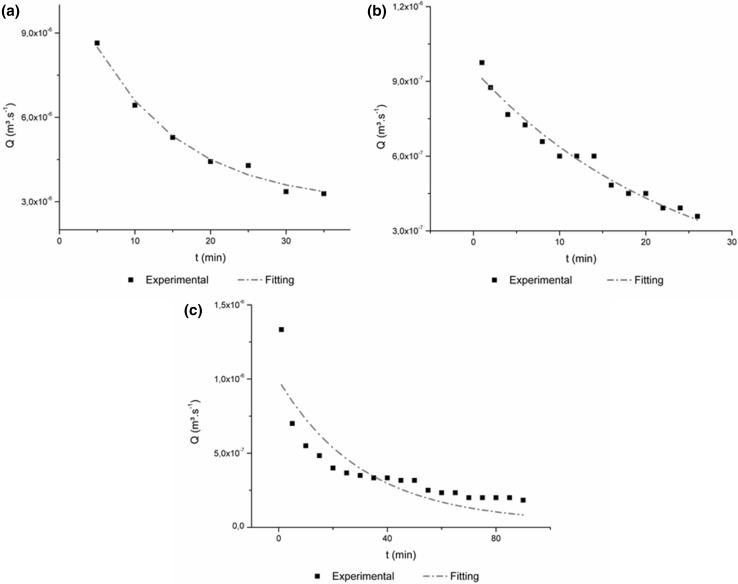
For all the sets of permeate flux versus time in this study (Fig. 2), the behaviors are in agreement to the one suggested by Marshall and Daufin (1995) which consist in a rapid flux decline on the first minutes of filtration time and then decrease gradually.

Fig. 2.

Adjustments for Ho and Zydney model for the NF IN (a), MF (b) and NF MF (c)

For fruit juices, the main foulants are polysaccharides as pectin, cellulose, lignin and hemicellulose. These substances increase the concentration of polarization, causing the sharp decline visualized in the beginning of the process, and then, at the later stages, form a cake layer on the membrane surface (Cassano et al. 2007; Verma and Sarkar 2015).

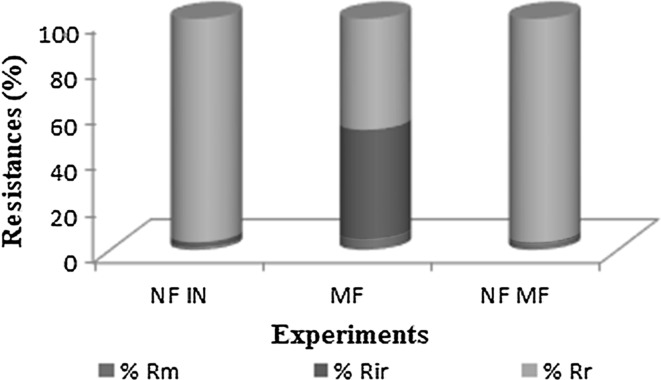
The knowledge of the resistances involved in the process is important, since the concentration of polarization can be reduced changing the hydrodynamic conditions. For the calculation of the resistances for permeate flux, the permeate viscosity for each experiment was obtained (data not shown) and water viscosity was considered 1.00 × 10⁻³ Pa s. These resistances can be observed on Fig. 1.

Fig. 1.

Percentage of resistance influence of reversible polarization of concentration (%R_r), membrane resistance (%R_m) and irreversible fouling resistance (%R_ir) on permeate flux

R_m values were higher when the NF membrane was utilized. MF presented lower membrane resistance values due to the porous structure. According to Mierzwa et al. (2008), the MF membranes have pore size between 100 and 200 nm while for NF this are 1 and 2 nm. Thus, larger pores are related with larger permeate flux and lower membrane resistance.

For both feed used in the NF processes (NF IN and NF MF) the main resistance was the polarization concentration while for MF was verified the presence of concentration polarization and fouling. Generally, process at higher pressures are more susceptible to solute deposition on the membrane surface, raising the polarization of concentration resistance. Meanwhile, processes like MF that use lower pressures are characterized by having high turbulence, reducing the polarization of concentration resistance (Kenneth et al. 2017).

Verma and Sarkar (2015) related the initial flux decline with the occurrence of different pore blocking mechanisms. So that, the pore blocking models are used to describe the main factor that influences in the processes. Higher values of R² are taken in account to determine the main factor for flux decline. The values obtained are shown on Table 2.

Table 2.

Parameters obtained from pore blocking models for MF, NF IN and NF MF processes

Experiment	Complete pore blocking
	Kb	R2
MF	0.0330	0.96
NF IN	0.0166	0.85
NF MF	0.0318	0.95

	Intermediate pore blocking
	Ki	R2
MF	0.0018	0.95
NF IN	0.0133	0.97
NF MF	0.0160	0.97

	Standard pore blocking
	Ks	R2
MF	0.0041	0.96
NF IN	0.0079	0.93
NF MF	0.0123	0.97

	Cake filtration layer
	Kc	R2
MF	0.0002	0.95
NF IN	0.0100	0.99
NF MF	0.0243	0.95

Resistance coefficient (k) is a phenomenological coefficient dependent of the resistance and concentration of cake layer and blocked surface. The main factor that influenced the k values was the pressure (de Bruijn et al. 2002; Razi et al. 2012). When comparing the k values obtained for the different processes it can be observed that both processes using NF presented close values, differing from MF.

MF process showed higher value of k_b, which according to Almandoz et al. (2010) was related to the number of blocked pores per filtered volume. The in natura juice has suspension particles which were bigger than the membrane pore, blocking this and resulting on bigger values of k_b parameter.

For k_c, k_i and k_s the higher values are obtained for NF MF, related with the adsorption of the small particles inside the pore, reducing their area and consequently blocking the surface. Furthermore, the NF MF have higher flux values, which is another factor related with these phenomena.

According to Torkamanzadeh et al. (2016) the good fit of the permeation data to the models suggests that the mechanism is dominant during the juice filtration. For the MF process, the best fitting was obtained for two distinct models, complete pore blocking and standard pore blocking, both with R² = 0.96. The larger pores of MF membrane allow the solutes to enter the membrane pore and be adsorbed. Salahi et al. (2010) related that the complete pore blocking occurs when the particle size is larger than the membrane pore and the standard pore blocking when the particles are adsorbed onto the membrane pores, reducing their diameter. As strawberry juice is a complex solution, with different sizes of solutes, these two different pore blockings mechanisms can occur simultaneously. Chang et al. (2011) related this same behavior when modelling the filtration of raw water, where all the pore blocking mechanisms occurred except for standard pore blocking.

With relation to the NF MF, the intermediate pore blocking model presented the best determination coefficient (R² = 0.97). Field et al. (1995) described the intermediate pore blocking as a dynamic situation where the blocking and unblocking of the pores occurs simultaneously and the solute particles can obstruct the entrance but not block completely the pore. As the large particles and macromolecules were removed by the MF the remaining particles were unable to completely block the pore, reducing some pore blocking mechanisms, and the removal of pulp and suspended solids reduced the cake filtration layer.

The best fitting, when analyzing the NF IN process, was for cake layer model (R² = 0.99). The cake layer model is related with the deposition of the particles or macromolecules with size greater than the membrane pores, so they do not enter in the membrane pores but is deposited in membrane surface (Field et al. 1995; Iritani 2013). The in natura juice has pulp and pectic substances with molar mass cut-off (MMC) much higher than the MMC of the membrane, facilitating the deposition of this compounds on the membrane surface, with consequent cake layer formation.

A relation between the pore blocking models and the permeate flux resistances can be performed. As described above, the main resistance verified for both processes using the NF membrane (NF IN and NF MF) is the polarization of concentration. In relation to the pore blocking models, NF IN presented the best fitting for cake filtration layer and for NF MF the intermediate pore blocking. The small pores of the NF membrane retain almost all the solutes, even the small ones. When using the NF IN, the macromolecules and suspended solids deposit on the membrane surface, leading to the cake layer filtration model, which result in the polarization of concentration due to the high pressures of the process. The NF MF process, the large particles are removed, but the small particles can deposit on other already deposited and form the polarization of concentration layer. According to Hafidi et al. (2003) this mechanism is initiate by the interaction between the solute and the membrane, where the chemical bonds and Van der Waals forces are the main phenomena involved.

Lin et al. (2007) affirm that the intermediate pore blocking was responsible for the sharp flux decline at the initial moments of the process, what justifies the flux decline visualized on NF MF process. In addition, according to Mello (2013) the polarization of concentration is directly linked with the standard, intermediate and complete pore blocking.

For the MF process the polarization of concentration and the fouling are the main permeate flux resistances and the complete and standard pore blocking showed the best R² when analyzing in regard to the pore blocking models. The different size of the solute particles occasioned this behavior, considering that the small particles enter the membrane pores and are adsorbed and the larger particles settle on the pores and block them. Rai et al. (2010) verified that cake filtration layer has the best correlation between the model and the experimental data when studying microfiltration of watermelon juice.

Even with good fit values, this classical models only evaluate one fouling mechanism at the same time, and are not able to describe the transition that occurs during the membrane process. Salgado et al. (2013) related that, for NF, the pore blocking mechanisms usually appears first, and it can be followed by the formation of a cake filtration layer. Therefore, both mechanisms must be considered to explain the membrane fouling (Corbatón-Báguena et al. 2015). The Hermia models evaluated in this study have as major advantage the simple and easy to implement, however, as only one variable is considered, it can present low accuracy when predicting the flux decline (Torkamanzadeh et al. 2016).

The model developed by Ho and Zydney (2000) combines the pore blocking mechanisms and the cake filtration layer and the results obtained by this model are presented in Fig. 2. This model proposed assumes that the particles present on the feed solution firstly deposit on the membrane surface or inside the pores, but even the blocked pores remains permeable to the permeate flow.

Feed solution used for each processes have significant differences, as particle size and removal of suspended solids. These characteristics have caused different initial pore blocking mechanisms for each processes, as described above. Over time, this pore blocking visualized promote the deposition of particles on each other and the cake layer grows.

With the growth of the cake layer, the second term of this new model starts to be dominant on the process. For MF and NF MF the R² was about, 0.97 and 0.99, respectively. This high adjustment values demonstrate clearly the evolution of the pore blocking models, occasioned by the particles entering or depositing on the pores and the later growth of the cake layer. For NF IN process, the R² was about 0.76, with poor fitting to this model. This was expect, once the in natura juice have suspended solids, that cannot enter on the pores, depositing on the membrane surface and starting the grow of the cake layer earlier, i.e., in the beginning of the process. The high values of R² obtained in this study for the model of Ho and Zydney (2000) demonstrate the accuracy of this model to predict the flux decline behavior for the processing of strawberry juice, even with different conditions of feed solution.

Conclusion

NF and MF flux decline presented sharp decline in the process beginning and followed by a gradual decline. This behavior is related with the development of polarization of concentration resistance. Due to the predominance of this resistance, incrustation could be detached using a sufficient shear force (i.e., physical flushing) increasing membrane lifespan, which is desired in the industry. Furthermore, each process presented a different behavior according to feed solution and membrane characteristics. Pore blocking models presented R² over 0.85 and Conjugated model presented R² between 0.76 and 0.99 demonstrating the efficiency of these models. Finally, these findings not only clarify the fouling mechanism involved in membrane process of strawberry juice, but also provide valuable knowledge about the concentration of its bioactive compounds.