Voluntary Head Rotational Velocity and Implications for Brain Injury Risk Metrics

Abstract

We investigated whether humans could sustain high head rotational velocities without brain injury. Rotational velocity has long been implicated for predicting concussion risk, and has recently been used to develop the rotational velocity-based Brain Injury Criterion (BrIC). To assess the efficacy of rotational velocity and BrIC for predicting concussion risk, we instrumented 9 male subjects with sensor-laden mouthguards and measured six-degree-of-freedom head accelerations for 27 rapid voluntary head rotations. The fastest rotations produced peak rotational velocities of 12.6, 17.4, and 25.0 rad/s in the coronal, sagittal, and horizontal planes, respectively. All of these exceeded the corresponding medians from padded sports impacts (8.9, 10.7, and 8.4 rad/s, respectively) and, in the case of sagittal and horizontal rotation, were within 1 standard deviation of published concussion averages. In the horizontal plane, four voluntary rotations exceeded the concussive impact median BrIC. The area under the precision-recall curve was lower in BrIC (0.49) than just using horizontal rotational acceleration (0.8), which distinguished concussive and subconcussive motions better. Voluntary motions produced less than 4% max principal strain (MPS) in finite element simulation, 5 times below predictions from dummy impacts used to develop BrIC. Despite having the highest critical velocity in BrIC, coronal rotation produced more tract-oriented strain in the corpus callosum than other planes. Baseline and post-experiment neurological testing revealed no significant deficits. We find that the head can tolerate high-velocity, low-acceleration rotational inputs too slow to produce substantial brain deformation. These findings suggest that the time regime over which angular velocities occur must be carefully considered for concussion prediction.

Introduction

Traumatic brain injury (TBI) is a leading cause of death and disability in the United States¹ and most common among injury-related deaths in children and young adults under the age of 24 in the United States and other industrialized countries.² Motor-vehicle–related injuries are the second-leading cause of TBI¹ in the United States, accounting for more than 30% of cases. Incidence rate of TBI-related deaths in motor vehicles and sports has declined in recent years,^1,3 likely attributed to the development and enforcement of safety standards and injury criteria, such as the Head Injury Criterion.^4–7 Although protective and preventive technology developed to follow these standards have reduced TBI-related death, incidence of mild TBI (mTBI; i.e., concussion, diffuse axonal injury) is on the rise.^8–11 Public health measures to prevent mTBI are limited because the precise physical mechanism of human injury is unclear.

Holbourn, a British physicist at Oxford University, previously hypothesized that rotation from blunt TBI caused injury whereas translation played an insignificant role.¹² He reasoned that the brain is largely incompressible (like water or gel) and thus deforms primarily under shearing loads during skull rotations (R1-5). Since then, numerous studies have investigated rotational mechanisms of brain injury. Multiple studies have measured head rotational velocity in concussion (Table 1),^13–15 whereas others have reported rotational velocities for milder, subconcussive head impacts (e.g., soccer headers).^13–17 In a recent study of six-degree-of-freedom (6DOF) head acceleration measurements of padded sports impacts,¹³ rotational velocity was more predictive of injury than criteria commonly used in football helmet and vehicle collision testing, though the sample of padded sports impacts contained only two diagnosed concussions.^4–7,18 Primate and analytical studies have also proposed rotational velocity thresholds that coincided with critical levels of brain strain.^19–21 In a computational study, varying pulses with different peak rotational accelerations but equal changes in rotational velocity produced similar levels of brain strain, suggesting that the latter may be a better metric of injury.²² Simple analytical models revealed that the sensitivity of mass response to acceleration and velocity changed according to the time scales in which these occurred.²³ These results suggest previous studies have largely been focused on the rotational velocity sensitive region.

Table 1.

Previous Measurements of Head Rotational Velocity

Study	Sample size	Activities	Coronal (rad s–1)		Sagittal (rad s–1)		Horizontal (rad s–1)		Magnitude (rad s–1)
			μ ± σ	Range	μ ± σ	Range	μ ± σ	Range	μ ± σ	Range
Concussive
Pellman et al., 2003	25	Football	—	—	—	—	—	—	34.8 ± 15.2	13–81
Rowson et al., 2012	57	Football	23.0 ± 5.2	—	22.1 ± 8.5	—	—	—	22.3 ± —	—
Hernandez et al., 2015	2	Football	—	19–36	—	15–22	—	18–24	—	27–38
Subconcussive, head impacts
Pellman et al., 2003	33	Football	—	—	—	—	—	—	26.1 ± 10.4	7–56
Funk et al., 2011	68	Soccer headers	—	—	5.9 ± 1.1	2–11	—	—	—	—
Rowson et al., 2012	300,977	Football	—	—	—	—	—	—	—	—
Hernandez et al., 2015	108	Football, combat	6.3 ± 4.3	1–35	9.3 ± 6.8	0–40	6.5 ± 4.3	1–38	12.7 ± 7.1	3–48
Wu et al. 2016	10	Soccer headers	—	—	—	—	—	—	4.4 ± 0.7	4–5
Subconcussive, nonimpact
Ewing et al., 1975	100	Volunteer sled tests	—	—	14.8 ± 7.6	1–32	—	—	—	—
Ewing et al., 1978	73	Volunteer sled tests	17.4 ± 6.5	5–35	—	—	—	—	—	—
King et al., 1994	15	Figure skating	—	—	—	—	25.3 ± 5.9	15–34	—	—
Siegmund et al., 2003	65	Volunteer sled tests	—	—	3.2 ± 0.8	—	—	—	—	—
Arbogast et al., 2009	180	Volunteer sled tests	—	—	6.6 ± —	2–15	—	—	—	—
Bussone et al., 2009	—	Playground activity	—	0–10	—	0–11	—	0–16	5.5 ± —	0–16
Funk et al., 2011	10	Everyday activity	—	—	4.2 ± 1.9	0–13	—	—	—	—

Dash (“—”) denotes that the values were not provided (or could not be calculated from the provided data).

Previous studies have implicated rotational velocity in concussion and have reported values in various subconcussive head motions, both with and without contact.^{13–17,24,26–30} Here is a compilation of previously reported rotational velocity values for mean ± standard deviation (μ ± σ) and range in each anatomical plane and magnitude. Direct measurement of nonimpact rotational velocities is limited, particularly in the coronal and horizontal planes.

The bounds of tolerable rotational head velocity are not well established, nor is it known how these bounds vary with type of input. Most studies have looked at rotational velocity in response to impact, but few have made direct measurements during nonimpact, subconcussive activities (Table 1). Several studies have contributed to our description of a “safe” envelope of head motion by measuring everyday activities such as sitting and jumping.^16,24,25 Volunteer sled tests have also contributed to our knowledge of tolerable rotational velocities in the sagittal plane.^26–29 In figure skating, video-estimated rotational velocity has exceeded 30 radians per second (rad s⁻¹).³⁰ Although this work has provided an initial envelope of minimal injury risk, direct measurement of rotational velocity for nonimpact motions is still limited, particularly in the coronal and horizontal planes (Fig. 1). Moreover, the measured tasks have largely been very mild. Peak human performance measurements characterizing the outer bounds of this envelope have not yet been reported.

FIG. 1.

Data collection and voluntary head movement experiments. (A) We used custom-fit, sensor-laden instrumented mouthguards to measure the six-degree-of-freedom (6DOF) accelerations of 9 male subjects during 27 rapid voluntary head movements. (B) The first 18 head movements involved isolated head rotations in all three planes of motion: coronal, sagittal, and horizontal. In each plane, subjects completed triplicate movements from each extreme to the other. (C) The second set of head movements involved tracking head rotations where subjects were instructed to follow a fast-moving soccer ball. Subjects tracked the soccer ball as it flew overhead, to the left, and to the right (three times each). Color image is available online.

The aim of this study was to expand the known range of tolerable head rotational velocities and, in doing so, evaluate rotational velocity (and derivative criteria like the Brain Injury Criteria [BrIC]) as predictors of concussion risk. To do so, we instrumented subjects with 6DOF measurement devices and aimed to characterize the fastest head movements subjects could produce voluntarily in each anatomical plane of rotation. We then contrasted these measurements with previously measured padded sports impacts and injury thresholds to test the hypothesis that voluntary head movements would not exceed concussion levels of padded sports impacts for any acceleration or velocity measure of rotation. We performed single-degree-of-freedom rigid body modeling, as well as finite element simulations and neurological testing, to investigate injury regimes and confirm the risk of injury was indeed minimal.

Methods

Subjects and instrumentation

Volunteer subjects were instrumented with mouthguards measuring 6DOF (translation and rotation) accelerations (Fig. 1A). We recruited male subjects between the ages of 18 and 40 that had no previous history of brain, neck, or spinal cord injury. To investigate whether past participation in a ball sport (where rapid head motion is common from following a target) affected head motion performance, we classified subjects as athletes if they had played a ball sport at the high school or college varsity level (including, but not limited to, baseball, basketball, football, golf, hockey, lacrosse, soccer, squash, tennis, volleyball, and water polo). All other subjects were considered nonathletes for the purposes of this study.

Each subject received a custom-fit instrumented mouthguard.^13,17,32,33 We made impressions of each subject's upper dentition, and embedded electronics in material that was pressure formed around the subject's dental mold (Fig. 1A). The custom fit provided tight coupling to the subject's skull through the maxillary dentition. Mouthguard electronics included a tri-axis accelerometer (measuring translational acceleration in the anterior-posterior, left-right, and superior-inferior directions), a tri-axis gyroscope (measuring rotational velocity in the coronal, sagittal, and horizontal planes), a microprocessor, 16-bit flash memory, and a battery. Activity that exceeded a programmed gyroscope threshold was recorded and downloaded at the conclusion of each experiment. Here, we used a rotational velocity magnitude trigger of 5 rad s⁻¹, modified from the 7g translational acceleration magnitude threshold we used in previous sports impact studies,^13,17,32,33 which we expected would be too high for these voluntary head motions. The embedded microprocessor recorded time-stamped sensor measurements at 500 Hz for 50 ms preceding the triggering velocity and 350 ms post-trigger (for a total record time of 400 ms). During all experiments, members of the research team noted the time of each head motion to later remove spurious false-positive mouthguard measurements that exceeded the rotational velocity threshold, but did not correspond to head motions. The kinematic accuracy of these devices was previously characterized in dummy head,^13,32 in vivo,¹⁷ and ex vivo experiments.³³

Kinematic measurements and processing

Accelerometer and gyroscope data were filtered using a second-order Butterworth low-pass filter with 200- and 110-Hz cut-off frequencies, respectively.^13,32 Sensor measurements were then transformed to express the translational acceleration of the head center of gravity and the rotational velocity and acceleration of a head anatomical reference frame (pointing in the anterior, left, and superior directions) using a previously published algorithm and assuming a 50th percentile male head size.³² Rotational acceleration was computed using a fourth-order central difference derivative of each rotational velocity component. Because the head motion experiments were mostly planar, we took a numerical integration of the primary rotational velocity to compute a change in orientation in the primary plane of motion.

In addition to peak kinematics values, we calculated the BrIC for each head motion. BrIC was developed by National Highway Traffic Safety Administration³¹ for inclusion in future vehicle safety standards and is a function of head rotational velocity (Eq. 1):

where ω_coronal, ω_sagittal, and ω_horizontal are the peak values for rotational velocity in each anatomical direction over time, and ω_cr,coronal, ω_cr,sagittal, and ω_{cr,horizontal} are the corresponding critical values determined from experimental data of pendulum dummy impacts. Though originally developed to assess severe brain injuries, BrIC has also been adapted to predict risk of mTBIs with critical angular velocity values of: 66.2, 59.1, and 44.2 rad s⁻¹, respectively.

To assess the performance of BrIC and other kinematic measurements as predictors of concussion risk, we constructed precision-recall curves. Precision, or positive predictive value, is the fraction of impacts predicted to be concussions that were actually concussions. Recall, or sensitivity, is the fraction of concussions that were correctly classified as concussions. Precision and recall can be summarized with the following equations (Eqs. 2 and 3):

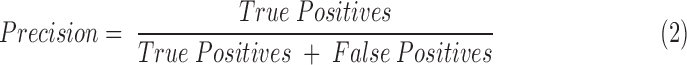The area under the precision-recall curve (AUC_PR), which ranges from 0 to 1, quantifies the degree to which both are achieved. A perfect classifier would have AUC_PR equal to 1. A random classifier would have AUC_PR equal to the fraction of concussions in the total data set. Precision-recall curves are better suited than receiver operating curves for use in assessing injury safety where the baseline probabilities of positive (injury) and negative (noninjury) classification are different (e.g., injuries are far rarer).

Head motion experiments

For all subjects, we measured a total of 27 rapid head movements using two experiments: 1) 18 isolated head motions and 2) nine tracking head motions. At the beginning of the experiments, we guided subjects through a series of neck stretches and rolls to warm them up. Subjects were then given their mouthguards and instructed to maintain a slack jaw throughout the entire duration of the study, given that this has been found to minimize mouthguard measurement errors.³³ We then conducted the isolated head motion experiments, where each subject was instructed to rotate their head as fast as possible in each of three rotation planes: coronal, sagittal, and horizontal (Fig. 1B). Starting with coronal plane rotation, subjects rotated their head from their leftmost extreme position (left ear on left shoulder) to the rightmost extreme position (right ear on right shoulder) three times. They then performed another triplicate in the reverse direction, right to left. The process repeated in the sagittal plane (looking up to down, and then down to up) and in the horizontal plane (looking right to left, and then left to right). Triplicates were performed to provide subjects an additional opportunity to warm up, get accustomed to the motion, and reach their peak performance/velocity. In addition, subjects were instructed to use only their head and neck, and minimize any movement or rotation of their arms and torso.

For the tracking head motions, each subject was instructed to follow a fast-moving (approximately 10 m s⁻¹) soccer ball (Fig. 1C). The first three head movements came from tracking a soccer ball flying approximately 3 feet directly overhead in a seated position with legs stretched forward and hands placed in front of them. The other six head movements came from tracking the soccer ball flying to the left and right in a standing position. In all cases and across all subjects, a soccer ball launcher (Sports Tutor, Burbank, CA) was used at the same setting to ensure consistency in the velocity and trajectory of launches across experiments. Markings on the ground were also used to keep subject placement consistent. Subjects were instructed to begin looking at the ball launcher and then follow the soccer ball with their eyes, only allowing their head and neck to rotate (and again minimize motion or the arms and torso). Subjects were also reminded to keep their jaw slack. All head motions, in both experiments, were videotaped just in case qualitative follow-up of the measurements were needed.

Head accelerations from these experiments were then compared with previously recorded padded sports impact data sets. The first set was collected at Stanford using similar instrumented mouthguards and consisted of 513 football, boxing, and mixed martial arts impacts, including two resulting in diagnosed concussion.¹³ The second set came from laboratory dummy reconstructions of NFL impact videos and consisted of 58 impacts, including 25 that resulted in diagnosed concussion.¹⁴ Finally, analysis of pendulum dummy tests that were used in the development of BrIC³¹ were included in this study for comparison.

Brain response modeling

To quantify potential brain tissue damage during these head motions, we simulated head motions using a combination of rigid body and finite element brain models that are commonly utilized in brain injury assessments and criteria. We performed rigid body simulations to predict brain response to varying inputs of velocity and acceleration. Using a previously published method of determining velocity and acceleration-dependent regimes,²³ we quantified brain displacement in a simple second-order system model. The model, briefly, consisted of a rigid brain mass with a single-degree-of-freedom pivot with respect to a rigid skull, located near the base of the brain. A torsional spring and damper were also included at the brain-skull pivot to provide the characteristic second-order dynamics, similar to an inverted pendulum with a spring damper.^34,35 We simulated a triangular acceleration pulse where the peak was set to a given acceleration, and the duration was set to produce a given velocity (area under the curve). We swept a rectangular grid of velocities and accelerations to find contour lines of constant peak response, taken as peak displacement of the mass from neutral. An additional injury threshold line, calculated and scaled from primate experiments,²⁰ was included for comparison.

We also simulated head movement measurements using a finite element (FE) model to estimate brain stress and strains. We used the FE head model developed at the KTH Royal Institute of Technology in Stockholm, Sweden,³⁶ which is sized to match an average adult male human head. Developed in LS-DYNA (LSTC, Livermore, CA), this model incorporates the brain, skull, meninges, scalp, cerebral spinal fluid, and eleven pairs of bridging veins. Brain tissue is modeled using an Ogden hyperelastic constitutive law (to account for large deformations of the tissue) with additional linear viscoelastic terms (to account for the rate dependence of the tissue). The model also accounted for material property differences between white and gray matter. The FE model was previously validated against intracranial pressure and displacement data from cadaver head impact experiments performed.³⁷ From the models, we analyzed the deformation of brain tissue in the primary direction of fiber tracts using a previously published technique using average diffuse tensor imaging of 81 healthy subjects.³⁸ Tract-direction strain was computed by projecting the Green–Lagrange strain tensor in the direction of preferred diffusion (which aligns with the primary direction of fiber tracts in a given direction). Principal strain was computed by taking the largest eigenvalue of the Green–Lagrange strain tensor. Strain rate in each brain element was determined using a fourth-order central difference derivative of strain over time.

We ran our data through similar analyses used to develop BrIC.³¹ Specifically, we correlated max principal strain (MPS) with peak values of rotational velocity, peak values of rotational acceleration, and BrIC. In all cases, we performed linear regression that was constrained to go through the origin. We also used the same formulation of r² coefficient of determination used by Takhounts and colleagues, for MPS data and regression through the origin.³¹

Neurological testing

To quantify deficits from performing these head motions, three different neurological tests were performed at four different time periods throughout the study: 1) baseline testing conducted 2–4 days preceding the head movement experiments at the time of obtaining written consent to participate in the study; 2) pre-experiment testing immediately preceding the experiments; 3) post-experiment testing immediately after the experiments; and 4) post-experiment testing approximately 20 min after the experiments. Tests were selected to span a variety of cognitive and neurological function, and the 20-min gap was selected based to allow for vestibular effects on balance to subside.³⁹ For all scores, we calculated differences from the subject's baseline.

The first test was the Balance Error Scoring System (BESS), which has been used previously to assess static postural stability.^39–45 As part of this test, subjects were instructed to close their eyes and hold three different stances (double leg, single leg, and tandem) and two different surfaces (firm floor and a foam pad). In the double leg stance, subjects stand straight, feet together (side by side), with hands on their hip. In the single-leg stance, subjects stand on their nondominant leg while the other leg is raised to maintain a knee flexion angle of approximately 90 degrees. In the tandem leg stance, subjects put one foot in front of the other, their dominant foot in front. To determine their dominant foot, subjects were asked to identify which foot they were more likely to kick a soccer ball. The BESS score for each test was the number of errors committed by the subject in a 20-sec period. Errors were defined as opening of the eyes, removing their hands from their hips, steps, stumbles, falls, and other failures to hold the specified stance. As such, a larger BESS score is thought to correspond with higher probability of brain injury. Live scoring was performed by the research team during the experiments and in video.

The second test was the King–Devick (KD) assessment.⁴⁶ This exam has been used to test oculomotor function, language function, and visual acuity by requiring subjects to read numbers on a tablet screen, as fast as possible, without committing any errors.^46–48 The numbers are to be read left to right, top to bottom, for three exams of increasing difficulty (rows get closer and guidelines are removed). As such, larger KD scores (time it takes to read the number) correspond with higher probability of brain injury.

The final test was the Standard Assessment of Concussion (SAC), which has been used to assess a wide variety of concussion symptoms.^40,49,50 The exam consists of four scored sections: 1) orientation, where subjects have to recite the current day, time, year, etc.; 2) memory, where subjects have to repeat back five words; 3) concentration, where subjects have to recite digits back in reverse order; and 4) delayed recall, where subjects have to remember the five words told to them in the memory section. Because points are provided for correct responses, lower SAC scores correspond with higher probability of brain injury.

Results

Head kinematics measurements

In this study, we recruited 9 male subjects with ages ranging from 21 to 33 (average and standard deviation of 24.7 ± 3.5). Eight days of experiments were conducted in a span of 1.5 months. Five of the 9 subjects were considered athletes because they reported playing a varsity ball sport in high school or college. We did not find significant differences in head kinematics, brain strains, or neurological scores between the athlete and nonathlete groups and thus refrain from presenting these data separately.

Across all 9 subjects, the fastest voluntary head movements produced peak rotational velocities of 12.6, 17.4, and 25.0 rad/s in the coronal, sagittal, and horizontal planes, respectively (Fig. 2). In all planes, rotational velocities usually peaked and returned to zero within 400 ms. On average, horizontal movements produced the highest rotational velocities (Fig. 2C), followed by sagittal (Fig. 2B) and then coronal (Fig. 2A). This corresponded with each subjects change in orientation in every plane, with subjects being able to span a greater range while rotating their head horizontally (Fig. 2F). During each subject's change in orientation, coronal rotations tended to peak just before the halfway mark, indicating subjects skewed toward starting fast at the beginning of the rotation and then decelerating slowly as they approached the other extreme (Fig. 2D). In contrast, rotational velocities peaked after the halfway mark in sagittal movements (Fig. 2E) and just at the halfway mark in horizontal (Fig. 2F).

FIG. 2.

Rotational velocities of rapid voluntary head movements. Across all subjects, the maximum, mean, and standard deviation of rotational velocity over time is shown for the (A) coronal, (B) sagittal, and (C) horizontal planes. (D–F) Rotational velocity as a function of change in orientation in the primary direction of motion is also shown for each of the three planes. Color image is available online.

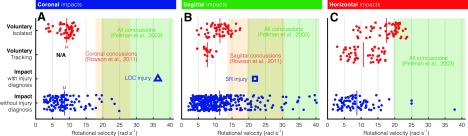
Voluntary movements in each plane exceeded corresponding sports-impact medians (8.9, 10.7, and 8.4 rad/s, respectively; Fig. 3). Human rotational velocity was most limited in the coronal plane and these did not exceed any previously reported mTBI values (Fig. 3A).^14,15 However, the fastest sagittal and horizontal movements were within 1 standard deviation of mTBI means.

FIG. 3.

Comparison of voluntary rotational velocities to sports impacts. (A) Coronal voluntary movements produced rotational velocities comparable to the sports impact median and below previously recorded concussion ranges (mean ±1 standard deviation). However, (B) sagittal and (C) horizontal voluntary movements cross into these published ranges and, in the latter, far exceed the sports impact median. N/A, not applicable. Color image is available online.

Rigid body modeling of brain displacement

Acceleration magnitudes separated voluntary movements from sports impacts far more than velocity (Fig. 4A,B). Using a simple second-order model and an idealized triangular loading pulse, we observe how increasing brain response is related to changes in acceleration and velocity. In translation, we observed that voluntary movements are clustered, and in a region of slow temporal dynamics (high velocity, low acceleration) where changes in translational velocities matter less (Fig. 4A). That is, higher-intensity voluntary movements seem to travel along contours of constant brain response, not perpendicular. Sports impacts appear to lie closer to the knee of the constant response contours, where both translational acceleration and velocity appear to matter. We see a similar relationship in rotation (Fig. 4B). Voluntary movements trended toward a temporal regime where changes in rotational acceleration matter more. Sports impacts crossed over the knee of the contours where both rotational acceleration and velocity seem to drive increasing brain response. Sled tests on seated, seatbelted volunteers²⁶ produced rotational kinematics in a middle regime where acceleration changes matter more for brain response than it does for sports impacts. An injury threshold developed from primate experiments²⁰ closely matched the contours of the rigid-body model results.

FIG. 4.

Temporal injury regimes of voluntary movements and sports impacts. Acceleration versus velocity in the voluntary head movements and sports impacts is shown for (A) translation and (B) rotation. These are compared with peak displacement contours of a mass-spring-damper brain model (mass of 1.5 kg and natural frequency of 15 Hz^34,35) with a triangular acceleration pulse input. In previously recorded volunteer seatbelted sled tests,²⁶ and more so in our recorded voluntary motions, rotational acceleration drives brain response more than rotational velocity. LOC, loss of consciousness. Color image is available online.

Finite element modeling of brain strain

Estimating brain response from finite element simulations, we found voluntary motions produced relatively small brain tissue deformation. At a given time, the largest average strains in these voluntary motions stayed below 0.3% (Fig. 5A). As a result, Cumulative Strain Damage Measure (CSDM25), or the percentage of the entire brain that is beyond a 25% threshold of strain, was zero for all voluntary movements. Tract-direction strain in the brain produced two peaks that temporally corresponded with those of peak rotational acceleration (Fig. 5B), approximately 180 ms apart. Pearson's correlation coefficient between average rotational acceleration and tract strain signals (0.85; 95% confidence interval, 0.82–0.88) was significantly stronger than the correlation between velocity and strain (0.51; 0.43–0.58). MPS and rotational acceleration magnitude were strongly correlated in the voluntary motions (r² = 0.96) and sports impacts (r² = 0.96), more so than in the pendulum dummy tests used to develop BrIC (r² = 0.77; Fig. 5C). However, the voluntary motion, sports impact, and pendulum test data all had slopes relating rotational acceleration to MPS (1e-04, 6e-05, and 4e-05, respectively) that were similar to one another (within 60%). Though all were strong, correlation between MPS and rotational velocity in voluntary motions (r² = 0.95) and sports impacts (r² = 0.91) were not as high as the pendulum tests (r² = 0.98; Fig. 5D). In voluntary motions, the slope relating MPS and rotational velocity (2e-03) was 5 times smaller than in sport impacts and pendulum tests (both 1e-02).

FIG. 5.

Brain strain during rapid voluntary movements. (A) On average, peak brain strains in the brain were below 1%. These have a strong temporal correlation (0.85) with (B) peaks in rotational acceleration at the beginning and end of each movement. (C) Peak rotational acceleration magnitude correlated strongly with maximum principal strain in the brain, and followed a similar trend to our sports impacts and pendulum tests performed for the development of the Brain Injury Criterion (BrIC).³¹ (D) Rotational velocity also correlated strongly with maximum principal strain, but in a different regime from the sports impacts and pendulum tests. (E) Coronal rotation produced more strain in the corpus callosum for a given peak rotational acceleration; however, it has the highest (most tolerable) critical velocity in BrIC. (F) Overall brain strain and strain rate distinguish voluntary movements from sports impacts. LOC, loss of consciousness; SR, strain rate. Color image is available online.

If we look at tract-oriented strain in the corpus callosum, a brain structure that has been previously implicated in concussion,^13,51 we see separation between rotational velocity in each anatomical plane (Fig. 5E). We see that horizontal rotations produce the largest strains in the corpus callosum (3%); however, coronal rotations tended to produce more strain in this structure for a given level of rotational velocity. This relationship between coronal rotation and corpus callosum strain was previously reported as a potential mechanism of mTBI.⁵¹ Strain and strain rate in the brain separate the voluntary motions from the sports impacts (Fig. 5F).

Criteria for injury prediction

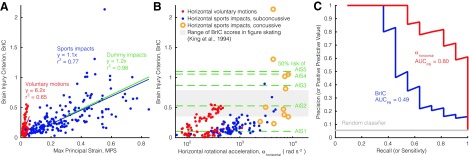
The inability of rotational velocity to distinguish between voluntary movements and sports impacts was the same for the velocity-based BrIC (Fig. 6). Along the y-axis, we saw little separation in the BrIC scores of voluntary movements (in red) to sports impacts (in blue) (Fig. 6A). BrIC was also much less correlated with MPS in the voluntary motions (r² = 0.65) and sports impacts (r² = 0.77) than in the pendulum impacts used to develop BrIC (r² = 0.98). Whereas the sports impacts and pendulum tests shared a similar relationship between MPS and BrIC (both slopes were 1.2), the voluntary motions had a slope (6.2) that was more than 5 times larger. We observed four horizontal voluntary motions, among 2 subjects, that exceeded the median concussion-level BrIC score (0.5) and a 50% risk of injury with an Abbreviated Injury Score (AIS) of 2, which describes a mild-to-moderate concussion (Fig. 6B). Moreover, two concussions from the NFL data set yielded BrIC scores exceeding a 50% risk of AIS5 injury, which describes the most severe, sometimes fatal, brain injuries. In contrast, even just a single axis of rotational acceleration (horizontal) does better to separate the voluntary movements (in red), subconcussive sports impacts (in blue), and concussive sports impacts (in yellow). The fastest voluntary movements were still below the slowest concussive impact. This improvement in classification performance is described by a larger area under the precision-recall curve (AUCPR = 0.80) compared to BrIC (AUCPR = 0.49; Fig. 6C). That is to say, horizontal rotational acceleration alone was more sensitive to detecting concussion impacts than BrIC.

FIG. 6.

Investigating the Brain Injury Criterion (BrIC). (A) BrIC values were moderately correlated with maximum principal strain for the voluntary motions and in a different regime from our sports impacts and previous pendulum tests performed in the criterion's development.³¹ (B) When BrIC is plotted against just horizontal rotational acceleration, we see little distinction between voluntary motions and concussive impacts in the former and much more separation in the latter. (C) This difference is quantified by a smaller area under the precision-recall curve for BrIC compared to just a single rotational acceleration axis. AUCPR, area under the precision-recall curve. Color image is available online.

Neurological testing

There were no patterns of neurological deficits across all tests and subjects (Fig. 7). For BESS, there was a significant improvement from the time of the consent meeting to the pre-test just before the experiments (Fig. 7A, Fig. S1; Supplementary material is available online at www.liebertpub.com/neu). This was likely attributed to a learning effect observed in other BESS studies³⁹ where subjects improved their ability to maintain the required postures after already having done the exam 2–4 days previously. This improvement vanishes in the first post-test, probably because balance impaired because of vestibular effects of the head movements. The learning improvement recovers in the second post-test, which is also significantly different from the consent baseline. In both KD (Fig. 7B) and all of the subtests of SAC (Fig. 7C), the subjects did not significantly differ from baseline.

FIG. 7.

Neurological testing before and after the voluntary head movements. Change in neurological testing from baseline at consent is provided at pre-experiment, post 1 (immediately after experiments), and post 2 (20 min after experiments) for (A) the Balance Error Scoring System (BESS), (B) King–Devick (KD) test, and (C) the Standard Assessment of Concussion (SAC). No significant neurological deficits were observed. Color image is available online.

Discussion

In this study, we investigated the maximum head rotational velocity that can be generated voluntarily. Here, we report the highest horizontal rotational velocities that were directly measured in humans and confirmed not to produce neurological deficit. In the sagittal and horizontal planes, we found rotational velocities in voluntary movements that exceeded those produced by (involuntary) head movements in padded sports impacts, including some that resulted in diagnosed concussion. Given these results, we must take into account the time regime or rotational acceleration exhibited during head motions to more accurately predict concussion risk. These high rotational velocities extend our previously known envelope of minimal injury risk given that they did not appear to produce neurological deficits associated with balance, oculomotor function, concentration, language function, and memory. These results cast doubt on the use of rotational velocity thresholds alone for assessing concussion risk.

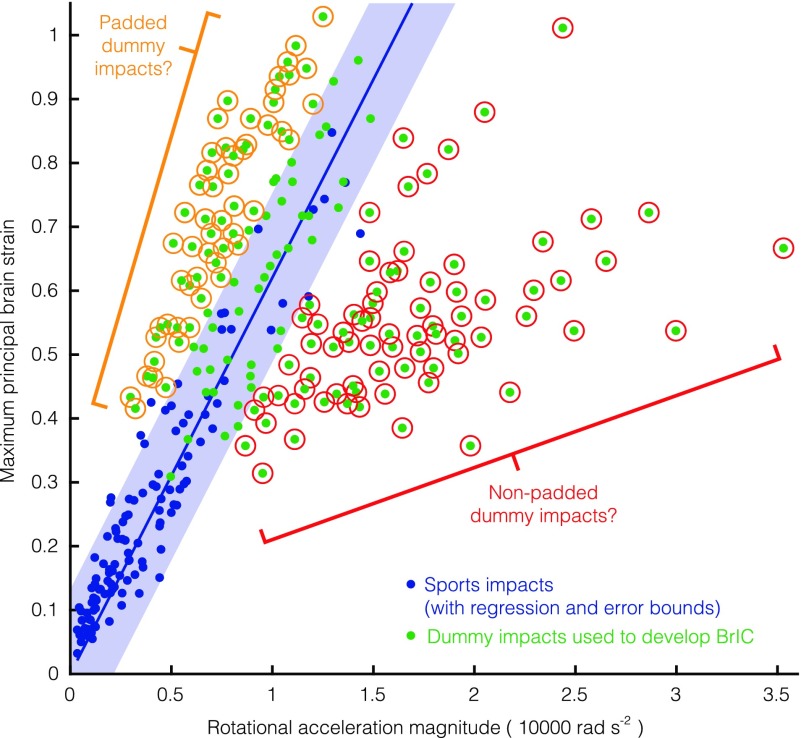
High voluntary rotational velocities without the presence of brain injury call into question previously proposed velocity-based criteria. The most notable of these is BrIC, which has been proposed by the National Highway Traffic Safety Administration (NHTSA) for potential adoption into their New Car Assessment Program (NCAP) vehicle safety standards.³¹ Whereas BrIC may be suitable for assessing severe brain injuries, it may have limitations in predicting injuries in the concussive regime. The reason for BrIC's limitations in the concussive regime could be attributed to the NHTSA's methods for relating head kinematics in dummy tests to brain tissue deformation. We found discrepancies between these relationships and those found in voluntary motions and sports impacts. Rotational acceleration was not used to develop BrIC due to poor correlation with MPS (Fig. 8).³¹ However, we found a strong correlation between rotational acceleration and MPS in sports impacts and voluntary movements (the latter in a much smaller range). The discrepancy in our findings may be attributed to Takhounts and colleagues, grouping padded and nonpadded dummy impacts together in their analysis. Whereas our (helmeted) sports impacts lie in a frequency regime sensitive to both velocity and acceleration (15 Hz), nonpadded dummy impacts have faster dynamics (>15 Hz) and push head motion into a regime sensitive to changes in rotational velocity, suggesting that the severe injuries that BrIC were developed to measure are most sensitive to short-duration, high-frequency events. As a result, these nonpadded impacts yield less MPS for increases in rotational acceleration and therefore poor correlation with the padded impacts overall.

FIG. 8.

Comparing BrIC dummy tests to sports impacts. In the development of BrIC, rotational acceleration was found to not correlate well with maximum principal strain (MPS) in the brain.³¹ This may be because padded and unpadded dummy impacts were grouped together. Sports impacts lie somewhere in the middle between these conditions and show tight correlation between rotational acceleration and MPS. BrlC, Brain Injury Criterion. Color image is available online.

Padded and nonpadded groups were tightly correlated in rotational velocity versus MPS because the presence of padding would be expected to affect rotational acceleration in the short time scale it peaks. For our very-low-frequency voluntary motion tests and sports impacts, MPS was most sensitive to changes in angular acceleration, suggesting that concussion risk should be additionally assessed with rotational accelerations or motion duration. Further, rotational acceleration and MPS trended similarly between voluntary motions and the dummy tests used to develop BrIC. However, a given rotational velocity in voluntary motions produced much less MPS than the dummy tests. This may suggest another fundamental limitation of BrIC: It may not apply to noncontact regimes where a passenger's head whips inside a car with high rotational velocity by low rotational acceleration. That is to say, the padded and nonpadded dummy impacts used to quantify severe brain injury risk do not represent the directly measured human head motions reported here for concussion risk assessment, as evidenced by the weaker correlation between BrIC and MPS for voluntary movements and sports impacts. Aside from MPS, Takhounts and colleagues used Cumulative Strain Damage Measure (CSDM) to describe the percentage of the brain exceeding a specified certain strain threshold. CSDM for a 25% threshold was zero for all voluntary movements, further suggesting a limited correspondence between the dummy impacts used to develop BrIC and the human head movements recorded here.

BrIC is essentially a combination of rotational velocity components weighted by the extent to which each can be tolerated. We found that multiple subjects could perform voluntary head movements with high enough rotational velocities to exceed the BrIC scores of recorded concussions. The same would probably be true for other high rotational velocity (and likely noninjury) head motions like figure skating.³⁰ Given that BrIC used measures of strain across the whole brain (MPS and CSDM), it is no surprise that horizontal rotation is weighted as the least tolerable rotation direction in BrIC given that it was previously found to produce more overall brain damage than other measures in a previous computational study.⁵² However, coronal rotation is weighted as the most tolerable direction in BrIC despite this direction producing the most severe diffuse axonal injuries (DAIs) in primates^53,54 and producing the highest tract strains in the body of the corpus callosum through excitation of lateral falx displacement.⁵¹ Perhaps a combination of multiple criteria is needed to predict risk of injury to specific structures in the brain.

Even a single direction of rotational acceleration separated voluntary motions from concussive impacts better than BrIC. Horizontal rotational acceleration had almost twice the area under the precision-recall curve as BrIC. This means that for the voluntary motion, and sports impact (subconcussive and concussive) data set, horizontal acceleration was better suited for correctly detecting concussions. Precision-recall is especially appropriate for concussion risk given that it considers disparate probabilities in the positive and negative classes. That is, precision-recall suits applications where the positive class (in this case, concussion) is rare or should be more heavily weighted. If it were possible to take a nonbiased, random sample in this high-velocity regime, we could conceivably amass more data that would further worsen the precision of BrIC (by increasing the number of false positives) whereas horizontal rotational acceleration would remain largely unaffected. Although we are not proposing the use of horizontal rotational acceleration as a stand-alone criterion, we note that rotational acceleration should be incorporated into classification of concussion in order to capture relevant loading regimes.

These loading regimes were captured by our second-order system model, whereby sports impacts lied in the knee of constant response lines where changes in both rotational acceleration and rotational velocity seem to contribute fairly equally to response of the mass (which represents the brain). However, coronal- and sagittal-plane sled tests of seat-belted volunteers are representative of certain motor vehicle collisions and occur in a lower-frequency, acceleration-sensitive regime similar to voluntary motions.^26,27 In this lower-frequency (noncontact) regime, head whiplash has been shown to produce DAI in primates^20,53,55 and humans.⁵⁶ Because BrIC only uses rotational velocity, it only applies to high-frequency impacts, such as those that are typically associated with severe brain injuries. BrIC fails to capture the importance of rotational acceleration (and insignificance of velocity) in producing brain deformation in the low-frequency regime that are typically associated with mTBI or concussion.

Finite element simulations and neurological testing suggest that voluntary head movements do not produce acute injury. Across all movements, we observed finite element strains that were much smaller than previous reported injury levels and thresholds. Temporally, strain had strong correspondence with rotational acceleration. Strain had a strong temporal correlation with acceleration, significantly more than velocity, providing further evidence that perhaps the latter is the likelier root cause of brain injury. Across all of the neurological testing, we observed no significant deficits from baseline. Although not significant, results from running the BESS revealed trends consistent with past findings.³⁹ Like previous studies, we found that a subject's pre-experiment BESS score was typically better than their baseline a few days before. Both tests were conducted before any head motion experiments, and the difference is likely attributed to a previously reported learning effect.^41,44 After the experiments, we found that BESS performance decreased (reported more errors per subject) back to baseline levels. This was likely attributed to the vestibular (dizzying) effects of repeated head rotations³⁹ that are not associated with mTBI, though decoupling these effects should be investigated further in future studies. At 20 min post-experiment, BESS values improved again, suggesting that the vestibular effects had faded. KD and SAC had no noteworthy trends aside from similar, previously reported learning effects.^46,48 That they have been previously found sensitive to brain injury^40,46–50 suggests the voluntary motion experiments produced little change in the subjects' oculomotor function, visual acuity, language processing, orientation, and memory.

There are several limitations to mention. The biggest and most obvious limitation is, in our assumption, that we have characterized peak human head rotation. It is possible that other subjects, perhaps with different neck sizes and strengths, may have produced even faster rotational velocities. It is also possible that our own subjects could have rotated faster, but did not, because of hesitation and the desire to protect themselves. We designed our study to minimize these risks. First, we collected an even split between ball sport athletes that are perhaps more accustomed to rapid head motion. Second, we asked each subject to perform each test in triplicates to allow them to warm up and get used to the motion. Finally, we measured head motions with and without a visual input in case some subjects responded more favorably to one over the other.

Accuracy of the finite element model is another limitation. The KTH model was previously validated against data from cadaveric drop tests.⁵⁷ However, the strains observed in this study are likely within the error bounds of the model (less than 5%). Although it is not advisable to consider these strain values in the absolute sense, it is safer to consider them relative to padded sports impacts (and injuries) that were previously simulated using the same model. Although we did not observe any significant finite element strains of neurological deficits indicative of an injury in the 9 subjects we tested, this does not mean that injuries cannot occur with voluntary head motions. It is possible that with a larger subject population, we might find very rare cases in which subjects are capable of inflicting minor injuries on themselves, though we believe this is unlikely.

Another limitation is the effect of confounding factors on the neurological assessments. We chose to evaluate subjects using these assessments because they are either standard in the field (components of SCAT3) or have been extensively studied (KD). However, we acknowledge that there are factors, such as learning effects or exercise, that can affect a subject's test score (R3-3). Other limitations of the study could come from confounding variables, such as tiredness, diet, and stress, that could have affected head motion performance.

Here, we find that humans are capable of producing head rotational velocities in the coronal and horizontal planes that can exceed previously measured concussion levels without neurological deficit. It therefore stands to reason that perhaps rotational acceleration is a better indicator of concussion risk. Given that BrIC was developed to assess severe brain injuries for vehicle safety testing, it is prudent to consider a different risk criteria for impact regimes resulting in mTBIs (concussions), such as an acceleration-inclusive alternative that distinguishes voluntary movements, subconcussive impacts, and concussions. Such a criterion could not only predict concussion risk, but also provide a basis on which to evaluate protective technology and the devices used to test them.⁵⁸ Of course, more data are necessary to confirm the findings of our study and determine whether BrIC or any other injury criteria would be most effective in predicting risk of concussion.

Author Disclosure Statement

No competing financial interests exist.