White Matter Connectome Edge Density in Children with Autism Spectrum Disorders: Potential Imaging Biomarkers Using Machine-Learning Models

Abstract

Prior neuroimaging studies have reported white matter network underconnectivity as a potential mechanism for autism spectrum disorder (ASD). In this study, we examined the structural connectome of children with ASD using edge density imaging (EDI), and then applied machine-learning algorithms to identify children with ASD based on tract-based connectivity metrics. Boys aged 8–12 years were included: 14 with ASD and 33 typically developing children. The edge density (ED) maps were computed from probabilistic streamline tractography applied to high angular resolution diffusion imaging. Tract-based spatial statistics was used for voxel-wise comparison and coregistration of ED maps in addition to conventional diffusion tensor imaging (DTI) metrics of fractional anisotropy (FA), mean diffusivity (MD), and radial diffusivity (RD). Tract-based average DTI/connectome metrics were calculated and used as input for different machine-learning models: naïve Bayes, random forest, support vector machines (SVMs), and neural networks. For these models, cross-validation was performed with stratified random sampling ( × 1,000 permutations). The average accuracy among validation samples was calculated. In voxel-wise analysis, the body and splenium of corpus callosum, bilateral superior and posterior corona radiata, and left superior longitudinal fasciculus showed significantly lower ED in children with ASD; whereas, we could not find significant difference in FA, MD, and RD maps between the two study groups. Overall, machine-learning models using tract-based ED metrics had better performance in identification of children with ASD compared with those using FA, MD, and RD. The EDI-based random forest models had greater average accuracy (75.3%), specificity (97.0%), and positive predictive value (81.5%), whereas EDI-based polynomial SVM had greater sensitivity (51.4%) and negative predictive values (77.7%). In conclusion, we found reduced density of connectome edges in the posterior white matter tracts of children with ASD, and demonstrated the feasibility of connectome-based machine-learning algorithms in identification of children with ASD.

Introduction

Autism spectrum disorder (ASD) represents a complex, heterogeneous neurodevelopmental condition characterized by deficits in social communication, as well as repetitive behaviors and atypical sensory reactivity (American Psychiatric Association, 2000). A 2013 survey by Centers for Disease Control and Prevention's National Center for Health Statistics showed that the prevalence of parent-reported ASD among children aged 6–17 has continued to increase from 1.16% in 2007 to 2.00% in 2011–2012, likely due to broader diagnostic criteria, increased awareness of the disorder among parents and providers, increased parental age, and environmental contributors affecting epigenetic factors (Blumberg et al., 2013). It is now clear that inherited and de novo genetic changes, including copy number variations and single nucleotide variants, in neurodevelopment genes contribute to the phenotype in 25–40% of cases with an evolving understanding of polygenetic and epigenetic factors (Chang et al., 2016; Ramaswami and Geschwind, 2018).

In addition to learning about genetic and epidemiologic factors, there has been increasing evidence from neuroimaging research suggesting that alterations in white matter microstructure and connectivity contribute to cognitive and behavioral deficits in affected children (Dean et al., 2016). Neuroimaging studies not only help illuminate the underlying mechanism of ASD phenotype in general (Falahpour et al., 2016; Libero et al., 2016) but also could provide objective biomarkers for timely identification of the ASD (Akshoomoff et al., 2004) as well as providing a marker for change with practice-based intervention (Sullivan et al., 2014).

Diffusion tensor imaging (DTI) and fiber tractography have provided quantitative evaluation of white matter microstructure and connectivity in children with ASD (Li et al., 2017). The structural connectome, representing the whole-brain network of macroscale white matter connectivity, has emerged during the past decade as a powerful formalism for the study of neurological and psychiatric diseases. The connectome is particularly relevant for ASD, which is hypothesized to result from short-range overconnectivity and long-range underconnectivity (Blanken et al., 2017; Shukla et al., 2011; Washington et al., 2014). However, to date there are no studies of ASD examining regional connectomic properties within the white matter. Edge density imaging (EDI) has recently been introduced as a framework to represent the anatomic embedding of connectome edges within the white matter (Owen et al., 2015, 2016). In EDI, the edges or links of the white matter are extracted by constraining probabilistic tractography to network nodes based on standard atlas parcellation of the cortical and deep gray matter nuclei (Owen et al., 2015, 2016).

Machine-learning analyses are also gaining popularity for pattern recognition and development of classification (or regression) models based on multidimensional data. These algorithms seem particularly suitable for devising classifiers based on multitude of variables extracted from diffusion and connectivity maps. In this study, we compared the white matter connectome and microstructure between children with ASD and typically developing children (TDC) using voxel-wise analysis. Then, we applied different machine-learning algorithms for identification of ASD based on the white matter tract-based average edge density (ED) and conventional DTI metrics.

Subjects and Methods

Participants and assessment

The participants in this study were recruited and prospectively enrolled through the UCSF Sensory Neurodevelopment and Autism Program clinical sites and research database (Chang et al., 2014, 2015; Owen et al., 2013). Children with ASD were diagnosed according to the Autism Diagnostic Interview-Revised (ADI-R) (Lord et al., 1994), Autism Diagnostic Observation Schedule (ADOS)-G (Lord et al., 2000), social communication questionnaire (SCQ) (Eaves et al., 2006), and Diagnostic Statistical Manual-IV criteria (American Psychiatric Association, 2000). In addition, all participants were screened and interviewed by a senior pediatric neurologist (E.J.M.) with expertise in neurodevelopmental disorders. The exclusion criteria were history of premature birth (<34 weeks), known genetic disorder associated with autism at time of enrollment (e.g., fragile X syndrome), or other neurological conditions that can potentially affect neurodevelopment (e.g., epilepsy). TDC did not meet diagnostic criteria for ASD or sensory processing disorders. To limit the confounding effects of age and gender, only boys aged 8–12 years were included in our analysis. Under the institutional review board approved protocol, informed consent was obtained from the parents or legal guardians, with the assent of all participants.

Magnetic resonance imaging protocol

All brain imaging was performed on a 3T MRI scanner (Siemens, Erlangen, Germany) using a 12-channel head coil. Anatomical scans were acquired using a three-dimensional T1-weighted magnetization-prepared rapid gradient echo sequence (field of view = 256 mm, 1 mm cubic voxels, time to repeat/echo time/inversion time = 2,300/2.98/900 ms, flip angle = 9°). The whole-brain high angular resolution diffusion imaging scan was acquired using a multislice two-dimensional single-shot twice-refocused diffusion-weighted echoplanar imaging sequence (repetition time, 8,000 ms; echo time, 109 ms; 100 × 100 matrix; field of view, 220 mm; voxel size, 2.2 × 2.2 × 2.2 mm); 64 noncollinear diffusion directions, uniformly distributed around a unit sphere with b value of 2,000 sec/mm²; and 1 brain volume with no diffusion weighting (Chang et al., 2014, 2015; Owen et al., 2013).

DTI postprocessing

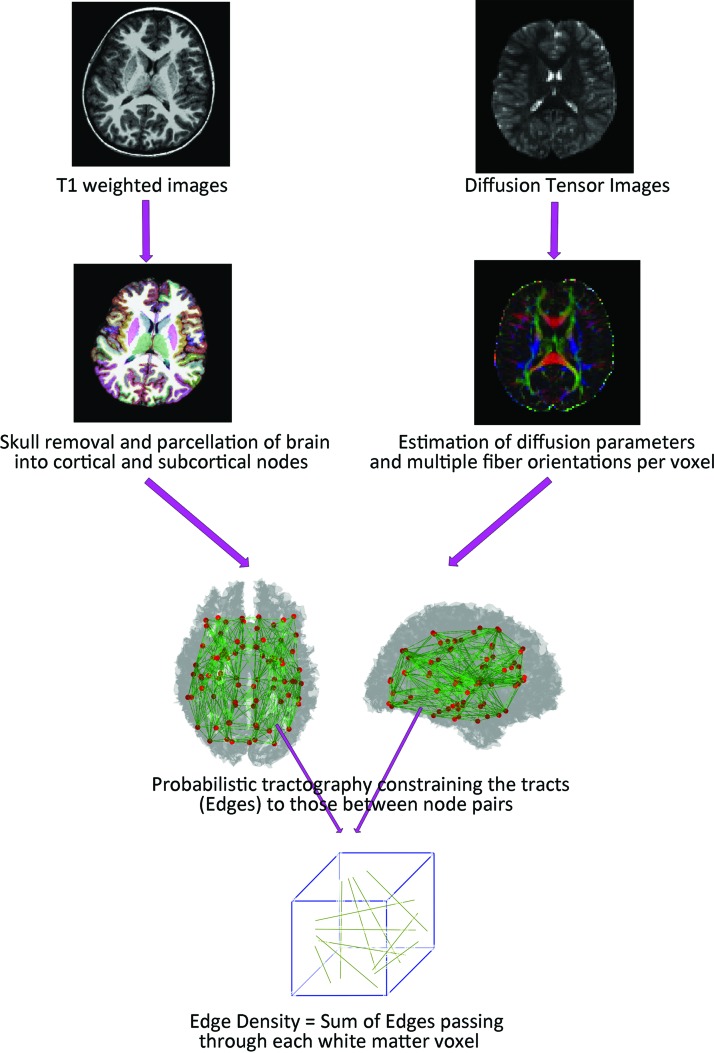
We used the software packages included in the Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library (FSL) version 5.0.8.^* The initial quality assurance involved eddy current and motion corrections, which was followed by removal of nonbrain tissue. The FSL's DTIFIT toolbox was used to compute the fractional anisotropy (FA), mean diffusivity (MD), and radial diffusivity (RD) maps. The Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques (BEDPOSTX2) package from FSL was used for estimation of diffusion parameters at each voxel and modeling of multiple fiber orientations per voxel (Chang et al., 2014, 2015; Owen et al., 2013). Figure 1 summarizes the image postprocessing pipeline.

FIG. 1.

EDI processing pipeline summary. EDI, edge density imaging. Color images are available online.

Edge density imaging

For computation of ED maps, the T1-weighted series were first parcellated into 68 cortical and 14 subcortical regions based on the Desikan–Killiany atlas from FreeSurfer software (Desikan et al., 2006). These 82 regions served as the connectome nodes (Fig. 1). Then, the T1-weighted volumes, and subsequently the 82 cortical and subcortical regions, were registered to the diffusion space. Using EDI methods reported previously (Owen et al., 2015, 2016; Wang et al., 2017), the cortical and subcortical regions were employed as seed and target regions for probabilistic tractography using the FSL probtrackx2 algorithm (Owen et al., 2015). The total number of structural connectome edges passing through each voxel in white matter was calculated as the ED value for that voxel (Fig. 1).

Tract-based spatial statistics and voxel-wise analysis

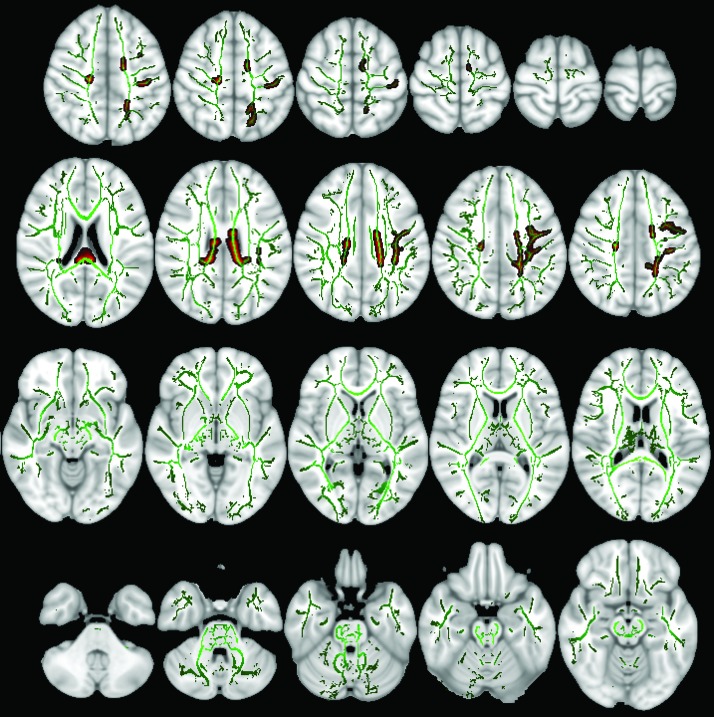
For tract-based spatial statistics (TBSS), each FA map was registered to all other FA maps to identify the most representative map of the cohort and use this representative FA map as the target image. This target image was then affine-aligned into MNI-152 standard space, and then the rest of FA maps were transformed into MNI-152 space, combining the nonlinear transform to the target and the affine transform from the target to standard space. The mean of aligned FA maps was used to create a skeletonized image representing the center of white matter tracts across all subjects. This white matter skeleton was thresholded to exclude voxels with FA values <0.2 (Fig. 2), which may represent regions of high intersubject variability. The ED maps were projected to MNI-152 using the registration matrix from the corresponding FA maps and threshold. For nonparametric voxel-wise statistics, we used “randomise” from FSL with 5,000 permutations and applied threshold-free cluster enhancement (TFCE) for multiple voxel-wise comparison correction. General linear model (GLM) designs were applied to correct for subjects' age as a covariate. For the ED maps, both ASD>control and control<ASD contrast designs were tested. The final statistical maps at a p-value <0.05 threshold were created and corrected for multiple comparisons (Fig. 2). For anatomic localization, we used the Johns Hopkins University white matter tractography atlas (ICBM-DTI-81) incorporated into FSL.

FIG. 2.

The mean skeletonized fractional anisotropy of all 47 subjects is overlaid on MNI-152 brain map in green color. Those white matter tracts with significantly lower ED in children with ASD compared with TDC are filled with red, based on voxel-wise TBSS analysis and after applying TFCE correction. ASD, autism spectrum disorder; ED, edge density; TBSS, tract-based spatial statistics; TDC, typically developing children; TFCE, threshold-free cluster enhancement. Color images are available online.

Extraction of tract-based DTI and connectome metrics

For univariate and multivariate analysis as well as machine-learning models, the average FA, MD, RD, and ED of white matter tracts from the ICBM-DTI-81 atlas were calculated. For this purpose, the ICBM-DTI-81 template was warped into each subject's native diffusion space applying the inverse spatial transformations from coregistration step described above (Chang et al., 2014, 2015; Owen et al., 2013). The average DTI/connectome metrics was then calculated for all 48 white matter tracts in the ICBM-DTI-81 atlas for each subject.

Voxel-based morphometry

We applied voxel-based morphometry (VBM) to investigate voxel-wise differences in the local gray and white matter volume and topography between children with ASD versus TDC. The VBM tool included in FSL was used.^† Initially, the brain in T1-weighted images was extracted using the Brain Extraction Tool. Next, brain-extracted images were segmented into gray matter, white matter, and cerebrospinal fluid. Then, the gray matter segments were aligned to ICBM-152 space applying the affine registration. These images were averaged to create a study-specific template, and finally all gray matter segments were nonlinearly registered and concatenated onto ICBM-152 space. These registered volume images were then modulated, and corrected for local expansion or contraction. These modulated segmented images were smoothed with an isotropic Gaussian kernel at a sigma of 3 mm. Similar to voxel-wise statistics for TBSS, we used “randomise” from FSL with 5,000 permutations and applied TFCE. We also used GLM for analysis of age as a covariate.

Machine learning

We evaluated different machine-learning algorithms for predicting cohort assignment as ASD versus TDC based on tract-specific average connectome/DTI metric: naïve Bayes, random forest, support vector machine (SVM) with linear kernel, and polynomial kernel, and neural networks. Combination of these models with different DTI and connectomic metrics was evaluated using the 48 white matter average FA, MD, RD, and ED values as input for each model. To evaluate the performance of these algorithms, the subject cohort was randomly divided into the training and validation datasets with preservation of ASD-to-TDC ratio. The stratified random sampling for training and validation samples was repeated 1,000 times for cross-validation. For each permutation, the machine-learning model was trained on training sample, and a confusion matrix was constructed in the corresponding validation sample based on the model predictions. The accuracy, sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) were calculated using the confusion matrix for each validation cohort, and the average across 1,000 permutations is presented. The accuracy was defined by the sum of true positive and true negative subjects (correctly classified) divided by total number of subjects in each validation sample. For each confusion matrix, the area under the curve (AUC) of receiver operating characteristics (ROCs) was also calculated.

For naïve Bayes, we applied the “naivebayes” “r” package with a Laplace smoothing value of 0.^‡ For random forest analysis, we applied the “randomForest” package. As recommended by the package authors, we used 500 random trees in each of the random forest models; and a 1/3 subset of variables was tried at each split. The averaged “mean decrease in Gini coefficients” is reported to depict the effect of different variables on classification accuracy of the final model. For SVM analysis, we used the “e1071” package in “r” project. We applied both linear and polynomial kernels for data classification. Tuning the SVM models, a cost of 0.1 returned the optimal error rate, and was applied for all linear kernels. For the polynomial kernel, a sigma of 1 was applied. For neural networks, we applied the “neuralnet” package using “resilient back propagation” methods. Using 2/3 rule, we included five hidden layers with 32, 21, 7, 4, and 2 neurons, consequentially.

Statistics

The data are expressed as number (frequency) or average ± standard deviation, where appropriate. For univariate analysis, Student's t-test was performed. Cohen's d coefficient was calculated to determine the effect size of the tract-based average DTI/connectome metrics using the “effsize” package from “r.” For multivariate analysis, we applied the penalized logistic regression with stepwise forward and backward selection using the “stepPlr” package. The penalized regression is suitable for multivariate analysis with substantial collinearity between independent variables.

Results

Participant characteristics

A total of 47 boys, 8–12 years of age, were included from the Sensory Neurodevelopment and Autism Program neuroimaging collection. Of these, 14 (30%) boys met criteria for ASD and 33 (70%) did not. All children with ASD exceeded screening criteria on either the ADI-R or SCQ parent report measures, with all these children exceeding autism score criteria on the ADOS. There was no significant difference in the average age of children with ASD (8.9 ± 2.7 years) versus the TDC (10.0 ± 3.3 years, p = 0.52).

Voxel-wise comparison of connectivity maps

On voxel-wise TBSS analysis, after applying TFCE, the body and splenium of the corpus callosum, bilateral superior and posterior corona radiata, and the left superior longitudinal fasciculus had significantly lower ED in children with ASD compared with TDC (Fig. 2). Conversely, there were no voxels in which the TDC cohort showed lower ED relative to the children with ASD. Table 1 lists the number of voxels in each of the white matter tracts from the ICBM-DTI-81 atlas with significant differences between the ASD and TDC study groups after applying TFCE. The GLM showed that children's age—in the restricted 8–12 years range examined—had no significant effect on voxel-wise ED values. In addition, there was no voxel-wise difference between children with ASD and TDC comparing FA (lowest voxel-wise p = 0.245), MD (lowest voxel-wise p = 0.275), and RD (lowest voxel-wise p = 0.240) maps.

Table 1.

The List of White Matter Tracts with Significant Difference in Edge Density Between the Children with ASD and TDC on Voxel-Wise TBSS Analysis

White matter tracts	No. of voxels
Body of corpus callosum	2,712
Splenium of corpus callosum	1,689
Left superior corona radiata	1,615
Right superior corona radiata	166
Left posterior corona radiata	435
Right posterior corona radiata	418
Left superior longitudinal fasciculus	1,243
Right sagittal stratum	8

Each cell represents the number of voxels with significantly lower edge density (p < 0.05) in children with ASD compared with TDC on voxel-wise TBSS analysis after correction for multiple comparison. There were no voxels with significantly higher edge density in children with ASD compared with TDC.

ASD, autism spectrum disorder; TBSS, tract-based spatial statistics; TDC, typically developing children.

Univariate and multivariate tract-based comparison

There was no significant difference between average ED and DTI microstructural metrics of select white matter tracts between ASD and TDC groups. Tables 2a–d list the results for select 22 white matter tracts chosen based on their Cohen's d effect size and results of voxel-wise analysis (Table 1). However, in multivariate stepwise penalized regression, the average ED of the left posterior corona radiata emerged as the only independent predictor of ASD (p = 0.046). In ROC analysis, the average ED of the left posterior corona radiata yielded an AUC of 0.665 (95% confidence interval: 0.491–0.838, p = 0.077) for distinction of children with ASD from TDC.

Table 2.

Univariate Comparison of DTI Microstructural and Connectome Metrics Between Select White Matter Tracts

	Edge density
a	ASD	TDC	t-test (p)	Cohen's d
Splenium of corpus callosum	98,064 ± 38,508	120,153 ± 27,940	0.067	−0.62
Body of corpus callosum	67,818 ± 28,892	83,668 ± 16,510	0.072	−0.61
Genu of corpus callosum	53,289 ± 19,884	62,095 ± 19,969	0.178	−0.44
Left cingulate gyrus	57,579 ± 21,190	65,918 ± 13,110	0.190	−0.43
Right cingulate gyrus	56,360 ± 18,261	63,704 ± 13,393	0.190	−0.43
Left fornix	30,340 ± 20,081	24,397 ± 9,107	0.305	0.34
Right fornix	4,340 ± 3,844	7,427 ± 8,530	0.094	−0.55
Left medial lemniscus	8,975 ± 6,520	6,551 ± 4,193	0.216	0.41
Right medial lemniscus	6,994 ± 4,648	9,070 ± 4,381	0.168	−0.45
Left superior longitudinal fasciculus	87,892 ± 24,300	100,197 ± 16,483	0.100	−0.55
Right superior longitudinal fasciculus	89,976 ± 29,152	93,908 ± 17,252	0.644	−0.15
Left superior corona radiata	51,781 ± 15,441	56,318 ± 8,407	0.315	−0.33
Right superior corona radiata	51,440 ± 18,157	58,002 ± 11,306	0.227	−0.40
Left posterior corona radiata	76,082 ± 23,974	90,637 ± 16,416	0.052	−0.66
Right posterior corona radiata	76,488 ± 27,227	83,469 ± 14,360	0.378	−0.29
Left sagittal stratum	81,545 ± 23,179	85,438 ± 15,748	0.573	−0.18
Right sagittal stratum	79,984 ± 15,392	82,581 ± 16,006	0.606	−0.17
Left superior cerebellar peduncle	2,630 ± 2,407	1,811 ± 1,817	0.267	0.36
Left superior cerebellar peduncle	2,945 ± 2,426	4,362 ± 2,142	0.071	−0.60
Left tapetum	35,561 ± 13,204	43,427 ± 16,420	0.093	−0.55
Right tapetum	44,099 ± 19,023	48,948 ± 14,266	0.402	−0.27

	Fractional anisotropy
b	ASD	TDC	t-test (p)	Cohen's d
Splenium of corpus callosum	0.655 ± 0.062	0.643 ± 0.020	0.494	0.22
Body of corpus callosum	0.578 ± 0.083	0.563 ± 0.031	0.521	0.21
Genu of corpus callosum	0.607 ± 0.068	0.591 ± 0.031	0.403	0.27
Left cingulate gyrus	0.401 ± 0.093	0.386 ± 0.034	0.556	0.19
Right cingulate gyrus	0.400 ± 0.096	0.373 ± 0.031	0.336	0.32
Left fornix	0.455 ± 0.087	0.441 ± 0.028	0.568	0.19
Right fornix	0.338 ± 0.093	0.358 ± 0.044	0.455	−0.24
Left medial lemniscus	0.547 ± 0.100	0.522 ± 0.029	0.377	0.29
Right medial lemniscus	0.538 ± 0.083	0.523 ± 0.027	0.513	0.21
Left superior longitudinal fasciculus	0.426 ± 0.079	0.416 ± 0.016	0.647	0.15
Right superior longitudinal fasciculus	0.433 ± 0.088	0.426 ± 0.014	0.757	0.10
Left superior corona radiata	0.464 ± 0.071	0.443 ± 0.015	0.291	0.35
Right superior corona radiata	0.453 ± 0.092	0.433 ± 0.017	0.431	0.26
Left posterior corona radiata	0.438 ± 0.066	0.417 ± 0.024	0.273	0.36
Right posterior corona radiata	0.430 ± 0.075	0.424 ± 0.023	0.764	0.10
Left sagittal stratum	0.446 ± 0.066	0.437 ± 0.023	0.621	0.16
Right sagittal stratum	0.434 ± 0.051	0.429 ± 0.025	0.770	0.09
Left superior cerebellar peduncle	0.570 ± 0.068	0.564 ± 0.042	0.745	0.10
Left superior cerebellar peduncle	0.553 ± 0.076	0.542 ± 0.036	0.629	0.16
Left tapetum	0.466 ± 0.083	0.441 ± 0.036	0.295	0.34
Right tapetum	0.482 ± 0.063	0.483 ± 0.035	0.953	−0.02

	Mean diffusivity (× 1,000)
c	ASD	TDC	t-test (p)	Cohen's d
Splenium of corpus callosum	0.622 ± 0.025	0.625 ± 0.021	0.726	−0.11
Body of corpus callosum	0.672 ± 0.035	0.675 ± 0.029	0.786	−0.09
Genu of corpus callosum	0.615 ± 0.036	0.621 ± 0.035	0.604	−0.17
Left cingulate gyrus	0.724 ± 0.033	0.707 ± 0.036	0.131	0.50
Right cingulate gyrus	0.701 ± 0.034	0.706 ± 0.042	0.668	−0.14
Left fornix	0.682 ± 0.068	0.677 ± 0.027	0.791	0.09
Right fornix	1.070 ± 0.261	1.008 ± 0.116	0.406	0.27
Left medial lemniscus	0.627 ± 0.056	0.642 ± 0.020	0.359	−0.30
Right medial lemniscus	0.619 ± 0.036	0.625 ± 0.020	0.534	−0.20
Left superior longitudinal fasciculus	0.635 ± 0.024	0.630 ± 0.024	0.496	0.22
Right superior longitudinal fasciculus	0.641 ± 0.032	0.647 ± 0.026	0.536	−0.20
Left superior corona radiata	0.621 ± 0.025	0.617 ± 0.019	0.560	0.19
Right superior corona radiata	0.618 ± 0.022	0.612 ± 0.019	0.384	0.28
Left posterior corona radiata	0.680 ± 0.030	0.678 ± 0.028	0.793	0.08
Right posterior corona radiata	0.682 ± 0.038	0.684 ± 0.029	0.840	−0.07
Left sagittal stratum	0.678 ± 0.029	0.668 ± 0.026	0.273	0.36
Right sagittal stratum	0.694 ± 0.033	0.684 ± 0.027	0.338	0.31
Left superior cerebellar peduncle	0.681 ± 0.034	0.679 ± 0.034	0.800	0.08
Left superior cerebellar peduncle	0.672 ± 0.030	0.669 ± 0.024	0.807	0.08
Left tapetum	0.754 ± 0.055	0.731 ± 0.034	0.156	0.47
Right tapetum	0.737 ± 0.043	0.720 ± 0.036	0.196	0.43

	Radial diffusivity (× 1,000)
d	ASD	TDC	t-test (p)	Cohen's d
Splenium of corpus callosum	0.342 ± 0.068	0.356 ± 0.023	0.479	−0.23
Body of corpus callosum	0.415 ± 0.078	0.429 ± 0.035	0.544	−0.20
Genu of corpus callosum	0.368 ± 0.059	0.383 ± 0.036	0.384	−0.28
Left cingulate gyrus	0.555 ± 0.073	0.551 ± 0.038	0.853	0.06
Right cingulate gyrus	0.539 ± 0.076	0.557 ± 0.044	0.401	−0.27
Left fornix	0.502 ± 0.091	0.502 ± 0.029	0.997	0.00
Right fornix	0.877 ± 0.270	0.809 ± 0.119	0.378	0.29
Left medial lemniscus	0.411 ± 0.083	0.432 ± 0.019	0.355	−0.30
Right medial lemniscus	0.410 ± 0.054	0.420 ± 0.021	0.525	−0.21
Left superior longitudinal fasciculus	0.481 ± 0.056	0.483 ± 0.024	0.875	−0.05
Right superior longitudinal fasciculus	0.483 ± 0.064	0.492 ± 0.025	0.606	−0.17
Left superior corona radiata	0.448 ± 0.043	0.456 ± 0.018	0.529	−0.20
Right superior corona radiata	0.449 ± 0.058	0.456 ± 0.017	0.672	−0.14
Left posterior corona radiata	0.504 ± 0.045	0.514 ± 0.031	0.482	−0.23
Right posterior corona radiata	0.511 ± 0.059	0.516 ± 0.031	0.765	−0.10
Left sagittal stratum	0.502 ± 0.040	0.499 ± 0.027	0.845	0.06
Right sagittal stratum	0.522 ± 0.036	0.517 ± 0.030	0.668	0.14
Left superior cerebellar peduncle	0.440 ± 0.050	0.438 ± 0.041	0.867	0.05
Left superior cerebellar peduncle	0.442 ± 0.054	0.445 ± 0.029	0.879	−0.05
Left tapetum	0.542 ± 0.070	0.539 ± 0.036	0.892	0.04
Right tapetum	0.523 ± 0.052	0.510 ± 0.037	0.401	0.27

The average ± standard deviation of edge density (a), fractional anisotropy (b), mean diffusivity (c), and radial diffusivity (d) are reported for select white matter tracts in each study group. Cohen's d was calculated as a measure of effect size (0.2: small; 0.5: medium; 0.8: large). Notably, of 48 white matter tracts in ICBM-DTI-81 atlas, those pairs with the largest effect size and/or those with significant voxel-wise difference (Table 1) were included.

DTI, diffusion tensor imaging.

Machine-learning classification

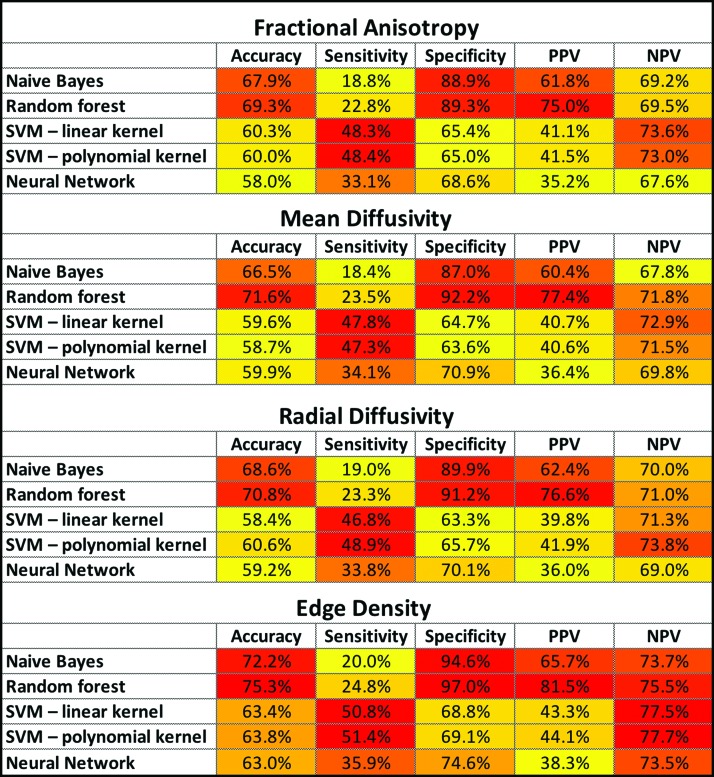
Applying a 3:7 ratio with preservation of the ASD-to-TDC proportion, we created 1,000 stratified random samples of training and validation datasets. The training datasets included 26 TDC and 11 ASD children, while the validation datasets included 7 TDC and 3 ASD children. Table 3 and Figure 3 demonstrate the test characteristics for different machine-learning models. Overall, the machine-learning models using tract-based ED had better performance in classification of children with ASD compared with those using FA, MD, or RD. Among all combinations, the greatest accuracy (75.3%), specificity (97.0%), and PPV (81.5%) were achieved by EDI-based random forest models, and the greatest sensitivity (51.4%) and NPV (77.7%) were achieved by EDI-based SVM with polynomial kernel (Fig. 3).

Table 3.

Comparative Test Characteristics for Combination of Different DTI/EDI Metrics with Machine-Learning Algorithms

	ROC AUC	Accuracy	Sensitivity	Specificity	PPV	NPV
Fractional anisotropy
Naive Bayes	0.66 (0.64–0.67)	67.9% (67.4%–68.4%)	18.8% (17.6%–20.1%)	88.9% (88.4%–89.5%)	61.8% (59.4%–64.2%)	69.2% (68.9%–69.6%)
Random forest	0.69 (0.68–0.70)	69.3% (68.8%–69.8%)	22.8% (21.4%–24.2%)	89.3% (88.9%–89.6%)	75.0% (73.1%–76.8%)	69.5% (69.1%–69.9%)
SVM—linear kernel	0.56 (0.54–0.58)	60.3% (59.5%–61.1%)	48.3% (46.7%–49.9%)	65.4% (64.3%–66.5%)	41.1% (39.7%–42.5%)	73.6% (72.9%–74.3%)
SVM—polynomial kernel	0.55 (0.51–0.57)	60.0% (59.2%–60.8%)	48.4% (46.8%–49.9)	65.0% (63.9%–66.0%)	41.5% (40.1%–42.8%)	73.0% (72.3%–73.7%)
Neural network	0.53 (0.51–0.57)	58.0% (57.2%–58.7)	33.1% (31.6%–34.5%)	68.6% (67.7%–69.5%)	35.2% (33.7%–36.8%)	67.6% (67.0%–68.1%)
Mean diffusivity
Naive Bayes	0.65 (0.64–0.67)	66.5% (65.9%–67.0%)	18.4% (17.2%–19.6%)	87.0% (86.5%–87.5%)	60.4% (58.1%–62.8%)	67.8% (67.4%–68.1%)
Random forest	0.71 (0.70–0.72)	71.6% (71.1%–72.1%)	23.5% (22.1%–25.0%)	92.2% (91.8%–92.6%)	77.4% (75.5%–79.3%)	71.8% (71.4%–72.1%)
SVM—linear kernel	0.56 (0.54–0.57)	59.6% (58.8%–60.4%)	47.8% (46.2%–49.4%)	64.7% (63.6%–65.8%)	40.7% (39.3%–42.0%)	72.9% (72.2%–73.6%)
SVM—polynomial kernel	0.55 (0.52–0.58)	58.7% (58.0%–59.5%)	47.3% (45.8%–48.9%)	63.6% (62.6%–64.6%)	40.6% (39.3%–41.9%)	71.5% (70.8%–72.1%)
Neural network	0.54 (0.52–0.56)	59.9% (59.1%–60.6%)	34.1% (32.6%–35.7%)	70.9% (69.9%–71.8%)	36.4% (34.8%–38.0%)	69.8% (69.2%–70.3%)
Radial diffusivity
Naive Bayes	0.66 (0.63–0.69)	68.6% (68.1%–69.2%)	19.0% (17.8%–20.3%)	89.9% (89.3%–90.4%)	62.4% (60.0%–64.8%)	70.0% (69.6%–70.3%)
Random forest	0.68 (0.66–0.70)	70.8% (70.3%–71.3%)	23.3% (21.9%–24.7%)	91.2% (90.8%–91.6%)	76.6% (74.7%–78.5%)	71.0% (70.6%–71.4%)
SVM—linear kernel	0.56 (0.53–0.58)	58.4% (57.6%–59.1%)	46.8% (45.2%–48.4%)	63.3% (62.3%–64.4%)	39.8% (38.5%–41.1%)	71.3% (70.6%–72.0%)
SVM—polynomial kernel	0.57 (0.54–0.60)	60.6% (59.8%–61.4%)	48.9% (47.3%–50.5%)	65.7% (64.6%–66.7%)	41.9% (40.6%–43.3%)	73.8% (73.1%–74.5%)
Neural network	0.54 (0.51–0.56)	59.2% (58.5%–60.0%)	33.8% (32.3%–35.3%)	70.1% (69.2%–71.1%)	36.0% (34.4%–37.6%)	69.0% (68.5%–69.6%)
Edge density
Naive Bayes	0.71 (0.69–0.72)	72.2% (71.7%–72.8%)	20.0% (18.7%–21.4%)	94.6% (94.0%–95.2%)	65.7% (63.2%–68.3%)	73.7% (73.3%–74.0%)
Random forest	0.75 (0.74–0.76)	75.3% (74.8%–75.9%)	24.8% (23.3%–26.3%)	97.0% (96.6%–97.4%)	81.5% (79.5%–83.5%)	75.5% (75.1%–75.9%)
SVM—linear kernel	0.59 (0.57–0.62)	63.4% (62.6%–64.3%)	50.8% (49.1%–52.6%)	68.8% (67.7%–70.0%)	43.3% (41.8%–44.7%)	77.5% (76.8%–78.2%)
SVM—polynomial kernel	0.60 (0.58–0.63)	63.8% (63.0%–64.7%)	51.4% (49.8%–53.1%)	69.1% (68.0%–70.3%)	44.1% (42.7%–45.6%)	77.7% (76.9%–78.4%)
Neural network	0.58 (0.55–0.61)	63.0% (62.2%–63.8%)	35.9% (34.3%–37.5%)	74.6% (73.6%–75.6%)	38.3% (36.6%–40.0%)	73.5% (72.9%–74.0%)

Detailed results for combination of different supervised machine-learning algorithms with DTI and EDI metrics for classification of children with ASD. The results are the average (95% confidence interval) performance for cross-validation of each algorithm among × 1,000 randomly selected validation samples.

AUC, area under the curve; EDI, edge density imaging; NPV, negative predictive value; PPV, positive predictive value; ROC, receiver operating characteristic; SVM, support vector machine.

FIG. 3.

Heat map summary for classification performance of different machine-learning algorithms using DTI and connectome metrics for identification of children with ASD. The accuracy, sensitivity, specificity, PPV, and NPV were calculated in validation datasets from × 1,000 cross-validation—details provided in Table 3. In each column, yellow to red color range is assigned to values from low to high, respectively. DTI, diffusion tensor imaging; SVM, support vector machine; PPV, positive predictive value; NPV, negative predictive value. Color images are available online.

The averaged “mean decrease in Gini coefficients” of random forest models from stratified cross-validation is reported to depict the effect of different variables on classification accuracy of the final model (Table 4). In EDI-based random forest models, the mean ED of left posterior thalamic radiation, right superior cerebellar peduncle, left sagittal stratum, left medial lemniscus, and left superior corona radiata had the highest averaged mean decrease in Gini coefficient.

Table 4.

Variables with the Largest “Mean Decrease in Gini Coefficient” in Random Forest Models

Fractional anisotropy		Mean diffusivity		Radial diffusivity		Edge density
White matter tracts	Mean decrease in Gini	White matter tracts	Mean decrease in Gini	White matter tracts	Mean decrease in Gini	White matter tracts	Mean decrease in Gini
Right posterior thalamic radiation	0.84	Left posterior thalamic radiation	0.82	Left posterior internal capsule	0.83	Left posterior thalamic radiation	0.89
Left posterior corona radiata	0.71	Left tapetum	0.59	Left posterior thalamic radiation	0.69	Right superior cerebellar peduncle	0.69
Left external capsule	0.51	Right tapetum	0.58	Left cingulate gyrus	0.56	Left sagittal stratum	0.56
Right superior cerebellar peduncle	0.42	Left anterior internal capsule	0.49	Right posterior thalamic radiation	0.52	Left medial lemniscus	0.52
Right fornix	0.41	Left cingulate gyrus	0.48	Right anterior internal capsule	0.51	Left superior corona radiata	0.51
Right uncinate fasciculus	0.41	Left sagittal stratum	0.45	Right uncinate fasciculus	0.44	Left superior longitudinal fasciculus	0.44
Right cingulate gyrus	0.40	Right superior fronto-occipital fasciculus	0.39	Right corticospinal tract	0.44	Right corticospinal tract	0.44
Left posterior thalamic radiation	0.38	Right posterior thalamic radiation	0.39	Middle cerebellar peduncle	0.42	Right medial lemniscus	0.42
Left posterior internal capsule	0.37	Pontine crossing tract	0.38	Pontine crossing tract	0.39	Left posterior internal capsule	0.39
Right anterior internal capsule	0.36	Left superior fronto-occipital fasciculus	0.37	Right posterior internal capsule	0.	Left posterior thalamic radiation	0.89

The 10 white matter tracts with the highest “mean decrease in Gini coefficient,” among random forest models (Table 3). The reported “mean decrease in Gini coefficient” represents the averaged values driven from 1,000 stratified random samples for the random forest models among different diffusion and connectomic metrics.

Voxel-based morphometry

The VBM analysis revealed no macrostructural difference between the two study groups. There was no significant difference in gray–white matter relative tissue concentration or regional volume comparing ASD children with TDC, in either ASD<control or control<ASD constructs.

Discussion

In voxel-wise analysis of the white matter connectome in children with ASD, we found lower ED in the body and splenium of corpus callosum, bilateral superior and posterior corona radiata, and the left superior longitudinal fasciculus compared with TDC. This measure of regional white matter connectome ED was more sensitive than conventional DTI metrics (i.e., FA, MD, and RD maps) as well as VBM of brain macrostructure, which failed to detect significant differences between the ASD and TDC groups at the studied sample size. While the voxel-wise analysis provides crucial information regarding the microstructural underpinning of the ASD, tract-based metrics extracted based on preset atlas might provide more feasible tool for distinguishing individual subjects with ASD. In this preliminary study, we showed the feasibility of applying different supervised machine-learning algorithms for identification of children with ASD based on tract-based DTI and connectomic metrics. While univariate tract-based variables fail to distinguish children with ASD from TDC, machine-learning models could construct imaging biomarkers for identification of ASD based on multitude of topographic DTI and connectomic information. In this study, the EDI-based models had better performance in identification of children with ASD compared with conventional DTI metrics, although the results should be confirmed in larger cohorts.

Numerous tractography and functional magnetic resonance imaging studies characterize ASD as a neurodevelopmental disorder due to underconnectivity between different brain regions (Li et al., 2017; Rane et al., 2015). The majority of prior DTI studies have demonstrated decreased FA and increased MD in white matter tracts (Di et al., 2018), most commonly in the corpus callosum and cingulum (Travers et al., 2012). The FA represents directional variation in apparent diffusion, and the MD is the average of eigenvalues measuring diffusion rate irrespective of direction. While the changes in FA and MD are sensitive measures of white matter microstructure, they are relatively nonspecific and may represent lower axonal density, thinner axons, or less myelination. In EDI, on the contrary, quantification of network edges represents the significance of each white matter voxel in the overall connectomic framework. Driven from the probabilistic calculation of tract density, ED provides a metric sensitive to directionality of diffusion at each voxel, and theoretically more likely representative of true neural fibers given the constraints in construction of edges originating from predetermined cortical and subcortical gray matter regions as connectome nodes. Although the number of cases in the current cohort was too small to draw a firm conclusion, these results suggest that ED is potentially more sensitive than FA, MD, and RD maps for identification of microstructural connectivity differences between children with ASD and the control cohort.

In our study, the results of EDI are consistent with the theory of decreased transcallosal fiber connectivity in children with ASD (Aoki et al., 2017). The commissural tracts connecting bilateral premotor, primary motor, and primary sensory cortex traverse through the body of corpus callosum (Hofer and Frahm, 2006); and the lower ED in the mid-corpus callosum may help explain sensory and motor processing deficits in ASD. The splenium, specifically, connects occipital, parietal, and temporal regions that are involved in visual processing. Lower ED in the splenium of corpus callosum in children with ASD may be related to deficits in visual processing (Di et al., 2018). Notably, callosal abnormalities, such as the diminished ED noted herein, are one of the most well-replicated findings for individuals with ASD, with implications for slower transmission of information leading to deleterious consequences for processing of nuanced and socially rich visual information (Demopoulos et al., 2015; Marco et al., 2012).

While voxel-wise comparison of EDI maps in children with ASD can elucidate the neural microstructural underpinning of autism, development of voxel-wise DTI/connectomic fingerprint for identification of individual subjects with ASD can be challenging. As a solution, atlas-based parcellation of white matter tracts can provide automated and reproducible tractometry variables for classification of individual subjects based on topographic pattern of connectivity changes. In our series, there was no significant difference in average tract-based DTI or connectomic metrics between children with ASD and TDC (Table 2). On the contrary, the average ED in the left posterior corona radiata was the only independent predictor of ASD in multivariate stepwise penalized regression. Still, the average ED of the left posterior corona radiata could not reach statistical significance in identification of children with ASD applying ROC analysis (p = 0.077). Nevertheless, multidimensional data from tract-based connectivity metrics could identify individuals with ASD using machine-learning algorithms.

In recent years, there has been increasing interest in the application of machine learning for objective and reproducible decision models in diagnosis or treatment planning. These models have been applied in neurological disorders, such as the diagnosis of Alzheimer's (Bryan, 2016) and Parkinson's disease (Haller et al., 2012), or lesion-symptom mapping in stroke patients (Zhang et al., 2014). Different machine-learning algorithms, however, vary in their implementation, mathematical logic, and computation. Given the small sample size and inherent variability in results of machine-learning algorithms depending on the randomly sampled training and validation datasets, we reported the averaged test characteristics among 1,000 stratified samples for cross-validation of each model. Thus, Table 3 results likely represent a realistic assessment of the classification accuracy for each combination of diffusion/connectomic metrics and machine-learning model in our cohort. The models using ED had better performance in identification of ASD compared with those using conventional DTI metrics. Also, the accuracy of random forest models was slightly higher than that of SVM models mostly due to higher PPV and specificity, although the results may not hold in a larger dataset (Table 3). It should be noted that the high accuracy achieved by random forest was in part due to assigning majority of participants to control cohort, achieving higher specificity and NPV at the expense of low sensitivity. This can affect clinical application of the model, given the cost of assigning a child with ASD to the TDC cohort, and thus preventing him/her from receiving proper and timely treatments. It is also noteworthy that, in a larger dataset, SVM models may outperform random forests for binary classification (Statnikov and Aliferis, 2007).

Of note, random forest models can also offer a glimpse into their classification constructs by reporting variable importance (mean decrease in Gini); however, the possible neurobiological translation of these outputs remains elusive—whether they are mere reflection of random forest algorithm computation or may indeed point out to neurobiologically important white matter tracts. Nevertheless, our preliminary results emphasize the importance of exploring different machine-learning options to identify the suitable solution in the development of image-based classifiers.

We found no significant difference in voxel-wise morphometric distribution of gray or white matter volume in our cohort. Prior studies also reported variable results regarding the cerebral and cerebellar volumetric differences between children with ASD and TDC (Boddaert et al., 2004; Chen et al., 2011; Girgis et al., 2007; Ismail et al., 2016; McAlonan et al., 2005). In a 2011 review of pooled density-based and volume-based voxel-wise morphometric studies on ASD, there was no consistent pattern of regional specificity with respect to gray and white matter differences (Chen et al., 2011). Also, while many studies on ASD children <6 years have shown regional increase in gray or white matter volumes; in ASD children >9 years, regional volumetric thinning is more commonly reported (Ismail et al., 2016). Aside from likely effects of age on volumetric changes of brain in children with ASD, the small sample size of our cohort might contribute to the lack of significant results in VBM analysis.

In addition to the small sample size, there are other limitations to our study. The unequal number of case and control participants can potentially affect the overall power of our voxel-wise study—particularly VBM. This may also affect the performance of machine-learning models, and contribute to uneven sensitivity and specificity values achieved by classifiers. The relatively low sensitivity of machine-learning models also raises question regarding their practical applicability. While restricting the inclusion criteria to boys between 8 and 12 years helped reduce the effects of age and gender as confounding factors, it limits the generalizability of our results. In addition, since this study focused on children with primary (i.e., idiopathic) ASD, the results may not be applicable to those with secondary forms of ASD due to genetic or chromosomal abnormalities.

While our investigation supports the potential value of white matter connectomics and application of machine-learning algorithms for identification of children with ASD, multisite and multimodal studies on large patient groups are the key to development of effective biomarkers for ASD and comprehensive characterization of the underlying mechanism. EDI is expected to benefit greatly in sensitivity and precision from multiband diffusion magnetic resonance imaging (MRI) sequences developed by the Human Connectome Project on the next generation of magnetic resonance scanners with faster and more powerful magnetic field gradients (Fan et al., 2016, 2017; Vu et al., 2015), as well as the application of more granular and robust cortical/subcortical atlases, such as from data-driven connectivity-based parcellation techniques (Tittgemeyer et al., 2018). Future studies can also integrate functional connectivity using resting-state functional MRI and magnetoencephalography with white matter microstructural and connectomic imaging, and apply machine-learning classifiers to identify objective patterns relevant to clinical diagnosis, prognostication, response to therapy, and/or treatment triage. Utilizing larger sample sizes and direct assessment of specific functional domains in ASD can also help gain a deeper understanding of how neural circuitry differences relate to individual patient symptoms.

Conclusion

Limited by small sample size and the present state of diffusion MRI acquisition and analysis technology for clinical research, we have reported the white matter connectomic correlates of ASD with topographic distribution of reduced white matter connectome Edges. Most notably, ED was more sensitive than conventional DTI metrics in identification of children with ASD. In addition, we have shown the potential for construction of multivariate classification models for identification of children with ASD, based on machine-learning analysis of white matter connectome EDI. The methodology introduced in this study can be applied to large cohorts in longitudinal trials using emerging diffusion MRI acquisition and tractography techniques for development of clinically useful imaging biomarkers of ASD from more sensitive and precise measurements of white matter connectomic ED. Such models can provide objective quantitative biomarkers for diagnosis, and potentially prognostication and treatment triage of children with ASD.

Author Disclosure Statement

No competing financial interests exist.