Impact of Microarray Preprocessing Techniques in Unraveling Biological Pathways

Abstract

To better understand the impact of microarray preprocessing normalization techniques on the analysis of biological pathways in the prediction of chronic fatigue (CF) following radiation therapy, this study has compared the list of predictive genes found using the Robust Multiarray Averaging (RMA) and the Affymetrix MAS5 method, with the list that is obtained working with raw data (without any preprocessing). First, we modeled the spiked-in data set where differentially expressed genes were known and spiked-in at different known concentrations, showing that the precisions established by different gene ranking methods were higher than working with raw data. The results obtained from the spiked-in experiment were extrapolated to the CF data set to run learning and blind validation. RMA and MAS5 provided different sets of discriminatory genes that have a higher predictive accuracy in the learning phase, but lower predictive accuracy during the blind validation phase, suggesting that the genetic signatures generated using both preprocessing techniques cannot be generalizable. The pathways found using the raw data set better described what is a priori known for the CF disease. Besides, RMA produced more reliable pathways than MAS5. Understanding the strengths of these two preprocessing techniques in phenotype prediction is critical for precision medicine. Particularly, this article concludes that biological pathways might be better unraveled working with raw expression data. Moreover, the interpretation of the predictive gene profiles generated by RMA and MAS5 should be done with caution. This is an important conclusion with a high translational impact that should be confirmed in other disease data sets.

1. Introduction

Microarray data analysis is used to identify important genes to predict at-risk phenotypes, understand biologic underpinning of health conditions, and identify therapeutic targets. However, microarray data are notorious for containing noise that historically contributed to issues around reproducibility, especially as related to gene/clinical phenotype relationships (Kooperberg et al., 2002; Larsson et al., 2005; Jeffery et al., 2006; Dinu et al., 2007). The effect of noise in inverse and classification problems has been theoretically analyzed by Fernandez-Martinez et al. (2014a,b). Furthermore, genomic noise also impedes accurate mechanistic conclusions by partially falsifying the biological pathways that are involved in the disease development (deAndrà-Galiana et al., 2016). To address this concern, it is common practice to apply different kinds of preprocessing techniques to the microarray data to amplify the gene signal and limit the noise caused by experimental factors (Irizarry et al., 2003). Noise might impact the results provided by the bioinformatic techniques used to identify the most discriminatory genes in phenotype prediction problems. Due to the high dimension and complexity of microarray data sets, filtering/ranking methods are often applied as a first step to preselect the set of most discriminatory genes.

In this article, we compared the precision of identifying biologically relevant genes obtained from a raw data set and preprocessed data sets using Robust Multiarray Average (RMA) and Affymetrix Microarray Suite 5.0 algorithm (MAS5). For that purpose, we used the most common ranking methods, Fisher's ratio (FR) and Fold Change (FC), to measure their predictive accuracy using a leave-one-out cross-validation approach. We first modeled the Affymetrix Latin Square Data for Expression Algorithm Assessment [Human Genome U133 Data Set Affymetrix (2015)], where 42 different control genes are spiked-in at known concentrations. This is commonly known as a spiked-in experiment. We observed that working with raw data provided better results than using the RMA and MAS5 preprocessed data sets to locate the spiked-in genes. To our knowledge, this is a novel observation that warrants confirmation in other disease data sets. In this study, we also present the results obtained for a radiotherapy-related fatigue data set in patients with prostate cancer (Saligan et al., 2014), obtaining some interesting and unexpected conclusions.

2. Microarrays Preprocessing Techniques

Microarrays are manufactured using photolithographic techniques to attach hundreds of thousands of different oligonucleotide sequences on the surface of a glass slide. These oligonucleotides correspond to known DNA or RNA sequences that are arranged in different probe sets. Quantification of the levels of transcripts in a sample is performed through hybridization to the specific probes and measurement of the expression through fluorescence-based methods. Generally, raw data contain about 20 pairs of oligonucleotides for each DNA or RNA target (gene) known as probe sets. The first component of these pairs is referred to as the Perfect Match (PM) probe. Each PM probe is paired with a Mismatch (MM) probe that is artificially created by changing the middle base with the intention of measuring nonspecific binding. Typically, to define a measure of gene expression, probe intensities are summarized for each probe set into a single value. Different studies have been performed to analyze the accuracy of these measurements and to correct the effect of noise in microarrays (Benito et al., 2004; Scherer, 2009; Chen et al., 2011). Two techniques of particular importance are RMA (Irizarry et al., 2003) and MAS5 (Affymetrix, 2001), and are analyzed in this article.

2.1. MAS5

The Affymetrix Microarray Suite 5.0 (MAS5) algorithm uses both PM and MM probes to summarize gene expression. The MAS5 signal of a probe set 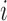is defined as the antilog of the Tukey's biweight robust mean (Huber and Ronchetti, 2009) of the following values:

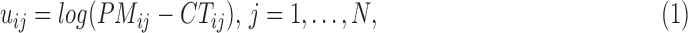where

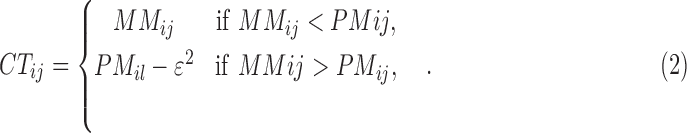being 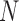the number of probes in the probe set (or gene) 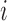and 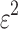a given positive amount that has to be individually adjusted for each probe set. Therefore, the robust Tukey's mean of a probe set 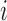is

where

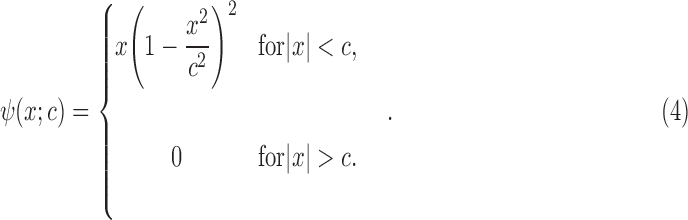2.2. RMA

Robust Multiarray Average (RMA) consists in three steps:

• 1. Background correction using the following additive probabilistic model:

  

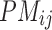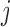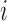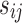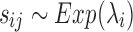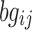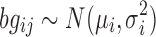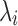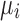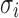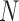  where is the PM of the probe in gene , is the gene signal and it is supposed to follow an exponential distribution , and is the background correction caused by the optical noise and nonspecific binding and it is supposed to follow a normal distribution . This identification problem has three unknown parameters (, , ) and different realizations for 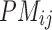. This problem can be typically solved by least squares and the maximum likelihood estimation.

• 2. Normalization across all arrays to make all distributions the same. This task is performed by quantile normalization and consists of normalizing the background corrected array to a common set of quantiles. This process is aimed at correcting array biases and avoiding the effect of outliers. This process provided a set of normalized probe values .

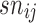• 3. Probe set summarizing where the final expression is calculated separately for each gene 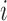using the following linear model in 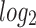scale:

  

  where 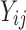are the background corrected, normalized, log-transformed probe intensities (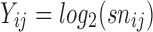), 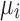is the log-expression level for gene 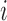, 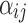is the probe affinity effect of probe 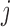in the gene 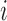, and 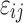is the independent identically distributed error term with zero mean. The probe affinities 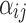should verify 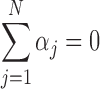. This linear model is solved using the median polish algorithm and provides the final summarized gene intensity value 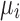, commonly used in phenotype prediction problems.

3. Materials and Methods

The methodology shown herein has two main parts as follows. (A) Analysis of the precision of the ranking methods using a synthetic data set for both raw and preprocessed data sets. (B) Analysis of the accuracy of predictive genes by inspecting the biological pathways for the cancer-related fatigue raw and preprocessed data sets.

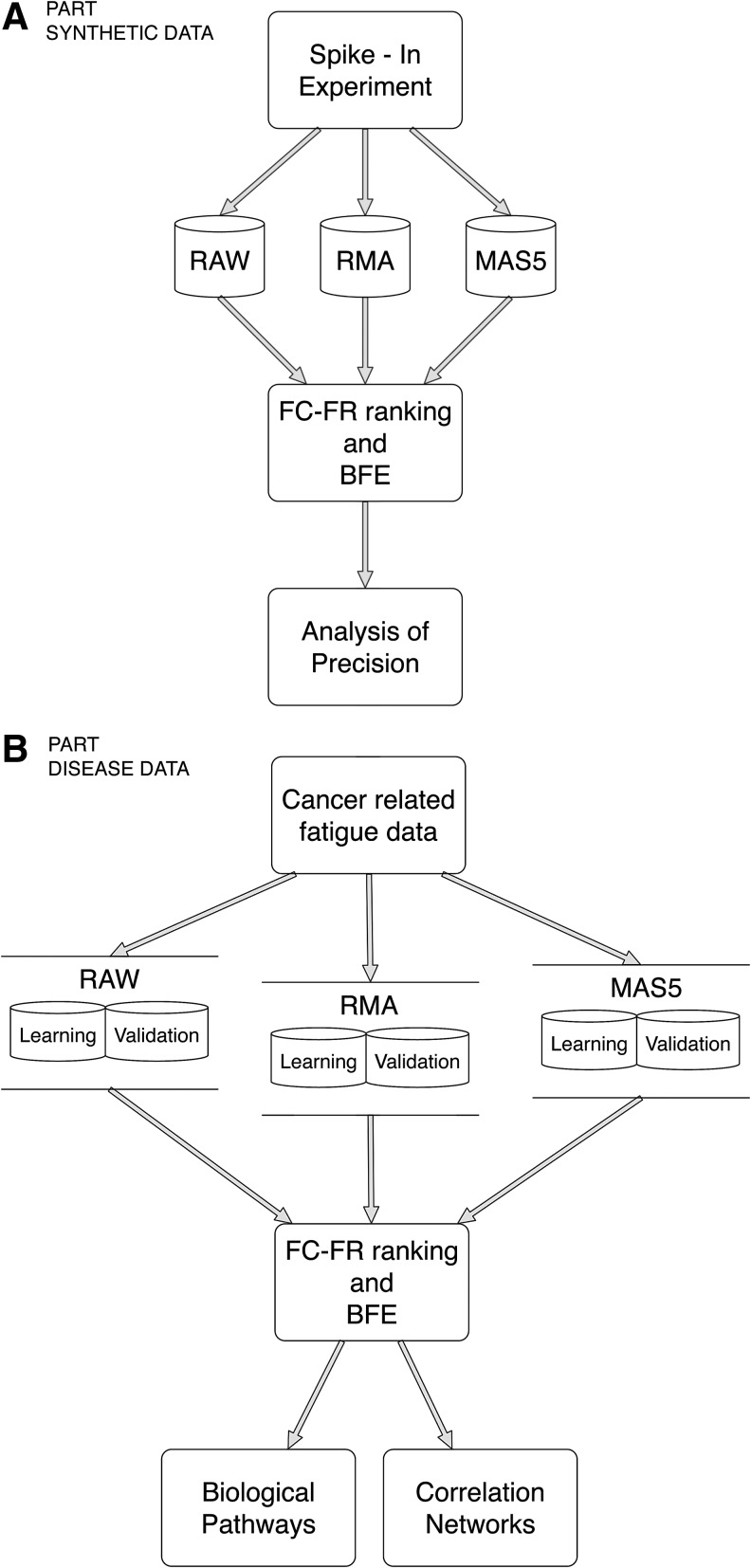
In part A, we used the Affymetrix Latin Square Data for Expression Algorithm Assessment. Knowing the genes that are differentially expressed, we first ranked the genes according to a combination of FC and FR and then analyzed the precision of the generated gene ranking using raw and preprocessed data. Subsequently, we performed gene selection to study the discrimination power of the selected genes in both cases (raw and preprocessed). In part B, we used a cancer-related fatigue data set. In this case, we did not know the differentially expressed genes, and therefore, we performed gene selection based on the same ranking methods used in the synthetic data set, identified the predictive genes, and conducted correlation networks and pathway analysis to understand the biological pathways that are associated with these selected genes. Then, we compared the biological pathways and correlation networks associated with the selected genes from the raw and preprocessed data. A flow chart of this methodology is shown in Figure 1.

FIG. 1.

Flow chart of the methodology.

3.1. Ranking methods and gene selection

To alleviate the high underdetermined character of the genomic phenotype prediction problem, filter methods were applied to reduce the dimensionality of the genomic data to select the most discriminatory genes. Filter methods rank the different genes according to different measures of their discriminatory power in the phenotype prediction problem. In this study, we analyzed the precision on the selection of the differentially expressed genes using a combination between the most common and well-known ranking methods as follows: FC and FR. The Precision 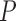was defined as follows:

where 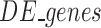is the set of differentially expressed genes and 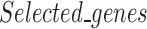is the set of selected genes/probes.

We work with binary classification problems, first knowing the gene expression in the different samples of each class. Our ranking algorithm is a combination of FC (Schena et al., 1996) and FR (Fisher, 1936). The algorithm first preselected the most differentially expressed genes above a certain absolute FC value, and then, the preselected genes are ranked according to their FR. The reason to first preselect with FC is to avoid low dispersions in both classes, which could provide high FR values, when in fact, the centers of both distributions in expressions are very close.

Once we rank the preselected genes, we identify the most discriminatory genes. The selection of the most predictive genes followed the same procedure that was described in Saligan et al. (2014) as follows: the shortest list of genes with the highest predictive accuracy was selected through the backward feature elimination (BFE) and a distance-based nearest-neighbor classifier. To measure the discriminatory power of the different embedded lists, we used the leave-one-out cross-validation (LOOCV) predictive accuracy. For comparison purposes, the same procedure was used for raw and preprocessed data through MAS5 and RMA preprocessing techniques.

3.2. The spike-in experiment

To check the precision of the above described ranking method using both raw and preprocessed data, we needed a data set where we know the genes that are differentially expressed. In such case, we used the Affymetrix Latin Square Data for Expression Algorithm Assessment (Human Genome U133 Data Set) that consists of 3 technical replicates of 14 separate hybridization of 42 spiked transcripts in a complex human background at concentrations ranging from 0.125 to 512 pM. The concentrations in the first experiment, composed by three replicas, were 0, 0.125, 0.25, 0.5, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 pM (Supplementary Material). Each subsequent experiment and its three replicas rotated the spiked-in concentrations by one group; that is, experiment 2 and its three replicas began with 0.125 pM and ended at 0 pM, up to experiment 14 and its three replicas, which began with 512 pM and ended at 256 pM. Further details can be consulted in Affymetrix (2015).

3.3. The cancer-related fatigue data set

The cancer-related fatigue microarray data set was obtained from men who were 18 years or older, diagnosed with nonmetastatic prostate cancer, with or without a history of prostatectomy, and scheduled to receive External Beam Radiation Treatment (EBRT) with or without concurrent androgen deprivation therapy (ADT). A total of 44 men with nonmetastatic prostate cancer were enrolled in an NIH IRB-approved study. Data from 27 subjects were used in the training set and data from 17 subjects were included in the validation blind set, Saligan et al. (2014). The training set was from the array outputs of 27 subjects, 18 high-fatigue (HF) and 9 low-fatigue subjects, phenotyped using a 3-point decline in fatigue score measured by the Functional Assessment of Cancer Therapy-Fatigue (Cella et al., 2002). We managed a raw microarray data set with 604,258 probes and the preprocessed data set with 54,675 different probes in both cases, using RMA and MAS5 preprocessing techniques.

Once the most discriminatory genes from raw and preprocessed data were selected, pathway analysis was performed using gene analytics software (Stelzer et al., 2009). Furthermore, we built correlation networks (Lastra et al., 2011) to understand how the expressions of the most discriminatory genes are interrelated. Correlation networks were generated using Pearson correlation coefficient (Pearson, 1895) and Kruskal's algorithm (Kruskal, 1956) to find the minimum spanning tree.

4. Results and Discussion

4.1. The spike-in experiment

Using the Affymetrix Latin Square Data for Expression Algorithm Assessment (Human Genome U133 Data Set), we checked the precision of the FC/FR ranking algorithm described in Section 3. There were 42 differentially expressed probes, and we selected the first 42 probes in the ranking. We compared the first group with the rest of the groups to cover all the possible concentration comparisons. In the first comparison (group 1 vs. group 2), the difference in concentration between all the differentially expressed probes was 0.125 pM. In the second comparison (group 1 vs. group 3), the difference was 0.5 pM up to the 12 comparisons (group 1 vs. group 13), which was 256 pM. Due to the rotation of the concentration, the last comparison (group 1 vs. 14) had again a difference of 0.125 pM in concentration among all the differentially expressed probes.

Table 1 shows the precision for each comparison using raw, RMA, and MAS5 data sets, showing the mean precision of the different comparisons. In almost all the comparisons, we obtained better results in terms of precision working with raw data than with RMA and MAS5 data sets. Also, the higher mean precision was achieved with raw data.

Table 1.

Precision on the Selection of the Differentially Expressed Genes Using Raw Data or Preprocessed Data with RMA and MAS5

Group comparison	raw	RMA	MAS5
1 vs. 2	7.14	9.52	4.76
1 vs. 3	26.19	16.67	16.67
1 vs. 4	38.10	11.90	14.29
1 vs. 5	28.57	28.57	16.67
1 vs. 6	26.19	28.57	28.57
1 vs. 7	40.48	26.19	23.81
1 vs. 8	35.71	21.43	30.95
1 vs. 9	40.48	23.81	23.81
1 vs. 10	35.71	19.05	21.43
1 vs. 11	38.10	14.29	21.43
1 vs. 12	23.81	16.67	9.52
1 vs. 13	23.81	23.81	14.29
1 vs. 14	7.14	4.76	9.52
Mean precision	28.57	18.86	18.13

The data are the Affymetrix Latin Square Data for Expression Algorithm Assessment. The selection is performed between the first group and the rest to include all the differences among the spike-in concentrations. The best result for each case (raw data, RMA preprocessed data, and MAS5 preprocessed data) is shown in boldface.

RMA, Robust Multiarray Average.

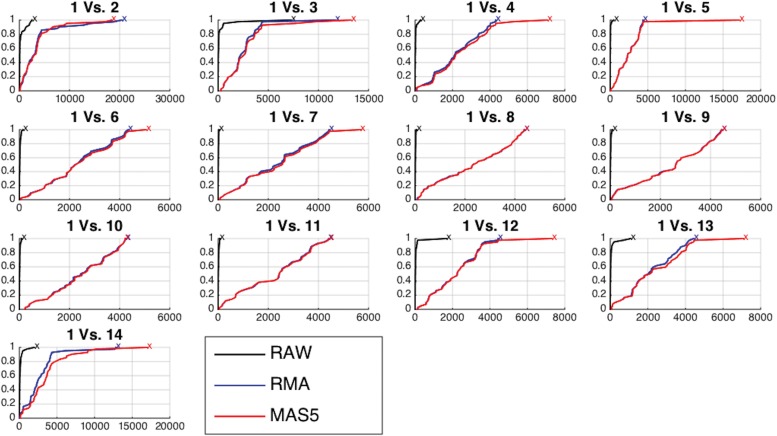
We also calculated the empirical cumulative distribution functions (CDFs) of the positions of the differentially expressed genes. A perfect CDF would be a straight line reaching the value of 1 at position 42, corresponding to the total number of differentially expressed genes. These curves served to visualize how many genes we have to select to locate all the differentially expressed genes. Figure 2 shows these CDF curves for each comparison and type of data. As the raw data obviously have more genes/probes (248,152 for raw data and 22,300 for preprocessed data, see Affymetrix (2015)), the positions given by the ranking method were divided by a correction factor as follows: 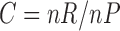where 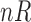is the number of raw probes/genes equal to 248,152 and 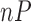is the number of preprocessed probes/genes equal to 22,300. Therefore, 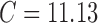, for the spiked-in experiment.

FIG. 2.

Empirical CDF of the positions of the differentially expressed genes ranked by the FC/FR methods for each comparison and different types of data. CDF, cumulative distribution function; FC, fold change; FR, Fisher's ratio.

In this figure, the x-axis represents the positions of the genes/probes given by the ranking method and the y-axis represents the percentage of differentially expressed genes that were located. Therefore, in the first comparison, we were able to find all the differentially expressed genes (42) selecting less than 5000 (0.5e4 in the x-axis of the graph) while working with preprocessed data, as we needed almost all the probes/genes (2.23e4). In all the comparisons, we were able to find all the differentially expressed genes selecting rather less number of genes with raw data than with preprocessed data.

4.2. The chronic fatigue data set

The aim of this study is to find the list of most discriminatory genes that serve to differentiate between high and low chronic fatigue (CF) induced by the radiotherapy in prostate cancer patients (Saligan et al., 2014). The differences on the selection of most discriminatory genes using raw and preprocessed data are shown. For the sake of clarity, we show the first 50 most discriminatory genes in each case.

Table 2 shows the LOOCV accuracy of the first 50 most discriminatory probes/genes in each case. The highest predictive accuracy we obtained was 92.59% of accuracy with only the first 3 probes/genes. However, using RMA and MAS5, we achieved 100% with 6 and 44 probes/genes, respectively. Obviously, the dimensionality of the raw data set is 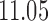times higher than the preprocessed data sets, that is, using the raw data, the probe sets have not been summarized in one gene such as in the preprocessed data. For that reason, the repetition of a probe in the raw data indicates the importance of the corresponding gene. This is the case of TUBB2A, HLA-DQA1, TUBB3, HLA-DQB1, and BTNL3. It can be observed that RMA also found these genes within the most discriminatory set, but not using MAS5.

Table 2.

Probe/Gene Name and Accuracy (Acc%) of the Selected Genes/Probes for Raw Data and Preprocessed Data with RMA and MAS5

raw		RMA		MAS5
Probe/gene	Acc(%)	Probe/gene	Acc(%)	Probe/gene	Acc(%)
TUBB2A	85.19	TUBB2A	88.89	SOCS3	85.19
HLA-DQA1	96.3	C11orf1	88.89	TMEM194A	92.59
TUBB2A	92.59	PPOX	96.3	1561478_at	92.59
TUBB2A	92.59	TTC2	92.59	CIB3	96.3
TUBB2A	88.89	NRIP3	96.3	ESYT2	92.59
TUBB2A	85.19	SCAMP4	100	ABHD1	92.59
TUBB2A	85.19	HLA-DQA1	100	JTB	92.59
HLA-DQA1	88.89	234253_at	100	1556412_at	92.59
TUBB2A	88.89	223313_s_at	96.3	207371_at	96.3
TUBB2A	88.89	BTNL3	100	LOC100131756	92.59
BTNL3	88.89	YSK4	96.3	CDK6	92.59
TUBB2A	88.89	236963_at	100	ALS2CR8	96.3
HLA-DQA1	92.59	ZCCHC2	100	SEL1L2	96.3
TUBB2A	88.89	DSG3	100	FLJ35220	96.3
TUBB3	88.89	TMEFF2	100	215626_at	96.3
HLA-DQB1	85.19	1566585_at	100	SPAM1	96.3
HLA-DQB1_LOC101060835	85.19	231141_at	100	FTCD	96.3
HLA-DQA1	88.89	SPATA20	100	1570285_at	96.3
IMMP1L	85.19	CSN1S2A	100	216795_at	96.3
BTNL3	85.19	RAB11FIP3	100	MAP3K2	96.3
_at	85.19	239587_at	100	MTSS1L	96.3
ZFPL1	85.19	RIMS3	100	GMEB1	96.3
GNRHR2	85.19	234548_at	100	SOCS7	96.3
DR1	88.89	C20orf103	100	GNA12	96.3
DOCK11	88.89	AGR2	100	244274_at	96.3
HLA-DQB1	88.89	SAT1	100	PLP2	96.3
FMR1	88.89	RGS18	100	ATG9B	96.3
ACAP2	85.19	1570044_at	100	1564056_at	96.3
HLA-DQB1	85.19	TUBB3	100	PCCB	96.3
ZEB1_LOC100996668	85.19	HDLBP	100	239370_at	96.3
FLJ32790	85.19	560087_a_at	100	ANK1	96.3
LOC100505812	88.89	AVL9	100	SCAND2	96.3
DENND4C	88.89	241238_at	100	1564872_at	96.3
PREPL	88.89	PHLDB3	100	SMAD2	96.3
LOC100505812	85.19	PIGK	100	CMTM3	96.3
FAM63B	88.89	F11	100	INSR	96.3
LYSMD3	85.19	C1orf21	100	PSG1	96.3
RP11-727A23.11_OTTHUMG00000183952	85.19	IL9	100	1560169_at	96.3
HIPK3	85.19	229733_s_at	100	MAP3K1	96.3
POLR2J4	85.19	241776_at	100	KCNRG	96.3
PHF17	85.19	WDR27	100	DOCK7	96.3
SP3	85.19	D21S2091E	100	1560995_s_at	96.3
MRGBP	85.19	239632_at	100	WNT5A	96.3
NAP1L1	85.19	HGSNAT	100	1562673_at	100
FAM126A	85.19	242839_at	100	GSK3B	100
EPS15P1	85.19	KCTD4	100	NCKIPSD	100
SMCR8	85.19	MECOM	100	215439_x_at	100
HLA-DQA1_LOC100509457	85.19	LOC257152	100	CDHR3	96.3
ZMYM2	85.19	MLH3	100	PCGEM1	96.3
EIF1AX_LOC101060318	85.19	DDX60	100	GNG13	96.3

Genes with the best accuracy are shown in boldface.

In addition, a blind validation of these results has been performed using the set of 17 subjects, independent of the training set, originally used in Saligan et al. (2014) to assess the validity of the learned predictive model. The result of this blind validation using raw data was 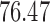accurate, while using MAS5 and RMA, the accuracy dropped to 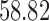and 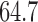, respectively. This result is very important and shows that RMA and MAS5 increase the accuracy in the learning process at the price of decreasing the accuracy in blind validation. Therefore, this implies that the biological pathways associated with the predictive genes found using raw data are more meaningful, and both preprocessing techniques (RMA and MAS5) highly impact the biological pathway analysis and the corresponding phenotype prediction problem.

4.3. Pathway analysis and correlation networks

In this section, we provide the main pathways associated with the discriminatory genes that can predict the CF phenotype using raw, RMA, and MAS5 data sets. These genes are shown in Table 2.

The raw data generated predictive genes associated with pathways mainly related to pathogenic infections (HLA-DQX genes), as well as pathways associated with oligomerization of connexins into connexons (TUBB2A and TUBB3) involved in intercellular signals and metabolic communication (Koval, 2006). These are crucial mechanisms in the development of many human diseases (Kelsell et al., 2001).

The main pathways associated with predictive genes generated by RMA are related to mitotic prometaphase (BIRC5, CLIP1, STAG2, TUBB3) that controls the nuclear membrane breaking apart into numerous membrane vesicles, cytoskeleton remodeling neurofilaments (EEPK1, KRT6A, TUBB2A, and TUBB3), and mitotic metaphase and anaphase (BIRC5, CLIP1, TUBB2A, and TUBB3). The beta-tubulin gene family controls the tubulin protein superfamily of globular proteins. Beta-tubulins polymerize into microtubules, which is a major component of the cytoskeleton formation. Microtubules function in many essential cellular processes, including mitosis. For instance, tubulin-binding drugs serve to kill cancerous cells by inhibiting microtubule dynamics that are required for DNA segregation and cell division. The main pathways associated with predictive genes generated by MAS5 are GADD45 pathway, EGFR1 signaling pathway, and interferon type I related to the MAP3KX genes (McKean et al., 2001; Jordan and Wilson, 2004).

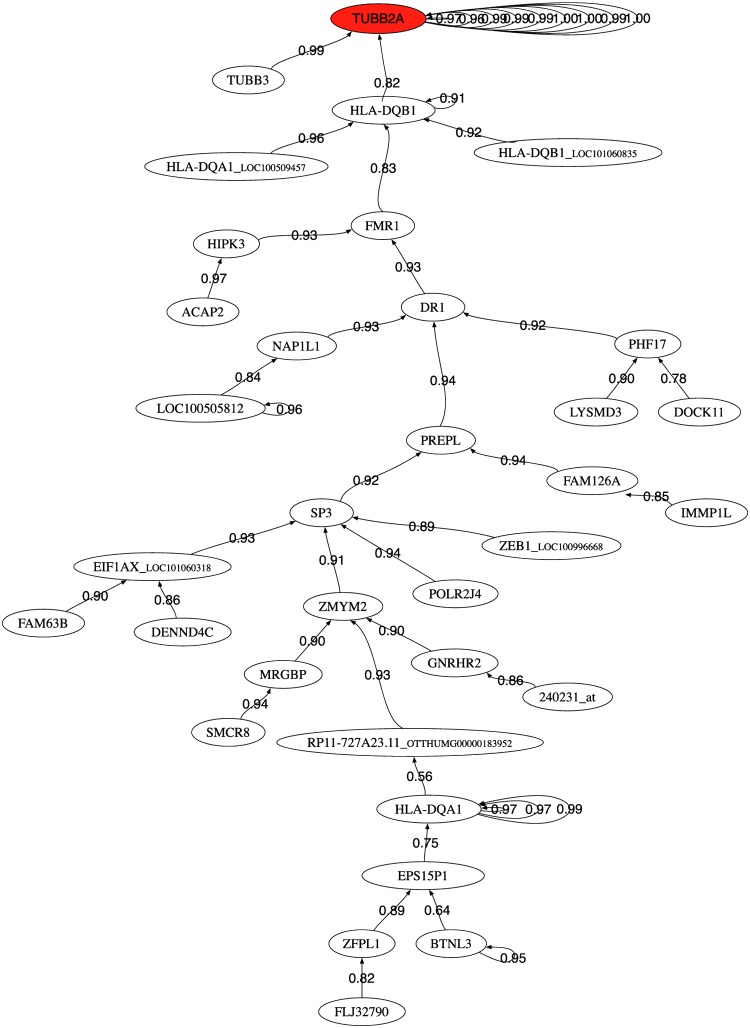
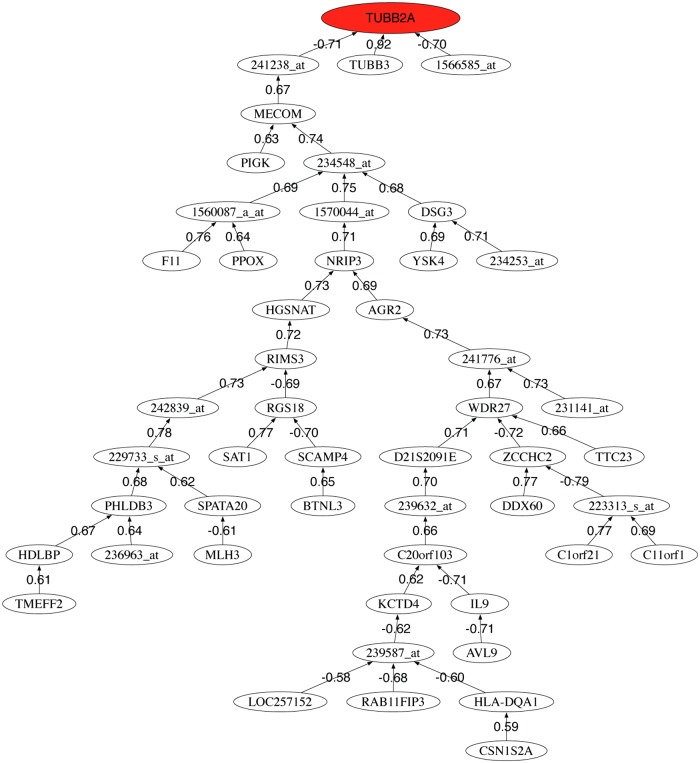
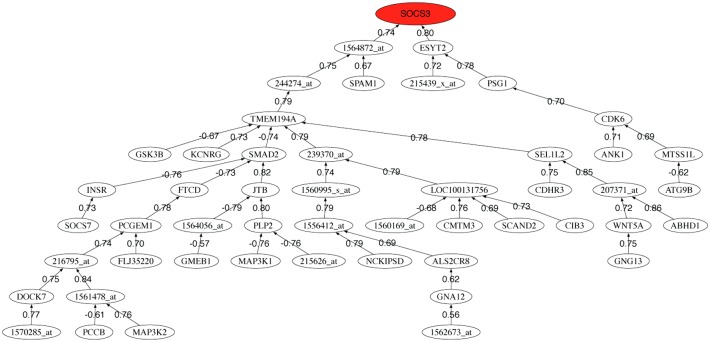
We also provide the correlation graphs for the 50 most discriminatory genes for each data set. Figures 3–5 show the correlation graphs for raw, RMA, and MAS5, respectively. In the case of raw data, we can observe one main tree connecting the tubulin genes to the major histocompatibility complex gene and other genes that serve to expand the tree. RMA privileges the connection between the beta-tubulin genes and two probes (241238_at and 1566585_at) whose gene name is unknown. MAS5 privileges the role of SOCS3. This gene encodes a member of the STAT-induced STAT inhibitor (SSI), also known as suppressor of cytokine signaling (SOCS), family. SSI family members are cytokine-inducible negative regulators of cytokine signaling. The expression of SOCS3 gene is induced by various cytokines, including interleukin (IL)6, IL10, and interferon-gamma (Masuhara et al., 1997; Minamoto et al., 1997).

FIG. 3.

Pearson correlation coefficient minimum spanning tree of the 50 first selected probes using raw data.

FIG. 4.

Pearson correlation coefficient minimum spanning tree of the 50 first selected probes using preprocessed data with RMA.

FIG. 5.

Pearson correlation coefficient minimum spanning tree of the 50 first selected probes using preprocessed data with MAS5.

5. Conclusions

We analyzed the impact of the main preprocessing microarray techniques (MAS5 and RMA) in identifying the biological pathways that are associated with discriminatory genes that can accurately predict the cancer-related fatigue phenotype. For such purpose, we first model a synthetic data set, the Affymetrix Latin Square Data for Expression Algorithm Assessment where 42 control genes are spiked-in at known concentrations; and a real case of radiotherapy-related fatigue data set (learning and validation) in patients with prostate cancer. We found that in the case of the Affymetrix synthetic data set, the mean precision along all the comparisons was higher using raw data than using preprocessed data. This difference is even more remarkable in the CDF curves for all the comparisons. We were able to find all the differentially expressed genes selecting rather less number of genes with raw data than with preprocessed data.

Regarding the cancer-related fatigue data set, we evaluated the goodness of the selected genes through BFE and a distance-based nearest-neighbor classifier through the LOOCV predictive accuracy. In addition, we built correlation networks and performed pathway analysis to understand how the expression of the most discriminatory genes is biologically relevant. With RMA and MAS5 data sets, we got better accuracy results in the learning phase than using raw data. However, in the blind validation, working with RAW data allowed us to generalize better than using preprocessed data (RMA and MAS5). Besides, the pathway analysis and the correlation networks were significantly different among raw, RMA, and MAS5. This would explain why some genetic signatures found in real practice fail to predict unseen samples. Consequently, it can be concluded that interpreting results from predictive gene profiles generated by RMA and MAS5 should be done with caution. This is an important conclusion with a high translational impact that should be confirmed in other disease data sets.

Author Disclosure Statement

Enrique J. de Andrés was supported by the Ministerio de Economia y Competitividad (grant TIN2011-23558).