Targeted Drug Delivery to Upper Airways Using a Pulsed Aerosol Bolus and Inhaled Volume Tracking Method

Abstract

The pulmonary route presents an attractive delivery pathway for topical treatment of lung diseases. While significant progress has been achieved in understanding the physical underpinnings of aerosol deposition in the lungs, our ability to target or confine the deposition of inhalation aerosols to specific lung regions remains meagre. Here, we present a novel inhalation proof-of-concept in silico for regional targeting in the upper airways, quantitatively supported by computational fluid dynamics (CFD) simulations of inhaled micron-sized particles (i.e. 1-10 μm) using an intubated, anatomically-realistic, multi-generation airway tree model. Our targeting strategy relies on selecting the particle release time, whereby a short-pulsed bolus of aerosols is injected into the airways and the inhaled volume of clean air behind the bolus is tracked to reach a desired inhalation depth (i.e. airway generations). A breath hold maneuver then follows to facilitate deposition, via sedimentation, before exhalation resumes and remaining airborne particles are expelled. Our numerical findings showcase how particles in the range 5-10 μm combined with such inhalation methodology are best suited to deposit in the upper airways, with deposition fractions between 0.68 and unity. In contrast, smaller (< 2 μm) particles are less than optimal due to their slow sedimentation rates. We illustrate further how modulating the volume inhaled behind the pulsed bolus, prior to breath hold, may be leveraged to vary the targeted airway sites. We discuss the feasibility of the proposed inhalation framework and how it may help pave the way for specialized topical lung treatments.

1. Introduction

The lungs are widely advocated as an attractive delivery pathway for treating lung diseases topically [1, 2]. In the past few decades, significant progress has been achieved in our physical understanding of respiratory flow phenomena and particle transport mechanisms in the pulmonary tree [3, 4]. Yet, leveraging such knowledge to target inhalation therapeutics to specific (e.g. inflamed or diseased) regions within the lungs remains overwhelmingly challenging [5]. One of the main obstacles for confined regional targeting lies in reducing particle dispersion throughout the lungs; a phenomenon caused on the one hand by flow turbulence (i.e. mixing) and shear flows within airways [6], but also as a result of the complex branching structure and large surface area of the lungs, estimated at ~100 m² for an average adult [7]. The vast dispersion of inhaled aerosols across the respiratory tract (e.g. extrathoracic, alveolar) renders the targeting of therapeutics for asthma [8], cystic fibrosis [9] and bronchitis [8] still suboptimal as these pulmonary conditions affect foremost the conductive airways, such that superfluous deposition in other regions should be broadly avoided.

While particle size alone is frequently regarded as the leading factor in determining the dynamics and deposition sites of aerosols in the lungs [5, 10, 11], any given particle size will to a large extent disperse along the respiratory tract. Namely, there is no single particle size choice that may be exploited for achieving generational targeting in the upper airways alone; that is to succeed in depositing aerosols within the tracheobronchial airways while minimizing deposition in the extra-thoracic (including oral) regions and the deep pulmonary acinar regions. It is widely acknowledged from in vivo and semi-empirical data [12] that for common inhalation aerosols, particles in the narrow size window of ~2-5 μm exhibit maximal tracheobronchial deposition. However, this local maximum represents a mere deposition fraction reaching on the order of ~5-10% [12]; the majority of inhaled aerosols (~80%) are thus filtered in the extra-thoracic airways, with a remaining ~10% anticipated to penetrate into the deeper alveolar regions. The deposition of such particles outside their intended targeting site may in turn lead to undesirable side effects such as reaching the systemic circulation, via translocation into the alveolar capillary bed, or indirectly through the digestive system, while other particles may reside in the alveolar regions for extended periods of time [13].

To overcome such targeting limitations various approaches have been sought as alternative strategies. For example, a first step towards increasing airway deposition fractions is to decrease premature deposition due to impaction in the extra-thoracic airways. A viable, yet simple, way to achieve such reduction in extra-thoracic deposition is, in principle, to decrease the particle Stokes’ number, a dimensionless number capturing a particle’s relaxation time and thus likelihood to deposit as a result of impaction [10, 14]. This may be for example achieved by reducing a patient’s inhalation flow rate [15]. Although such considerations have been implemented in some modern inhalers (e.g. AKITA®JET), the improvements they bring are still widely deemed insufficient [16]; indeed, particle screening of the dose initially inhaled remains strong across the extra-thoracic regions. Alternatively, a strategy to reduce the particle Stokes’ number has been advocated through the use of porous particles [17, 18]. For these latter particles the aerodynamic diameter is maintained low (due to the particle’s reduced density) while the geometric diameter may be increased, thus leading to higher drag forces. Despite showing reduced impaction rates, this method has to date not been translated into therapeutic practice. Furthermore, reducing a particle’s Stokes’ number to cross through the first obstacle of extra-thoracic deposition may result in particles eventually passing through the upper airways and reaching the acinar regions. Parallel to such efforts, other in vivo and in vitro works [19, 20] have advocated for example the use of hygroscopic particulate matter or droplets (e.g. sodium chloride aqueous solution droplets) for targeting upper airway deposition. Here, aerosols are selected to be small enough to evade impaction in the oral cavity during the initial inhalation phase, following which they deposit with higher deposition rates in the upper airways as a result of hygroscopic growth leading to more impaction and sedimentation. Although this method has shown promising results, to the best of our knowledge, it is still far from having matured into a clinically-available aerosol therapy [19, 20].

Beyond such approaches, more radical inhalation strategies featuring magnetic particles have also been suggested as a means for generational airway targeting. Here, particles are typically loaded with super paramagnetic iron oxide nanoparticles (SPIONs) and are pulled by an external magnet located in proximity of the targeted lung regions. In analogy to the hygroscopic particle method, aerosols are prematurely deposited due to the external pulling of the magnetic force. In a seminal in vivo animal study, an external magnet was located on one of the rodents’ lungs thereby leading to increased deposition of inhaled SPIONs. However, airways could not be specifically targeted and deposition was prevalent in the alveoli [21]. In a subsequent computational fluid dynamics (CFD) study, tracheal targeting was attempted by placing a magnet in proximity of a patient’s neck. Yet, the drag force exerted on particles by the inhaled air was too strong such that aerosols transited beyond the targeted region and a mild deflection in their trajectories was observed [22]. Although this method is still in its infancy, magnetic particles potentially add a useful control mechanism to deposit aerosols in targeted regions. It should be noted though that this method also presents possible disadvantages and hurdles due to the added complexity of the technique itself, as well as possible health risks stemming from deposition of SPIONs along with the medicine [22, 23].

Driven by ongoing shortcomings, we explore in silico a new methodology for inhalation drug delivery, adjusted to target and confine deposition within upper airways. In contrast to traditional inhalation methodologies based on continuous drug inhalation, a short aerosol bolus is injected and the inhaled volume of clear air (devoid of particles) following the aerosol bolus is monitored. By tracking this inhaled volume, the location (i.e. depth) of the aerosol bolus can be assessed. Once the aerosol bolus reaches the targeted region, a breathhold maneuver is initiated. During breath hold, aerosols within the targeted airway region are left to sediment until deposition. To evaluate the feasibility of such concept, we have conducted CFD-DEM (discrete element method) simulations, where particle dynamics of the pulsed aerosol bolus are investigated in an anatomically-realistic, multi-generation airway tree model. Specifically, we investigate the case of simulating an intubated patient; a first clinical scenario motivated by specialized therapies (e.g. acute asthma exacerbations [24]). To cast this work most relevant to available inhalation therapies, specific attention is given to the selection of particle sizes typical of common inhalation devices (i.e. 1-10 microns). Following our in sicilo results, we identify an optimal particle size range for such suggested technique and quantify ensuing targeting efficiencies. Finally, we discuss opportunities and limitations of such inhalation technique, including its potential implementation for clinical applications. The suggested method would require control or monitoring of the inhaled volume; a feature not typically integrated in commonly-available inhalation devices. Although such additional functionality would lead plausibly to increased design and manufacturing costs, we anticipate nevertheless that the advocated generational targeting technique can prove cost effective and provide additional therapeutic value across various aerosol delivery applications. This could lead to better treatment outcomes and reduced side effects, such as in chemotherapy.

2. Methods

In the present in silico study, a scenario is considered whereby a patient is intubated and mechanically ventilated (see clinical relevance below). The aerosol targeting methodology is initiated by ventilating the lungs using a constant flow rate of 3 liters per minute (LPM), assuring laminar flow (as discussed below). After the flow has stabilized to a steady state (~0.5 s), a short bolus of particles is released. The bolus is carried deeper into the airway tree as it crosses over each airway bifurcation. During the inhalation phase, the bolus location in the airways is tracked via monitoring of the clear air volume (CAV) injected after the bolus. Once the bolus reaches the targeted depth (i.e. the target volume of clear air is reached, denoted tCAV), a breath hold maneuver (BH) is initiated whereby particles are left to settle under gravity for 9 s, corresponding to a sufficiently short time period causing no harm to the patients [25]. Following the BH period the flow is then reversed, and the remaining airborne particles are exhaled (see supplementary material video, Online Resource 1). This protocol is repeated in silico for various tCAVs (corresponding to different BH onset times), resulting in scenarios of targeting different lung generations. Following such methodology, we note that the 3 LPM inhalation flow rate is used only once, i.e. while inhaling the short-pulsed aerosol bolus, and is not intended for continuous ventilation of the intubated patient.

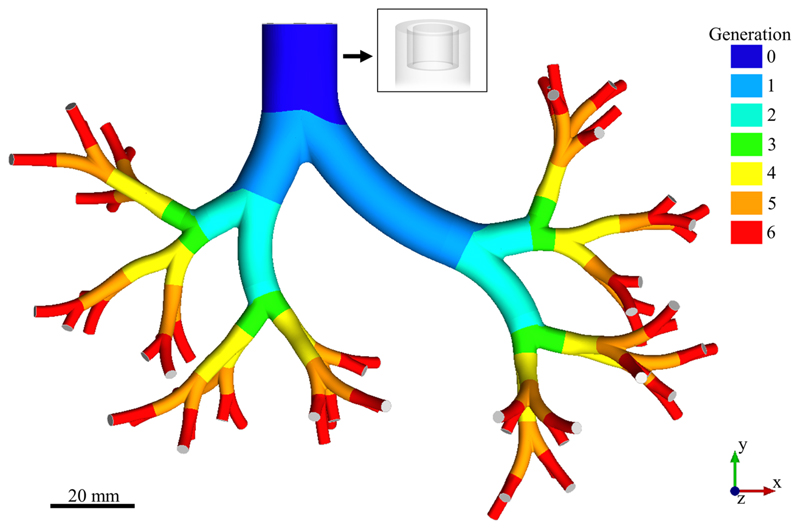
Our CFD simulations are based on the construction of a computer-aided design (CAD) of a morphometrically-faithful upper airway tree for an average human (male) adult, featuring seven generations (the trachea is generation 0) of dichotomously branching, asymmetric airways (Fig. 1). In accordance with the seminal morphometric models of Weibel [7] and Horsfield [26, 27], these were combined into a hybrid geometry, following previously reported methods [28]. As noted above, we restrict our in silico proof-of-concept to the specific case of an intubated patient, applicable to clinical cases such as drug delivery to intubated patients with acute asthma and COPD exacerbations [24, 29]. A standard size 9 endotracheal intubation tube is fitted to the tracheal region of the geometry [30]; the cuff is modeled as an impermeable rigid wall, and the tracheal geometry is thus truncated above the bottom wall of the cuff (Fig. 1, inset). Finally, the model is rotated relative to gravity to mimic an inhalation scenario where the patient is lying down.

Fig. 1.

Three-dimensional (3D) computer-aided design (CAD) model of the intubated upper airway tree spanning seven generations. The generations are color-coded (0 through 6), and the outlets are marked in grey. Inset: Semi-transparent view of the inlet region, illustrating the fitting of the endotracheal tube (including a cuff) in the distal tracheal region

In our simulations, air inhaled into the airway model is assumed to be incompressible, Newtonian, and isothermal, and its motion is governed by the continuity and momentum conservation (Navier-Stokes) equations. For the boundary conditions, a flow rate of 3 LPM is imposed at the inlet (i.e. intubation tube), to assure laminar flow and thus minimize turbulent particle dispersion. Specifically, this flow rate yields a Reynolds number of Re=400 in the trachea (defined by Re= v_air d_airway/υ_air, where d_airway represents the airway diameter, v_air is air velocity, and υ_air is air kinematic viscosity). Such choice follows previous studies in adult human tracheal models where turbulence was shown to subside almost entirely for inhalation flow rates under 3.75 LPM (Re=500) [31, 32]. To remain below such threshold, a uniform velocity-inlet condition was used with v_air–inlet =0.69 m/s (Re=400). We note that due to the increase in total cross section of the airways in more distal branches, the Reynolds number gradually falls, dropping to ~25 in the model’s most distal airway branches (i.e. generation 6). A constant equal flow rate is enforced on all airway outlets (i.e. outflow boundary condition). Although this latter condition comes short of accurately capturing the anticipated regional (i.e. lobal) ventilation distribution in the lungs [33], this condition may nevertheless be appropriate as a first approximation as thoroughly discussed by Nowak et al. [34]. This is especially true in the case of relatively slow inhalation flow rates, unobstructed airways, and sequential bifurcations with 90° azimuthal rotation (i.e. unlike sequential co-planer bifurcations, which promote unequal flow distribution between branches) [34]. Finally, the airway walls are assumed to be rigid with no slip, including at the intubation tube walls (Fig. 1, inset). To model the ensuing aerosol dynamics following the onset of BH, the velocity field was reset to zero throughout the computational domain. In the absence of severe airway obstruction, we note that despite the simplifying assumptions presented, we do not anticipate such choices to play a dominant role in determining the ensuing particle dynamics or qualitatively changing the nature of the presented results.

The dynamics of the inhaled particles are described within a discrete Lagrangian framework (one-way coupled to the flow [19, 35]), neglecting electrostatic and hygroscopic effects. Their motion is governed by the force balance [36]

$$m_p\frac{d{\mathbf{\text{v}}}_p}{dt}={\mathbf{\text{F}}}_{gravity}+{\mathbf{\text{F}}}_{drag}+{\mathbf{\text{F}}}_{Brownian},$$ (1)

where m_p is the particle mass and v_p is the particle velocity vector, t is the time, F_gravity is the gravitational force, F_drag is the drag force and F_Brownian is the Brownian force, as described in detail elsewhere [36]. As noted above, the direction of the gravitational force corresponds to a patient laying down, i.e. in the +z direction, as shown in Fig. 1. Due to the low particle Reynolds numbers (defined by Re_p = v_aird_p/υ_air, where d_p is the particle diameter), Stokes’ drag law is used where the Cunningham correction factor for air is applied. Finally, the Brownian force is added to account for the random diffusive motion of the particles. We note that particle diffusion and the Cunningham correction factor are relevant in particular for the smaller particles considered in the current work (i.e. 1 μm) [36].

Particles enter through the intubation tube during a short bolus period of 50 ms, which corresponds to the approximate time it takes the bolus to cross the larger generations (i.e. trachea and main first bronchi). This short bolus period is intentionally chosen to maximize the inhaled aerosol dose meanwhile guaranteeing accurate generational targeting within the simulated upper airway generations. We note that for the specific inhalation flow rate of 3 LPM, this short pulse results in a bolus volume of 2.5 ml of air containing aerosols. For comparison, the total volume of the trachea is 30.5 ml, the bronchi 11.3 ml and ~4 ml down to 1.5 ml for each of the subsequent generations, i.e. spanning 2 through 6 [7]. During the bolus injection period, particle injection is uniform in time and spatially-shaped as a parabola-weighted towards the center of the intubation tube (i.e. more particles are injected from the center of the tube) [37]. Once injected inside the upper airway domain, particles that contact the airway walls are assumed to have immediately deposited. Particles that evade deposition on the walls can either (i) reach one of the airway outlets (i.e. generation seven), where they are assumed to travel deeper (and deposit) in more distal generations, or alternatively, (ii) particles may remain airborne within the airway tree until the end of the BH period, in which case they are assumed to be exhaled.

The inhaled aerosols are assumed to have a density of ρ_p =1000 kg/m³, equivalent to a nebulized aqueous solution. Numerical simulations are presented for 4 different monodispersed particle diameters, namely 1, 2, 5 and 10 μm (typical of nebulizers [38]), covering the window size of effective tracheobronchial deposition [12]. For each particle diameter the BH maneuver is initiated following four distinct tCAVs, i.e. 0, 2.5, 5 and 10 ml, resulting in four different penetration depths of the particle bolus. Assuming a constant ventilation flow rate of 3 LPM during the inhalation maneuver, these tCAVs correspond to BH initiation times of 0.05, 0.10, 0.15 and 0.25 s, respectively (timed from the beginning of the injection of the bolus).

The CAD model of the flow domain (Fig. 1) was meshed by tetrahedral cells in conjunction with wall prism layers (ANSYS ICEM CFD 16.0). Subsequently, a finite volume solver (ANSYS Fluent 16.0) was used to solve the conservation equations (mass and momentum) on the resulting numerical grid. Rigorous mesh convergence tests were first performed to select the optimal numerical setup. Namely, tetrahedral Delaunay meshes spanning 1.7M to 8.3M cells were compared. For each mesh size, mass conservation was verified, and velocity residuals converged within 0.01% tolerance in the entire domain. The final mesh was selected with 2.4M cells featuring 3 near wall prism layers and a velocity convergence error below 2% throughout the domain (when compared to the finest mesh examined). Finally, convergence tests were also used to select the appropriate accuracy of the numerical models used: a Coupled pressure-velocity coupling scheme was selected, along with Least Squares Cell Based for the gradients, 2^nd Order for the pressure and 2^nd Order Upwind for the momentum. Note that for easier reproducibility, the model names are stated here according to the terminology provided in the commercial software (ANSYS Fluent).

To track the motion of micron sized particles (i.e. 1-10 μm), flow (CFD) simulations were combined with a previously validated in-house DEM (Discrete element method) code [36], where the rigid body dynamics of each particle are individually solved following momentum conservation (Newton’s second law). This amalgamation was achieved using one-way coupling between the continuous (air) and discrete (particles) phases, as inhaled therapeutic aerosols are typically dilute [19, 35], where the dynamics of the particles were solved separately using first-order explicit Euler temporal integration. Finally, convergence tests were also performed to select the time step and the number of particles to simulate. Eventually, a time step of 1·10⁻⁷ s was used to ensure adequate temporal resolution in the Lagrangian tracking, and a total of 2’000 injected particles were simulated for each combination of particle size and tCAV to assure accurate deposition statistics [36]. We note that this number of particles does not represent a specific inhalation device, but rather a general generic case which can be applied to most existing devices.

3. Results

To give the reader some initial quantitative insight into the nature of the dominant particle transport phenomena anticipated prior to the onset of BH maneuver, we begin by briefly examining the relevant governing dimensionless parameters during steady inhalation flow conditions. These can be described using two non-dimensional particle numbers, namely the Stokes and gravity numbers [10]. We note that a detailed discussion of ensuing air flow patterns in the modeled respiratory tract is omitted here for brevity; flow topologies qualitatively resemble extensive works on the topic [39, 40]. However, for an intubated patient the abrupt diameter change from the tip of the intubation tube to the trachea (Fig. 1, inset) creates a small recirculation zone around the annular region between the tracheal wall and the outer diameter of the intubation tube, bounded by the cuff on the proximal side. Nevertheless, this recirculation has little effect on ensuing particle motion (see supplementary material video, Online Resource 1).

The Stokes number captures the role of particle impaction (i.e. the tendency of a particle to deviate from a flow streamline) and is defined as

$$Stk=\frac{{\rho }_p{d}_p^2{U}_0{C}_c}{18{\mu }_{air}{d}_{airway,0}},$$ (2)

where d_p is the particle diameter, U₀ is the characteristic flow velocity of air in the trachea, C_c is the Cunningham slip correction factor, μ_air is the viscosity of air, and d_airway,0 is the diameter of the trachea. For the examined particle diameters (i.e. 1, 2, 5 and 10 μm), Stokes numbers in the region of the trachea yield Stk = 3.9· 10⁻⁵, 1.5 · 10⁻⁴, 8.7· 10⁻⁴ and 3.4· 10⁻³, respectively. For these cases Stk ≪0.1 such that impaction is unlikely to play a central role in the fate of the inhaled particles. In more distal airway branches, values of the Stokes numbers further decrease, further underlining such anticipated dynamics. In parallel, the particle gravity number compares the importance of sedimentation to convection and can be expressed in the trachea by

$$H=\frac{g{\rho }_p{d}_p^2{C}_c}{18{\mu }_{air}{U}_0},$$ (3)

where g is the gravitational acceleration. The corresponding gravity numbers for the range of particle sizes in the trachea yield H = 1.8· 10⁻⁴, 6.7· 10⁻⁴, 4.0· 10⁻³ and 1.6· 10⁻², respectively. In contrast to the Stokes number, the gravity number increases in more distal generations, following an increase in the total cross section of the airways (and hence a decrease in flow velocity) [7]. As the total cross section gradually increases from the trachea to the 6^th generation (i.e. the model’s most distal airway generation), gravity numbers increase by ~56% thereby emphasizing the rapidly increasing role of sedimentation with airway depth.

To further understand the governing sedimentation dynamics, dimensional numbers may also be examined. The largest tCAV simulated in the present study is 10 ml, corresponding to a period of 0.25 s, throughout which inhaled aerosols are convected prior to initiation of the BH maneuver. In parallel to their initial convective motion during 0.25 s, the 1, 2, 5 and 10 μm particles are anticipated to sediment 7.5 μm, 30 μm, 0.18 mm and 0.76 mm, respectively. Comparing such sedimentation distances to the airway diameters at generation 6 (i.e. 2.8 mm), we may hence expect that a fraction of the 10 μm particles might deposit prematurely; that is, before the initiation of the BH. For further comparison, 20 μm particles sediment 3.05 mm within 0.25 s; the majority of these large particles would deposit prior to reaching generation 6 and are hence not likely candidates for targeted delivery in the conducting airways following the prescribed methodology. We anticipate that during inhalation the majority of simulated particles (i.e. 1 to 10 μm) will follow streamlines as nearly perfect tracers whereas during the BH maneuver, gravitational forces become the dominant factor affecting particle dynamics.

A final point to consider is the sedimentation distances achieved within the 9 s of BH. Here, we note that the 1, 2, 5 and 10 μm particles will sediment 0.27, 1.08, 6.75 and 27.4 mm, respectively. This order-of-magnitude assessment thus points to the fact that the smaller 1 and 2 μm particles are expected to be insufficient for efficient airway targeting and instead are anticipated to be mostly exhaled after BH before coming in contact with the airway walls.

3.1. Generational targeting

We now turn our attention to results from the numerical simulations. Figure 2 presents deposition maps of the various particle sizes as a function of the investigated tCAVs (i.e. 0, 2.5, 5 and 10 ml), corresponding to BH initiation times of 0.05, 0.10, 0.15 and 0.25 s, respectively; supplementary material video 1 (Online Resource 1) exemplifies the transport and deposition dynamics of 10 μm particles with a tCAV of 5 ml. Other tCAV values examined (not shown for brevity) include 7.5 ml where deposition results fall well in line between 5 and 10 ml (Fig. 2; third and fourth row). In contrast, simulations for tCAVs of 12.5, 15 and 17.5 ml yield scenarios for which inhaled aerosols overwhelmingly exit the airway outlets (not shown here) and are thus too large inhaled volumes for targeting generations 0 through 6. Comparing the different columns of Fig. 2, we observe that small 1 μm size particles are the least efficient, and hence relevant, for our intended targeting technique (Fig. 2; first column). Indeed, while such particles are inhaled and halted in proximity of their targeted locations, their slow settling velocities hinder their adequate deposition (i.e. very small fractions) within the imposed BH period (see Fig. 3). The vast majority is eventually exhaled. Somewhat in contrast to the 1 μm particles, 2 μm particles display a clear pattern of successful generational targeting. However, these particles still exhibit low deposition fractions (Fig. 2; second column). Focusing on the two larger particle sizes (Fig. 2; third and fourth columns), we notice how the results of the 5 and 10 μm particles are qualitatively alike. This observation hints to the fact that increasing particle size any further would have limited benefits in terms of targeting efficacy. Rather, larger particles (>10 μm) would augment the tendency for premature deposition under sedimentation, as discussed earlier.

Fig. 2.

Deposition maps for different particle diameters (columns) as a function of different target clear air volume (tCAV) following a 9 s breath-hold (BH) maneuver (rows). Deposited particles are displayed in blue (exhaled particles are not shown). The direction of gravity is in the +z direction

Fig. 3.

Particle deposition efficiencies. Deposition fractions are shown as a function of time for the four different particle sizes examined. The different figures capture four different target clear air volumes (tCAVs) investigated, namely a tCAV = 0, b 2.5 ml, c 5 ml and d 10 ml, corresponding to four different BH initiation times of 0.05, 0.10, 0.15 and 0.25 s, respectively. In each sub-figure, the onset of tracked tCAV is marked

For a tCAV of 0 ml, aimed at tracheal targeting (Fig. 2, first row), particles with d_p ≤2 μm are hardly deposited (as quantitatively discussed below in Figs. 3 and 4), while particles with d_p =5 and 10 μm show good qualitative results, with a continuous deposition pattern covering the entire trachea. Interestingly, examining Fig. 2 (second through fourth row), we note that deposition for the 2 μm particles gradually improves compared to the first row; however, deposition still remains quite sparse. This improvement is due to the smaller airway diameters in distal generations, which shorten the sedimentation path of the particles until deposition. In contrast, for the larger particles (5 and 10 μm), deposition appears dense and continuous across all rows.

Fig. 4.

Distribution of deposited particles according to airway generation, including deposition on the intubation tube and exhaled particles. The different sub-plots capture four different target clear air volumes (tCAVs), namely a tCAV = 0, b 2.5 ml, c 5 ml and d 10 ml. A control case in the absence of a BH maneuver is presented in (e)

Figure 3 presents deposition fractions as a function of time for four different tCAVs (i.e. different targeted lung depths). Here, each sub-plot (a-d) corresponds to a different row shown in Fig. 2. The different BH onset times (corresponding to the different tCAVs) are marked with a vertical dashed line in each sub-plot. During the inhalation phase, particles gradually move into the deeper airways with some reaching the outlets; we recall that particles that exit via an outlet are counted as deposited (i.e. namely, these are likely to deposit past generation 6 in more distal airways during BH). In turn, this visually leads to a jump in the deposition rates prior to reaching tCAV (i.e. prior to the onset of BH); an artefact most clearly visible in Fig. 3d, where the deposition rate of 1 μm particles is exceptionally high before the onset of BH. The same effect also helps explains why deposition rates are strikingly similar for the different particle diameters prior to BH initiation (e.g. t < 0.25 s in Fig. 3d). During the inhalation phase all inhaled particles act as near perfect tracers reaching the outlets almost simultaneously. Another trend witnessed most clearly for the 10 μm particles in Fig. 3 is the increase in deposition rate with increasing tCAV (increase in BH onset time), i.e. the larger the tCAV (the later the onset of BH), the steeper the average slope of the deposition fraction. To understand this phenomenon, we recall that particles that reach more distal branches are still airborne within narrower airways upon the onset of BH. Hence, these particles sediment across relatively shorter distances before depositing.

Perhaps the most visually striking result in Fig. 3 is the drastic change in deposition rates for the different particle sizes, which clearly follows from the considerable differences in sedimentation velocity (i.e. gravity number) across the various particle diameters. Indeed, only minute fractions of the 1 μm particles (well below 0.05) are deposited after the 9 s BH for any of the 4 targeting maneuvers (Fig. 3a and d). This low deposition fraction explains the sparse deposition witnessed for these particles in Fig. 2 (first column). We note the exception of a higher total deposition fraction in Fig. 3d that may be mostly attributed to 1 μm particles exiting the airway outlets. Similarly, low fractions of the 2 μm particles are deposited when the trachea or main bronchi are targeted (Fig. 3a and b). However, for the more distal (and narrow) airways, the deposition efficiency of the 2 μm particles on the airways (neglecting deposition on the outlet, prior to the BH) is increased to 0.1-0.2 (Fig. 3c and d). We underscore that although these two latter cases (2 μm in Fig. 3c and d) are far from ideal targeting scenarios, they would nevertheless surpass traditional targeting methods used; it is typically possible to reach ~5-10% tracheobronchial deposition following ICRP data [12]. Most importantly, the majority of the 5 μm particles (>0.65) are deposited in the targeted region (Fig. 3). We note that for 10 μm particles, targeted deposition yields unity within just ~4 s BH.

We next quantify the efficiency of targeting according to airway generation (Fig. 4), including deposition on the intubation tube, particles reaching past generation 6 and those exhaled. Each subplot (Fig. 4a and d) represents the corresponding tCAVs of 0, 2.5, 5 and 10 ml, respectively. As a control case, we also compare simulation results in the absence of a BH (Fig. 4e). In the latter case, the inhalation flow rate is also kept constant at 3 LPM with an inhaled volume of 0.5 L, resulting in a total inhalation time of 10 s. Perhaps one of the more noteworthy points in Fig. 4 is the amount of exhaled 1 and 2 μm particles, emphasizing the low deposition fractions for these sizes noted in Figs. 2 and 3.

As can be seen from Fig. 4a, a tCAV of 0 ml leads to deposition in the trachea and the two main bronchi, i.e. generations 0 and 1. Similarly, confined targeting is also achieved for a tCAV of 2.5 ml (Fig. 4b), where deposition is restricted almost completely to generations 1 and 2. However, when more distal generations are targeted, the specificity of regional targeting is somewhat compromised. For example, for a tCAV of 5 ml (Fig. 4c) deposition is evenly distributed between generations 1-4 whereas for a tCAV of 10 ml (Fig. 4d), deposition is rather homogeneously spread across generations 1-6, with ~10% of the particles reaching past generation 6. Interestingly, although tCAVs of 5 and 10 ml leads to the deposition of particles across more generations, we note that the bolus spreads rather homogenously. For example, with 5 μm particles and a tCAV of 7.5 ml, deposition yields 0.22±0.03 in each of the generations 1 through 4 (Fig. 4c); for a tCAV of 10 ml deposition yields 0.14± 0.09 in each of the generations 1-6 (Fig. 4d).

3.2. Discussion and summary

Despite extensive work done on the design of inhalers and drug formulations to treat diseases of the pulmonary tract, there is still an ongoing debate regarding the selection of the most fundamental parameters, such as what constitutes the optimal inhaled particle diameter, for any given inhalation application [11]. These uncertainties arise in part due to the vast dispersion of therapeutics across the lungs [12], underlining the difficulty in achieving targeted delivery specifically to the conducting airways. In the present study, motivated by the pitfalls of current drug delivery paradigms to treat airway diseases (e.g. asthma [8], cystic fibrosis [9] and bronchitis [8]), we have attempted to explore in silico the feasibility of a novel technique, in targeting aerosols specifically within the proximal upper airway generations. Such targeted delivery would allow superfluous deposition in other regions (e.g. acinar) to be broadly avoided, potentially reducing side effects. Using a pulsed aerosol bolus and inhaled volume tracking method, we exemplify a specific targeting protocol on an intubated and ventilated patient. Our in silico results show how using an accurately timed BH maneuver can assist in uniformly targeting the bolus to selected generations, by leveraging particles’ intrinsic sedimentation towards our goal.

Before discussing further implications of our findings, we review some of the main limitations of the current study. In the present in silico study we have explored the case of an intubated patient. Although this first clinical scenario has many applications in specialized therapies, such as acute COPD and asthma exacerbations [24, 29], cancer therapy [41], voluntary oral inhalation through an inhaler device would significantly broaden the applicability of the suggested technique. Although beyond the scope of the present work, such scenario could be realized by requesting for instance the patient to breathe through the device and comply with the prescribed flow or alternatively by monitoring voluntarily inhaled volumes using a spirometer. Moreover, our rigid, generic, airway geometry model represents only a small fraction (< 5%) of total lung volume and is thus limited in its ability to capture the intricate flow distribution in an elastic and dynamic, and importantly diseased lung. Finally, the neglect of airway narrowing, typical of obstructive diseases and advocated as a possible application for the targeting technique hereby discussed, may result in biased deposition outcomes [6, 42]. Yet, despite these shortcomings, we do not anticipate the general picture drawn in this work to be significantly modified.

Oral deposition during voluntary inhalation of particulate matter has been thoroughly studied in the past, yielding useful semi-empirical models of deposition efficiency [43]. Calculating the so-called impaction parameter ${\rho }_p{d}_p^{2}Q$ (where Q is the flow rate), for the examined 1, 2, 5 and 10 μm particles, results in 50, 200, 1250, 5000 g μm² s⁻¹, respectively. Based on these values we can anticipate oral deposition fractions below 0.05 for the 1, 2, and 5 μm particles, and deposition fractions of ~0.1 for 10 μm particles [43], suggesting that targeted delivery in line with the present results may be achievable under oral inhalation (using a mouth piece). Although a constant flow rate was simulated in this work, we anticipate minimal change in the results for voluntary breathing. As the airborne particles are convected as near perfect tracers, their location during the onset of BH depends mostly on tCAV. As a final note, the duration of the BH was shown to be achievable by voluntarily breathing asthmatic patients and is thus not anticipated to pose a significant obstacle [11].

It is also important to consider the fate of inhaled particles that are convected beyond the simulated domain, and thus the possibility of targeting those deeper regions; a relevant point for obstructive diseases such as asthma [11]. As presented in our results, their behavior can be assessed by comparing the airway diameters with the particle sedimentation distances during BH. For example, in generations 7 through 10, airway diameters typically decrease to 2.3-1.3 mm; whereas during a 9 s BH, the 1, 2, 5 and 10 μm particles will sediment 0.27, 1.08, 6.84 and 27.4 mm respectively. We can therefore anticipate that 1 μm particles will be mostly exhaled, whereas the majority of the 2 μm particles and all the 5 and 10 μm particles are expected to deposit. As airways become even narrower (down to 0.6 mm in the 16^th generation [7]), 10 μm particles will sediment prematurely and smaller particles (e.g. 2 μm) are expected to present more favorable targeting results. It is therefore plausible that the optimal formulation for targeting all the conducting airways would be a polydisperse mixture of diameters, with larger particles (e.g. 5-10 μm) depositing in proximal generations and smaller particle (e.g. 2 μm) targeting more distal airway generations.

One application for our advocated method could be increasing the efficiency of currently available inhalers. By achieving targeted delivery to the upper airways, the inhaled drug doses can be reduced (while maintaining similar dosing in diseased regions), falling in line with currently advocated official medical guidelines [44]. Some specific drug examples could include Corticosteroids and β2 adrenergic agonist used to treat inflammatory diseases such as asthma and COPD, antibiotics like Rifampin and Isoniazid used to treat tuberculosis [45], and other inhalable antibiotics, antivirals and antifungals [1]. Furthermore, successful implementation of this method could pave the way for novel lung therapies. One prominent example is the emerging field of inhaled chemotherapy for lung cancer treatments, where the extreme toxicity of the drugs and the highly localized disease (e.g. bronchogenic carcinoma) render targeted delivery of utmost relevance [41]. Overall, our CFD-DEM simulation results highlight how novel inhalation drug delivery techniques may introduce considerable improvement to the efficiency of currently used inhalation devices. To the best of our knowledge, our results demonstrate for the first time the feasibility of a relatively simple airway targeting technique that is directly applicable with many currently used drug formulations and devices.

Supplementary Material

Electronic supplementary material The online version of this article (https://doi.org/10.1007/s10494-018-9927-1) contains supplementary material, which is available to authorized users.