From networks to optimal higher-order models of complex systems

Standfirst

Rich data is revealing that complex dependencies between the nodes of a network may escape models based on pairwise interactions. Higher-order network models go beyond these limitations, offering new perspectives for understanding complex systems.

Network science provides powerful analytical, statistical, and computational methods to describe the behaviour of complex systems [1]. Complex systems are typically composed of a large number of components. Each of them interacts directly only with relatively few others components, while influencing more indirectly via chains of direct interactions. Since both direct and indirect interactions determine the behaviour and function of a system, network models of complex systems capture both — generally in two steps. First, components are represented as nodes x_i. Direct interactions between them are represented with possibly weighted and directed pairwise links $\overrightarrow{x_i{x}_j},$ which are captured in adjacency matrices or associated to random walk and Laplacian matrices. Second, non-adjacent nodes are transitively connected by matrix algebraic methods; in applications such as eigenvector centrality or spectral clustering, for example, these would be given by products of matrices or eigenvalue decompositions. The application of these methods assumes that, given adjacent pairwise links $\overrightarrow{x_i{x}_j}$ and $\overrightarrow{x_j{x}_k},$ a node x_i can indirectly influence another node x_k through a transitive path $\overrightarrow{x_i{x}_j{x}_k}$ with two independent steps. This assumption is ubiquitous in network science. It is at the root of node-ranking and community detection algorithms [2, 3, 4, 5], of scalable techniques to calculate shortest paths, optimal flows and cuts [6], as well as of visualisation methods [7].

The success of network models across the sciences rests on their ability to connect the structure, dynamics and function of arbitrary systems on the basis of abundant data on pairwise interactions between their components. Compared with mean-field approaches, where the interactions between all elements are summarized through a single averaged field, network models often have greater explanatory power because they account for the sparse and non-random topologies of social, biological, and technological systems [1]. However, new forms of high-dimensional and time-resolved data have now also shed light on the limitations of these models.

Rich data indicates who interacts with whom, but also what different types of interactions exist, when and in which order they occur, and whether interactions involve pairs or larger sets of nodes. These seemingly disparate types of data have something in common: they provide us with information on higher-order dependencies between the components of a system, which lay beyond the reach of models that exclusively capture pairwise links. This has profound consequences for network models of relational data— a cornerstone in the interdisciplinary study of complex systems. For example, higher-order dependencies have been shown to either speed up or slow down dynamical processes [8, 9, 10], change node rankings [11, 12, 13], and alter community structures [12, 14, 15, 16, 17, 18].

An active community of researchers is developing higher-order network models that account for different types of higher-order dependencies in data on complex systems. Such models better capture how the components of complex systems directly and indirectly influence each other, promising improved explanatory power at the expense of increased model complexity. Further progress will require integrative approaches that combine novel network-analytic methods for rich data with scalable statistical inference and machine-learning techniques. These will allow addressing open questions, such as finding models that optimally balance under- and over-fitting in dependence of available data, or establishing the existence and scalability of a single framework that can capture different types of higher-order dependencies. Finding good answers can in turn further improve our understanding of the structure, dynamics, and function of complex systems.

In this perspective article, after a brief overview of different classes of higher-order network models, we illustrate the effects of non-Markovian paths in time-series data, which have become the focus of one modelling approach. We show how their consideration affects fundamental network science methods that span different disciplines—community detection, node ranking, and modelling dynamical processes. Finally, we discuss challenges in developing optimal higher-order models that take advantage of rich data on higher-order dependencies while avoiding the risk of overfitting.

Modelling higher-order dependencies in complex systems

Recent work on higher-order network models can be divided into three different yet related lines of research. The first line challenges the assumption that the influence between a system’s components can be decomposed into links of a single type, introducing instead multilayer higher-order models with multiple link types [19, 8]. The second line questions the assumption that the influence between components in a complex system can be decomposed into pairwise links, developing models that generalise pairwise links to arbitrary node sets, which we refer to as combinatorial higher-order models [20, 21, 22, 14]. The third line challenges the idea that the indirect influence between the components of a system can be understood based on transitive paths formed by independent links. Leveraging information on real paths inferred from time series data, this research has introduced non-Markovian higher-order network models. They account for correlations in the sequence of nodes traversed by paths that cannot be captured by first-order Markov models [12, 10].

Multilayer models account for the fact that many real complex systems exhibit multiple types of interactions that require a generalisation of network models. Examples include multi-modal transportation systems [23], interdependent layers of power and communication infrastructures [24], multilayer financial networks [25], or multi-faceted relationships between individuals in social systems [26]. Multilayer generalisations of networks seek to account for these features in, for example, the modelling of spreading processes [8], the detection of modular structures [27], and the ranking of nodes [28, 29].

Combinatorial models reproduce many-body interactions, which appear in many systems and necessitate higher-order models that capture information beyond pairwise interactions. Examples include triangles, which are known to be fundamental building blocks of social networks [30], cliques in scientific co-authorship networks [31], feed-forward loop network motifs in biochemical transcription networks [32] and temporal social networks [33], spatial coexistence relations between species in an ecosystem [34], and trigenic interactions in gene regulatory networks [35]. Research on combinatorial models has introduced high-dimensional generalisations of graphs from topological data analysis. These include hypergraphs, in which links can join any set of nodes [36], and more recently simplicial complexes, in which simplices can join any set of nodes and all subsets of those nodes [37, 38].

The need for non-Markovian models has been highlighted by a number of studies, which have used high-resolution time series data to reveal complex higher-order patterns in paths that are not captured by standard network models. Examples include flight itineraries of passengers, patients moving between hospital wards [39], time-stamped interactions in social networks [40, 41, 42], scholarly citation networks [12], temporal patterns in trade relations [43, 44], human mobility [10, 12, 45], navigation paths of humans in information networks [46, 17], patient pathways in hospital networks [47], and traces of dynamical processes in networked systems [15]. By leveraging applications of higher-order Markov chains in time series analysis [48], sequence mining [49, 50, 51], behavioural modelling [52, 53], and natural language processing [54, 55], recent research on non-Markovian higher-order models has generalised networks to higher-dimensional representations that account for higher-order dependencies in paths.

Despite differences in motivation and mathematical underpinning, these approaches share a motivation: that standard network models are too simple to explain the complex paths of influence in high-dimensional and time-resolved data on biological, technical, economic, and social systems, and thereby cannot adequately connect their structure, dynamics, and function. In practice, this is achieved by modelling higher-order dependencies in complex systems and further constraining paths beyond what is expected from the network topology.

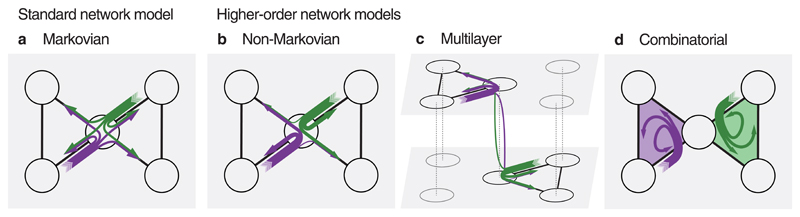
As an illustration, consider an ego network with five nodes in which ego communicates by different means with two friends and two colleagues, but rarely passes on information between them (Fig. 1). A standard network model would wash out this kind of higher-order node dependencies, whereas a random walk as an information flow model would form paths across independent pairwise links (Fig. 1a). In contrast, all higher-order network models better capture the constraints on the information paths so that they tend to stay among friends or colleagues. This is achieved by considering node dependencies in the underlying data in different ways: a non-Markovian model records the temporal order of messages so that paths continue depending on where they come from (Fig. 1b), a multilayer model differentiates communication means so that paths mainly stay within associated layers (Fig. 1c), and a combinatorial model combines group and multiple pairwise communication in a simplicial complex and considers paths that move between links that share a triangle (Fig. 1d). In this way, higher-order network models further constrain the indirect paths by which different parts of a system influence each other.

Figure 1. Different approaches to model an ego network with higher-order dependencies between nodes.

Ego (central node) communicates by different means with two friends (left nodes) and two colleagues (right nodes). Green and purple arrows highlight paths from one friend (purple) and one colleague (green) through ego. To which nodes these paths can continue depends on the constraints set by (a) a standard network model with Markovian dynamics, (b) a non-Markovian network model, (c) a multilayer network with Markovian dynamics within layers, and (d) a simplicial complex where the paths move between links that share a triangle.

In the following, we review how modeling of higher-order dependencies between nodes with proper constraints on paths can provide a better understanding of complex systems. Therefore, we focus on non-Markovian higher-order network models, which explicitly question the assumption that indirect influence between distant nodes happens through transitive paths — common in standard network models.

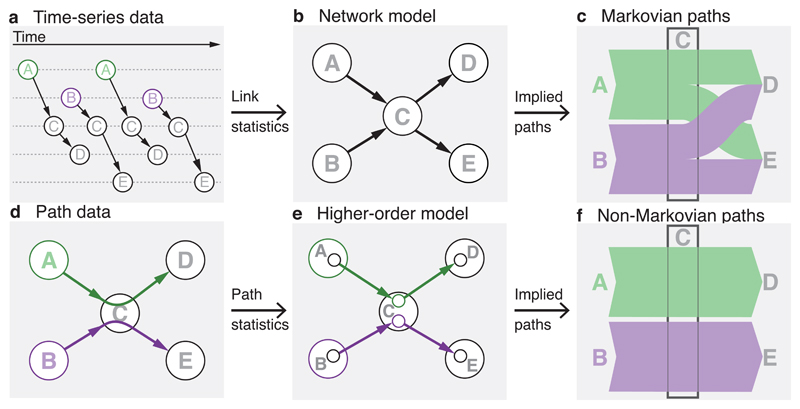
A useful example to illustrate this concept is the reconstruction of paths from time-series data (Fig. 2a). The temporal information available in this data helps either directly infer the paths or cascades through which information propagates in a system, or indirectly capture time-stamped links that define the concept of causal, or time-respecting, paths [9]. Considering pairwise interactions, a standard network model would portray the link topology of the underlying system as shown in Fig. 2b. This representation discards information on the links contribution to paths, implicitly suggesting that nodes can indirectly influence each other via transitive paths that traverse nodes in a memoryless, Markovian fashion. In our example, nodes A and B can both indirectly influence D and E via four transitive, Markovian paths: $\overrightarrow{\mathit{\text{ACD}}},\overrightarrow{\mathit{\text{ACE}}},\overrightarrow{\mathit{\text{BCD}}},\text{and}\overrightarrow{\mathit{\text{BCE}}}$ (Fig. 2c). However, a closer look at the interaction order in the time-series data (Fig. 2a) reveals that only two of these four possible paths exist in the sequence (Fig. 2d). Network analytic methods that assume transitive, Markovian paths, are therefore not valid. This shortcoming can be overcome by a path-centric view that generalises networks to higher-order models of paths [12, 10, 11, 15, 17, 56]. Figure 2e illustrates this idea with a second-order model that accounts for the topology of paths of length two. In the spirit of higher-order Markov chain models, this model can be represented with a memory network [12], where state nodes represent states in a second-order state space and links encode possible transitions between states. Depending on the topology of paths, each of the five physical nodes A, B, C, D, and E, which typically are the objects of interest in the real world, has one or more state nodes (Fig. 2e). These state nodes enable efficient higher-order network models of paths. A path described by a Markovian model on the state nodes, directed from one state node to the next with a probability that does not depend on previously visited state nodes, appears non-Markovian on the physical nodes (Fig. 2f). This modelling approach can be generalised to arbitrary order m by adding one state node for each prefix of m – 1 nodes that precedes the current physical node on a path. In this way, we can construct network models that capture higher-order effects in paths for any given order m.

Figure 2. Non-Markovian higher-order models can better capture the topology of paths in complex systems.

A rich source of path information is time-series data that capture interaction sequences between the components of a system (a). Focusing on pairwise interactions, network models abstract a system’s topology with nodes and links (b) while assuming that paths are transitive and Markovian (c). Due to the chronological ordering of interactions, the actual paths of indirect influence in time- series data (d) can deviate from this assumption. Focusing on paths rather than pairwise interactions, higher-order network models with, for example, state nodes (e) can capture the actual topology of indirect influence (f).

Non-Markovian paths and community detection

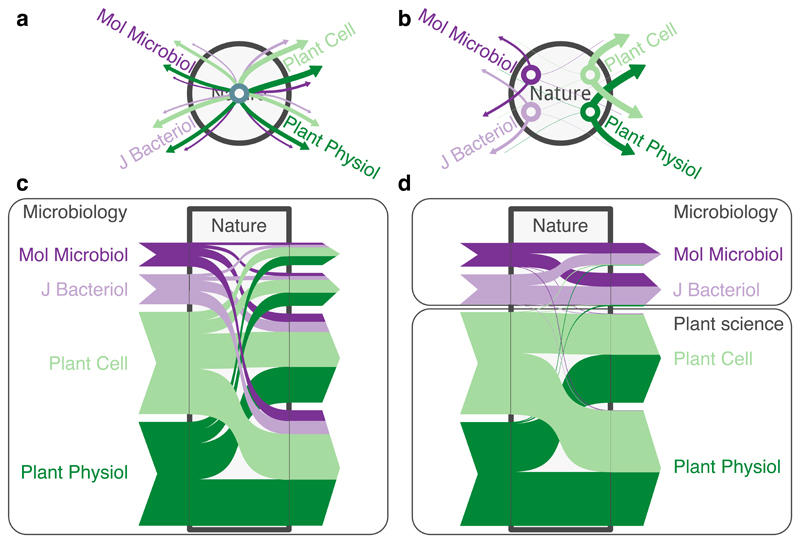
Community detection [57] is an umbrella term for a large number of algorithms that group nodes into distinct modules to simplify and highlight essential structures in the network topology. As higher-order network models can capture more complex forms of interactions, generalised community-detection algorithms can capture more complex forms of relational regularities. An example is citation flows between journals and scientific communities with long flow persistence times. A standard network model where journals are connected by weighted directed links that are built by aggregating citations between their articles fails to capture the complex citation flows through multidisciplinary journals such as Nature (Fig. 3a,c) [12].

Figure 3. Community detection of paths can capture overlapping communities.

The underlying data from Thomson Reuters Web of Science [64] are chains of citing articles aggregated in journals, like in Fig. 2(a) with nodes interpreted as articles in journals A–E. A standard first-order Markov representation of citation flows from four specialised journals through multidisciplinary Nature (a). A second-order representation with one state node for each citing journal (b). The standard network representation mixes flows and washes out the boundary between fields (c). A second-order Markov model captures the fact that citation flows through a multidisciplinary journal depends on where they come from and highlights overlapping fields in Nature (d).

Citation flows from different fields mix and move in a non-realistic way across fields, as the output citation flow from the multidisciplinary journal depends only on the total number of citations directed to another journal, irrespective of where the citations are coming from. For example, Fig. 3c illustrates that, within a standard first-order Markov model, most citation flows from two microbiology journals would continue to two plant science journals. As a result, all these journals would be best assigned to the same field. This showcases how community detection based on a standard network model can wash out boundaries between modules and fail to assign nodes to multiple overlapping modules.

In contrast, a second-order Markov representation of citation flows, which takes into account where citations come from, captures the fact that most citation flows coming to Nature from one field return to the same field (Fig. 3b,d). For example, when going from a first- to a second-order Markov representation, the relative amount of citation flows that return to the same journal after two steps, averaged over all journals, increases from 11% to 22% [12]. Moreover, the non-returning citation flows behave in a more realistic way: Figures 3b and d illustrate how citation flows from the Journal of Microbiology and the Journal of Bacteriology in microbiology mostly return to either journal and, similarly, how citation flows from Plant Cell and Plant Physiology in plant science mostly return to those journals. As a consequence, citation flows stay within their respective fields, highlighting the multidisciplinary character of the journal Nature. Averaged over all journals, the flow persistence within fields, the probability that citation flows stay within the same field in the next step, increases by 38 percent [58]. A higher-order representation of non-Markovian citation paths is critical for capturing overlapping research fields in multidisciplinary journals.

Non-Markovian paths and node centralities

Algorithms that identify important nodes are among the success stories of network science. They help us to locate critical elements in networked infrastructures, identify influential actors in social systems, or find relevant pages in the World Wide Web. At the heart of these applications are measures for the centrality of nodes— based on, for example, their occurrence on the shortest paths between other nodes, their role in flow processes, or their influence on the steady state of stochastic dynamics [1, 59, 60]. These methods assume that node centrality can be characterised based on the topology of pairwise interactions between system components.

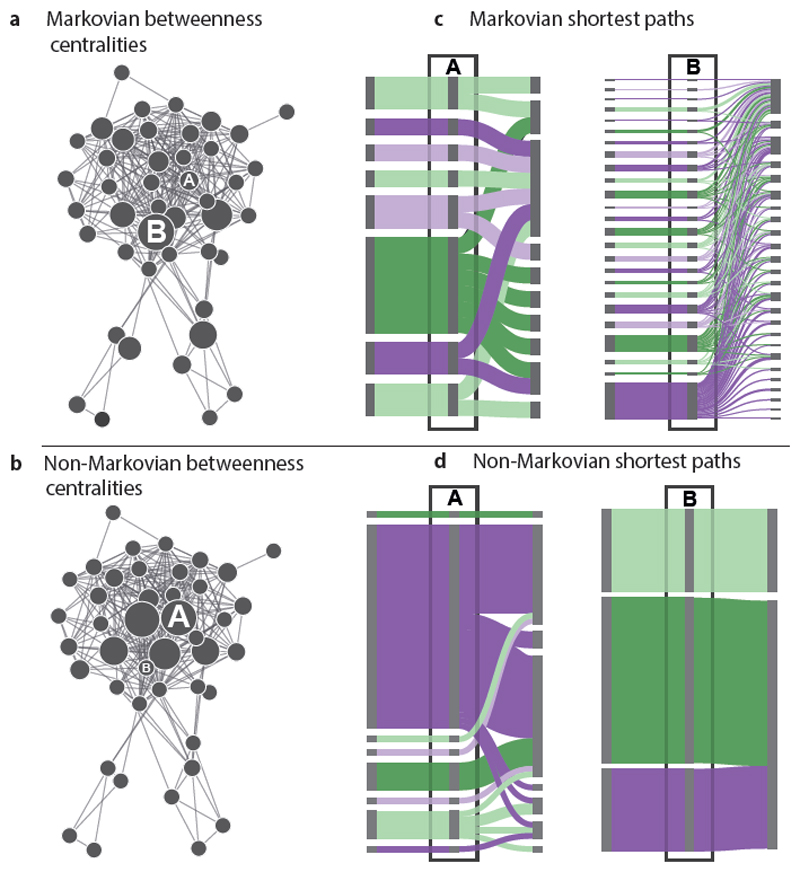
However, to better capture the importance of nodes we must go beyond network models and account for the complex structure of paths in high-dimensional, time-resolved data. An example is shown in Figure 4, which is based on time-stamped social interactions between software developers in a major Open Source project. The network model of these interactions (Fig. 4a) allows us to estimate the importance of nodes, for example, using betweenness centrality, a measure that assigns high centrality to a node v if many shortest paths between pairs of other nodes pass through v [65]. The resulting node centralities are represented by node sizes in Fig. 4a, indicating that node B is the most important node in the system.

Figure 4. Non-Markovian paths change the centrality of nodes in time-stamped social network data.

Betweenness centralities calculated based on shortest paths in a network model of time-stamped interactions (a) do not capture the true importance of nodes calculated based on causal paths that respect causality in the underlying time-series data (b). The alluvial diagrams highlight the fact that the chronological order of interactions alters the shortest causal paths passing through nodes A and B (d), compared to what we would expect based on the topology of direct interactions (c), thus considerably changing the betweenness centrality of nodes.

But is this a good estimate for the relative importance of different developers? We can answer this question by inferring causal paths in the underlying time-series data. That is, we consider which paths exist based on the chronological ordering and timing of time-stamped interactions. In a nutshell, for two interactions $\overrightarrow{\mathit{\text{AB}}}\text{and}\overrightarrow{\mathit{\text{BC}}},$ a causal path $\overrightarrow{\mathit{\text{ABC}}}$ can only exist if $\overrightarrow{\mathit{\text{AB}}}$ occurs before $\overrightarrow{\mathit{\text{BC}}}.$ Hence, time-stamped network data allow us to calculate causal path statistics that may or may not be consistent with the assumptions in transitive, Markovian paths of standard network models [17]. In the example shown in Fig. 4, a calculation of betweenness centralities based on actual shortest causal paths [11] considerably shifts the relative importance of different developers. The alluvial diagrams in Fig. 4a and b visualise these differences, revealing that the shortest causal paths passing through node B are considerably more constrained than expected. This is due to temporal patterns in human communication behaviour that are not captured by a standard network model. As a result, node B is less central than we would assume based on the network topology. In contrast, node A, which ranks among the least central nodes from a topology perspective, turns out to be the most important node in terms of causal paths in the interaction sequence.

Higher-order models open new ways to address these limitations of existing centrality measures. We can, for instance, generalise networks to higher-order network models that resemble high-dimensional De Bruijn graphs [61, 10, 17]. Each node in such an m-dimensional model represents a path of length m – 1. Relative frequencies of paths of length m in time-series data are represented by weighted links, connecting nodes that overlap by m – 1 nodes. This simple construction generalises standard network models to higher-order generative models of paths, each model of order m being a line graph of the model with order m – 1 (Fig. 5). Similar to memory networks, we can use such models to define higher-order generalisations of path-based centrality measures such as betweenness or closeness [11]. Moreover, spectral measures such as PageRank or eigenvector centrality can be redefined based on eigenvectors of linear operators derived from De Bruijn graphs or memory networks [12, 17, 15]. These novel measures help us better quantify the importance of elements in a complex system, considering a system’s topology as well as temporal patterns in non-Markovian paths. Besides statistical methods that can be used to detect correlations that warrant higher-order models, cross-validation analyses show that the predictions generated by such models indeed outperform those of standard network models [17], which confirms that higher-order models can better capture unseen data.

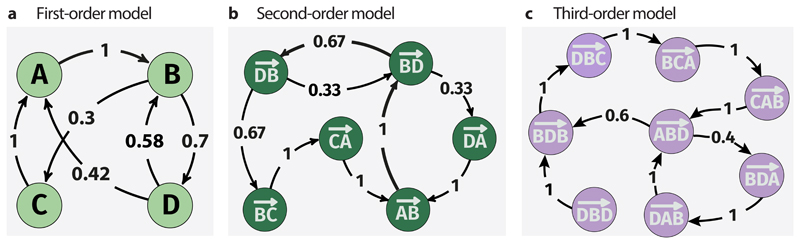
Figure 5. De Bruijn graphs with m dimensions help generalise network analytic methods to higher-order models.

(a) shows a first-order model with dimensionality m = 1 for a set of observed causal paths between four nodes A, B, C, and D. (b) shows a second-order model with m = 2 and (c) shows a third-order model with m = 3. Starting from a a first-order network model, higher-order models can be generated by an iterative line graph construction. The absence of transitions that correspond to a possible transitive path in the underlying first-order network, such as $\overrightarrow{BDB}\to \overrightarrow{DBD},$ indicates constraints in the observed paths that change the causal topology of the system.

Non-Markovian paths and dynamical processes

Along with giving us the ability to reason about topological features including like community structures or node centralities, network science enables us to understand how the topology of a system influences dynamical processes, and thus its function. Much of this research is based on the analytical study of linear dynamical systems in which Laplacian, adjacency, or transition matrices encode direct pairwise interactions between a system’s elements. The eigenvalues and eigenvectors of these matrix operators capture how the topology of a system influences the efficiency of diffusion and propagation processes, whether it enforces or mitigates the stability of dynamical systems, or if it hinders or fosters collective dynamics.

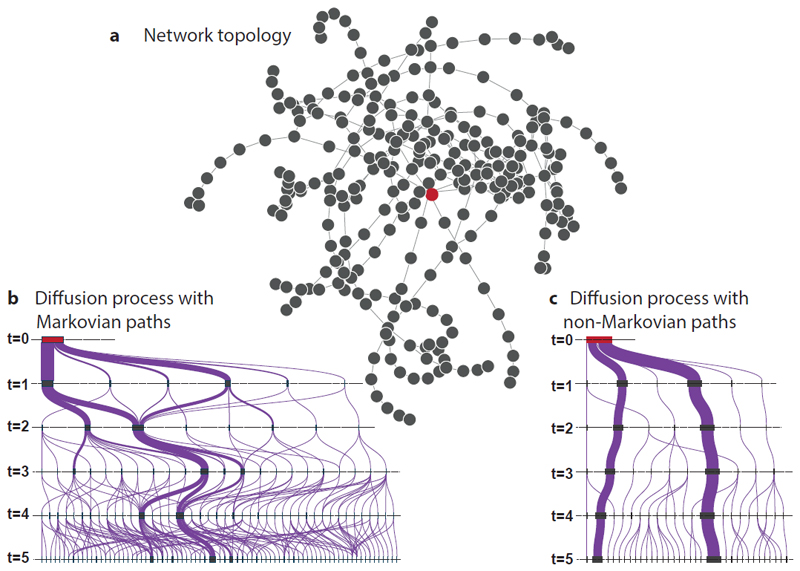
Although such algebraic methods help to relate the structure and dynamics of complex systems, they also come with the assumption of transitive, Markovian paths, which is not justified in many real systems. Figure 6a illustrates an example of such a system — the London Tube modelled as a network, where nodes represent train stations and links capture direct train connections between them. To understand how the topology of this transportation network influences its efficiency and robustness, it is common to study its influence on dynamical processes. As a simple example, consider a discrete-time model for the diffusion of passengers who start their journey at a single station at time t = 0 and travel one station per discrete time step. We further adjust each passenger’s probability to continue across a given link based on data on average passenger volumes between London Tube stations, making the passenger more likely to continue through links with high passenger volume. The flow diagram in Fig.6b shows the first five steps in this process. Assuming transitive, Markovian paths, it highlights how the system’s topology shapes diffusion dynamics. Alternatively, using available data on actual passenger itineraries, we can study this diffusion process based on real paths (Fig. 6c). This study reveals that the topology of the system is not sufficient to explain the complex non-Markovian paths and flows in the system [10]. Specifically, Fig. 6c reveals a strong directional preference – which would be better captured by a non-backtracking random walk – rooted in the non-Markovian characteristics of paths and the underlying geography. These patterns considerably influence the process and limit what the topology alone can tell us about the robustness and efficiency of real transportation networks.

Figure 6. Non-Markovian paths in networked systems influence the evolution of diffusion processes.

(a) shows a network model of the London Tube, where links capture direct train connections between metro stations. The flow diagrams in (b,c) show the first five steps of a discrete-time diffusion process starting in node highlighted in red in (a). The widths of flows capture the number of passengers moving on paths between particular nodes in the process. While (b) shows the dynamics of the process using transitive and Markovian paths in the network, (c) shows the evolution of diffusion across the non-Markovian paths created by the specific ordering of train connections in the London Tube. The causal topology created by such non-Markovian paths influences dynamical processes and challenges our understanding of real complex systems.

Non-Markovian higher-order models help us to overcome these issues. We can, for instance, generalise Laplacian and transition matrices to high-dimensional De Bruijn graph models [10] that capture the causal topology shaped by non-Markovian paths. Such higher-order representations enable the generalisation of methods for dynamical systems, such as eigendecompositions, spectral analysis or stability theory, to systems with non-Markovian paths. They make it possible to analytically study the complex interplay between time and topology in networked systems, and explain why non-Markovian characteristics of paths can both decelerate and accelerate dynamical processes and collective dynamics [10, 62].

Perspectives

To explain the behaviour of complex systems, we must understand how the components of a system influence each other. Network science provides powerful tools to address this challenge based on network abstractions of direct, pairwise interactions. They help us to explain emergent phenomena that are tied to essential features of the topology of the network that models a system, rather than to the details of a particular system. Moreover, by combining graph-theoretic methods with ensemble-based techniques, network science provides a solid foundation for statistical analysis, inference, and machine learning in relational data. However, the limits of what network models can teach us about real systems are becoming increasingly evident as a result of rich, recently available data on social, technical, and biological systems. Capturing complex paths in these data requires advanced modelling techniques, which comes with new challenges but also exciting opportunities for interdisciplinary exchanges between physics, computer science, and statistics.

Model selection is an epistemological challenge. Given rich, high-dimensional, and time-stamped data on complex systems, how do we know that our selected model explains how a system’s components influence each other? Referring to Ockham’s razor, a good model should be maximally parsimonious: It should make minimal assumptions to enable generalisable statements that go beyond the specific system under study. However, a good model must also be sufficiently sophisticated to explain paths observed in real systems, which is where standard network models often fall short. In other words, much like network science has exposed patterns in the link topology, we need higher-order models that best compress information by modelling higher-order dependencies in complex systems. Effectively, finding such optimal models based on rich data becomes a machine learning problem, where standard networks are merely one of many possible outcomes.

Scalability is a computational challenge. The size of non-Markovian models often grows exponentially with their order so that analysis becomes quickly infeasible. Moreover, statistically reliable inference of such models typically requires vast volumes of data, which may not be available. Finally, fixed higher-order models can simultaneously under- and over-fit paths in real systems. These issues highlight the need for computational and statistical methods that use variable-order [58, 15] or multi-order models [17], and model order reduction techniques [16] to generate computationally tractable models that neither under- nor overfit the data (see box 1). While model selection and statistical learning can be used to fit non-Markovian higher-order models in time-series data [17], little is known about how we can address this challenge for other classes of higher-order models and data.

Box 1. useful software.

The Infomap software package, available online at http://www.mapequation.org, provides code for clustering paths modeled by any fixed or variable higher order. Infomap is the search algorithm for an objective function known as the map equation, whose multilevel version can identify overlapping and nested modules that capture network flows modeled with flexible sparse memory networks. Together they provide a general solution that reveals overlapping modular patterns in higher-order network flows through complex systems [56].

The software package pathpy, available at http://www.pathpy.net, implements statistical techniques to learn optimal multi-order generative models for paths in time-series data. Operationalising Occam’s razor, these models balance model complexity with explanatory power for empirically observed paths in data on complex systems. Standard network analysis is justified if the inferred optimal model is a first-order network model. Optimal models with orders larger than one indicate higher-order dependencies and can be used to improve the analysis of dynamical processes, node centralities, and clusters [17].

A unified, higher-order modelling framework is an interdisciplinary challenge. While multilayer, combinatorial, and non-Markovian higher-order models enrich network science in different ways, a unified framework can potentially combine their strengths. For example, generalised links and paths in combinatorial models, which define them between arbitrary node sets, as well as multilayer models, which include heuristic inter-layer links, can benefit from the path-centric view of non-Markovian models with generalised links from data on paths. Similarly, the non-Markovian perspective can benefit from advances made by the other approaches. For example, these other approaches offer generalisations of generative models [63] that help us to detect structural patterns and identify the simple mechanisms by which they emerge. Since little is known about the mechanisms by which similar non-Markovian patterns emerge across different systems, a new class of higher-order generative network models would provide a step forward. Finally, a unified mathematical language can enable universal methods to select optimal models across different modelling approaches.

Addressing these challenges, higher-order modelling techniques will be able to leverage existing network methods and extend them toward optimal models that better explain the inner workings and behaviour of complex systems.