Multiscale Methods in Drug Design Bridge Chemical and Biological Complexity in the Search for Cures

Abstract

Drug action is inherently multiscale: it connects molecular interactions to emergent properties at cellular and larger scales. Simulation techniques at each of these different scales are already central to drug design and development, but methods capable of connecting across these scales will extend understanding of complex mechanisms and the ability to predict biological effects. Improved algorithms, ever-more-powerful computing architectures and the accelerating growth of rich datasets are driving advances in multiscale modeling methods capable of bridging chemical and biological complexity from the atom to the cell. Particularly exciting is the development of highly detailed, structure-based, physical simulations of biochemical systems, which are now able to access experimentally relevant timescales for large systems and, at the same time, achieve unprecedented accuracy. In this Perspective, we discuss how emerging data-rich, physics-based multiscale approaches are of the cusp of realizing long-promised impact in the discovery, design and development of novel therapeutics. We highlight emerging methods and applications in this growing field, and outline how different scales can be combined in practical modelling and simulation strategies.

Introduction

Biomolecular simulations are essential tools for drug design and development, and for our understanding of the molecular bases of disease^1,2. Simulations provide a ‘computational microscope’ to reveal biological mechanisms in atomic detail.³ They can reveal cryptic drug binding sites⁴ and predict important biological properties such as drug resistance⁵. Molecular dynamics (MD) simulations are the most widely used biomolecular simulation method: they apply empirical molecular mechanics (MM) force fields and can now be used to explore in atomic detail time-dependent phenomena at the scale of viral capsids⁶ even over microseconds⁷, given sufficient computational power. MM methods are increasingly applied routinely in structure-based drug design, e.g. for free energy calculations to predict binding affinities of pharmaceutical leads to their targets, accelerating drug development⁸. Their importance and algorithmic efficiency (resting on years of development by many pioneers) have made atomistic molecular dynamics simulations one of the largest scientific consumers of computing time globally. These methods (and Monte Carlo simulations) can be applied in rigorous free energy calculations of relative binding affinities of small molecules to protein targets. However, computational demands in terms of the sizes of systems and timescales limit the use of MD methods, but at the same time, the relatively simple potential functions used to achieve computational efficiency somewhat limit their range of application and accuracy. Different types of simulation methods are therefore required for different types of problems. Each of these different simulation methods has strengths, weaknesses and practical limitations in terms of the size of system that can be simulated, length of simulation that can be achieved, and type of phenomena that can be modeled. For example, various types of coarse-grained methods allow simulations on large spatiotemporal scales phenomena, including protein-protein interactions, protein orientation in membranes and packaging of nucleic acids. Simple molecular docking approaches offer a limited level of detail of molecular interactions, conformational flexibility and solvation in favor of increased computational efficiency for the rapid identification of potential leads from large databases. At the other extreme of computational molecular science, quantum chemical methods can be used to model chemical reactions (e.g., the mechanisms of enzyme catalysis) and calculate spectra. First principles (ab initio) electronic structure techniques for the structure optimisation of proteins⁹, and atomistic simulations to investigate dynamics of systems of appreciable size and complexity over nano- to microsecond ^10,11 and even millisecond timescale¹² (for smaller systems) exemplify the upper limits of current capability for atomic and molecular methods¹³.

Multiscale modelling approaches are emerging in drug design with potentially enormous impact on human health. Drugs act at the molecular scale but obviously have macroscopic effects, so we must consider multiple length scales to understand how they exert their effects. The dynamic nature of drug targets and the breathtaking complexity of biological systems challenge our scientific understanding from the level of molecular structure all the way up to cellular organization (and beyond). Each level provides challenges and fascination in its own right, but a holistic approach requires an understanding of how changes at different levels are linked together and influence each other. No single simulation method can address all of the many questions involved, nor explain how phenomena at various spatiotemporal scales are coupled and linked. Multiscale simulation methods aim to model and analyse the connections across scales, e.g. how changes on one scale lead to changes at another. An obvious challenge is the integration of data and simulations across lengthscales and timescales. Current multiscale approaches are potentially capable of overcoming these limits by directly combining different levels of description, bringing a new perspective to drug discovery.

The award of the 2013 Nobel Prize in Chemistry to Karplus, Levitt, and Warshel for their seminal contributions in developing multiscale methods for modeling complex biochemical systems recognized the essential role of theoretical and computational methods as a direct and necessary complement to experiment, and the birth of multiscale molecular modelling in biochemistry¹⁴. Today, nearly half a century after the advent of these methods, multiscale simulations offer the tantalizing possibility of understanding biology in intricate and exquisite detail. For example, multiscale modelling offers an understanding of how a chemical reaction occuring at an enzyme active site can affect other proteins and extend through the hierarchy of biological complexity - from subcellular neighborhoods, to cells, and tissues. The power of multiscale methods lies in the possibility to create a fluid knowledge landscape synthesizing disparate modelling and experimental data at different spatiotemporal scales. Practical insight will depend on combining diverse approaches, linking chemistry at the atomic scale with biological function at the cellular and higher levels to elucidate the mechanisms of emergent phenomena, and doing so in a way that circles back to drive drug design and development.

[H3] Unleashing the potential of emerging experimental data sources

Technological innovations for the in situ acquisition of biological structural data, including advances in direct detector and phase plate technologies¹⁵ for X-ray beamlines and electron microscopes (EMs), give access to new and vastly more detailed information across a range of previously inaccessible scales and, in some instances, time resolutions (Figure 1). Multiscale computational approaches are needed to fill in and connect datasets, which include data obtained from: serial block wide-field EM illumination of tissue and cellular ultrastructure to within tens of nanometers isotropic resolution for biologically real (endogenous, not cultured) samples¹⁶; cryoelectron tomography (cryoET) to localize supramolecular complexes and yield glimpses into cells with molecular resolution ( ~2–4 nm resolution in individual tomograms),^17–19; soft x-ray tomography to image whole hydrated (not stained or frozen) cells in their near-native state²⁰; near-atomic cryoelectron microscopy (cryoEM)¹⁹; small angle x-ray (SAXS) and neutron scattering (SANS); x-ray crystallography, diffuse scattering for an ensemble-based view of x-ray structures²¹; x-ray free electron lasers ^22, time resolved x-ray ²³ and neutron diffraction²⁴. In parallel, ongoing innovations in biophysical techniques such as NMR spectroscopy (e.g.,used for intein protein segmentation²⁵) and hydrogen-deuterium exchange mass spectrometry (HDX-MS)²⁶ continue to enrich our understanding of the dynamics and interactions of molecular and macromolecular ensembles. Interpretation, refinement and understanding of the high-resolution data from all these techniques challenge current modelling approaches. In addition all these new data call for the development of models and provide tests for their validation.

Figure 1: Multiscale structure- and physics-based methods bridging from atoms to cells.

Emerging multiscale computational methods coupled with increasingly accurate structural data on biological and chemical systems enables the development of highly detailed and predictive models of drug action across spatial scales ranging from angstroms to microns and temporal scales ranging from femtoseconds to minutes. Such approaches can be gainfully used to address a number of outstanding challenges in drug discovery and design (Table 1).

[H3] The coming fusion of simulation and data science

The convergence of improved and increased biophysical data, together with impressive algorithmic advances, occurs against a backdrop of an ever-expanding, increasingly diverse and more capable computing landscape. Porting simulation methods to the growing range of novel hardware architectures (e.g., graphics processing units (GPUs), advanced RISC machine (ARM)-based high performance computing (HPC), cloud computing, petascale HPC machines, and the emerging horizon of exascale computing²⁷) is extending the scope and range of simulations. The rapid growth of data science also offers transformative possibilities, not only in the manipulation of simulation data and linking across spatiotemporal scales, but also in its seamless integration with experimental data. Examples include the systematic development of Jupyter notebooks²⁸ and automated workflows^29,30, improved data sharing²¹, integration³¹, and analytics²⁰. These developments are driving cultural shifts towards improved reproducibility, openness, sharing, robustness and, ultimately, predictive ability of the computational approaches discussed in this Perspective.

[H3] Potential applications of multiscale methods in drug discovery

Multiscale methods span two or more spatial or temporal domains, or combine different types of treatment, aiming to give insight across scales. We note that the concept of multiscale modeling has been developed in several disciplines. Here, we focus on multiscale simulation methods that relate to the molecular level, that are based on fundamental physics, and are potentially relevant to drug discovery. Multiscale techniques can be constructed in different ways, depending on how different levels of description are combined or coupled, and how information is passed between the different levels³⁴. Multiscale methods can combine different levels of theory or resolution, e.g., combining MD with Brownian dynamics (BD) to access long timescales and larger lengthscales (MD/BD³⁵) or combining quantum mechanics (QM) with molecular mechanics (MM) in (QM/MM³⁶) to study electronic properties in a single simulation. Another class of multiscale methods comprises the hierarchical integration of sets of approaches carried out at different scales, which leads to one ultimate cohesive model. In this case, the final result is obtained through the interchange of key parameters across model scales^{37– 40}, even though the simulation platform itself may not directly interface two distinct physical regimes. A related form of multiscale modeling is based on the connection (and synthesis) of different types of biological, chemical, structural and biophysical data — a particularly exciting approach, given technological advances across a spectrum of experimental techniques. The development of increasingly accurate integrative models as an initial framework on which multiscale simulation methods subsequently operate presents a powerful emerging paradigm for drug discovery.

The study of multiscale methods for drug design is a wide and rapidly growing field; it is rich in potential but yet to realise its enormous promise. The diversity of approaches and applications means that we can only cover a few relevant examples in this Perspective to indicate the vast potential of this field. Here, we focus on some recent exciting methodological advances, as well as challenges for development and applications that highlight the promise of simulations to bridge scales from atoms to cells.

[H1] Cellular to Subcellular

The ongoing surge of high-resolution structural data is providing detailed views into many previously inaccessible biological compartments (e.g., the cell nucleus) and enabling the development of correspondingly realistic molecular models of cells and subcellular organelles. New tools such as CellPack¹², which interoperates with CellView⁴¹ and LipidWrapper¹³, can be used to model complex biomolecular systems at the mesoscale, reaching atomic resolution. Combining different datasets across scales of resoultion enables direct multiscaling from the standpoint of data integration (Box 1). The accessible spatial range now reaches the micron dimension, with essentially no limits on the complexity of the constituents of the system under investigation. A key advance is the ability to develop many ensembles of such models compatible with multiple sources of experimental data (e.g., proteomics, structural data from x-ray through cell tomography, etc.). This allows researchers to modify the construction of a system (for example, changing the expression level of a particular protein, introducing a structural perturbation to membrane or organelle shape, varying the molecular composition of viral strains (reassortment), or adding post-translational modifications) in order to test consistency against different types of data and predict the effects induced by these changes on the system.

Box 1: Multiscale Data-Driven System Assembly.

CellPACK⁴² is a system-construction framework allowing the integration of information from cellular ultrastructure, genomics and proteomics, and atomic structure to build integrated, data-centric 3D models of subcellular environments at molecular detail.

Data Input Sources

CellPack can connect to (ingest) many types of relevant datasets such as proteomics and genomics (for contents, stoichiometry of molecules in various compartments), X-ray crystallography (for atomic-resolution of molecular components), as well as various types of electron microscopies and tomographies (for macromolecular assemblies, subcellular and cellular ultrastructure).

Compartment Construction Methods

Once the compartments have been defined, polygonal models define membrane ultrastructure. If atomic membranes are desired, atomic structures of lipid membrane are modeled with LipidWrapper⁴³. Membrane-embedded selective orientation and placement of membrane-bound macromolecules based on the Orientations of Proteins in Membranes (OPM) methodology¹³⁷.

Solid voxelisation techniques are used to discretize the volume to be filled. Afterwards, crowded soluble environments are constructed with a size-priority voxel based method; where needed, schematic fibrous structures can be modeled with a random walk algorithm that “grows” the structures in situ.

Recipe Parameterization

The various data input sources and methods are integrated into a “recipe” that describes how to build a model. Namely, the recipe defines the “what” (ingredient description extracted from proteomics and structural biology), the “where” (cellular localization, e.g., surface, interior, organelle, etc.), the “how” (packing methods and constraints) and “how many” (based on molarity or copy number extracted from literature or experimentation).

Model Generation

Based on the recipe, and given a random seed, cellPACK generates a unique 3D model, which is simply a list of ingredients and their respective positions and orientations. By sampling different parameters (concentration, priority, order, packing methods) CellPack can easily generate hundreds of models to study statistical distributions, taking molecular models a step closer towards addressing biological heterogeneity, in hopes of understanding and, ultimately, accurately predicting emergent phenomena.

Once structural models are assembled, researchers can explore biological heterogeneity at the molecular level, and statistical distributions of biological and chemical components within these complex environments. Monte Carlo based methods such as MCell, ⁷ and continuum-based methods such as SubCell, ⁶ enable researchers to investigate biological phenomena without explicitly accounting for molecular (particle) collision and interaction. Reaction-diffusion master equation (RDME) methods combine network- and particle-based approaches on discretized grids/lattice sites; in doing so, these approaches allow the development of whole-cell based models of drugs and their dynamical interactions with receptors. Two exemplary GPU-accelerated RDME programs are: Lattice Microbe ^46–48, which splits the reaction and diffusion operators to allow efficient models of in vivo crowding on particle diffusion; and ReaDDyMM⁴⁹, which combines reactions at lattice sites with particle-particle interactions at off-lattice sites, as determined by MD. Another promising multiresolution method — lattice Boltzmann MD (LBMD) — employs a mixed approach in which (dynamic) proteins are represented as coarse-grained particles and the solution through which the proteins diffuse is represented probabilistically, such that multiple physical elements (including hydrodynamic and thermodynamic forces) can be included⁵⁰.

Particle-based approaches range from coarse-grained (each particle represents a group of atoms, from part of an amino acid residue to a whole protein) to fully atomistic (every atom represented individually) representations of the molecular constituents. Although coarse-grained techniques offer the possibility of simulating the behavior of larger systems on longer time-scales compared to the fully atomistic approaches, the choice of particle representation (i.e., how atoms are grouped) and the related force field development still presents challenges⁵¹. Atomic details are neglected entirely in coarser models, such as fluctuating finite element analysis (FFEA). In this approach, the macromolecules are essentially treated as density maps, subject to thermal fluctuations within a continuum medium that encodes the material properties, such as shear and elastic. Lower resolution data, such as SAXS or cryoEM can be directly linked to FFEA, effectively bypassing the requirement of starting with a detailed molecular model⁵². Such approaches can be essential when, for example, higher resolution structural data for system components is not available, or not all of the molecular components in a particular system are known.

Particle-based simulations in which the molecular components are represented with atomic detail —rigid-body BD and fully-flexible atomistic MD simulations — are proving ever more capable ^6,53–55. Rigid-body BD uses fully atomistic representations of molecules, but neglects the molecular internal degrees of freedom. In this representation, rigid molecules (e.g. proteins) are free to tumble and rotate as they diffuse relative to each other in a viscous medium (with water represented as a continuum solvent) and subject to random motion according to the fluctuation-dissipation theorem. The intermolecular forces that govern the interaction and collisions of the particles are electrostatic in nature and represented with a modified form of the Poisson–Boltzmann equation. In contrast, internal motions and conformational changes are considered in fully-flexible MD simulations. BD and MD can be used to explore the dynamics of molecules in crowded biological milieus, improving understanding of detailed biological and chemical interactions^10,53. They can be combined in multiscale approaches such as SEEKR (Box 2). Recent efforts linking particle-based simulation to higher-level systems biology or network-based models exemplify how handoffs between such methods can be gainfully achieved. For example, association rates determined with BD, MD, and SEEKR in network-based Markov chain of states models have been combined in order to define the mechanisms underlying the cooperative nature of cAMP activation of protein kinase A³⁷. Systems biology models and MD simulations have been combined e.g. to generate predictions of the effects of enzyme--substrate binding affinity changes due to genetic variation in human erthyrocytes³⁸. In both cases, linking molecular and cell-based models allowed mechanistic insights and predictions at the atomic-level to inform network-based whole-cell models of disease. Collectively, multiscale approaches spanning cellular to subcellular scales will help to address the challenge of better predictive models for off-target effects (e.g. binding of drugs to targets other than that desired). They also enable more complete understanding of chemical mechanisms of action and their effects at larger scales, especially for complex signalling pathways that require a broad view of molecular complexity. Hence, particle-based multiscale approaches at this scale may be particularly useful for understanding drug action.

Box 2: A Multiscale Method for Drug Binding and Residence Time Prediction.

SEEKR is a directly multiscale simulation approach that combines fully atomistic molecular dynamics simulations and rigid body Brownian dynamics simulations (i.e. two different dynamical propagators) with milestoning theory to calculate association and dissociation rates as well as binding free energies for protein ligand complexes. Fictitious ‘milestone’ surfaces (depicted with different colours) are placed at increasing distances from the determined ligand binding site. Short simulations are initiated from each milestone surface and are monitored until they touch an adjacent surface, where they are subsequently terminated. Each milestone surface is assigned a particular simulation type. These types can encompass a broad range of methods, as milestoning theory is agnostic to the simulation type implemented. Typical SEEKR simulations span the spectrum of potential simulation detail, implementing fully atomistic MD regions and rigid body BD regions. This approach has demonstrated significant increases in both speed and accuracy for the calculation of kinetic parameters compared to “brute force” molecular dynamics simulations, which often require simulation timescales that are inaccessible by conventional computer simulations. The combination of a multiscale simulation approach with milestoning enables SEEKR to predict ligand dissociation events in a statistically robust and computationally efficient manner, facilitating the accurate computation of drug residence times, a particularly important property linked to the in vivo efficacy of drug molecules.

Yellow regions in the figure represent regions that are simulated using fully atomistic molecular dynamics simulations (red arrows represent these trajectories). These regions correspond to milestones close to the binding site, where an atomistic description of molecular interactions is required to model of the binding and unbinding processes. Blue regions instead are simulated using Brownian dynamics. These correspond to the outermost milestones of the figure, where atomistic detail is less important and rigid body dynamics with implicit solvent can rapidly sample long trajectories. The green region represents an area sampled by both molecular dynamics and Brownian dynamics simulations, which are brought together with milestoning theory.

A typical milestoning procedure consists of multiple simulation steps. First an equilibrium distribution for each milestone surface is obtained, typically through umbrella sampling. The equilibrium distribution is then converted to a first hitting point distribution (FHPD) by initiating simulations from each point in the equilibrium distribution with reversed velocities to determine if they had been in a previous state. Any trajectories that cross the same milestone surface they were initiated from are excluded from the FHPD. Finally, trajectories are initiated from each point in the FHPD and allowed to propagate forward in time until it crosses another milestone surface. The trajectory is then terminated, and the transition, as well as the transition time, is recorded. This data can be used to compute a transition kernel, K, where each element is computed by the formula:

$$K_{ij}=\frac{n_{i\to j}}{{\sum }_k{n}_{i\to k}}$$

The mean first passage time (MFPT), τ:, can then be computed by the equation:

$$\langle \tau \rangle =p\cdot {\left(I-\widehat{K}\right)}^{-1}\langle \tau \rangle$$

Where p is the initial probability distribution and I is the identity matrix. The unbinding rate constant, k_off, is then simply the inverse of the calculated MFPT.

Challenges at cellular and subcellular scales will continue to include the experimental determination of the constituents of cellular compartments (e.g., protein counts, mRNA expression levels, etc.) with enough detail (spatial and temporal resolution) to enable the development of biologically accurate structural models. New tools for segmentation and refinement of tomographic data are needed, particularly when the data are highly complex. For example, recent ultrastructural 3D mapping of the cell nucleus shows how new imaging techniques, such as ChromEMT, can directly reveal details of the higher order structure of chromatin; at the same time, it underscores the need for new tools that are able to segment and refine the structural data at the level of individual chromatin fibers⁵⁶. These data will transform our understanding of the relationship between chromatin structure and dynamics and the regulation of gene expression, which is an inherently multiscale challenge ⁵⁷. Additionally, once these structures are refined, new tools for developing numerically computable meshes from these reconstructions are required to create models that can be extended and interrogated with physics-based simulation. Innovations in simulation approaches are required to effectively handle hydrodynamic interactions⁵⁸, as well as different concentration and diffusion regimes within a complex, crowded cell scene ⁵⁹. Finally, a major set of challenges relates to the ability of researchers to set up and execute complex models and simulations. Also, the substantial complexity of highly detailed large-scale models can make the interpretation of the simulated phenomena difficult. These challenges are intimately linked with data analysis and visualization, and will benefit from technological advances such as machine learning ⁶⁰ and virtual reality⁶¹.

[H1] Subcellular to molecular and atomistic

The action (and metabolism) of many drugs is fundamentally based on the changes in and interactions among individual molecules. Multiscale methods are needed to connect molecular changes to changes induced in subcellular levels and and beyond. Increasingly informed integrative models of macromolecular complexes ^62,63 are providing atomically detailed views of complex drug targets and drug-target interaction⁶⁴, thanks particularly to advances in cryoEM. The 2017 Nobel Prize in Chemistry recognised these developments ⁶⁵. However, moving beyond the traditional paradigm of studying single drug targets in isolation to tackle the dynamics of macromolecular complexes and, for example, their interactions with the genome⁶⁴ poses a challenge to atomic-scale modeling. The ability to model protein–protein complexes more accurately (e.g. allowing for changes in conformation driven by intermolecular interactions and chemical changes) will improve protein and antibody design for vaccine development.^66–69 Indeed, the resolution-revolution taking place in cryoEM and cryoET will drive methods development for multiscale simulation across the subcellular and molecular scales. Multiscale simulations will offer an expanded perspective of drug targets, elucidating their detailed and often critical interactions with realistically complex membranes and other proteins. The new structural understanding provided by diverse approaches has already helped industrial research teams reconcile seemingly divergent or otherwise inexplicable experimental assay results⁷⁰.

There has been significant recent progress in the development of methods enabling the exploration and characterization of the dynamics of molecular scale systems. An example particularly relevant to drug discovery is provided by simulation-based approaches for the identification of so-called cryptic (hidden) pockets or sites of allosteric activation, which are not evident in x-ray crystallographic structures and can be novel drug-target sites ^4,71,72. Another promising class of techniques is based on Markov state models (MSMs), which enable the extension of temporal scales achievable in ensemble-based approaches through the extraction of long timescale dynamics from many short timescale simulations. MSMs take a more statistics-oriented view to trajectory analysis: individual states are defined or identified, and the dynamics between the interconnected states, assumed to be Markovian, are modelled as a transition probability matrix, populated from independent simulations. Dynamic information relating the states is typically obtained through many short timescale MD simulations that are integrated into one cohesive framework ^73–75 MSMs have been used to predict the thermodynamic and kinetic landscapes for the activation of multiple kinases ^76,77 and protein–protein association pathways⁷⁸, characterizing biological processes that occur over timescales from microseconds to hours. Notably, MSMs make use of the statistical sampling necessary for the analysis of larger lengthscale (e.g., subcellular or cell-scale) simulations, which by their nature contain many independent copies of one particular drug target. One can use relatively short timescale (e.g., tens of nanoseconds) simulations of large and/or multicomponent systems, potentially comprising multiple hundreds of millions of atoms, in combination with MSMs to extract long timescale (e.g., kinetics on the order of milliseconds) information for the individual molecular components of a biological scene. These methods will facilitate an increasingly accurate understanding of how drugs act at a particular site and subsequently alter the dynamical landscape of their receptors, including, for example, for the highly dynamic G-protein coupled receptors ⁷⁹, one of the most important classes of pharmaceutical targets. MD based methods also stand to benefit from and connect to advances in experimental structure characterization methods. These methods include diffuse x-ray scattering, which gives improved characterization of protein flexibility and ligand binding, and the detailed picture of biomolecular heterogeneity emerging from high resolution cryoEM, both of which can feed back into the development of more accurate MD force fields ^21.

The development of effective drugs is becoming increasingly reliant on our understanding and ability to quantify and optimize the kinetics of drug binding (associated with a rate contstant kon) and unbinding (koff). Drugs must bind quickly enough to their target to avoid being cleared from the body before they can act, and must also remain bound long enough to exert an effect; such considerations are more important than the thermodynamic binding affinity in many cases. Drugs with slow rates of dissociation have longer interaction times (also referred to as residence times) with their targets and therefore are often found to be more efficacious^80,81. The ability to quantify and predict binding and unbinding rates and residence times therefore represents a major and growing requirement in drug discovery and development programs. As such, the past few years have seen a dramatic increase in simulation and associated modeling methods to predict such quantities, and analyse the molecular and dynamical features that determine them⁸¹. These methods include direct quantification through enhanced sampling techniques⁸² such as MSMs ^76,83, smoothed-potential MD^84,85, and metadynamics ⁸⁶ (e.g. with path collective variables and parallel tempering to calculate free energy profiles, and transition state-partial path transition interface sampling ⁸⁷ for kinetics) or through multiscale simulation methods, such as SEEKR. SEEKR is a novel method that uses milestoning theory to combine atomic-scale rigid-body Brownian dynamics (if the two interacting molecular species are sufficiently far apart, with fully-flexible MD simulations when the particles are in close proximity (Box 2) ^35,88,89. The combined use of different dynamical propagators enables efficient computation of accurate binding kinetics and free energies of binding using a directly multiscale approach.

Predicting membrane permeability is another area of intense interest to drug discovery programs for which multiscale physics-based simulations promise significant advantages over phenomenological (or descriptor-based) models. Both the potential of mean force for a small molecule crossing the membrane and its position-dependent diffusion constant can be simulated in several ways and combined to predict the passive permeation of drugs through membranes (reviewed in ^90,91). Recent resurgence of interest in this area has included multiscale efforts to tackle system complexity, e.g. for notoriously challenging systems such as gram-negative bacterial membrane transport ^92–94; multiresolution methods that mix coarse-grained models of membranes with all-atom models of antibacterial compounds ⁹⁵; and methods that enable multiscaling in time through the integrated use of MSMs ⁹⁶ or milestoning ^97,98.

Despite the developments described above, the ability of present methods to enable crossing of subcellular to molecular scales — ensuring biological and chemical realism — is not without technical and intellectual challenges. Sampling of slow conformational dynamics in all of these systems remains a key problem. Development of new approaches to accelerate otherwise slow dynamics (e.g., multiensemble MSMs⁹⁹) will be required. Innovative solutions to the challenges posed by slow dynamics are likely to require continued development of approaches for hierarchical coarse-graining^57,100–104. As simulations over increasingly longer timescale become routine, research efforts must continue to shift from manual human-driven data curation (which remains the current de facto standard) to machine-learning-based methods that will enable the detection of new patterns, correlations, etc. within the vast amount of data being generated¹⁰⁵.

[H1] Atomistic to electronic

Molecular structure, dynamics, and reactivity arise fundamentally from quantum mechanics. Calculations of the electronic structure of molecules are essential for the study of certain properties. In principle, as Dirac stated long ago, quantum mechanics provides the theoretical route to calculating all molecular properties, the “only” challenge being computational tractability. The utility of quantum mechanics has been amply demonstrated for small molecules (~tens of atoms), for which reaction barriers and spectra can be calculated from first principles ab initio electronic structure methods with accuracy often at least as good as experiment. The electronic structure of larger systems (~hundreds of atoms) can be calculated with density functional theory (DFT) methods. These are in general somewhat less accurate and are not systematically improvable, but have nevertheless revolutionized the role of computation in chemistry by providing useful insight (e.g., into reaction mechanisms) at a manageable computational cost. More approximate methods based on semiempirical molecular orbital theory or approximate DFT allow calculations on even larger systems (~thousands of atoms). Algorithmic developments (such as implementation on GPUs⁹) and methodological developments continue to extend the reach of quantum chemical calculations, both in terms of system size (for example, the thousands of atoms for modelling transition states in enzymes and properties of ion channels) and scope (for example, to MD and Monte Carlo simulations), bringing electronic structure calculations into new biological regimes¹⁰⁶. All of these techniques address molecular electronic structure, which is inherently quantum mechanical, and are usually applied with a classical description of molecular dynamics/nuclear motion. Quantum dynamical effects such as quantum tunneling (which is significant in the determining the rate of transfer of hydrogen) can also be investigated, by methods that include the effects of quantum dynamics for nuclei.

In principle, quantum mechanical methods offer higher accuracy than empirical force fields, but in practice, it may often be more feasible — or indeed preferable — to apply a hybrid approaches, combining a quantum mechanical description of a small region (e.g., enzyme active site) with an empirical (MM) treatment of most of the system (e.g., protein, solvent, membrane, etc). Such QM/MM methods were a focus of the 2013 Nobel Prize in Chemistry and now provide an attractive combination of practicality and versatility for a range of problems. Applications in drug development include: informing inhibitor design from knowledge of interactions of transition states and intermediates ¹⁰⁷; understanding the reactivity and specificity of (and resistance to) covalent inhibitors ^108; analysing the coupling of chemical and conformational changes in biomolecules; predicting NMR and electronic spectra (e.g., to identify binding modes); developing of in situ structure-activity relationships, and predicting drug metabolism ^109–111 (Figure 2). It is possible to extend beyond DFT to highly accurate first principles ab initio methods, e.g., by applying projector-based embedding techniques, which can be applied in a QM/MM framework to treat large systems such as proteins. ^112,113,114 QM/MM MD simulations are possible with lower-level QM treatments and are increasingly practical with DFT methods. A combination of such methods can predict chemically accurate barriers for enzyme-catalysed reactions ^35,110. QM/MM methods can also now be applied in areas that were previously the domain of empirical force fields, such as in calculations of binding affinities and solvation energies using multilevel sampling approaches. ^8,117–121 QM/MM methods can be applied in multiscale schemes coupling sampling at different levels, to combine the accuracy of the higher-level method with a more computationally efficient lower-level treatment (see Box 3). Potentially, this can overcome some limitations of empirical (MM) atomistic force fields (such as oversimplified descriptions of electrostatics and lack of electronic polarization), which may be particularly important for some target classes, such as metalloproteins¹²². For example, the binding affinity of water molecules to proteins is affected by changes in the polarization of water molecules ¹²³. This effect is larger for larger drug-like molecules and may affect predictions of drug binding/unbinding kinetics because of the important changes in solvation involved in these processes. Just as QM methods can generate data to inform development of atomistic force fields¹²⁴, which are increasingly driven by machine learning approaches and integrated with experimental data, multiscale QM/MM schemes also offer the potential of testing and developing lower-level methods, e.g., in on-the-fly (re)parameterization¹²⁵.

Figure 2: Multiscale Simulation Methods to Predict Drug Metabolism by Cytochrome P450 Enzymes.

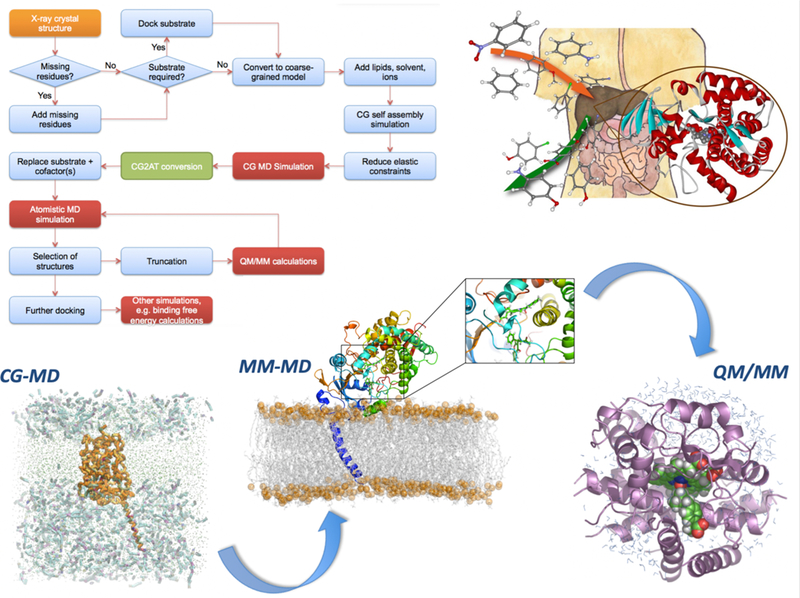
Cytochrome P450 enzymes (CYPs) play a central role in metabolizing most drugs. Understanding their reactivity and selectivity is a central goal in predicting drug metabolism, and provides an example of a drug development challenge requiring multiscale simulation approaches. The flowchart shows a practical workflow for multiscale modeling of metabolic reactions of pharmaceuticals in CYPs¹⁰⁹. Mammalian CYPs are membrane-bound enzymes, but typically only the structures of the soluble portions are determined experimentally, lacking the membrane-anchoring helix, and the membrane. The intact CYP, in situ, can be modeled by adding the transmembrane helix and assembling the membrane around the protein, which occurs spontaneously in coarse-grained (CG) molecular dynamics (MD) simulations. CG methods allow MD simulations on timescales of microseconds to milliseconds, showing how the protein is oriented in the membrane and how drug molecules such as warfarin move through the membrane and associate with the protein. Understanding how the drug accesses and binds within the active site requires more detailed, fully-flexible MD simulations with an atomistic molecular mechanics (MM) representation in which every atom in the simulation is represented explicitly, in contrast to the representation of amino acids by a small number of ‘beads’ that group atoms together at the CG level. The CG model is converted into an atomistic (AT) model, which can be used for MD simulations of drug binding. Typical MM methods cannot be used to model chemical reactivity, therefore for potentially reactive poses of the enzyme/drug complex, the system is converted to a quantum mechanics/molecular mechanics (QM/MM) model, in which the reactive Compound I and the drug are included in the QM region for modeling of chemical reactions of the drug in the enzyme.

Box 3: Combining QM/MM and MM simulations for calculations of Protein-Ligand Binding Affinity.

Multiscale sampling allows for efficient connection of high and low levels of simulation, combining a more accurate, high level method, with the greater computational efficiency of a lower-level method^{34, 115, 120}. Free energy calculations are increasingly important in drug discovery and development. Typically, the relative binding affinity of different ligands is calculated (for example, via free energy perturbation simulations); alternatively, the absolute binding free energy of a ligand to its protein target, ΔG_bind, can be calculated, as shown here, (for example using enhanced sampling molecular dynamics methods). Typically, such calculations apply empirical ‘molecular mechanics’ models, which are computationally efficient and provide atomic-level detail, but have limitations in their description of molecular interactions (due for example to the use of an invariant atomic charge model). Methods based on quantum mechanics (QM) are potentially more accurate because they treat the electronic structure of molecules, but they are much more computationally expensive, making direct application in free energy simulations impractical. A coupled multiscale approach, combining quantum mechanics (QM) calculations with MM simulations, allows protein-ligand binding affinities to be calculated at the combined QM/MM level, which may help overcome limitations of empirical MM force fields, potentially improving the accuracy of predictions, and improving models. This is achieved by the thermodynamic cycle shown here, where the free energy change for going from a QM to a MM description of the ligand $\left(\Delta G^{\text{QM}\to \text{MM}}\right)$ is calculated, here for the ligand when bound to the protein, and when free in solution. Replica exchange thermodynamic integration can be used to calculate $\left(\Delta G^{\text{MM}\to \text{QM}}\right)$ efficiently. This transformation from a MM to a QM representation of the molecule takes advantage of efficient sampling at the lower (MM) level. The Metropolis-Hastings algorithm is used to accept a configuration into the higher level (QM/MM) ensemble. Replica exchange simulations across the QM<->MM coordinate enhance sampling, and free energy differences can be calculated by thermodynamic integration, or other methods. Combined with the MM free energy of binding, these give the free energy of binding, ΔG_bind.at the QM/MM level. This can test (and correct) limitations of MM methods such as lack of changes in electronic polarization115–118. This type of scheme also allows rigorous connection between different levels in generalized multiscale simulation schemes.

Methods capable of modelling and predicting chemical reactivity in detail offer opportunities in a number of emerging challenging areas in drug discovery. A particularly important area of application is in the study of covalent inhibitors. There is renewed and growing interest in developing covalent binders and inhibitors (for enzymes and other targets), for increased affinity and e.g. altered pharmacokinetics ¹²⁶. There is a need to understand what governs the reactivity of covalent modifiers in vivo to maximise specificity and minimise off-target effects, and to understand resistance to covalent drugs¹²⁷. The ideal covalent modifier is only activated at the specific target site. Just as for the prediction of drug metabolism, approaches based on the ligands alone cannot capture all the factors relevant for reactivity. Challenges include prediction of pK_as of target residues for modification (for cysteines, in particular), treatment of conformational effects and identification of unusual mechanisms. For modelling of reactivity, empirical valence bond (EVB) methods are a highly efficient alternative to QM or QM/MM calculations, being significantly less computationally demanding than electronic structure methods, but they require substantial effort in parameterization ¹²⁸. QM and QM/MM methods (and/or experimental data) can be used to parameterize EVB models ¹¹⁵. Pratical challenges in applying QM/MM methods ¹²⁹ include the choice of the size of QM region for optimal efficiency and accuracy ¹³⁰. Adaptive schemes, in which the QM region changes during the simulation, are potentially useful for some applications, such as long-range electron transfer ¹³¹. Consistency between the particular level of QM treatment and the MM force field is also important. Also, QM/MM simulations typically apply relatively low levels of QM theory, and connecting to higher levels of theory (for example, via embedding or perturbation approaches) can be important to achieve high accuracy. For large systems, models combining QM/MM and coarse grained methods will be useful¹³². Generating reaction pathways and reactive configurations requires effective and efficient simulation methods and enhanced sampling techniques. A long-cherished goal is to use knowledge of transition states to design enzyme inhibitors, based on Pauling’s proposal that transition state analogues should be high affinity ligands. Whilst it is naive to think that this is a universal approach to enzyme inhibition, there is real potential in using structurally detailed knowledge of the interactions of transition state structures in some enzymes, and reaction intermediates in others, to design and optimise binding interactions of drug leads.

Methods for understanding and predicting chemical reactivity in large biological systems also bring into view a range of other exciting possibilities relevant to drug design and development. Simulations of biochemical reactions will be important for understanding the modulation and control of reactivity by conformational effects and allosteric regulation. A fundamentally important theme is understanding how chemical and conformational changes are coupled in biomolecular systems. This is essentially a multiscale problem in itself: it requires knowledge of the role of macromolecular conformational changes in catalytic cycles, and how reactions such as the hydrolysis of ATP drive molecular motors and other biomolecular machines. Linking to larger scales will help in designed manipulation of metabolic cycles and signaling cascades, as noted above. More speculative practical challenges are also coming into sight: the control and manipulation of reactivity within biological systems promises entirely new types of therapy. Enzyme inhibitors are obviously important as pharmaceuticals and, in a few cases, enzymes are used as drugs, such as thrombolytics, and in enzyme replacement and enhancement therapies to correct genetic deficiencies, usually in rare conditions. The activation of prodrugs often depends on enzymes and therefore improved understanding of prodrug–enzyme reactivity will help the in the design and development of all types of directed enzyme prodrug therapy^133,134. Potentially, engineered or evolved enzymes, catalytic antibodies or hybrid bio/chemocatalysts, could be used to control selective prodrug reactivity in cells. Photodynamic therapy is another area in which electronic structure calculations can potentially aid drug design, understanding and predicting photoactivation and contributing to improved selectivity of photoactivation ¹³⁵. More radical is the use of designed catalysts to remodel or destroy biological targets in situ ¹³⁶. One example is the possibility of gene editing offered by systems such as CRISPR/Cas 9. Application of catalysts in human patients will be accelerated by techniques for understanding and designing determinants of specificity and reactivity and their interactions in vivo. Multiscale simulation methods capable of modelling reactions and predicting their effects in complex biological systems will contribute to such developments.

[H1] The changing role of computational science

An expanding range of chemical, biological, biophysical, spectroscopic and structural techniques is increasingly integral to drug discovery and design programs. The scale and complexity of the data that they generate demand the concerted development of data-centric computational models to interpret and connect them. The combination of a range of data with multiscale models will provide detailed knowledge of drug targets, including their time dependence and dynamics, transforming our ability to understand and predict drug action. An exciting prospect is the development of interconnected multiscale models spanning the full range of complexity, from chemical action at a target binding site through complex cellular interactions and beyond. Multiscale models of this scope will also help to identify and analyse adverse drug reactions, arising from drug–drug interactions and off-target effects. Developing reliable, integrated multiscale methods poses significant challenges, but they promise significant payoffs in the drug discovery arena. They will drive the generation of experimentally testable hypotheses and assist in experimental design. Understanding of biology will undoubtedly advance faster and more reliably through effective combination of experimental and multiscale computational science.

The role of biomolecular simulation in drug design and development (and in analysing mechanisms relevant to health and disease) is evolving rapidly. Whereas previously simulation provided simple models to help develop or illustrate hypotheses, increasingly simulations can be used as another form of experiment: a computational experiment or assay. As such, simulators must apply similar standards of statistical rigor in assessing the significance of their findings. Computational assays can be used to assess and predict biological properties, such as drug resistance in mutant systems. Simulations can also be used to explore and analyse processes that are otherwise inaccessible or unachievable with experiment. Ongoing increases in computer power, together with improvements in the reliability and scope of simulation methods (with detailed validation against experiment), mean that computational assays will become ever more important in drug development, offering speed and affordability, and complementing and managing the growing deluge of experimental data.

No single simulation technique can address all the many levels of challenge and understanding required for modelling of biological systems from the molecular to the cellular level: this is the essential driving motivation for the development of multiscale methods. As the examples outlined here highlight, the potential of multiscale modelling and simulation, and of its close integration with experiment, is only just starting to be realized in drug discovery. We expect that, within the next decade, multiscale methods are likely to be central in drug discovery and development programs. They will form the basis of, and inform, cohesive data-rich models for drug–target systems. Together, these will rationalize and synthesize experimental data, accelerate drug development and help discover effective therapeutics with novel mechanisms of action.

Table 1:

Drug Discovery Challenges and Multiscale Computational Methods that Address Them

Drug Discovery Challenge	Relevant Multiscale Computational Method(s) and Examples
Mechanism of Action: Small molecule or protein-protein binding, transition or activation pathway analysis	Combined MD/BD (SEEKR) 88, Markov state models (MSM) 78
Mechanism of Action: Reaction mechanisms. Covalent inhibition/binding/modification	Combined quantum mechanics/molecular mechanics (QM/MM) 5,36,115, including embedding methods 116; empirical valence bond methods
Mechanism of Action: Off-target effects	MD, BD of large-scale multi-component systems 6,10,11, reaction diffusion master equation 47,49, lattice Boltzmann MD50
Predicting Drug Resistance	QM/MM (e.g. for antimicrobial resistance due to beta-lactamases36, and for covalent binders124); MD with free energy calculations (e.g. influenza neuraminidase) 5
Drug Residence Time	SEEKR 88, metadynamics 138, MSM 83
CYP P450 Drug Metabolism	Combined coarse grained MD, MD, QM/MM 109,110
Small Molecule Membrane Permeability	Milestoning97,98, mixed coarse-grained/all-atom approaches 95, combined PMF/MSM method 96