Abstract
Background
Vertical jump highs are used to quantify performance in the lower extremities. The aim of this study was to validate a wearable inertial measurement unit (IMU) for purpose of estimating countermovement jump height using the following methods: numerical double integration (NDI), takeoff velocity (TOV) and flight-time (FT).
Methods
Fifteen students each performed three jumps in two different sessions, four weeks apart. Jump-heights calculated from motion capture and force plate were used as gold standard for global IMU position and center of mass (CoM) displacement, respectively.
Results
The NDI method showed higher estimates for global position (1.39 cm, p = 0.025), and for CoM displacement (4.20 cm, p < 0.001). Narrow limits of agreements (LoA) were found (<4.8 cm). Further, a low tolerance level of determining equivalence (delta) between the two sessions regarding both global and CoM displacement (±2.80 and ± 2.90 cm) suggesting reasonable test-retest reliability.
Similar bias was found for TOV and FT (p < 0.015) and wide LoAs were found for global position and for CoM displacement (TOV: ±7.05 and ± 9.36 cm, AT: ±9.27 and ± 8.49 cm). Further, high delta between the two sessions (TOV: ±3.50 cm, FT ±4.00 cm) showed poor test-retest reliability.
Conclusion
Estimation of countermovement jump height using an IMU leads to the most accurate measurements applying the NDI-method. Countermovement jump estimated with an IMU can reliably evaluate functional performance in the lower extremities in young or in sports active patients after surgery or after rehabilitation. Countermovement jump with an IMU allows performing the test without a force plate and thus serves as an objective outcome measure in clinical practice.
Keywords: countermovement jump, Wearable, Inertial measurement unit, Test-retest
Introduction
Vertical jump highs are widely used to quantify performance in the lower extremities. Since a subject will not be able to maintain a squat position without impairing output, the most reliable jumping method for gauging vertical movement is a countermovement jump (CMJ).1 Force plates (FP) have been used to analyze CMJ in children,2,3 elderly4, 5, 6 and athletes.7, 8, 9 FP accurately determine the vertical acceleration of the center of mass (CoM), but are expensive and difficult to transport.10, 11, 12, 13 Instead contact mats are often used for field tests, e.g. Optojump14 and Ergojump.15,16 In these cases, flight-time (FT) is used to estimate vertical displacement, which requires the assumption that takeoff and landing posture are identical.11,13,17 This assumption is problematic, especially in children,18 non-athletes10, orthopaedic patients and to lesser extent in physically active students17 and sports students.11
Inertial measurement units (IMU) have become popular for various movement analyses,19, 20, 21, 22 presumably because of its size, ease of use and affordability. An IMU is a sensor containing an accelerometer and a gyroscope. A few studies have validated different accelerometers with regards to estimating vertical displacement, e.g. two biaxial accelerometers mounted on the ankles23 and one triaxial accelerometer mounted with a rubber band around the waist.24 The vertical displacement is in both cases estimated from FT and thus, different takeoff- and landing postures may limit the applicability. Further, these studies ignored rotational movement of the sensor in the sagittal plane due to e.g. hip flexion, which has been found to influence estimated vertical displacement.25 Hence, an IMU is more applicable to estimate vertical displacement during a CMJ. However, to estimate the vertical displacement, Picerno et al.25 like the previous include the FT as a variable which might limit the validity of the measurements.
There are three ways of estimating vertical displacement of the CoM when using a FP, which also can be applied when using an IMU: Numerical double integration (NDI) of acceleration, takeoff velocity (TOV) and FT. Both the NDI and TOV method overcome the requirement of the same posture, FT, takeoff and landing during a CMJ. Hence, we hypothesized that an IMU can replace a force plate when estimating vertical displacement in a counter movement jump. This was done by firstly validate an IMU to determine CMJ height by NDI, TOV and FT using both FP and motion capture (MC) as gold standards, and secondly to investigate the reliability by test-retest.
Materials and methods
Subjects: Fifteen sports students (12 males, age 26 (4.61) years (mean (SD)), body mass 81.0 (8.90) kg, height 187 (8.57) cm, BMI 23.42 (0.91) kg m−2 and 3 females, 26 (1.15) years, 69.2 (8.38) kg, 170 (2.36) cm, 23.98 (2.84) kg m−2) gave their written, informed consent to participate in this study. Due to non-study related issues only eleven of the subjects participated in the second test session (9 males, 26 (4.86) years mean (SD)), 82.3 (7.71) kg, 188 (8.20) cm, 23.00 (0.72) kg m-2 and 2 females, 25 (0) years, 67.0 (10.54) kg, 169 (0.71 cm, 23.60 (3.91) kg m-2). The regional ethical committee was contacted regarding initiation of the study and reviewed the study as non-notifiable.
Equipment: An IMU (MicroStrain, Inertia-Link - 3DM-GX2, Williston, USA) containing a triaxial accelerometer and a triaxial gyroscope with wireless connection and 100 Hz sampling frequency was used. An 8-camera (ProReflex MCU 1000, Qualisys, Gothenburg, Sweden) MC system sampled FT at 240 Hz and an AMTI OR6-7 force plate (Advanced Medical Technology Inc., Watertown, MA, USA) sampled FT at 960 Hz was used as gold standard. Qualisys Track Manager (Gothenburg, Sweden) was used to record and synchronize these data.
Procedure: The subjects were informed about the purpose of the study, after which they performed approximately 5 min warm up, primarily on an exercise bike. Subsequently, they were instructed how to perform CMJ without arm swing to minimize the change in posture and thereby a vertical displacement of the CoM between takeoff and landing. There were no restrictions on the depth of the counter movement.10,11,17,26 The subjects were allowed two habituation jumps after which the IMU was mounted with local positive y-axis upwards at the level of L5, identified by palpation as the midpoint between the posterior superior iliac spines. The IMU was secured by double sided tape (3 M Company, St. Paul, Minneapolis, USA) and Fixomull stretch (BSN medical GBH, Hamburg, Germany) as underlying layer for better attachment. The IMU battery was taped next to the IMU also using Fixomull. Testing involved four jumps separated by approximately 2 min, of which the last three jumps were used in the data analysis.
Data processing: To perform the data analysis, a computer program was written in MATLAB (MathWorks, Natick, Massachusetts, USA).
The IMU outputs six channels: three accelerations [g] with respect to the IMU's local coordinate system and three rotations [deg] with respect to the global coordinate system. For each sample, the acceleration was transformed from the local IMU to the global coordinate system using Euler angles, and subsequently converted to m/s2 and corrected for gravitation. For a subject standing still, this gives a baseline acceleration of the IMU very close to zero in the global coordinate system.
The estimated vertical displacement by the IMU was calculated by three different methods. The first method, NDI, was calculated by integrating the non-filtered vertical acceleration twice using the trapezoidal rule.27 The initial condition assumes the acceleration to be zero, which means that the jump height will be equivalent to the maximum vertical displacement value. The second method, TOV, is based on the assumption that the subject is not affected by other forces than gravity during FT and therefore can be considered as a particle with a constant acceleration (g), air resistance being neglected: , where is takeoff velocity, is gravitational acceleration and is the vertical displacement relative to the initial position. Takeoff velocity is determined by integration of the filtered acceleration data measured before the instant of takeoff. This instant is defined as the time when the subject leaves the platform and the filtered acceleration equals g. The third method, FT, considers the subject as a particle by the free fall equation: , where is flight-time, is gravitational acceleration and is the vertical displacement relative to the initial position. Flight-time is defined as the time period between the instant of takeoff and the instant of landing. Takeoff is defined as the instant when the subject leaves the platform and the filtered acceleration becomes less than . Landing is defined as the instant when the subject returns to the platform and is identified as the last observation of the filtered acceleration less than g. The displacement is in both TOV and FT determined by integrating the filtered acceleration twice.10,17
The previous mentioned three methods were also applied for the FP. The vertical force component was converted into acceleration by Newton's second law , where is force, is the acceleration and is body mass. The is determined while the subject stands still on the FP prior to the downward movement, as the mean of the FP's baseline signal divided by . For the MC method, the same period is used as baseline to measure the maximum vertical displacement.
To estimate the point of takeoff and landing the IMU-acceleration data were filtered by a lowpass Butterworth filter, which is often used for skin-mounted sensors gauging human movement(25,28). To quantify the cutoff frequency and order number, the vertical acceleration data needed to be synchronized. The FP and MC data were automatically synchronized by Qualisys Track Manager. It was not possible to sample the IMU data with the same system due to technical difficulties. Instead, mathematical optimization was used to synchronize the data by phase time shifting the IMU acceleration data with respect to FP-acceleration data until the lowest root-mean-square (rms) was found. In order to execute the mathematical optimization, FP and MC were downsampled respectively from 960 Hz and 240 Hz to 100 Hz, which is the same sample frequency as the IMU data. Subsequently, the original data (FP, MC and IMU) were cutoff 2 s before and 1 s after the landing, which is located as FP peak.
For each jump, the synchronized FP and IMU data was used to determine the optimal filtering window and cutoff frequency and order number by optimizing the minimum rms value. The normalized cutoff frequency and order are investigated in the ranges of 0.01–0.99 with steps of 0.01 and in the range of 1–10 with steps of 1, respectively. The general lowpass filter applied on the IMU's acceleration data, was a 1. Order filter with a cutoff normalized frequency of 0.13 (6.5 Hz) which was found as the median of the optimal lowpass filter for each jump.
Statistical analysis
The median of the subjects estimated jump heights were used for the analysis. Bland Altman plots (differences versus mean) were presented to visualise systematic differences between the measurement methods.29 Systematic differences between the methods were determined by a Students two-tailed t-test, while limits of agreement (LoA) were used to estimate the likelihood of difference.29 Pitman-test was applied to test equal variation between two different comparisons.30 To determine the margin of equivalence between two different methods (delta) a Two One-Sided Test (TOST) was used.31 The Intra-tester reliability was visualized with Bland and Altman plots and Students two-tailed t-test was used to test if there were systematic differences between the first and second measurement. MATLAB was used for statistical analysis with a significance level of 0.05.
Results
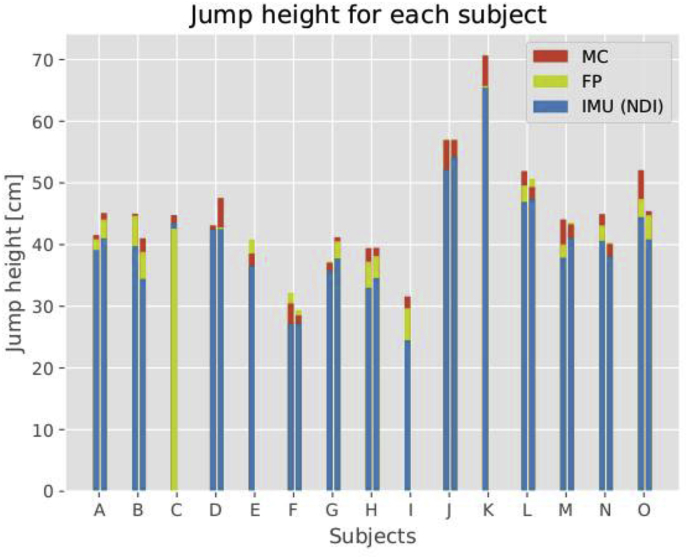
The vertical displacement of the MC in the first test session (n = 15) ranged from 29.71 cm to 65.74 cm (43.43 ± 9.08 cm), while the second test session (n = 11) ranged from 29.37 cm to 57.02 cm (42.73 ± 7.07 cm). The vertical displacement of the IMU with the NDI calculation method in the first test session (n = 15) ranged from 30.45 cm to 70.67 cm (44.81 ± 10.15 cm), while the second test session (n = 11) ranged from 28.51 cm to 56.96 cm (43.45 ± 7.08 cm). The vertical displacement of the FP in the first test session (n = 15) ranged from 24.52 cm to 65.43 cm (40.61 ± 9.88 cm), while the second test session (n = 11) ranged from 27.21 cm to 54.26 cm (43.45 ± 7.08 cm). Estimates for each subject are presented in Fig. 1. The results for the first and second test session are listed in Table 1, Table 2, respectively. The comparison between the first and second test session for the three methods are listed in Table 3.
Fig. 1.
Bar plot of each subject (A–O) presenting the median vertical displacement estimated with MC, FP, and IMU (NDI) for each session. The left bar for each subject is the estimate from the first session and the right bar is the estimate from the second session. The four subjects with only 1 bar are the ones who were not able to participate in the second session.
Table 1.
Mean difference with 95% confidence interval (m), Bland & Altman's limits of agreement lower and upper respectively with 95% confidence interval (m) pitman-test as correlation of variation between IMU-MC and FP-MC (corr), and tolerance level of equivalence (delta in m) (alfa = 0.05).
| NDI | Mean difference (95% CI) | LoA (95% Cl) lower | LoA (95% Cl) upper | corr | delta |
|---|---|---|---|---|---|
| IMU - MC | 0.0139 [0.0020; 0.0258]* | -0.0322 [-0.0587; −0.0198] | 0.0599 [0.0476; 0.0865] | 0.67 | 0.0280 |
| FP - MC | -0.0281 [-0.0387; −0.0175]** | -0.0693 [-0.0930; −0.0582] | 0.0131 [0.0021; 0.0368] | 0.0410 | |
| IMU - FP | 0.0420 [0.0296; 0.0544]** | -0.0060 [-0.0337; 0.0068] | 0.0900 [0.0771; 0.1177] | – | 0.0570 |
| TOV | |||||
| IMU - MC | 0.0575 [0.0393; 0.0757]** | -0.0130 [-0.0536; 0.0059] | 0.1280 [0.1091; 0.1686] | 0.27 | 0.0790 |
| FP - MC | -0.0270 [-0.0377; −0.0164]** | -0.0683 [-0.0921; −0.0572] | 0.0142 [0.0032; 0.0380] | 0.0400 | |
| IMU - FP | 0.0845 [0.0603; 0.1087]** | −0.0091 [-0.0631; 0.0160] | 0.1781 [0.1530; 0.2321] | – | 0.1130 |
| AT | |||||
| IMU - MC | 0.0309 [0.0070; 0.0548]* | -0.0618 [-0.1153; −0.0370] | 0.1236 [0.0988; 0.1771] | 0.05 | 0.0590 |
| FP - MC | -0.0146 [-0.0250; −0.0043]* | -0.0548 [-0.0780; −0.0440] | 0.0255 [0.0148; 0.0487] | 0.0270 | |
| IMU - FP | 0.0455 [0.0236; 0.0675]** | -0.0394 [-0.0884; −0.0166] | 0.1304 [0.1077; 0.1794] | – | 0.0710 |
*p < 0.05 **p < 0.001.
Table 2.
Mean difference with 95% confidence interval (m), Bland & Altman's limits of agreement lower and upper respectively with 95% confidence interval (m) pitman-test as correlation of variation between IMU-MC and FP-MC (corr), and tolerance level of equivalence (delta in m) (alfa = 0.05).
| NDI | Mean difference (95% CI) | LoA (95% Cl) lower | LoA (95% Cl) upper | corr | delta |
|---|---|---|---|---|---|
| IMU - MC | 0.0072 [-0.0041; 0.0185] | -0.0303 [-0.0586; −0.0190] | 0.0447 [0.0334; 0.0729] | 0.19 | 0.0210 |
| FP - MC | -0.0280 [-0.0353; −0.0206]** | -0.0523 [-0.0707; −0.0450] | -0.0036 [-0.0110; 0.0147] | 0.0370 | |
| IMU - FP | 0.0352 [0.0241; 0.0462]** | -0.0016 [-0.0293; 0.0095] | 0.0719 [0.0608; 0.0997] | – | 0.0480 |
| TOV | |||||
| IMU - MC | 0.0413 [0.0308; 0.0519]** | 0.0063 [-0.0202; 0.0169] | 0.0764 [0.0658; 0.1028] | 0.28 | 0.0570 |
| FP - MC | -0.0270 [-0.0343; −0.0196]** | -0.0513 [-0.0697; −0.0440] | -0.0026 [-0.0100; 0.0158] | 0.0360 | |
| IMU - FP | 0.0683 [0.0543; 0.0823]** | 0.0218 [-0.0134; 0.0358] | 0.1148 [0.1008; 0.1500] | – | 0.0880 |
| AT | |||||
| IMU - MC | 0.0398 [0.0145; 0.0651]* | -0.0441 [-0.1075; −0.0189] | 0.1237 [0.0984; 0.1870] | 0.34 | 0.0700 |
| FP - MC | -0.0625 [-0.0977; −0.0273]* | -0.1793 [-0.2674; −0.1441] | -0.0543 [0.0191; 0.1424] | 0.1030 | |
| IMU - FP | 0.1023 [0.0580; 0.1466]** | -0.0446 [-0.1555; −0.0004] | 0.2492 [0.2049; 0.3601] | – | 0.1570 |
*p < 0.05 **p < 0.001.
Table 3.
Difference between first and second session. Mean difference with 95% confidence interval (m), Bland & Altman's limits of agreement lower and upper respectively with 95% confidence interval (m) pitman-test as correlation of variation (corr) and tolerance level of equivalence (delta in m) (alfa = 0.05).
| NDI | Mean difference (95% CI) | p-værdi | LoA (95% Cl) lower | LoA (95% Cl) upper | corr | delta |
|---|---|---|---|---|---|---|
| IMU - MC (1 vs. 2) | 0.0056 [-0.0132; 0.0244] | 0.5206 | -0.0567 [-0.1038; −0.0379] | 0.0680 [0.0492; 0.1150] | 0.68 | 0.0280 |
| FP - MC (1 vs. 2) | -0.0022 [-0.0113; 0.0068] | 0.5957 | -0.0323 [-0.0550; −0.0232] | 0.0278 [0.0188; 0.0505] | 0.28 | 0.0130 |
| IMU - FP (1 vs. 2) | 0.0078 [-0.0103; 0.0260] | 0.3580 | -0.0523 [-0.0977; −0.0342] | 0.0680 [0.0499; 0.1134] | 0.4201 | 0.0290 |
| TOV | ||||||
| IMU - MC (1 vs. 2) | 0.0114 [-0.0085; 0.0312] | 0.2305 | -0.0543 [-0.1039; −0.0346] | 0.0770 [0.0573; 0.1266] | 0.07 | 0.0350 |
| FP - MC (1 vs. 2) | -0.0021 [-0.0117; 0.0074] | 0.6271 | -0.0337 [-0.0576; −0.0242] | 0.0295 [0.0199; 0.0533] | 0.30 | 0.0140 |
| IMU - FP (1 vs. 2) | 0.0135 [-0.0070; 0.0340] | 0.1726 | −0.0544 [-0.1056; −0.0339] | 0.0814 [0.0609; 0.1326] | 0.02 | 0.0380 |
| AT | ||||||
| IMU - MC (1 vs. 2) | -0.0063 [-0.0352; 0.0226] | 0.6363 | -0.1022 [-0.1754; −0.0733] | 0.0895 [0.0606; 0.1619] | 0.65 | 0.0400 |
| FP - MC (1 vs. 2) | 0.0462 [0.0017; 0.0908] | 0.0433* | -0.1015 [-0.2130: −0.0570] | 0.1940 [0.1495; 0.3055] | <0.01 | 0.0980 |
| IMU - FP (1 vs. 2) | -0.0526 [-0.0977; −0.0074] | 0.0267* | -0.2023 [-0.3153; −0.1572] | 0.0971 [0.0520; 0.2101] | 0.08 | 0.1050 |
*p < 0.05.
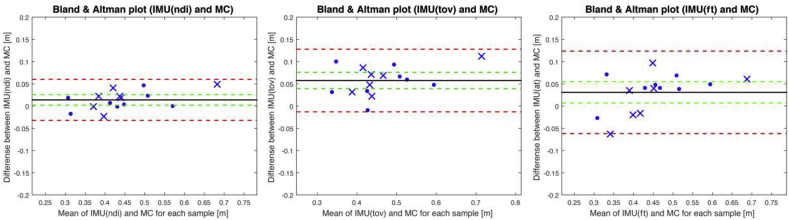
For all comparisons, Bland-Altman plots (Fig. 2) and regression plots (Fig. 3) were constructed. However, only the plots for IMU compared to MC are shown. Each of these compares the IMU and MC with the three methods in the first session. In the first session, the IMU estimates significant higher compared to global position and CoM displacement for both NDI, TOV and AT. Contrary, the FP compared to MC estimates significantly lower vertical displacement for NDI, TOV and AT. LoA for IMU-MC is smallest for NDI (±4.60 cm) while LoA for TOV (±7.05 cm) and FT (±9.27 cm) are larger. Similar results were found for IMU-FP with the smallest LoA for NDI (±0.048 cm) while LoA for TOV (±9.36 cm) and FT (±8.49 cm) are larger. FP-MC has the same narrow LoA relative to the IMU (ndi) MC for both NDI (±4.12 cm), TOV (±4.13 cm) and FT (±4.02 cm). The pitman-test shows significantly different variation between the IMU-MC and FP-MC related to FT (p = 0.0491), while the strongest correlation is found for NDI (p = 0.67) compared to TOV (p = 0.27).
Fig. 2.
Bland-Altlman plot of IMU and motion capture (MC) (first session) for the three calculation methods NDI, TOV and FT respectively. Mean difference with confidence interval and limits of agreement is indicated. The dots and crosses represent measures done by two different testers.
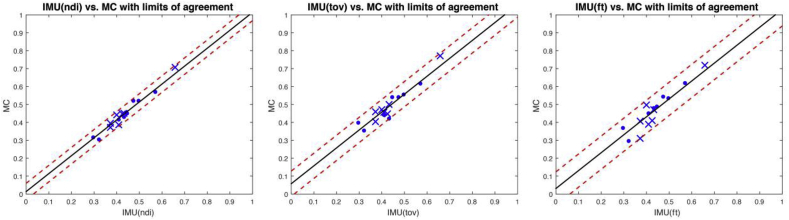
Fig. 3.
Regression plots of IMU and motion capture (MC) (first session) for the three calculation methods NDI, TOV and FT respectively, with indicated limits of agreement indicated. The dots and crosses represent measures done by two different testers.
The same relationships are observed in the second test session for both IMU-MC and FP-MC, though with narrower LoA, in general. For FP-MC related to AT, a larger LoA was observed. For IMU-MC related to AT, LoA was on par with the first session. The pitman-test shows significant difference between the two sessions of FT (p = 0.0462), while no significant differences are observed for NDI (p = 0.52) and TOV (p = 0.23). Additionally, the NDI method indicates the least systematic difference between the two sessions (0.56 cm) relative to TOV (1.14 cm).
Fig. 3 illustrates a clear linear relationship between the IMU and MC since the data for all three methods are observed within the LoA's. This also holds true for the second test session. The same trend is observed for FP-MC and IMU-FP in the second session, while regards to AT, the same straight line does not emerge.
Discussion
Vertical displacement is a very useful measure of physical function in relation to rehabilitation of the lower extremities.2, 3, 4, 5, 6, 7, 8, 9 The use of a force plate is usually associated with the most reliable method to quantify lower extremity performance, but this method is highly expensive and difficult to transport. Thus, the purpose of this study was to investigate whether a FP can be replaced by an IMU when estimating vertical displacement to quantify functional performance in the lower extremities. The performance of an IMU using different computational methods was compared to data from both a FP and MC. The method of the NDI reveals to be the most exact. However, this study is based on a small sample, hence the results should be interpreted with caution.
To determine the best estimate of the vertical displacement performed by each of the subjects, the median of each subject's three jumps were applied. As Miller & East (1976) found little variability of vertical displacement across individual subjects,12 an observation that is substantially apart from the other two estimates is likely not to represent the subject's performance. Further, the sample size of three observed jumps per subject is not large enough to be assumed normally distributed. Adding these arguments together, the median, ahead of mean and mode, proves to be the best method to reduce the effect of variation in the three jumps.
Comparing the position of the IMU to the estimate of the vertical displacement of the FP the assumption of L5 representing the CoM is necessary. The estimate of the IMU only represents the position with respect to the global reference system, which is identical to the reflective marker placed at the IMU (earlier refered to as MC) and not the CoM of the subject. The position of the CoM depends on the body posture. In previous studies strong agreement were found between FP and MC although means were significantly different. This holds true both when the CoM is calculated by anthropometric tables11,17,32 and when markers are placed on the trochanter.10 Above results are identical with the results of this study's estimation of vertical displacement based on FP for NDI and TOV in both the first and second session. For FT this is only the case in the first session. Palazzi et al.32 finds the highest consistency between the displacement of CoM in the standing position prior to the jump and FT the peak (maximum vertical displacement). This indicates that the posture before the jump and FT the peak is similar when the hands are placed on the hips during the jump. However, Palazzi et al.32 used a 39-marker full-body Plug-in Gait model to estimate the CoM whereas this study used the level of L5. The general picture of the results of the NDI method showed significant difference between both the IMU-FP and FP-MC. The IMU compared to the FP overestimates while the FP compared to the MC underestimates. This exhibits the position of L5 as not being a preferable/optimal assumption. However, comparing the two sessions both the IMU-FP and FP-MC shows similar mean difference and additionally LoA. This indicates that, within this population, the IMU is applicable when comparing vertical displacement within a subject. Further, in the comparison of the IMU to the MC a small difference was found for both sessions for the NDI method, which indicates good kinematic estimates of the IMU.
Picerno et al. (2010) estimated the vertical displacement from the following kinematic equation and found a small insignificant mean difference (Mdiff = 0.6 ± 5.4 cm) between devices.25 Similar systematic difference was found in this study but only for NDI, it is found in both the first and second session of the IMU-MC. The differences were 1.39 cm with CI: [0.20, 2.58] cm and 0.72 cm with CI: [-0.41, 1.85] cm, respectively, while the LoA are respectively 0.8 cm and 1.63 cm narrower in relation to Picerno et al.25 Regarding the TOV method (IMU-MC), the second session have the same narrow LoA (±3.51 cm), while the first session has a wider LoA (±7.05 cm). The FT method (IMU-MC) shows wide LoA for both the first and second session ± 9.27 cm and ±8.39 cm, respectively. The mean difference for TOV is significantly greater than the NDI in both the first and second session, although there is a small systematic difference for both TOV and FT between the two sessions. This study cannot confirm the results of Picerno et al.,25 but it appears that NDI is a better method to estimate the vertical displacement.
The lowest mean systematic difference for test-retest is also found for NDI FT IMU-MC (0.56 cm). This is only 0.34 cm greater than the FP-MC comparison, while TOV is 1.35 cm greater. Further, the TOST also found the smallest required difference to achieve equivalence. Due to the study design a real inter-test for reliability was not possible. However, Fig. 2, Fig. 3 indicate that the tester has no impact on the results as they are distributed equally.
The study of Picerno et al.25 involves methodological uncertainty. Both the numerical integration and in particular the posture requirement FT takeoff and landing, can be the reason for the higher LoA, and will result in a lower accuracy compared to this study's LoA found FT NDI. The inclusion of FT when estimating vertical displacement reduces the potential population since the posture requirement FT takeoff and landing can not necessarily be assumed. The assumption of the same posture FT takeoff and landing can be avoided by using NDI or TOV, which are reflected FT the wide LoA for FT (IMU-MC) in both first and second session, and also the wide LoA FT AT (FP-MC) in the second session compared to the first. While there is a narrow LoA for both NDI and TOV.
An additional problem with FT and to a lesser extent TOV, can be an inaccurate identification of takeoff and landing, caused by the relatively lower sample frequency of the IMU (100 Hz) compared with FP (960 Hz). The relatively low LoA for IMU-MC FT the second test session for TOV (±3.51 cm) compared to the first session, may be the result of an accidentally more precise match between the estimated and actual takeoff and landing point. This may illustrate that the IMU by TOV potentially can achieve the same precision as NDI if the IMU is sampled FT higher frequency. Precision may be even better as the uncertainty factor by numerical integration can be reduced because TOV is only integrated once in a shorter period. The uncertainty from the sensor's small fluctuations caused by soft tissue33 may also affect the accuracy of identifying takeoff and landing. This does also affect the NDI but to lesser degree. A potential reduction of these fluctuations should be investigated in further studies.
Conclusion
Countermovement jump estimated with an IMU can be used to evaluate functional performance in the lower extremities in young or in sports active patients after surgery or after rehabilitation. Countermovement jump with an IMU allows performing the test without a force plate and thus serves as an objective outcome measure in clinical practice. Of the presented three methods to estimate CMJ height, NDI is the most reliable and accurate IMU method of estimating the vertical displacement of the COM. Therefore, IMU using the NDI method is deemed reliable and valid to estimate CMJ height and in turn assess and monitor CMJ height changes over-time.
Conflicts of interest
The authors have no conflicts of interest relevant to this article.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Contributor Information
Emil Toft Nielsen, Email: emiltn@clin.au.dk.
Peter Bo Jørgensen, Email: pbjr@clin.au.dk.
Inger Mechlenburg, Email: inger.mechlenburg@clin.au.dk.
Henrik Sørensen, Email: hs@ph.au.dk.
References
- 1.Markovic G., Dizdar D., Jukic I., Cardinale M. Reliability and factorial validity of squat and countermovement jump tests. J Strength Condit Res. 2004;18(3):551–555. doi: 10.1519/1533-4287(2004)18<551:RAFVOS>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 2.Harrison A.J., Gaffney S. Motor development and gender effects on stretch-shortening cycle performance. J Sci Med Sport. 2001;4(4):406–415. doi: 10.1016/s1440-2440(01)80050-5. [DOI] [PubMed] [Google Scholar]
- 3.Hassani A., Kotzamanidou M.C., Tsimaras V., Lazaridis S., Kotzamanidis C., Patikas D. Differences in counter-movement jump between boys with and without intellectual disability. Res Dev Disabil. 2014;35(7):1433–1438. doi: 10.1016/j.ridd.2014.03.034. [DOI] [PubMed] [Google Scholar]
- 4.Caserotti P., Aagaard P., Simonsen E.B., Puggaard L. Contraction-specific differences in maximal muscle power during stretch-shortening cycle movements in elderly males and females. Eur J Appl Physiol. 2001;84(3):206–212. doi: 10.1007/s004210170006. [DOI] [PubMed] [Google Scholar]
- 5.De Vito G., Bernardi M., Forte R., Pulejo C., Macaluso A., Figura F. Determinants of maximal instantaneous muscle power in women aged 50-75 years. Eur J Appl Physiol Occup Physiol. 1998;78:59–64. doi: 10.1007/s004210050387. [DOI] [PubMed] [Google Scholar]
- 6.Bosco C., Komi P.V. Influence of aging on the mechanical behavior of leg extensor muscles. Eur J Appl Physiol Occup Physiol. 1980;45(8318):209–219. doi: 10.1007/BF00421329. [DOI] [PubMed] [Google Scholar]
- 7.Shan X. Biomechanical analysis of vertical jump performance of volleyball. In: hong Y., editor. Proceedings of XVIII International Symposium on Biomechanics in Sports. The Chinese University of Hong Kong; Hong Kong: 2000. pp. 76–79. [Google Scholar]
- 8.Chelly M.S., Ghenem M.A., Abid K., Hermassi S., Tabka Z., Shephard R.J. Effects of in-season short-term plyometric training program on leg power, jump- and sprint performance of soccer players. J Strength Condit Res. 2010;24(10):2670–2676. doi: 10.1519/JSC.0b013e3181e2728f. [DOI] [PubMed] [Google Scholar]
- 9.Kyriazis T a, Terzis G., Boudolos K., Georgiadis G. Muscular power, neuromuscular activation, and performance in shot put athletes at preseason and at competition period. J Strength Condit Res. 2009;23(6):1773–1779. doi: 10.1519/JSC.0b013e3181b3f91e. [DOI] [PubMed] [Google Scholar]
- 10.Ache Dias J., Pupo J.D., Reis D.C. Validity of two methods for estimation of vertical jump height. J Strength Condit Res. 2011;25(7):2034–2039. doi: 10.1519/JSC.0b013e3181e73f6e. [DOI] [PubMed] [Google Scholar]
- 11.Kibele A. Possibilities and limitations in the biomechanical analysis of countermovement jumps: a methodological study. J Appl Biomech. 1998;14(1):105–117. [Google Scholar]
- 12.Dowling J.J., Vamos L. Identification of kinetic and temporal factors related to vertical jump performance. J Appl Biomech. 1993;9(1977):95–110. [Google Scholar]
- 13.Linthorne N.P. Analysis of standing vertical jumps using a force platform. Am J Phys. 2001;69(11):1198–1204. [Google Scholar]
- 14.Tessitore A., Meeusen R., Cortis C., Capranica L. Effects of different recovery interventions on anaerobic performances following preseason soccer training. J Strength Condit Res/Natl Strength Condit Assoc. 2007;21(3):745–750. doi: 10.1519/R-20386.1. [DOI] [PubMed] [Google Scholar]
- 15.Ramírez-Campillo R., Meylan C., Alvarez C. Effects of in-season low-volume high-intensity plyometric training on explosive actions and endurance of young soccer players. J Strength Condit Res. 2014;28(5):1335–1342. doi: 10.1519/JSC.0000000000000284. [DOI] [PubMed] [Google Scholar]
- 16.Malliou P., Ispirlidis I., Beneka A., Taxildaris K., Godolias G. Vertical jump and knee extensors isokinetic performance in professional soccer players related to the phase of the training period. Isokinet Exerc Sci. 2003;11(3):165–169. [Google Scholar]
- 17.Aragón-Vargas L.F. Evaluation of four vertical jump tests: methodology, reliability, validity, and accuracy. Meas Phys Educ Exerc Sci. 2000;4(4):1–5. [Google Scholar]
- 18.Isaacs L.D. Comparison of the vertec and just jump systems for measuring height of vertical jump by young children. Percept Mot Skills. 1998;86:659–663. doi: 10.2466/pms.1998.86.2.659. [DOI] [PubMed] [Google Scholar]
- 19.David Li Y., Hsiao-Wecksler E.T. Gait mode recognition and control for a portable-powered ankle-foot orthosis. IEEE Int Conf Rehabil Robot. 2013;2013:6650373. doi: 10.1109/ICORR.2013.6650373. [DOI] [PubMed] [Google Scholar]
- 20.Hundza S., Hook W., Harris C. Accurate and reliable Gait cycle detection in Parkinson's disease. IEEE Trans Neural Syst Rehabil Eng. 2013;22(1):127–137. doi: 10.1109/TNSRE.2013.2282080. [DOI] [PubMed] [Google Scholar]
- 21.Luinge H.J., Veltink P.H. Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Med Biol Eng Comput. 2005;43(2):273–282. doi: 10.1007/BF02345966. [DOI] [PubMed] [Google Scholar]
- 22.Bonnet V., Mazza C., Fraisse P., Cappozzo A. Real-time estimate of body kinematics during a planar squat task using a single inertial measurement unit. IEEE T Bio-Med Eng. 2013;60(7):1920–1926. doi: 10.1109/TBME.2013.2245131. [DOI] [PubMed] [Google Scholar]
- 23.Quagliarella L., Sasanelli N., Belgiovine G., Moretti L., Moretti B. Evaluation of standing vertical jump by ankles acceleration measurement. J Strength Condit Res. 2010;24(5):1229–1236. doi: 10.1519/JSC.0b013e3181cb281a. [DOI] [PubMed] [Google Scholar]
- 24.Castagna C., Ganzetti M., Ditroilo M., Giovannelli M., Rocchetti a, Manzi V. Concurrent validity of vertical jump performance assessment systems. J Strength Condit Res. 2013;27(3):761–768. doi: 10.1519/JSC.0b013e31825dbcc5. [DOI] [PubMed] [Google Scholar]
- 25.Picerno P., Camomilla V., Capranica L. Countermovement jump performance assessment using a wearable 3D inertial measurement unit. J Sports Sci. 2011;29(2):139–146. doi: 10.1080/02640414.2010.523089. [DOI] [PubMed] [Google Scholar]
- 26.Meylan C.M.P., Nosaka K., Green J., Cronin J.B. The effect of three different start thresholds on the kinematics and kinetics of a countermovement jump. J Strength Condit Res. 2011;25(4):1164–1167. doi: 10.1519/JSC.0b013e3181c699b9. [DOI] [PubMed] [Google Scholar]
- 27.Hornbeck R.W. 1967. Numerical Methods. [Google Scholar]
- 28.Fong D.T.-P., Chan Y.-Y. The use of wearable inertial motion sensors in human lower limb biomechanics studies: a systematic review. Sensors. 2010;10(12):11556–11565. doi: 10.3390/s101211556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bland J.M., Altman D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1(8476):307–310. [PubMed] [Google Scholar]
- 30.Pitman E.J.G. A note on normal correlation. Biometrika. 1939;31(1-2):9–12. [Google Scholar]
- 31.Lauzon C., Caffo B. Easy multiplicity control in equivalence testing using two one-sided tests. Am Statistician. 2009;63(2):147–154. doi: 10.1198/tast.2009.0029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Palazzi D.A., Williams B.K., Pitre C. 31th ISBS Conference. 2001. Accuracy and precision of the kinetic analysis of counter movement jump performance; pp. 1–4. [Google Scholar]
- 33.Forner-Cordero A., Mateu-Arce M., Forner-Cordero I., Alcántara E., Moreno J.C., Pons J.L. Study of the motion artefacts of skin-mounted inertial sensors under different attachment conditions. Physiol Meas. 2008;29(4):N21–N31. doi: 10.1088/0967-3334/29/4/N01. [DOI] [PubMed] [Google Scholar]