Efficiency measures the conversion of agonist binding energy into receptor conformational change

Receptors convert agonist-binding energy into conformational change. Nayak et al. describe a new agonist trait, efficiency, as the fraction of binding energy transformed into the mechanical work of conformational change and suggest that it is a general attribute of agonist action at receptor-binding sites.

Abstract

Receptors alternate between resting↔active conformations that bind agonists with low↔high affinity. Here, we define a new agonist attribute, energy efficiency (η), as the fraction of ligand-binding energy converted into the mechanical work of the activation conformational change. η depends only on the resting/active agonist-binding energy ratio. In a plot of activation energy versus binding energy (an “efficiency” plot), the slope gives η and the y intercept gives the receptor’s intrinsic activation energy (without agonists; ΔG₀). We used single-channel electrophysiology to estimate η for eight different agonists and ΔG₀ in human endplate acetylcholine receptors (AChRs). From published equilibrium constants, we also estimated η for agonists of K_Ca1.1 (BK channels) and muscarinic, γ-aminobutyric acid, glutamate, glycine, and aryl-hydrocarbon receptors, and ΔG₀ for all of these except K_Ca1.1. Regarding AChRs, η is 48–56% for agonists related structurally to acetylcholine but is only ∼39% for agonists related to epibatidine; ΔG₀ is 8.4 kcal/mol in adult and 9.6 kcal/mol in fetal receptors. Efficiency plots for all of the above receptors are approximately linear, with η values between 12% and 57% and ΔG₀ values between 2 and 12 kcal/mol. Efficiency appears to be a general attribute of agonist action at receptor binding sites that is useful for understanding binding mechanisms, categorizing agonists, and estimating concentration–response relationships.

Introduction

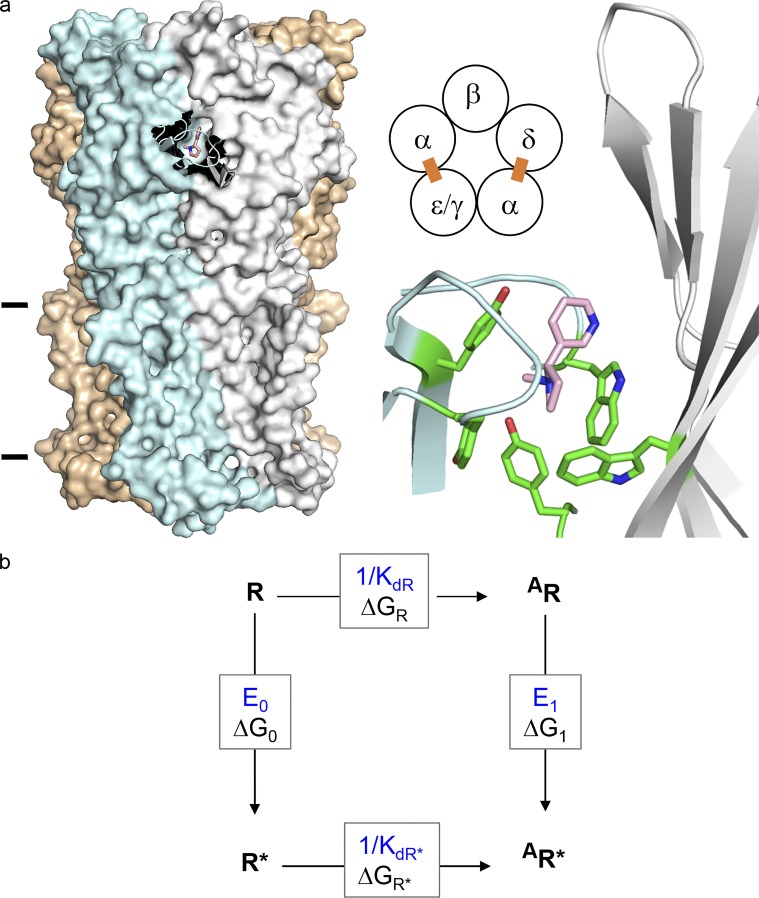
Nicotinic acetylcholine receptors (AChRs) from vertebrate skeletal muscle have two neurotransmitter-binding sites located in the extracellular domain, at α−δ and either α−ε (adult) or α−γ (fetal) subunit interfaces (Fig. 1 a). At adult sites, 4 α-subunit aromatic amino acids combine to determine neurotransmitter-binding energy, and at the fetal site a tryptophan in the γ subunit also contributes (Cohen et al., 1991; Kearney et al., 1996; Zhong et al., 1998; Brejc et al., 2001; Nayak et al., 2014; Purohit et al., 2014). AChRs operate by a cyclic mechanism (Fig. 1 b) in which the global, activation (“gating”) conformational change, R↔R*, occurs either with or without a bound agonist, and agonists bind weakly to R (free-energy ΔG_R) or strongly to R* (ΔG_R*).

Figure 1.

AChR structure and function. (a) Neurotransmitter binding sites. Left, each site is at a subunit interface (PDB ID 5KXI; Morales-Perez et al., 2016). α-subunit (blue), nicotine (pink), and lines mark approximately the membrane. Middle, each endplate AChR has two neurotransmitter binding sites (ε is adult and γ is fetal). Right, at each site a cluster of aromatic amino acids surrounds the agonist. (b) A cyclic scheme describes receptor operation. Horizontal, agonist binding; vertical, receptor gating. R, resting state (low affinity and closed channel); R*, active state (high affinity and open channel); A, agonist. ΔG_R and ΔG_R*, binding free energy changes (in direction of arrow) to R and R*; ΔG₀ and ΔG₁, gating free energy changes with zero and one bound agonist. Corresponding equilibrium constants, blue. Agonists are ligands that bind more strongly to R*.

In mouse AChRs and for a series of acetylcholine (ACh)–like agonists, ΔG_R is a constant fraction of ΔG_R* (Jadey and Auerbach, 2012). A fixed ΔG_R/ΔG_R* ratio generates a linear correlation between the log of the receptor gating equilibrium constant and the agonist resting equilibrium dissociation constant (Auerbach, 2016). Recently, free-energy changes in each step of the activation cycle were measured experimentally for small, ACh-class agonists at individual mouse AChR-binding sites (Nayak and Auerbach, 2017). Despite a wide range in resting affinity, at all sites and for all tested agonists, ΔG_R* was always approximately twice ΔG_R. That is, at all three kinds of neurotransmitter-binding sites, the interaction energy of each ligand in the resting conformation was approximately half as strong as in the active conformation. Here, we show that the ΔG_R/ΔG_R* ratio defines η, which is the energy-conversion efficiency, and that a fixed binding-energy ratio pertains to other classes of nicotinic receptor agonist and other receptors.

The new nicotinic agonists we investigated have an azabicycloheptane (Aza) group. Some of these occur naturally, such as anatoxin (from cyanobacteria) and epibatidine (Epi; a frog toxin), and other bridged, bicyclic compounds have been approved for treatment of neurodegenerative diseases (memantine, amantadine, and biperiden). We used single-channel kinetics to estimate binding energies of these and ACh-class agonists and compared energy efficiencies at individual α−ε, α−δ, and α−γ neurotransmitter-binding sites of human AChRs.

So far, a fixed binding-energy ratio has been observed only in endplate AChRs. To explore the generality of this result, we estimated from published values of binding and gating equilibrium constants agonist energy efficiencies at binding sites of BK channels (K_Ca1.1) and muscarinic, GABA_Α, NMDA, glycine, and aryl-hydrocarbon receptors. We also estimated for the first time the intrinsic gating energy (ΔG₀ in Fig. 1 b) of adult- and fetal-type human AChRs and of these other receptors. ΔG₀ not only determines the basal activity level but also contributes to the high-concentration asymptote and midpoint of the concentration–response curve (CRC). An increase or decrease in ΔG₀ caused, for example, by a mutation or an allosteric modulator can alter the CRC and the physiological response enough to cause disease, often without a noticeable change in baseline activity (Zuo et al., 1997; Zhou et al., 1999; Lester and Karschin, 2000; Labarca et al., 2001; Hatton et al., 2003).

The results regarding energy efficiency indicate that (a) Epi-class nicotinic agonists are less efficient than ACh-class agonists, (b) the same agonist can have different efficiencies at different binding sites, and (c) many receptors have a fixed binding-energy ratio. The structural correlates of energy efficiency in AChRs are considered elsewhere (Tripathy et al., 2019).

Materials and methods

Electrophysiology

Human embryonic kidney (HEK) 293 cells were maintained in Dulbecco’s Minimal Essential Medium supplemented with 10% FBS and 1% penicillin–streptomycin, pH 7.4. AChRs were expressed in HEK293 cells by transient transfection (CaPO₄ precipitation method) of mouse α,β,δ,ε/γ subunits in a ratio of 2:1:1:1. Most electrophysiological experiments were started ∼24 h after transfection. Single-channel currents were recorded in the cell-attached patch configuration (23°C). The bath solution was (in mM) 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, and 10 HEPES/KOH, pH 7.4. Because of the high extracellular [K⁺], the cell membrane potential (V_m) was ∼0 mV. Unless noted otherwise, the pipette potential was +100 mV.

Patch pipettes were fabricated from borosilicate glass, coated with Sylgard (Dow Corning), and fire polished to a resistance of ∼10 MΩ when filled with pipette solution (Dulbecco’s PBS; in mM): 137 NaCl, 0.9 CaCl₂, 2.7 KCl, 1.5 KH₂PO₄, 0.5 MgCl₂, and 8.1 Na₂HPO₄, pH 7.3/NaOH). Single-channel currents were recorded using a PC505 amplifier (Warner Instruments), low-pass filtered at 20 kHz, and digitized at a sampling frequency of 50 kHz, using a National Instruments data acquisition board (SCB-68). For unliganded-activation experiments, the pipette holder and pipettes were never exposed to agonists.

For ligand-activation experiments, agonists were added to the pipette solution at the desired concentrations. The ACh-class agonists were the neurotransmitter ACh, carbamylcholine (CCh; Martin et al., 2017), tetramethylammonium (TMA), and choline (Cho), and the Epi-class agonists were the arrow toxin Epi, its synthetic analogue epiboxidine (Ebx), the very fast death factor anatoxin (Anx), and azabicyclo heptane (Aza). To estimate gating equilibrium constants, a saturating concentration of agonist (≥10 times K_dR) was used.

The patches were unstable in the presence of high concentrations of the hydrophobic compound Aza (>1 mM). Therefore, we used a modified pipette back-fill method (Auerbach, 1991). In brief, the pipette tip was capillary filled to a height of <0.5 mm with pipette solution (no agonist), and the shank was syringe filled with the desired [Aza]. We estimated the diffusion constant of Aza (D_Aza) to be 0.52 × 10⁻⁵ cm^2·s⁻¹ based on published values for cyclohexane, pyrimidine, and benzene (Wang and Tingjun, 2011). We estimate that [Aza] at the tip of the pipette was within 10% of that in the shank after ∼50 s (Eq. 1, a and b, in Auerbach, 1991). The channel activity (cluster P_O; see below) increased as [Aza] diffused into the tip. We estimated the opening rate constant after ∼120 s of diffusion time.

For experiments with α-conotoxin, cells were incubated in 100 nM α-conotoxin MI (CTx MI), a specific blocker of the α−δ site (Bren and Sine, 2000) for 15 min before patching. The membrane potential was −100 mV when low [agonist] was used and +100 mV when high [agonist] was used.

Protein engineering

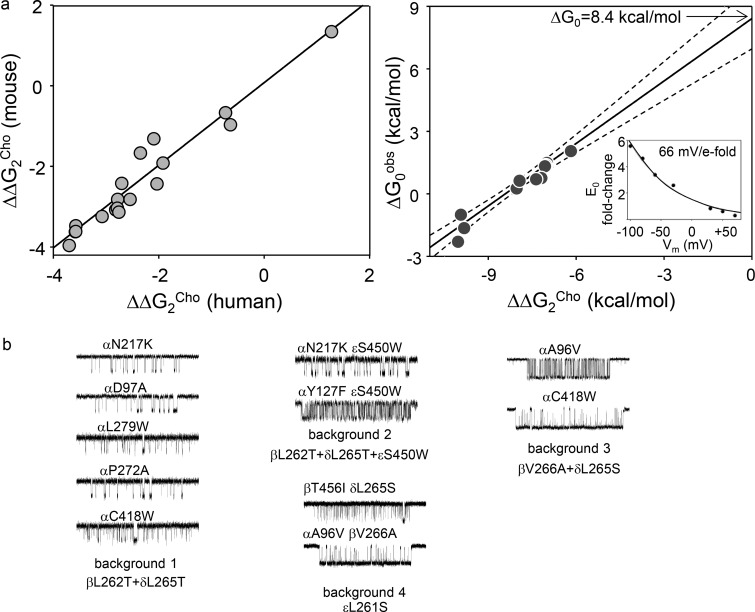
Mutations were incorporated into AChR subunits using the QuikChange site-directed mutagenesis kit (Agilent Technologies) and were verified by nucleotide sequencing. These “background” mutations were ≥20 Å away from the agonist-binding sites, had no effect on agonist binding, and were added to facilitate the kinetic analyses (Jadey et al., 2011). We could not resolve completely components of interval duration distributions having time constants briefer than ∼100 µs or longer than ∼200 ms (see below). Hence, with WT AChRs, we could estimate accurately rate constants only over a narrow range of ∼50 s⁻¹ to 10,000 s⁻¹. To extend this range almost indefinitely, we added mutations that only changed the unliganded gating equilibrium constant (ΔG₀) to known extents in order to place the interval durations into a readily measurable range. The mutations had no effect on binding to either the active or resting state. We multiplied the observed values by the fold changes caused by the mutations to obtain parameters for the WT condition. The effect of each background mutation on unliganded gating was estimated by measuring its effect on gating with the weak partial agonist Cho and by assuming the change in open-channel probability (P_O) was entirely due to changes in unliganded gating (Fig. 4 a).

Figure 4.

Intrinsic gating of human AChRs. (a) Left: Mutations far from the binding sites produce similar changes in the diliganded gating energy with Cho (ΔΔG₂^Cho) in mouse and human AChRs (slope, 1.0 ± 0.1; R² = 0.95). Each symbol is a different mutation. Right: In adult-type human AChRs, ΔΔG₂^Cho is caused exclusively by a change in the unliganded gating energy (ΔG₀^obs; slope = 1.0 ± 0.1, R² = 0.91; dashed lines, 95% confidence limits). The y intercept (no change in ΔΔG₂^Cho) is ΔG₀ in the WT. Inset: Voltage dependence of E₀ in adult-type human AChRs. (b) Example unliganded single-channel current clusters from mutations added to four different background constructs. The clusters (top to bottom) and the backgrounds (left to right) are arranged with increasing open-channel probability (excluding long openings).

To study AChRs having just one functional binding site, a disabling mutation (see below) was added to the ε, γ, or δ subunit to effectively eliminate binding and activation at α−ε, α−γ, or α−δ, respectively (Gupta et al., 2013). In mouse AChRs, this mutation reduces the coupling constant (K_dR/K_dR*) for ACh from ∼5,700 to ∼12, to effectively eliminate activation from just the mutated site. We incorporated δP123R to make AChRs having only a functional α–γ or α−ε site, and εP121R (adult type) or γP121R (fetal type) to make AChRs having only a functional α−δ site. These mutations also change unliganded gating (ΔG₀) to an extent that was measured for each construct, in order to correct for the background. The results from the δP123R experiments were corroborated independently by using the α−δ site-specific inhibitor CTx MI.

To reduce the fast channel block by the agonist apparent at high concentrations, the membrane was depolarized to +100 mV (pipette potential, −100 mV). The effect of depolarization on unliganded gating of human AChRs was taken into account in the same way as with background mutations—namely, by correcting for the effect of voltage on the ΔG₀. Fig. 4 a (inset) shows that in adult-type human AChRs, there is an e-fold reduction in ΔG₀ with a 66-mV depolarization. In mouse endplate AChRs, membrane potential does not influence agonist binding. All of the rate constants reported below have been corrected for the background perturbations (mutations and voltage) and pertain to WT AChRs at −100 mV.

Kinetic modeling

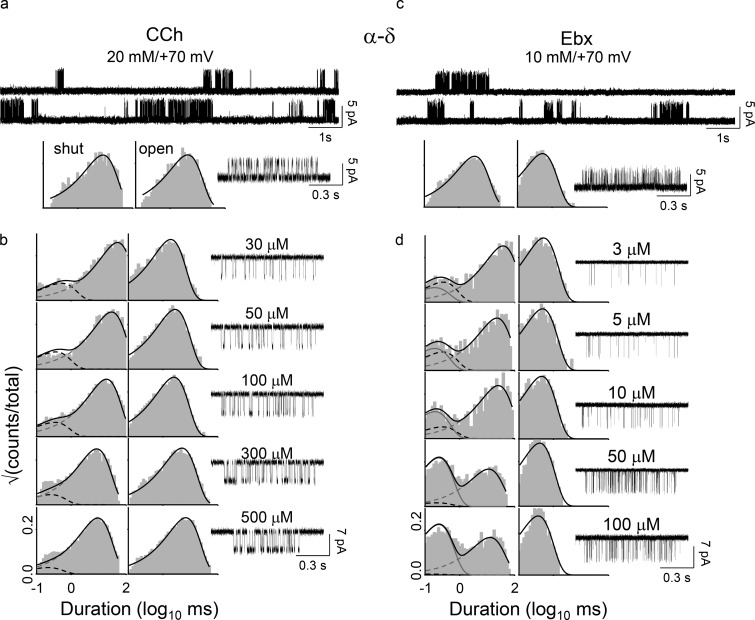
Kinetic analyses of single-channel currents were performed by using the QuB software suite (Nicolai and Sachs, 2013). Rate constants were obtained by analyzing clusters of single-channel activity (representing binding and gating) flanked by nonconducting intervals ≥20 ms (representing desensitization; see Fig. 2, top). The currents within clusters were idealized into noise-free intervals by using the segmental K-means algorithm after digitally filtering the data at 12 kHz (Qin, 2004). At the highest [agonist] (in mM: 10 Epi; 20 ACh, CCh, TMA, Ebx, and Anx; 50 Aza; and 100 Cho), the forward (channel-opening) rate constant (f_n; n, number of bound agonists) and backward (channel-closing) rate constant (b_n) were estimated from the idealized intracluster interval durations by fitting the data to a C⇄O⇄D scheme, where C is resting (closed channel and low affinity), O is active (open channel and high affinity), and D is a short-lived desensitized state (closed channel and high affinity) that was inside clusters (Salamone et al., 1999; Elenes and Auerbach, 2002). The rate constants of the model were optimized by using a maximum interval likelihood algorithm after imposing a dead time of 20–50 µs (Qin et al., 1997). The gating equilibrium constants were calculated from the ratios of the forward/backward rate constants, and the gating free energies in kilocalories per mole were calculated by taking the natural log and multiplying by −0.59 (−RT; R, universal gas constant and T= absolute temperature in K). The error limit on the energy values is ±0.6 kcal/mol (Gupta et al., 2017).

Figure 2.

Energy measurements from electrophysiology. The α−δ site of the adult-type human AChRs was studied in isolation after disabling the α−ε site by adding the mutation εP121R. (a) Gating with CCh. Top: Gating with CCh. [CCh] = 20 mM (to fully saturate the α−δ site) and V_m = +70 mV (to reduce channel block by CCh). Openings (top) are clustered; intercluster gaps reflect desensitization and intracluster intervals mainly reflect ^AR⇄^AR* gating. Intracluster interval duration histograms (bottom) and an example cluster. (b) CCh binding. Association and dissociation rate constants were estimated by fitting across [CCh] (see Materials and methods). (c and d) Ebx gating and binding. Free energies were calculated from the equilibrium constants estimated from the forward/backward rate constant ratios.

The gating properties of unliganded AChRs are complex. There are multiple exponential components apparent in both the shut (nonconducting) and open (conducting) dwell-time distributions. Therefore, a simple shut⇄open kinetic scheme is inadequate to describe unliganded gating activity. In mouse AChRs, unliganded gating schemes have three shut and two open states, irrespective of background mutations (Grosman and Auerbach, 2000; Gonzalez-Gutierrez and Grosman, 2010; Nayak and Auerbach, 2017). We did not carry out elaborate modeling of unliganded gating in human AChRs. Instead, we estimated the unliganded gating forward and backward rate constants, f₀ and b₀, from the inverse of time constant of the predominant components of the shut and open dwell-time distributions (Nayak et al., 2012). Hence, the occasional, unliganded long openings were excluded.

To estimate the single-site association and dissociation rate constants to resting AChRs (k_on and k_off) we fitted globally intracluster interval durations across ~μM [agonist], using a bind-and-gate activation scheme (the clockwise activation pathway in Fig. 1 b):

$$A+R{\rightleftarrows }^{A}R{\rightleftarrows }^{A}R\ast ,$$

where R is a resting receptor, R* is an active receptor, and superscript A is the agonist. The first step is binding to the resting state, and the second step is the global gating isomerization. The resting affinity (K_dR) was estimated as the ratio of the rate constants for the first step, k_off/k_on. K_dR* values were calculated from the cycle by assuming microscopic reversibility.

A free energy change (ΔG) is proportional to the logarithm of the equilibrium constant (K_eq), ΔG = −RTlnK_eq, where R is the gas constant and T is the absolute temperature (RT = 0.59 at 23°C). In the cycle, ΔG_R and ΔG_R* are the free-energy changes associated with low- and high-affinity binding to resting and active conformations (equilibrium dissociation constants K_dR and K_dR*).

Statistical analyses of efficiency plots for nonnicotinic receptors

In the analyses of published data from receptors other than endplate AChRs, we assumed equivalent and independent binding sites. In some reports, a gating equilibrium constant (E) was given, and in others, we calculated it from the maximum response (P_O^max),

$$P_O^{max}={\left(1-1/E\right)}^{-1}.$$

To estimate more accurately the slopes and intercepts of the efficiency plots of nonnicotinic receptors, outliers were identified statistically by a forward search algorithm (Hadi and Simonoff, 1993; Atkinson, 1994). In brief, the method orders the points by their closeness to the fitted model (in this instance, see Eq. 3, in Results) starting with an initial set of fewer observations and extending the regression to a larger dataset, with outliers identified by estimating the residuals. The method is insensitive to the choice of initial subset so long as it is free of “unmasked” (obvious) outliers. We calculated the residuals for each dataset using Excel and plotted them versus the predicted y values from the fitted model to identify the outliers.

Mutations

As described above, in order to make the low-P_O AChR constructs more amenable to single-channel kinetic analysis, we added background mutations that made ΔG₀ (and, hence, ΔG₁) more favorable but did not influence binding (Jadey et al., 2011). For example, the monoliganded gating equilibrium constant with CCh (E₁^CCh) at α−δ was measured using 20 mM CCh with the added background perturbations αP272A + δL265T (to make ΔG₀ less positive), εP121R (to disable the α−ε binding site), and V_m = +100 mV (to reduce channel block by CCh). These four perturbations changed the unliganded gating equilibrium constant by 182-, 37-, 0.1416-, and 0.1-fold, respectively, and together increased the unliganded gating equilibrium constant (E₀) by ∼100-fold. The observed E₁^CCh was 0.15 (f₁ = 89 s⁻¹/b₁ = 583 s⁻¹), which was corrected to the WT condition by dividing by 100 (1.5 × 10⁻³). For weaker agonists, a larger boost in unliganded gating was required; for instance, αD97A + αY127F + αS269I + εP121R, which, in combination, increase E₀ by 2,981-fold.

Chemicals

NaCl, KCl, CaCl₂, MgCl₂, HEPES, NaOH, KOH, KH₂PO₄, Na₂HPO₄, ACh chloride, CCh, TMA, Cho, and Ebx were purchased from Sigma. Epi (±) and anatoxin A fumarate were obtained from Tocris Biosciences. 7-Azabicyclo [2.2.1] heptane was purchased from AstaTech. CTX-MI was obtained from the Alomone Laboratories.

Results

Efficiency definition

Fig. 1 b shows the activation cycle for a receptor having one functional binding site. Microscopic reversibility is satisfied (Nayak and Auerbach, 2017), so

$$\mathrm{\Delta }{\text{G}}_1-\mathrm{\Delta }{\text{G}}_0=\mathrm{\Delta }{\text{G}}_{\text{R}*}-\mathrm{\Delta }{\text{G}}_{\text{R}}.$$ (1)

Each side of Eq. 1 is the “coupling” constant energy that determines the extent to which one bound agonist molecule increases activity above the basal level.

The energy conversion efficiency (η) of a machine is the useful output energy divided by the total input energy (Schroeder, 1999). In a receptor, the useful output energy is that for activation above the baseline that from Eq. 1 is equal to the active-resting difference in binding free energy, ΔG_R* − ΔG_R. The total input energy is the maximum from the ligand, ΔG_R*. Hence, agonist energy efficiency at a given binding site is

$$\eta =1-\mathrm{\Delta }{G}_R/\mathrm{\Delta }{G}_{R*}.$$ (2)

An energy efficiency can be calculated for any agonist at any binding site of any receptor (that operates by a cyclic mechanism) from the resting/active binding energy ratio, that is equal to the ratio of the logarithms of the equilibrium dissociation constants (logK_dR*/logK_dR).

In endplate AChRs and for a series of ACh-class agonists, experiments show that the binding-energy ratio is a constant (Jadey and Auerbach, 2012),

$$\kappa =\mathrm{\Delta }{G}_R/\mathrm{\Delta }{G}_{R*}.$$

Rearranging Eq. 1 and substituting,

$$\mathrm{\Delta }{\text{G}}_1=\mathrm{\Delta }{\text{G}}_0+\mathrm{\Delta }{\text{G}}_{\text{R}}(1/\mathrm{\kappa }-1),$$

and from Eq. 2,

$$\mathrm{\Delta }{G}_1=\mathrm{\Delta }{G}_0+\mathrm{\Delta }{G}_R(\eta /(1-\eta )).$$ (3)

Eq. 3 describes an “efficiency” plot, which is a plot of ΔG₁ versus ΔG_R (logE₁ versus logK_dR) for a series of agonists. If the energy efficiency is the same for all of the agonists, then the points will fall on a straight line with slope η/(1 − η) and y intercept ΔG₀. An average η value is estimated from the slope,

$$\eta =slope/\left(slope+1\right).$$ (4)

Human endplate AChRs

To study one human endplate AChR neurotransmitter–binding site at a time, a mutation (or toxin) was added to disable the companion site, and background mutations were added to make ΔG₀ more favorable so that a single agonist molecule would produce an easily measured response. The background mutations only decreased ΔG₀ and had no effect on either ΔG_R or ΔG_R*. The decrease in ΔG₀ resulted in an equivalent decrease in ΔG₁ (Eq. 3) and, hence, an increased level of activity that allowed rate constants to be estimated from single-channel interval durations at different agonist concentrations (Fig. 2). Rate constant ratios for binding and gating are equilibrium constants (Table 1), the logs of which are proportional to ΔG_R and ΔG₁ (Table 2).

Table 1. Human AChR rate and equilibrium constants .

Site	Agonist	f1(s−1)	b1(s−1)	E1	kon(M−1s−1)	koff(s−1)	KdR (μM)	KdR* (nM)
α–ε	ACh	55.8	6,771	8.2 × 10−3	5.2 × 107	3,662	70.8	5.5
	CCh	32.0	7,884	4.05 × 10−3	1.7 × 107	2,236	182	21
	TMA	20.1	10,615	1.9 × 10−3	7.8 × 106	4,448	573	195
	Cho	2.12	12,325	1.72 × 10−4	2.04 × 106	5,884	2,884	10,867
α–δ	ACh	24.3	5,292	4.6 × 10−3	3.6 × 107	4,631	130	18.1
	CCh	10.4	6,830	1.5 × 10−3	8.1 × 106	3,345	413	176
	TMA	7.1	8,540	8.3 × 10−4	4.6 × 106	3,559	773	587
	Cho	1.1	12,950	8.5 × 10−5	1.6 × 106	7,601	4,750	34,697
α–δ	Epi	39.2	20,804	1.94 × 10−3	2.2 × 108	1,674	7.5	2.52
	Ebx	26.9	22,427	1.2 × 10−3	7.4 × 107	3,606	48.7	25.4
	Anx	6.72	23,150	2.9 × 10−4	3.7 × 107	4,273	115	247
	Aza	3.11	31,211	9.9 × 10−5	7.7 × 106	7,195	934	6,053
α–γ	ACh	377	6,658	5.6 × 10−2	2.9 × 108	4,020	13.8	0.02
	CCh	65.4	8,167	8.0 × 10−3	6.9 × 107	7,689	111	1.25
	TMA	23.5	12,071	1.9 × 10−3	2.7 × 107	8,696	322	14.9
	Cho	5.5	13,598	4.1 × 10−4	8.8 × 106	10,456	1,188	230

The active-state equilibrium constant was calculated from the activation thermodynamic cycle (Fig. 1 b) assuming microscopic reversibility, K_dR* = (K_dRE₀/E₁), where E₀ is the unliganded gating equilibrium constant and is equal to 6.6 × 10⁻⁷ (ΔG₀ = 8.4 kcal/mol) in adult-type and 8.6 × 10⁻⁸ (ΔG₀ = 9.6 kcal/mol) in fetal-type AChRs. f₁ and b₁, monoliganded forward and backward gating rate constants (E₁ = f₁/b₁); k_on and k_off, agonist association and dissociation rate constants to a resting receptor (K_dR = k_off/k_on).

Table 2. Human AChR gating and binding free energy changes.

Site	Agonist	ΔG1	ΔGR	ΔGR*
α–ε	ACh	2.8	−5.6	−11.2
	CCh	3.3	−5.1	−10.4
	TMA	3.7	−4.4	−9.1
	Cho	5.1	−3.4	−6.7
α–δ	ACh	3.2	−5.3	−10.5
	CCh	3.8	−4.6	−9.2
	TMA	4.2	−4.2	−8.5
	Cho	5.5	−3.2	−6.1
α–δ	Epi	3.7	−7.0	−11.7
	Ebx	4.0	−5.9	−10.4
	Anx	4.8	−5.0	−8.7
	Aza	5.4	−4.1	−7.1
α–γ	ACh	1.7	−5.2	−13.1
	CCh	2.9	−5.4	−12.1
	TMA	3.7	−4.7	−10.6
	Cho	4.6	−4.1	−9.0

All values are kilocalories per mole. ΔG₁, gating with one bound agonist; ΔG_R, binding to the resting conformation; ΔG_R*, binding to the active conformation (Fig. 1 b).

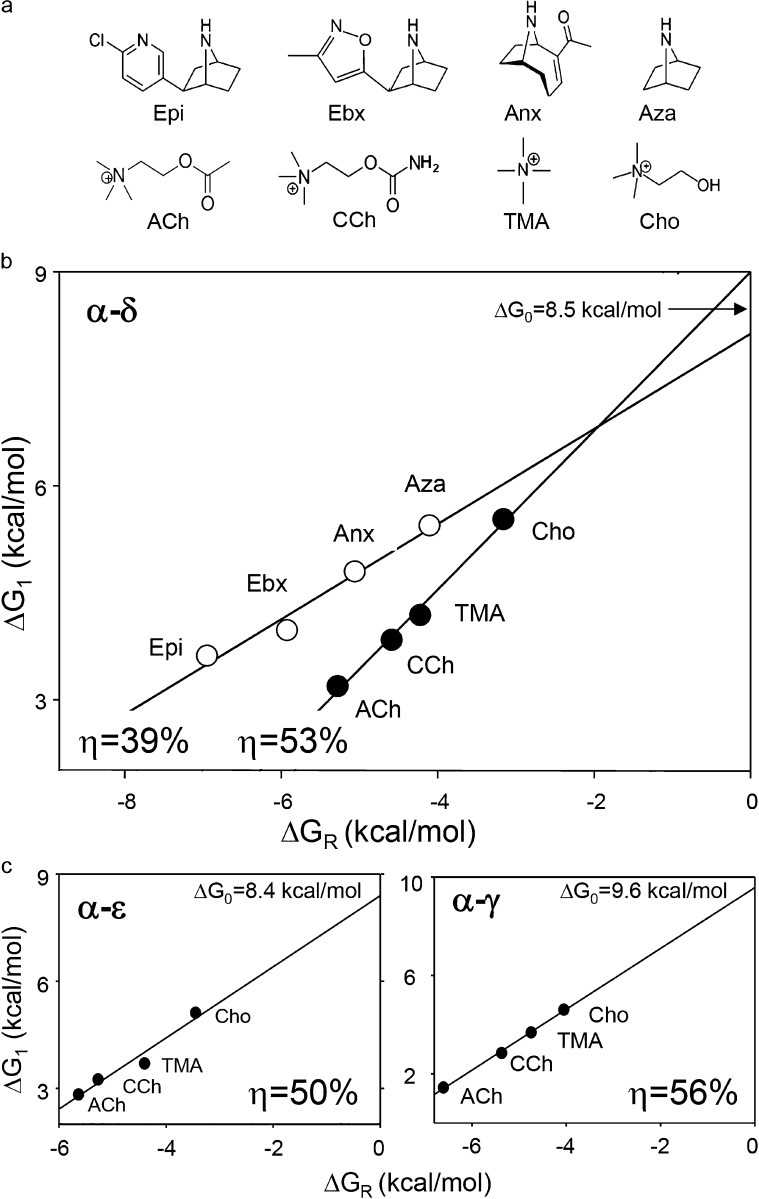
Fig. 3 b shows efficiency plots for ACh- and Epi-class agonists at the α−δ binding site. Within each agonist family, there is a range of ΔG_R and ΔG₁ values, but because the points fall on the same line we conclude that all four ligands within each class have approximately the same energy efficiency. From the slopes of the linear fits (Eq. 4), we estimate that η_ACh-class = 0.53 ± 0.04 and η_Epi-class = 0.39 ± 0.05 (mean ± SD). At the α−δ binding site (that is common to adult and fetal AChRs), ACh-class agonists are ∼35% more efficient than Epi-class agonists at converting agonist-binding energy into kinetic energy for gating. The average of the y intercepts, +8.5 kcal/mol, estimates ΔG₀ in adult-type human AChRs (at −100 mV) and is the same value as in adult-type mouse AChRs.

Figure 3.

Efficiency plots for human AChR-binding sites. (a) Agonists. Epi, epibatidine; Ebx, epiboxidine; Anx, anatoxin; Aza, azabicycloheptane; ACh, acetylcholine; CCh, carbamylcholine; TMA, tetrmethylammonium; Cho, choline. (b) Efficiency plot for the AChR α−δ neurotransmitter binding site. The y-axis is the gating free energy change and the x-axis is the binding free energy change. The line is the fit by Eq. 3, with energy efficiency (η) calculated from the slope and intrinsic gating energy (ΔG₀) from the y intercept. ACh-class agonists are more efficient than Epi-class agonists. (c) Efficiency plots for α−ε and α−γ sites. ACh-class agonists are most efficient at α−γ. The intrinsic gating energy of adult-type AChRs (with an ε subunit) is less positive (more favorable) than of fetal-type (with a γ subunit) AChRs.

We repeated these experiments with ACh-class agonists and AChRs having only a functional α−ε or α−γ binding site (Fig. 3 c). The results were η_ACh-class = 0.50 ± 0.08 and 0.56 ± 0.02. ACh-class agonists have approximately the same energy efficiency at the two adult sites (α−δ and α−ε) but, perhaps, a slightly greater efficiency at the fetal α−γ site. It appears that the same ligand can have different efficiencies at different binding sites. As expected, the y intercept of the α−ε plot gives the same ΔG₀ as in the α−δ plot, but that from the α−γ plot estimates the intrinsic gating energy of fetal-type human AChRs to be +9.6 kcal/mol, again similar to the mouse fetal-type AChR value.

It is of considerable importance to know the intrinsic gating energy of a receptor, so we applied two additional methods to measure it more accurately in adult-type human AChRs. Many mutations away from the binding sites have the same effect on gating with two bound Cho molecules (ΔG₂^Cho) in human and mouse AChRs (Fig. 4 a, left). We assumed that, as in mouse, the observed changes relative to the WT (ΔΔG₂^Cho; Table 3) were caused exclusively by equivalent changes in intrinsic gating (ΔΔG₀). We measured ΔG₀ for human AChR mutants (Table 4) and plotted the values against the corresponding values of ΔΔG₂^Cho (Fig. 4 a, right). The slope of the fitted straight line was 1.0 ± 0.1, validating the assumption. The y intercept of the plot in Fig. 4 b provides a second estimate of ΔG₀, +8.4 ± 0.8 kcal/mol.

Table 3. Effect of mutations on ΔG₂^Cho in human AChRs.

Mutation	f2(s−1)	b2(s−1)	E2Cho	E2mut/Cho/E2WT	ΔΔG2Cho (kcal/mol)
—	76	2,252	0.034	1	0
αE45R	4,002	2,095	1.91	56	−2.4
αA96V	3,380	885	3.82	112	−2.8
αD97A	6,624	1,533	4.3	126	−2.8
αY127F	3,471	1,001	3.47	102	−2.7
αS266E	30	3,023	0.01	0.30	0.7
αS269I	1,832	706	2.6	77	−2.6
αP272A	1,458	236	6.2	182	−3.1
αC418W	731	184	3.98	116	−2.8
βL262T	844	675	1.25	36	−2.1
βV266A	424	28	15.1	445	−3.6
βT456I	101	826	0.14	3.6	−0.8
βT456F	314	342	0.92	27	−1.9
δI43Q	200	1,893	0.105	3.1	−0.7
δI43H	20.5	5,067	0.004	0.12	1.3
δL265T	190	148	1.48	37	−2.1
δL265S	172	9.2	18.7	550	−3.7
εL261S	1,956	134	14.6	429	−3.6
εL269F	831	197	4.2	124	−2.8

E₂ = f₂/b₂. ΔΔG₂^Cho, gating free energy change with two bound Cho molecules; f₂ and b₂, diliganded forward and backward gating rate constants.

Table 4. Mutant AChR construct unliganded gating rates, equilibrium constants and free energies.

Construct	f0(s−1)	b0(s−1)	E0mut	ΔG0Obs	E2mut/E2wt	ΔΔG2Cho	n
αN217K βL262T δL265T	22.5 (6)	786 (192)	0.028 (0.01)	2.1 (0.18)	3.9 × 104	−6.25	3
αD97A βL262T δL265T	19 (2)	260 (17)	0.073 (0.009)	1.5 (0.07)	1.7 × 105	−7.08	2
αL279W βL262T δL265T	56 (4)	633 (54)	0.088 (0.01)	1.4 (0.067)	1.7 × 105	−7.1	2
αC418W βL262T δL265T	85 (7)	879 (92)	0.095 (0.013)	1.4 (0.08)	1.6 × 105	−7.1	5
αP272A βL262T δL265T	225 (58)	889 (78)	0.25 (0.06)	0.8 (0.12)	2.4 × 105	−7.3	4
αN217K βL262T δL265T εS450W	35 (4.3)	126 (13)	0.27 (0.04)	0.8 (0.09)	2.9 × 105	−7.43	2
αY127F βL262T δL265T εS450W	433 (14)	752 (3.5)	0.58 (0.02)	0.3 (0.02)	9.3 × 105	−8.1	3
αC418W βV266A δL265S	5285 (236)	120 (14)	44.1 (5.1)	−2.2 (0.07)	2.9 × 107	−10.1	4
βT456I δL265S εL261S	269 (34)	825 (93)	0.32 (0.06)	0.7 (0.11)	8.4 × 105	−8.0	2
αA96V βV266A δL265S	735 (55)	160 (17)	4.6 (0.22)	−0.9 (0.07)	2.7 × 107	−10.0	3
αA96V βV266A εL261S	6,925 (655)	477 (126)	14.6 (4.0)	−1.6 (0.16)	2.1 × 107	−9.9	5

Free energies are in kilocalories per mole. E₀ = f₀/b₀; ΔΔG₂^Cho = −0.59*ln(E₂^mut/E₂^wt); ΔG₀^obs = −0.59*ln(E₀); f₀ and b₀, unliganded forward and backward gating rate constants (±SEM, n patches); ΔΔG₂^Cho, change in gating free energy with two bound Cho molecules.

A third method of estimating ΔG₀ does not require extrapolation or mutations (Jha and Auerbach, 2010). When the binding sites operate independently (see below), the difference between gating energies with two versus one bound agonist is the same as the difference between one versus none,

$$\mathrm{\Delta }{\text{G}}_2-\mathrm{\Delta }{\text{G}}_1=\mathrm{\Delta }{\text{G}}_1-\mathrm{\Delta }{\text{G}}_0,$$

where ΔG₁ is the average of the two, single-site gating energies. We measured ΔG₂ and calculated ΔG₁ from the single-site ΔG₁ values. The calculated average ΔG₀ for the four agonists at adult-type binding sites was +8.3 kcal/mol.

All three methods of estimating ΔG₀ produced the same result. We estimate that the human AChR intrinsic gating energies are 8.4 kcal/mol in adult-type and 9.6 kcal/mol in fetal-type AChRs, which correspond to unliganded gating equilibrium constants (constitutive P_O values) of 6.6 × 10⁻⁷ in adult-type and 8.6 × 10⁻⁸ in fetal-type AChRs.

To learn if the two WT binding sites interact with each other with regard to receptor activation, we compared the two-site gating energies with the sums of one-site gating energies. The two were the same in both adult- and fetal-type human AChRs, for all agonists. As in mouse AChRs (Nayak and Auerbach, 2017), the human AChR-binding sites operate independently with regard to activation by agonists.

Other receptors

Next, we investigated energy efficiency in other receptors. In terms of equilibrium constants, Eq. 2 is

$$\eta =1-\log \left({\text{K}}_{\text{dR}*}\right)/\log \left({\text{K}}_{\text{dR}}\right),$$ (5)

where K_dR* is the equilibrium dissociation constant of the active conformation and K_dR is the equilibrium dissociation constant of the resting conformation (Fig. 1 b). For example, K_dR* and K_dR for ACh measured at the mouse AChR α−ε site are 12 nM and 153 µM (Nayak and Auerbach, 2017), from which we calculate η_ACh = 52%.

We used Eq. 5 to estimate the efficiency of the agonist Ca⁺² at binding sites of K_Ca1.1 (BK; a potassium-selective ion channel) using published values of the equilibrium dissociation constants (Sweet and Cox, 2008). At Ca-bowl sites, K_dR = 3.1 mM and K_dR*=0.9 µM, from which we calculate η_Ca = 9%. At RCK1 sites, K_dR = 15.8 mM and K_dR* = 2.1 µM, from which we calculate η_Ca = 13%. So far, binding equilibrium constants have been published only for Ca⁺², so we could not make an efficiency plot and ascertain if other agonists of K_Ca1.1 have the same energy efficiency.

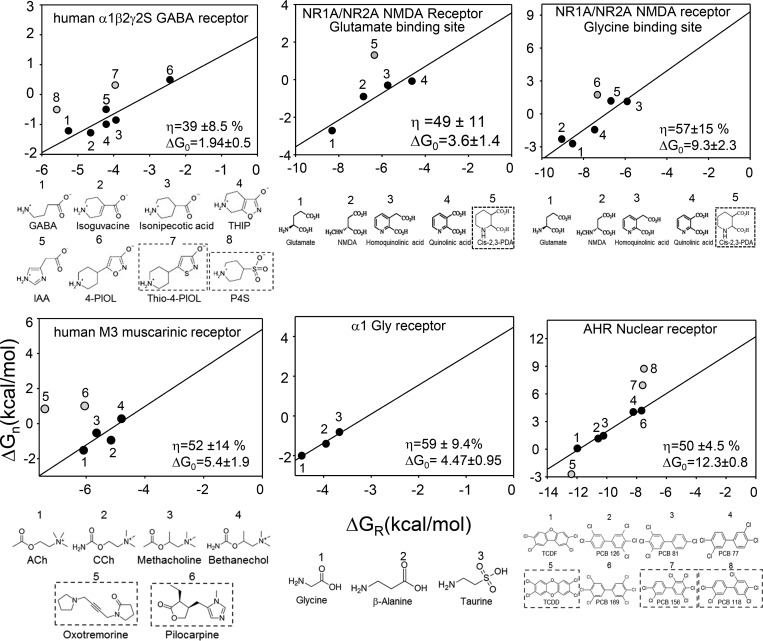
Affinities and efficacies for agonist series have been reported for several other receptors, including M3 muscarinic (Sykes et al., 2009), GABA_A (Mortensen et al., 2004), glycine (Lewis et al., 2003), NMDA (Priestley and Kemp, 1994; Priestley et al., 1995), and aryl-hydrocarbon (Hestermann et al., 2000). From these, we could calculate gating and binding energies and construct efficiency plots to estimate η and ΔG₀ (Fig. 5). In all of these receptors except M3, a positive correlation between binding and gating energies is apparent. We considered that the scatter in these plots was caused, in part, by including agonists that belong to different energy efficiency classes. For example, combining all of the points for ACh- and Epi-class agonists at the human AChR α−δ site (Fig. 2 a) would obscure the linear relationship between gating and binding energies apparent for each agonist family.

Figure 5.

Efficiency plots for other receptors. In each panel, top is the efficiency plot and bottom is the agonist structures. Energies were calculated from literature values (see text for citations). Gray symbols and boxed ligands are agonists having a different efficiency from the main group, identified statistically and excluded from the linear fit. ΔG₀ is kilocalories per mole.

To improve the accuracy of the slope and intercept estimates for the non-nicotinic receptors, we used an unbiased, statistical method to identify outliers (see Materials and methods). After their removal, the activation versus binding free energies all fell on the same line, including for M3. This result suggests that in these receptors and for these agonists there is a constant energy efficiency and, hence, a fixed binding-energy ratio. In Fig. 5, the η values estimated from the slopes are in the range of 39–59% and the ΔG₀ values estimated from the y intercepts are in the range of 1.9–12 kcal/mol (Table 5).

Table 5. Energy efficiencies (η, for the native agonist) and intrinsic gating energies (ΔG₀).

Receptor	η %	ΔG0 (kcal/mol)
Endplate AChR
Human
α−ε	47	8.4
α−δ	51
α−γ	56	9.6 (w/α−δ)
Mouse
α−ε	55	8.4
α−δ	58
α−γ	59	9.8 (w/α−δ)
Human α1β2γ2S GABAA receptor	39	1.9
Human NR1A/NR2A NMDA receptor (unliganded Glu site, Gly site saturated)	49	3.6
Human NR1A/NR2A NMDA receptor (unliganded Gly site, Glu site saturated)	57	9.3
Human M3 muscarinic receptor	52	5.4
Human α1 GlyR	59	4.5
Fish aryl-hydrocarbon nuclear receptor	50	12.3

ΔG₀ values for endplate AChRs are for adult (α−ε and α−δ) or fetal types (α−γ).

In some cases, the “outlier” ligands had structures that differed from the main group. For example, in GABA_A receptors, the outliers were the only agonists with a sulfur atom, and in M3 muscarinic receptors, the outliers were large and with rings. This result supports the hypothesis that combining data from agonists belonging to different efficiency classes creates scatter in the efficiency plots. However, for other receptors, the basis for the scatter was less clear and possibly can be attributed to experimental errors.

Rate-equilibrium free energy relationships (REFERs)

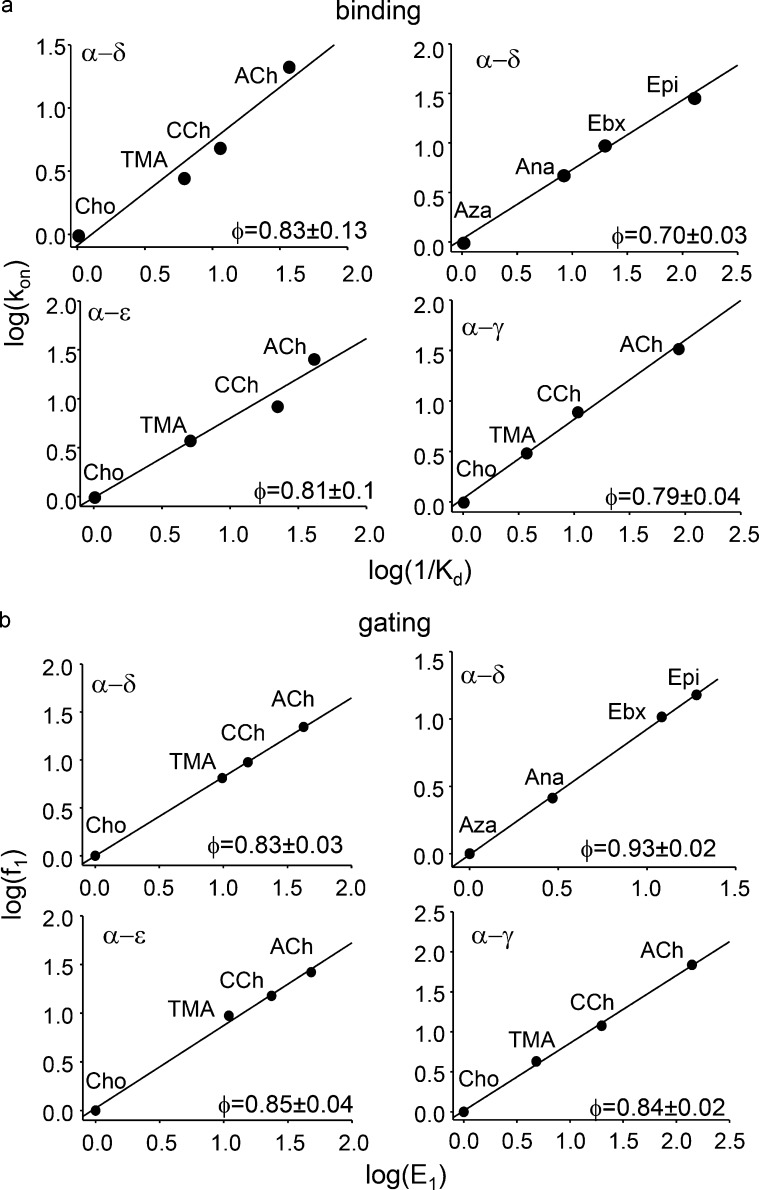
Our fundamental measurements were rate constants, so we were also able to probe the transition states of binding and gating in human AChR activation. Fig. 6 shows REFERs for binding and gating in human AChRs activated by different agonists. The REFER slope (φ) gives the relative extent to which the agonist dependence of the equilibrium constant is determined by changes in the forward versus backward rate constant on a scale from 1 to 0. For ACh-class agonists, the single-site φ-value for both binding and gating is ∼0.83, indicating that differences between the agonists are caused mainly by differences in the forward processes, namely agonist association and channel opening. The binding and gating φ-values were similar at α−δ, α−ε and α−γ sites. For Epi-class agonists at α−δ, the binding φ-value was smaller (0.70) and the gating φ-value larger (0.93) than for ACh-class agonists. That is, with Epi compared with ACh, the transition state for binding is earlier (when achieved, the ligand is more “free-like” in energy) and that for gating is later (the ligand is a more “open-like” in energy).

Figure 6.

Human AChRs REFERs. The slope (φ) of each REFER reports the extent to which a change in equilibrium constant is caused by a change in the forward versus backward rate constant. (a) Binding to the resting state. k_on (M⁻¹s⁻¹), association rate constant; K_dR, equilibrium dissociation constant. At all sites, agonists differ mainly with regard to association rate constant (ACh-class more so than Epi-class agonists). (b) Gating with one bound agonist. f₁ (s⁻¹), forward, channel-opening rate constant; E₁, monoliganded gating equilibrium constant. At all sites, agonists differ mainly with regard to the channel-opening rate constant (Epi-class more so than ACh-class agonists).

Discussion

Energy conversion efficiency (η) is the fraction of the stimulus energy transformed into the mechanical work of a global conformational change. In energy terms, affinity is ΔG_R or ΔG_R*, relative efficacy is ΔG_R − ΔG_R*, and efficiency is 1 − ΔG_R/ΔG_R*.

Any kind of input energy at any sensor site of any allosteric protein (that activates according to a cycle) can be associated with an efficiency. In receptors, the input energy is from agonist binding and the resting/active binding-energy ratio determines η. η is a positive number for agonists, zero for antagonists, and a negative number for inverse agonists.

The main results are as follows. (a) An efficiency plot, of activation energy versus binding energy (log equilibrium constants), estimates energy efficiency and the intrinsic gating energy. (b) Structurally related agonists have the same efficiency at a given binding site; different agonist families have different efficiencies at the same binding site; it appears that agonists can have different efficiencies at different binding sites (Fig. 3). (c) Efficiency plots for muscarinic, GABA_A, glycine, NMDA, and aryl-hydrocarbon receptors are linear (Fig. 5). Below, we discuss η and ΔG₀ values, consider some implications of η, and compare mouse and human endplate AChRs.

We consider the structural correlates of energy efficiency in nicotinic AChRs in a separate report (Tripathy et al., 2019). Briefly, the active/resting ratio of distances between a key agonist atom and the center of the binding pocket determines energy efficiency.

η and ΔG₀

Table 5 shows η values for different agonist/site combinations and ΔG₀ values for seven kinds of receptor. The overall, average efficiency for the native agonist was ∼51%, with values ranging between 39% (GABA_A receptors) and 59% (glycine receptors). Human endplate AChR-binding sites are typical in this regard, with an average efficiency of ∼51%. Apparently, many diverse receptors dedicate about half of the available ligand-binding energy to the activation conformational change. Ca²⁺ at K_Ca1.1-binding sites is substantially less efficient, for unknown reasons. It is possible that the low per-site efficiency is compensated by the large number of binding sites (n = 8).

The spread in receptor ΔG₀ values is substantial. The estimate for GABA_A receptors suggests a relatively high level of constitutive activity (P_O∼4 × 10⁻²), consistent with literature reports (Wagner et al., 2005; Shin et al., 2017). M3 muscarinic, glycine, and NMDA receptors appear to be less active in the absence of agonists (∼10⁻⁴). Interestingly, the intercepts of the efficiency plots for the glycine versus glutamate agonist series suggests that NMDA receptors have an even lower level of constitutive activity in the absence of the coagonist glycine compared with the neurotransmitter glutamate. Adult-type neuromuscular synapses (mouse and human) and K_Ca1.1 channels have about the same probability of being active constitutively (10⁻⁷). Of the receptors we examined, the fetal endplate and aryl-hydrocarbon receptors have the most positive ΔG₀ and, hence, the smallest estimated level of constitutive activity (∼10⁻⁸). Even in this small sample, there is a wide range in constitutive P_O.

In mouse AChRs, only a few amino acids at the neurotransmitter binding site determine the agonist-binding energies, whereas a large number of amino acids throughout the protein determine ΔG₀ (Corringer et al., 2000; Sine, 2012; Auerbach, 2013; Purohit et al., 2013). The physiological reasons for the wide variation in the level of constitutive activity are not known (∼15-fold smaller in fetal versus adult endplate AChRs and ∼70-fold larger in GABA_A versus glycine receptors). However, the wide range in ΔG₀ values and the participation of many side chains suggest that the level of intrinsic activity is fine tuned by natural selection. We note that the lower intrinsic activity of fetal versus adult endplate receptors pertains to both mouse and human AChRs.

Implications of η

In this section, we discuss the value of knowing energy efficiency. First, η informs of the binding mechanism. The main activation pathway connecting R with ^AR* (Fig. 1 b) involves the formation of a low-affinity complex followed by a switch (within the gating isomerization) to a high-affinity complex: A+R⇄^AR⇄^AR*. The corresponding ligand-dependent free energy changes in this two-step sequence are ΔG_R and (ΔG_R* − ΔG_R). A linear efficiency plot indicates that ΔG_R/ΔG_R* is the same for all agonists, or that ΔG_R is a constant fraction of ΔG_R* for all agonists in the family. Hence, a shared efficiency implies that the energy changes in the two steps in the above reaction sequence are correlated linearly.

Several lines of evidence suggest that in endplate and other receptors, both steps involve local rearrangements of the binding sites. In mouse AChRs (Nayak and Auerbach, 2017) and all of the receptors shown in Fig. 5, the resting association rate constant (k_on) is slower than diffusion (Grewer, 1999; Lewis et al., 2003; Dravid et al., 2008; Sykes et al., 2009; Mortensen et al., 2010). This suggests that the formation of the low-affinity complex is not by diffusion alone. Also, k_on can be highly temperature dependent in AChRs (Gupta and Auerbach, 2011) and independent of the agonist’s diffusion constant in nicotinic and GABA_A receptors (Zhang et al., 1995; Jones et al., 2001; Jadey and Auerbach, 2012). These results suggest that A+R⇄^AR involves a local rearrangement of the binding site (“catch”). Certainly, the subsequent ^AR⇄^AR*, affinity-changing step that triggers the global isomerization ("hold") involves structural changes at the binding sites.

The linear efficiency plots suggest that in AChRs and the receptors shown in Fig. 5, the energy change associated with low-affinity binding (ΔG_R) is correlated linearly with the energy change in the switch to high affinity (ΔG_R* − ΔG_R, which in an efficiency plot is the agonist-dependent part of the y axis). This correlation between catch and hold energies, however, does not necessarily imply a correlation in the catch and hold structural changes. It is possible that in some receptors, distinct ligand–protein interactions govern the energy changes in each step of the reaction sequence.

Second, η can be used to categorize agonists. Defining an agonist family by members that have the same energy efficiency (fall on the same straight line in an efficiency plot) is a new way to classify ligands. In AChRs, it appears that the relative movement of the ligand toward the center of the binding pocket is greater for ACh-class versus Epi-class agonists (Tripathy et al., 2019). We speculate that the classification of agonists by efficiency will become increasingly useful as we learn more about the structural basis of low- versus high-affinity binding in other receptors.

Third, η simplifies CRC analysis. There are four free energies in the activation cycle, but one is constrained by microscopic reversibility and ΔG₀ is agonist independent, leaving just two to be measured for each ligand. If the agonist’s efficiency is known, then only one energy value needs to be measured in order to construct a full CRC. An experimental measurement of either the resting affinity or gating equilibrium constant is sufficient (Auerbach, 2016). Once the receptor and agonist family have been calibrated (ΔG₀ and η have been measured), an entire CRC, including absolute efficacy and EC₅₀, can be calculated from just one affinity estimate, either for a resting or active site.

Human versus mouse AChRs

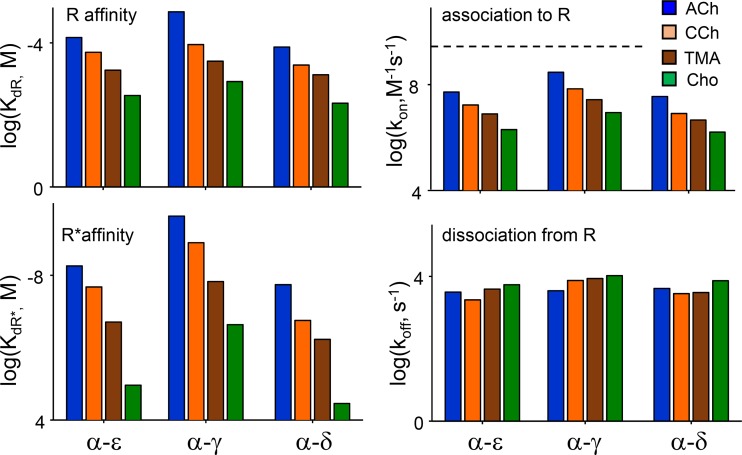
Our study of human AChRs involved a comprehensive analysis of binding and gating rate and equilibrium constants for eight different agonists at three kinds of binding sites (Fig. 7). Some values for adult-type human AChRs were reported previously based on kinetic modeling of single-channel currents from receptors having two functional binding sites (Wang et al., 1997; Mukhtasimova et al., 2016). These previous reports suggested that α−δ and α−ε have distinctly different affinities for ACh, CCh, Epi, and Cho, whereas our results show unambiguously that these affinities are almost the same at the two human adult neurotransmitter-binding sites (within a factor of ∼2, or ∼0.5 kcal/mol; Tables 1 and 2). As pointed out elsewhere (Salamone et al., 1999), this discrepancy can be traced to a modeling error in the previous experiments. In AChRs, there is an approximately millisecond shut interval component apparent at all agonist concentrations that may reflect sojourns in a short-lived desensitized state (Elenes and Auerbach, 2002). If, as in the previous analyses, this state is not included in the modeling scheme, then the equilibrium dissociation constant of one binding step will be underestimated, leading to the incorrect conclusion that the two sites have different affinities. Our results using individual binding sites show definitively that the adult sites of human AChRs have approximately the same affinities for the tested agonists and, furthermore, operate independently.

Figure 7.

Summary of human AChR-binding constants. Left: Equilibrium constants. For all ACh-class agonists, resting- and active-state–binding energies are greater at the fetal α−γ site than at the adult α−ε and α−δ sites. Right: Rate constants. For all agonists, association to R is slower than diffusion (dashed line, 5 × 10⁹ M⁻¹s⁻¹) and greatest at α−γ. Dissociation rate constants are similar for all agonists and at all sites.

Binding and gating constants of human endplate AChRs are almost the same as those in mouse endplate AChRs, for both fetal and adult types. For a complete list of the results for mouse AChRs, see Nayak and Auerbach (2017). Receptor ΔG₀ values, too, are nearly identical. In both species, agonists at the fetal α−γ site have higher affinities, relative efficacies, and energy efficiencies than those at either adult site. The only significant difference between human and mouse AChRs we have detected so far is that binding and gating φ-values for ACh-class agonists are lower in human AChRs (∼0.8 versus ∼0.9; Fig. 6), but for unknown reasons. We also observed that there is greater kinetic heterogeneity in human versus mouse AChRs that may be caused by amino acid differences in the δ subunit in the region that flanks a conserved glycine in loop E (Vij et al., 2015).

Mouse and human AChRs share ∼90% sequence identity. There are n = 10 (α−γ) or n = 21 (α−δ or α−ε) amino acid mismatches between human and mouse AChRs within 20 Å of the aromatic cluster of the binding site. The similarity in function between species suggests that these mismatches (in combination) have little effect on binding, efficacy, energy efficiency, or intrinsic gating. The conservation of the fetal versus adult ΔG₀ difference between species suggests that the specific values are optimal, but different, at developing versus mature neuromuscular synapses.