4D Liver Tumor Localization using Cone-Beam Projections and a Biomechanical Model

Abstract

Purpose:

To improve the accuracy of liver tumor localization, this study tests a biomechanical modeling-guided liver cone-beam CT (CBCT) estimation (Bio-CBCT-est) technique, which generates new CBCTs by deforming a prior high-quality CT or CBCT image using deformation vector fields (DVFs). The DVFs can be used to propagate tumor contours from the prior image to new CBCTs for automatic 4D tumor localization.

Methods/ Materials:

To solve the DVFs, the Bio-CBCT-est technique employs an iterative scheme that alternates between intensity-driven 2D-3D deformation and biomechanical modeling-guided DVF regularization and optimization. The 2D-3D deformation step solves DVFs by matching digitally reconstructed radiographs of the 3D deformed prior image to 2D phase-sorted on-board projections according to imaging intensities. This step’s accuracy is limited at low-contrast intra-liver regions without sufficient intensity variations. To boost the DVF accuracy in these regions, we use the intensity-driven DVFs solved at higher-contrast liver boundaries to fine-tune the intra-liver DVFs by finite element analysis-based biomechanical modeling.

We evaluated Bio-CBCT-est’s accuracy with seven liver cancer patient cases. For each patient, we simulated 4D cone-beam projections from 4D-CT images, and used these projections for Bio-CBCT-est based image estimations. After Bio-CBCT-est, the DVF-propagated liver tumor/cyst contours were quantitatively compared with the manual contours on the original 4D-CT ‘reference’ images, using the DICE similarity index, the center-of-mass-error (COME), the Hausdorff distance (HD) and the voxel-wise cross-correlation (CC) metrics. In addition to simulation, we also performed a preliminary study to qualitatively evaluate the Bio-CBCT-est technique via clinically acquired cone beam projections. A quantitative study using an in-house deformable liver phantom was also performed.

Results:

Using 20 projections for image estimation, the average (± s.d.) DICE index increased from 0.48±0.13 (by 2D-3D deformation) to 0.77±0.08 (by Bio-CBCT-est), the average COME decreased from 7.7±1.5 mm to 2.2±1.2 mm, the average HD decreased from 10.6±2.2 mm to 5.9±2.0mm, and the average CC increased from −0.004±0.216 to 0.422±0.206. The tumor/cyst trajectory solved by Bio-CBCT-est matched well with that manually obtained from 4D-CT reference images.

Conclusions:

Bio-CBCT-est substantially improves the accuracy of 4D liver tumor localization via cone-beam projections and a biomechanical model.

I. INTRODUCTION

Primary liver carcinoma is a leading cause of morbidity worldwide that affects an increasingly large population [1], with incidence and mortality both on the rise in the United States [2]. The liver is also one of the most common sites of metastatic disease from primary cancers such as breast, colorectal, and melanoma. Historically, radiation therapy has played a limited role in treating liver cancer, especially primary liver cancer, because of normal liver tissues’ low tolerance for radiation [3]. The role of radiation therapy in liver cancer treatment has become more promising as technological developments, such as stereotactic body radiotherapy, have enabled the delivery of a highly focused radiation dose to tumors while sparing normal liver tissue [4]. The success of this delivery depends on the accuracy of daily tumor localization immediately prior to each treatment or during each treatment, which is however complicated by liver motion. The commonly applied, x-ray-based cone-beam CT (CBCT) imaging is considered sub-optimal for liver due to the low-contrast of the liver tumor within the liver parenchyma. While contrast agents are frequently used during CT simulation to enhance tumor contrast, they are rarely used in CBCT to guide daily treatments because of the additional workload, the potential toxicity of the contrast agents, and uncertainties regarding the timing of contrast administration [5]. Many institutions use fiducial markers implanted near the liver tumor to assist localization [6]. However, this method requires invasive marker implantation, can lead to liver inflammation, and is susceptible to potential marker migrations during the course of treatment. Other clinics rely on anatomical surrogates, mostly diaphragms, to localize the tumor. However, the degree of motion correlation between the surrogates and the liver tumors can affect the accuracy of anatomical surrogates-based localization [7]. Some clinics use the rigid translation of the whole liver volume in 3D-CBCT to localize the liver tumor, but this method fails to capture the 4D liver motion, with accuracy affected by motion blurriness. The above techniques also rely on rigid registration for tumor localization. Rigid registration is error-prone, as previous studies have found the average liver motion difference determined by rigid registration and deformable registration on magnetic resonance images (MRIs) is approximately 10 mm [8].

Recently, a new CBCT/4D-CBCT estimation technique has been developed that generates new CBCTs by deforming a high-quality prior CT or CBCT image [9–15]. The deformation approach can help to accurately solve the 4D liver motion by estimating 4D-CBCTs from phase-sorted cone-beam projections. The deformation vector fields (DVFs) solved by 2D-3D deformation can be used to automatically propagate tumor contours from prior images to new images for localization, without the need to perform the challenging task of visual tumor identification. However, for liver imaging, the liver tumors’ low contrast also limits the accuracy of 2D-3D deformation, as the liver tumor fails to provide sufficient intensity variation from the liver parenchyma to drive the intensity difference-based deformation. As a result, most of these 2D-3D deformation methods are limited in applications to the lung sites, where the in-lung contrast is sufficiently high to drive the accurate deformation of bulk lung tumors [9, 10, 12–15]. Only one study [11] has performed a preliminary liver deformation study using scatter-free and noise-free CT-simulated data, and the deformation accuracy evaluation is limited to the liver surface contours (instead of intra-liver tumors). It also specifically acknowledges the limitation of the 2D-3D deformation algorithm in deforming low-contrast intra-liver regions. Thus, improving the image estimation accuracy of low-contrast liver tumors is critical to improving patient setup and tumor localization in image-guided radiation therapy.

Recently, we developed a biomechanical modeling-guided CBCT estimation technique (Bio-CBCT-est) [16] that combines the 2D-3D deformation technique with a biomechanical modeling DVF regularization and optimization step [17–20]. The biomechanical modeling step uses the organ boundary condition solved by 2D-3D deformation to regularize and optimize the DVF at low-contrast, intra-organ regions. The technique models each organ of interest as a mesh composed of discrete tetrahedral finite elements. The collective movements of these finite elements, representing the intra-organ deformation, can be solved by finite element analysis based on tissue elasticity properties and organ boundary motion. The physics-driven deformation can potentially boost the deformation accuracy of low-contrast regions within each organ, because it does not rely on intensity variations to solve intra-organ DVFs.

This study evaluates the Bio-CBCT-est technique for 4D liver tumor localization using cone-beam projections. We used seven liver cancer patient cases to validate the technique. For each patient, we simulated 4D cone-beam projections from 4D-CT images, and used these projections for Bio-CBCT-est based image estimations. We compared the tumor/cyst contours automatically propagated by Bio-CBCT-est against the tumor/cyst volumes manually contoured on the 4D-CT reference images. We also evaluated the estimation accuracy of Bio-CBCT-est for different projection sparsity levels to assess the technique’s potential to reduce imaging dose. We also performed a preliminary study to qualitatively evaluate Bio-CBCT-est using clinically acquired cone beam projections. A clinical study using an in-house deformable liver phantom was also conducted to quantitatively evaluate the clinical feasibility of the Bio-CBCT-est technique.

II. MATERIALS AND METHODS

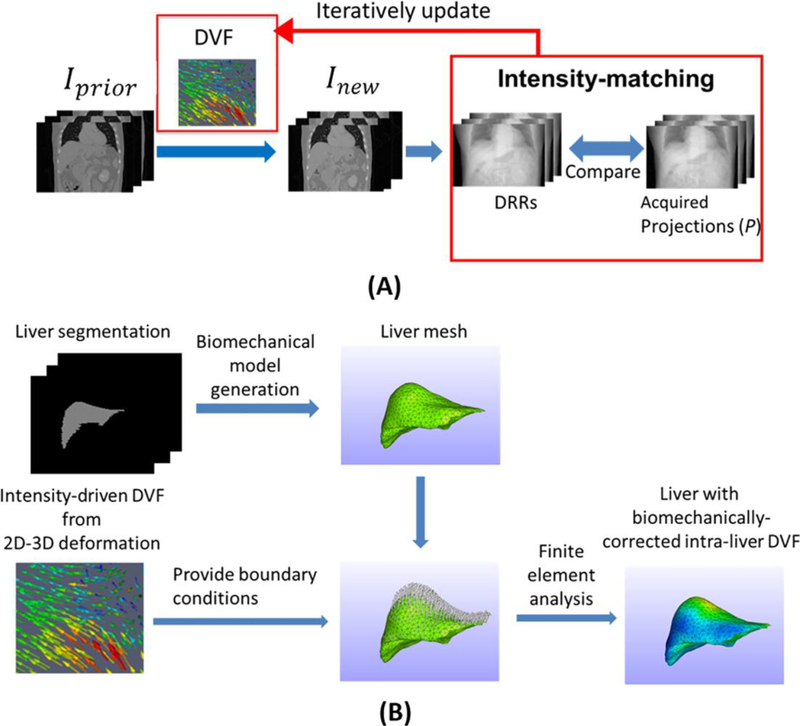
The Bio-CBCT-est technique solves the DVF by two alternating steps: 2D-3D deformation (Fig. 1 (A)) and finite element analysis-based biomechanical modeling (Fig. 1 (B)). The following section introduces each step.

Figure 1:

(A). General scheme of the intensity-driven 2D-3D deformation technique. The DVF is iteratively updated so that the DRRs of the deformed I_prior (I_new ) will match the cone-beam projections in the intensity domain. (B). Workflow of the liver biomechanical modeling. A liver tetrahedral mesh is generated from the liver contour. The liver boundary DVF solved by 2D-3D deformation is then used as the boundary conditions to drive the finite element analysis of the liver tetrahedral mesh to solve biomechanically-corrected intra-liver DVF.

II.A. 2D-3D deformation

The 2D-3D deformation technique uses an intensity-driven approach to solve the DVF (DVF), which generates the new CBCT image through trilinear interpolation-based deformation on the prior image:

$$I_{new}(\mathit{x})=I_{prior}(\mathit{x}+\mathit{DVF})$$ (1)

I_prior denotes the prior image and I_new denotes the deformed I_prior The 2D-3D deformation algorithm optimizes the DVF so that the DRRs of I_new will match the cone-beam projections in the intensity domain (Fig. 1 (A)). We call I_new an estimated CBCT image, to reflect the fact that it is updated from I_prior (either CT or CBCT) with the guidance from new cone-beam projections. The same naming approach has been used in previous 2D-3D deformation studies [11, 12, 15].

The deformation field DVF is defined on the voxel grid of the new image I_new and pointed to the prior image I_prior For differentiation, we further denoted it as DVF_forward. For Bio-CBCT-est we need to perform biomechanical modeling on the prior image’s organ of interest (liver in this study). It necessitates us to solve concurrently an inverse deformation field DVF_inverse, which is defined on the voxel grid of the prior image I_prior and pointed to the new image I_new. Thus for Bio-CBCT-est, we enforced a symmetric, dual-directional objective function to optimize DVF_forward and DVF_inverse concurrently:

$$\mathit{DV}{\mathit{F}}_{\mathit{forward}}=argmi{n}_{\mathit{D}\mathit{V}{\mathit{F}}_{\mathit{forward}}}\left\{\begin{array}{c}{\Vert \left(a*\mathcal{A}{I}_{prior}\left(\mathit{x}+\mathit{D}\mathit{V}{\mathit{F}}_{\mathit{forward}}\right)+b\right)-P\Vert }_2^2+\frac{\omega }{2}*E\left(\mathit{D}\mathit{V}{\mathit{F}}_{\mathit{forward}}\right)\\ +\Vert \mathcal{A}\left[\left(I_{prior}\left(\mathit{x}+\mathit{D}\mathit{V}{\mathit{F}}_{\mathit{forward}}\right)\right)(\mathit{x}+\mathit{D}\mathit{V}{\mathit{F}}_{\mathit{inverse}})\right]-P_{prior}{\Vert }_2^2+\frac{\omega }{2}*E\left(\mathit{D}\mathit{V}{\mathit{F}}_{\mathit{inverse}}\right)\end{array}\right\}$$ (2)

In Eq. 2, $\mathcal{A}$ denotes the projection matrix that generates DRRs with imaging geometry matched to the cone-beam projections. P denotes all the cone-beam projections used for the estimation. The sum of squared intensity differences [16] is used as the metric to measure the differences between the DRRs and the cone-beam projections (P) over various angles. a and b are intensity scaling and shift factors to account for the inherent, non-deformation-induced intensity mismatch between DRRs and on-board projections, which are computed using least-squares-based fitting. In addition to the intensity-matching term, the E(*) term in Eq. 2 defines the deformation energy in quadratic forms [13]. The E(*) term is minimized to regularize the smoothness of the deformation vector field. It also serves the purpose of reducing the deformation vector field solution space to achieve stable and fast convergence. The intensity-matching term and the energy term are balanced by the energy weighting factor ω, which is empirically set to 0.05 based on previous studies [13, 21, 22]. P_prior in Eq. 2 denotes the projections generated from I_prior as counterparts to the onboard projections, serving to enforce the projection matching in the inverse direction. In this study, we set DVF_inverse as the negative of DVF_forward, a simple, validated strategy that enables fast optimization [21]. The gradient of the objective function in Eq. 2 can be explicitly calculated, thus the objective function can be conveniently optimized through the nonlinear conjugate gradient descent algorithm. More implementation details of the algorithm can be found in [13].

As shown, the DVF_forward and DVF_inverse can be solved after optimizing the intensity-driven objective function in Eq. 2. However, because of their limited accuracy in low-contrast regions with insufficient intensity variations, the solved DVFs need to be regularized and optimized using the following biomechanical modeling step.

II.B. Biomechanical modeling

There is currently no consensus about the “optimal model” for biomechanical modeling of biological tissues. In this study, we describe the liver using the Mooney-Rivlin material model, a hyper-elastic biomechanical model that is often applied to biological soft tissues [16, 23, 24]. Based on the strain energy density function of the Mooney-Rivlin model, the intra-liver DVF can be solved for a liver mesh of tetrahedral elements, with boundary conditions provided by DVFs of 2D-3D deformation (Fig. 1(B)).

Based on liver contours segmented from the prior image I_prior, a liver mesh composed of tetrahedral elements is generated (Fig. 1(B)). The actual number of nodes in the mesh vary among patient cases, depending on the liver volume. On average we used around ~4000 nodes for the liver volume. The intensity-driven DVF_inverse solved by 2D-3D deformation at the liver boundaries is fed as the boundary condition for finite element analysis, to regularize and fine-tune the intra-liver DVF of the tetrahedral elements. Since 2D-3D deformation has been validated to work effectively at high-contrast regions such as organ boundaries [11, 12, 25], the DVF solved by 2D-3D deformation at higher-contrast liver boundaries is well-suited to serve as the boundary condition to fine-tune the DVF at low-contrast regions including the liver parenchyma. We connected image voxels to the tetrahedron element via the barycentric coordinates [26]. An image voxel is considered to be within a tetrahedron element only if all the corresponding barycentric coordinates (four in total) of the voxel in the tetrahedron are nonnegative. If none such tetrahedron element exists, we select the one closest to the voxel. The image voxel’s DVF is then the weighted DVFs of the four nodes of the matched tetrahedron element.

II.C. The whole iterative workflow of Bio-CBCT-est

Using a prior high-quality CT or CBCT image and cone-beam projections, the Bio-CBCT-est technique applies the 2D-3D deformation step to generate a pair of intensity-driven DVFs: DVF_inverse and DVF_forward. This DVF_inverse is fed as the input for the biomechanical modeling step to yield a biomechanically-corrected DVF. The biomechanically-corrected DVF is further fed back into 2D-3D deformation as a new initial DVF_inverse for further optimization and fine-tuning, and the output results are assessed for convergence based on the projection matching term. Bio-CBCT-est iteratively optimizes and regularizes the DVFs back and forth between the 2D-3D deformation step and the biomechanical modeling step until it meets the convergence criteria (the absolute change of the projection intensity matching term < 0.005 * the previous projection intensity matching term), which converges in around 10–15 iterations. After convergence, the final DVF_inverse and DVF_forward are obtained with the estimated CBCT image (generated by deforming the prior image using the final DVF_forward). The workflow applies the same way when estimating 4D-CBCT images at different phases, which can be performed in parallel.

II.D. Evaluation

To evaluate the accuracy of Bio-CBCT-est, we retrospectively studied seven liver cancer patient cases. We obtained three of these cases from the ITK medical image open library (http://midas.kitware.com/community/view/47). The other four patients were treated at our institute, with this study conducted under an institutional review board protocol. Four of the seven liver cancer patients (patients 1–4) have 10-phase 4D-CT sets acquired with an injected contrast agent to enhance visualization. The other three patients (patients 5–7) have contrast-enhanced CT images at the end-inspiration (0%) and the end-expiration (50%) phases only. We used each patient’s end-inspiration phase (0%) CT as the high-quality prior image and simulated sparse-view cone-beam projections from the other “target” CT phases for CBCT estimation. For one of the patients (patient 4), we have two 4D-CTs acquired, one of which was used to evaluate Bio-CBCT-est for inter-scan image estimation. We used the end-inspiration phase (0%) of one 4D-CT set (Pa4–1) as the prior image to estimate the other 4D-CT set (Pa4–2). Note that Bio-CBCT-est does not use any motion information from 4D-CT for 4D-CBT estimation, and is immune to potential motion pattern differences between the 4D-CT and the to-be-solved 4D-CBCT in real applications. To simulate projections that are best matched to the clinical projections, we used a GPU-accelerated Monte-Carlo approach [27] previously developed and validated against the clinically-benchmarked EGSnrc package [28]. This Monte-Carlo package (gDRR) has been used in multiple studies to simulate projections matched to the real, clinical counterparts [29–32]. The photoelectric absorption, Compton scattering and Raleigh scattering effects were all included in the simulations of photon interactions with matter. A realistic detector response curve was included in the projection simulation. In addition to the primary and scatter signals, the Monte-Carlo package also simulated noise signals calibrated with a real CBCT scanner. More detailed simulation processes and validations can be found in [27]. The projections were generated to contain 512 × 384 pixels (0.776 mm x 0.776 mm in dimension per pixel), with 120 kVp peak energy and 80 mA/10 ms exposure per projection. The source-to-axis distance was simulated as 100 cm and the detector-to-axis distance was simulated as 50 cm.

We simulated different numbers of projections, including 5, 10, and 20, to evaluate Bio-CBCT-est’s potential for imaging dose reduction. For three of the patients (patients 1, 6 and 7), the liver tumors were difficult to contour even with contrast enhancement. Using the tumor for evaluation will introduce additional contouring uncertainties and bias the evaluation. Thus for those patients, we contoured the liver cysts instead, obtaining a more accurate ‘gold-standard’ to assess the contour propagation accuracy. Since Bio-CBCT-est solves deformation and motion within the whole liver, the anatomical sub-structures within the liver should all provide a good reference to evaluate the deformation and motion estimation accuracy. We contoured the tumor/cyst volumes from the prior images of all the patients to facilitate DVF-driven tumor/cyst contour propagation. We also manually contoured the tumor/cyst volumes on each patient’s “target” CT reference phase images to evaluate the accuracy of the automatically propagated tumor/cyst contours by Bio-CBCT-est. Quantitatively, we compared the automatically propagated tumor/cyst contours at each phase to their manual counterparts using the DICE similarity index:

$$DICE=2*\frac{V_{Automatic}\cap V_{Manual}}{V_{Automatic}+V_{Manual}}$$ (3)

The V_Automatic symbol denotes the automatic tumor/cyst contour estimated through DVF-driven contour propagation. The V_Manual symbol denotes the tumor/cyst volume manually contoured on the “target” CT reference phase images. The DICE index calculates the degree of geometrical and volumetric match between the two volumes, a metric frequently applied in radiotherapy studies [33]. The DICE value ranges from 0 to 1, with 1 indicating a perfect match. Besides DICE, we also calculated the voxel-wise Pearson cross-correlation (CC) coefficient of the area enclosed by the automatic tumor/cyst contour and the manual tumor/cyst contour, which is defined as:

$$CC=\frac{{\mathrm{\Sigma }}_x\left(I_{new}(x)-\overline{I_{new}(x)}\right)*\left(I_{ref}(x)-\overline{I_{ref}(x)}\right)}{\sqrt{{\mathrm{\Sigma }}_x{\left(I_{new}(x)-\overline{I_{new}(x)}\right)}^2}*{\sqrt{{\mathrm{\Sigma }}_x\left(I_{ref}(x)-\overline{I_{ref}(x)}\right)}}^2},x\in V_{Automatic}\cup V_{Manual}$$ (4)

I_new denotes the deformed image (Eq. 1) and I_ref denotes the “target” CT reference image. x denotes the voxel coordinates within the union region of V_Automatic and V_Manual. We use the union region to account for the mismatches between V_Automatic and V_Manual. In addition to DICE and CC, we calculated the center-of-mass-error (COME) and the bidirectional Hausdorff distance (HD) between the automatically propagated tumor/cyst contour and the manual contour by Eqs. 5 and 6:

$$COME=\sqrt{{(CO{M}_x^{Automatic}-CO{M}_x^{Manual})}^2+{(CO{M}_y^{Automatic}-CO{M}_y^{Manual})}^2+{(CO{M}_z^{Automatic}-CO{M}_z^{Manual})}^2}$$ (5)

$$HD=\max ({\max }_{a\in V_{Automatic}}{\min }_{b\in V_{Manual}}\Vert a-b\Vert ,{\max }_{b\in V_{Manual}}{\min }_{a\in V_{Automatic}}\Vert b-a\Vert )$$ (6)

The COM symbol denotes the center-of-mass coordinates, with subscripts denoting the coordinates along the three Cartesian axes: x, y, and z. In Eq. 6, a denotes points within V_Automatic, and b denotes points within V_Manual. The COME and HD metrics calculate the overall distance between two volumes, an important indicator for on-board image guidance accuracy. To better benchmark the efficacy of Bio-CBCT-est, we also compared its results with those from the intensity-driven 2D-3D deformation technique.

To further demonstrate that our technique can be applied towards real clinical projections for inter-fractional tumor localization, we extracted the clinical cone-beam projections of patient 4, which were acquired for 3D CBCT imaging on an Elekta Synergy XVI system (Elekta AB, Stockholm, Sweden). The projections were acquired of 512 × 512 pixels, with each pixel measuring 0.8 mm x 0.8 mm in dimension. The source-to-axis distance is 100 cm and the detector-to-axis distance is 53.6 cm. The acquisition used 120 kVp x-ray energy, with an exposure of 40 mA/40 ms per projection. We sorted all the projections (~680 projections) into 10 phase bins by the Amsterdam Shroud technique [34], and used Bio-CBCT-est to estimate a 10-phase 4D-CBCT image set. Qualitatively, we compared the solved 4D liver tumor motion of Bio-CBCT-est against that solved by the 2D-3D deformation technique, with the 4D-CT liver tumor motion as a reference. In the end, to further evaluate the clinical feasibility of our technique quantitatively, we conducted an additional deformable liver phantom study. We designed and constructed a motion and deformation-enabled liver phantom for this study. In the liver phantom, we implanted small metallic ball bearings (BBs) to track the intra-liver motion (‘gold-standard’), and compared the tracked ‘gold-standard’ motion to that solved by our method. We exported a patient’s liver contour and 3D-printed a liver shell based on the patient’s liver contour. A commercial liquid silicone (EcoFlex 00–30, Smooth-on Inc., Macungie, PA) was poured into the shell and cured into a solid, elastic liver (Fig. 2. (A) and (B)). The liver phantom can be compressed and stretched to large extents and rebound to its original shape and size without tearing, serving as a deformable liver phantom. We inserted 9 BBs into the liver phantom at different locations to use as motion landmarks. The liver phantom was housed inside a body shell, with one end touched by a moveable Styrofoam plate (Fig. 2. (C)). The body shell was then mounted onto an in-house motion platform (Fig. 2. (D) and (E)) which drives the motion and deformation of the soft liver phantom, through pressing the Styrofoam plate using a rod moving with programmed trajectories.

Figure 2.

(A). Anterior view of the soft, elastic liver phantom. (B). Posterior view of the liver phantom. (C). A hard body shell to house the liver. (D). The in-house motion platform. (E). The whole motion-enabled deformable liver phantom platform.

We acquired a CBCT scan of the relaxed liver phantom (phase 0%) on a LINAC (TrueBeam, Varian Medical Systems, Palo Alto, CA), which serves as the prior image. And we acquired two new CBCT scans of the liver phantom at phase 25% and phase 50%, corresponding to the mid-motion position and max-motion position of the liver phantom as driven by the motor system. The projections of the new CBCT scans were extracted, down-sampled and fed into the Bio-CBCT-est and the 2D-3D deformation algorithms for new CBCT estimation. Before the CBCT estimation, in these sparse projections we removed the BBs to assess the algorithms in solving intra-liver DVFs at low-contrast regions without the BBs’ guidance. On the other hand, the BB locations on the fully-sampled, clinically-reconstructed phase 0%, phase 25% and phase 50% CBCT scans were manually tracked to derive the ‘gold-standard’ intra-liver DVFs. The solved DVFs by the Bio-CBCT-est and the 2D-3D deformation techniques were compared against the ‘gold-standard’ DVFs for evaluation.

III. RESULT

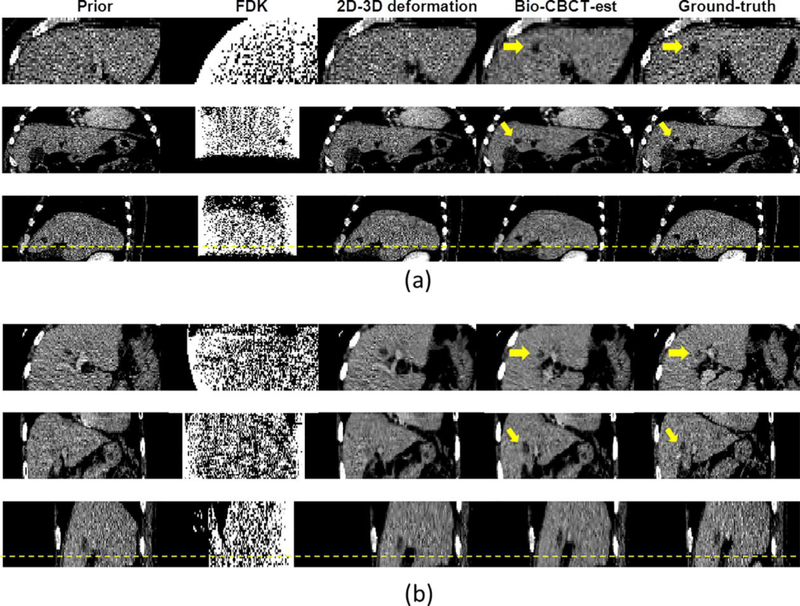
The clinical FDK algorithm generated CBCT images with excessive artifacts that prevent accurate tumor localization, because of the 20 sparse-view projections used for reconstruction. In contrast, the 2D-3D deformation and Bio-CBCT-est algorithms preserved the high-quality information from the prior CT volume through the DVF-driven image estimation approach (Fig. 3). However, 2D-3D deformation did not accurately deform the low-contrast tumor regions. By comparison, the Bio-CBCT-est technique deformed low-contrast tumor regions that matched better with the “target” CT reference image. Note that both cases in Fig. 3 show the most challenging estimation scenarios, where the prior (0%) and “target” (50%) CT volumes have the greatest deformation.

Figure 3:

From left to right: three-view slice cuts of the prior CT image at phase 0%, the CBCT image reconstructed by the clinical Feldkamp-Davis-Kress (FDK) algorithm at phase 50%, the CBCT image estimated by 2D-3D deformation at phase 50%, the CBCT image estimated by Bio-CBCT-est at phase 50%, and the “target” CT reference image at phase 50%. The CBCT reconstructions/estimations used 20 Monte-Carlo projections simulated from the “target” CT reference image. The arrows point to the tumor regions. The images are from (a) patient 3 and (b) patient 4.

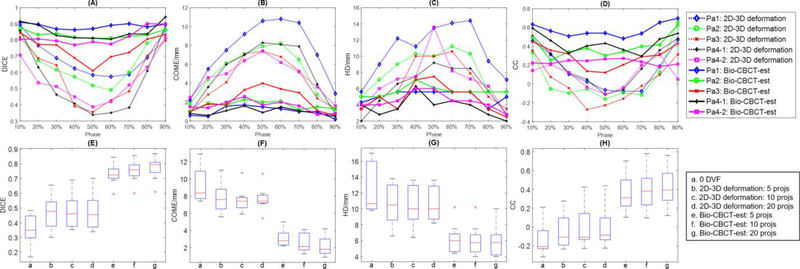
Fig. 4 (A)-(D) plots the DICE, COME, HD and CC metrics for patients 1–4 at phases 10–90%. Fig. 4 (E)-(H) shows the boxplots of DICE, COME, HD and CC metrics for patients 1–7 at phase 50%, using different numbers of projections (5, 10, or 20). In each boxplot, the upper edge, the central line and the lower edge of the box represent the 75 percentile (Q3), median and 25 percentile (Q1) of the data, respectively. The lower whisker extends to the datum no smaller than Q1–1.5 × (Q3 – Q1), and the upper whisker extends to the datum no larger than Q1–1.5 × (Q3 – Q1). The ‘+’ in the plots are outliers outside the whiskers. The same setup applies to all boxplots in this study. For phase 50%, the “target” CT volume has the greatest deformation from the prior image, which demonstrates the estimation accuracy for the most challenging scenario of each patient. Even when enhanced by contrast agents, the liver tumor/cyst contrast in 2D cone-beam projections was still limited, and the sparse-view projection-based 2D-3D deformation failed to deform the tumor/cyst volume to the correct locations. When applied to estimate all 9 respiratory phases, the Bio-CBCT-est technique automatically propagated liver tumor/cyst contours with significantly improved DICE values as compared to the intensity-driven 2D-3D deformation technique (<10^–8 by Wilcoxon signed-rank test) (Fig. 4 (A)). Substantially improved results can also be observed for the COME (Fig. 4 (B), HD (Fig. 4 (C)), and CC (Fig. 4 (D)) metrics. The accuracy of tumor contour propagation towards intra-scan phase images (Pa4–1) and inter-scan phase images (Pa4–2) is comparable for Bio-CBCT-est. Note that the CC metric is consistently lower for Pa4–2 than Pa4–1, mostly due to the inter-scan contrast wash-out in Pa4–2. In general, larger deformation from the prior image leads to larger errors in tumor localization (Fig. 4 (A)-(D)). Increasing the number of projections used for estimation helped to improve accuracy for Bio-CBCT-est (Fig. 4 (E)-(H)). Using 20 projections, Bio-CBCT-est increased the average DICE value from 0.48 (2D-3D deformation results) to 0.77, reduced the average COME from 7.7 mm to 2.2 mm, reduced the average HD from 10.6 mm to 5.9 mm, and increased the average CC from −0.004 to 0.422. The CC results in general appear low in our study, which is mostly due to the homogeneity of the liver region. Without sufficient intensity variations to establish the cross-correlation, CC is largely affected by the random noise in the liver. Thus a small displacement will lead to a substantial CC decrease. To benchmark the true performance of Bio-CBCT-est, we simulated a scenario of shifting the ‘gold-standard’ CT image in the longitudinal direction by one voxel (2 mm), and re-calculated the CC results. After the one voxel shift, the average CC between the shifted ‘gold-standard’ CT and the original ‘gold-standard’ CT reduced from 1 to 0.425, which is very close to the result of Bio-CBCT-est by using 20 projections (0.422). The results suggest that Bio-CBCT-est can localize the tumor to an accuracy of around one voxel (2 mm) by using 20 projections, which is also consistent with the average COME result (2.2 mm).

Figure 4:

(A)-(D). Plots of the DICE, COME, HD, and CC metrics. Results of two methods (2D-3D deformation and Bio-CBCT-est) are shown for patients 1–4 (patient 4 has two image sets) at different phases (10%−90%), by using 20 Monte-Carlo projections simulated from 4D-CT. (E)-(H). Boxplots of the DICE, COME, HD, and CC metrics. Results of two methods (2D-3D deformation and Bio-CBCT-est) are shown for patients 1–7 at phase 50%, by using 5, 10, or 20 Monte-Carlo projections simulated from the “target” CT reference image at phase 50%.

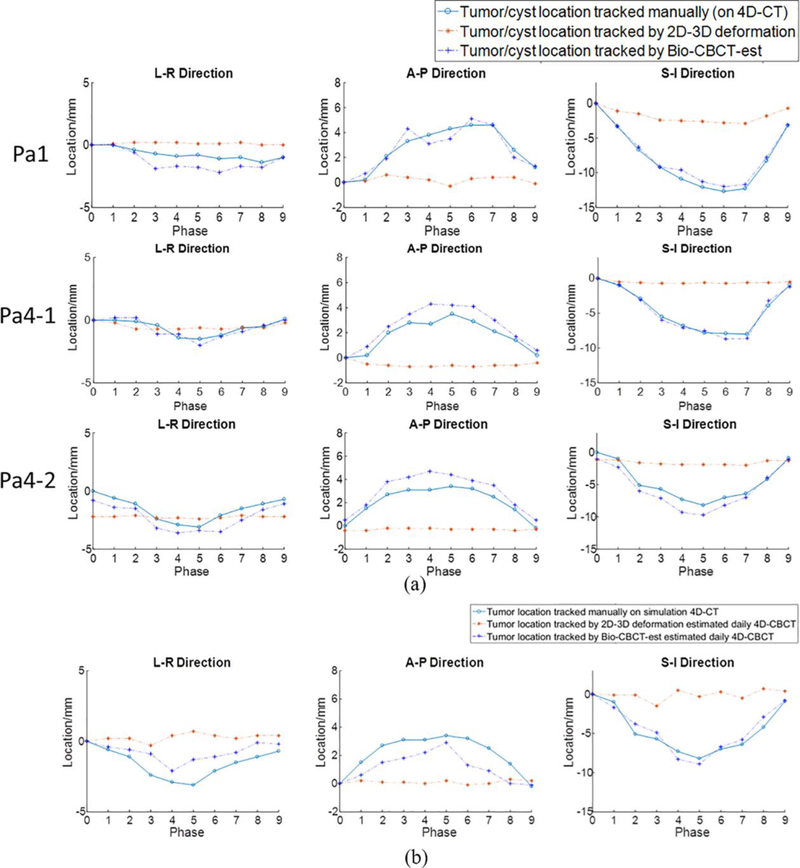
Fig. 5 compares the localization of the contours at different phases between manual contouring, Bio-CBCT-est based propagation, and 2D-3D deformation based propagation. The trajectories were shown along the left-right (LR), anterior-posterior (AP), and superior-inferior (SI) directions, respectively. The tumors/cysts localized by Bio-CBCT-est matched well with those localized by manual contouring on 4D-CT reference images, especially along AP and SI directions (Fig. 5 (A)). In Fig. 5 (B), compared to the tumor motion curve solved by 2D-3D deformation, the tumor motion curve solved by Bio-CBCT-est was closer to that observed during 4D-CT acquisition. For this patient (Patient 4), we used abdominal compression to reduce motion and improve motion reproducibility between the simulation and the treatment. A substantial discrepancy as seen in Fig. 5 (B) between the 4D-CT trajectory and the on-board trajectory solved by 2D-3D deformation is less likely.

Figure 5:

(A). Comparison of tumor/cyst centroid locations at different phases between manual localization (based on manually contoured tumors on 4D-CT reference images), automatic localization by 2D-3D deformation solved DVFs, and automatic localization by Bio-CBCT-est solved DVFs. The results are for patients 1 and 4 (rows 1–3), using 20 Monte-Carlo projections simulated from 4D-CT for automatic localization. Patient 4 has two 4D-CT sets: Pa4–1 shows the results of intra-scan localization, and Pa4–2 shows the results of inter-scan localization. (B). Comparison of tumor centroid locations at different phases between manual localization on simulation 4D-CT, automatic localization by 2D-3D deformation solved DVFs, and automatic localization by Bio-CBCT-est solved DVFs. Clinically acquired projections of Patient 4 were used for automatic localization. The manual localization was based on the 4D-CT set of Pa4–2.

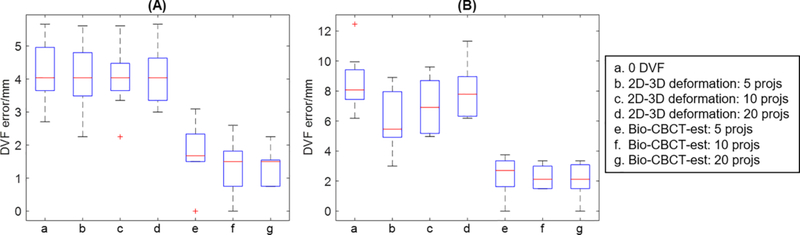
Fig. 6 shows the results of the deformable liver phantom study for phase 25% (Fig. 6 (A)) and phase 50% (Fig. 6 (B)) of the liver phantom. Bio-CBCT-est accurately estimated the intra-liver DVFs of the liver phantom, using cone-beam projections acquired on a LINAC. By 20 projections, the mean (s.d.) Euclidean DVFs errors of Bio-CBCT-est were 1.3 mm (0.5 mm) and 2.1 mm (1.1 mm) for phase 25% and phase 50% of the liver phantom, respectively. The corresponding errors of 2D-3D deformation were 4.1 mm (0.9 mm) and 8.0 mm (1.8 mm), respectively. Increasing the number of projections led to better Bio-CBCT-est results, which, however, were not observed for 2D-3D deformation.

Figure 6.

Boxplots of Euclidean errors of solved intra-liver DVFs for (A). phase 25% and (B). phase 50% of the liver phantom by different techniques, as indicated by (a-g) in each subfigure. Each boxplot contains results of 9 BBs implanted at different locations of the liver phantom.

IV. DISCUSSION

In contrast to the current x-ray based liver imaging techniques, the Bio-CBCT-est technique can estimate high-quality 4D-CBCT liver images with full volumetric and motion (deformation) information. By combining intensity-driven 2D-3D deformation with physics-driven DVF optimization through biomechanical modeling, Bio-CBCT-est offers the possibility of accurate 4D localization of liver tumors by using only limited on-board projections with no contrast enhancement needed. The liver tumor areas estimated by Bio-CBCT-est matched well with those on “target” CT reference phase images through visual evaluations (Fig. 3). The corresponding quantitative evaluations showed strong agreements between automatically propagated tumor/cyst contours estimated by Bio-CBCT-est and manual CT contours (Fig. 4, Fig. 5). By biomechanical modeling, the Bio-CBCT-est technique does not rely on the limited intra-liver intensity information to solve intra-liver DVFs, which provides consistent and stable results. Increasing the number of projections led to better Bio-CBCT-est results, which, however, were not observed for 2D-3D deformation (Fig. 4, Fig. 6). The lack of an accurate intra-liver deformation model may have contributed to the amplified errors seen in 2D-3D deformation when more projections were used for estimation.

In this study, we used the liver boundary DVF solved by 2D-3D deformation as the boundary condition, to drive finite element analysis based biomechanical modeling to solve the intra-liver DVF. The liver boundary, especially that on the cranial side at lung-liver interfaces, has much higher contrast than inner liver parenchyma to allow accurate 2D-3D deformation [11]. The caudal liver boundary, though higher in contrast than the liver parenchyma, has less contrast than the cranial side boundary and potentially leads to less accurate boundary DVF from 2D-3D deformation. Despite this potential inaccuracy, in our study the Bio-CBCT-est technique provided substantially improved tumor localization as compared to the intensity-driven technique, with the average DICE around 0.77, COME around 2.2 mm, and HD less than 6 mm by using only 20 projections. Nonetheless, we believe that the accuracy of Bio-CBCT-est can further improve after introducing methods to boost the lower-liver boundary deformation accuracy. We performed a pilot study by using motion modeling to further improve the DVF accuracy at the caudal liver side [35]. By motion modeling, the DVF accuracy at the caudal liver boundary further improves, leading to more accurately localized liver tumor. However, the method relies on a prior motion model built on a 4D-CT set, which is prone to errors caused by mismatched motion patterns between 4D-CT and on-board acquisition. The improvement is neither much substantial. Future studies investigating methods to further enhance the lower boundary deformation accuracy are warranted.

In this study, we used liver 4D-CTs with injected contrast agents for evaluation, which allowed us to visualize and manually contour the tumor/cyst volumes of each CT phase image. 4D cone-beam projections were simulated from these 4D-CT images, and used for 4D-CBCT estimation. Since the 4D cone-beam projections are generated from the 4D-CT, the motion in the corresponding 4D-CBCT should match perfectly with that in the 4D-CT. Thus we can compare our solved 4D-CBCT motion using the simulated cone-beam projections against the ‘gold-standard’ 4D-CT motion for evaluation. To better evaluate Bio-CBCT-est for its clinical applicability, we used a Monte-Carlo based simulation approach [27] to enable fast, realistic cone-beam projection simulation from the 4D-CTs. Currently the major obstacle of using real CBCT projections is the lack of a correspondingly high-quality, on-board 4D-CBCT as the ‘gold-standard’ reference to evaluate the accuracy of the estimated 4D-CBCT set. To evaluate the estimated 4D motion of the liver tumor, we would need a contrast-enhanced, fully-sampled 4D-CBCT to reveal the low-contrast liver tumor volumes at each respiratory phase. However, in current clinical practice, contrast agent is not administered for CBCT imaging on daily fractional treatments (contrast administration is only performed in CT simulation). In addition, fully-sampled high-quality 4D-CBCT imaging would need substantially more projections than traditional 3D-CBCT [36]. Due to these limitations, it is challenging to perform a comprehensive clinical 4D-CBCT study at the current stage. Another potential evaluation scheme is to compare the liver tumor motion trajectory on the 4D-CBCT estimated by Bio-CBCT-est against the averaged motion curve of the implanted fiducial markers solved from the same projection set [6].

Unfortunately, our institution currently does not implant fiducial markers into liver cancer patients and does not have access to such data. To conduct a preliminary study, we extracted the clinical projections acquired for one patient’s 3D CBCT, sorted them into 10 phases using the Amsterdam Shroud technique, and used both Bio-CBCT-est and 2D-3D deformation for 4D-CBCT estimation (Fig. 5 (B)). The Bio-CBCT-est solved liver tumor location trajectory was closer to that observed in 4D-CT images than 2D-3D deformation solved tumor location trajectory. We used abdominal compression on this patient to reduce motion and improve motion reproducibility between the simulation and the treatment. A drastic tumor trajectory change as seen in the curve solved by 2D-3D deformation is less likely. However, we acknowledge that without ‘gold-standard’ on-board tumor location trajectory, quantitative evaluation and definitive conclusions cannot be drawn. Considering the lack of a ‘gold-standard’ for the preliminary clinical patient study, we also designed an in-house deformable liver phantom with implanted BBs to evaluate the intra-liver DVFs solved by Bio-CBCT-est quantitatively. The results further validated Bio-CBCT-est as an accurate method to solve intra-liver DVFs at low-contrast regions (Fig. 6).

In this study, for three patients we localized the liver cysts instead of the liver tumors. Localizing the actual liver tumors rather than the liver cysts will be a better choice, as the liver tumors are more relevant to treatments. Unfortunately, for the three patients the liver tumors are challenging to contour with poor visibility. The physicians involved in our study concerned about the potential biases of using them as the study object and suggested using cysts as surrogates. Although not tumors, these cysts are well within the liver and of adequate sizes/locations to represent intra-liver motion/deformation. They also serve well to evaluate our method in solving the full intra-liver DVF (not only limited to that around the tumors). Future studies involving more patients are warranted to evaluate the estimation accuracy of Bio-CBCT-est at different intra-liver regions, especially the tumor regions.

In this study, we modeled the liver as a homogeneous organ with consistent biomechanical properties across tetrahedron elements for simplicity and achieved encouraging results. Such approximations have been found adequate in other biomechanical modeling studies [17, 18, 37]. In reality, the material composition and elasticity may vary between different liver lobes and between the liver and the tumor. Future studies of liver heterogeneity may improve the estimation accuracy of the Bio-CBCT-est technique, though at the cost of increased complexity and more heterogeneity among patients. MRI can potentially serve as a good surrogate to differentiate the components of the liver and enable customized area-specific biomechanical modeling. The elastic properties of cirrhotic livers may also differ from normal livers. Future studies could examine corresponding patient cases to determine the most appropriate biomechanical modeling parameters.

With the promising results from this study, Bio-CBCT-est can be readily applied for further clinical evaluation in a prospective patient study, which is currently being planned in our institution. We aim to compare its accuracy with the current clinically-applied, surrogates-based liver tumor localization techniques. We will use the fiducial marker-based localization technique as the ‘gold-standard’ for reference. We will implant three fiducial markers around the liver tumor to minimize the effect of marker migration [38]. In the prospective study, we will also quantitatively evaluate the accuracy of using a prior contrast-enhanced CT to estimate on-board CBCTs from non-contrast-enhanced projections, as the objective function of Bio-CBCT-est might be affected by the contrast signal change. If we find the impact to be significant in some scenarios, its effect can be conveniently minimized by overriding the HU values of the contrast-enhanced CT. In our retrospective patient study, encouraging results are achieved by using very sparse projection sets (5–20 projections per phase). In the prospective clinical study, patient breathing irregularity and sorting errors can cause more motion artifacts for sparser projections sets, which may increase the number of projections required per phase for more reliable tumor localization and needs to be further investigated. In these scenarios, motion management techniques like respiration coaching and audio-visual feedback can help to regularize the breathing signal [39]. With validated accuracy from the prospective study, Bio-CBCT-est will make a non-invasive, contrast-agent-free technique for accurate on-board liver tumor localization.

Highlights.

Delivering effective radiation therapy for liver requires daily tumor localization at each treatment, but the respiration-induced liver motion and the low tumor visibility complicate this task in the clinic.

We have developed a biomechanical modeling-guided cone-beam CT (CBCT) estimation technique. It can generate 4D liver CBCT images and corresponding deformation vector fields (DVFs) from deforming a prior high-quality liver CT or CBCT image.

The DVFs enable automatic 4D liver tumor localization by propagating the liver tumor contour from the prior image.

Our study demonstrates that the new method can accurately localize liver tumors in 4D to ~ 2 mm in center-of-mass-errors.