Robust Network-Based Regularization and Variable Selection for High-Dimensional Genomic Data in Cancer Prognosis

Abstract

In cancer genomic studies, an important objective is to identify prognostic markers associated with patients’ survival. Network-based regularization has achieved success in variable selections for high-dimensional cancer genomic data, due to its ability to incorporate the correlations among genomic features. However, as survival time data usually follow skewed distributions, and are contaminated by outliers, network-constrained regularization that does not take the robustness into account leads to false identifications of network structure and biased estimation of patients’ survival. In this study, we develop a novel robust network-based variable selection method under the accelerated failure time (AFT) model. Extensive simulation studies show the advantage of the proposed method over the alternative methods. Two case studies of lung cancer datasets with high dimensional gene expression measurements demonstrate that the proposed approach has identified markers with important implications.

2. Introduction

In cancer research, profiling studies have been extensively conducted to identify prognostic markers that may contribute to the development and progression of cancer. Important prognostic markers have the potential to shed deep insight in elucidating the genetic basis of cancer, and provide assistance in cancer prevention, diagnosis and treatment selection. The generation of unprecedented amount of high dimensional genomics data from the high-throughput profiling studies has led to the development of extensive regularized variable selection methods(Fan and Lv (2010)). The genomics features, such as gene expressions and single nucleotide polymorphism (SNPs), are treated as variables within the regularization (or penalization) framework. As the correlations among genomics features have been widely recognized, multiple studies have developed network based regularization methods to accommodate interconnections among these features, including gene expressions (Li and Li (2008)), SNPs (Ren et al. (2017)), copy number variations (Peng et al. (2012); Shi et al. (2015)) and DNA methylations (Sun and Wang (2012)).

The network based methods have unique strength to effectively capture correlations by incorporating prior biological information via the network (or graph) structure, where the vertices of networks are the genomic features and the edges of the networks denote certain regulatory relationship among the features. Incorporation of the network structure in regularized variable selection has led to significant improvement in both identification accuracy and predictive performance, as demonstrated in aforementioned studies, as well as many other studies. Nevertheless, these methods have limitations. First, network–constrained regularization methods under survival outcomes have not received much attention. As markers identified under patients’ survival have important implications in cancer prognosis, the network–based regularized variable selection will improve accuracy in both identifying prognostic markers and predicting patients’ survival. However, the disease outcome investigated from published studies are mainly continuous (Li and Li (2008); Peng et al. (2012); Shi et al. (2015)), binary (Ren et al. (2017); Sun and Wang (2012); Min et al. (2018)) and multi-nomial (Tian et al. (2014)). Markers identified from these studies, though important, cannot be treated as potential prognostic markers directly. Second, existing network (or graph) based methods lack robust properties, which are critical to accommodate data contamination and long-tailed distributions. In studies that investigate the regulations of between CNVs and gene expressions (Peng et al. (2012); Shi et al. (2015)), as gene expressions may have heavy tailed distributions (especially at high expression levels) or be contaminated, inference of gene regulatory relationship based on non-robust methods might be biased.

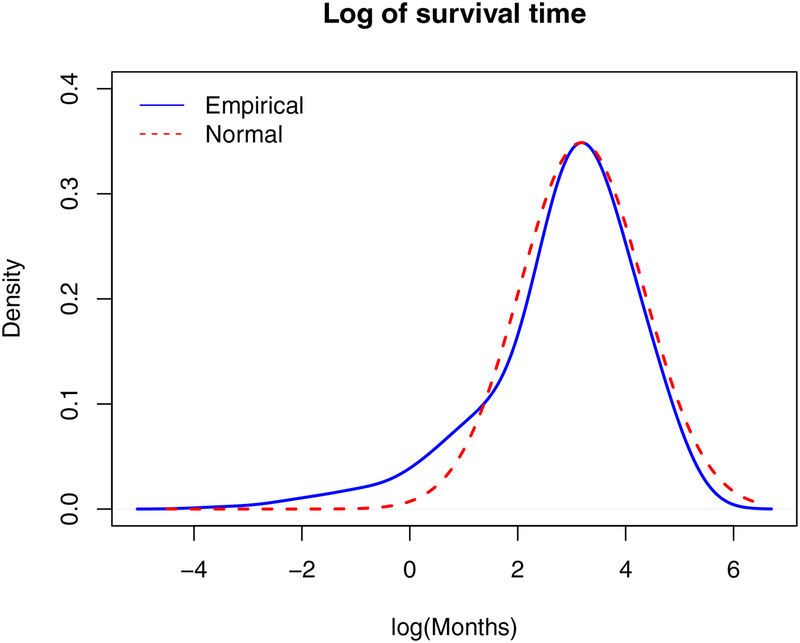
We use the lung squamous cell carcinoma (LUSC) data collected by The Cancer Genome Atlas (TCGA) as a motivating example. For the 461 subjects analyzed in this study, five subjects have survival time 150.13, 151.15, 154.20, 156.54 and 173.69 months, respectively, while the rest 456 subjects have survival times ranging from 0.03 to 139.98 months. Figure 1 shows the plots of both empirical density function of the log survival time as well as the corresponding best-fitted normal density. The deviation from normal is observed. Moreover, the Kolmogorov-Smirnov test yields a pvalue less than 0.01, which suggests a significant difference from normal distribution. Such a pattern may happen for multiple reasons. For example, when multiple cancer subtypes exist, the largest subtype can be viewed as being “contaminated” by small subtypes. Contamination of survival can also be caused by misclassification of causes of death (Rampatige et al. (2013)) and unreliable extraction of survival times from medical records (Fall et al. (2008)). Without taking robustness into consideration, non-robust network based methods will lead to biased estimation and thus false identification of network structure, even in the presence of only one contaminated observation. As shown in Wu and Ma (2015), for high-dimensional genomic data, the robust variable selection methods are still not well developed, which is particularly true for the network–constrained approaches, possibly due to the extra complexity from incorporating network structure to accommodate interconnections among genomic features.

Figure 1:

Distribution of log(survival time) in the TCGA LUSC dataset.

In this article, we propose a robust network–based regularization and variable selection method for high-dimensional genomics data in cancer prognosis. Our method has the following novel features to distinguish itself from existing ones. First, we adopt the least absolute deviation (LAD) loss function to accommodate heavy-tailed distribution and data contamination. Although no robust loss function universally outperforms the rest, the LAD loss function, as a special case of quantile-based loss functions, is especially appealing for high-dimensional data due to its L₁ form (Wu and Ma (2015); Huang et al. (2007); Wu et al. (2018)). Other robust loss functions, including exponential square loss (Wang et al. (2013b)) and rank based loss (Shi et al. (2014); Wu et al. (2015)), do not enjoy such a computational convenience for data with high-dimensionality. Second, as our goal is to robustly identify important genomic signatures while accommodating correlations under survival outcomes, we develop robust network based penalization under the accelerated failure time (AFT) model with Kaplan-Meier weights. The proposed penalty function is of an “MCP + L₁” form, where MCP, the Minimax Concave Penalty, encourages sparsity (Zhang (2010)) and the L₁ term promotes network structure. Besides, although the weighted LAD estimator has been investigated in Huang et al. (2007), the strength of its regularized counterpart has not been fully explored, especially for network structure estimation and identification. Third, we develop an effective algorithm within the coordinate descent framework. On the contrary, the computational cost for many robust variable selection methods are prohibitively high under complicated data and model settings (Wu and Ma (2015)). The advantage of our method over alternatives has been convincingly demonstrated in both simulation studies and two case studies. To the best of our knowledge, identifying important genomic features in cancer prognostic studies through robust penalization by incorporating network structures has not been reported before. It is also noting that our method is not restricted to cancer survival only. Instead, it can be readily extended to other types of response, such as the continuous disease phenotypes.

3. Statistical Methods

We consider the AFT model for cancer prognosis. For high-dimensional genomics data, the AFT model is adopted over the Cox model and other alternatives due to its lower computational cost. From now on, we use gene expression as a representative example of genomics features.

3.1. The LAD Regression for Censored Data

Denote the ith subject by using the subscript i. Let (T_i, X_i, Z_i) (i = 1,…, n) be n independent and identically distributed random vectors, where T_i is the logarithm of survival time, X_i = (x_i1, x_i2…, x_ip)^T is the p–dimensional vector of gene expressions, and Z_i = (z_i0, z_i1…, z_iq)^T is the (q + 1)–dimensional vector of which the first component z_i0 = 1 and the last q components are clinical/environmental covariates. Usually, q and p are of low and high dimensionality, respectively. The AFT model postulates that

$$T_i=Z_i\alpha +X_i\beta +{\epsilon }_i$$

α = (α₀, α₁,…, α_q)^T where α₀ is the intercept and the last q components are the regression coefficients for the clinical covariates. β = (β₁,…, β_p)^T is the regression coefficient vector for the gene expressions, and ε_i is the error term with an unspecified distribution. Denote C_i as the logarithm of the censoring time. Under right censoring, we observe (Y_i, δ_i, Z_i, X_i), where Y_i = min(T_i, C_i), and δ_i = I(T_i ≤ C_i) is the indicator of event. Without loss of generality, we assume that {(Y_i, δ_i, Z_i, X_i), i = 1,…,n} have been sorted with respect to Y_i in an ascending order.

We adopt the Kaplan-Meier weights for censoring. Let ${\widehat{F}}_n$ be the Kaplan–Meier estimator of the distribution function F of T. Then by following Stute and Wang (1993), we have ${\widehat{F}}_n(y)=\sum _{i=1}^n{v}_{i}1\left\{Y_i\le y\right\}$, where the Kaplan–Meier weights v_i (i = 1,…, n.) are defined as

$$v_1=\frac{{\delta }_1}{n},v_i=\frac{{\delta }_i}{n-i+1}\prod _{j=1}^{i-1}{\left(\frac{n-j}{n-j+1}\right)}^{{\delta }_j},i=2,\dots ,n.$$

To accommodate data contamination, consider the weighted LAD loss function

$$L(\alpha ,\beta )=\frac{1}{n}\sum _{i=1}^n{v}_i\left|Y_i-Z_i\alpha -X_i\beta \right|$$ (1)

The robustness comes from the L₁ form of the loss function. For a contaminated observation with Y_i significantly deviating from $Z_i\widehat{\alpha }+X_i\widehat{\beta }$, the predicted value from model (1), the L₁ based loss down-weighs such a deviation, while the non-robust loss, for example, least square based loss, results in a much larger deviation.

3.2. Robust Network-based Penalized Identification

As only a small subset of gene expressions is associated with cancer prognosis, and the total number of gene expressions is much larger than the sample size, identification of important prognostic markers is of a “large p, small n” nature, and can be achieved through regularized variable selection. Consider the regularized loss function:

$$Q(\alpha ,\beta )=L(\alpha ,\beta )+P(\beta ;\mathrm{\lambda },\mathrm{\gamma })$$ (2)

where λ and γ are tuning parameters. A nonzero component of regularized estimate $\widehat{\beta }$ indicates that the corresponding gene expression is associated with cancer prognosis. One possible choice for the penalty function is

$$P(\beta ;\mathrm{\lambda },\mathrm{\gamma })=\sum _{m=1}^p{\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}\left(\left|{\beta }_m\right|\right),$$

where ${\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}(t)={\mathrm{\lambda }}_1{\int }_0^{|t|}{\left(1-\frac{x}{\mathrm{\gamma }{\mathrm{\lambda }}_1}\right)}_{+}dx$ is the Minimax Concave Penalty (MCP) with tuning parameter λ₁ and regularization parameter γ (Zhang (2010)).

The effects of gene expressions are represented by β, the vector of regression coefficients. We impose MCP on β, and components of non-zero regularized estimate suggests that the corresponding gene expressions are associated with cancer prognosis. A major disadvantage of this penalty is that correlations among gene expressions are not considered. Multiple studies, including aforementioned ones, have shown that failure to accommodate correlations results in biased estimation and false identification of important effects. To overcome this issue, we use a network structure to describe the interconnections among gene expressions. In the gene expression network, a node corresponds to a gene expression, and two nodes are connected by the edge if corresponding gene expressions are associated statistically or biologically. We propose the following penalty function to incorporate network information:

$$P(\beta ;\mathrm{\lambda },\mathrm{\gamma })=\sum _{m=1}^p{\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}\left(\left|{\beta }_m\right|\right)+{\mathrm{\lambda }}_2\sum _{1\le m<k\le p}|a_{mk}\Vert {\beta }_m-\text{sgn}\left(a_{mk}\right){\beta }_k|,$$ (3)

where ρ_λ1,γ(·) is the MCP defined above, β_m is the coefficient corresponding to the m-th gene expression and a_mk measures the strength of connection between the m-th and k-th gene expression. The first term of (3) imposes MCP on all the p components of β, thus it encourages sparsity in the regularized estimate. The second term promotes the smoothness among pairwise coefficient profiles of correlated gene expressions. It encourages their regression coefficients to be of similar magnitude. The extent of “encouragement” is adjusted by a_mk. The penalty shares certain similarity with the sparse Laplacian penalty (Huang et al. (2011)). However, it also has remarkable difference due to the L₁ form, which is adopted for the “consistency” purposes with the weighted LAD loss function.

In (3), |a_mk| is the network adjacency which plays a critical role in quantifying the strength of connection between two nodes. We consider the approach from Zhang and Horvath (2005) to specify adjacency. Denote r_mk as the Pearson correlation coefficient between the mth and kth gene expression. Let A = (a_mk, 1 m, k ≤ p) be the adjacency matrix, where $a_{mk}=r_{mk}^{\alpha }\cdot I\left\{\left|r_{mk}\right|>r\right\}$ with α = 5. A properly defined network adjacency measure can keep the sign of r_mk, retain strong correlations and tune down weak ones (that are possibly noises). We choose the power transformation and the value of α following existing studies (Huang et al. (2011); Zhang and Horvath (2005)). We calculate the cuto r based on Fisher transformation z_mk = 0.5log((1 + r_mk)/(1 − r_mk)). If the correlation between mth and kth gene expressions is 0, $\sqrt{n-3}{z}_{mk}$ approximately follows N(0, 1), which can then be adopted to calculate a threshold δ for $\sqrt{n-3}{z}_{mk}$. Then the threshold for r_mk is $r=\text{exp}(2\delta /\sqrt{n-3})-1)/(\text{exp}(2\delta /\sqrt{n-3})+1)$. The network is weighted and sparse. Please refer to Huang et al. (2011) and Zhang and Horvath (2005) for more details. There are alternative ways of constructing network adjacency. For instance, biological information (like pathway) is used to define adjacency in some studies. We conjecture that they are equally applicable. As our objective is not to compare different network constructions, we focus on this specific network structure.

3.3. Computation

Consider the following iterative algorithm:(a) initialize $\widehat{\alpha }$ and $\widehat{\beta }$; (b) update $\widehat{\alpha }$ as the minimizer of (1) with β fixed at $\widehat{\beta }$; (c) update $\widehat{\beta }$ as the minimizer of (2) with α fixed at $\widehat{\alpha }$; (d) iterate step (b) and (c) until convergence. The non-convexity of MCP in the penalty function (3) makes that computation of step (c) particularly challenging. Here, we develop an effective algorithm that borrows strength from MM (majorization-minimization) within the coordinate descent (CD) framework. More specifically, the nonconvex MCP in (3) is replaced by its majorization function to create a surrogate regularized loss function first, then optimization is conducted over the surrogate loss function with respect to one predictor at a time, and cycled through all predictors untill convergence.

We define a majorization function for the MCP function ${\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}(\left|\beta \right|)$ at the d-th iteration (d = 1, 2, …) as

$${\varphi }_{{\beta }_m^{(d-1)}}\left(\left|{\beta }_m\right|\right)={\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}\left(\left|{\beta }_m^{(d-1)}\right|\right)+{\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}^{\prime }\left(\left|{\beta }_m^{(d-1)}\right|+\right)\left(\left|{\beta }_m\right|-\left|{\beta }_m^{(d-1)}\right|\right),m=1,\dots ,p$$

where ${\beta }_m^{(d-1)}$ is the value of β_m at the end of the (d-1)-th iteration, and ${\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}^{\prime }\left(\left|{\beta }_m\right|+\right)$ is the limit of ${\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}^{\prime }\left(t\right)$ as $t\to \left|{\beta }_m\right|$ from the above. ${\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}^{\prime }\left(\left|{\beta }_m\right|+\right)$ exists for all β_m due to the piecewise differentiability of MCP. We can see that

$${\varphi }_{{\beta }_m^{(d-1)}}\left(\left|{\beta }_m\right|\right)\ge {\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}\left(\left|{\beta }_m\right|\right)\text{\hspace{1em} for all }m$$

where the equality holds when ${\beta }_m={\beta }_m^{(d-1)}$. Hence, ${\varphi }_{{\beta }_m^{(d-1)}},m=1,\dots ,p$ majorizes the MCP function ${\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}(\left|\beta \right|)$. Subsequently, the regularized loss function in (2) is majorized at the d-th iteration by

$$Q_{{\beta }^{(d-1)}}(\alpha ,\beta )=L(\alpha ,\beta )+\sum _{m=1}^p{\varphi }_{{\beta }_m^{(d-1)}}\left(\left|{\beta }_m\right|\right)+{\mathrm{\lambda }}_2\sum _{1\le m<k\le p}|a_{mk}\Vert {\beta }_m-\text{sgn}\left(a_{mk}\right){\beta }_k|$$

Next, we update the value of β at the d-th iteration by minimizing the surrogate regularized loss function:

$${\beta }^{(d)}=\underset{\beta }{\text{argmin}}{Q}_{\beta (d-1)}(\alpha ,\beta )$$ (4)

This minimization can be conducted within the coordinate descent framework. With α and β_−m held fixed at the current estimate, we have

$$\begin{gathered} {\beta }_m^{(d)}=\underset{{\beta }_m}{\text{argmin}}\{\frac{1}{n}\sum _{i=1}^n{v}_i|Y_i-Z_i\alpha -\sum _{j\ne m}{X}_{ij}{\beta }_j-X_{im}{\beta }_m|+\sum _{j\ne m}{\varphi }_{{\beta }_j^{(d-1)}}\left(\left|{\beta }_j\right|\right)+{\varphi }_{{\beta }_m^{(d-1)}}\left(\left|{\beta }_m\right|\right)+{\mathrm{\lambda }}_2\sum _{j\ne m}\sum _{j<k\le p}\left|a_{jk}\right|\left|{\beta }_j-\text{sgn}\left(a_{jk}\right){\beta }_k\right|+{\mathrm{\lambda }}_2\sum _{m<k\le p}\left|a_{mk}\right|\left|{\beta }_m-\text{sgn}\left(a_{mk}\right){\beta }_k\right| \\ =\underset{{\beta }_m}{\text{argmin}}\{\frac{1}{n}\sum _{i=1}^n{v}_i|Y_i-Z_i\alpha -\sum _{j\ne m}{X}_{ij}{\beta }_j-X_{im}{\beta }_m|+{\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}^{\prime }\left(\left|{\beta }_m^{(d-1)}\right|+\right)\left|{\beta }_m\right|+{\mathrm{\lambda }}_2\sum _{m<k\le p}|a_{mk}\Vert {\beta }_m-\text{sgn}\left(a_{mk}\right){\beta }_k|\} \end{gathered}$$

Therefore, (4) can be equivalently expressed as a minimization problem for weighted median regression. We re-write (4) as

$${\beta }_m^{(d)}=\underset{{\beta }_m}{\text{ argmin }}\left\{\frac{1}{n+1+p-m}{\sum }_{i=1}^{n+1+p-m}{w}_{im}\left|u_{im}\right|\right\}$$ (5)

where

$$u_{im}^{(d)}=\{\begin{array}{ll}\frac{Y_i-Z_i\alpha -\sum _{j\ne m}^p{X}_{ij}{\beta }_j^{(d-1)}}{X_{im}}-{\beta }_m\hfill & i=1,2,\dots ,n\hfill \\ 0-{\beta }_m\hfill & i=n+1\hfill \\ \text{ sgn }\left(a_{mk}\right){\beta }_k-{\beta }_m\hfill & i=n+2,\dots ,n+1+p-m\hfill \end{array}$$ (6)

and

$$w_{im}^{(d)}=\{\begin{array}{ll}\frac{1}{n}{v}_i\left|X_{im}\right|\hfill & i=1,2,\dots ,n\hfill \\ {\rho }_{{\mathrm{\lambda }}_1,\mathrm{\gamma }}^{\prime }\left(\left|{\beta }_m^{(d-1)}\right|+\right)\hfill & i=n+1\hfill \\ {\mathrm{\lambda }}_2\left|a_{mk}\right|\hfill & i=n+2,\dots ,n+1+p-m\hfill \end{array}$$ (7)

where m and k follow the same definition as in (3). The minimizer of (5) is the weighted median of (n + 1 + p − m) pseudo observations. Similarly, we can update the (q + 1)− dimensional vector α^(d) component-wisely by minimizing the loss function (1) using weighted median regression. Specifically, for each l = 0, …, q, update ${\alpha }_l^{(d)}$ using the weighted median in (1) with β and α_−l held fixed. With fixed tuning parameters, the coordinate descent algorithm is described in Table 1

Table 1:

Coordinate descent algorithm.

Algorithm Coordinate descent for the robust penalized network-based regularization

Initialize d = 0, α(0) and β(0)

Repeat

update α(d+1) component-wisely using weighted median regression

for m = 1, 2, … , p

compute um and wm via (6) and (7)

update ${\beta }_m^{\left(d+1\right)}$ using the weighted median in (5)

m ← m + 1

end for

d ← d + 1

until convergence

Selection of proper tuning parameters is crucial to the proposed method. Here, we have tuning parameters λ₁ and λ₂, as well as a regularization parameter γ. In MCP, γ balances between the concavity and unbiasedness. As suggested by Zhang (2010), Shi et al. (2015) and other studies, in our numerical study, we experiment γ with a sequence of values, including 1.5, 3, 5, 7 and 10, and find that the results not sensitive to the choice of γ. Therefore, we set γ=5. We choose the optimal pair of tuning parameters (λ₁, λ₂) via a two-dimensional grid search on independent testing data sets. That is, we first obtain regularized estimates from training data, then evaluate prediction performance over independently generated testing data. In simulation, the tunings determined from V-fold cross validation are very close to those based on independent testing data, but computationally more intensive. In real data analysis, we use cross validation to choose optimal tuning parameters since independent testing data sets are not available. In both simulation study and case study, convergence has been achieved in a small to moderate number of iterations. We compute the CPU time of running 100 replicates of simulated 300 × 500 gene expression data with AR structure and fixed tuning parameters on a regular laptop. The CPU time in seconds are 53.0 (LAD_Network), 36.1 (LAD MCP), 34.9 (LAD LASSO), 39.1 (Network), 24.3 (MCP) and 24.7 (LASSO), respectively.

To facilitate computation, we implement the proposed method, as well as the alternatives in C++ and provide the R package regnet with detailed documentation and examples (Ren et al. (2018)).

4. Simulation

To demonstrate the utility of the proposed approach, we evaluate the performance through simulation study. In particular, we consider right censored survival data under the accelerated failure time (AFT) model. We generate datasets for different correlation structures and correlation levels, each with 300 subjects. For each subject, we simulate 5 clinical covariates and the expression of 500 genes, from multivariate normal distributions with marginal means equal to zero and variances equal to one. Among the 500 genes, there are 100 clusters with 5 genes per cluster. For the gene expression, we consider three correlation structures. (1) the auto-regression (AR) structure, in which gene i and j within the same cluster have correlation coefficients ${\rho }^{\left|i-j\right|}$, and they are independent cluster–wisely. We consider ρ = 0.5 and 0.8, representing moderate and strong correlation, respectively. (2) banded correlation structure where the ith and jth genes have ρ = 0.5 if |i − j| = 1 and ρ = 0 otherwise. Gene expressions in different clusters are independent. (3) banded correlation structure where the ith and jth genes have correlation coefficient 0.5 if |i − j| = 1, 0.25 if |i − j| = 2 and 0 otherwise. 10% of clusters are randomly selected to have nonzero regression coefficients generated from Unif[0.2, 0.8]. For the clinical covariates, we simply use a multivariate normal distribution with ρ = 0.7 in all scenarios. All clinical covariates have non-zero coefficients generated independently from Unif[0.2, 0.8]. The log event times are generated under the AFT model with random errors from N(0, 1) (Error1), T(1) (Error2), 85%N(0,1) + 15%Cauchy(0, 1) (Error3) or 75%N(0,1) + 25%Cauchy(0, 1) (Error4). The log censoring times are generated from uniform distribution. The average censoring rate is about 30%. We choose the tuning parameters based upon the prediction performance of the corresponding model in an independently simulated validation dataset.

For comparison, besides the developed robust network-constrained approach (LAD_Network), we also consider two robust approaches, robust MCP (LAD MCP) and robust LASSO (LAD LASSO), as well as three non-robust approaches, Network (Huang et al. (2011)), MCP and LASSO. All the robust methods adopt the weighted LAD loss function, while non-robust methods adopt the weighted least square loss. In particular, robust MCP is equivalent to the proposed approach when λ₂ = 0 in (3). Similarly, Network reduces to MCP when the tuning parameter corresponding to the Laplacian term is 0. Comparison between robust and non-robust methods has fully demonstrated the advantage of not only robustness in accommodating data contamination in survival response, but also the network based penalty from LAD_Network in accommodating interconnections among genetic measurements.

Simulation results for the gene expression data under AR structure are tabulated in Table 2. We can observe that from the upper panel of Table 2 where ρ = 0.5, LAD_Network has better performance than LAD_MCP and LAD_LASSO for all four error types. For example, under Error2, LAD_Network identifies 31.63(sd 13.55) out of the 50 true positives, with a relatively small number of false positives 14.93(sd 9.85). LAD_MCP identifies a lower number of true positives 23.1(sd 9.64) with a higher number of false positives 56.17(sd 81.31). LAD_LASSO has a true positives 30.33(sd 6.57), but a much higher false positives 103.17(sd 49.89). Compared with non-robust methods, the proposed method has significant advantage when heterogeneity exists in the data (Error2, Error3 and Error4). When there is no heterogeneity (Error1), performance of the proposed method is comparable to that of the non-robust Network method and outperforms MCP and LASSO.

Table 2:

Simulation for gene expression data (n, p) = (300, 505). 50 genes have nonzero regression coefficients. 5 clinical covariates are not subject to selection. The gene expressions have AR structure with ρ = 0.5 (upper panel) and ρ = 0.8 (lower panel). mean(sd) of true positives (TP) and false positives (FP) based on 100 replicates.

		LAD_Network	LAD_MCP	LAD_LASSO	Network	MCP	LASSO
AR ρ = 0.5
Error1	TP	44.90(5.65)	40.67(4.59)	38.90(5.19)	40.07(4.70)	28.53(3.92)	48.27(1.20)
	FP	9.77(7.59)	8.63(8.16)	121.93(36.26)	8.13(5.37)	7.67(3.96)	75.57(10.64)
Error2	TP	31.63(13.55)	23.10(9.64)	30.33(6.57)	1.57(2.84)	1.50(2.76)	4.07(6.35)
	FP	14.93(9.85)	56.17(81.31)	103.17(49.89)	3.37(7.73)	3.27(7.94)	11.40(19.09)
Error3	TP	43.68(7.64)	36.28(5.79)	34.88(7.74)	20.03(12.84)	15.42(9.45)	31.83(16.71)
	FP	16.05(29.77)	12.64(20.27)	114.35(57.49)	9.81(6.57)	7.97(5.47)	60.73(33.39)
Error4	TP	39.03(10.15)	31.57(4.70)	34.10(6.26)	11.83(10.91)	9.73(8.51)	20.57(16.26)
	FP	14.33(11.20)	13.50(19.47)	109.87(40.55)	8.93(8.02)	7.67(7.77)	38.83(30.69)
AR ρ = 0.8
Error1	TP	46.93(5.77)	41.00(6.36)	43.70(4.94)	49.60(0.62)	23.93(2.97)	48.27(1.14)
	FP	5.27(6.35)	2.43(2.58)	94.20(38.45)	12.00(8.39)	7.70(5.38)	61.67(15.77)
Error2	TP	43.80(12.34)	23.93(5.46)	38.57(5.9)	10.97(15.16)	4.77(7.68)	9.47(10.68)
	FP	15.07(13.55)	14.20(22.23)	101.42(41.99)	18.50(33.77)	16.07(64.74)	21.82(25.00)
Error3	TP	47.23(7.11)	37.07(5.93)	43.90(4.37)	33.33(20.10)	15.47(10.68)	30.60(18.05)
	FP	4.53(5.06)	11.87(35.83)	91.37(24.94)	27.93(40.69)	19.07(66.48)	49.33(27.36)
Error4	TP	44.37(10.23)	32.30(5.03)	44.30(3.28)	32.57(19.21)	13.63(8.72)	28.27(14.97)
	FP	10.17(9.43)	6.03(8.22)	105.00(32.13)	26.90(20.39)	10.73(6.20)	47.60(26.05)

As correlation increases, the proposed one outperform other alternatives more significantly. As what we can observe from the lower panel of Table 2 where ρ = 0.8 under AR structure, LAD_Network achieves ideal true positives and satisfactory false positives. For example, LAD_Network has a TP 43.8(sd 12.34) and a FP 15.07(sd 13.55) for Error 2 and a TP 47.23(sd 7.11) and a FP 4.53(sd 5.05) for Error 3, outperforming all other alternatives. To further examine the performance of the proposed approach, we also conduct simulation under banded structures. Results are summarized in Table 3 in the Appendix. The proposed LAD_Network delivers a consistent performance under different covariance structures: it outperforms robust alternatives when moderate to strong correlation exists among genetic variants, and it has significant advantage over non-robust methods when heterogeneity exists in the data.

In the second set of simulation, we consider more realistic correlation structures. Specifically, We generate gene expression datasets based on correlation structure extracted from real data in cancer studies. 500 genes are selected from Non-small cell lung cancer (NSCLC) data and Lung squamous cell carcinoma (LUSC) data, respectively. Two gene expression datasets, each with 300 subjects, are simulated with a multivariate normal distribution with marginal means zero and correlation matrix computed from genes selected from NSCLC data and LUSC data, respectively. 10% of genes are assigned to have nonzero regression coefficients generated from Unif[0.2, 0.8]. The 500 genes from real data are selected in a way that they form group-wise correlation structure. Unlike the first set of simulation where there are 5 genes per cluster, the clusters in this setting form more closely to real data based upon the calculated correlation coefficient. Results are shown in Table 4 and 5 in the Appendix. In Table 4, under Error 3, LAD_Network has the highest TP, 43.00(6.79), and the lowest FP, 3.14(3.91), among all the six approaches. The superior performance has also been observed under other heavy-tailed distributions. With standard normal error (Error 1), LAD_Network is comparable with the non-robust Network method, and outperforms the other two non-robust methods. Similar patterns have also been observed from Table 5. The conclusions from the simulations based on real gene expression data are consistent with the ones we have from the first setting.

In the third set of simulation, we examine whether the proposed one demonstrates superior performance over the alternatives on simulated single-nucleotide polymorphism (SNP) data. We consider two schemes to simulate SNP data. With the first SNP generating scheme, the SNP data are simulated by dichotomizing expression values of each gene at the 1st and 3rd quartiles, with the 3–level (2,1,0) for genotypes (AA,Aa,aa) respectively, where the gene expresison values are generated under the first set of simulation. Results are given in Table 6 and 7 under AR structure and banded structure respectively in the Appendix. Under the second approach, the SNP genotype data are simulated based on a pairwise linkage disequilibrium (LD) structure. Let q₁ and q₂ be the minor allele frequencies (MAFs) of two alleles A and B for two adjacent SNPs. We denote LD as δ, and the frequencies of four haplotypes are calculated as p_AB = q₁q₂ + δ, p_Ab = q₁(1 − q₂) − δ, P_aB = (1 − q₁)q₂ − δ, and P_ab = (1 − q₁)(1 − q₂) + δ. Under Hardy-Weinberg equilibrium, SNP genotype (AA, Aa, aa) at locus 1 can be generated from a multinomial distribution with frequencies $\left(q_1^2,2q_1\left(1-q_1\right),{\left(1-q_1\right)}^2\right)$. Based on the conditional genotype probability matrix (Cui et al. (2008)), we can simulate the genotypes for locus 2. With MAFs 0.3 and pairwise correlation r = 0.6, we have $\delta =r\sqrt{q_1\left(1-q_1\right)q_2\left(1-q_2\right)}$. The simulation results based on LD structure are given in Table 8 in the Appendix. Under both SNP generating schemes, the patterns are similar as those observed from the gene expression data.

5. Real Data Analysis

We analyze lung cancer data with gene expression measurements from two studies, separately. The first dataset is from the study of Xie et al. (2011), and the second one is the Lung squamous cell carcinoma (LUSC) data from TCGA (https://cancergenome.nih.gov/).

5.1. Non-small cell lung cancer (NSCLC) data

In the USA, lung cancer is the most common cause of cancer death. About 80% to 85% of lung cancers are non-small cell lung cancer (NSCLC). To identify genetic markers associated with the prognosis of NSCLC, gene profiling studies have been extensively conducted. As individual studies usually have small sample sizes, we follow the study of Xie et al. (2011) and collect data from four independent studies with gene expression measurements. After matching clinical variables and gene expression data, we have total 348 subjects and 22,283 gene expressions. Among the 348 subjects, 180 died during follow up, with survival times ranging from 0.03 to 204 months (median 26.19 months). To reduce the computational cost, we rank the probes by their variations and select the top 700 for downstream analysis. We include five clinical covariates, age, gender, smoking history, tumor stage and chemotherapy. Age is a normalized continuous variable, and dummy variables are created for categorical variables: smoking history, tumor stage and chemotherapy.

We apply all the methods to the lung cancer dataset. First, we conduct the logrank test to evaluate the prediction performance after splitting the patient group into training and testing sets. By dichotomizing the patients according to the median risk scores from the testing set, two risk groups can be created. Larger log rank test statistic indicates more significant survival difference between the low-risk and high-risk groups, thus better prediction performance. The log-rank statistics are 206.5 (LAD_Network), 130.7 (LAD_MCP), 132.7 (LAD_LASSO), 77.0 (Network), 11.1 (MCP) and 133.0 (LASSO), respectively. The proposed method has the best predictive performance, as indicated by the log-rank test statistic.

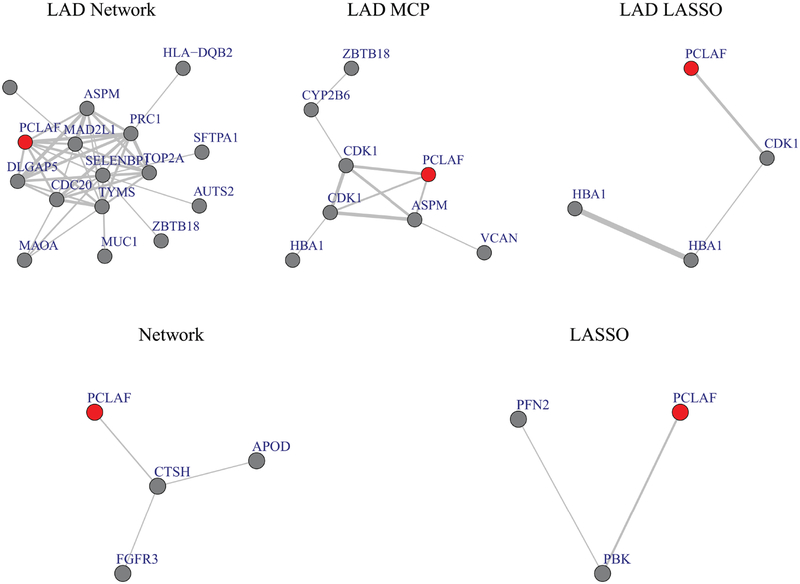
As a representative example, we examine the sub-network of gene PCLAF, PCNA Clamp Associated Factor. PCLAF is identified by five methods (all methods except MCP) as one of the most important genes. PCLAF encodes a PCNA-binding protein and is a regulator of DNA repair during DNA replication. It has been found to be overexpressed in various tumors, including lung tumor tissues (Yu et al. (2001); Hosokawa et al. (2007); Kato et al. (2012b)). Figure 2 shows the sub-network of PCLAF, where the red nodes indicate the probe of PCLAF. Thickness of the edges denotes the strength of correlation between genes. Comparing different methods, it can be clearly observed that the proposed approach has identified much more highly correlated prognostic genes, since the interconnections among genes have been accommodated by the approach that incorporates the network structure information. Eight genes are directly connected to PCLAF in the sub-network identified by the proposed approach. They are TOP2A, ASPM, SELENBP1, MAD2L1, CDC20, PRC1, TYMS and DLGAP5. All of them are positively correlated to PCLAF, except SELENBP1. PRC1 (Protein regulator of Cytokinesis 1) has the highest correlation with PCLAF (r=0.83). It is interesting that PCLAF and PRC1 are located closely on Chromosome 15. Similar as PCLAF, PRC1 is overexpressed in lung cancer cells. Higher level of PRC1 is found to be associated with poor survival of lung cancer patients (Zhan et al. (2017); Hanselmann et al. (2017)). However, none of the alternative methods capture this important prognostic marker in the PCLAF network. In addition, TOP2A (DNA Topoisomerase II Alpha) (Hou et al. (2017); Huang et al. (2015)), CDC20 (Cell Division Cycle 20) (Kato et al. (2012a); Wang et al. (2013c)), DLGAP5 (DLG Associated Protein 5) (Schneider et al. (2017); Shi et al. (2017)) and MAD2L1 (MAD2 mitotic arrest deficient-like 1) (Shi et al. (2016)) have been identified as negative prognostic markers in NSCLC by recent studies. Studies report that the over-expression of TYMS (thymidylate synthase) (Wang et al. (2013a); Chamizo et al. (2015)) and ASPM (Kuo et al. (2015)) are related to drug-resistance in advanced NSCLC. Among the genes, SELENBP1 (selenium-binding protein 1) is negatively correlated with PCLAF and other genes in the network. Selenium-binding proteins are known to play important roles in cancer prevention effects of selenium. Down-regulation of SELENBP1 is associated with poor prognosis in NSCLC patients (Zeng et al. (2013); Tan et al. (2016)). Overall, the proposed approach identifies more informative prognostic markers.

Figure 2:

Sub-network for PCLAF.

5.2. Lung squamous cell carcinoma (LUSC) data

Lung squamous cell carcinoma (LUSC) is one of the most common types of NSCLC. It comprises 25–30% of all lung cancer cases (Zappa and Mousa (2016)). LUSC is more strongly correlated with cigarette smoking history than most other subtypes of NSCLC (Kenfield et al. (2008)). We analyze TCGA (The Cancer Genome Atlas) data on the prognosis of LUSC (The Cancer Genome Atlas Research Network (2012)). We consider four clinical covariates: age at diagnosis, gender, smoking history and tumor stage. The total number of genes is 20,499 and the sample size is 461. 203 died during follow-up among all the subjects. The survival times range from 0.03 to 173.69 months, with a median of 17.84 months. Similar as the NSCLC study, we select the top 700 genes for further analysis.

We applied the six methods to the working dataset. The log-rank statistics are 155.0 (LAD_Network), 116.9 (LAD_MCP), 102.8 (LAD_LASSO), 76.4 (Network), 40.6 (MCP) and 96.1 (LASSO), respectively. The proposed method has the largest log-rank statistic and thus superior prediction performance.

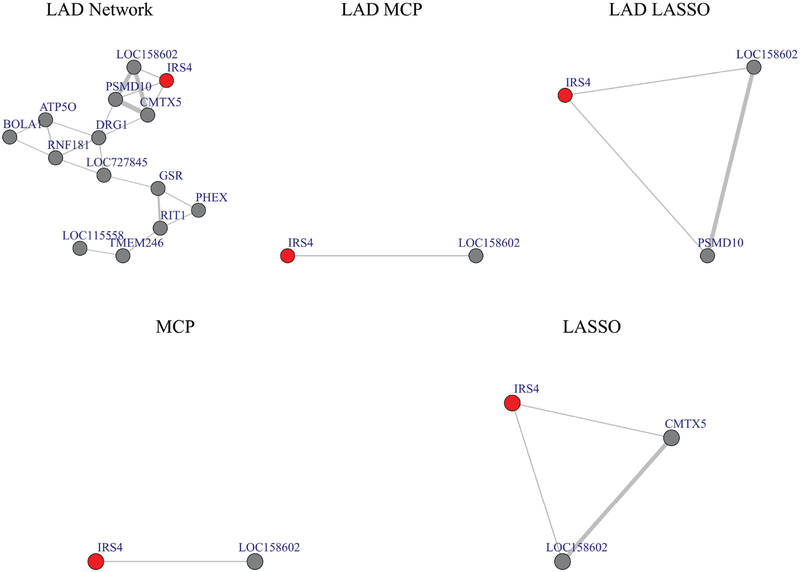
We use the sub-network of gene IRS4 (Insulin receptor substrate 4) as a representative example. IRS4 is identified by five methods (all expect Network) as a prognostic gene. IRS4 plays a tumor-promoting role in NSCLC (Hoxhaj et al. (2013); Weischenfeldt et al. (2017)). The proposed method identifies 13 genes in the sub-network of IRS4 (Figure 3). Ten genes are uniquely identified by the proposed method, and the rest three (PSMD10, CMTX5 and LOC158602) are also identified by other methods. Both PSMD10 (Proteasome 26S Subunit, Non-ATPase 10) and CMTX5 (also known as PRPS1, phosphoribosyl pyrophosphate synthetase 1) are positively correlated with IRS4 and have been reported as oncogenes (He et al. (2017); Luo et al. (2016)). Among the 13 genes in IRS sub-network, three of them (PSMD10, CMTX5, PHEX) are located on chromosome X, the same as IRS4. LOC158602 is a gene with unknown function, but highly correlated with both PSMD10 and CMTX5. DRG1 (Developmentally regulated GTP binding protein 1) is only identified by the proposed method. DRG1 plays important roles in regulating cell growth. Overexpression of DRG1 leads to chromosome missegregation and promotes tumor progression in NSCLC (Lu et al. (2016)). GSR (glutathione reductase) is one of enzymes in the glutathione (GSH) metabolism system, which is a major redox regulatory systems in mammals that support increased tumor growth (Tobe et al. (2015)). It has been reported that GSH levels in cells, regulated by GSH-synthesising enzymes such as GSR, is associated with resistance to epidermal growth factor receptor (EGFR) inhibitors in NSCLC (Li et al. (2016)). In this network, GSR has a strong correlation with RIT1 (Ras Like Without CAAX 1) (r =0.69). RIT1 encodes a RAS-family small GTPase. It has been reported as an oncogene. Mutations in RIT1 may also induce resistance to EGFR inhibition, but in a MEK-dependent manner (Berger et al. (2014)).

Figure 3:

Sub-network for IRS4.

6. Discussion

In cancer genomics studies, much effort has been devoted to developing variable selection methods to identify important genomics features associated with survival outcomes (Tibshirani (1997); Huang and Ma (2010); Sha et al. (2006)). In recent decades, it has been recognized that network (or graph) based regularization methods are particularly effective in accommodating the correlation among genomic variants in a number of studies, nevertheless, their development and application in cancer survival studies are quite limited. Besides, although the lack of robustness might lead to biased estimation and false identification of sparse network structures, robust network–based variable selection has not received much attention in cancer prognosis studies. Motivated by the limitations of existing studies and analysis of the cancer genetic data, we have proposed a robust network constrained regularization and variable selection method to accommodate correlations among gene expressions in the search of important prognostic markers. The proposed method outperforms alternatives, both robust and non-robust, under a diversity of simulation setups. In the analysis of cancer prognosis data with high-dimensional gene expression measurements, it leads to biologically sensible findings and improved prediction.

Our method significantly distinguishes from and complements existing ones in the following aspects. We adopt a weighted LAD objective function to accommodate data contamination, with Kaplan-Meier weights for censoring. To incorporate the interconnections among gene expressions, we propose a network-constrained penalty of the “MCP+L₁” form, and develop an efficient algorithm within the coordinate descent framework. The MM step is critical for the formulation of the convex surrogate objective function, which naturally leads to a weighted median regression problem. The effectiveness of smoothing the non-convex penalty function has been demonstrated in Peng and Wang (2015) and studies alike.

Here we describe the correlation among genomic variants through network structures. We acknowledge that, first, different network structures can be constructed (Huang et al. (2011)) and, second, there exists a variety of ways to incorporate correlations in penalized estimation and identification, not necessarily through network based penalty functions. For example, the spatial correlation among CNVs can be taken into account by using the adaptive fused LASSO penalty (Gao and Huang (2010a)). Comparisons to other network structures and structures other than networks are not the focus of this paper, thus not pursued. We also acknowledge that Bayesian methods can be robust depending on the prior distribution assumptions. For example, Sha et al. (2006) consider AFT models with the t prior distribution. Note that the robustness of our proposed method is not only restricted to certain type of heavy–tailed distribution or data contamination, and Sha et al. (2006) will not lead to networks among genomic variants. Moreover, comparisons between frequentist and Bayesian methods is beyond of the scope of this paper, and will be postponed to the future.

The proposed algorithm for LAD_Network under survival response is essentially a first order method. The first order method, such as gradient descent and proximal gradient descent, can enjoy a linear convergence rate when the objective function has strong convexity (Boyd and Vandenberghe (2004)). The LAD_Network loss function is, however, not differentiable and not strongly convex, which poses challenge on establishing the rate of convergence. We conjecture that the rate of convergence of LAD_Network can be shown by following that of the subgradient method (Bertsekas (2010)). It is also worth noting that Wu and Lange (2008) has given a detailed discussion of LASSO in LAD regression, although the rate of convergence has not been provided. The iteration cost of our algorithm is not cheap, due to the MM step and the sorting step for solving weighted median regression. From a practical point of view, the fast convergence of our algorithm is guaranteed by the C++ core module of R package regnet. In addition, Gao and Huang (2010b) has investigated estimation and selection consistency of LAD_LASSO, which is important for developing consistency properties of LAD_Network case. In this paper, we focused on the development of statistical methodology. Investigations on the theoretical properties will be conducted in future studies.

Regularized objective function of robust penalization methods share a common structure of “robust objective function + penalty function” (Wu and Ma (2015)). The computational advantage of the proposed method roots in the L₁ form of the objective function. It is conjectured that the robustness can be achieved by coupling the penalty function with other robust loss functions, such as the exponential squared loss (Wang et al. (2013b)) and rank based loss (Shi et al. (2014); Wu et al. (2015)). However, since additional tunings and smoothing are demanded for these loss functions, the computational expenses are even high under low dimensional settings.

In this study, we focus on prognostic outcomes. Extension of our method to continuous disease phenotypes can be made readily by changing Kaplan-Meier weights to equal weights. In addition, the proposed method is not limited to the analysis of gene expression measurement. The network structure has been widely adopted to describe correlations among other genomics features, such as SNPs (Ren et al. (2017)), CNVs (Peng et al. (2012); Shi et al. (2015)) and DNA methylations (Sun and Wang (2012)), where robust network based penalization is also of great interest.

A. Appendix

Table 3:

Simulation for gene expression data (n, p) = (300, 505). 50 genes have nonzero regression coefficients. 5 clinical covariates are not subject to selection. The gene expressions have Banded.1 (upper panel) or Banded.2 structure (lower panel) with ρ = 0.5. mean(sd) of true positives (TP) and false positives (FP) based on 100 replicates.

		LAD_Network	LAD_MCP	LAD_LASSO	Network	MCP	LASSO
			Banded.1	ρ = 0.5
Error1	TP	41.30(6.26)	36.87(3.16)	32.80(6.73)	35.37(4.41)	27.93(2.35)	45.30(2.38)
	FP	13.43(10.74)	8.57(8.39)	105.53(45.21)	8.37(3.65)	8.63(6.67)	85.40(10.19)
Error2	TP	24.93(9.84)	19.77(15.93)	26.93(12.59)	2.00(5.55)	2.47(8.90)	3.17(5.34)
	FP	23.00(24.92)	79.87(124.43)	105.27(67.09)	11.93(44.98)	17.97(79.54)	14.10(33.67)
Error3	TP	39.63(9.88)	32.00(4.88)	33.70(6.93)	18.77(10.76)	16.87(9.36)	30.17(14.13)
	FP	11.80(9.28)	17.97(31.91)	111.17(46.28)	9.40(6.98)	7.03(4.06)	60.30(32.13)
Error4	TP	36.03(11.87)	30.43(5.37)	30.33(7.91)	12.97(11.78)	11.40(10.67)	22.80(16.40)
	FP	11.90(10.46)	21.57(29.67)	109.40(48.10)	8.23(8.18)	6.73(7.25)	52.83(36.92)
			Banded.2	ρ = 0.5
Error1	TP	43.63(7.89)	42.43(3.22)	33.53(9.72)	34.20(4.34)	25.20(4.13)	47.40(1.69)
	FP	8.07(7.72)	10.83(14.28)	101.17(48.16)	9.17(4.89)	10.07(4.64)	80.93(12.3)
Error2	TP	31.77(11.31)	26.60(10.75)	33.33(5.57)	3.43(8.64)	3.27(7.98)	6.27(8.48)
	FP	24.73(43.87)	100.50(119.98)	129.90(45.73)	17.00(69.35)	15.03(61.68)	19.40(24.64)
Error3	TP	41.40(8.58)	35.50(5.47)	33.50(7.66)	15.17(11.58)	12.37(8.46)	29.93(15.21)
	FP	12.97(27.18)	10.80(17.94)	114.40(54.39)	8.80(8.26)	7.33(5.57)	61.27(30.46)
Error4	TP	37.57(11.66)	32.87(5.69)	34.03(7.3)	14.87(13.23)	11.83(10.39)	26.33(16.11)
	FP	9.60(8.62)	19.00(31.61)	113.30(50.56)	9.30(9.34)	7.97(7.45)	55.17(33.04)

Table 4:

Simulation for gene expression data using correlations calculated from LUSC data. (n, p) = (300, 505). 50 genes have nonzero regression coefficients. 5 clinical covariates are not subject to selection. mean(sd) of true positives (TP) and false positives (FP) based on 100 replicates.

		LAD_Network	LAD_MCP	LAD_LASSO	Network	MCP	LASSO
Error1	TP	46.88(3.61)	46.29(2.89)	40.47(6.29)	45.66(2.21)	43.42(2.38)	48.09(1.18)
	FP	1.28(2.00)	3.83(4.83)	1.97(2.69)	1.44(1.92)	1.58(2.20)	13.27(3.66)
Error2	TP	33.65(6.54)	32.59(8.21)	33.69(5.54)	11.02(7.35)	18.25(7.12)	18.14(8.35)
	FP	9.92(23.64)	28.03(45.27)	13.27(14.75)	23.94(52.35)	73.50(71.82)	17.14(21.58)
Error3	TP	43.00(6.79)	41.63(5.95)	41.15(6.03)	30.24(11.93)	28.81(8.41)	39.35(9.46)
	FP	3.14(3.91)	5.58(6.60)	3.85(6.80)	5.52(12.42)	12.43(29.37)	21.83(11.31)
Error4	TP	40.91(6.53)	40.02(5.67)	39.72(5.82)	22.99(11.13)	23.39(8.16)	35.02(9.72)
	FP	3.07(3.41)	8.60(10.37)	3.12(6.07)	7.07(22.44)	18.22(37.61)	26.29(25.11)

Table 5:

Simulation for gene expression data using correlations calculated from NSCLC data. (n, p) = (300, 505). 50 genes have nonzero regression coefficients. 5 clinical covariates are not subject to selection. mean(sd) of true positives (TP) and false positives (FP) based on 100 replicates.

		LAD_Network	LAD_MCP	LAD_LASSO	Network	MCP	LASSO
Error1	TP	43.10(6.57)	43.32(3.41)	41.01(6.91)	47.12(3.08)	39.67(3.12)	45.91(1.65)
	FP	1.40(2.00)	3.02(3.77)	5.68(9.65)	0.83(1.44)	1.44(2.27)	23.01(12.09)
Error2	TP	36.44(9.83)	33.73(6.75)	34.46(5.28)	25.23(6.41)	11.27(3.03)	19.72(5.92)
	FP	13.80(25.85)	34.36(55.80)	23.14(42.02)	43.94(34.98)	15.86(18.95)	14.23(8.96)
Error3	TP	41.51(8.41)	39.23(6.68)	38.17(6.52)	38.20(10.43)	24.93(9.19)	35.45(8.77)
	FP	4.75(6.41)	11.10(12.24)	13.47(20.48)	13.66(37.16)	8.64(34.40)	22.71(21.76)
Error4	TP	42.13(7.50)	38.58(6.86)	39.72(6.14)	34.56(10.60)	19.90(9.03)	30.23(9.58)
	FP	7.03(9.27)	13.33(25.09)	16.63(28.77)	30.02(72.28)	13.17(42.50)	19.57(27.40)

Table 6:

Simulation for SNP data (n, p) = (300, 505) under AR structures. 50 genes have nonzero regression coefficients. 5 clinical covariates are not subject to selection. The SNPs have AR structure with ρ = 0.5 (upper panel) and ρ = 0.8 (lower panel). mean(sd) of true positives (TP) and false positives (FP) based on 100 replicates.

		LAD_Network	LAD_MCP	LAD_LASSO	Network	MCP	LASSO
AR ρ = 0.5
Error1	TP	39.97(9.05)	39.77(3.54)	34.50(6.24)	33.50(6.60)	29.83(6.88)	46.03(2.30)
	FP	8.83(5.80)	9.33(7.71)	106.03(37.94)	9.13(6.26)	8.77(5.17)	84.53(11.25)
Error2	TP	23.23(10.57)	22.43(10.93)	27.43(8.64)	5.17(9.41)	6.93(14.32)	6.10(8.79)
	FP	23.93(40.56)	57.97(95.48)	110.17(66.55)	32.03(86.43)	45.67(126.72)	23.67(39.83)
Error3	TP	37.03(10.07)	36.17(4.53)	34.30(6.39)	16.17(11.50)	15.07(10.51)	28.30(16.74)
	FP	9.00(6.44)	15.93(26.06)	107.77(43.29)	8.50(5.76)	8.30(5.45)	58.40(34.86)
Error4	TP	38.13(7.35)	34.17(6.01)	34.90(7.04)	10.63(10.55)	9.83(9.89)	19.90(17.49)
	FP	10.17(6.86)	27.17(41.85)	109.70(45.23)	6.73(6.10)	6.07(6.49)	40.63(41.16)
AR ρ = 0.8
Error1	TP	46.87(5.11)	45.30(2.87)	42.87(6.06)	48.70(1.42)	26.07(3.49)	48.73(1.01)
	FP	3.80(2.96)	3.47(2.66)	104.20(30.42)	10.00(7.89)	6.67(3.39)	60.00(12.99)
Error2	TP	38.80(10.71)	26.17(6.93)	35.93(4.16)	5.97(10.07)	6.10(12.41)	5.70(7.53)
	FP	12.20(8.02)	44.20(83.64)	105.40(32.2)	35.30(89.14)	43.57(111.1)	25.77(42.43)
Error3	TP	46.70(6.02)	39.90(5.94)	43.17(3.65)	33.23(16.9)	18.10(9.78)	33.97(15.77)
	FP	6.77(5.88)	6.10(10.6)	105.63(28.03)	18.97(16.06)	20.83(65.59)	60.93(29.47)
Error4	TP	42.87(10.92)	36.03(6.83)	42.17(4.47)	25.93(16.99)	13.43(8.39)	29.33(15.39)
	FP	5.67(4.56)	10.30(21.71)	120.90(48.61)	19.77(13.39)	7.57(6.82)	50.30(31.1)

Table 7:

Simulation for SNP data (n, p) = (300, 505) under banded structures. 50 genes have nonzero regression coefficients. 5 clinical covariates are not subject to selection. The SNPs have Banded.1 (upper panel) or Banded.2 structure (lower panel) with ρ = 0.5. mean(sd) of true positives (TP) and false positives (FP) based on 100 replicates.

		LAD_Network	LAD_MCP	LAD_LASSO	Network	MCP	LASSO
			Banded.1	ρ = 0.5
Error1	TP	39.17(9.57)	36.87(8.19)	30.13(8.40)	31.80(3.95)	26.57(4.39)	43.97(3.18)
	FP	9.10(5.92)	13.53(21.54)	91.63(43.74)	8.27(5.30)	8.53(6.22)	81.93(12.6)
Error2	TP	19.17(9.70)	18.30(13.42)	25.43(8.69)	2.83(7.39)	3.60(9.97)	3.17(5.17)
	FP	14.93(13.16)	57.30(93.44)	97.63(51.97)	17.30(60.78)	24.20(89.50)	13.10(27.14)
Error3	TP	33.33(10.57)	32.47(4.61)	29.97(8.37)	14.60(13.06)	12.83(11.25)	24.40(17.98)
	FP	8.00(4.61)	18.57(38.32)	101.23(52.47)	8.13(7.21)	6.63(6.19)	53.10(37.71)
Error4	TP	33.53(13.54)	29.43(8.05)	31.00(6.77)	11.43(8.63)	10.83(7.73)	24.40(12.76)
	FP	16.37(12.94)	18.30(36.76)	108.90(39.14)	7.07(7.91)	6.53(5.78)	56.57(30.96)
			Banded.2	ρ = 0.5
Error1	TP	41.23(8.78)	40.57(3.30)	34.23(7.57)	32.23(6.74)	27.77(5.10)	45.93(1.76)
	FP	10.83(7.68)	9.17(7.45)	113.63(46.59)	9.63(6.7)	9.30(4.23)	84.00(12.91)
Error2	TP	21.10(7.69)	20.53(13.05)	27.27(8.2)	1.60(1.96)	1.63(2.11)	3.03(4.19)
	FP	17.27(10.43)	76.43(122.77)	93.57(49.76)	5.10(10.5)	5.00(10.3)	11.40(15.40)
Error3	TP	35.60(9.11)	34.90(4.48)	34.20(5.11)	15.30(10.17)	14.37(9.68)	28.67(16.14)
	FP	10.60(7.02)	15.63(38.21)	117.63(38.53)	9.80(7.23)	9.50(7.10)	66.77(37.00)
Error4	TP	38.50(8.44)	36.47(5.17)	33.20(7.07)	12.43(10.86)	11.80(10.26)	21.80(18.26)
	FP	18.77(13.23)	41.57(69.17)	109.73(42.16)	11.13(26.16)	12.90(30.37)	45.90(38.12)

Table 8:

Simulation for SNP data based on the linkage disequilibrium (LD) structure. (n, p) = (300, 505). 50 genes have nonzero regression coefficients. 5 clinical covariates are not subject to selection. mean(sd) of true positives (TP) and false positives (FP) based on 100 replicates.

		LAD-Network	LAD_MCP	LAD_LASSO	Network	MCP	LASSO
Error1	TP	46.47(4.62)	42.94(5.09)	43.10(3.54)	46.25(2.17)	44.94(2.62)	45.93(2.03)
	FP	4.30(6.29)	9.43(16.91)	28.10(13.34)	2.59(3.12)	2.85(4.23)	21.52(5.25)
Error2	TP	38.22(7.42)	34.44(7.76)	27.45(4.70)	23.90(5.28)	12.15(9.04)	10.34(9.56)
	FP	18.84(18.76)	46.88(69.94)	49.31(16.43)	95.05(59.21)	36.10(82.64)	20.73(22.59)
Error3	TP	45.38(4.71)	40.16(5.59)	39.12(5.01)	26.16(15.89)	27.16(13.09)	33.03(13.71)
	FP	5.85(6.66)	11.17(23.56)	35.25(12.73)	10.22(32.97)	25.37(77.51)	36.70(18.09)
Error4	TP	42.65(6.21)	39.28(5.35)	36.40(5.03)	21.66(15.24)	25.14(12.31)	28.30(14.80)
	FP	5.99(5.63)	17.00(31.33)	39.82(14.83)	13.95(38.37)	44.58(108.55)	36.91(21.17)