Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
letter
. 2018 Sep 19;21(12):1833–1844. doi: 10.1111/ele.13158

Climatically controlled reproduction drives interannual growth variability in a temperate tree species

Andrew J Hacket‐Pain 1,✉, Davide Ascoli 2, Giorgio Vacchiano 3, Franco Biondi 4, Liam Cavin 5, Marco Conedera 6, Igor Drobyshev 7,8, Isabel Dorado Liñán 9, Andrew D Friend 10, Michael Grabner 11, Claudia Hartl 12, Juergen Kreyling 13, François Lebourgeois 14, Tom Levanič 15, Annette Menzel 16,17, Ernst van der Maaten 18, Marieke van der Maaten‐Theunissen 18, Lena Muffler 13, Renzo Motta 19, Catalin‐Constantin Roibu 20, Ionel Popa 21, Tobias Scharnweber 13, Robert Weigel 13, Martin Wilmking 13, Christian S Zang 22
PMCID: PMC6446945  PMID: 30230201

Abstract

Climatically controlled allocation to reproduction is a key mechanism by which climate influences tree growth and may explain lagged correlations between climate and growth. We used continent‐wide datasets of tree‐ring chronologies and annual reproductive effort in Fagus sylvatica from 1901 to 2015 to characterise relationships between climate, reproduction and growth. Results highlight that variable allocation to reproduction is a key factor for growth in this species, and that high reproductive effort (‘mast years’) is associated with stem growth reduction. Additionally, high reproductive effort is associated with previous summer temperature, creating lagged climate effects on growth. Consequently, understanding growth variability in forest ecosystems requires the incorporation of reproduction, which can be highly variable. Our results suggest that future response of growth dynamics to climate change in this species will be strongly influenced by the response of reproduction.

Keywords: Dendrochronology, drought, European beech, Fagus sylvatica, forest growth, masting, path analysis, SEM, structural equation modelling, trade‐off

Introduction

Tree growth and reproduction are key controls on the dynamics of forest ecosystems at a range of timescales, including their response to ongoing climate change. Both growth and reproduction are influenced by climate and resource availability. This makes them related, inducing growth‐reproduction trade‐offs in many species (Thomas 2011). Growing‐season climate influences growth via physiological processes including leaf phenology, photosynthesis and xylogenesis (e.g. Leuschner et al. 2001; Breda et al. 2006). However, the direction, duration, and timing of climate relationships with growth are not always consistent across space and time, and the processes accounting for the observed relationships are poorly understood, limiting our ability to predict future changes in tree growth (Babst et al. 2013; Guillemot et al. 2017; Peltier et al. 2018). A major source of such uncertainty are the processes that cause lagged effects of climate on growth (Piovesan et al. 2005; Hacket‐Pain et al. 2016). However, lagged effects of climate on growth are not well reproduced by vegetation models (Babst et al. 2013; Rammig et al. 2015). Despite recognition that they can be key drivers of tree growth responses to climate change (‘ecological memory’), the processes responsible are poorly understood (Ogle et al. 2015; Peltier et al. 2018). In some cases, lagged correlations can result from lagged effects within the physical environment (Woodhouse 2003). Alternatively, they have been attributed to ‘carry‐over’ or ‘legacy’ impacts within trees after unfavourable years (Anderegg et al. 2015). For example the depletion of internal carbohydrate reserves (Galiano et al. 2011) may reduce growth the following year (Skomarkova et al. 2006), although this has been difficult to demonstrate empirically, in part due to complexities of linking tree‐level resources and growth (Mund et al. 2010; Richardson et al. 2013). Additionally, leaf area index, xylem conductivity or fine root dynamic responses to climate may influence growth in subsequent years, creating mechanisms for lagged correlations between climate and growth (e.g. Breda et al. 2006; Galiano et al. 2011).

Allocation to reproduction is a key functional trait of plants, and varies both at interannual timescales, and across tree lifespan (Thomas 2011; Muller‐Haubold et al. 2013; Allen et al. 2014). Variation in reproductive effort is strongly influenced by climate, especially in species that display ‘masting’, i.e. highly variable interannual seed production synchronised among individuals and populations (Pearse et al. 2016; Vacchiano et al. 2017). Trade‐offs between growth and reproduction have been repeatedly observed, and can indirectly affect climate‐growth relationships, causing the emergence of lagged climate effects (Piovesan & Schirone 2000; Hacket‐Pain et al. 2015). Additionally, the strength of growth‐reproduction trade‐offs varies with abiotic stresses such as summer drought (Sletvold & Agren 2015; Hacket‐Pain et al. 2017), so the magnitude of growth reductions associated with investment in reproduction is also dependent on climate.

Here, we use a masting tree species (Fagus sylvatica L.) to investigate the interplay of climate, reproduction, and tree growth. We hypothesise that climate drives both resource availability and its allocation, including via lagged effects (Fig. 1). This implies that climatically controlled allocation to reproduction may be an important additional mechanism by which climate influences interannual variation in tree growth. Testing this hypothesis will improve our ability to understand and predict responses of trees to climate change (Selas et al. 2002; Drobyshev et al. 2010; Davi et al. 2016). We show that temperature and precipitation influence growth in this species both directly, and indirectly through controls on resource allocation to reproduction. Allocation to reproduction is a key driver of growth, and due to its predominant dependence on previous summers’ temperature, it is responsible for creating lagged climate effects on growth. Consequently, we argue that including variable resource allocation in models of tree growth will improve their ability to reproduce observed patterns of growth and improve predictions of future tree growth.

Figure 1.

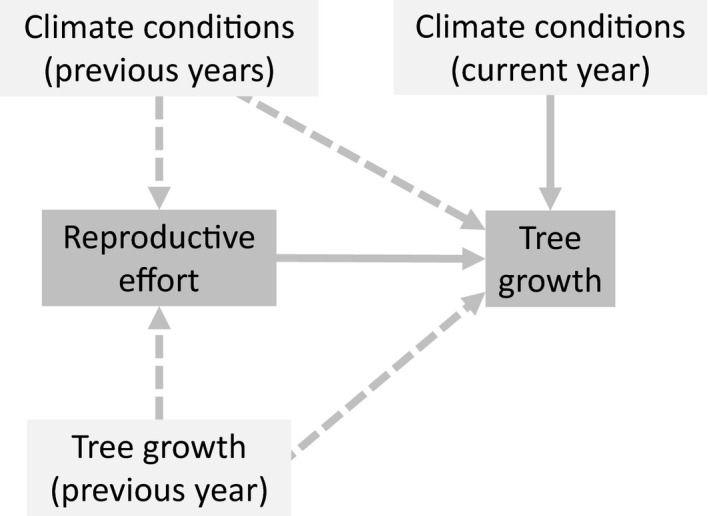
Figure 1

Open in a new tab

Theoretical model linking climate conditions across multiple years, tree reproductive effort and tree growth. Dashed lines indicate effects operating across years.

Methods

Data

Tree‐ring widths were used to characterise tree growth, with data taken from a tree‐ring network covering the whole geographic distribution of F. sylvatica (Fig. 2) (Zang et al. 2018). The dataset used in this study includes 321 sites, and extends from southern Scandinavia to the Mediterranean Basin, and from western Europe to the Balkans. Sites were selected to represent locally typical closed‐canopy F. sylvatica forest, and sampling was not designed to specifically target climatically stressed sites or individuals. Each site included a minimum of five trees. As our focus was to understand interannual variation in growth, low‐frequency ring‐width variation was removed using 32‐year spline detrending with a frequency cut‐off of 0.5 (Cook & Peters 1981), and individual trees were averaged to create mean site chronologies of ring‐width indices (RWI). Reproductive effort (RE) was characterised using a five‐class ordinal index of seed production (Ascoli et al. 2017a), with seed production chronologies for each NUTS‐1 (Nomenclature of Territorial Units for Statistics, see Appendices S1 and S2) region of Europe developed by Vacchiano et al. (2017). Ordinal data were reclassified to binary, comprising of ‘mast’ (category 4 and 5) and ‘non‐mast’ years (category 1, 2 and 3). This approach was designed to maintain linear relationships and reduce the degrees of freedom in the models. RWI series from individual sites were further averaged to create regional NUTS‐1 growth chronologies (Fig. 2), with correlations between sites in each NUTS‐1 checked to ensure growth synchrony within each region (Appendix S3). The number of individual site chronologies contributing to each mean NUTS‐1 chronology varied from 3 to 41. Data for monthly mean maximum temperature (MAX) and monthly total precipitation (PRE) were obtained from the CRU TS 3.23 gridded dataset (Harris et al. 2014). Regional climate time‐series were calculated by averaging pixel‐level climate data across NUTS‐1 using the cruts package (Taylor & Parida 2016) in R version 3.3.1 (R Development Core Team 2016). Homogeneity of climate within regions was checked by calculating the mean pairwise correlation between all individual grid cells in each region, and we checked that regional climate chronologies represented the climate of the sampled tree‐ring sites. Growing season conditions were represented by a 3‐month window (May–July, MJJ). While the time window corresponding to the strongest relationship with annual growth may vary between populations, previous studies have indicated this window captures the main signal for populations of F. sylvatica across Europe (Hacket‐Pain et al. 2016; Cavin & Jump 2017). Previous summer climate signals (t‐1 and t‐2) were represented using a 2‐month window (June–July, JJ), which acts as a consistent climate cue of mast years across Europe (Drobyshev et al. 2010; Muller‐Haubold et al. 2013; Vacchiano et al. 2017).

Figure 2.

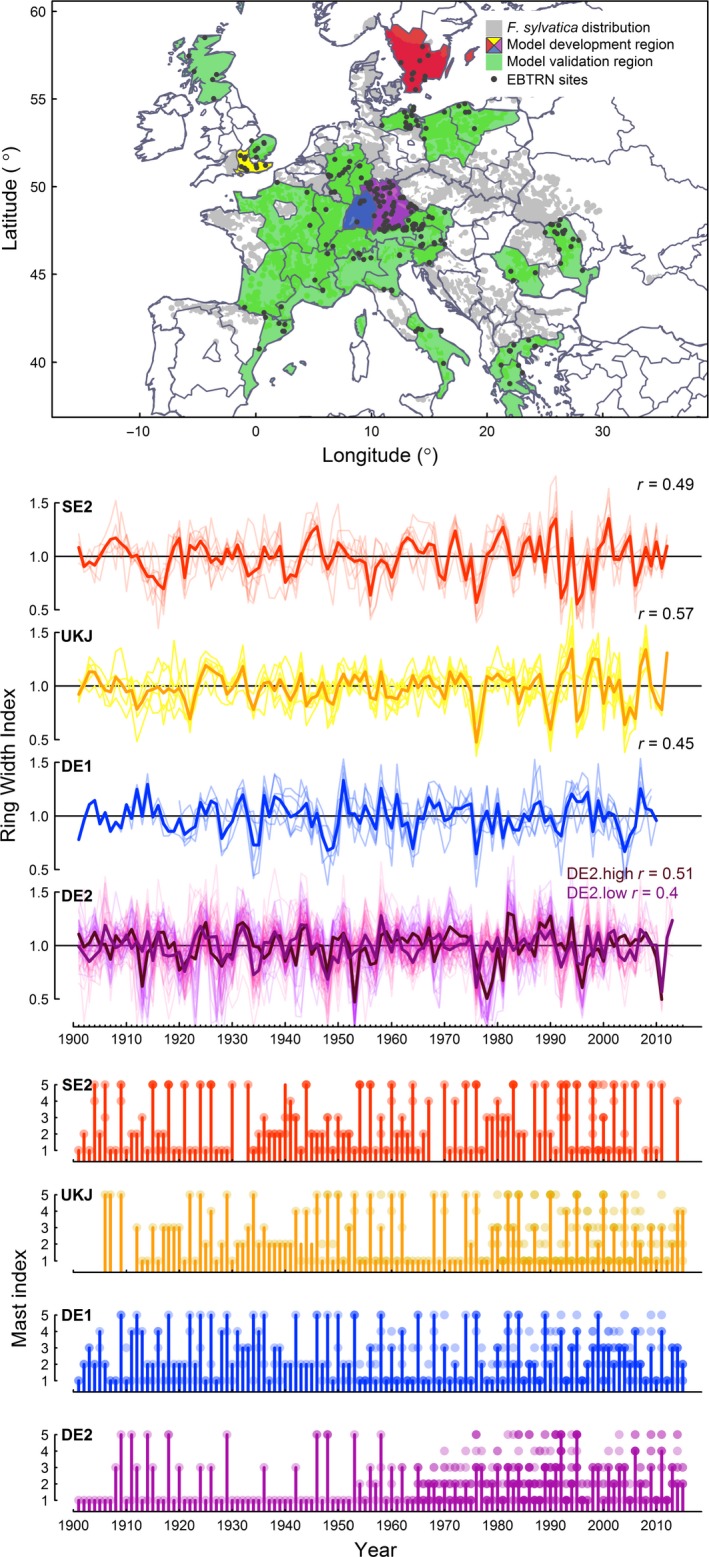
Figure 2

Open in a new tab

Study location and summary of data. (a) Study regions (NUTS‐1) including the geographic distribution of Fagus sylvatica (EURFORGEN 2009), and locations of individual RWI chronologies. (b) Ring‐width index chronologies for each region. Individual chronologies plotted in pale colours, and the mean regional chronology in dark colours. r represents the mean correlation between sites in each regional chronology. For DE2, cluster analysis revealed two distinct groups of chronologies, which correspond to high (paler purple) and low (darker purple) elevation (see Appendix B) (c) Annual reproductive effort (RE) (1‐2‐3 = non‐mast year; 4–5 = mast year) of Fagus sylvatica in each region. Individual records are plotted as points (colour intensity represents the number of records in a class), with the modal values plotted as bars.

Structural equation modelling (SEM)

We used SEM (path analysis) to examine relationships between climate variables, reproductive effort, and growth (Fig. 1), with analysis conducted at the NUTS‐1 regional level. SEM provides a tool to statistically test conceptual models with empirical datasets, including direct and indirect dependency structures (Fig. 1) (Grace 2006). In our initial model, growth was influenced directly by climate conditions in the growing season, which influence physiological processes including phenology, photosynthesis and xylogenesis (Leuschner et al. 2001; Breda et al. 2006). Links were also included to represent lagged effects of previous summer temperature on growth, which is commonly reported in this species (Piovesan et al. 2005). Additional climatic factors such as winter or spring temperature in the year of growth may be important locally, but are not consistently relevant across populations (Lebourgeois et al. 2005; Hacket‐Pain & Friend 2017), and so were not included in this analysis. Links were also included between current growth and annual reproductive effort (Muller‐Haubold et al. 2013; Hacket‐Pain et al. 2017), and between current‐ and prior‐year growth. Annual reproductive effort was influenced by previous summers’ climate and previous year growth (Drobyshev et al. 2010; Vacchiano et al. 2017). A full description and justification of our initial model is included in Appendix S4. Aggregated (NUTS‐1) data for RWI, RE and climate variables were tested for multivariate normality and multivariate outliers, using the MVN package in R (Korkmaz et al. 2014) (Appendix S5), and the linearity of bivariate relationships was checked by graphical plotting (Appendix S6). In SEM, the estimation of parameters aims to minimise the discrepancy between the observed covariance matrix and the covariance matrix implied by the hypothetical model (Grace 2006). SEMs were fitted using diagonally weighted least‐squares estimation (DWLS) in the R package lavaan (Rosseel 2012) in order to adjust for the categorical endogenous variables included in our data (RE). SEMs test the strength, sign and significance of relationships between variables. We used standardised path coefficients to represent these relationships, which can be interpreted as equivalent to partial correlation coefficients. For categorical variables we also plot the raw coefficients to aid interpretation (Grace & Bollen 2005). Indirect effects are estimated by multiplying coefficients along indirect pathways. The raw coefficients and P‐values are provided in Appendix S7.

Model fitting and validation

Following the recommendation of Kline (2005), we focused the model development and fitting on regions with > 100 years of complete data, a threshold met by four regions: two in northern Europe (UKJ and SE2) and two in central Europe (DE1 and DE2) (Fig. 2). Initial analysis of the tree‐ring chronologies showed high within‐region synchrony between individual RWI chronologies in SE2, UKJ and DE1 (see Fig. 2), but lower synchrony in DE2. Cluster analysis revealed a strong dependence of RWI to elevation (see Appendix S8), therefore all analyses for DE2 were conducted using two mean chronologies (high and low elevation). Model development and fitting followed the two‐stage process recommended by Grace (2006). The first step focused on the concept of goodness‐of‐fit (GOF) and compared the specified model with the variance‐covariance matrix of observed data. This was essentially a test that no important links between variables were omitted. To estimate the GOF we used the χ 2 test (threshold value, P > 0.05), the Comparative Fit Index (CIF, threshold value > 0.9), and the Standardised Root Mean Square Residual (SRMSR) and Root Mean Square Error of Approximation (RMSEA) (threshold value < 0.1 and < 0.05 respectively) (Kline 2005; Grace 2006; Rosseel 2012). The second stage of evaluation investigated whether all links included in the model were supported by the data. Insignificant links (P > 0.05) were excluded from the model – but only if doing so did not reduce GOF (Grace 2006). As a final check, we compared models with and without the insignificant links using anova. This procedure was used to develop an optimal model for the prediction of RE and RWI based on climate and prior growth. To estimate confidence intervals around predicted RWI we randomly resampled model parameters 1000 times, assuming a normal distribution and using the estimated standard error for each parameter. A 95% confidence interval was based on the distribution of the set of 1000 predicted RWI (± 2 SD).

We then used independent regions with more limited data availability to validate our models using two approaches. First, we used the multi‐modelling approach (Rosseel 2012) to estimate a single model for all discrete regions used in the development of the optimal model structure. Then we ran this multi‐group model to predict RWI in 26 independent validation regions, based only on climate data, with RE predicted using previous summer temperatures. We used this model structure for further validation for eight of these 26 regions where we had at least 45 years of complete RWI, RE and climate data. Here we used the same optimal model structure, but the parameters were fitted individually in each region, allowing for local differences in sensitivity of growth and masting to climate. As these regions had not been used in model development and fitting, this was a form of model‐structure validation, testing the generality of our underlying assumptions of the controls of growth.

Results

Selection of optimal model linking climate, reproduction and tree growth

Tree growth was significantly correlated with climate and reproductive effort in the five regions used for model development and fitting (Fig. 3 and Appendix S6). These models passed the GOF tests, showing that our proposed model structure linking climate, reproduction and growth was consistent with our datasets (Fig. 1). Growth was reduced in years of high reproductive effort, and was positively correlated with growing season precipitation (Fig. 3). However, not all the linkages in the original models were significant, and comparison of alternative models demonstrated that the effects of MAX JJ‐1 and MAX JJ‐2 on RWI could be adequately explained by indirect pathways involving RE (Appendices S9 and S10). In all five regions, a model that included only indirect effects of MAX JJ‐1 and MAX JJ‐2 via RE was statistically indistinguishable from a model that included both direct and indirect pathways, and significantly better than a model where previous summers’ temperatures could only influence growth directly (Appendix S10). This indicated that the indirect pathway via RE is the dominant (although not necessarily the exclusive) pathway for previous summers’ temperature influence on RWI. Consequently, as direct linkages between previous summers’ temperature and RWI were not supported by the data they were removed from the optimal model. The linkage between RWI ‐1 and RE was also insignificant, and removing it had no effect on prediction of RE. MAX JJ had no significant influence on growth in any of the five regions in the saturated models (Appendix S9). However, when models were optimised individually for each of the five regions (Appendix S11), MAX JJ was retained in DE2‐high, becoming significant when PRE MJJ was removed. We therefore decided to retain the linkage between MAX JJ and RWI in the optimal models (Fig. 3). In conclusion, our optimal model structure predicted RWI on the basis of growing season climate (PRE MJJ and MAX JJ), reproductive effort (RE) and previous year growth (RWI ‐1), with additional indirect effects of previous summers’ temperature as RE was predicted on the basis of previous summers’ climate (MAX JJ‐1 and MAX JJ‐2).

Figure 3.

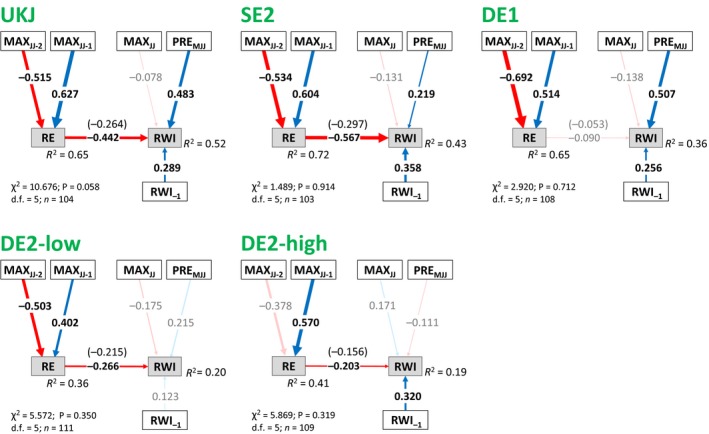
Figure 3

Open in a new tab

Structural Equation Models for model development and fitting regions, representing the effects of temperature and precipitation on radial growth, with indirect pathways involving the effects of allocation to reproduction (RE). Following mediation analysis, direct pathways from MAXJJ ‐1 and MAXJJ ‐2 to RWI, and from RWI ‐1 to RE, have been removed. Blue and red arrows indicate positive and negative relationships respectively. Numbers on the arrows indicate the standardised path coefficients, with arrow thickness proportional to the coefficient strength. Coefficients in parenthesis refer to raw coefficients. Pale colours indicate non‐significant pathways (P < 0.05). The proportion of explained variance (R 2) for each endogenous variable is also shown.

The optimal models explained a higher proportion of observed variance in RWI in northern Europe (R 2 = 55% and 43% in UKJ and SE2 respectively). Interpretation of coefficients is not straightforward in models with categorical variables (Grace & Bollen 2005), but in SE2 the raw coefficient for RE, which represents the change in RWI in a mast year (i.e. RE = 1), was greater than the standardised coefficient for MAX JJ or PRE MJJ , which represents the change in RWI for a ± 1 SD change in these climate variables. As a mast year occurred on average every 3 years in SE2 (Fig. 2), we suggest that RE was the variable with the strongest influence on RWI in this region. In UKJ, RE was also an important control on growth, but PRE MJJ had an additional strong influence. In DE1, the model explained 36% of the variance in RWI, and PRE MJJ was the strongest influence on growth (RE was insignificant). In DE2‐low and DE2‐high the models had lower explanatory power, and RE was the only significant linkage with RWI. In SE2, UKJ and DE1, the models reproduced observed patterns of RWI successfully, including multi‐year growth reductions (Fig. 4). However, fitted models for all regions failed to consistently reproduce the magnitude of growth reductions in years with the narrowest observed rings (Appendix S12). Consequently, the models did not adequately capture an observed increase in interannual growth variability during recent decades in UKJ and SE2.

Figure 4.

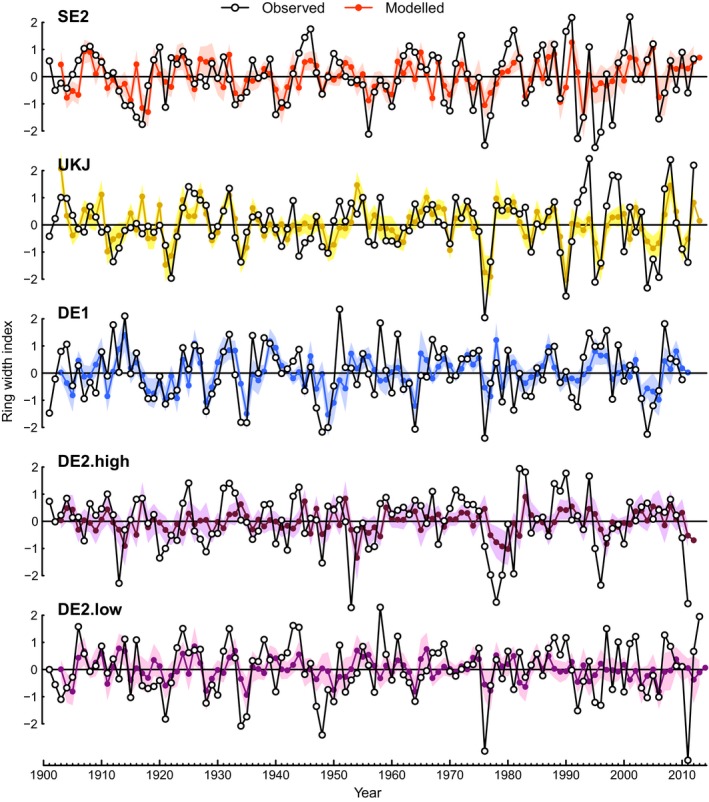
Figure 4

Open in a new tab

Comparison of observed and predicted RWI for model development regions (models described in Fig. 3). Shading represents 95% confidence interval for model predictions. Note that RWI is modelled as a function of PREMJJ,MAXJJ , and RWI ‐1 , and predicted RE (predicted from MAXJJ ‐1 and MAXJJ ‐2) – i.e. observed RE is not used to predict RWI.

There were differences in the relative importance of different pathways between regions (pathway coefficients) (Fig. 3). RE had a significant negative impact on growth in all regions except DE1, so that high RE (a mast year) resulted in reduced growth. Generally, summer precipitation (PRE MJJ) had a significant positive influence on growth, but this relationship was weaker in the most northerly region, SE2 and DE2‐low, and was insignificant in the high elevation region DE‐high. Summer temperature in the year of growth (MAX JJ) had no significant impact on growth in any of the study regions. While always insignificant, it had a weak negative influence on growth in all chronologies except DE2‐high, where the relationship was positive.

Consequently, in SE2 the main climate influence on radial growth was an indirect effect of temperature during the two summers prior to the year of growth, via RE (masting); i.e. the indirect influence of MAX JJ‐1 and MAX JJ‐2 were both greater than the direct influence of either PRE MJJ or MAX JJ (Fig. 3). In UKJ the influence of growing season precipitation (PRE MJJ) was stronger than in SE2, but previous summers’ temperature, through their influence on masting, also had a strong impact on growth. Radial growth in the previous year had a significant positive influence on growth (i.e. positive autocorrelation) in all five models.

Model validation

A multi‐group model was fitted using the optimal model structure (Fig. 3), although restricted to UKJ, SE2 and DE2‐low. DE2‐high was excluded from the multi‐group model due to opposite influences of PRE MJJ and MAX JJ on RWI, and DE1 was excluded due to the insignificant link between RE and RWI. Including either of these regions in the multi‐group resulted in the model failing the GOF tests. The resulting multi‐group model was consistent with the results of the individual models (Appendix S13). The model captured the key features of growth in many of the 26 independent validation chronologies from across Europe for the period 1951–2015 (Fig. 6), including individual and multi‐year growth depressions, although the magnitude of these growth depressions was not reproduced by the models (Appendices S12 and S14). While correlations were low in some regions, it should be noted that errors in the prediction of RE propagate into the prediction of RWI. Indeed, in several of the regions where the model performed poorly, this was associated with lower model skill at predicting observed RE.

Figure 6.

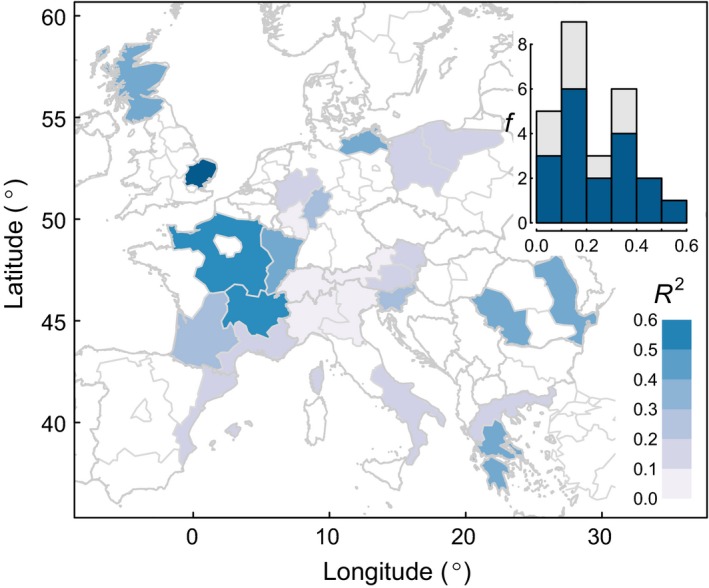
Figure 6

Open in a new tab

Comparison of predicted and observed tree ring chronologies from independent validation regions. RWI was predicted for each region using the multi‐group model. Note that in these models, RE was predicted using climate data, and predicted RE is then used in the model predicting RWI. The inset frequency plot shows the distribution of R 2, with light grey bars indicating regions where the regional RWI chronology shows low intraregion synchrony (mean correlation between sites < 0.3, see Appendix S3).

Then, we fitted the model structure in Fig. 3 individually to eight regions that had not been used in the model development due to smaller sample sizes. The reduced number of linkages in the optimal model allowed model fitting for regions with ≥ 45 years of data (Kline 2005) These individually fitted models (Fig. 5) supported the results of the optimal models for the five model development regions (Fig. 3), demonstrating that RE and PRE MJJ are major drivers of growth. Seven of the eight models passed the GOF tests (DE8 failed, and was not included further). RE had a significant negative influence on RWI in six of these seven remaining validation models (in addition to the significant negative influence in four of the five original models), and was the largest direct or indirect effect on growth in five regions. PRE MJJ had a significant positive influence on growth in one region (DEA), and was positive but insignificant in all other regions except AT3. The influence of MAX JJ was always insignificant, and was negative in all regions except DEB and AT3.

Figure 5.

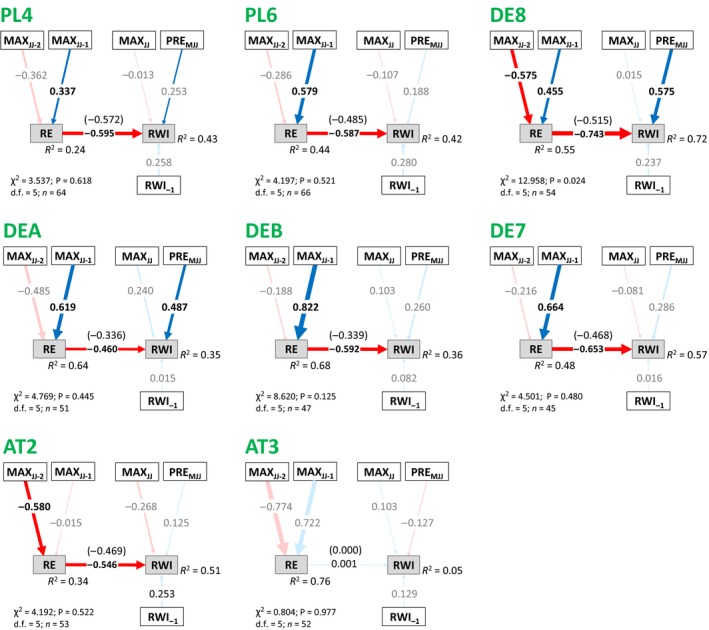
Figure 5

Open in a new tab

Model in Figure 3 fitted individually to each of an additional eight validation regions with ≥ 45 complete observations. Blue and red arrows indicate positive and negative relationships respectively. Numbers on the arrows indicate the standardised path coefficients, with arrow thickness proportional to the coefficient strength. Coefficients in parenthesis refer to raw coefficients. Pale colours indicate non‐significant pathways (P < 0.05). The proportion of explained variance (R 2) for each endogenous variable is also shown.

Discussion

Across a wide geographical region, a simple model structure with direct influences of summer precipitation and temperature, a negative impact of reproductive effort and an autoregressive term was consistent with observed data (12 of 13 models passed the GOF tests), and explained a high proportion of observed variation in growth in most regions. While the coefficients associated with each linkage showed regional variability (Figs 3 and 5), our results show that interannual variation in growth in F. sylvatica can be adequately explained by a framework of direct growing‐season climate effects and climatically driven variation in annual allocation to reproduction. Importantly, in eight of twelve individually fitted models (Figs 3 and 5), the main factor driving interannual variation in ring width was allocation to reproduction (RE) (Figs 3 and 5). The influence of climate on growth varied in importance (and direction) between regions, but RE had a consistently negative effect on growth; i.e. mast years reduced growth. Importantly, the RE influence was consistent across the species’ geographic distribution, generalising the results of regionally focused studies (Drobyshev et al. 2010; Muller‐Haubold et al. 2013; Hacket‐Pain et al. 2017). In our analysis, in seven of the twelve individually fitted models, high RE (a mast year) was associated with a larger growth reduction than a dry summer with precipitation one standard deviation below the mean (and in an additional region the coefficients were equal in magnitude). As years of high RE usually occur more frequently than dry or warm summers, this implies that RE has a greater effect on growth than these climate variables. We note that the window used for growing season climate influences on growth was fixed for all regions, and other climatic influences on growth were not included in our analysis, such as late frost events (Príncipe et al. 2017). If the climate window were optimised for individual regions, the relative importance of direct climate influences and RE may change and the overall variance explained by the models would increase (Lebourgeois et al. 2005; Hartl‐Meier et al. 2014). Weaker relationships between intraregion RE and RWI were found in some regions, which may result from variation in the strength of growth‐reproduction trade‐offs among populations (Sletvold & Agren 2015), perhaps due to differences in non‐structural carbohydrate (NSC) storage. However, variation between regions could also be related to the data used to characterise reproductive effort (Ascoli et al. 2017a). Intraregions RE correlations were generally high (Fig. 2 and Appendix S2), but fine‐scale variations in reproduction effort may not be captured by the data used in this study (Wohlgemuth et al. 2016). Nevertheless, our results provide strong evidence that allocation to reproduction has a consistent negative effect on the growth of F. sylvatica, and can explain a substantial part of the observed interannual variation in ring width (Drobyshev et al. 2010; Muller‐Haubold et al. 2013; Hacket‐Pain et al. 2017).

Furthermore, because RE was itself correlated with temperature from previous summers (Fig. 3, and see also Vacchiano et al. 2017), an important indirect temperature control on growth was revealed. RWI is frequently reported to be negatively correlated with previous summer temperatures (Babst et al. 2013; Hartl‐Meier et al. 2014; Hacket‐Pain et al. 2016), but comparing alternative models indicated that for our data, the most parsimonious model included only indirect pathways through RE (Figs 3 and 5). In other words, adding direct links between previous summer temperature and growth did not improve the model skill at reproducing RWI. We interpret this to suggest that lagged correlations between growth and previous years temperature are largely a consequence of the interplay with reproduction (masting) (Hacket‐Pain et al. 2015), rather than resulting from other ‘carry‐over’ effects. Further evidence to support this conclusion comes from the consistent direction of the indirect temperature influences. While the coefficients associated with the direct MAX JJ ‐RWI linkage varied from positive to negative with elevation in central Europe, the influences of previous summers’ temperature through RE were consistently negative (Figs 3 and 5). This indicates that the lagged negative correlations between RWI and previous summer temperature (MAX JJ‐1) are not primarily driven by ‘carry‐over’ effects of hot summers on internal resources levels (e.g. NSC) (Guillemot et al. 2017), as the influence of growing season temperature (and precipitation) on growth switches sign, but the lagged effects do not. Furthermore, regions with weaker RE‐RWI relationships also had weaker bivariate correlations between MAX JJ‐1 and RWI (Fig. 3 and Appendix S6). However, we acknowledge that other mechanisms act over multiple years to create lagged effects on growth, including NSC dynamics, and needle, leaf and root dynamics (e.g. Fritts 1976). These climate‐dependent processes are also important controls of growth in F. Sylvatica, and may be the main drivers of lagged climate correlations in species that do not exhibit one or more of the key characteristics that underpin the climate‐reproduction‐growth interplay that we have explored here. Many tree species or populations do not have synchronised and highly variable investment in reproduction (masting) (Herrera et al. 1998), show weak relationships between climate and reproductive effort (Vacchiano et al. 2017; Patterson & Knapp 2018), or do not exhibit a strong negative relationship between reproductive effort and radial growth (e.g. Lebourgeois et al. 2018; Patterson & Knapp 2018). For example interplay with reproduction seems unlikely to explain the lagged effects of drought on growth in non‐masting conifers growing in the southern and western North America (e.g. Anderegg et al. 2015; Peltier et al. 2018).

Consequently, the indirect influence of MAX JJ‐1 on growth (through RE) was an important climatic driver of growth, and in half of the regions (6/12) the total effect of MAX JJ‐1 on growth was greater than the direct influence of growing season climate (MAX JJ or PRE MJJ). Furthermore, in this study we characterised RE using a binary measure of allocation to reproduction. Higher resolution data may reveal that the variation in RWI explained by reproductive effort is greater than we found here (Hacket‐Pain et al. 2017). It is also notable that alternative models that only included indirect pathways for the effects of MAX JJ‐1 and MAX JJ‐2 through RE captured observed variation in RWI more successfully than when only direct links were included (Appendix S10). This indicates that the ability of MAX JJ‐1 and MAX JJ‐2 to predict RWI is improved when they are combined to predict the probability of a year with high RE (i.e. a mast year). In other words, models that included climate effects through RE were better at predicting growth than alternative models that included direct lagged effects on growth (MAX JJ‐1 and MAX JJ‐2) but no influence of RE (Appendix S10).

Our results imply that adequately explaining observed variation in tree growth requires accounting for flexible allocation of resources, including reproduction, which is a major sink for carbohydrates and nutrients and is highly variable across years (Muller‐Haubold et al. 2013; Pearse et al. 2016). In particular, the effect of reproductive allocation on growth will be an important factor determining the response of growth to future climate changes. Some studies have reported increased investment in reproduction in recent decades (Allen et al. 2014), which may have negative effects on forest productivity over short and longer timescales, analogous to the effects of changes in the occurrence of insect outbreaks (Peters et al. 2017). Indeed, our results show that a major source of uncertainty in the prediction of future changes in tree growth may originate from uncertainty in the response of tree reproductive effort to climate change (Ascoli et al. 2017b; Pearse et al. 2017). The proximate drivers of variable seed production in F. sylvatica are still uncertain, but the positive correlation between previous summer temperature and seed production has been linked to floral primordia differentiation (Drobyshev et al. 2010; Vacchiano et al. 2017). The negative correlation with MAXJJ‐2 may be related to climate effects on resource accumulation (Pearse et al. 2016; Allen et al. 2017; Ascoli et al. 2017b).

Our simple models explain a high proportion of the observed variance in growth. In the twelve regions where models were fitted individually, the combination of growing season precipitation, temperature, previous summer's growth and RE could explain ≥ 35% of the observed variance in interannual growth in half of the regions (R 2 ≥ 50% in three of the twelve regions) (Figs 3 and 5). Generally, the lowest tree growth was associated with a combination of high RE and dry summers. While these terms were included in the final models, they did not fully reproduce the magnitude of observed growth reductions in years of extreme low growth (e.g. 1976). This may be due to nonlinear responses of growth to climate, particularly under climate extremes (Appendix S6), and to interactions, such as between low precipitation and/or high vapour pressure deficit and high temperature, or interactions between low precipitation and reproductive effort. A potential effect of tree age on allocation to reproduction was also not included in our model (Thomas 2011). Other climate factors that we did not include in our models may be important controls on growth locally (Piovesan & Schirone 2000; Skomarkova et al. 2006; Drobyshev et al. 2010). For example in mountain and upland regions late spring frost events occurring after leaf‐out are associated with narrow tree rings (Dittmar et al. 2006; Príncipe et al. 2017), and low growth in the DE2‐high chronology in 1927, 1928, 1953 and 2011 correspond to late frost events reported in the region by Dittmar et al. (2006) and Menzel et al. (2015).

Our multi‐group model reproduced elements of the independent RWI series across the species’ geographic distribution, with higher correspondence between observed and predicted RWI in Romania, France and the UK (Fig. 6). As expected, the explained variance in these regions was lower than for the individually fitted models (Figs 3 and 5), as the multi‐group model used for predicting RWI in the independent datasets did not allow for geographic variation in the sensitivity of RWI to growing season climate or RE, which was observed in this and previous studies (Piovesan et al. 2005; Cavin & Jump 2017). For example the coefficient associated with summer precipitation was highest in westerly regions (UKJ, DE7, DE1), and was frequently insignificant in eastern regions (AT2, AT3, DE2, PL6). In particular, the model was less successful at predicting RWI in the Alpine region (Austria, Switzerland, northern Italy). It should be noted that interannual growth synchrony was low in many of these topographically complex regions (Appendix S3), indicating diverse drivers of growth or microclimatic variation in topographically complex regions (Hartl‐Meier et al. 2014; Hacket‐Pain & Friend 2017). Additionally, previous analysis has revealed that while broad‐scale climate cues of mast years are consistent between populations in F. sylvatica (Vacchiano et al. 2017), there are some differences in the seasonality and nature of cues between populations. Consequently, we would expect the multi‐group model to vary in its ability to accurately predict RE.

Conclusions

We have found that climatically driven variation in reproductive effort is an important control on interannual growth variability in F. sylvatica and appears to be the dominant factor determining interannual radial growth variability in many populations. Additionally, the climatic control of reproductive effort creates indirect climate effects on growth, generating lagged correlations between summer temperature and growth. A similar interplay may be important in explaining antecedent climate effects on growth in other species (Anderegg et al. 2015; Peltier et al. 2018), but this remains to be fully tested. Importantly, this study also demonstrates that categorical and regional‐resolution data on mast years can provide useful information to untangle the interplay of climate, reproduction, and tree growth. These results have important implications for models of tree growth, including those that resolve annual ring width or simulate tree growth or NPP. Such models have tended to focus on the direct effects of growing season climate on growth, using approaches that range from phenomenological (e.g. Tolwinski‐Ward et al. 2011) to physiologically focused process‐based models (e.g. Friend & White 2000). Our results demonstrate that climatically controlled variation in allocation to reproduction is an important control on tree growth (at least for beech), and contribute to a growing body of research that indicates that variable resource allocation at a variety of timescales is a key factor influencing tree growth (Drobyshev et al. 2010; Thomas 2011; Muller‐Haubold et al. 2013; Hacket‐Pain et al. 2017). For example Guillemot et al. (2015) suggest that increased investment in reproduction with tree age could explain age‐related declines in stem biomass increment (see also Thomas 2011). Decadal variations in reproductive effort (e.g. frequency of ‘mast years’) (Drobyshev et al. 2014; Ascoli et al. 2017b) may have effects on growth trends analogous to the influence of cyclic insect outbreaks (Peters et al. 2017). Consequently, we argue that including variable resource allocation in models will increase the ability to reproduce observed variability in tree growth and growth‐climate relationships. It may also improve predictions of future changes in tree growth, which will at least in part be dependent on the response of reproduction to environmental change.

Statement of authorship

AJHP conceived and designed the study, conducted analysis and wrote the manuscript. CZ contributed to study design, preliminary analysis and the manuscript preparation. GV and DA helped to conceive the study, prepared datasets and contributed to the manuscript preparation. ADF contributed to the initial development of the study concept. All authors contributed data and contributed to manuscript revision and editing.

Supporting information

 

Click here for additional data file. (3.3MB, pdf)

Acknowledgements

We are grateful to Wolfram Elling, Christoph Dittmar and ITRDB contributors who provided data, and Janet Maringer who helped to assemble the masting database ‘MASTREE’. We thank Andrew Tanentzap for advice and guidance on the use of SEM. We are grateful to the three anonymous reviewers whose comments and suggestions improved the manuscript. AJHP acknowledges funding support from the John Fell Oxford University Press (OUP) Research Fund REF161/025. Dataset assembly and preliminary discussions between AJHP, GV and DA occurred with support from the European Union (EU) COST Action PROFOUND (FP1304). AM and CZ acknowledge funding from the European Research Council (FP7/2007‐2013)/ERC grant agreement no. 282250. JK, LM, MM‐T, RW, MW acknowledge support by the research training group RESPONSE funded by the German Research Council (DFG Fi 846/8‐1, DFG GRK2010). FB was supported, in part, by a grant from the Office of Research and Innovation at the University of Nevada, Reno (USA).

References

  1. Allen, R.B. , Hurst, J.M. , Portier, J. & Richardson, S.J. (2014). Elevation‐dependent responses of tree mast seeding to climate change over 45 years. Ecol. Evol., 4, 3525–3537. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Allen, R.B. , Millard, P. & Richardson, S.J. (2017). A resource centric view of climate and mast seeding in trees In: Progress in Botany (eds Cánovas F., Lüttge U. & Matyssek R.). Springer, Cham, pp. 233–268. [Google Scholar]
  3. Anderegg, W.R.L. , Schwalm, C. , Biondi, F. , Camarero, J.J. , Koch, G. , Litvak, M. et al (2015). Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models. Science, 349, 528–532. [DOI] [PubMed] [Google Scholar]
  4. Ascoli, D. , Maringer, J. , Hacket‐Pain, A. , Conedera, M. , Drobyshev, I. , Motta, R. et al (2017a). Two centuries of masting data for European beech and Norway spruce across the European continent. Ecology, 98, 1473. [DOI] [PubMed] [Google Scholar]
  5. Ascoli, D. , Vacchiano, G. , Turco, M. , Conedera, M. , Drobyshev, I. , Maringer, J. et al (2017b). Inter‐annual and decadal changes in teleconnections drive continental‐scale synchronization of tree reproduction. Nat. Commun., 8, 2205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Babst, F. , Poulter, B. , Trouet, V. , Tan, K. , Neuwirth, B. , Wilson, R. et al (2013). Site‐ and species‐specific responses of forest growth to climate across the European continent. Glob. Ecol. Biogeogr., 22, 706–717. [Google Scholar]
  7. Breda, N. , Huc, R. , Granier, A. & Dreyer, E. (2006). Temperate forest trees and stands under severe drought: a review of ecophysiological responses, adaptation processes and long‐term consequences. Ann. For. Sci., 63, 625–644. [Google Scholar]
  8. Cavin, L. & Jump, A.S. (2017). Highest drought sensitivity and lowest resistance to growth suppression are found in the range core of the tree Fagus sylvatica L. not the equatorial range edge. Glob. Change Biol., 23, 362–379. [DOI] [PubMed] [Google Scholar]
  9. Cook, E.R. & Peters, K. (1981). The smoothing spline: a new approach to standardizing forest interior tree‐ring width series for dendroclimatic studies. Tree‐ring Bull., 41, 45–53. [Google Scholar]
  10. Davi, H. , Cailleret, M. , Restoux, G. , Amm, A. , Pichot, C. & Fady, B. (2016). Disentangling the factors driving tree reproduction. Ecosphere, 7, e01389. [Google Scholar]
  11. Dittmar, C. , Fricke, W. & Elling, W. (2006). Impact of late frost events on radial growth of common beech (Fagus sylvatica L.) in Southern Germany. Eur. J. Forest Res., 125, 249–259. [Google Scholar]
  12. Drobyshev, I. , Overgaard, R. , Saygin, I. , Niklasson, M. , Hickler, T. , Karlsson, M. et al (2010). Masting behaviour and dendrochronology of European beech (Fagus sylvatica L.) in southern Sweden. For. Ecol. Manage., 259, 2160–2171. [Google Scholar]
  13. Drobyshev, I. , Niklasson, M. , Mazerolle, M.J. & Bergeron, Y. (2014). Reconstruction of a 253‐year long mast record of European beech reveals its association with large scale temperature variability and no long‐term trend in mast frequencies. Agric. For. Meteorol., 192, 9–17. [Google Scholar]
  14. EURFORGEN (2009). Distribution map of Beech (Fagus sylvatica). Available at: www.euforgen.org. Last accessed 1 April 2017.
  15. Friend, A.D. & White, A. (2000). Evaluation and analysis of a dynamic terrestrial ecosystem model under preindustrial conditions at the global scale. Global Biogeochem. Cycles, 14, 1173–1190. [Google Scholar]
  16. Fritts, H. (1976). Tree Rings and Climate. Academic Publishers, New York. [Google Scholar]
  17. Galiano, L. , Martinez‐Vilalta, J. & Lloret, F. (2011). Carbon reserves and canopy defoliation determine the recovery of Scots pine 4 yr after a drought episode. New Phytol., 190, 750–759. [DOI] [PubMed] [Google Scholar]
  18. Grace, J. (2006). Structural Equation Modeling and Natural Systems. Cambridge University Press, Cambridge, UK. [Google Scholar]
  19. Grace, J.B. & Bollen, K.A. (2005). Interpreting the results from multiple regression and structural equation models. Bull. Ecol. Soc. Am., 86, 283–295. [Google Scholar]
  20. Guillemot, J. , Martin‐StPaul, N.K. , Dufrene, E. , Francois, C. , Soudani, K. , Ourcival, J.M. et al (2015). The dynamic of the annual carbon allocation to wood in European tree species is consistent with a combined source‐sink limitation of growth: implications for modelling. Biogeosciences, 12, 2773–2790. [Google Scholar]
  21. Guillemot, J. , Francois, C. , Hmimina, G. , Dufrene, E. , Martin‐StPaul, N.K. , Soudani, K. et al (2017). Environmental control of carbon allocation matters for modelling forest growth. New Phytol., 214, 180–193. [DOI] [PubMed] [Google Scholar]
  22. Hacket‐Pain, A.J. & Friend, A.D. (2017). Increased growth and reduced summer drought limitation at the southern limit of Fagus sylvatica L., despite regionally warmer and drier conditions. Dendrochronologia, 44, 22–30. [Google Scholar]
  23. Hacket‐Pain, A.J. , Friend, A.D. , Lageard, J.G.A. & Thomas, P.A. (2015). The influence of masting phenomenon on growth‐climate relationships in trees: explaining the influence of previous summers’ climate on ring width. Tree Physiol., 35, 319–330. [DOI] [PubMed] [Google Scholar]
  24. Hacket‐Pain, A.J. , Cavin, L. , Friend, A.D. & Jump, A.S. (2016). Consistent limitation of growth by high temperature and low precipitation from range core to southern edge of European beech indicates widespread vulnerability to changing climate. Eur. J. Forest Res., 135, 897–909. [Google Scholar]
  25. Hacket‐Pain, A.J. , Lageard, J.G.A. & Thomas, P.A. (2017). Drought and reproductive effort interact to control growth of a temperate broadleaved tree species (Fagus sylvatica). Tree Physiol., 37, 744–754. [DOI] [PubMed] [Google Scholar]
  26. Harris, I. , Jones, P.D. , Osborn, T.J. & Lister, D.H. (2014). Updated high‐resolution grids of monthly climatic observations – the CRU TS3.10 Dataset. Int. J. Climatol., 34, 623–642. [Google Scholar]
  27. Hartl‐Meier, C. , Dittmar, C. , Zang, C. & Rothe, A. (2014). Mountain forest growth response to climate change in the Northern Limestone Alps. Trees‐Struct. Funct., 28, 819–829. [Google Scholar]
  28. Herrera, C.M. , Jordano, P. , Guitian, J. & Traveset, A. (1998). Annual variability in seed production by woody plants and the masting concept: Reassessment of principles and relationship to pollination and seed dispersal. Am. Nat., 152, 576–594. [DOI] [PubMed] [Google Scholar]
  29. Kline, R.B. (2005). Principles and Practice of Structural Equation Modeling. Guilford Publications, New York. [Google Scholar]
  30. Korkmaz, S. , Goksuluk, D. & Zararsiz, G. (2014). MVN: an R package for assessing multivariate normality. R. J., 6, 151–162. [Google Scholar]
  31. Lebourgeois, F. , Breda, N. , Ulrich, E. & Granier, A. (2005). Climate‐tree‐growth relationships of European beech (Fagus sylvatica L.) in the French Permanent Plot Network (RENECOFOR). Trees‐Struct. Funct., 19, 385–401. [Google Scholar]
  32. Lebourgeois, F. , Delpierre, N. , Dufrêne, E. , Cecchini, S. , Macé, S. , Croisé, L. et al (2018). Assessing the roles of temperature, carbon inputs and airborne pollen as drivers of fructification in European temperate deciduous forests. Eur. J. Forest Res., 137, 1612–4677. [Google Scholar]
  33. Leuschner, C. , Backes, K. , Hertel, D. , Schipka, F. , Schmitt, U. , Terborg, O. et al (2001). Drought responses at leaf, stem and fine root levels of competitive Fagus sylvatica L. and Quercus petraea (Matt.) Liebl. trees in dry and wet years. For. Ecol. Manage., 149, 33–46. [Google Scholar]
  34. Menzel, A. , Helm, R. & Zang, C. (2015). Patterns of late spring frost leaf damage and recovery in a European beech (Fagus sylvatica L.) stand in south‐eastern Germany based on repeated digital photographs. Front. Plant Sci., 6, 110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Muller‐Haubold, H. , Hertel, D. , Seidel, D. , Knutzen, F. & Leuschner, C. (2013). Climate responses of aboveground productivity and allocation in Fagus sylvatica: a transect study in mature forests. Ecosystems, 16, 1498–1516. [Google Scholar]
  36. Mund, M. , Kutsch, W.L. , Wirth, C. , Kahl, T. , Knohl, A. , Skomarkova, M.V. et al (2010). The influence of climate and fructification on the inter‐annual variability of stem growth and net primary productivity in an old‐growth, mixed beech forest. Tree Physiol., 30, 689–704. [DOI] [PubMed] [Google Scholar]
  37. Ogle, K. , Barber, J.J. , Barron‐Gafford, G.A. , Bentley, L.P. , Young, J.M. , Huxman, T.E. et al (2015). Quantifying ecological memory in plant and ecosystem processes. Ecol. Lett., 18, 221–235. [DOI] [PubMed] [Google Scholar]
  38. Patterson, T. & Knapp, P. (2018). Long‐leaf pine cone‐radial growth relationships in the southeastern USA. Dendrochronologia, 50, 134–141. [Google Scholar]
  39. Pearse, I.S. , Koenig, W.D. & Kelly, D. (2016). Mechanisms of mast seeding: resources, weather, cues, and selection. New Phytol., 212, 546–562. [DOI] [PubMed] [Google Scholar]
  40. Pearse, I.S. , LaMontagne, J.M. & Koenig, W.D. (2017). Inter‐annual variation in seed production has increased over time (1900–2014). Proc. R. Soc. B Biol. Sci., 284, 20171666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Peltier, D.M.P. , Barber, J.J. & Ogle, K. (2018). Quantifying antecedent climatic drivers of tree growth in the Southwestern US. J. Ecol., 106, 613–624. [Google Scholar]
  42. Peters, R.L. , Klesse, S. , Fonti, P. & Frank, D.C. (2017). Contribution of climate vs. larch budmoth outbreaks in regulating biomass accumulation in high‐elevation forests. For. Ecol. Manage., 401, 147–158. [Google Scholar]
  43. Piovesan, G. & Schirone, B. (2000). Winter North Atlantic oscillation effects on the tree rings of the Italian beech (Fagus sylvatica L.). Int. J. Biometeorol., 44, 121–127. [DOI] [PubMed] [Google Scholar]
  44. Piovesan, G. , Biondi, F. , Bernabei, M. , Di Filippo, A. & Schirone, B. (2005). Spatial and altitudinal bioclimatic zones of the Italian peninsula identified from a beech (Fagus sylvatica L.) tree‐ring network. Acta Oecol., 27, 197–210. [Google Scholar]
  45. Príncipe, A. , van der Maaten, E. , van der Maaten‐Theunissen, M. , Struwe, T. , Wilmking, M. & Kreyling, J. (2017). Low resistance but high resilience in growth of a major deciduous forest tree (Fagus sylvatica L.) in response to late spring frost in southern Germany. Trees, 31, 743–751. [Google Scholar]
  46. R Development Core Team (2016). R: A Language and Environment for Statistical Computing. 3.3.1 edn R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
  47. Rammig, A. , Wiedermann, M. , Donges, J.F. , Babst, F. , von Bloh, W. , Frank, D. et al (2015). Coincidences of climate extremes and anomalous vegetation responses: comparing tree ring patterns to simulated productivity. Biogeosciences, 12, 373–385. [Google Scholar]
  48. Richardson, A.D. , Carbone, M.S. , Keenan, T.F. , Czimczik, C.I. , Hollinger, D.Y. , Murakami, P. et al (2013). Seasonal dynamics and age of stemwood nonstructural carbohydrates in temperate forest trees. New Phytol., 197, 850–861. [DOI] [PubMed] [Google Scholar]
  49. Rosseel, Y. (2012). lavaan: an R package for structural equation modeling. J. Stat. Softw., 48, 1–36. [Google Scholar]
  50. Selas, V. , Piovesan, G. , Adams, J.M. & Bernabei, M. (2002). Climatic factors controlling reproduction and growth of Norway spruce in southern Norway. Can. J. For. Res., 32, 217–225. [Google Scholar]
  51. Skomarkova, M.V. , Vaganov, E.A. , Mund, M. , Knohl, A. , Linke, P. , Boerner, A. et al (2006). Inter‐annual and seasonal variability of radial growth, wood density and carbon isotope ratios in tree rings of beech (Fagus sylvatica) growing in Germany and Italy. Trees‐Struct. Funct., 20, 571–586. [Google Scholar]
  52. Sletvold, N. & Agren, J. (2015). Climate‐dependent costs of reproduction: Survival and fecundity costs decline with length of the growing season and summer temperature. Ecol. Lett., 18, 357–364. [DOI] [PubMed] [Google Scholar]
  53. Taylor, B. & Parida, B. (2016). Cruts: Interface to climatic research unit time‐series version 3.21 data. Available at: https://CRAN.R-project.org/package=cruts. Last accessed 1 April 2017.
  54. Thomas, S.C. (2011). Age‐related changes in tree growth and functional biology: the role of reproduction In: Size‐ and Age‐Related Changes in Tree Structure and Function (eds Meinzer F., Lachenbruch B. & Dawson T.). Springer, Dordrecht, pp. 33–64. [Google Scholar]
  55. Tolwinski‐Ward, S.E. , Evans, M.N. , Hughes, M.K. & Anchukaitis, K.J. (2011). An efficient forward model of the climate controls on interannual variation in tree‐ring width. Clim. Dyn., 36, 2419–2439. [Google Scholar]
  56. Vacchiano, G. , Hacket‐Pain, A. , Turco, M. , Motta, R. , Maringer, J. , Conedera, M. et al (2017). Spatial patterns and broad‐scale weather cues of beech mast seeding in Europe. New Phytol., 215, 595–608. [DOI] [PubMed] [Google Scholar]
  57. Wohlgemuth, T. , Nussbaumer, A. , Burkart, A. , Moritzi, M. , Wasem, U. & Moser, B. (2016). Muster und treibende Kräfte der Samenproduktion bei Waldbäumen. Schweiz Z Forstwes, 167, 316–324. [Google Scholar]
  58. Woodhouse, C.A. (2003). A 431‐yr reconstruction of western Colorado snowpack from tree rings. J. Clim., 16, 1551–1561. [Google Scholar]
  59. Zang, C. , Hacket‐Pain, A.J. , Jump, A.S. , Biondi, F. , Menzel, A. , Buras, A. et al (2018). Climate and drought responses in a continent‐wide tree‐ring network of European beech (Fagus sylvatica) In: Geophysical Research Abstracts Gottigen, Germany: EGU2018‐13454. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

 

Click here for additional data file. (3.3MB, pdf)

Articles from Ecology Letters are provided here courtesy of Wiley

RESOURCES