Evaluating vaccination strategies for tuberculosis in endemic and non-endemic settings

Abstract

According to the World Health Organization, tuberculosis (TB) is the leading cause of death from infectious disease worldwide (WHO, 2017). While there is no effective vaccine against adult pulmonary TB, more than a dozen vaccine candidates are in the clinical trial pipeline. These include both pre-exposure vaccines to prevent initial infections and post-exposure vaccines to prevent reactivation of latent disease. Many epidemiological models have been used to study TB, but most have not included a continuous age structure and the possibility of both pre- and post-exposure vaccination. Incorporating age-dependent death rates, disease properties, and social contact data allows for more realistic modeling of disease spread. We propose a continuous age-structured model for the epidemiology of tuberculosis with pre- and post-exposure vaccination. We use uncertainty and sensitivity analysis to make predictions about the efficacy of different vaccination strategies in a non-endemic setting (United States) and an endemic setting (Cambodia). In particular, we determine optimal age groups to target for pre-exposure and post-exposure vaccination in both settings. We find that the optimal age groups tend to be younger for Cambodia than for the US, and that post-exposure vaccination has a significantly larger effect than pre-exposure vaccination in the US.

1. Introduction

Tuberculosis (TB) is an infectious disease caused by the bacterium Mycobacterium tuberculosis (Mtb), and is currently the leading cause of death from infectious disease worldwide. TB most commonly infects the lungs and is spread through aerosol when an infected individual coughs, sneezes, speaks, or sings. Upon infection, most people do not develop symptoms; this is called latent TB infection (LTBI). People with latent TB are not infectious, but may reactivate and develop active TB disease later in life. It has been estimated that one-third of the world’s population is infected with latent TB [1].

There have been many modeling efforts to understand TB epidemiology. Previous models have explored the effects of socio-demographic factors [2], age structure [2, 3, 4, 5], treatment regimens and diagnostics [4, 6], pre-exposure vaccination [4, 6, 7, 8, 5, 9, 10, 3, 11], post-exposure vaccination [4, 9, 10, 11], and vaccine cost-effectiveness [12]. A review of mathematical models for epidemiological impact of TB vaccines is provided in [13]. Despite substantial work in this field, there has been a lack of models that include continuous age-structure and both pre- and post-exposure vaccination. [4] includes pre- and post-exposure vaccination, but the pre-exposure vaccine is only administered to newborns and the age structure is implemented via compartments in an ordinary differential equation (ODE) model rather than a continuous age variable. [3] utilizes a continuous age structure and includes pre-exposure vaccination, but does not consider effects of post-exposure vaccination. [2] utilized an age-structured individual-based model, but did not study vaccination.

Since TB is spread directly from person to person, mixing patterns have a large influence on its epidemiology. Research on social contacts and mixing patterns reveals significant age preferences that drive disease spread, which supports the use of an age-structured model [14]. Data on mixing patterns by age can be found in [15] (for 8 European countries), [16] (Netherlands), and [17] (United States). Mixing patterns for more than 100 other countries have been estimated in [18]. The application of such mixing patterns to age-structured epidemiological models is discussed in [19]. Using an age-structured model also allows us to study vaccination strategies targeted toward specific age groups, and to predict optimal vaccination strategies in different settings.

Pre- and post-exposure vaccines for TB

Currently, the only licensed vaccine for tuberculosis is the bacille Calmette-Guérin (BCG) vaccine. While it is not widely used in the United States, it is often given to infants and children in low-income countries where TB is common [20]. BCG is effective in protecting against certain types of non-pulmonary TB in children, but can be ineffective at preventing pulmonary TB in adults. Estimates of protection by BCG against pulmonary TB range from 0 to 80% efficacious [21]. More than a dozen other TB vaccines are in clinical trials as of 2017 [22, 23].

BCG is currently used as a pre-exposure vaccine, i.e. it is given to individuals who have not previously been infected with TB to prevent future infection. These types of vaccines are also referred to as prophylactic or preventive vaccines. Other pre-exposure vaccines currently in clinical trials include the H1 and H4 subunit vaccines [24, 25].

Another vaccination option is post-exposure vaccines which are designed to prevent reactivation or reinfection in people who have already been infected with Mtb and are clinically latent, or LTBI. Recent advances in post-exposure TB vaccines could prove highly effective at reducing overall incidence given the high burden of latent TB infection globally. The recombinant BCG vaccine, VPM1002, is currently being developed as a post-exposure vaccine [26]. The most promising post-exposure vaccine candidate to date is the M72/AS01_E vaccine [27]. Some vaccines, such as the H56, ID93, and M72 subunit vaccines, are designed to provide both pre-exposure and post-exposure protection and are currently being evaluated in both non-human primate and human settings [28, 29, 30, 31].

Vaccines may lose efficacy over time, a process referred to as vaccine waning. For example, it has been shown that BCG may lose more than half of its efficacy within 10–15 years after vaccination, though the rate of waning varies significantly across different populations [32]. Vaccine waning rates can be difficult to measure because they require long-term follow up of vaccinated individuals. Further, for recently developed vaccines such as those discussed above, these type of data are not available. Still, this effect should be considered in determining the best age groups to target for vaccination. Since vaccine efficacy can wane over time, it is not always optimal to vaccinate young children; rather, it may be more beneficial to target age groups that are at high risk of infection.

In this paper, we present an SEIR model for TB epidemiology that incorporates a continuous age structure. First, we use this model to explore differences between TB dynamics in endemic (high prevalence) and non-endemic (low prevalence) settings. In this work, we compare model predictions for the United States and Cambodia. We choose to focus on Cambodia as an endemic setting due to its high prevalence of TB and its low prevalence of HIV-TB coinfection and multi-drug-resistant TB to control somewhat for those variables in the system. Next, we consider both pre- and post-exposure vaccination strategies. Since the efficacy of a vaccination strategy may depend heavily on population demographics and prevalence of TB in the area, we expect that strategies for vaccination will be different. We also identify optimal vaccination strategies; as expected, the results are quite different between these two demographic settings.

2. Age-structured model with vaccination

Model formulation

To study vaccination outcomes, it is useful to consider the age structure of a population since vaccines are often targeted at specific age groups. Further, by including age-dependent death rates, disease properties, and contact rates, we are able to obtain a more detailed and realistic model than the traditional SEIR model. One benefit of using a PDE model rather than an agent-based model (ABM) is that computational time does not increase with the population size. For an ABM, it may become computationally infeasible to do a parameter search within a large population such as the United States.

In the United States, immigration plays a major role in the spread of tuberculosis, so to make the model as accurate as possible, it is crucial to include immigration dynamics. In 2016, 68.5% of reported TB cases in the U.S. occurred among non-US–born persons, and 12% of cases occurred among non-US–born persons who had been in the U.S. for less than one year [33]. We assume that immigrants do not have active infection at the time of arrival in the US, so immigrants may only contribute to the susceptible, exposed, and latent populations.

The total population is compartmentalized according to disease status: susceptible (S), exposed for the first time (E₀), latent (L), primary infection (I_p), endogenously reactivated (I_n), secondary exposure (E_s), and exogenously reinfected (I_x). Exposed refers to an individual who has been recently exposed to Mtb but has not yet cleared or contained the infection nor developed active disease. We incorporate age structure by adding a transport term to all of the equations. All state variables are functions of both time and age. Model parameters can also vary with age (this is left out of the notation for ease of readability). The birth rate b, is incorporated into the boundary conditions, i.e. S(t, 0) = b. All other populations are 0 at a = 0 (i.e. nobody is born exposed to TB).

We then include terms for vaccination to the SEIR scheme. Vaccination is incorporated by adding a compartment V_S of vaccinated susceptibles (pre-exposure) and V_L of vaccinated latent individuals (post-exposure). Individuals in V_S become infected at a lower rate than unvaccinated individuals. Individuals in V_L are less likely to develop an active infection than those in L. Vaccination rates and vaccine efficacy for both cases can be age-dependent. The full model structure is shown in Figure 1. The pathways S ↔ V_S and L ↔ V_L are bidirectional to represent vaccine waning. Any of these pathways can be turned off by setting the relevant model parameter to zero.

Figure 1: Model diagram with vaccination of susceptibles and the latently infected.

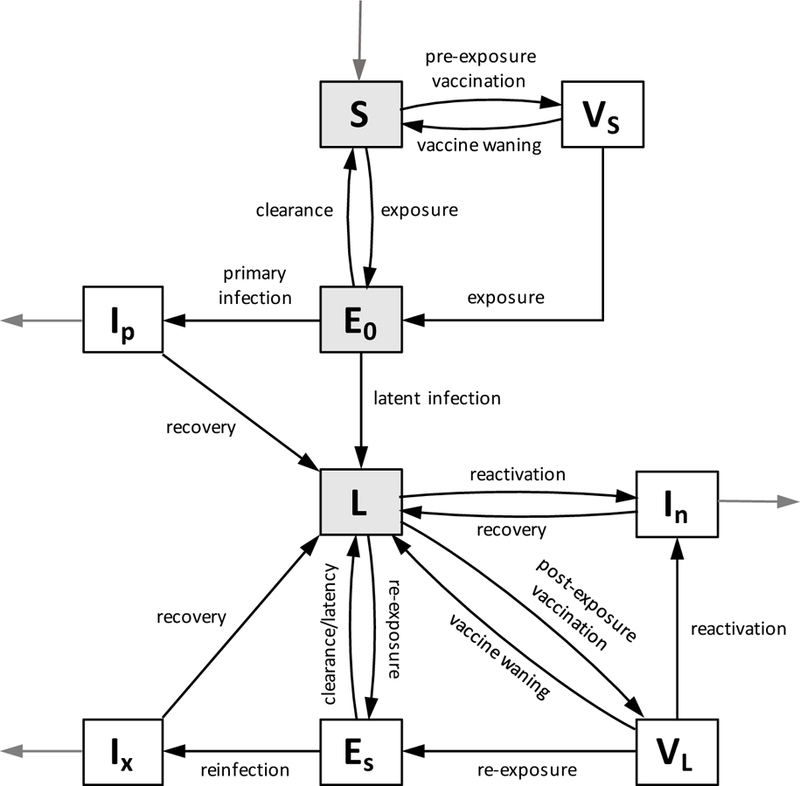
Gray compartments indicate compartments affected by immigration. Black arrows indicate movement between compartments, and gray arrows indicate birth and TB-related death.

The model equations are as follows.

$$\begin{gathered} \left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)S(t,a)=k\chi (1-p)E_0(t,\hspace{0.33em}a)-(\beta B(t,\hspace{0.33em}a)+\mu +{\psi }_s)S(t,\hspace{0.33em}a)+w_s{V}_s(t,\hspace{0.33em}a) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+(1-{\nu }_s)(1-u_e-u_{\ell })M(a) \end{gathered}$$

$$\left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)E_0(t,a)=\beta B(t,\hspace{0.33em}a)S(t,\hspace{0.33em}a)+{\text{γ}}_{s}B(t,\hspace{0.33em}a)V_s(t,\hspace{0.33em}a)-(k+\mu )E_0(t,\hspace{0.33em}a)+u_{e}M(a)$$

$$\left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)I_p(t,\hspace{0.33em}a)=pk{E}_0(t,\hspace{0.33em}a)-(d+\mu +{\mu }_T)I_p(t,\hspace{0.33em}a)$$

$$\begin{gathered} \left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)L(t,a)=k(1-p)(1-\chi )E_0(t,a)+k(1-(1-\sigma )p)E_s(t,a)+d{I}_{tot}(t,a) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-(\beta B(t,\hspace{0.33em}a)+r+\mu +{\psi }_{\ell })L(t,\hspace{0.33em}a)+w_{\ell }{V}_L(t,\hspace{0.33em}a)+(1-{\nu }_{\ell })u_{\ell }M(a) \end{gathered}$$

$$\left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)I_n(t,a)=rL(t,\hspace{0.33em}a)+r_v{V}_L(t,\hspace{0.33em}a)-(d+\mu +{\mu }_T)I_n(t,\hspace{0.33em}a)$$

$$\left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)E_s(t,a)=\beta B(t,\hspace{0.33em}a)L(t,\hspace{0.33em}a)+{\text{γ}}_{\ell }B(t,\hspace{0.33em}a)V_L(t,\hspace{0.33em}a)-(k+\mu )E_s(t,\hspace{0.33em}a)$$

$$\left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)I_x(t,\hspace{0.33em}a)=(1-\sigma )pk{E}_s(t,\hspace{0.33em}a)-(d+\mu +{\mu }_T)I_x(t,\hspace{0.33em}a)$$

$$\left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)V_S(t,\hspace{0.33em}a)={\psi }_{s}S(t,\hspace{0.33em}a)-({\text{γ}}_{s}B(t,\hspace{0.33em}a)+\mu +w_s)V_S(t,\hspace{0.33em}a)+{\nu }_s(1-u_e-u_{\ell })M(a)$$

$$\left(\frac{\partial }{\partial t}+\frac{\partial }{\partial a}\right)V_L(t,\hspace{0.33em}a)={\psi }_{\ell }L(t,\hspace{0.33em}a)-({\text{γ}}_{\ell }B(t,\hspace{0.33em}a)+r_v+\mu +w_{\ell })V_L(t,\hspace{0.33em}a)+{\nu }_{\ell }{u}_{\ell }M(a)$$

where

$$I_{tot}(t,\hspace{0.33em}a)=I_p(t,\hspace{0.33em}a)+I_n(t,\hspace{0.33em}a)+I_x(t,\hspace{0.33em}a)$$

$$B(t,\hspace{0.33em}a)=c(a){\int }_0^A\frac{I_{tot}(t,\hspace{0.33em}a\prime )}{N(t,\hspace{0.33em}a\prime )}P(t,\hspace{0.33em}a,a\prime )da\prime$$

$$N(t,\hspace{0.33em}a)=S(t,\hspace{0.33em}a)+E_0(t,\hspace{0.33em}a)+I_p(t,\hspace{0.33em}a)+L(t,\hspace{0.33em}a)+I_n(t,\hspace{0.33em}a)+E_s(t,\hspace{0.33em}a)+I_x(t,\hspace{0.33em}a)$$

This model is based on the work of Guzzetta et al. [2], and the functional form for B(t, a) is based on the system presented in [3]. Here, N (t, a) represents the total population of age a at time t. P (t, a, a′) gives the probability that an individual of age a has contact with an individual of age a′ given that it has a contact with a member of the population. A represents the maximum age of individuals; we use 100 years, but this can be varied. Thus B(t, a) gives the total probability that an individual of age a has contact with an infectious individual. c(a) is an age-specific per-capita activity rate in [0, 1] that modulates the maximal transmission rate β. M (a) represents the population density (by age) of incoming migrants. For initial conditions, we assume the V_S and V_L compartments to be empty. Descriptions of all parameters can be found in Table 1.

Table 1: Description of model parameters with units.

Values used for these parameters are given below in Table 2.

Parameter	Description	Unit
b	birth rate	ppl/yr
µ	natural mortality	yrs−1
µT	TB-related mortality	yrs−1
β	transmission rate	yrs−1
k	rate of flow out from exposure	yrs−1
p	probability of active disease upon infection	%
χ	clearance of first infections	%
σ	protection from exogenous reinfection	%
r	rate of endogenous reactivation	yrs−1
d	successful treatment rate	yrs−1
ue	proportion of migrants recently exposed to TB	%
Uℓ	proportion of migrants with latent TB	%
ψs, ψℓ	vaccination rates	yrs−1
νs, νℓ	proportion of susceptible/latent immigrants that are vaccinated	%
ws, wℓ	rates of vaccine waning	yrs−1
γs, γℓ	rates of transmission to vaccinated individuals	yrs−1
rv	reactivation rate of vaccinated latent individuals	yrs−1

Parametrization of the model in a non-endemic setting (US)

We refer to [2] for functional forms of age-dependent probability of primary infection (p) and protection from reinfection (σ).

$$p(a)=\left\{\begin{array}{ll}{p}_c\hfill & a\le 10\hspace{0.33em}\text{yrs}\hfill \\ a\frac{p_a-p_c}{10}+2p_c-p_a\hfill & 10\hspace{0.33em}\text{yrs}<a<20\hspace{0.33em}\text{yrs}\hfill \\ p_a\hfill & a\ge 20\hspace{0.33em}\text{yrs}\hfill \end{array}\right.$$

$$\sigma (a)=\left\{\begin{array}{ll}{\sigma }_c\hfill & a\le 10\hspace{0.33em}\text{yrs}\hfill \\ a\frac{{\sigma }_a-{\sigma }_c}{10}+2{\sigma }_c-{\sigma }_a\hfill & 10\hspace{0.33em}\text{yrs}\le a\le 20\hspace{0.33em}\text{yrs}\hfill \\ {\sigma }_a\hfill & a\ge 20\hspace{0.33em}\text{yrs}\hfill \end{array}\right.$$

These functional forms will be used for both the non-endemic and endemic settings. Parameter values given in [2] are σ_c = 0%, σ_a = 40%, p_c ∈ [1%, 10%], and p_a ∈ [6%, 20%]. In [2], an increasing function (linear growth followed by quadratic growth) was also used for reactivation rates. However, in our preliminary numerical experiments we found that this functional form makes it difficult to maintain low case rates (as observed in the US) while also maintaining more reactivated infections than primary infections. According to [34], only 14% of genotyped tuberculosis cases in the US in 2011–2014 were attributed to recent infection. Further, published data on United States case statistics show that reactivation risk is not a monotonic function with age [35]. We thus choose to use a constant value for the reactivation risk r.

Natural death statistics by age can be found in [36], and immigration data are listed in [37]. We base immigration in the model on data for immigrants obtaining legal permanent residence. It is assumed that one-third of immigrants either have latent TB or have been exposed to TB, in accordance with published global TB prevalence data reported in [38]. Model parameter values/ranges are given in Table 2.

Table 2:

Values and ranges for model parameters.

Parameter	US value/range	Cambodia value/range	References
b	4 × 106	3 × 105	[42, 39]
µ(a)	fit to data	fit to data	[36, 44]
µT	0.133 – 0.25	0.133 – 0.25	[2, 4]
β	0.1 – 200	0.1 – 200	[2]
k	0.2 – 3	0.2 – 3	[2]
pc	1 – 10%	1 – 10%	[2]
pa	6 – 20%	6 – 20%	[2]
Χ	1 – 99%	1 – 99%	[2]
σc	0 – 10%	0 – 10%	[2, 5]
σa	30 – 50%	30 – 50%	[2, 5]
r	10−4 – 1.6 × 10−3	10−4 – 1.6 × 10−3	[2, 35]
d	0.5 – 2	0.5 – 2	[2]
B(t, a)	fit to data	fit to data	[18]
E0/Itot	1–15	1–15
Percent latent	1–10 %	50–75%	[41, 46]
M (a)	fit to data	–	[37]
ue	0–0.1	–
uℓ	0.33 – ue	–	[38]
n (Hill coefficient)	–	0.5–2

The age-dependent contact probability, P (t, a, a′) can be taken from published contact patterns; we use United States time-of-exposure contact data between the years 1987 and 2003 from [17]. We also use these data to estimate contact rates c(a) by considering total numbers of contacts of an individual of age a with others in all age groups. We scale c(a) so that its values lie in [0, 1].

We initialize the model to match reported data in the United States from the year 2000. Population distributions by age group can be found in [39] (see Figure 2), and tuberculosis incidence rates (active disease) by age group can be found in [33]. [38] estimates that the prevalence of active TB in the United States is approximated 0.8 times the incidence. In numerical simulations, we assume that prevalence and incidence have the same age distribution. Cubic splines were used to approximate the population and case rate age distributions in numerical simulations. Estimates of latent TB prevalence by age group can be found in [40] (this data comes from Tarrant County, Texas). The total number of latent infections is determined by a percentage of the total population, which we vary from 1 to 10%. According to [41], prevalence of LTBI in the United States in 2011–2012 was between 4.7 and 5%, which equates to approximately 15 million people. The age distribution for latent TB was approximated by a cubic spline for numerical simulations. The age distribution of total infectious cases is taken from [33]. The initial infectious cases are assumed to be 14% primary cases [34], 85% reactivated cases, and 1% reinfected cases. We initially assume that E₀ is proportional to the total infectious cases I_tot, and we assume that E_s is initially empty.

Figure 2: Age distribution data for the US and Cambodia in the year 2000.

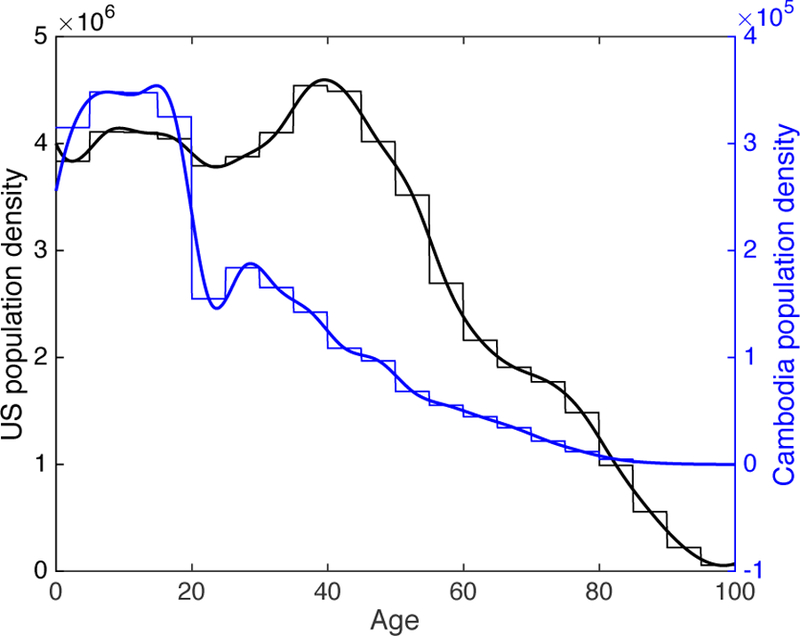
Thin lines indicate age-group data from [39, 42] and thick lines indicate cubic spline fits to the data. United States is shown in black and Cambodia is shown in blue.

Parametrization of the model in an endemic setting (Cambodia)

For a high burden population we consider Cambodia, due to its high rates of TB infection and low rates of multi-drug-resistant TB and HIV co-infection [43].

Population age structure data and estimated birth rate for the year 2000 are taken from [42]. The population age structure is shown in Figure 2. Age-dependent death rates in 2000 were obtained from the WHO [44]. Death rates were approximated by a sum of two exponential functions to account for the decreasing death rates in the first few years of life (due to high infant mortality) followed by increasing death rates with increasing age. We neglect immigration in this case since the net migration rate in Cambodia has been negative for many years [42]. Estimated age-dependent contact rates are taken from [18].

TB prevalence data by age group is taken from [45]. It should be noted that the prevalence data is from the year 2002; since TB incidence in Cambodia had only a slight decrease from 2000 to 2002 (approximately 3%), we assume that the prevalence distribution is also similar. According to [46], prevalence of LTBI in Cambodia has been estimated at 64%. We let the LTBI prevalence vary in a wide range from 50 to 75%. For the age distribution of LTBI cases, we use a Hill equation based on the general trends estimated for WHO regions [47] and data from Ca Mau, Vietnam [48].

The Hill equation takes the form

$$f(x)=\frac{A{x}^n}{x^n+B^n}$$

for some parameters n, A, B > 0. We let the exponent n vary as a parameter in our uncertainty analysis (described below), and use coordinate descent optimization to determine A and B such that: (1) the overall LTBI prevalence matches the assumed value, and (2) the prevalence for any age group is always less than 100%.

Values and ranges for model parameters are summarized in Table 2.

Model calibration using incidence data

We use CDC and WHO data for tuberculosis incidence rates in the US and Cambodia, respectively, for the years 2000–2016 [33, 43] to calibrate the model and determine baseline parameter values in each setting. We calculate the incidence for the model as the number of new cases of infectious TB per 100,000 population per year,

$$C_{sim}(t)=\frac{100,000}{N(t)}{\int }_0^A(pk{E}_0(t,\hspace{0.33em}a)+rL(t,\hspace{0.33em}a)+\beta B(t,\hspace{0.33em}a)L(t,\hspace{0.33em}a))\hspace{0.33em}da$$

To perform parameter fitting, we use Latin hypercube sampling (LHS) with a uniform distribution to explore the parameter space within the ranges in Table 2 and identify parameter sets that match well with available data. LHS was performed on the full parameter space with 10,000 samples.

Next, the best fitting parameter set, call it P_opt, was chosen as the parameter set from the LHS samples that minimized an error function. For the US case, the error is defined by

$$E_{US}={\left[{\sum _{i=0}^{16}{(C_{sim}(i)-C_{data}(i))}^2+10\left(\frac{\int I_p(16,\hspace{0.33em}a)\hspace{0.33em}da}{I_{tot}(16)}-0.14\right)}^2\right]}^{1/2}$$

where C_sim(i) and C_data(i) are the case rates at t = i for the simulation and CDC data [33] respectively, I_p(16, a) is the simulated age distribution for primary infections at t = 16, and I_tot is the total number of simulated infections at t = 16. The value of 0.14 for the proportion of primary infections is taken from [34]. The weighting factor of 10 was chosen somewhat arbitrarily to weight the importance of the proportion of primary infections in determining an optimal parameter set. We found that using smaller weights led to solutions with unrealistically large proportions of primary infections, while using much larger weights led to excessive error in incidence rates. For Cambodia, there is no available data on the relative proportions or primary, reactivated, and reinfected cases; thus we consider only the case rates in determining the error, i.e.

$$E_{Cambodia}={\left[\sum _{i=0}^{16}{(C_{sim}(i)-C_{data}(i))}^2\right]}^{1/2}$$

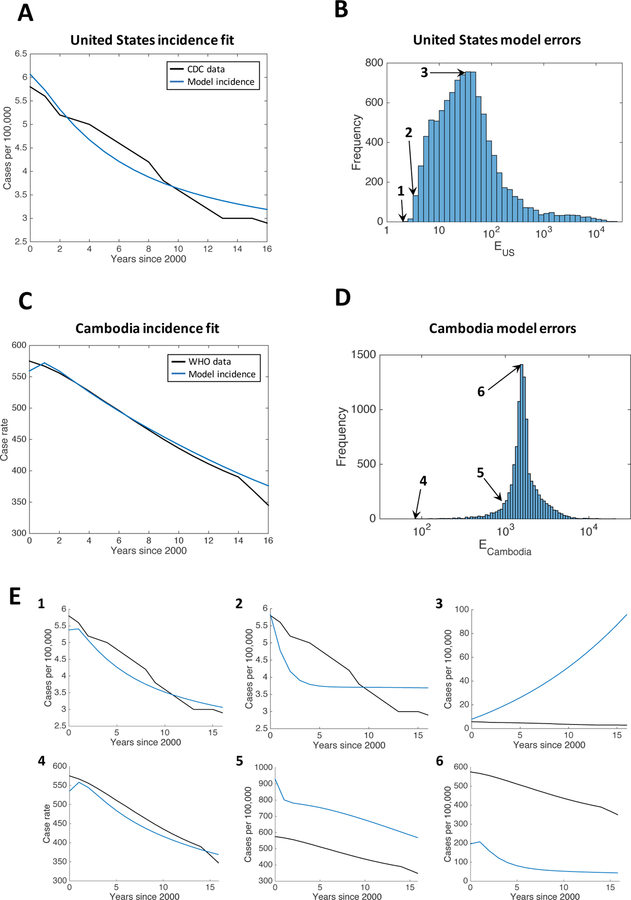
Distributions of values for the two error functions E_US and E_Cambodia for the full parameter ranges are shown in Figure 3, along with examples of incidence curves for different levels of error. We see that, in both settings, parameter sets that provide a good model fit are rare in the parameter space.

Figure 3: Error distributions with examples for the US and Cambodia.

(A) Incidence rates for the best fitting parameter set for the United States compared to CDC incidence data from [33]. (B) Histogram of the error function E_US among the 10,000 LHS samples in the full parameter range for the United States. (C) Incidence rates for the best fitting parameter set for Cambodia compared to WHO incidence data from [43]. (D) Histogram of the error function E_Cambodia among the 10,000 LHS samples in the full parameter range for Cambodia. (E) Three examples are given for both the US and Cambodia, for different values of the error function: 1) E_US = 10^0.3 (minimum error), 2) E_US = 10^0.5, 3) E_US = 10^1.5, 4) E_Cambodia = 10^1.9 (minimum error), 5) E_Cambodia = 10³, and 6) E_Cambodia = 10^3.2. The locations of these error values in the histograms are shown with arrows in (B) and (D).

Lastly, another LHS was then performed in the parameter ranges given by Popt ± 20% (note this may allow the parameter values to go outside the ranges prescribed in Table 2). This procedure was then repeated several times to obtain successively better fitting parameter sets. Comparing the best-fitting parameter sets for the US and Cambodia (see Table 3), we see that the primary differences are in the contact rates (β), initial prevalence of latent TB, and treatment rates (d). In the United States, the transmission rate β is approximately 75, meaning that if a susceptible individual with the largest age-dependent activity rate were exposed to an exclusively infected population, there would be a 50% chance of them being infected after $\frac{\log 2}{75}=3.4\hspace{0.33em}\text{days}$. In contrast, the transmission rate for Cambodia is approximately 234, meaning the 50% chance of infection is reached after $\frac{\log 2}{234}=1.1\hspace{0.33em}\text{days}$ days. There are also notable differences in values for the successful treatment rate (d), proportion of active disease upon infection for adults (pa), and reactivation rate (r).

Table 3:

Best fitting parameter sets identified by LHS for the US and Cambodia, respectively.

Parameter	US value	Cambodia value
µT	0.14164	0.17314
β	74.997	233.92
k	0.27672	0.48772
pc	0.023375	0.025514
pa	0.23181	0.12609
χ	0.73242	0.35385
σc	0.087282	0.044396
σa	0.33939	0.51859
r	2.1225 × 10−4	9.5896 × 10−4
D	2.1032	0.78465
E0/Itot	14.917	11.232
Percent latent	0.095037	0.53381
ue	0.0011811	–
n	–	0.79424

The model behavior for the best fitting parameter sets are shown in Figure 4. We see two major differences between the two demographic settings. First, the latent population is much younger on average in Cambodia than in the US. Second, the active TB cases in Cambodia are primarily comprised of primary infections and reinfections, with a relatively small proportion of endogenously reactivated infections. In contrast, the majority of active TB cases in the US are due to reactivation, in agreement with observed data [34].

Figure 4: Solution profiles for the best-fitting parameter sets for the US and Cambodia without vaccination.

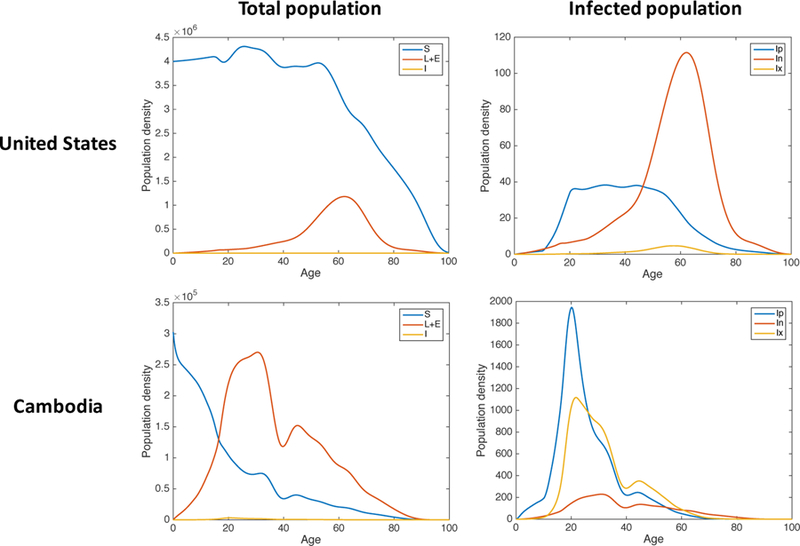
Left: Simulated age distributions of the susceptible (S, blue), latent and exposed (L+E, red), and infected (I, yellow) classes in the year 2016 for the best fitting parameter set obtained via LHS. Right: Simulated age distributions of the three infected classes in 2016 for the same parameter set. Ip (blue) denotes primary infections, In (red) denotes endogenous reactivation, and Ix (yellow) denotes exogenous reinfection.

3. Effects of vaccination

Sensitivity analysis with constant vaccination parameters

Our goal is to explore the effects of uncertainty and sensitivity of the model outputs to different vaccination levels and to compare this across demographics. Using constant parameters, we used LHS to explore the model behavior for parameter values within the broad ranges given in Table 4. Since we are using hypothetical efficacious vaccines, there are no data available to calibrate these parameters. Vaccination was applied beginning at t = 20, corresponding to the year 2020. Model parameters not associated with vaccination are held constant at the best fitting values identified in the previous section. The median, minimum, and maximum incidence curves obtained in the LHS are shown in Figure 5. We observe that for most parameter sets, there is a sharp drop in incidence at the beginning of the vaccination campaign followed by gradual decline in later years. To assess the importance of each parameter for determining case rates, we use the partial rank correlation coefficient (PRCC) at each time point. PRCC was computed in Matlab using the partialcorr function. These values are shown graphically in Figure 6.

Table 4:

Vaccination parameter ranges used for both demographic populations.

Parameter	Description	Min	Max
ψs, ψℓ	vaccination rates	0	1
ws, wℓ	rates of vaccine waning	0	1
vs, vℓ	proportion of immigrants vaccinated	0	1
γs, γℓ	transmission rates to vaccinated individuals	0	5
rv	reactivation rate of vaccinated latents	1e-8	1e-4

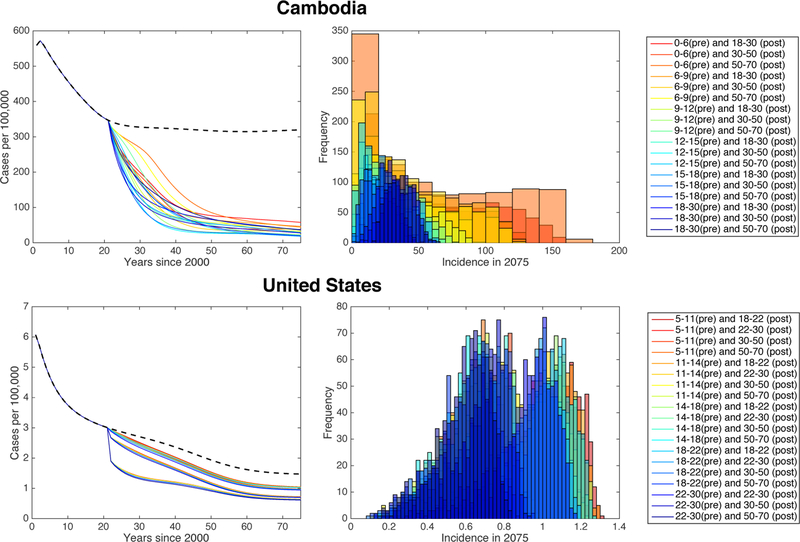
Figure 5: TB incidence in the US and Cambodia under constant vaccination.

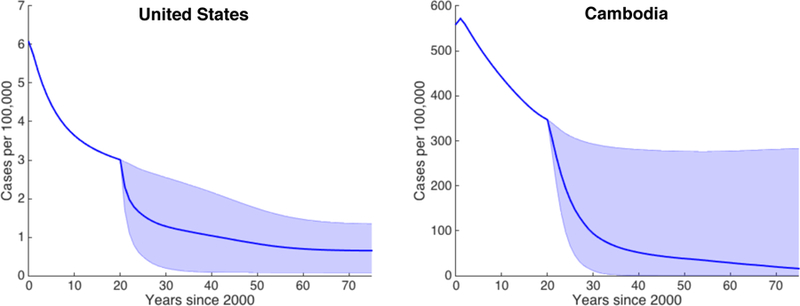
Simulated case rates for the US (left) and Cambodia (right) from the year 2000 to 2075 for constant vaccination parameters within the ranges in Table 4. Vaccination is started at t = 20. The blue line indicates the median case rate and the shaded region indicates the full range of case rates obtained via 1,000 LHS samples.

Figure 6: Sensitivity results identifying important vaccination mechanisms in the US and models.

Partial rank correlation coefficients (PRCC) for each parameter at each time point after beginning vaccination (t = 20). Results for the United States are shown on the left graph, and for Cambodia are shown on the right graph. Parameters included in the analysis are (from red to blue) reactivation rate, transmission rates, proportions of immigrants that are vaccinated (US), vaccine waning, and vaccination rates.

We see that for the US, the post-exposure (latent) vaccination parameters ψ_ℓ and w_ℓ appear to have the greatest effect at all time points, followed by the pre-exposure (susceptible) vaccination parameters ψ_s and w_s. Vaccination rate is negatively correlated with TB incidence and the rate of vaccine waning is positively correlated with TB incidence. The vaccination rates ψ_s and ψ_ℓ and the rate of waning w_ℓ for the post-exposure vaccine have PRCCs significantly different from zero at all time points, with p < 0.001. Further, the post-exposure vaccination parameters ψ_ℓ and w_ℓ are significantly more sensitive (p < 0.001) than the pre-exposure vaccination parameters ψ_s and w_s (respectively) for all years after the start of vaccination. The proportion of susceptible immigrants that are vaccinated (υ_s) and the transmission rate for vaccinated latent individuals (γ_ℓ) are not significantly different from zero at any time point.

For Cambodia, since we do not consider immigration, the parameters υ_s and υ_l are eliminated. We observe in this case that differences in sensitivity of the pre- and post-exposure vaccination parameters are much less substantial than in the low-burden case. At later times, the pre-exposure vaccination parameters become more significant. This is in contrast to the United States simulation, in which the post-exposure vaccination parameters remained most sensitive for all time. The pre-exposure vaccination rate for Cambodia is significantly more sensitive than the post-exposure vaccination rate in all years after 2040, and the rate of pre-exposure vaccine waning is significantly more sensitive than post-exposure vaccine waning in all years after 2059 (p < 0.01). We also see that the transmission rates γ_s and γ_ℓ for vaccinated individuals are the least sensitive parameters, with PRCCs that are never significantly different from zero.

Age-dependent vaccination parameters reveal different optimal strategies for the US and Cambodia

In practice, vaccination campaigns are often targeted toward specific age groups who will receive the greatest benefit from a vaccine. To study the effect of age group targeting, we can apply a pre-exposure vaccine to one group and a post-exposure vaccine to another age group. This can be incorporated into the model by making the vaccination rate parameters age-dependent, so that the vaccination rate is very high for a particular age demographic and zero (or low) for other groups. Here, we base our age group choices on the public school systems in both countries respectively [49, 50]. The age groups we consider for Cambodia are 0–6, 6–9 (first cycle primary), 9–12 (second cycle primary), 12–15 (lower secondary), 15–18 (upper secondary), 18–30, 30–50, and 50–70. The age groups we consider in the United states are 0–5, 5–11 (elementary), 11–14 (middle), 14–18 (high), 18–22 (college), 22–30, 30–50, and 50–70. We consider all possible combinations of targeting a single age group for pre-exposure vaccination and a single age group for post-exposure vaccination, with the constraint that the post-exposure age group be older than the pre-exposure age group.

For each case, we evaluate 1,000 LHS samples in the ranges given in Table 5. We let vaccination rates vary from 1.6 to 5, corresponding to immunization coverage of 80–99% within one year. This is consistent with reported immunization coverage for routine vaccines in the US and Cambodia [51, 52]. These values are higher than the values we used for the constant vaccination rates earler (Table 4) because it is easier and more efficient to target age groups than to vaccinate an entire population. We also restrict the rates of vaccine waning to be less than 0.14, corresponding to a half-life of at least 5 years. This restriction is based on data suggesting that BCG efficacy typically wanes after 10–15 years [32].

Table 5:

Parameter ranges for vaccination by age group used for both demographic settings.

Parameter	Description	Min	Max
${\widehat{\psi }}_s$, ${\widehat{\psi }}_{\ell }$	vaccination rates for age group	1.6	5
ws, wℓ	rates of vaccine waning	0	0.14
vs, vℓ	proportion of immigrants vaccinated	0	1
γs, γℓ	transmission rates to vaccinated individuals	0	5
rv	reactivation rate of vaccinated latents	1e-8	1e-4

Results for the Cambodia are shown in Figure 7. We find that the average Cambodian incidence in 2075 is minimized by choosing the age group 12–15 for pre-exposure vaccination and 50–70 for post-exposure vaccination. The optimal choice of age group varies slightly depending on the timeline: incidence is minimized in 2050 by choosing 12–15 for pre-exposure and 30–50 for post-exposure, and incidence in 2030 is minimized by choosing 15–18 for pre-exposure and 30–50 for post-exposure. The worst performance (i.e. highest median incidence) and the largest variation is observed for targeting ages 0–6 for pre-exposure vaccination; this is likely due to vaccine waning. Currently, this is the age group that is most commonly targeted for the BCG vaccine in countries such as Cambodia. However, it should be noted that our model considers only pulmonary TB, while BCG is most effective in protecting against forms of extrapulmonary TB, which is most often what occurs in children [43].

Figure 7: Vaccination by selected age groups in Cambodia and the US.

Left: Median incidence rates by year for different vaccination strategies (see legends on right), calculated via 1,000 LHS samples. Black dashed line shows the predicted incidence with no vaccination. Right: Histograms of the entire uncertainty analysis (LHS) runs.

Results for the US look vastly different when compared with Cambodia (Figure 7, as there is significantly more overlap between the histograms of 2075 incidence rates for the different vaccination strategies. Still, there are some age group combinations that have clear benefits over others in terms of median US TB incidence over time. The median incidence curves appear to be clustered, with each cluster corresponding to a different choice of age group for post-exposure vaccination. For all years following the start of vaccination, incidence is minimized by choosing the age group 22–30 for pre-exposure vaccination and 50–70 for post-exposure vaccination. In general, the age group that is targeted for post-exposure vaccination has a much larger effect on disease incidence than the one chosen for pre-exposure vaccination, with 50–70 being the optimal choice among the age groups considered. This effect is not observed in the results for Cambodia, and is likely due to the relatively small proportion of primary TB infections in the United States.

Including neonatal vaccination effects

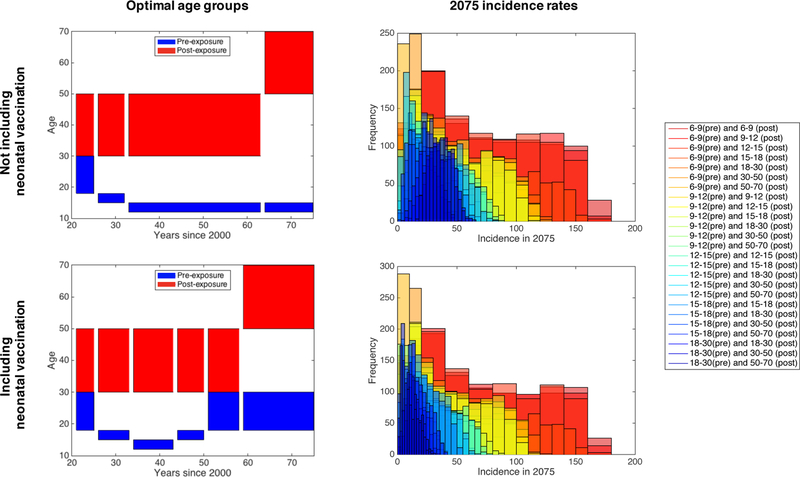
To more accurately reflect what is currently done in endemic settings, we also consider another scenario: the case where pre-exposure vaccinations are provided to infants (age 0–1) with 99% immunization coverage, as is currently the case with BCG in Cambodia [51], in addition to targeting age groups for additional pre-exposure and post-exposure vaccination. In this case, the second round of pre-exposure vaccination can be seen as a booster. We compare these results with the previous results (see Figure 7) not including neonatal vaccination, shown in Figure 8. We find that incorporating neonatal vaccination can decrease median 2075 incidence by up to 70% for some choices of vaccination age groups, and that older age groups become more effective for pre-exposure vaccination campaigns. Incorporating neonatal vaccination shifts the optimal “booster” pre-exposure age group to 18–30, which is older than the optimal age group for the non-neonatal campaign above, for minimizing median incidence by 2075. For earlier time points (up to around 2045), neonatal vaccination makes no difference in the optimal vaccination age groups. We do not consider neonatal vaccination for the United States, since it is not currently performed.

Figure 8: Effects of neonatal vaccination with a booster and post-exposure vaccine in Cambodia.

Left: Optimal age groups for pre- and post-exposure vaccination, in terms of minimizing median incidence, from years 2021–2075 when not including neonatal vaccination (top) and when including neonatal vaccination (bottom). Right: Histograms of the 2075 incidence rates from uncertainty analysis (LHS) runs.

4. Discussion

In this paper, we have presented a novel age-structured SEIR model for tuberculosis epidemiology with pre- and post-exposure vaccination. We choose not to incorporate HIV co-infection and drug resistance into the model for the sake of simplicity. These factors are not major influences in the two populations that we consider, but would need to be added to the model in order to study areas such as Sub-Saharan Africa, which has a high incidence of HIV, or India, which has a high incidence of multi-drug resistant TB [43]. Co-infection with HIV and TB has been shown in many studies to worsen the effects of both diseases and shorten survival [53, 54, 55]. We calibrated the model using published data for an endemic setting (Cambodia) and a non-endemic setting (US) using parameter values from previously published models. We allowed model parameters such as proportion of active disease upon infection, protection from re-infection, and contact rates to vary with age, as has been done in previous models [2, 5, 3]. In previous work, the rate of reactivation of latent TB has also been assumed to be increasing with age [2, 5]. However, this assumption is not necessarily supported by data [35]. In numerical experiments for our model, we found that by letting r be an increasing function of age, the curve of incidence over time could not match reported case rates [33, 43] due to an unreasonably large number of simulated infections arising from an aging latent population.

In performing model calibration to incidence data, we observed that good-fitting parameter sets are rare within the established parameter ranges. However, this does not prove definitively that the parameter values are identifiable from incidence trends alone, and we recognize that this could influence the interpretation of results. In addition, since there are no available error estimates for the CDC and WHO incidence data, we are unable to obtain statistics on the parameter estimates, such as confidence intervals. To assess the differences in parameter values, we considered the distributions of parameter values in the top 1 percentile of model fits from the full LHS (data not shown) and found statistically significant differences for the parameters pa, r, β, and d, with p-values less than 0.001.

Through uncertainty and sensitivity analysis via LHS/PRCC, we found that post-exposure vaccination is significantly more effective at reducing TB incidence than pre-exposure vaccination in a non-endemic setting (US). This finding is further supported by our study of vaccination by age group, where we found that the age group selected for post-exposure vaccination has a much larger effect on the efficacy of the vaccination strategy than the age group selected for pre-exposure vaccination. The importance of post-exposure vaccination is likely due to the large proportion of reactivated infections compared to primary infections. In an endemic setting, there is a larger incidence of primary infections, so pre-exposure vaccination becomes more important. In the case of Cambodia, we found that pre-exposure vaccination becomes significantly more effective at reducing incidence over a sufficiently longer time frame.

We also found that optimal age groups to target for vaccination tend to be younger for an endemic setting than for a non-endemic setting. In the endemic setting we found that early adolescents (ages 12–15) should be targeted for pre-exposure vaccination to best reduce incidence, whereas in the non-endemic setting we found that young adults (ages 22–30) should be targeted. However, if we assume that infants are also vaccinated in the endemic setting, as is currently the case with BCG, then the optimal age group for further pre-exposure vaccination is also young adults. In both settings, older adults (ages 50–70) are optimal for targeting post-exposure vaccination over a sufficiently longer time frame. Over shorter time frames, however, the optimal age group for post-exposure vaccination in the endemic setting is younger, ages 30–50.

The optimal age groups that we predict for vaccine targets are older than the age groups currently targeted for BCG vaccination. This is in agreement with previous modeling results that indicate that vaccines should be targeted at adolescents and adults rather than infants [12]. Currently, the WHO recommends vaccination with BCG as soon as possible after birth [43]. One reason for this discrepancy is the high mortality associated with of non-pulmonary forms of TB in young children, such as TB meningitis and miliary TB [56]. Since extrapulmonary TB is typically not infectious and thus does not contribute to the epidemiology of the disease, we do not consider these types of infection in our model. Since vaccine efficacy can wane significantly over time [32], vaccinating age groups that are at higher risk for developing pulmonary TB leads to a greater decrease in incidence. However, it has also been shown that prior exposure to Mtb or environmental mycobacteria can decrease efficacy of BCG [57], implying that vaccination may be less effective when given to older individuals. This effect is not observed for more recent TB subunit vaccines [58], and thus we did not include it in the model.

Our work provides a framework for determining how to best vaccinate a population when efficacious pre- and post-exposure vaccines for pulmonary TB become available. Our results utilize broad ranges for parameter values that could be refined when further data about new vaccines becomes available, such as rates of vaccine waning. In the absence of such data, with the assumption that vaccine efficacy decreases by no more than 50% in the first five years following vaccination, we have predicted optimal age groups to target in order to minimize incidence over a 55-year vaccination campaign.

Appendix A Technical details

A.1. PDE solver

To solve the age-structured PDE model, we use upwinding. The upwind scheme for the transport equation u_t + u_x = 0 is given by

$$u_i^{n+1}=u_i^n+\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x}\left(u_i^n-u_{i-1}^n\right)$$

where $u_i^n$ denotes the numerical approximation of the solution u(t_n, x_i) [59]. The scheme is stable provided the CFL condition $\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x}\le 1$ is satisfied. The scheme is first order accurate in time and space.

With a forcing function F(t, x) on the right hand side, the scheme becomes

$$u_i^{n+1}=u_i^n+\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x}\left(u_i^n-u_{i-1}^n\right)+\mathrm{\Delta }tF(t_n,x_i).$$

This scheme is implemented in Matlab.

In numerical experiments we used ∆x = 0.1 and ∆t = 0.05. Simulations were performed in Matlab 2015a.