Ensemble-Based Replica Exchange Alchemical Free Energy Methods: The Effect of Protein Mutations on Inhibitor Binding

Abstract

The accurate prediction of the binding affinity changes of drugs caused by protein mutations is a major goal in clinical personalized medicine. We have developed an ensemble-based free energy approach called thermodynamic integration with enhanced sampling (TIES), which yields accurate, precise, and reproducible binding affinities. TIES has been shown to perform well for predictions of free energy differences of congeneric ligands to a wide range of target proteins. We have recently introduced variants of TIES, which incorporate the enhanced sampling technique REST2 (replica exchange with solute tempering) and the free energy estimator MBAR (Bennett acceptance ratio). Here we further extend the TIES methodology to study relative binding affinities caused by protein mutations when bound to a ligand, a variant which we call TIES-PM. We apply TIES-PM to fibroblast growth factor receptor 3 (FGFR3) to investigate binding free energy changes upon protein mutations. The results show that TIES-PM with REST2 successfully captures a large conformational change and generates correct free energy differences caused by a gatekeeper mutation located in the binding pocket. Simulations without REST2 fail to overcome the energy barrier between the conformations, and hence the results are highly sensitive to the initial structures. We also discuss situations where REST2 does not improve the accuracy of predictions.

1. Introduction

Mutations enable proteins to tailor molecular recognition with small-molecule ligands and other macromolecules, and can have a major impact on drug efficacy. Rapid and accurate prediction of drug responses to protein mutations is vital for accomplishing the promise of personalized medicine. The use of targeted therapeutics will benefit cancer patients by matching their genetic profile to the most effective drugs available. Examples of such drugs are gefitinib and erlotinib which belong to a class of targeted cancer drugs called tyrosine kinase inhibitors. A subgroup of patients with nonsmall-cell lung cancer (NSCLC) have specific point mutations and deletions in the kinase domain of epidermal growth factor receptor (EGFR), which are associated with gefitinib and erlotinib sensitivity. Screening for these mutations may identify patients who will have a better response to certain inhibitors.

In silico free energy calculation is one of the most powerful tools to predict the binding affinity of a drug to its target proteins. It employs all-atom molecular dynamics (MD) simulation, a physics-based approach for calculating the thermodynamic properties. The accurate prediction of the binding affinities of ligands to proteins is a major goal in drug discovery and personalized medicine.¹ The use of in silico methods to predict binding affinities has been largely confined to academic research until recently, primarily due to the lack of their reproducibility, as well as lack of accuracy, time to solution, and computational cost.

Recent progress in free energy calculations, marked to some extent by the advent of Schrödinger’s FEP+,² has initiated major interest in their potential utility for pharmaceutical drug discovery. The improvements include new sampling protocols in order to accelerate phase space sampling,^3,4 such as Hamiltonian-replica exchange (H-REMD)⁵ and its variants, including replica exchange with solute tempering (REST2)⁶ and FEP/REST.⁷ The replica exchange methods run multiple concurrent (parallel) simulations and occasionally swap information between replicas to improve sampling. For a given set of simulation samples, different free energy estimators⁸ can be applied with varying accuracy and precision, of which the multistate Bennett acceptance ratio (MBAR)⁹ has become increasingly popular. MBAR makes use of all microscopic states from all of the replica simulations, by reweighting them to the target Hamiltonian. The implementation of an enhanced sampling protocol such as REST2⁶ and the use of the free energy estimator MBAR⁹ has been shown to improve the accuracy of the free energy calculations. The rapid growth of computing power and automated workflow tools has also contributed significantly in the wider application of free energy approaches in real world problems.

We have recently developed an approach called thermodynamic integration with enhanced sampling (TIES)¹⁰ which utilizes the concept of ensemble simulation to yield accurate, precise, and reproducible binding affinities. TIES is based on one of the alchemical free energy methods, thermodynamic integration (TI), employing ensemble averages and quantification of statistical uncertainties associated with the results.¹¹ TIES has already been shown to perform well for a wide range of target proteins and ligands.¹⁰⁻¹³ TIES provides a route to reliable predictions of free energy differences meeting the requirements of speed, accuracy, precision, and reliability. The results are in very good agreement with experimental data while the methods are reproducible by construction. Variants of TIES incorporate enhanced sampling techniques REST2 and the free energy estimator MBAR.¹¹ TIES has been shown to have a positive impact in the drug design process in the pharmaceutical domain.^12,13

Some protein mutations may fortuitously bring therapeutic benefit to some patients who use a specific drug treatment, while others may impair the ability of a drug to bind with the protein, one of the reasons for the target proteins developing drug resistance. Studying the effect of protein mutations on binding affinity is important for both drug development and for personalized medicine. The purpose of the present paper is to apply the ensemble-based TIES approach¹⁰ to study point mutations in proteins, a variant which we name TIES-PM. TIES-PM employs the TIES methodology to yield rapid, accurate, precise, and reproducible relative binding affinities caused by the protein variants when bound to a ligand.

Here we apply TIES-PM to fibroblast growth factor receptor 3 (FGFR3), one of the four members of the human FGFR family. FGFRs play a critical role in many physiological processes and are recognized therapeutic targets in cancer.¹⁴ Point mutations in FGFRs are among the main genomic alterations, along with fusions and amplifications, contributing to tumor generation and progression. Considerable effort has been dedicated to the development of effective FGFR inhibitors for cancer therapy, some of which are at various phases within clinical trials.¹⁴ In a previous study,¹⁵ we calculated binding free energy differences of inhibitors upon mutations in FGFR1. That study was a critical first step in initiating the TIES protocol.¹⁰ We have also used FGFR1 as one of the molecular systems with which to establish uncertainty quantification within ensemble approaches.¹¹ In the current study, we consider four FGFR tyrosine kinase inhibitors (TKIs): AZD4547, BGJ-398, JNJ42756493, and TKI258 (see Figure 1), of which the first three are selective and highly potent.¹⁶ Some activating mutations result in distinct changes in drug efficacy. Three single amino acid residue mutations in the kinase domain of FGFR3—V555M, I538V, and N540S—are considered here, of which V555M is the most common gatekeeper mutation.¹⁷ They are among the most frequently observed FGFR3 variants, and confer resistance to these inhibitors in most cases (see the experimental binding affinity changes in Table 1).¹⁶

Figure 1.

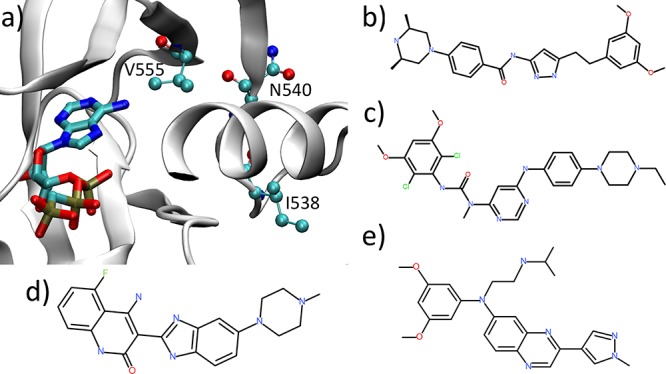
Structures of FGFR3 and inhibitors studied in this work: (a) the binding site of tyrosine kinase domain for FGFR3 in complex with ACP, an ATP-analogue (PDB ID: 4K33). FGFR3 is depicted in cartoon and ACP in bond representation. Mutations of three residues, V555, I538, and N540 (ball-and-stick representation), are among the most common genetic variants in FGFR3. The chemical structures of four ATP competitive inhibitors are shown in panels b–e: (b) AZD4547, (c) BGJ-398, (d) TKI258, and (e) JNJ4275649.

Table 1. Relative Binding Free Energies Calculated Using TIES, Incorporating Schemes λR2 and λR2-M as Well as Determined from Experimental K_i Values for All the Inhibitor-Mutant Complexes Studied^a.

		ΔΔGcalc
mutant	drug	TIES	λR2b	λR2-Mb	ΔΔGexp
V555M	AZD4547-linear	–3.56(0.31)	–2.76(0.12)	–2.70(0.12)	–1.75(0.33)
	AZD4547-bent	0.55(0.41)	–2.07(0.11)	–1.98(0.12)
	BGJ-398	–3.02(0.44)	–3.66(0.12)	–3.60(0.12)	–1.19(0.08)
	TKI258	0.26(0.25)	–1.17(0.13)	–1.11(0.13)	0.97(0.22)
	JNJ42756493	–5.19(0.38)	–3.99(0.16)	–3.92(0.15)	–3.08(0.17)
	MAE	1.75	1.37	1.30
	RMSE	1.84	1.59	1.54
I538V	AZD4547-linear	0.25(0.33)	0.09(0.11)	0.05(0.11)	–2.11(0.32)
	BGJ-398	0.44(0.35)	0.46(0.11)	0.45(0.11)	–0.74(0.21)
	TKI258	–0.65(0.38)	0.47(0.13)	0.38(0.12)	–1.91(0.13)
	JNJ42756493	0.62(0.34)	0.30(0.12)	0.28(0.12)	–2.18(0.10)
	MAE	1.90	2.06	2.02
	RMSE	2.02	2.13	2.08
N540S	AZD4547-linear	–0.43(0.43)	0.91(0.14)	0.95(0.14)	–0.76(0.33)
	BGJ-398	–1.00(0.52)	1.13(0.14)	1.16(0.13)	0.25(0.19)
	TKI258	–1.77(0.60)	1.02(0.14)	1.11(0.14)	–0.90(0.15)
	JNJ42756493	–0.87(0.45)	1.06(0.14)	1.11(0.14)	–1.75(0.21)
	MAE	0.83	1.82	1.87
	RMSE	0.89	1.94	2.00

^aThe mean absolute error (MAE) and root mean square error (RMSE) are also shown for all complexes of each mutant using each free energy scheme. Production runs are 4 ns in all cases. All values are in kcal/mol. The statistical uncertainties associated with each value are shown in brackets.

^bHighest T_eff for λ-REST2 simulations is 800 K for receptor and 1500 K for complexes in case of mutants I538V and N540S. In the case of mutant V555M, it is 1500 K for the AZD4547 complexes and 600 K for all other complexes; 600 K is used for the receptor.

2. Methods

In this study, ensemble-based λ-REST2 simulations (TIES-λ-REST2)¹¹ are performed for four TKIs binding to wild-type and mutant FGFR3s (Figure 1). The free energy differences upon mutations are predicted with their associated uncertainties, and compared with experimental data. There are a range of issues and artifacts which affect the reliability and accuracy of MD results.¹⁸ Here we use the latest Amber force fields (see the Simulation Setup section) which are known to be reliable for the present systems, and the same procedures to setup the protein–ligand systems as we recently reported and validated.¹⁰⁻¹³

2.1. Hybrid Topology

A dual topology scheme is used in the current study, similar to that used in our previous studies for the alchemical transmutation of one ligand to another¹⁰ but adapted to handle the transmutation of amino acids in the current study. The reason for this choice is dictated by our use of NAMD.¹⁹ A hybrid residue is introduced, which consists of both the disappearing and appearing amino acids (Figure 2), exclusively belonging to the initial and the final states, respectively. The hybrid potential energy function is set in such a way that the disappearing and appearing parts do not interact with each other. For an alchemical transformation from one amino acid to another, the hybrid structure file is prepared by aligning the mainchain and the common side chain atoms of the appearing residue to those of the disappearing residue.

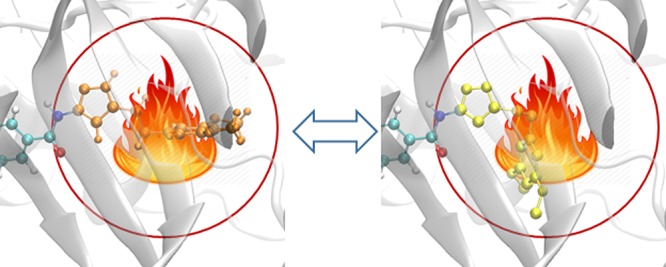
Figure 2.

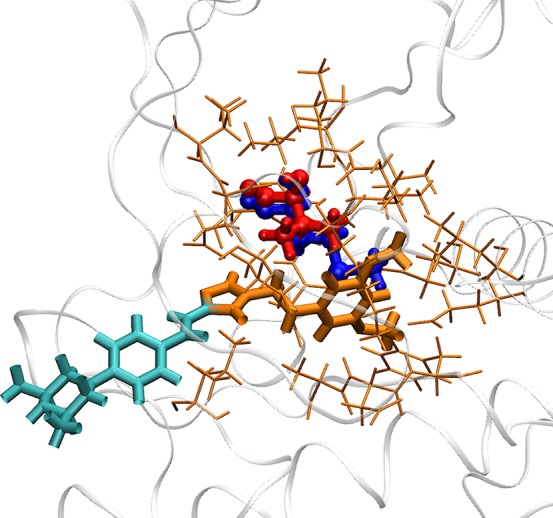
Different regions in the λ-REST2 simulations. The AZD4547-V555M complex is shown here as an example. The hybrid residue, denoted as the alchemical region, is depicted as a ball-and-stick model. It consists of disappearing (red) and appearing (blue) groups which are slightly separated for reasons of clarity. They can fully or partially overlap in the simulation as there are no interactions between them. The REST2 region, including the alchemical region (red and blue ball-and-stick), part of the ligand (orange bond), and surrounding protein residues (orange stick), is designated as the “hot” region. The selection of the REST2 region is described in the main text (section 2.3 REST2 region).

2.2. Free Energy Schemes

Thermodynamic integration with enhanced sampling (TIES)¹⁰ is used to calculate the free energy differences (ΔΔG_binding) of ligands binding to wild-type and mutant proteins. An alchemical pathway is defined, which corresponds to the transformation of a residue at one end into another at the other end of the pathway. An alchemical coupling parameter, λ, is introduced to define intermediate states with a hybrid potential function V(λ,x), where λ ranges between 0 and 1 corresponding to the initial and final states, respectively. In thermodynamic integration, the alchemical free energy change ΔG_alch is given by the following equation:

1

where ⟨∂V(λ,x)/∂λ⟩_λ denotes an ensemble average of the potential energy derivative in state λ. Ensemble MD simulations are run at each λ window for both apo protein and ligand–protein complex. Equation 1 is evaluated using a stochastic integration method since the integrand is generated from a Gaussian random process,²⁰ and the associated uncertainty is calculated accordingly.¹⁰ The free energy difference ΔΔG_binding is then calculated as the difference of the alchemical free energy changes ΔG_alch of apoprotein and complex, and the uncertainty as the propagation of the errors. Three schemes¹¹ are used in the current study, as (i) the standard TIES,¹⁰ (ii) an ensemble of λ-REST2 simulations termed as TIES-λ-REST2 (λR2), and (iii) TIES-λ-REST2 with MBAR estimator termed TIES-λ-REST2-M (λR2-M).¹¹ All of the three schemes use ensemble-based simulations.^10,11 In standard TIES, simulations are run indepedently at each predefined λ value and at a constant temperature (300 K). In TIES-λ-REST2 simulations, a predefined number of parallel REST2 replicas are run with regular exchange attempted between neighboring replicas of which both the alchemical parameters λ and the effective temperatures T_eff differ. The calculated binding free energy differences from these schemes are denoted as ΔΔG_calc^TIES, ΔΔG_calc and ΔΔG_calc^λR2–M, respectively, which all are obtained from eq 1 but differ in the ways of deriving the integrands. In standard TIES (i), the potential energy in the integrand is a function of λ (the temperature is a constant), and the average includes samples from a specific λ window. In λ-REST2 (ii), the potential energy is a function of (λ, T_eff), and the average includes samples from a specific λ window. In λ-REST2-M (iii), the potential energy is a function of (λ, T_eff), and the average includes samples from multiple λ windows using MBAR.

2.3. REST2 Region

As described in Bhati et al.,¹⁰ a small region of the molecular system is designated as the so-called “hot” region for all λ-REST2 simulations (Figure 2). This region is usually referred to as the REST2 region. It is critical to properly define the region for the REST2 simulations in order to improve the sampling of conformations relevant to binding. If the region is too small, the overall impact of applying REST2 may be insufficient to prevent the molecule from getting trapped in one or more local energy minima. It has been shown²¹ that using the default FEP+ protocol,² in which only perturbed ligand groups are included in the REST2 region, is not sufficient for some cases to obtain proper sampling. Another study²² shows that choosing only a mutant residue as the hot region has no effect on binding free energy prediction in most cases. On the other hand, when the region is too big, a large number of replicas within the replica exchange process may be required to cover a given range in effective temperatures, while the sampled conformations may not be relevant to stable binding of the inhibitor at all. It has been suggested to include key protein residues within the REST2 regions, which are identified either by visual inspection²¹ or by analyses of preliminary simulations performed prior to FEP+ runs.²³

In this study, the REST2 region for all mutations is defined as follows: for unbound protein calculations, it includes the mutant residue and all protein residues within 3 Å distance of the former; for bound protein calculations, it comprises the mutant residue, all protein residues within 3 Å of the mutant residue and 4 Å of the ligand, and all ligand atoms within 4 Å of the mutant residue. The nonbonded interactions of the atoms in the “hot” region are reduced by a scaling factor based on an effective temperature (T_eff). The alchemical region (Figure 2), which is part of the “hot” region, is also scaled by the alchemical coupling parameter, λ. The λ value increases linearly from 0 to 1 with replicas, whereas T_eff varies such that it attains its maximum at the midpoint and decreases to 300 K at the end-points. Samples from a specific REST2 replica are used to calculate ∂V/∂λ at that state for each λ-REST2 simulation followed by standard TIES analysis to yield ΔG_alch and its associated uncertainty.¹⁰

2.4. Simulation Setup

The structure of FGFR3 was taken from the protein data bank (PDB ID: 4K33, Figure 1). The missing residues in the file were built by ModLoop,²⁴ and the mutant/engineered residues were restored to their wild-type forms. The inhibitors were manually positioned into the binding site on the basis of their existing X-ray structures as follows: BGJ-398 from PDB ID 3TT0, JNJ42756493 from PDB ID 5EW8, TKI258 from PDB ID 5AM7, and AZD4547 from PDB IDs 4V05 and 4RWK as there are two distinct conformations for it, denoted as “linear” and “bent” in the current study.²⁵ The crystal water molecules of 4K33 were retained unless they overlapped with the aligned inhibitors. The inhibitors were optimized at the Hartree–Fock level with the 6-31G* basis (HF/6-31G*) in Gaussian 03²⁶ and parametrized using Antechamber and restrained electrostatic potential (RESP) modules in AmberTools 17²⁷ with the general AMBER force field (GAFF).²⁸ The Amber ff14SB force field²⁹ was used for the protein. All systems were solvated in orthorhombic water boxes with a minimum extension from the protein of 14 Å. The TIP3P water model was used. The molecular systems were neutralized with Na⁺ or Cl^– ions.

2.5. Simulations

The customized version of the NAMD 2.11 package,¹⁹ with implementation of REST2 for alchemical simulations,³⁰ was used for all the TIES-PM simulations. The systems were maintained at a temperature of 300 K and a pressure of 1 bar in an NPT ensemble. A time step of 2 fs was used. We used the protocol established in our previous publications^10,11 in which an ensemble of five replicas was used; 2 ns of equilibration and 4 ns of production were conducted for each replica. To check the convergence of the calculated free energies, some simulations were extended up to 20 ns. A soft core potential was used for the van der Waals interactions which were scaled up/down linearly across the full λ range (0 to 1) for the appearing/disappearing atoms, respectively. The electrostatic interactions of the disappearing atoms were linearly decoupled from the simulations between λ values of 0 and 0.55 and completely turned off beyond that, while those of the appearing atoms were not turned on until λ = 0.45, and then linearly coupled to the simulations from λ value 0.45 to 1. An exchange of configurations between two neighboring λ replicas was attempted every 1 ps, and conformations were saved every 10 ps.

2.6. Computational Resources

The TIES-λ-REST2 simulations require a large number of MD runs to be performed. On modern large scale high performance computers, all simulations can be run in parallel and completed in the same wall clock time as needed for a single MD simulation. All simulations were run on the BlueWaters supercomputer at the National Center for Supercomputing Applications of the University of Illinois at Urbana–Champaign (https://bluewaters.ncsa.illinois.edu) and Titan at Oak Ridge National Laboratory (https://www.olcf.ornl.gov/olcf-resources/compute-systems/titan/). For a 2 ns equilibration and 4 ns production MD simulation, it took 14.6 h on 4 nodes (128 cores) of BlueWaters, and 8.7 h on 15 nodes (240 cores) of Titan. Collectively about 27.8 million core hours were consumed in the course of this study.

3. Results

Table 1 contains the calculated as well as experimental relative binding affinities (ΔΔG) for all the mutant-inhibitor complexes studied. ΔΔG_calc values from three free energy schemes, namely TIES,¹⁰ TIES-λ-REST2, and TIES-λ-REST2-M,¹¹ are reported. Some significant improvements are observed from TIES-λ-REST2 simulations, while the inclusion of MBAR only slightly improves the accuracy and precision (Table 1). In the following analyses, we mainly focus on the comparisons of TIES and TIES-λ-REST2. The experimental values are determined using the K_i values reported by Patani et al.¹⁶ Mean absolute error (MAE) and root-mean-square error (RMSE) values for all complexes of every mutant using each free energy scheme are included as a measure of the accuracy of the simulation results. The inhibitor AZD4547 has been reported to bind with the FGFR kinase gatekeeper mutant in two distinct conformations—linear and bent—experimentally.²⁵ Results for both are shown in Table 1. It should be noted that the FGFR3 gatekeeper mutation V555M occurs inside the binding pocket (“local”), while the other two mutations (I538V and N540S) occur away from the binding pocket (“remote”). The effect of local mutations on the binding of inhibitors can be attributed to the changes in the local environment of the binding pocket altering the direct interaction between protein and inhibitor. On the other hand, remote mutations do not have any direct interaction with the inhibitor and hence can be expected to affect the inhibitor binding through indirect means such as large scale conformational changes in the protein. Such events may occur on a time scale of the order of μs to ms. Below, we discuss the results from these two categories of mutations separately.

3.1. Local Mutation

In the case of the V555M mutant, ΔΔG_calc^TIES predicts the resistance behavior of all inhibitors correctly except AZD4547 starting from the bent conformation; that is, the predicted ΔΔG_calc values have the same signs as those of the corresponding experimental values ΔΔG_exp (Figure 3). In other words, the predictions agree directionally with the experimental values. We find that, for standard TIES, the accuracy of the predictions is not very good, most of the complexes having an absolute error close to 2 kcal/mol with a MAE and RMSE of 1.75 and 1.84 kcal/mol, respectively. In addition, the predicted relative binding affinity of the AZD4547–V555M complex is sensitive to its initial structure. The ΔΔG_calc values for the linear and bent conformations of AZD4547 differ by about 4 kcal/mol. It has been shown experimentally that AZD4547 coexists in its linear as well as bent conformations only when binding to the gatekeeper mutant.²⁵ This means that, during an alchemical transformation from valine to methionine (V555M), AZD4547 should exhibit only its linear conformation at the λ = 0 end-point (V555), but have an increasingly mixed population of both linear and bent conformations on approaching the λ = 1 end-point (M555). It appears that the energy barrier between these two conformations is too high to be overcome using standard MD simulations at 300 K. Thus, the inhibitor remains trapped in its starting conformation throughout a standard TIES calculation. This explains why the TIES prediction ΔΔG_calc is so sensitive to its initial structure and does not agree directionally with its experimental value in the case of the bent conformation of AZD4547.

Figure 3.

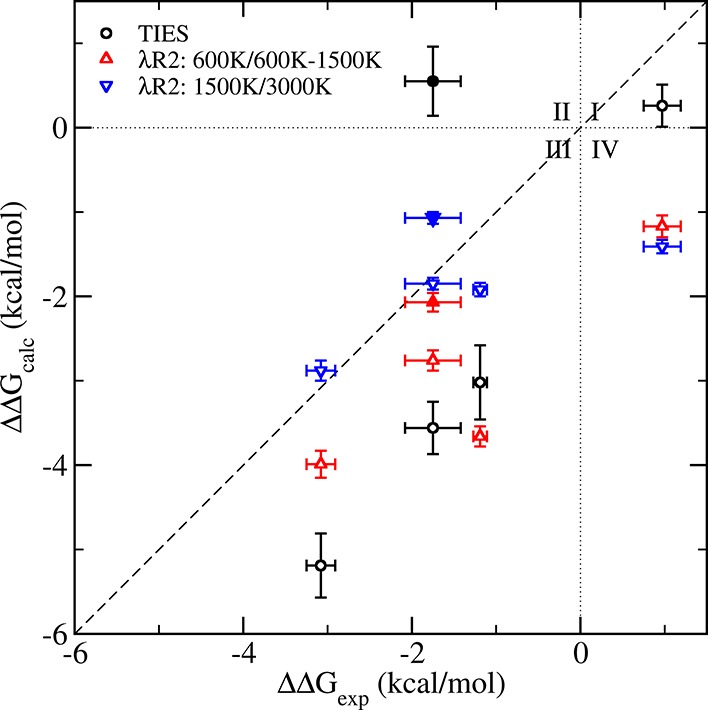
Comparison of the predicted ΔΔG_calc values using TIES (black circles), TIES-λ-REST2 (λR2, up/down triangles) with those from experiments for V555M mutant complexes with the highest T_eff of the chosen REST2 region at 600 K for receptor and complexes except those with AZD4547 which are at 1500 K (red triangles pointing up), and at 1500 K for receptor and 3000 K for complexes (blue triangles pointing down). Results of AZD4547 from the bent conformation are represented using filled circles and triangles. The dotted lines (x = 0 and y = 0) create four quadrants. Data points in quadrants I (x > 0 and y > 0) and III (x < 0 and y < 0) indicate that the calculated binding free energy differences agree directionally with those from the experimental data. The results from TIES-λ-REST2-M (λR2-M) are very close to those from λR2 (Table 1), and are not shown for reasons of clarity.

To overcome the large energy barrier between the two conformations of AZD4547 and also to study the effect of the accelerated sampling method, λ-REST2,⁷ on ΔΔG predictions in general, we performed TIES-λ-REST2 simulations to get ΔΔG_calc^λR2 and ΔΔG_calc (refer to Table 1 and Figure 3). On comparing them with ΔΔG_calc^TIES, we find an overall improvement in the relative binding affinity predictions, the MAE and RMSE reducing by 0.38 and 0.25 kcal/mol with scheme λR2 and by 0.45 and 0.30 kcal/mol with scheme λR2-M, respectively. The AZD4547, both for the linear and the bent conformations, benefit from REST2 with their ΔΔG_calc predictions improving drastically. However, it is clear from Figure 3 that, out of the five complexes (including the two conformations of AZD4547), ΔΔG predictions for only three complexes improve using TIES-λ-REST2. The relative binding affinity for the V555M-BGJ-398 complex remains the same as in the case of standard TIES while that for the V555M–TKI258 complex is less accurate than standard TIES using TIES-λ-REST2. This is because some conformations are sampled in the TIES-λ-REST2 simulations that are irrelevant to stable ligand binding and lead to the deviations of the predictions from the experimental values (see more details in the Discussion section).

To investigate the effects of the highest REST2 temperature (T_eff) on the predictions, we increased T_eff value from 600 to 1500 K for the receptor and 600/1500 to 3000 K for the complexes. As can be clearly seen from Figure 3, increasing the temperature of the “hot” region improves the accuracy of the results in most cases and reduces MAE and RMSE by up to 0.6 kcal/mol (Table 2). Three out of the five inhibitors bound to the V555M mutant then generate predictions closer to experiment by more than 0.7 kcal/mol (BGJ-398, by 1.74 kcal/mol; JNJ42756493, by 0.71 kcal/mol; AZD4547-linear, by 0.91 kcal/mol). Although the absolute error (0.68 kcal/mol) increases slightly for the AZD4547-bent using the higher T_eff, it is still well on the level of accuracy expected from such alchemical approaches.¹¹ Increasing the temperature allows greater flexibility within the system being simulated and facilitates access to key regions of phase space by allowing high energy barriers in the potential energy surface to be crossed. The inhibitor TKI258, when bound to the V555M mutant, remains an exception as its predicted relative free energy is displaced from the perfect correlation line on increasing the temperature. This exceptional behavior of TKI258 is due to an even higher population of irrelevant conformations sampled in the simulations when a higher temperature is used (see the Discussion section).

Table 2. Relative Binding Free Energies Calculated Using Schemes λR2 and λR2-M with Different Highest Effective Temperature (T_eff) Compared with Corresponding Experimental Values for All the Inhibitor-Mutant Complexes Studied^a.

		ΔΔGcalc
mutant	drug	λR2b	λR2-Mb	λR2c	λR2-Mc	ΔΔGexp
V555M	AZD4547-linear	–2.76(0.12)	–2.70(0.12)	–1.85(0.07)	–1.82(0.06)	–1.75(0.33)
	AZD4547-bent	–2.07(0.11)	–1.98(0.12)	–1.07(0.07)	–1.11(0.06)
	BGJ-398	–3.66(0.12)	–3.60(0.12)	–1.92(0.08)	–1.96(0.06)	–1.19(0.08)
	TKI258	–1.17(0.13)	–1.11(0.13)	–1.41(0.08)	–1.42(0.06)	0.97(0.22)
	JNJ42756493	–3.99(0.16)	–3.92(0.15)	–2.88(0.12)	–2.87(0.11)	–3.08(0.17)
	MAE	1.37	1.30	0.82	0.82
	RMSE	1.59	1.54	1.16	1.16
I538V	AZD4547-linear	0.09(0.11)	0.05(0.11)	–0.12(0.08)	–0.04(0.07)	–2.11(0.32)
	BGJ-398	0.46(0.11)	0.45(0.11)	0.01(0.08)	0.09(0.07)	–0.74(0.21)
	TKI258	0.47(0.13)	0.38(0.12)	0.01(0.08)	0.12(0.08)	–1.91(0.13)
	JNJ42756493	0.30(0.12)	0.28(0.12)	–0.01(0.07)	0.11(0.07)	–2.18(0.10)
	MAE	2.06	2.02	1.71	1.80
	RMSE	2.13	2.08	1.80	1.89
N540S	AZD4547-linear	0.91(0.14)	0.95(0.14)	0.72(0.11)	0.74(0.11)	–0.76(0.33)
	BGJ-398	1.13(0.14)	1.16(0.13)	0.67(0.11)	0.67(0.11)	0.25(0.19)
	TKI258	1.02(0.14)	1.11(0.14)	0.71(0.12)	0.72(0.12)	–0.9(0.15)
	JNJ42756493	1.06(0.14)	1.11(0.14)	0.72(0.12)	0.72(0.12)	–1.75(0.21)
	MAE	1.82	1.87	1.50	1.50
	RMSE	1.94	2.00	1.66	1.67

^aThe mean absolute error (MAE) and root mean square error (RMSE) for all complexes of each mutant using each free energy scheme are also shown. Production runs are 4 ns in all cases. All values are in kcal/mol. Statistical uncertainties associated with each value are shown in the brackets.

^bHighest T_eff for λ-REST2 simulations is 800 K for receptor and 1500 K for complexes in case of mutants I538V and N540S. In the case of mutant V555M, it is 1500 K for the AZD4547 complexes and 600 K for all other complexes; 600 K is used for the receptor.

^cHighest T_eff for λ-REST2 simulations is 1500 K for receptor and 3000 K for complexes.

3.2. Remote Mutations

In the case of remote mutations, the calculated relative free energies do not agree well with the experimental values (Table 1 and Figure 4). This is not surprising given that the predictions are made using 4 ns long simulations. As mentioned earlier, the effect of remote mutants on the binding of an inhibitor is not due to a change in the direct interaction between the inhibitor and the protein. It generally involves a change in the protein conformation which indirectly affects the binding of the inhibitor. Such conformational changes are close to impossible to capture with molecular dynamics simulations of short temporal duration. This is further confirmed by the fact that the predicted ΔΔG_calc^TIES values for all inhibitors (except TKI258 whose unusual behavior is further discussed in the next section) using standard TIES are very close to each other in the cases of both the I538V as well as the N540S mutant. This essentially means that short duration simulations are only able to capture the changes in the immediate vicinity of the alchemical transformation (i.e., the mutation in this case).

Figure 4.

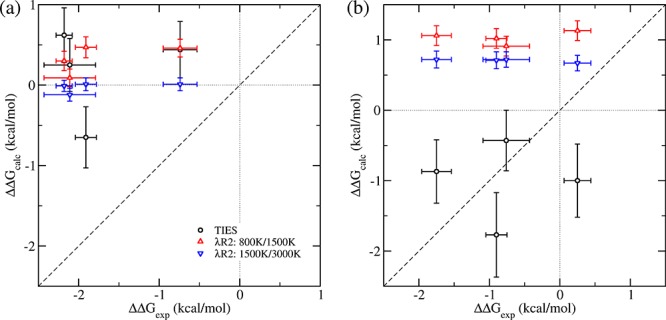
Comparison of the predicted ΔΔG_calc values using TIES (black circles), TIES-λ-REST2 (λR2, up/down triangles) with those from experiment for for all inhibitors bound to FGFR3: (a) I538V mutant and (b) N540S mutant, when the highest T_eff for the chosen REST2 region is at 800 K for receptor and 1500 K for complexes (red triangles pointing up) and at 1500 K for receptor and 3000 K for complexes (blue triangles pointing down). The dotted lines (x = 0 and y = 0) create four quadrants. Data points in quadrants I (x > 0 and y > 0) and III (x < 0 and y < 0) indicate that the ΔΔG_calc values agree directionally with ΔΔG_exp. The results from TIES-λ-REST2-M (λR2-M) are very close to those from λR2 (Table 1), and are not shown for reasons of clarity.

The predicted ΔΔG_calc values for complexes with the I538V mutant using all three free energy schemes are statistically close to zero. Among the three mutations investigated, I538V is the most distant from the bound inhibitors. The I538V mutation involves alchemically transforming isoleucine to valine which are both nonpolar amino acids. Thus, this transformation does not significantly affect the charge distribution of the protein and hence also does not affect its long-range interactions. The mutation does not directly affect the two calculated ΔG_alch values (eq 1) in the presence and absence of an inhibitor, from which the free energy difference ΔΔG_calc is calculated. The experimentally detected ΔΔG_exp must be generated from a mechanism which is not captured in the simulations.

Although the ΔΔG_calc values are not close to zero for the N540S mutation, the predictions are consistently positive. This means that the two calculated ΔG_alch values for the alchemically transforming protein residue differ in the presence and absence of an inhibitor. In the case of remote mutations, the two ΔG_alch values can differ when there is a considerable change in long-range interactions of the mutant with the inhibitor. The N540S mutation involves changing asparagine to serine (effectively −CONH₂ to −OH) which alters the charge distribution of the protein as well as its long-range interactions. Another reason for the nonzero ΔΔG_calc predictions in this case is that the mutation is closer to the inhibitors as compared to the I538V mutant. The shortest distance between the hybrid N540S residue and the inhibitor is 6 Å while for the I538V mutation it is 9 Å. Thus, one would expect that there would be a greater likelihood of standard TIES being able to capture the effect of the N540S than the I538V mutant. Indeed, it should be noted that the complexes bound to the N540S mutant in Table 1 have the least MAE/RMSE among all mutants with standard TIES predictions.

We also performed TIES-λ-REST2 simulations of duration up to 4 ns for the remote mutations but they do not improve the accuracy of results. This may be because the indirect mechanisms which potentially affect the inhibitor binding in such cases occur on time scales longer than can be computed by the simulations performed in this study and hence the “correct” region of the phase space is not sampled even using TIES-λ-REST2 simulations. Remote mutations may modulate the inhibitor–protein interactions via induced allosteric conformational changes occurring over a wide range of space and time scales. A number of computational methodologies have been developed for modeling large-scale motions of proteins, including coarse-grained molecular dynamics and accelerated MD. The prediction of binding free energies may be improved by taking into account all of the conformations, with statistical reweighting techniques to optimally merge data obtained from the enhanced approaches. It is interesting to note in Figure 4 that the ΔΔG_calc^{λR2/λR2–M} values for all inhibitors are close to each other for both the remote mutations unlike in the case of standard TIES, for which TKI258 was an exception. Thus, TIES-λ-REST2 brings all ΔΔG_calc values to the same baseline irrespective of the inhibitor bound.

Increasing the temperature of the “hot” region, from 800 to 1500 K for the receptor and 1500 to 3000 K for the complexes, improves the accuracy of the results and reduces MAE and RMSE of predicted ΔΔG_calc for both of the remote mutants (Table 2). However, the predictions do not agree with the experimental values (Figure 4). In contrast with the observation for the local mutation (section 3.1), the ΔΔG calculations do not benefit from REST2 for the remote mutants studied here.

3.3. Effect of Extending Simulation Time

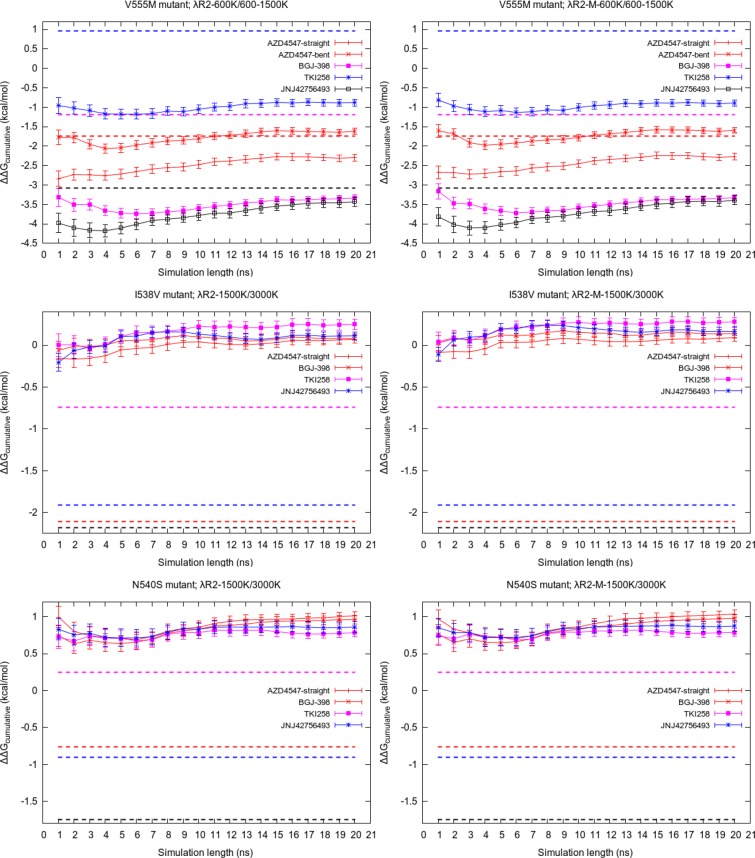
As we explained earlier, short duration simulations are usually unable to correctly predict the relative binding free energies of remote mutations. In this section, we present the outcome of our attempts to extend the duration of simulations. Figure 5 displays the variation of cumulative average of ΔΔG_calc values using standard TIES with the length of simulation extended up to 20 ns for the complexes involving I538V mutant. Apart from small variations, the predicted ΔΔG_calc values remain constant and do not exhibit any signs of getting closer to the corresponding experimental values for all inhibitors except JNJ42756493. In the case of JNJ42756493, the ΔΔG_calc value seems to be drifting toward the experimental value but is still quite far from it after 20 ns. This suggests that 20 ns of standard MD simulation is not sufficiently long to sample the relevant conformations of the complexes involving remote mutants.

Figure 5.

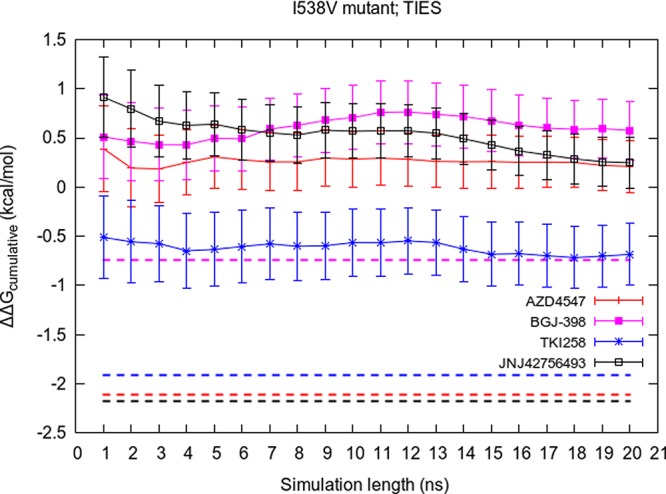
Variation of the cumulative average of ΔΔG_calc^TIES with simulation length for all inhibitors bound to the FGFR3 I538V mutant. The corresponding experimental value for each inhibitor is shown by a dashed line of the same color.

We also extended the TIES-λ-REST2 simulations to see if “heating” a local portion of the complexes around the mutant residue and/or the binding pocket has any impact on the predicted free energies. Figure 6 displays the variation of cumulative average of the calculated ΔΔG_calc values with the simulation length up to 20 ns for all complexes of the three mutants. In the case of complexes involving the V555M mutant, the general trend is that the predicted ΔΔG_calc values get closer to the experimental values. However, it should be noted that, out of the five complexes, the largest difference between the predicted values of ΔΔG_calc at 4 and 20 ns is 0.75 kcal/mol for the V555M–JNJ42756493 complex (see the black line in Figure 6; from −4.18 kcal/mol at 4 ns to −3.43 kcal/mol at 20 ns). The corresponding values for the other V555M complexes are less than or equal to 0.5 kcal/mol. This is a marginal gain measured against the expense of the computation leading to a very high cost–benefit ratio. This observation is in line with our previous studies where we have shown that “long” simulations furnish little to no advantage when the alchemical transformation is local, that is, when it occurs in the binding site.^10,11

Figure 6.

Variation of the cumulative average of ΔΔG calculated using schemes λR2 and λR2-M with simulation length for all complexes. The highest T_eff for receptor and complex are 1500 and 3000 K, respectively, in the case of I538V and N540S mutants, while the corresponding values in the case of V555M mutant are 600 and 600 K/1500 K. The corresponding experimental values for each inhibitor are shown by a dashed line of the same color.

Unlike the V555M mutant, in the case of remote mutants, we extended the λ-REST2 simulations with the highest T_eff of 1500 K for receptor and 3000 K for complexes up to 20 ns. The length of the simulation does not affect the predicted ΔΔG_calc values in these cases either. The predictions remain quite stable, consistently away from the experimental values and close to each other for all complexes involving remote mutations.

4. Discussion

In this section, we discuss how the application of λ-REST2 may be useful in some cases while degrading the quality of results in others. We provide details on the variation in the predicted ΔΔG values for the V555M–AZD4547 complex with the two conformations of the inhibitor AZD4547 using the standard TIES and then how λ-REST2 simulations bring them closer. We also explain the anomalous behavior of the inhibitor TKI258 in detail and provide evidence for how “heating” adversely affects the results in this case. On the basis of the discussion in this section, we formulate some caveats and recommendations concerning the application of the λ-REST2 technique in general for free energy predictions.

4.1. Improved Sampling of AZD4547 on “Heating”

As noted earlier, the inhibitor AZD4547 has been found to bind with the FGFR gatekeeper mutation in two distinct conformations—linear and bent—as shown in Figure 7. However, in the case of the wildtype (WT) FGFR kinase and its other mutants, AZD4547 occurs only in the linear conformation. This suggests that while simulating an alchemical transformation corresponding to the FGFR3 WT to V555M mutant, the inhibitor AZD4547 should occur only in the linear conformation at λ = 0 end-point (WT), while adopting an increasingly mixed population of both conformations on approaching λ = 1 end-point (V555M). In this section, we quantify the occurrence of both conformations of AZD4547 among the MD trajectories of the V555M–AZD4547 complex in the case of different free energy schemes and discuss its impact on the predicted relative free energies.

Figure 7.

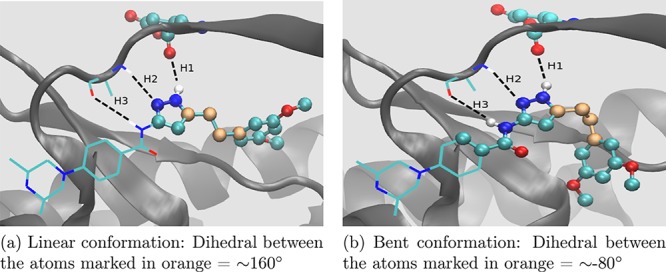
Two distinct conformations of inhibitor AZD4547 found experimentally when bound to the FGFR gatekeeper mutant. The three hydrogen bonds, marked with black dashed lines and labeled as H1, H2, and H3, keep the middle portion of the inhibitor stable. The value of the dihedral angle between the four carbon atoms highlighted in orange can be used as an indicator of the occurrence of the two conformations. The atoms displayed as balls lie in the REST2 region while the ones displayed as lines reside outside it.

In Figure 7, the three hydrogen bonds, which AZD4547 forms with the glutamic acid and alanine residues of the hinge region of FGFR kinase, are marked with black dashed lines and labeled as H1, H2, and H3. These hydrogen bonds keep the middle portion of AZD4547 stable. Figure 8 displays the normalized frequency distributions of these three hydrogen bonds in the λ-REST2 trajectories at the λ = 1 end-point of V555M–AZD4547 complexes with the linear as well as the bent starting structures. H1 and H2 peak around 2 Å while H3 peaks around 2.5 Å. This makes it clear that AZD4547 remains stably bonded to the hinge region of the FGFR3 V555M mutant. The four carbon atoms which connect this stable middle portion of AZD4547 with its free head portion are highlighted in orange in Figure 7. It can be seen that the dihedral angle between these four carbon atoms may be used as a reliable indicator of the type of conformation AZD4547 exists in at a given point in the MD trajectory. Therefore, we use this information to quantify the occurrence of the two conformations of AZD4547.

Figure 8.

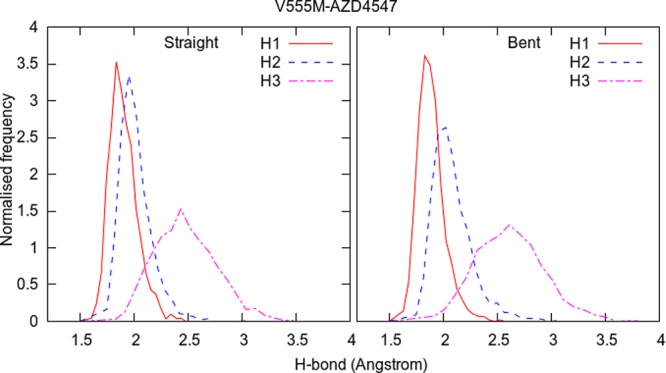
Normalized frequency distributions of the three hydrogen bonds (H1, H2, and H3 from Figure 7) in λ-REST2 trajectories at the λ = 1 end-point of the V555M–AZD4547 complexes when using the linear as well as the bent starting structures.

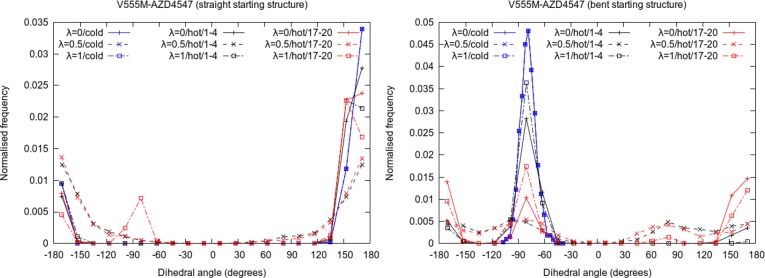
Figure 9 displays the normalized frequency distributions of the dihedral between the four carbon atoms highlighted in orange in Figure 7 from the standard TIES as well as λ-REST2 trajectories at λ = 0, 0.5, and 1 for V555M–AZD4547 complexes with both the linear and the bent starting structures. The peaks centered around +160° correspond to the linear conformation whereas the peaks around −80° correspond to the bent conformation. It is easy to recognize from Figure 9 that, in the case of standard TIES (shown in blue), the type of conformations sampled is entirely dependent on the starting structure of the complex and that there is absolutely no mixing of the states during such simulations. Thus, there are negligible peaks around −80° and +160° when starting with the linear and the bent conformations, respectively. This explains why the predicted ΔΔG values are sensitive to the starting structure and are very different for the two different starting structures using TIES. The plots in black and red denote the distributions from the first and the last 4 ns of the 20 ns long λ-REST2 trajectories. It is evident that λ-REST2 allows sampling the states from both conformations irrespective of the starting structure. This is possible through regular exchanges of conformations between the neighboring states and heating of the REST2 region in the intermediate states. As becomes obvious from Figure 9, the distributions at λ = 0.5 are relatively smoother with non-negligible proportions of both the conformations. However, the picture is not so simple in the case of end-points as discussed next.

Figure 9.

Normalized frequency distributions of the dihedral angle between the four carbon atoms highlighted in orange in Figure 7 for different λ states of V555M–AZD4547 complexes in standard TIES (in blue) as well as λ-REST2 simulations showing the relative populations of the two conformations of AZD4547. In the case of λ-REST2 simulations, the distributions from the first (1–4 ns; in black) and the last 4 ns (17–20 ns; in red) are shown separately.

Ideally, the λ = 0 end-point should have samples predominantly if not exclusively from the linear conformations while the λ = 1 end-point should have samples from both the conformations. However, we find that there is some mixing during the first 4 ns of λ-REST2 simulations which is not enough to reach the ideal situation and hence a dependence on the starting structure persists. In the case of the linear starting structure, there are predominantly linear conformations even at the λ = 1 end-point during the first 4 ns. Similarly, in the case of the bent starting structure, predominantly the bent conformations persist even at the λ = 0 end-point. However, during the last 4 ns of λ-REST2 simulations, there is a noticeable improvement in both situations. In the case of the linear starting structure, there is a visible peak around −80° at λ = 1 end-point. In the case of the bent starting structure, there is an almost equal proportion of both conformations at λ = 1 end-point. Moreover, the peak around −80° is much smaller as compared to the first 4 ns at λ = 0 end-point. It is interesting to note that the −80° peak is always lower for the λ = 0 end-point as compared to the λ = 1 end-point in the case of λ-REST2 simulations. Indeed, the switching from bent to linear conformation appears to be easier than the converse through λ-REST2 simulations. This is because both of the end-points accept the linear conformation, while only the λ = 1 end-point tolerates the bent conformation. Through this selective pressure, the linear conformation is more likely to spread than the bent one during the replica exchange simulations.

4.2. The Exceptional Case of TKI258: Limitations of λ-REST2

The inhibitor TKI258 is an anomaly in this study. As is clear from Figure 4 and Table 1, its ΔΔG prediction consistently becomes less accurate on applying λ-REST2 as compared to the standard TIES in case of all three mutants. The absolute errors of the TKI258 complexes increase by 1.43, 1.12, and 1.05 kcal/mol when bound with V555M, I538V, and N540S, respectively, on using λ-REST2. In addition, its relative binding affinity predictions using λR2 as well as λR2-M become less accurate on increasing the highest T_eff to 3000 K in the case of the V555M mutant. In this section, we provide an explanation for such behavior of TKI258. Figure 10 displays the binding pose of TKI258 found experimentally. It forms two hydrogen bonds with glutamic acid and alanine residues of the hinge region of the protein (labeled as H1 and H2 in Figure 10). Figures 11, 12, and 13 show the normalized frequency distributions of H1 and H2 for λ = 0 and λ = 1 end-points of TKI258 complexes in the case of the standard TIES as well as λ-REST2 simulations. Below we discuss them in detail.

Figure 10.

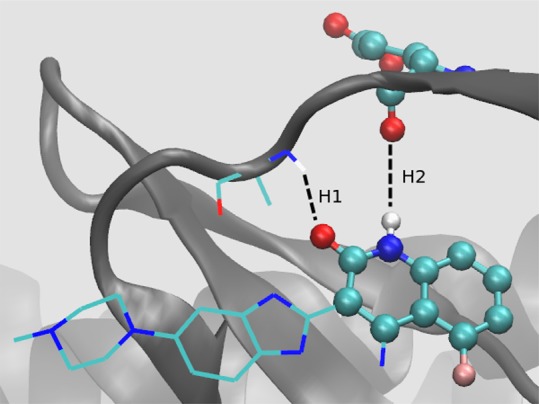
Inhibitor TKI258 bound to V555M mutant. It forms two hydrogen bonds with the hinge region of the protein which are displayed with black dashed lines and labeled as H1 and H2. The atoms shown as balls lie in the “hot” region. The atoms are shown in the standard color code: carbon in green, oxygen in red, nitrogen in blue, hydrogen in white, and fluorine in pink.

Figure 11.

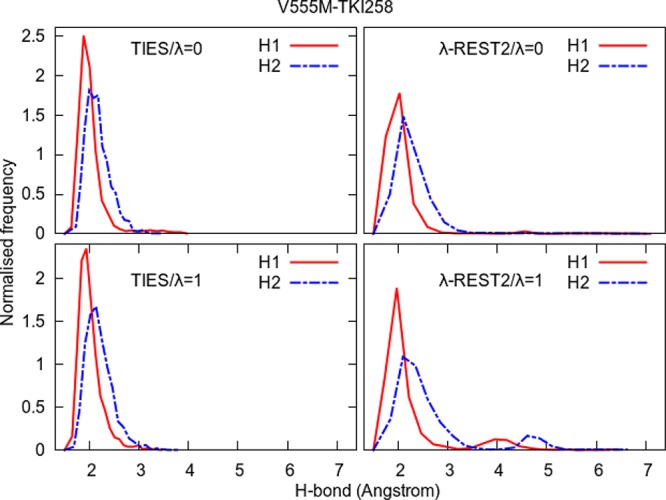
Normalized frequency distributions of H1 and H2 from Figure 10 for the two end-points in the case of the standard TIES as well as λ-REST2 simulations of the V555M–TKI258 complex. λ-REST2 simulations sample a larger comformational space than TIES, as evidenced by the lower and wider distributions of the distances, and the second peaks in the λ = 1 end-point (V555M).

Figure 12.

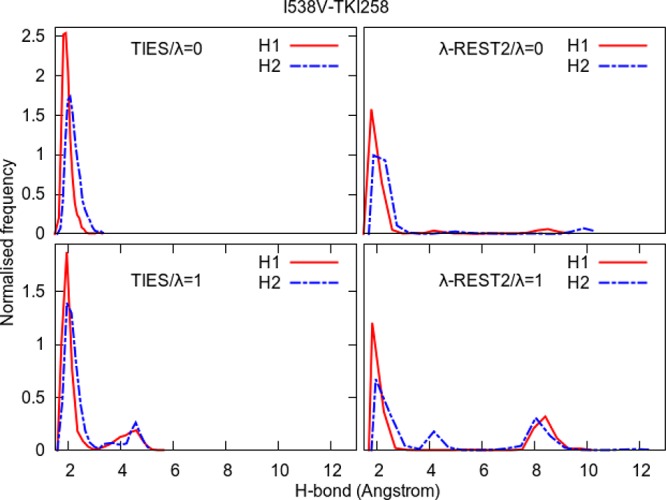
Normalized frequency distributions of H1 and H2 from Figure 10 for the two end-points in the case of standard TIES as well as λ-REST2 simulations of the I538V–TKI258 complex. The long tails and additional peaks beyond 4 Å indicate that λ-REST2 simulations sample some conformations irrelevant to stable inhibitor binding.

Figure 13.

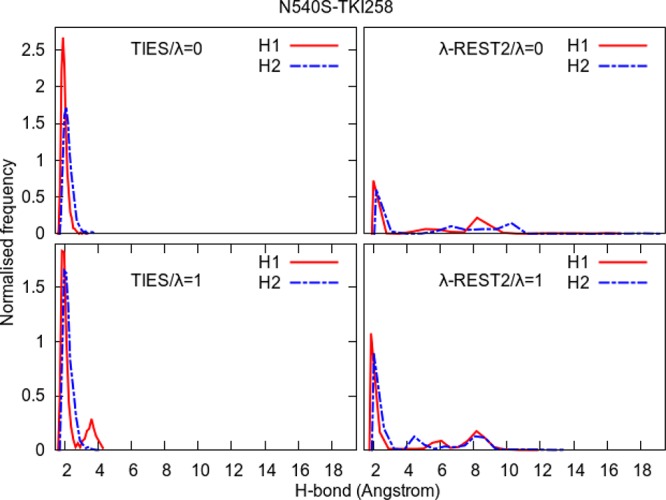
Normalized frequency distributions of H1 and H2 from Figure 10 for the two end-points in the case of standard TIES as well as λ-REST2 simulations of the N540S–TKI258 complex. The long tails and additional peaks beyond 4 Å indicate that λ-REST2 simulations sample some conformations irrelevant to stable inhibitor binding.

Figure 11 compares the normalized frequency distributions of H1 and H2 in the ensemble of conformations for the two end-points (λ = 0 and λ = 1) of the standard TIES calculation as well as λ-REST2 calculation. Both H1 and H2 have peaks around 2 Å with almost negligible frequencies between 3 and 4 Å and vanish for distances greater than 4 Å. This is true for both the end-points which suggests that the inhibitor remains quite stable and tightly bound to the protein via the two hydrogen bonds throughout the simulations at both the end-points. This explains why ΔΔG_calc^TIES for the V555M–TKI258 complex is close to zero.

On the other hand, in the case of λ-REST2 simulations, the right-hand tails of the H1 and H2 distributions extend to 7 Å. However, in the case of the λ = 0 end-point, they have negligible frequencies beyond 3 Å unlike the λ = 1 end-point where there are small peaks for both H1 and H2 around 4 and 5 Å, respectively. This happens because, due to the “heating”, the inhibitor drifts away from the protein and hence binds only weakly to it at one of the end-points as compared to the other end-point. This explains the negative value of ΔΔG_calc^λR2(−M) for the V555M–TKI258 complex. The important thing to note here is that the “heating” in the intermediate λ-windows and regular exchanges between the neighboring REST2-replicas causes the complex to visit some “unwanted” high energy conformations leading to degraded results. The smaller peaks of the H1 and H2 distributions at λ = 1 end-point suggest that the V555M–TKI258 complex has a higher energy minimum which is not sampled by standard MD simulations and is probably not observed experimentally to the extent realized by the λ-REST2 simulations (X-ray structures show that all reversible ATP-competitive inhibitors form one or more stable H-bond(s) with the hinge region of the receptors). The more heating there is, the greater is the population of this higher energy minimum and hence the more negative is the ΔΔG_calc prediction (refer to Figures 3, 4, and Table 2).

Comparing Figure 11 with Figure 8, it is clear that such a drifting of the inhibitor does not occur in the case of V555M–AZD4547 complex even though the highest T_eff for the latter is 1500 K against 600 K in the case of the former. To find out if a similar process arises in other complexes, we performed a hydrogen-bond analysis for all complexes whereby we determined the occupancies of all the hydrogen bonds formed between glutamic acid and alanine residues of the hinge region of the protein and the inhibitor (refer to Table S7 of the Supporting Information; the bond and angle cut-offs used to determine the occurrence of the hydrogen bonds were 3 Å and 135°). We found that, except for JNJ42756493, all inhibitors form one or more hydrogen bonds with at least one of the two residues such that their occupancies are greater than 50%. The occupancies of the strongest hydrogen bond (the one with the largest occupancy) do not change much for all such inhibitors except TKI258. This can be attributed to the absence of the 2,4-dimethoxy phenyl group in TKI258 unlike other inhibitors (refer to Figure 1) which provides enough empty space in the binding pocket for it to drift away from the protein.

The ΔΔG predictions for the complexes of TKI258 in case of remote mutants also become less accurate on “heating” as compared to standard TIES. In order to understand this, we accumulated the normalized frequency distributions of H1 and H2 for these complexes too as shown in Figures 12 and 13. It is interesting to note that, in the case of both remote mutants, the distributions are different at the two end-points of the standard TIES calculations such that there are additional small peaks in H1 and/or H2 distributions around 4 Å at the λ = 1 end-point. This may be related to the negative ΔΔG_calc^TIES predictions for both complexes of TKI258 (refer to Table 1 and Figure 4). However, in the case of λ-REST2 simulations, the situation appears to be even worse than the V555M–TKI258 complex with H1/H2 values reaching as high as 12 and 18 Å for I538V–TKI258 and N540S–TKI258 complexes, respectively. Both these complexes have peaks centered around 8 Å in the case of λ-REST2 simulations which correspond to the flipped conformation of the inhibitor when the fluorine atom of the TKI258 faces the hinge region of the protein while the H and O atoms involved in H1 and H2 point toward the opposite side (refer to Figure 10). This is further confirmed by the hydrogen bond analysis where the starred occupancies correspond to the hydrogen bonds formed by the inhibitor atoms facing opposite to the H and O involved in H1 and H2 (refer to Table S7 in the Supporting Information). Such flipped conformations correspond to a higher energy minimum which is inaccessible using standard MD simulations (and probably unobserved in experiments) but, due to the “heating” and exchanging of conformations between neighboring REST2-replicas, are observed in λ-REST2 simulations. This explains why the ΔΔG predictions using λ-REST2 become less accurate as compared to standard TIES. It should be noted that no such flipped conformations are observed in other inhibitors. This is partly due to the absence of the 2,4-dimethoxy phenyl group in the case of TKI258, which leaves an empty space in the binding pocket, and partly to relatively weaker interactions between TKI258 and the hinge region of the protein as compared to other inhibitors due to inclusion of an extra residue in the “hot” region (refer to Table S7 of the Supporting Information).

From the above discussion, it can be concluded that blind application of the λ-REST2 technique with the hope to improve sampling is not wise and may lead to potentially “unwanted” conformations. This can be further understood by considering a hypothetical situation where there are two potential energy minima separated by a barrier such that the lower energy minimum corresponds to the “wanted” conformation while the higher energy minimum corresponds to the “unwanted” conformation. During a λ-REST2 simulation, the intermediate λ-windows are “hot” and will sample both minima as well as the peak of the energy barrier. Although enhanced sampling is preferred in many cases, correctly predicting a physical observable of interest requires not only sufficient representative conformational states but the corresponding weights that describe the likelihoods of individual states. The latter are usually calculated based on the total energy of a system while the energy distributions of different states can be highly overlapping. It is therefore difficult to assess the relative likelihood of a state and its contribution to the prediction of the observable. Thus, while λ-REST2 can be a valuable technique, it should be used with care. Constraints from experiments, wherever available, should be used to infer the relevance of conformational space sampled by an enhanced MD simulation. In cases where there are no experimental data at all, many binding poses may need to be generated and evaluated, by methods such as docking and enhanced MD simulation, and the most plausible poses should be chosen based on their ranking scores. There are also data driven approaches such as random forests³¹ and state-of-the-art neural network methods³² which show some promise in this respect. As opposed to theory-led approaches, these data-driven machine learning approaches have a general limitation in biomedical research,³³ and their accuracies usually depend on the size and quality of training sets.

5. Conclusions

In this article, we describe the applications of ensemble-based approaches, with or without enhanced sampling protocols, to predict relative binding free energies of inhibitors to wild-type and mutant proteins. These approaches have been shown to be accurate and precise with effective control of errors for a range of target proteins and ligands.¹¹ Two challenging cases are investigated in the current study: one is a protein mutation within the binding site, which induces a large conformational change within one of the inhibitors;²⁵ another is the protein mutations remote from the binding site which do not have significant impact on the stability of the protein yet have an influence on inhibitor binding.¹⁶

The calculation of free energy changes caused by local mutations can benefit from enhanced sampling techniques such as REST2. The correct conformations are sampled in TIES-λ-REST2 simulations for the inhibitor AZD4547: while only one comformation is sampled for the inhibitor complexed with wild-type FGFR3, two conformations emerge when the gatekeeper residue is mutated from valine to methionine (V555M). Without enhanced sampling, the inhibitor remains trapped in its initial conformations, making the predicted free energy changes either overestimated or underestimated. TIES-λ-REST2, on the other hand, correctly predicts the free energy changes regardless of what initial conformation is used. As in our previous work,¹¹ the free energy estimator, MBAR, only offers a marginal improvement in the precisions of predictions but does not affect their accuracy.

For local mutations, the choice of a “hot” region is important in determining the efficiency and convergence of the free-energy calculations in simulations with REST2 approach. If the region is too small, the functionally relevant conformational space may not be explored sufficiently; while if it is too large, the system may drift away from those conformations leading to deteriorated predictions. Therefore, one requires some preliminary knowledge of the topological and physical properties of the protein–ligand systems for selection of an appropriate REST2 region. We do not question the utility of classical atomistic MD as a predictive tool for biomolecular systems, as many studies have proven the predictive ability of the method, including our two collaborative studies with pharmaceutical companies,^12,13 which were performed, initially blind, to investigate the binding affinities of compounds to protein targets. Our current study serves as a caution against the blind application of enhanced sampling approaches.

For remote mutations, however, the TIES-λ-REST2 approach does not generally improve the binding free-energy predictions. This is not surprising given that the mutations are far away from the bound inhibitors and affect the binding through an allosteric mechanism. Allostery involves conformational changes on length and/or time scales that are greater than standard atomistic molecular simulations can access. They only sample local conformational changes on a nanosecond time scale, which are not affected by remote mutations.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b01118.

• Tables containing individual ΔG_alch values for all the relative free energy calculations, and a table for the comparison of occupancies of hydrogen bonds between the inhibitors and the protein (PDF)

• Topology and coordinate files for all ligand–protein complexes (ZIP)

The authors would like to acknowledge the support of the MRC Medical Bioinformatics project (MR/L016311/1), the Qatar National Research Fund (7-1083-1-191), the EU H2020 projects ComPat (http://www.compat-project.eu/, Grant No. 671564), and CompBioMed (http://www.compbiomed.eu/, Grant No. 675451), NSF Award (https://www.nsf.gov/pubs/2017/nsf17542/nsf17542.htm, Award No. NSF 1713749) and funding from the UCL Provost. We made use of the BlueWaters supercomputer at the National Center for Supercomputing Applications of the University of Illinois at Urbana–Champaign (https://bluewaters.ncsa.illinois.edu), access to which was made available through the aforementioned NSF award, and the Titan supercomputer at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. A.P.B. was supported by an Overseas Research Scholarship from UCL and an Inlaks Scholarship from the Inlaks Shivdasani Foundation.

The authors declare no competing financial interest.