Delay Differential Analysis for Dynamical Sleep Spindle Detection

Abstract

Background

Sleep spindles are involved in memory consolidation and other cognitive functions. Numerous automated methods for detection of spindles have been proposed; most of these rely on spectral analysis in some form. However, none of these approaches are ideal, and novel approaches to the problem could provide additional insights.

New Method

Here, we apply delay differential analysis (DDA), a time-domain technique based on nonlinear dynamics to detect sleep spindles in human intracranial sleep data, including laminar electrode, stereoelectroencephalogram (sEEG), and electrocorticogram (ECoG) recordings.

Results

We show that this approach is computationally fast, generalizable, requires minimal preprocessing, and provides excellent agreement with human scoring.

Comparison with Existing Methods

We compared the method with established methods on a set of intracranial recordings and this method provided the highest agreement with human expert scoring when evaluated with F₁ score while being the second-fastest to run. We also compared the results on the DREAMS surface EEG data, where the method produced a higher average F₁ score than all other tested methods except the automated detections published with the DREAMS data. Further, in addition to being a fast and reliable method for spindle detection, DDA also provides a novel characterization of spindle activity based on nonlinear dynamical content of the data.

Conclusions

This additional, non-frequency-based perspective could prove particularly useful for certain atypical spindles, or identifying spindles of different types.

1. Introduction

1.1. Sleep Spindles

Sleep spindles are discrete events consisting of 11 to 16 Hz oscillations (the precise frequency range varies across subjects) recorded primarily in stage 2 non-REM sleep, and to a lesser extent in stage 3 non-REM sleep (Berry et al., 2012). Spindles display a characteristic waxing and waning pattern in amplitude, and generally last between 0.3 and 3 seconds, recurring every 5 to 15 seconds (Bonjean et al., 2012;Leresche et al., 1991). Sleep spindles arise from the activity of thalamocortical circuitry. They have become a subject of study for their potential roles in memory consolidation and other cognitive functions (Sejnowski and Destexhe, 2000; Schabus et al., 2004; Fogel et al., 2007), as well as in psychiatric and neurological disorders (Ferrarelli et al., 2007; Petit et al., 2004; Ktonas et al., 2007).

Numerous methods for automated spindle detection have been proposed, most of which rely on spectral analysis in some form (Warby et al., 2014; O’Reilly and Nielsen, 2015). Here, we propose an alternative approach using a nonlinear time-domain algorithm which is computationally fast and therefore capable of detecting spindles in real time.

1.2. Delay Differential Analysis

Delay differential analysis (DDA) is a time-domain classification framework based on embedding theory in nonlinear dynamics (Kremliovsky and Kadtke, 1997; Lainscsek et al., 2013). An embedding reveals the nonlinear invariant properties of an unknown dynamical system (here the brain) from a single time series (here intracranial recordings). The embedding in DDA serves then as a sparse nonlinear functional basis onto which the data are mapped. Since the basis is built on the dynamical structure of the data, preprocessing (such as filtering) is not necessary. DDA yields a small number of features (around 4), far fewer than traditional spectral techniques, which provide a power at each frequency (often 100-200 frequencies). In either case, the size of the feature set might vary depending on the parameters used. Also, either set of features can be combined or collapsed to yield a measure that can be thresholded. However, working with a constrained feature space is often desirable. This approach greatly reduces the risk of overfitting, and therefore helps to ensure that a model that was selected using a single EEG channel from one subject can be applied to a wide range of data from different subjects, channels, and recording systems.

One can also view DDA models as sparse Volterra series (Volterra, 1887, 1959). A general nonlinear real-valued function can be expressed as a Taylor series expansion of functionals of increasing complexity around a fixed point. Rather than retain all low-order terms in the expansion, DDA imposes restricted complexity on the analysis by using a low-dimensional sparse delay differential equation (DDE) model. In a model of this type, linear and nonlinear components of the data are analyzed in an interconnected manner. This reduces the computational load, and further, by leaving some of the non-relevant dynamics unmodeled, it is possible to greatly reduce the effect of artifacts and other signals unrelated to the particular classification task of interest.

DDEs combine differential with delay embeddings as a functional embedding where (non-) linear polynomial functions of the delay terms are used (Lainscsek et al., 2017). The general form of the DDEs is

$$\stackrel{.}{x}(t)=\sum _{i=1}^I{a}_i\prod _{n=1}^N{x}_{{\tau }_n}^{m_{n,i}}\text{for}{\tau }_n,m_{n,i}\in {\mathbb{N}}_0$$ (1)

where I is the number of monomials in the model, N is the number of delays, m_n,i is the order of the n^th term in the i^th monomial, and x_τn represents x(t − τ_n). The time derivative of the data, x̄(t), is estimated with a weighted center derivative (Miletics and Molnárka, 2005):

$$\stackrel{.}{x}(t)=\frac{1}{2M}\sum _{m=1}^M\frac{x(t+m)-x(t-m)}{m}$$ (2)

where M is the number of points used.

For a given model, we compute a small set of features, which are the estimated coefficients a_i in Eq. (1) as well as the least-squares error. The error is defined as:

$$\rho =\sqrt{\frac{1}{K}\sum _{k=1}^K{\left({\stackrel{.}{x}}_{t_k}-\sum _{i=1}^I{a}_i\prod _{n=1}^N{x}_{{\tau }_n,t_k}^{m_{n,i}}\right)}^2}$$ (3)

where K is the number of time points, and x_τn,tk represents x(t_k − τ_n).

2. Methods

2.1. Data

DDA was applied to laminar, stereoelectroencephalogram (sEEG), and electrocorticogram (ECoG) recordings from patients with intractable epilepsy.

The laminar recordings studied here come from five patients, designated L1 to L5. Recordings and data were obtained under Institutional Review Board (IRB) approval with informed consent from participants in accordance with the Declaration of Helsinki.

The additional recordings used for this study consisted of sEEG (depth electrode) recordings from five patients, designated S1 to S5, and ECoG recordings from two patients, designated E1 and E2, with long-standing pharmaco-resistant complex partial seizures. These recordings used a standard clinical recording system (XLTEK, Natus Medical Inc., San Carlos, CA) with sampling rates of 500, 512, or 1024 Hz. The reference for the sEEG electrodes was an electrode placed over the C2 spinous process on the posterior neck. For the ECoG (cortical surface electrode) recordings, the reference channel was a strip of electrodes located outside the dura mater and facing the skull at a region remote from other grid and strip electrodes. Placement of the intraparenchymal (sEEG) electrodes and subdural electrode arrays was chosen to confirm the hypothesized seizure focus and locate epileptogenic tissue in relation to essential cortical areas, thus directing surgical treatment.

The decision to implant, as well as the electrode targets and the duration of implantation were entirely clinically based with no input from this research study. All data were handled following protocols approved by the IRB of the Massachusetts General Hospital according to National Institutes of Health guidelines.

sEEG data used for this study consist of three channels from subject S1, four channels from subject S2, one channel each from subjects S3 and S5, and two channels from subject S4. ECoG data used here consist of three channels from subject E1 and one channel from subject E2. All data selected for use in this study were exclusively from stage two sleep, during time periods when no seizures were occurring.

2.2. Spindle Marking

Both the data used for developing the detector and those used for testing were drawn from human expert-scored intracranial recordings: 23-channel laminar electrodes in five subjects (L1-L5) and single-channel scored sEEG and ECoG recordings from subjects S1-S5 and E1-E2. In the laminar data set, the scorer marked a single time point for each identified spindle based on evaluation of all 23 channels (here designated type I scoring). In the sEEG and ECoG data, the beginning and end of all spindles were marked on the basis a single channel (type II scoring). In type II scoring, therefore, the beginnings of spindles are defined as the point where spindle oscillations become visually apparent to the scorer, and the end is defined as the point where these oscillations are no longer apparent. Also, in type II scoring, the scorer marked all potential spindles, regardless of clarity. By including both types of human scoring as well as a range of spindle quality, we aim to develop a robust detector that can function even with non-ideal data.

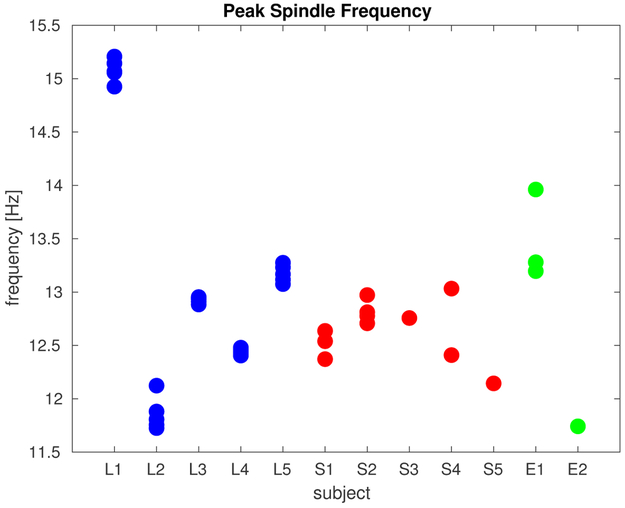
Since only a single time point was marked in type I scoring, a window of one second around each marker was taken as the spindle (that is, the beginning of each spindle was defined as 0.5 seconds before the mark and the end was defined as 0.5 seconds after the mark), and a wider window of one to three seconds around each marker was excluded from classification as non-spindle data (only data at least 1.5 seconds before or after a mark were considered non-spindle data). Table 1 summarizes the properties of the marked spindles in both data sets: the recording type (laminar electrodes, sEEG, or ECoG), the scoring type (I or II), the sampling rate f_s, the number of marked spindles, the mean spindle duration, and the mean peak frequency (between 11 and 17 Hz) for all spindles in each recording. Since type I scoring involved marking spindles on the basis of multiple channels, the peak frequencies are computed as the mean of the peak frequency across the five channels in which spindles are most visually apparent. The peak frequencies for all channels for each subject are plotted in Fig. 2.

Table 1:

Human-marked spindle properties for the fifteen recordings.

Subject	Channel**	Type	Scoring	fs [Hz]	Number	Mean duration [s]	Mean peak freq. [Hz]
L1	1-23, left frontal	Laminar	I	2000	144	1*	15.0580
L2	1-23, right frontal	Laminar	I	2000	48	1*	11.8063
L3	1-23, right frontal	Laminar	I	2000	137	1*	12.8836
L4	1-23, right frontal	Laminar	I	2000	50	1*	12.4320
L5	1-23, right temporal	Laminar	I	2000	72	1*	13.2750
S1	1 (RCIN3)	sEEG	II	500	57	0.84	12.5395
S1	2 (LCIN4)	sEEG	II	500	135	0.91	12.8115
S1	3 (LSF6)	sEEG	II	500	47	0.72	12.6363
S2	1 (LCIN3)	sEEG	II	500	213	1.79	12.7073
S2	2 (LSF3)	sEEG	II	500	218	1.42	13.1963
S2	3 (RCIN5)	sEEG	II	500	146	1.25	12.9723
S2	4 (LFR1)	sEEG	II	500	227	1.57	12.3713
S3	1 (OF7)	sEEG	II	500	138	0.87	12.7769
S4	1 (RPF5)	sEEG	II	512	152	1.15	12.7569
S4	2 (ROF4)	sEEG	II	512	81	0.98	13.9615
S5	1 (RAF6)	sEEG	II	512	124	0.96	13.0326
E1	1 (GR28)	ECoG	II	512	82	1.05	12.4093
E1	2 (GR53)	ECoG	II	512	13	1.36	11.7415
E1	3 (GR38)	ECoG	II	512	92	1.18	13.2799
E2	1 (AGR52)	ECoG	II	1024	47	0.71	12.1440

^*The mean duration cannot be determined from Type I scoring because only a single time point was marked across all channels (1-23). One second of data is designated as spindle data for structure selection.

^**RCIN–right cingulate, LCIN–left cingulate, LSF–left subfrontal, LFR–left frontal, OF–orbitofrontal, RPF–right posterior frontal, ROF–right orbitofrontal, RAF–right anterior frontal, GR–grid (subject E1 grid channels 28, 38, and 53 were all located over posterior frontal cortex with 28 the most inferior and 53 the most superior), AGR–anterior grid (subject E2 anterior grid channel 52 was located over middle posterior frontal cortex)

Figure 2:

Spindle frequencies. For each of the five laminar, five sEEG, and two ECoG subjects, the peak frequency (between 11 and 17 Hz) was computed for all human-marked spindles and the mean peak frequency across all spindles is plotted as one point for each channel. For laminar subjects, five of the channels are plotted–spindles were marked based on evaluation of all channels. For the sEEG and ECoG subjects, spindles were marked on an individual-channel basis, and all scored channels are plotted. Color indicates the type of recording. Note that laminar recordings were collected from cortex identified as probably epileptogenic.

2.3. Supervised Structure Selection

Structure selection of the model ultimately relied on data from one channel from one subject. Since DDA uses specific time delays, adjustments need to be made for sampling rate, and to facilitate this, the model (polynomial form and delays) was selected using data with the lowest sampling rate in the available data set (this allows for easy adjustment to higher sampling rates). Here, we used an sEEG recordings sampled at 500 Hz. Data from these subjects and channels were divided into half-second epochs and marked as spindle or non-spindle based on how each epoch had been marked by a human expert in the manner described above. Among these 500 Hz recordings, the one for which spindle and non-spindle epochs proved most separable was used to select a model for use with new data.

In order to select the model from these training data, the set of models to be considered was first subjected to constraints based on model forms that had proven effective in previous applications of DDA, ensuring the sparsity of the model. The general form of the model shown in Eq. (1) was constrained to two delays (N ≤ 2), three terms (I = 3), and up to third-order nonlinearities (∑_n m_n,i ≤ 3). This resulted in a total of 188 unique DDE model forms, upon which we performed an exhaustive search. The delays T₁ and T₂ were allowed to vary between approximately 1 and 80 ms at intervals of 1/f_s.

We performed repeated random subsampling cross-validation (Kohavi et al., 1995) to evaluate the performance of each model. This method involves repeatedly dividing the data at random into training and testing sets. (Note that throughout we use the terms “training” and “testing” to refer to these repeated random splits of the data for cross-validation. New data, not used in the structure selection of a particular model, are referred to as “validation” data.) This prevents overfitting of the model and ensures generalizability. Here, the repeated random splits were carried out for the model selection data, assigning 70% of spindle and non-spindle epochs to the training set, and the remaining 30% to the testing set. Using the model coefficients a_k,i and error ρ_k obtained from each epoch k of the training data, we used the human expert-scored labels l_k (i.e. 0 for non-spindle and 1 for spindle) to obtain a vector of weights W for the features by finding a least-squares solution to:

$$\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill a_{1,1}\hfill & \hfill a_{1,2}\hfill & \hfill a_{1,3}\hfill & \hfill {\rho }_1\hfill \\ \hfill 1\hfill & \hfill a_{2,1}\hfill & \hfill a_{2,2}\hfill & \hfill a_{2,3}\hfill & \hfill {\rho }_2\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill a_{k,1}\hfill & \hfill a_{k,2}\hfill & \hfill a_{k,3}\hfill & \hfill {\rho }_k\hfill \end{array}\right)W=\left(\begin{array}{c}\hfill l_1\hfill \\ \hfill l_2\hfill \\ \hfill ⋮\hfill \\ \hfill l_k\hfill \end{array}\right).$$ (4)

The additional constant term avoids constraining the separating hyperplane to pass through the origin in feature space. The weights W can be applied to the features computed from the testing data which provides a one-dimensional distance D from an optimal hyperplane of separation between spindle and non-spindle feature sets. We can evaluate how well this distance corresponds to the human expert-scored labels of the testing data by computing the area under the receiver operating characteristic (ROC) curve or F₁ score. The ROC is constructed by plotting the hit rate against the false alarm rate for various spindle detection thresholds for D. The area under the curve defined by the plotted points, A′, should be equal to 0.5 for random chance detection, and 1 for perfect separation of the groups (Hand and Till, 2001). A′ can be obtained by taking

$$A^{\prime }=\frac{S_0-n_0(n_0+1)}{2n_0{n}_1}$$ (5)

where n₀ and n₁ represent the number of points in each of two classes labeled 0 and 1 (here, non-spindle and spindle epochs), and S₀ is obtained by first ranking all points by their probability of being classified as 0, then summing the ranks of the true class 0 points. In practice, once a specific model form has been selected, it is often sufficient to use a single feature for classification.

While A′ is useful for structure selection of the DDA model, we evaluate final performance with another measure, the F₁ score, which is more widely used for evaluating spindle detection (Dice, 1945; Sørensen, 1948). F₁ scores are computed from the confusion matrix according to:

$$F_1=\frac{2TP}{FN+FP+2TP}$$ (6)

where TP is the number of true positives, FN is the number of false negatives, and FP is the number of false positives. For this purpose, the human scoring is considered the “ground truth”. F₁ scores are used in Sec. 3.1 for comparison between the outputs of several spindle detection methods. As additional measures, we also compute the false discovery rate $(FDR=\frac{FP}{TP+FP})$ and false negative rate $(FNR=\frac{FN}{FN+TP})$.

The cross-validation was repeated 100 times and the maximal A′ was used to select the optimal model form and values of the delays. Using this procedure, for spindle detection in the laminar, sEEG, and ECoG data at all sampling rates, an effective DDE model is:

$$\stackrel{.}{x}=a_1{x}_{{\tau }_1}+a_2{x}_{{\tau }_2}+a_3{x}_{{\tau }_1}^2$$ (7)

with T₁ = 16 δt = 32 ms and T₂ = 25 δt = 50 ms for 500 Hz data. For spindle detection, we find that the single feature a₂ provides sufficient information for good detection performance. In general, the threshold for spindle detection is set to 1.2 standard deviations above the mean of a₂. This threshold has been empirically determined to provide good agreement with human scoring and was fixed throughout.

Despite the fact that these data come from subjects with different types of electrodes and different sampling rates, it is possible to obtain spindle detection which agrees with human scoring across multiple recordings as well as multiple human scorers would tend to agree with each other (Basner et al., 2008). Because we use nonlinear models, all terms are connected and linear as well as nonlinear terms contain both linear and nonlinear information. For this reason the delays do not correspond to particular frequencies as one might expect (Lainscsek and Sejnowski, 2015). Adjustments need to be made for data with different sampling rates. In order to apply a selected DDA model to data with a higher sampling rate, we need to change the delays and derivatives in the following way: The delays can be just the approximate multiples (e.g. from 500 Hz to 1000 or 1024 Hz they would be doubled). For the derivatives we keep the number of total points constant but take for this example every second data point. For data with lower sampling rates (e.g. the DREAMS data in Sec. 3.1), results can only be obtained by upsampling the data to the minimum sampling frequency of 500 Hz before applying the model.

2.4. Application to Full-Time Data

Having selected a model form and delay pair according to the above procedures, we compute the corresponding a2 coefficient in sliding time windows across the full length of all recordings. We use windows of length around 650 ms, shifted by around 200 ms per step. Since the number of spindle and non-spindle epochs in the training data are not equal, the optimal threshold for spindle detection may vary slightly between recordings. Nevertheless, for the sake of testing a fully automated method, we maintained the aforementioned 1.2 standard deviation above mean a₂ threshold for all results shown here. The beginning of each detected spindle is therefore defined as the point at which the normalized a₂ value increases this threshold, and the end is defined as the point at which it subsequently decreases below the threshold. (Note that threshold-setting does not affect A′, since this is a threshold-independent measure, but does determine the F₁ scores, which are computed from the confusion matrix for a particular threshold.) As a final step, any threshold crossings less than 300 ms in length are excluded and marked as non-spindle. The remaining threshold-crossings are the identified spindles. We evaluate detector performance by comparing these time points identified as spindle by the detector with those identified by the human expert.

3. Results

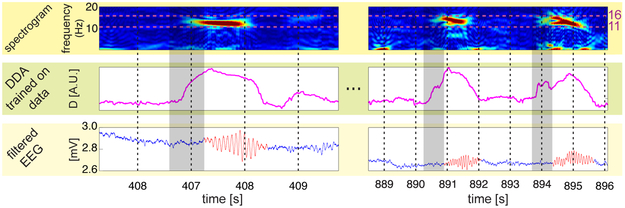
Applying the detector to laminar, sEEG, and ECoG data, we obtain a mean area under the ROC curve, A′, of 0.82 and a mean F₁ score of 0.50. For the laminar data, we take just one central channel from each electrode array for evaluating all methods. Since these data were scored based on all channels, but some superior and inferior channels lacked clearly visible spindles, one of the channels (channel 11) with apparent spindles was chosen for evaluating spindle detection performance. All available (individually scored) sEEG and ECoG channels were used. For comparison, DDA frequency-band detectors (discussed in Appendix A) for 11-14 Hz and 11-17 Hz yield mean A′ values of 0.72 and 0.77 and mean F₁ scores of 0.21 and 0.18 respectively. Such a difference in performance indicates that in addition to the frequency characteristics of spindles, nonlinear information might also be relevant. Fig. 3 shows the output the data-trained DDA spindle detector. Since the data-trained DDA detector shows higher agreement with human scoring than the frequency-based DDA detector, it is used exclusively for the remainder of the manuscript.

Figure 3:

Spindle detection. The lowest row in the plot shows the data with the spindles in red, as marked by a human expert. In the middle row, a DDA spindle detection output (trained on one channel from a different subject) is shown. We also show the spectrograms (in the top row) for reference. The gray-shaded regions indicate the width of the time windows used for computing both the DDA features and the spectrogram (650 ms). Since we plot the time points on the x-axis for the start points of the sliding windows, all points within a shaded region use windows that include some amount of spindle data.

The A′ values, F₁ scores, false discovery rates, and false negative rates for the DDA spindle detector on all subjects are listed in Table 2. Note that in Sec. 3.1, F₁ scores are used to compare methods. Where cross-recording averages are reported, two recordings are excluded since all automated detectors perform poorly, and these were originally selected as recordings that were difficult to score.

Table 2:

DDA spindle detection performance on all recordings

Subject	Channel	A′	F1	False discovery rate	False negative rate
L1	11	0.6023	0.2685	0.5323	0.8117
L2	11	0.6934	0.2991	0.7107	0.6903
L3	11	0.7423	0.2892	0.4701	0.8011
L4	11	0.7784	0.4948	0.5590	0.4365
L5	11	0.7529	0.3679	0.6682	0.5872
Laminar mean		0.7139	0.3439	0.5881	0.6654
S1	1 (RCIN3)	0.8785	0.5404	0.5924	0.1983
S1	2 (LCIN4)	0.9066	0.7685	0.2340	0.2290
S1	3 (LSF6)	0.8716	0.4345	0.6953	0.2428
S2	1 (LCIN3)	0.9120	0.3464	0.0380	0.7887
S2	2 (LSF3)	0.9170	0.5410	0.0265	0.6254
S2	3 (RCIN5)	0.8514	0.5601	0.1723	0.5768
S2	4 (LFR1)	0.9262	0.3970	0.0386	0.7499
S3	1 (OF7)	0.9062	0.8211	0.1718	0.1858
*S4	1 (RPF5)	0.4886	0.0749	0.8372	0.9514
S4	2 (ROF4)	0.8421	0.7201	0.1541	0.3731
S5	1 (RAF6)	0.8186	0.6290	0.3222	0.4133
sEEG mean		0.8830	0.5758	0.2445	0.4383
E1	1 (GR28)	0.8385	0.6081	0.3954	0.3884
*E1	2 (GR53)	0.6254	0.0462	0.9722	0.8636
E1	3 (GR38)	0.7726	0.5128	0.4000	0.5522
E2	1 (AGR52)	0.8112	0.3478	0.7692	0.2941
sEEG mean		0.8074	0.4896	0.5215	0.4116

^*These recordings are excluded from the means and further analysis due to poor quality.

3.1. Comparison with Established Methods

Warby et al. (2014) presented a comparison of several automated methods for spindle detection with scoring by human experts and non-experts. Here, we compare the DDA spindle detector to two of the automated methods considered there (Mölle et al., 2002; Martin et al., 2013) and a modified version (Andrillon et al., 2011) of a third (Ferrarelli et al., 2007), as well as an additional method designed for intracranial data (Hagler et al., 2018). Warby et al. used two additional detectors (Bódizs et al., 2009; Wendt et al., 2012) which are excluded here due to their reliance on the comparison of specific channels from a standard EEG montage, making them unsuitable for use with intracranial recordings from disparate locations.

It is important to note that for all of these methods, spindle detection performance may be lower here than with some other data, since no preprocessing or artifact removal steps have been applied here prior to the core processing steps for spindle detection intrinsic to each method. Further, these data present a mix of recordings of different quality and spindle clarity, as evaluated by human expert scoring.

Mölle et al. used a 12-15 Hz bandpass finite impulse response (FIR) filter and subsequently computed a root mean square (RMS) signal with 50 ms time resolution and a 100 ms time window from the filtered data. Spindles were then detected using a thresholding procedure, with beginning and end threshold crossings between 0.4 and 1.3 s required for spindle detection. This threshold was set automatically by the algorithm for each subject as originally published, but was always greater than 5 μV (Mölle et al., 2002).

The approach of Martin et al. was similar: data were first bandpass filtered from 11 to 15 Hz using an FIR filter applied both forward and reverse. The RMS of the signal was then computed using 0.25 s windows. The threshold for spindle detection was set at the 95th percentile and required two consecutive RMS time points (corresponding to 0.5 s) for a spindle (Martin et al., 2013).

We also use a slightly modified version of the detector of Andrillon et al., itself a modified version of the method of Ferrarelli et al. (2007). Putative spindles were identified by applying a zero-phase fourth-order Butterworth bandpass filter for 9 to 16 Hz. Instantaneous amplitude was computed using a Hilbert transform, and the threshold for detection was set at three standard deviations from the mean, with a threshold for the beginning and end of spindles set at one standard deviation. Only events with durations between 0.5 and 2 s were marked as spindles, and spindles separated by less than 1 s were merged.

Finally, we also apply a method developed for and previously applied to intracranial recordings of the type we consider here, which was developed by Hagler et al. This technique relies on an initial detection based on instantaneous power in the spindle band (11-17 Hz) using a smoothed wavelet convolution. Any initially identified spindles under 0.5 s in duration are excluded. Further, the ratio of Fourier power in the spindle band relative to power in the 4 to 9 Hz range is used to remove artifacts and weak spindles. (Hagler et al., 2016).

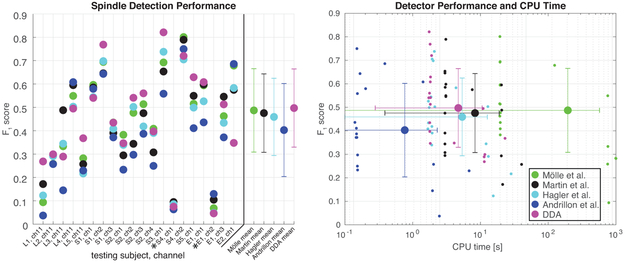
In order to compare these various techniques with differing methodologies, we convert the raw outputs of each technique to a binary index of spindle or non-spindle for each time point. These binary detection indices are then compared by computing the F₁ score of each method against the human expert-marked spindles. The mean across subjects of the number of spindles detected (expressed as a percentage of the number of spindles marked by the human expert), spindle length, F₁ score, and false positive and negative rates (relative to human expert scoring) for each of these methods are shown in Table 3. The F₁ scores as well as CPU time for all methods and recordings are shown in Fig. 4. DDA provides the highest average F₁ score and the second lowest average CPU time.

Table 3:

Comparison of detection methods for all data

Method	Mean percentage of human-scored spindles	Mean length [s]	Mean F1	False discovery rate	False negative rate	CPU* time [s] per recording
Mölle	105.0457	0.4871	0.4871	0.2856	0.5994	30.5645
Martin	141.9600	0.4754	0.4754	0.3427	0.5441	2.5615
Andrillon	46.3362	0.4028	0.4028	0.2078	0.7022	0.3922
Hagler	116.2967	0.4591	0.4591	0.2963	0.6225	1.8177
DDA	89.8979	0.4970	0.4970	0.3861	0.4969	1.6389

^*All methods were implemented in MATLAB 9.4 (R2018a) and tested on the same 12-core (Intel Xeon X5690 @ 3.47 GHz) system. The DDA detector calls an executable written in C for a key step in the procedure.

Figure 4:

Detection methods comparison. In the left panel, F₁ score is plotted for a set of automated spindle detection methods and DDA for the various Laminar, sEEG, and ECoG recordings. The means (points) and standard deviations (bars) across all recordings for each detector are plotted at the far right-these exclude two recordings (denoted by *) of poor quality for which all methods yield low performance. These recordings are also omitted from the right panel. At right, the F₁ score for all recordings is plotted against CPU time for each detection method. Each detector was run on twenty intracranial recordings, the mean across all recordings (except the two noted exclusions) is plotted with a larger marker, standard deviations across all recordings are plotted as bars in both CPU time and F₁ score. Note that not all recordings are of equal length, so some variation in the CPU time is to be expected.

Notably, as shown in Fig. 2, one of the recordings (L1) had a higher mean peak spindle frequency than all others. That recording has a low F₁ score (see Fig. 4) for all comparison methods. DDA, in contrast, detected those spindles relatively well since the goal was to detect dynamical patterns in the data.

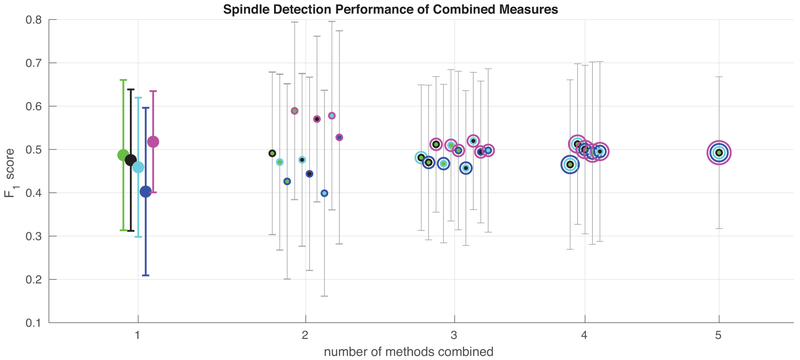
To assess the advantage provided by using DDA features in addition to spectral features, Fig. 5 and Table 4 show the mean F₁ scores for various combinations of the different detection methods. Of note is the fact that combining the DDA measure of spindle activity with other measures generally provides a better measure than combining two or more spectral methods, since it provides different information. Note that the F₁ scores for the DDA detector alone in Fig. 5 and Table 4 do not match exactly the scores in the earlier figures and tables. This is due to an additional step of averaging the DDA features across the overlapping windows at each time point. This provides a measure with time resolution equal to original data which can then be combined with other measures on a point-by-point basis.

Figure 5:

Combining features from the various methods. Spindle detection measures from the various tested methods were combined by taking a mean at each time point, and the agreement of these averaged measures with human scoring was evaluated via F₁ score. Two recordings with poor detector performance for all methods were omitted here. Colors correspond to the different methods, when methods are combined, concentric circles corresponding to the combined measures are plotted at one point. For all methods and combinations of methods, the mean across all recordings is shown. Error bars represent the standard deviation across recordings. Mean F₁ scores for these combinations of detectors are also shown in Table 4. It is noteworthy that there is a significant boost in detection performance only when combining DDA with any one of the spectral methods. No other combination of methods provides such a boost.

Table 4:

Combining detection measures from the various methods. The highest-performing combinations of detectors are marked in red.

# combined	Mölle et al.	Martin et al.	Hagler et al.	Andrillon et al.	DDA	F1 score
1	0.4871	0.4754	0.4591	0.4028	0.5179
	X	X				0.4912
	X		X			0.4709
	X			X		0.4264
	X				X	0.5892
2		X	X			0.4761
		X		X		0.4439
		X			X	0.5704
			X	X		0.3991
			X		X	0.5781
				X	X	0.5280
	X	X	X			0.4813
	X	X		X		0.4701
	X	X			X	0.5119
	X		X	X		0.4674
3	X		X		X	0.5098
	X			X	X	0.4978
		X	X	X		0.4571
		X	X		X	0.5197
		X		X	X	0.4943
			X	X	X	0.4979
	X	X	X	X		0.4653
	X	X	X		X	0.5125
4	X	X		X	X	0.5000
	X		X	X	X	0.4917
		X	X	X	X	0.4954
5	X	X	X	X	X	0.4927

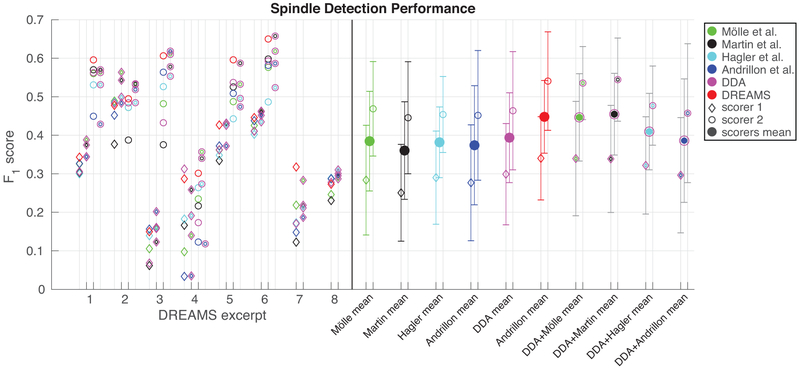
Finally, for comparison, DDA and the other detection methods were applied to the DREAMS dataset, collected and made available by Université de Mons, TCTS Laboratory (Stéphanie Devuyst, Thierry Dutoit) and Université Libre de Bruxelles, CHU de Charleroi Sleep Laboratory (Myriam Kerkhofs) (Devuyst et al., 2011). The DREAMS data consist of surface EEG with spindles marked by two human experts. Using these data allow the above detection methods to be compared on surface EEG data, as well as compared to automated spindle detections from a method implemented by the original authors and made available with the data. This technique is based on bandpass filtering and applying a recording-specific threshold. While the DREAMS automated detections provide better agreement with the human scorers than the intracranial data-trained DDA detector or any of the other tested methods (Devuyst et al., 2011). We cannot compare directly with this method since only the data and automated detections are available, and not the code. We therefore cannot test the DREAMS method on our dataset. Further, as can been seen in Fig. 6, there is also a large discrepancy between the two human scorers, with one scorer also only having scored six of the eight subjects. Issues with the scoring of these data were previously noted by O’Reilly and Nielsen (2015). Further, it is noteworthy that DDA still provides reasonable spindle detection after structure selection based solely on intracranial data. Most significantly, however, we also show the combinations of two detectors (as shown in Fig. 5). For these data, combining our DDA measure with the measure produced by the method of Martin et al. provides the highest average agreement with the two human scorers among all tested methods and combinations of methods.

Figure 6:

Spindle detection on DREAMS data. F₁ score is plotted for a set of automated spindle detection methods and DDA for the eight surface EEG excerpts included in the DREAMS data set. For six of the eight excerpts, two human experts scored the data. For these six recordings, F₁ scores based on the first expert’s markings are plotted as diamonds at left, and the scores based on the second expert’s markings are plotted as open circles at right. The means (diamonds and open circles) and standard deviations (bars) across all recordings for each detector’s agreement with both experts are plotted at the far right with the same markers, and the means of each method’s agreement with both scorers are plotted as larger filled circles. Combinations of the other measures with DDA, as shown in Fig. 5 are shown with the colors for each of the methods combined. In addition to the six methods shown previously, we also show here the F₁ scores of the automated spindle detections included with the DREAMS data with both human experts in red.

4. Discussion and Conclusions

DDA is a powerful novel tool for detecting sleep spindles in EEG and intracranial recordings. DDA requires minimal pre-processing of signals and can be rapidly applied to large datasets. When compared with several well-established and reliable frequency-based methods, DDA provides the highest level of agreement with human scoring (evaluated here with F₁ score). Further, DDA is the second fastest of the tested methods, where the only faster method produces the lowest F₁ scores. DDA therefore holds great promise for real-time applications. We also tested all methods on the publicly available DREAMS data, consisting of surface EEG recordings scored by two expert scorers. Again, DDA provides the highest F₁ score of the previously tested methods when taking the average across both scorers. The automated detections made available with the DREAMS data however, do provide better agreement with the human scorers. It should be noted that the DREAMS data is a small and heterogeneous data set, and therefore somewhat limited for evaluation purposes (O’Reilly and Nielsen, 2015).

An important caveat for the results from intracranial data presented here is that they are based on comparison with the spindle markings by a single human expert. Despite this, the fact that several automated methods produce similar detections indicates that the markings are reasonable. Further, similar results are achieved using the same approaches on an EEG data set scored by two experts. It is also important to note the classic bias that our implementation of other previously published detectors may not be as fully perfected as the novel method developed for this paper. Other implementations on other data and comparing to other human scoring might not produce the same relative performance numbers. However, this is only a concern when looking at each method separately. As shown in Figs. 5 and 6, combining our nonlinear time-domain method with any of the tested spectral-based methods, the performance is increased dramatically, beyond the relatively differences between individual methods. This indicates that spectral and nonlinear methods account for different information in the original signal: DDA looks for dynamical differences while spectral methods look for content in a specific spindle frequency band.

Combining two spectral measures does not provide the same advantage as combining linear and nonlinear features. Additionally, we have demonstrated that DDA models built on the data show superior performance to those built to detect specific frequencies, which indicates that using the nonlinear signature of the spindle provides access to additional information. Accessing this type of information could prove especially useful in future studies focused on spindles of different types, or occurring in patients with neuropsychiatric disorders. Finally, it is worth emphasizing again the robustness of DDA measures in general to noise and artifacts due to the sparsity of the feature space. This is a significant advantage for many data sets.

A version of the DDA spindle detector for use on Linux systems using MATLAB has been made available at http://snl.salk.edu/∼asampson/SPINDLES/index.html.

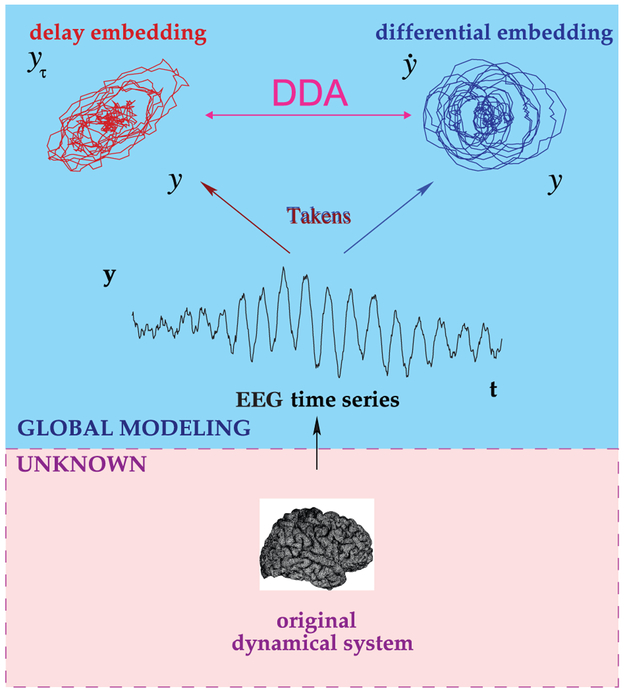
Figure 1:

Delay Differential Analysis (DDA). For an unknown dynamical system (such as the brain) from which we can record a single variable over time (such as ECoG data), embedding theory states that we can recover the nonlinear invariant properties of the original system. DDA combines delay and differential embeddings in a functional form which allows time-domain classification of the data. For a given polynomial model form, we estimate the coefficients and least-squares error, which form a low-dimensional feature space. This figure is adapted from Lainscsek and Sejnowski (2015).

Delay Differential Analysis (DDA) is a powerful non-linear tool for EEG data analysis

DDA features can be used to detect sleep spindles quickly and reliably

DDA provides a novel and unique time-domain measure of spindle activity

DDA is the best and one of the fastest of the tested sleep spindle detectors

Appendix A Frequency-Based Spindle Detection

All spindle detection techniques DDA is compared to are based on decomposing the signal into oscillatory components, and therefore have very different assumptions: while DDA assumes nonlinearity of the (unknown) underlying dynamical system, spectral methods assume linear superposition of stationary sinusoids. To interpret the differences in detector performance we need to answer the question of what is gained by using nonlinear instead of linear analysis.

In Lainscsek and Sejnowski (2015) a connection between DDA and spectral analysis was made: a one term linear DDE can be used for frequency detection while a one term nonlinear DDE can detect frequency/phase couplings in the time domain. A DDE with linear and nonlinear terms will have vanishing nonlinear coefficients for purely harmonic signals. For data that contain nonlinear couplings between frequencies or other nonlinear signal components, linear as well as nonlinear terms contain both linear and nonlinear information. Superposition does not work due to nonlinearities in the model. Therefore no connection between frequencies and delays can be made for real-world signals that are generally nonlinear.

Applying the same three-term, nonlinear DDE used for the spindle data to simulated data (noise-diluted sinusoids) can serve as a test of what can be gained by adding nonlinear information, and as a bridge between this technique and traditional wavelet or other spectral methods. The effectiveness of the frequency detector at detecting spindles is also informative as to how much of the relevant dynamical information is related to the dominant frequencies, which is of interest since many spindle detection techniques rely on spectral analysis (Warby et al., 2014).

The DDA frequency detector relies on the same structure selection framework as the data-trained spindle detector, but the DDE model form is fixed to match the model selected using the real data, and only the values of the delays are selected based on the simulated data. For the purposes of comparison with the data-trained detector, we select for frequency bands in the simulated data that correspond to sleep spindles in the EEG sigma band, defined alternately as 11-14 Hz or 11-17 Hz. By comparing the delays which are most successful at detecting these frequencies with those that are selected for the task of sleep spindle detection, we can gain insight into the information added by nonlinear analysis.

The simulated data is generated according to:

$$S_i=A_i\cos ({\omega }_{i}t+{\phi }_i)+ϵ$$ (8)

with ω_i = 2πf_i for 9991 equally-spaced frequencies f_i between 0.1 and 100 Hz, equal amplitudes A_i = 1, random phases 0 < φ_i ≥ 2π, and added white noise ϵ with a signal-to-noise ratio of 5 dB. Starting from the full set of frequencies, we divide into nearly-equal groups for training and testing, with training data consisting of frequencies f_i from 0.1 to to 100 Hz, and the testing data consisting of frequencies f_i from 0.11 to 99.99 Hz, both sets with 0.02 Hz frequency intervals. This ensures that we validate on slightly different frequencies from the training data, still in the desired range. For our simulated training data, we select data with frequencies f_i in the sigma band. As was the case for the data-driven detector, we train separately for each sampling rate, generating simulated data to match each of the sampling rates in the laminar, sEEG, and ECoG data. We then choose delays for each sampling rate f_s

Selecting a model to provide sensitivity to specific frequency bands requires an additional step, in that we first select “high-pass delays” which are sensitive to frequencies above the lower bound we wish to set (here, 11 Hz), and then additional “low-pass delays” which are sensitive to frequencies below the upper bound (here, 14 or 17 Hz).

The delays chosen for each sampling rate for each definition of the sigma band (11-14 Hz or 11-17 Hz) are shown in Table 5. Note that in some cases, the same delays can be used in both the “high-pass DDE” and “low-pass DDE”, since different weights can be applied to the features to select for different frequency ranges.

As with the data-driven detector, we apply a vector of weights to the features for both the lower and upper bounds, in this case obtaining two values of D, which we call D₁ and D₂.

Table 5:

Selected delays (τ₁,τ₂) for specified bands, units of δt = 1/f_s

	delays [δt]
fs	11-14 Hz		11-17 Hz
	> 11 Hz	< 14 Hz	> 11 Hz	< 17 Hz
2000	(8,105)	(8,105)	(8,69)	(7,39)
1024	(1,44)	(19,4)	(4,37)	(4,20)
512	(23,43)	(8,2)	(17,19)	(10,2)
500	(39,18)	(10,2)	(2,17)	(2,9)

We combine them by summing their absolute values and applying the sign of the lesser of d₁ and d₂:

$$D=\frac{\text{min}(D_1,D_2)}{\mid \text{min}(D_1,D_2)\mid }(\mid D_1\mid +\mid D_2\mid ).$$ (9)

We will therefore obtain positive values only in the region where both are positive, which should correspond to the “DDA pass band”.

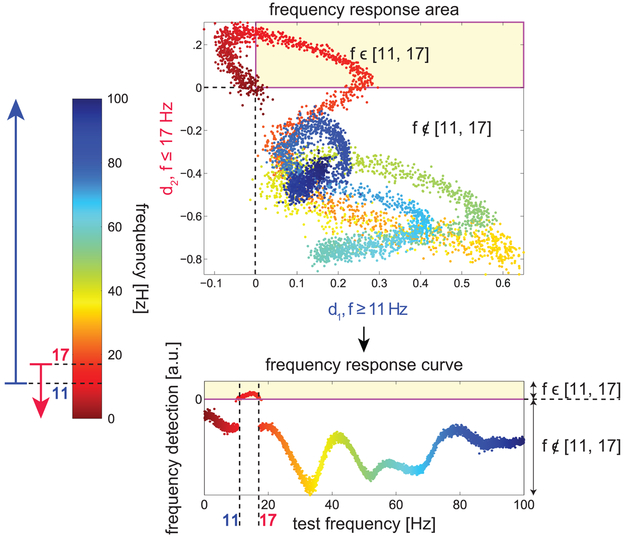
Fig. 7 shows the frequency response of the detector on simulated data. Given its strong selectivity for frequencies in the desired range, it was applied to the sleep spindle data as a means of detecting frequency content in the spindle band which uses the same methodology as the data-based DDA spindle detector. This allows for direct comparison between the frequency-based and data-based DDA approaches.

Figure 7:

Frequency band detection. Applying the DDE model with two different delay pairs, one sensitive to frequencies above 11 Hz and one sensitive to frequencies below 17 Hz, we can obtain an output which is positive only in the desired band. In the top panel, the distance from the hyperplane values computed from both DDEs (d₁ and d₂) are plotted for test frequencies ranging from 0.1 to 100 Hz. The frequency of the test data is color-coded according to the color bar at left, from 0.1 (red) to 100 Hz (blue). Points falling into the upper right quadrant (shaded yellow) have positive values for both d₁ and d₂, and we select delays such that only frequencies in the desired range (11-17 Hz) fall into this area. In the lower plot, d₁ and d₂ are combined according to Eq. (9) to obtain a one-dimensional index that is positive only for frequencies in the desired range. This procedure was also used to obtain delays and corresponding weights for frequency ranges 11-14 Hz and 12-15 Hz.