Atomistic Modeling of Intrinsically Disordered Proteins Under PEG Crowding: Quantitative Comparison with Experimental Data and Implication of Protein-Crowder Attraction

Abstract

The malleability of intrinsically disordered proteins (IDPs) has generated great interest in understanding how their conformations respond to crowded cellular environments. Experiments can report gross properties such as fluorescence resonance energy transfer (FRET) efficiency, but cannot resolve the conformational ensembles of IDPs and their interactions with macromolecular crowders. Computation can in principle provide the latter information but in practice has been hampered by the enormous expense for realistic modeling of IDPs and crowders and for sufficient conformational sampling. Here, taking advantage of a powerful method called FMAP (FFT-based Modeling of Atomistic Protein-crowder interactions), we computed how the conformational ensembles of three IDPs are modified in concentrated polyethylene glycol (PEG) 6000 solutions. We represented the IDPs at the all-atom level and the PEG molecules at a coarse-grained level, and calculated the experimental observable, i.e., FRET efficiency. Whereas accounting for only steric repulsion of PEG led to overestimation of crowding effects, quantitative agreement with experimental data was obtained upon including mild IDP-PEG attraction. The present work demonstrates that realistic modeling of IDPs under crowded conditions for direct comparison with experiments is now achievable.

Graphical Abstract

Introduction

Over one third of proteins are intrinsically disordered or contain large disordered regions, and the disorder is of critical importance for cellular functions.^1–4 The conformational preferences and the conformational responses upon interacting with other molecules are crucial determinants for the functions of intrinsically disordered proteins (IDPs). Notably, some IDPs undergo disorder-to-order transitions upon binding structured targets,^5–7 or Zn⁺² ions and drug molecules.^8–11 Other IDPs, upon forming high-affinity complexes, while preserving structural disorder, experience conformational shifts such as compaction.¹² Much less attention has been paid to the fact that, in cells, IDPs encounter a high concentration of bystander macromolecules or crowders, at over 300 g/l or 30% of volume fraction.¹³ The malleability of IDPs makes them especially susceptible to the influence by interactions with macromolecular crowders.¹⁴ The aim of this study was to reveal conformational shifts of IDPs produced by realistically modeled protein-crowder interactions.

A number of experimental techniques have been used to characterize IDP conformations under macromolecular crowding. Bulk and single-molecule fluorescence resonance energy transfer (FRET) have indicated conformational compaction of an unfolded protein and IDPs by polymer crowders.^15–16 Using small-angle neutron scattering (SANS), one study found no apparent effect on the radius of gyration (R_g) of an IDP by protein crowders,¹⁷ while another study presented evidence for compaction of the IDP FlgM at moderate concentrations of polymer and protein crowders but recovery in IDP size upon a further increase in crowder concentrations.¹⁸ Moreover, based on fitting scattering profiles with an ensemble of IDP conformations, the latter study suggested that protein crowders can simultaneously induce compaction and expansion of FlgM, leading to two segregated conformational populations. Different NMR experiments have provided residue-specific information on IDPs under crowding. In an early study, backbone amide resonance broadening of FlgM C-terminal residues in the presence of a protein crowder as well as in Escherichia coli cells was interpreted as indicating gain of structure ¹⁹, although in retrospect the observation is also consistent with nonspecific binding with crowders. For the IDP α-synuclein, backbone chemical shifts have indicated no change in secondary structure under polymer crowding ²⁰ and in E. coli cells,²¹ whereas paramagnetic resonance enhancement have suggested compaction under polymer and protein crowding as well in mammalian cells.^{20, 22} Interestingly, the extent of compaction was more modest for protein crowders relative to polymer crowders. Furthermore, NMR relaxation data suggested weak interactions of N- and C-terminal residues with cytoplasmic components in mammalian cells, which were partially recapitulated by protein crowders but not polymer crowders.²² Recently hydrogen-exchange mass spectrometry (HX-MS) showed faster exchange throughout the binding domain of the activator for thyroid hormone and retinoid receptors (ACTR) at 300 g/L Ficoll but slower exchange for one segment at 400 g/L Ficoll.²³ The former observation can be interpreted as indicating ACTR expansion, whereas the latter observation is probably due to Ficoll-induced ACTR aggregation, as found for other IDPs.^{18, 20} Techniques such as FRET and SANS report on gross properties (e.g., FRET efficiency and scattering profile) and hence lack the power to resolve conformational ensembles. Although NMR spectroscopy and, to some extent, HX-MS generate residue-level data and may give hints on IDP-crowder interactions, unequivocal, detailed interpretation is extremely challenging.

Computation, in principle, can provide detailed answers on how protein-crowder interactions alter conformational ensembles of IDPs. However, due to the enormous expense for realistic modeling of IDPs and crowders and for sufficient conformational sampling, most computational studies have been limited to simplified models of IDPs and crowders, which nonetheless have generated valuable insight. Computer simulations using a coarse-grained representation (one bead per residue) have shown that IDPs always exhibit compaction in the presence of steric spherical crowders, which exert only steric repulsion, and the extent of compaction depends on the intrinsic flexibility of the IDPs.²⁴ Similar simulation results have been formulated into scaling relations for the extent of compaction.²⁵ The effects of steric spherical crowders have been generalized to IDPs modeled as chains of mixed types of beads, to mimic amino-acid compositions of proteins.²⁶ The extent of compaction was found to depend on bead composition, which affects intrinsic flexibility; hence the dependence on composition recapitulates the dependence on intrinsic flexibility noted in the earlier study.²⁴ Very recently, Banks at el.¹⁸ reported simulation results for coarse-grained IDPs in the presence of attractive spherical crowders. Adding weak protein-crowder attraction led to moderation of the crowder-induced compaction; with stronger protein-crowder attraction, IDPs exhibit compaction at moderate crowder concentrations but subsequent expansion at higher crowder concentrations. The latter result is qualitatively consistent with the SANS data reported in the same study. In the past few years, all-atom explicit solvent molecular dynamics simulations have shown promise in studying some aspects of proteins under crowded cell-like conditions.²⁷ For IDPs in particular, though, inaccuracy of force fields and under sampling of conformations still present major obstacles even in dilute solutions,^28–31 let alone in crowded solutions. The problem is underscored by a recent study using all-atom explicit solvent simulations,³² where a 47-residue C-terminal fragment of ACTR exhibited significant expansion in the presence of 200 g/l of PEG 500, in contrast to the compaction of ACTR by PEG revealed by single molecule FRET.¹⁶

It is highly desirable to make direct comparison between experimental observables and computational results based on realistic modeling of IDPs and crowders. As emphasized above, interpreting experimental data alone to gain detailed information on crowding-induced shifts in IDP conformations or the underlying IDP-crowder interactions is extremely challenging. For example, to interpret the FRET efficiency measured in a single-molecule FRET experiment in terms of the IDP size, specifically the mean R_g, one has to assume both a certain distribution for R_g and a certain conditional probability for the FRET donor-acceptor distance at a given R_g value.¹⁶ SANS can yield the mean R_g of an IDP but it is silent on IDP-crowder interactions. In particular, when the mean R_g does not change under crowding, it does not necessarily mean absence of crowding effects, because the observation is also compatible with near cancelation of IDP compaction due to crowder steric repulsion and IDP expansion due to weak IDP-crowder attraction.^17–18 In the latter study, scattering profiles of FlgM under protein crowding were interpreted as indicating segregation of compacted and expanded conformations. Simulations of coarse-grained IDPs in the presence of attractive spherical crowders then suggested that compacted conformations fit into a void and wrap around a single bordering crowder, whereas expanded conformations snake through interstitial crevices and bind multiple crowders simultaneously. However, the crudeness of the IDP and crowder models precluded a quantitative comparison with the experimental data, therefore blocking an opportunity to test the conformational segregation hypothesis and assess the IDP-crowder interaction strengths of the experimental systems.

In the past few years we have developed a computational approach that opens the door to realistic modeling of IDPs under crowded conditions for direct comparison with experiments.^33–38 The basic idea is to determine how crowding biases the statistical weight of each conformation of the protein; in particular, these biases alter the conformational ensemble of an IDP. To implement this approach, we sample the conformations of the protein in the absence of crowders; each crowder-free conformation is then “postprocessed”, to determine the crowding bias, which is the Boltzmann factor of the chemical potential, Δμ, of the protein inside the crowders. Our latest method implementing this approach is called FMAP, or FFT-based Modeling of Atomistic Protein-crowder interactions, in which protein-crowder interactions are expressed as correlation functions and evaluated via fast Fourier transform in order to calculate Δμ.^37–38 FMAP has been applied to determine the conformational shift of coarse-grained IDPs by repulsive spherical crowders, resulting in IDP compaction identical to that obtained by direct simulations of the IDPs inside the crowders.²⁴ Most recently we have used FMAP to determine the chemical potential of an atomistic protein at a wide range of concentrations, leading to a phase diagram for liquid-liquid phase separation.³⁹

Here we applied FMAP to make quantitative comparison with the FRET efficiency data of Soranno et al.¹⁶ for four fluorescence donor-acceptor pairs in three IDPs under PEG 6000 crowding. We represented the IDPs at the all-atom level and PEG 6000 at a coarse-grained level. Accounting for steric repulsion of PEG produced stronger compaction than experimentally observed, but quantitative agreement was obtained upon including mild IDP-PEG attraction.

Methods

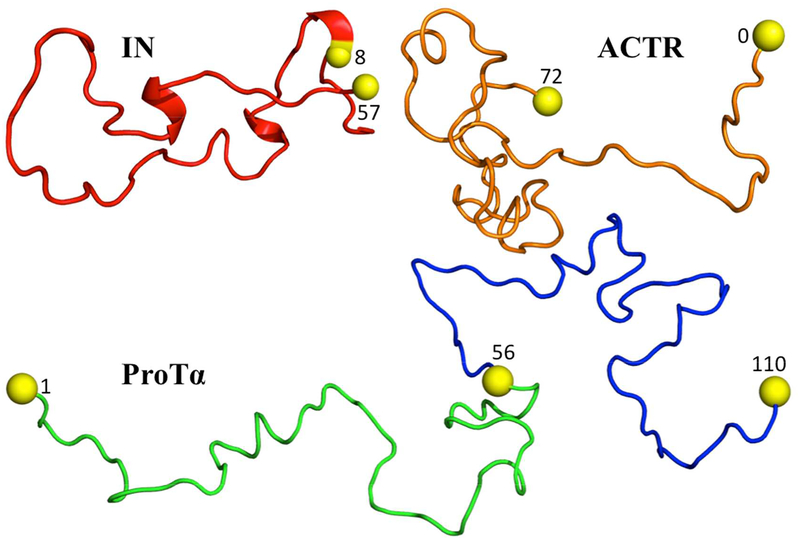
The three IDPs studied here are the 56-residue N-terminal domain of HIV-1 integrase (IN), the 71-residue ACTR, and the 110-residue prothymosin α (ProTα) (Fig. 1). In the experimental study,¹⁶ Cys residues were appended at the N- or C-termini or substituted into internal or terminal positions in order to attach fluorescence donors and acceptors (Alexa Fluor 488 and Alexa Fluor 594, respectively). Specifically, four fluorescence donor-acceptor pairs were positioned at residue 8 and the C-terminal extra residue in IN, at the N- and C-terminal extra residues in ACTR, and at either residues 1 and 56 or residues 56 and 110 in ProTα (referred to as ProTαN or ProTαC). The amino-acid sequences with these Cys additions and substitutions can be found in Table S2 of ref ¹⁶. We modeled these Cys residues but not the fluorescence donors and acceptors. Below we detail the procedures for generating IDP conformations and calculating FRET efficiencies in the absence and presence of crowders.

Figure 1.

The three IDPs studied. In each proteins, the Cys residues, with residue number indicated, for attaching fluorescence donors and acceptors are shown as yellow spheres. For ProTα, two fluorescence pairs were studied: one at residues 1 and 56 and the other at residues 56 and 110.

Generation of IDP Conformations.

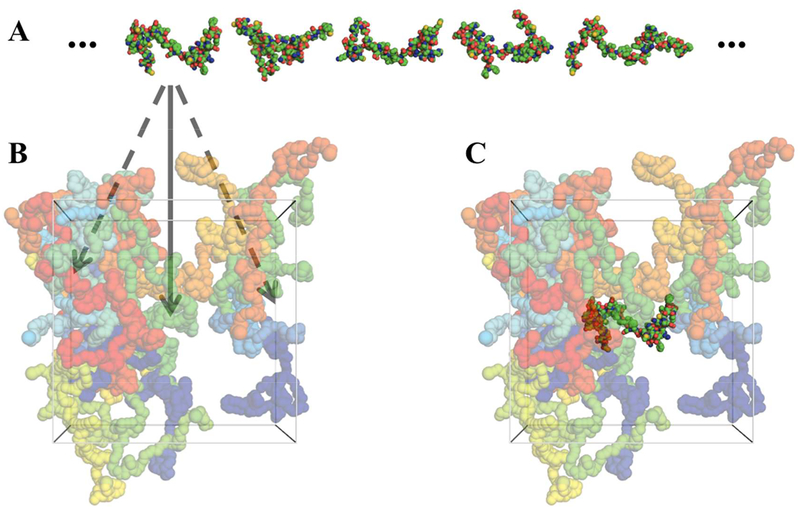
For each IDP, with the amino acid sequence as input, we used two methods, flexible-meccano (http://www.ibs.fr/research/scientific-output/software/flexible-meccano/)⁴⁰ and TRaDES, (http://trades.blueprint.org/)⁴¹ to generate 100,000 all-atom conformations to represent the conformational ensemble (Fig. 2A). Similar to our earlier work,⁴² both methods randomly choose conformers for each residue in Ramachandran space (i.e., with backbone ϕ,ψ torsion angles as coordinates), and eliminate steric clashes. TRaDES is slightly more elaborate, including a bias in the (ϕ,ψ) probability density of each residue by secondary structure prediction and with clash detection checked at the atom level rather than residue level.

Figure 2.

Representative IDP conformations and PEG configurations and illustration of FMAP. (A) Representative conformations of IN. (B) A representative configuration of PEG 6000 at a 10% weight fraction. Arrows indicate fictitious insertions of an IN molecule into different positions inside the box of PEG molecules. (C) A successful insertion, whereby the inserted IN molecule is free of steric clashes with any PEG molecules.

Calculation of FRET Efficiencies.

At a given donor-acceptor distance r, the FRET efficiency is $E\left(r\right)=1/\left(1+r^6/R_0^6\right),$ where R₀ is the Foster radius of the donor-acceptor pair (approximately 54 Å for the experimental systems). An IDP samples a range of r values, and the observed FRET efficiency is an average over the r values:

$$\overline{E}=\int drE\left(r\right)P\left(r\right)$$ (1)

where P(r) is the probability density of r.

We took r to be the C_α−C_α distance between the two Cys residues to which the fluorescence donor and accepters were attached. For each IDP, the average over r was done by assigning conformation n out of the N = 100,000 conformations a statistical weight w_n. Then

$$\overline{E}=\frac{{\displaystyle \sum }_{n=1}^{N}E\left(r_n\right)w_n}{{\displaystyle \sum }_{n=1}^N{w}_n}$$ (2)

If flexible-meccano or TRaDES conformations were used directly, we would have equal weights for all the conformations. The resulting $\overline{E}$ values disagreed with the experimental values for the IDPs in the absence of crowders. To remove this discrepancy, we reweighted the conformational ensemble by an r−dependent statistical weight,

$$w_{0n}=\text{exp}\left(b{r}_n\right)$$ (3)

where “0” in the subscript signifies that the weight is for the crowder-free case, and the parameter b was tuned for each IDP to reach agreement between predicted and experimental crowder-free $\overline{E}$ values. The resulting b values are listed in Table 1 and Table S1 flexible-meccano and TRaDES conformations, respectively. The raw and reweighted r distributions are compared in Fig. S1.

Table 1.

Conformational properties of IDPs in the absence and presence of crowders.^a

	0%			10%			20%
IDP	b (Å−1)	mean Rg (Å)		$\overline{E}$			$\overline{E}$
		raw	reweighted	Expt	st only	st + at	Expt	st only	st + at
IN	−.0029	21.13	20.94	0.672	0.698	0.670	0.689	0.819	0.733
ACTR	−.0021	23.61	23.43	0.523	0.565	0.529	0.560	0.727	0.614
ProTαN	.0450	28.66	31.42	0.398	0.422	0.385
ProTαC	.0708	28.62	32.60	0.330	0.342	0.309

^aIDP conformations generated by flexible-meccano.

We also explored other forms of reweighting, such as one that depended on the radius of gyration of the protein. The latter reweighting led to a substantial population of conformations with R_g values much too high for the sequence length of a protein.

The crowding-induced shifts in protein conformations can be accounted for by a biasing weight,^{24, 34–35}

$$w_{cn}=\text{exp}\left(-\beta \Delta {\mu }_n\right)$$ (4)

where Δμ_n is the chemical potential for inserting a protein molecule into the crowder solution, and β is the inverse of the product between the Boltzmann constant and absolute temperature. All our calculations were for room temperature. Note that w_cn is to be multiplied with w_0n so that the total statistical weight in the presence of crowders is w_0nw_cn.

The calculation of Δμ_n involved: (1) preparing PEG 6000 solutions by coarse-grained (CG) simulations; (2) selecting an appropriate IDP-PEG interaction energy function; and (3) implementation of FMAP for the IDP-PEG systems. Next we describe these steps.

Coarse-Grained Simulations of PEG 6000 Solutions.

The trajectories of PEG 6000 solutions were kindly provided to us by Dr. Tamio Yamazaki, simulated as in his published work.⁴³ In brief, each oxyethylene unit of PEG and every three water molecules were represented by a single particle. The energy function for each PEG chain has a bonded term and an angle term; and all particles interact via a Lennard-Jones potential. The parameterization was validated against experimental data on diffusion constant and shear viscosity.

The CG simulations were run for 1 microsecond each, in triplicates for PEG 6000 at 10%, 20%, and 30% weight fractions. The simulation boxes were cubic with side length at approximately 150 Å. The final snapshots of the triplicates were used as representatives of each PEG 6000 solution (Fig. 2B).

IDP-PEG Interaction Energy Function.

We modeled the IDP-PEG interaction energy as pairwise additive. The interaction between IDP atom i and PEG particle j consisted of two parts. Steric repulsion operated when the pair distance r_ij was below a nominal contact distance d_ij:

$$u_{st}\left(r_{ij}\right)=\infty \text{ if }{r}_{ij}<d_{ij}$$ (5)

Weak attraction, modeled by a Lennard-Jones potential, was then present beyond the hard core:

$$u_{\text{at}}\left(r_{ij}\right)={\epsilon }_{ij}\left[{\left({\sigma }_{ij}/r_{ij}\right)}^{12}-{\left({\sigma }_{ij}/r_{ij}\right)}^6\right]\text{ if }{r}_{ij}>d_{ij}$$ (6)

The total IDP-PEG interaction is then

$$U_{\text{int}}={\Sigma }_{ij}{u}_{\text{st}}\left(r_{ij}\right)+\alpha {\Sigma }_{ij}{u}_{\text{at}}\left(r_{ij}\right)\equiv U_{\text{st}}+U_{\text{at}}$$ (7)

For the FMAP implementation of the steric term, we took d_ij as the algebraic average of σ_ii and σ_jj:^37–38

$$d_{ij}=\left({\sigma }_{ii}+{\sigma }_{jj}\right)/2$$ (8)

On the other hand, for the FMAP implementation of the attractive term, a combination rule for both ε_ij and σ_ij based on the geometric mean had to be used:

$${\epsilon }_{ij}={\left({\epsilon }_{ii}{\epsilon }_{jj}\right)}^{1/2}$$ (9)

$${\sigma }_{ij}={\left({\sigma }_{ii}{\sigma }_{jj}\right)}^{1/2}$$ (10)

Initial values of Lennard-Jones parameters (ε and σ) were taken from the Amber force field for protein atoms⁴⁴ and from ref ⁴³ for PEG CG particles. All ε_ij values were then scaled by a uniform factor α to adjust the magnitude of the IDP-PEG attraction.

FMAP Implementation.

The starting point of FMAP is the Widom expression⁴⁵ for the chemical potential for inserting a protein molecule into the crowder solution:

$$\text{exp}\left(-\beta \Delta {\mu }_n\right)={\langle \text{exp}\left[-\beta {\text{U}}_{\text{int};n}\left(R\right)\right]\rangle }_{R,\text{c}}$$ (11)

where U_int;n is the energy of the IDP in the nth conformation interacting with the crowders, and R is the position of the IDP inside the crowder solution, and 〈⋯〉_R,c signifies averaging over IDP position and crowder configuration (Fig. 2B,C). The averaging over R was achieved by using fast Fourier transform (FFT). In essence, we expressed exp[−βU_st (R)]and U_st (R) as correlation functions and evaluated them via FFT. Details are reported in our previous work. ^37–38

The discretization required for FFT calculations introduces numerical errors, which can be eliminated by using smaller and smaller grid spacings but result in significant increases in computational times. Note that the averaging over R can be split,

$${\langle \text{exp}\left[-\beta {\text{U}}_{\text{int};n}\left(R\right)\right]\rangle }_R={\langle \text{exp}\left[-\beta {\text{U}}_{\text{st};n}\left(R\right)\right]\rangle }_0{\langle \text{exp}\left[-\beta {\text{U}}_{\text{at};n}\left(R\right)\right]\rangle }_1$$ (12)

where 〈⋯〉₀ and 〈⋯〉₁ mean averaging over all grid points and over only grid points that are free of steric clashes between the IDP and crowders. If only a single crowder configuration is used for Δμ_n, then eq 12 corresponds to

$$\Delta {\mu }_n=\Delta {\mu }_{\text{st},n}+\Delta {\mu }_{\text{at},n}$$ (13)

That is, Δμ_n would be decomposable into steric and attractive contributions. As we found previously,³⁸ the numerical errors due to discretization are systematic and can be compensated by artificially inflating the nominal contact distances d_ij. Here we found that, at a grid spacing of 0.6 Å, the errors in both Δμ_st,n and Δμ_at,n are nearly compensated by a 6% inflation in d_ij (Figs. S2 and S3).

With averaging over crowder configuration, Δμ_n is no longer decomposable. Here we used the final snapshots of the triplicate simulations for each PEG 6000 solution for averaging over crowder configuration. Specifically, we first determined the chemical potential, denoted as Δμ_n,I, Δμ_n,II, or Δμ_n,III, in each of the three crowder configurations, and then obtained the average chemical potential according to

$$\text{exp}\left(-\beta \Delta {\mu }_n\right)=\left[\text{exp}\left(-\beta \Delta {\mu }_{n,\text{I}}\right)+\text{exp}\left(-\beta \Delta {\mu }_{n,\text{II}}\right)+\text{exp}\left(-\beta \Delta {\mu }_{n,\text{III}}\right)\right]/3$$ (14)

For comparison, we also determined the chemical potential when only the steric contribution was accounted for (equivalent to setting the scaling factor α on ε_ij to 0).

Results

Assessment of Crowder-Free Conformational Ensembles.

For IN, the mean FRET efficiency calculated from the conformational ensemble generated by flexible-meccano is 0.634, which is already very close to the experimental value of 0.649. The mean R_g calculated from this ensemble was 21.1 Å (Table 1), which agrees closely with a value of 21.0 Å predicted by a scaling relation, ${\overline{R}}_{\text{g}}=2.54N_{\text{aa}}^{0.522}\text{Å},$ where N_aa denotes the number of amino acids, that was compiled from a list of IDPs.⁴⁶ A very mild exp(br_n) reweighting with b = −0.0029 Å⁻¹ (Fig. S1A) brought the mean FRET efficiency to agreement with the experimental value, and decreased the mean R_g slightly to 20.9 Å. Recently IN was studied by molecular dynamics simulations²⁹ and by fluorescence correlation spectroscopy and photoinduced electron transfer.⁴⁷ While the molecular dynamics simulations suggested transient helix formation, the latter experimental study concluded that local structure formation has relatively little effect on single-molecule FRET measurements because they probe only long chain segments within IDPs.

For ACTR, the flexible-meccano conformational ensemble likewise needed only a mild exp(br_n) reweighting, with b = −0.0021 Å⁻¹ (Fig. S1A), in order to reproduce the experimental $\overline{E}$ value of 0.498. The mean R_g values before and after the reweighting are 23.6 and 23.4 Å, respectively, in close agreement with a value of 23.8 Å from the scaling relation and suggesting that ACTR, like IN, in buffer has a size typical of IDPs. Using small-angle X-ray scattering (SAXS), Kjaergaard et al.⁴⁸ found a decrease in mean R_g from 26.3 Å at 5 °C to 23.9 Å at 45°C for ACTR. In the same study, NMR spectroscopy detected only low levels of transient helical content. By simultaneous fitting single molecule FRET and SAXS data using ensemble reweighting, Borgia et al.⁴⁹ found a mean R_g of 24.8 Å at room temperature. Our mean R_g is consistent with these latter values.

The decrease in mean FRET efficiency from 0.649 for IN to 0.498 for ACTR is commensurate with the increase in donor-acceptor sequence separation from 49 to 72 peptide bonds (Fig. 1). In contrast, the experimental $\overline{E}$ values for ProTαN and ProTαC are much lower, at 0.35 and 0.28, respectively, even though the donor-acceptor sequence separations, at 55 and 54 peptide bonds, are close to that of IN. As a result, significant increases in mean donor-acceptor distance are required in reweighting the flexible-meccano conformational ensembles (Fig. S1A). The resulting b values of the exp(br_n) weight for ProTαN and ProTαC are 0.045 and 0.0708, respectively, with mean r increasing from 49.3 to 64.6 Å and from 46.9 to 68.9 Å. The corresponding increases in mean R_g are more modest, from 28.7 Å to 31.4 Å and from 28.6 to 32.6 Å, respectively, for the two variants of ProTα. For reference, the afore-mentioned scaling relation predicts a ${\overline{R}}_{\text{g}}$ of 29.5 Å for a 110-residue IDP like ProTα. Using SAXS, Uversky et al.⁹ reported a mean R_g of 37.8 Å for this protein. The reweighted flexible-meccano conformational ensemble slightly underestimates the latter value.

While R_g provides a good measure for the size of an IDP, the asphericity provides a very useful measure on the shape of the IDP.^{31, 49–50} The latter is defined as

$$\delta =1-3\frac{{\lambda }_1^2{\lambda }_2^2+{\lambda }_1^2{\lambda }_3^2+{\lambda }_2^2{\lambda }_3^2}{{\left({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2\right)}^2}$$ (15)

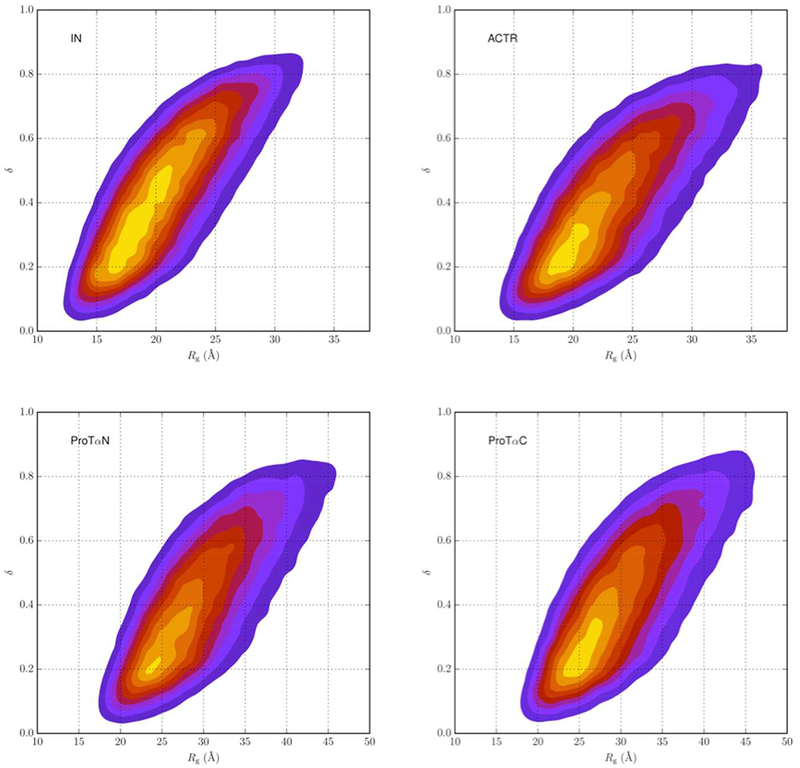
where λ_1,2,3 are the eigenvalues of the moment of inertia tensor. The value of δ ranges from 0 to 1, with 0 representing a sphere and 1 representing a thin rod. The mean asphericities calculated from the reweighted flexible-meccano conformational ensembles for IN, ACTR, ProTαN, and ProTαC are 0.44, 0.41, 0.45, and 0.47, respectively. These values are typical of IDPs.⁵⁰ The mean asphericity determined by Borgia et al.⁴⁹ using ensemble reweighting was between 0.4 and 0.45 for ACTR.

As expected of IDPs, both R_g and q span a wide range in each protein. Fig. 3 displays the 2-dimensinal probability densities in R_g and δ. All the results by the other IDP conformation-generation method, TRaDES, are very similar to those by flexible-meccano, and hence are presented only in Supporting Information. The r distributions before and after reweighting TRaDES conformations are presented in Fig. S1B, and the corresponding 2-dimensinal probability densities in R_g and δ are presented in Fig. S4.

Figure 3.

Two-dimensional probability densities in radius of gyration and asphericity for four IDPs, calculated from reweighted flexible-meccano conformational ensembles.

IDPs Are Over-Compacted If PEG Exerts Only Steric Repulsion.

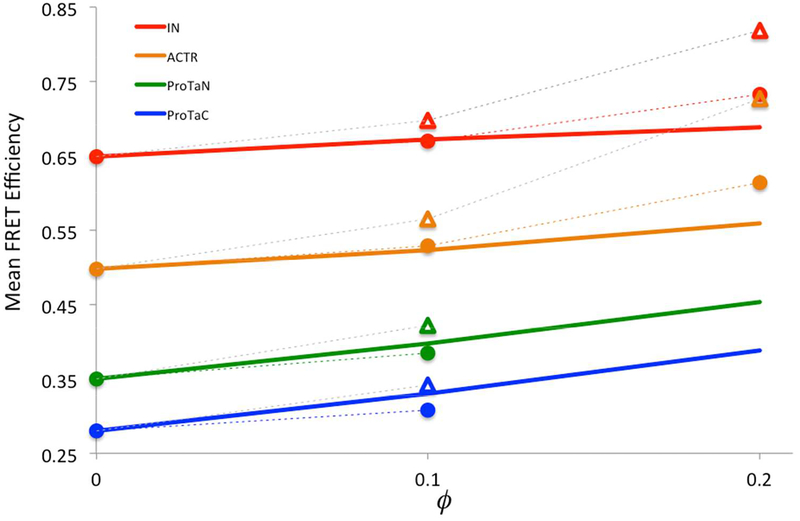
We now consider the effects of PEG crowding on the conformational ensembles of the four IDPs. Experimentally, the mean FRET efficiencies of the four proteins increase with increasing PEG weight fraction (Fig. 4, solid lines), indicating that the proteins become more and more compact under PEG crowding. PEG has often been thought of as a steric crowder, which exerts only steric repulsion. Qualitatively, steric repulsion by crowders is expected to compact IDPs.

Figure 4.

Experimental and calculated mean FRET efficiencies. Experimental results are shown as solid lines, calculated results are shown as triangles or circles (connected by dash), when only steric repulsion or both steric repulsion and weak attraction between IDPs and PEG are accounted for. Calculated results are from applying FMAP on reweighted flexible-meccano conformational ensembles; errors, as estimated by bootstrapping, are less than the size of the symbols.

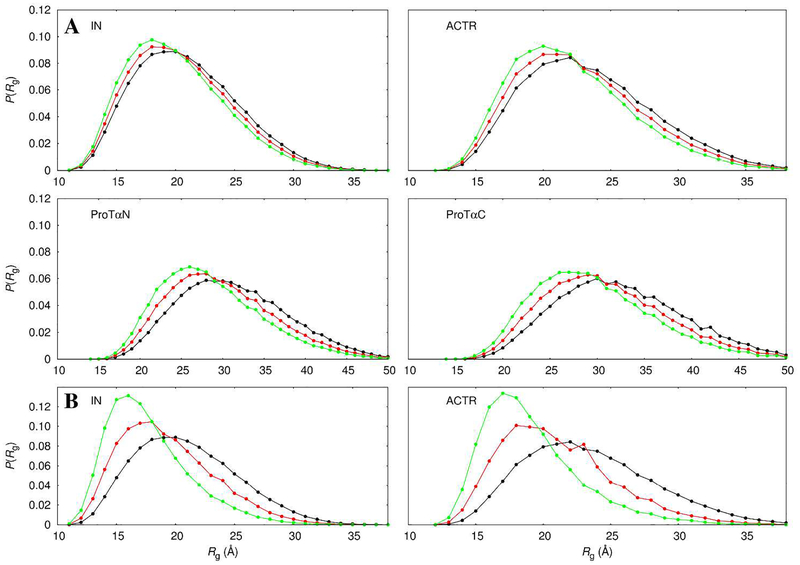
However, when only steric repulsion is accounted for (by FMAP), the mean FRET efficiencies are overestimated for all the four proteins in the presence of 10% PEG 6000 and for IN and ACTR in the presence of 20% PEG 6000, and the overestimation is more severe at the higher PEG weigh fraction (Figs. 4 and S5, triangles connected by dash). In other words, with only steric repulsion by PEG, the IDPs conformations are shifted too far into the compact end. For example, the mean R_g of IN decreases from 20.9 Å in the absence of crowders to 20.0 Å in the presence of 10% PEG 6000 and further down to 17.8 Å at a 20% weight fraction (Figs. 5 and S6, green curves).

Figure 5.

R_g distributions of the four proteins in the absence and presence of PEG 6000. (A) 10% PEG 6000. (B) 20% PEG 6000. Results calculated from reweighted flexible-meccano conformational ensembles are in black; those shifted by PEG modeled with steric repulsion only are in green; and those shifted by PEG modeled with both steric repulsion and weak attraction are in red.

We were unable to obtain reliable results for ProTαN or ProTαC at 20% PEG 6000, because, in this denser crowder solution, the occurrence of large voids is extremely rare, and hence the probability for successful insertion of these longer IDP chains becomes exceedingly low.

Mild IDP-PEG Attraction Permits Quantitative Agreement With Experiment.

The effect of steric repulsion can be counteracted by mild IDP-crowder attraction. Indeed, with the scaling parameter α (eq 7) at 0.06, the PEG-induced compaction is sufficiently moderated so that the predicted $\overline{E}$ (Figs. 4 and S5, circles connected by dash) comes into reasonable agreement with the experimental values. With both steric repulsion and mild attraction, the compaction by PEG is more modest. For example, the mean R_g of IN decreases from 20.9 Å in the absence of crowders to 20.5 Å in the presence of 10% PEG 6000 and to 19.3 Å at a 20% weight fraction (Figs. 5 and S6, red curves).

Discussion

By modeling IDPs at the all-atom level, we have made quantitative comparison with experimental data on the their conformational shifts under PEG 6000 crowding. We directly computed the experimental observable, namely the mean FRET efficiency, from the IDP conformations, after accounting for the conformational bias exerted by the crowder. This bias was treated by a unique method called FMAP, which computes IDP-crowder interactions via FFT. Whereas including only steric repulsion between the IDPs and PEG led to overly compact conformations, quantitative agreement with experimental data was obtained upon including mild IDP-PEG attraction.

Interestingly, mild attraction between IDPs and polymer crowders was implicated in a recent experimental study.¹⁸ The SANS data in this study showed reduction in R_g for an IDP at moderate concentrations of dextran and Ficoll, but then an uptick in R_g at higher concentrations of these polymer crowders. The latter observation is a strong indication for the presence of IDP-crowder attraction. This attraction is much milder than that exerted by protein crowders, as the latter were apparently able to induce conformational expansion to such an extent as to produce segregation between the expanded and compacted populations.

In addition to PEG 6000, Soranno et al.¹⁶ measured the effects of crowding over a wide range of PEG chain length. The degree of IDP compaction was similar for PEG chains longer than PEG 6000, but much less for shorter PEG chains (all at a fixed weight fraction). The latter observation contradicts a classical theory for steric crowders, namely the scaled particle theory, which predicts stronger IDP compaction for smaller crowders. IDP-PEG attraction counteracts the compaction due to steric repulsion, and may provide an explanation for the lesser degree of IDP compaction under crowding by shorter PEG chains. This issue will be addressed in the future.

An underlying assumption of FMAP is that the important conformations of an IDP under crowding are all present in the crowder-free ensemble used for calculation. This assumption is likely valid when IDP-crowder interactions are purely steric or at most mildly attractive. Stronger IDP-crowder attraction may induce conformations, such as an IDP chain wrapping around a crowder, that are unlikely sampled in the absence of crowders. Under those circumstances, FMAP may fail. FMAP may also not work well when inserting large IDPs into dense crowder solutions, as illustrated by inserting ProTαN or ProTαC into 20% PEG 6000.

In cellular environments, crowding-induced conformational shifts may be important for IDP functions. Such conformational shifts may also affect the efficacy of drugs targeting IDPs. There is much still to be learned about the influences of specific and nonspecific interactions on IDPs, nevertheless the present work demonstrates that realistic modeling of IDPs under crowded conditions for direct comparison with experiments is now achievable.

ABBREVIATIONS

ACTR

binding domain of the activator for thyroid hormone and retinoid receptors

FFT

fast Fourier transform

FMAP

FFT-based modeling of atomistic protein-crowder interactions

FRET

fluorescence resonance energy transfer

HX-MS

hydrogen-exchange mass spectrometry

IDP

intrinsically disordered proteins

IN

N-terminal domain of HIV-1 integrase

PEG

polyethylene glycol

ProTα

prothymosin α

SANS

small-angle neutron scattering

SAXS

small-angle X-ray scattering