Signal clarity: an account of the variability in infant quantity discrimination tasks

Abstract

Infants have shown variable success in quantity comparison tasks, with infants of a given age sometimes successfully discriminating numerical differences at a 2:3 ratio but requiring 1:2 and even 1:4 ratios of change at other times. The current explanations for these variable results include the two-systems proposal - a theoretical framework that suggests that there are multiple systems at play and that these systems do not communicate early in infancy, leading to failure in certain numerical comparisons. An alternative proposal is that infants may be attending to continuous extent dimensions in these tasks rather than number per se. However, neither of these two main proposals is independently capable of accounting for the previously published data. Recently the Signal Clarity Hypothesis was proposed to account for and predict the variability (Cantrell & Smith, 2013). According to this hypothesis, infants’ variable success may be understood from a framework of statistical learning taken together with the signal-to-noise ratio generated by control procedures in habituation tasks. Here we test specific predictions made by the Signal Clarity Hypothesis. Across four experiments assessing 9-month old discriminations of small and large sets (2 vs. 4 and 3 vs. 4), we demonstrate that infant success can be predicted by this novel approach and, further, that infants may discriminate smaller ratios of change than previously believed (3:4 numerical change and 2:3 cumulative area change).

Introduction

Evidence suggests that infant numerical discriminations are imprecise and ratio dependent (see Feigenson, Dehaene & Spelke, 2004). For example, the data indicate that at 6 months of age infants discriminate changes in number involving a 1:2 ratio difference (e.g. they recognize the differences between 8 versus 16 and between 16 versus 32 items; Brannon, Abbott & Lutz, 2004; Cordes & Brannon, 2009a; Xu & Spelke, 2000; Xu, Spelke & Goddard, 2005). This ability improves with age such that by 9 months infants discriminate 2:3 ratio differences (Lipton & Spelke, 2003, 2004; Wood & Spelke, 2005; Xu & Arriaga, 2007). These data support the existence of an imprecise Approximate Number System (ANS) - a preverbal system responsible for tracking number via noisy analog magnitude representations. However, there are a few findings that do not fit within the proposed traits of the ANS system.

Here we test an explanation of those findings - the Signal Clarity Hypothesis - based on the idea that umans show biased attention to regularity (e.g. Fiser & Aslin, 2001; Saffran, Aslin & Newport, 1996; Zhao, Al-Aidroos & Turk-Browne, 2013), and that the presence of these regularities leads to more refined discrimination (Wyart, Nobre & Summerfield, 2012). The account is derived from the general properties of the habituation procedure (the task by which number discrimination is generally tested in infants) but may also be informative about how the number systems develop. We first summarize the findings that are discrepant with the proposed traits of the ANS and briefly review the current explanations for these discrepancies. Second, we describe the Signal Clarity Hypothesis that should apply to any habituation task (not just number tasks). We then consider how this hypothesis may explain the observed discrepancies in the infant number discrimination literature and describe the rationale for the four experiments we report. Finally, we consider the broader implications of the Signal Clarity Hypothesis for understanding the dimensions that are relevant in numerical comparison, and how we as a field might - from this approach - study the relative saliencies of various dimensions and how they may change over development.

The ratio varies with set size and stimuli presentation

A key assumption that has, to date, been described as a trait of the ANS is its ratio dependency: the discrimination of any two values occurs if their ratio of difference exceeds some threshold. The ratio threshold approaches one over the course of development, such that discriminations become more precise with age, but is presumed to be relatively stable within an infant at a particular age (e.g. an infant who discriminates 16 and 24 also tends to be able to discriminate 24 and 36 - a stable ratio of 2:3). There are, however, cases in which this principle of ratio dependency is violated. For example, although 6-month-old infants fail to make 2:3 ratio comparisons of large numerosities (e.g. 8 versus 12), they have in some instances succeeded with this ratio comparison when the set sizes of the compared quantities were both small (i.e. < 4 such as in a comparisons of 2 versus 3 items) and number was confounded with other visual, non-numerical quantities (i.e. density, surface area, contour; Antell & Keating, 1983; Cordes & Brannon, 2009a; Wynn, 1996) or when the task stimuli were presented intermodally (Jordan & Brannon, 2006; Jordan, Suanda & Brannon, 2008; Kobayashi, Hiraki & Hasegawa, 2005). An additional discrepancy is that 6-month-old infants oftentimes fail to discriminate a 1:2 ratio difference (e.g. 1 vs. 2, 2 vs. 4, as well as 3 vs. 6), despite at times discriminating a 2:3 ratio at the same age (Cordes & Brannon, 2009b; Lipton & Spelke, 2004; Wood & Spelke, 2005; Xu, 2003; Xu et al., 2005).

There are two main explanations for this pattern of findings. The first is the two-systems hypothesis (Feigenson et al., 2004). According to this hypothesis, in addition to the ratio dependent ANS, infants use a second system - an object file system - which has a limit of three items and is more precise than the ANS in processing small numerosities (see Feigenson et al., 2004; Feigenson & Carey, 2003; Xu, 2003). Current interpretations of this hypothesis further propose that the representations formed in each of the two systems cannot be directly compared to one another (Cordes & Brannon, 2009b; Feigenson, Carey & Spelke, 2002; Xu, 2003). Therefore, the two-systems hypothesis could account for many of the observed results: young infants successfully compare 2 versus 3 at times because these small sets may be represented by the more precise object file system, large number discriminations are not as precise because they are handled by the ANS, and infants fail in comparisons that involve small (1–3 items) and large (> 4) numbers such as 2 versus 4 and 3 versus 6 because of a systems interfacing problem. The two- systems hypothesis, however, does not provide an explanation for repeated failure in 1 versus 2 comparisons (Feigenson et al., 2002; Xu et al., 2005), nor does it - without making certain additional assumptions - seamlessly handle the observed success of young infants in small-large set comparisons that involve quantities at ratios greater than 1:2 such as 1 versus 4 and 2 versus 8 (Cordes & Brannon, 2009a; see also Vanmarle, in press).

Another explanation previously proposed to account for the variability in infants’ number discrimination is that they are in fact attending to continuous extent rather than number per se (Clearfield & Mix, 1999; Mix, Huttenlocher & Levine, 2002). When one item is added to a set of two to make three, not only does the numerical value of the set change but so does the total area covered by the set, the total edge length of the items (cumulative contour), and density (within the confines of some limited space) - and these variables do not change at the same rate as number.¹ If infants are in fact using one of these other dimensions to detect set size changes, then mapping out discrimination with respect to number may lead to what appears to be variability in the numerical ratio needed for successful comparison (see Cantrell & Smith, 2013, for an example). However, this proposal cannot be the whole story, either. If attention to continuous extent alone were the sole determinant of discrimination, then the ratio for discrimination of these variables would be expected to be more reliable and predictable. Based on current data, however, this does not appear to be the case: infants demonstrate wide variability in their ability to discriminate changes in dimensions such as cumulative surface area and item size. For example, infants do not show a stable discrimination ratio for surface area, succeeding in 1:2 ratio differences when judging the area of one item but requiring up to a 1:4 ratio for judging the cumulative area over a set of items at the same age (Brannon et al., 2004; Brannon, Lutz & Cordes, 2006; Cordes & Brannon, 2008; Hespos, Dora, Rips & Christie, 2012). Infants also appear imprecise in item size comparisons, and interpretations of some studies show similar inattention to cumulative contour (Cordes & Brannon, 2009a; Cordes and Brannon, 2011).

In brief, the pattern of findings across studies in the field shows variability in numerical discrimination that does not fit the proposal of a stable ratio-dependent system; infants have at times discriminated 2:3 ratio differences in number, but in other cases infants at the same age have required 1:4 ratio differences for successful comparison. The two-systems hypothesis - intended to account for the variability - does not, in its current state, explain the full range of results. The alternative hypothesis - that infants may be using one or more continuous extent variables - is also not complete as there are still instances of unpredictable discrimination behavior based on these other variables. Given the gaps in these hypotheses, how might the pattern of findings be explained?

The Signal Clarity Hypothesis

Over the past 30 years, the dominant method used to investigate infant discrimination has involved habituation. The procedure is at its root about the categorical representation of a series of exemplars. In the task infants are shown sequentially presented displays that have some commonality, they are expected to form a representation of that series, and at test a novel stimulus from a different category is presented; an increase in looking to the novel stimulus is interpreted as successful discrimination of the categorical representation and the novel stimulus category. In numerical tasks, the expectation is that the representation across the series is primarily about number and, in fact, researchers often vary the non-number dimensions (e.g. surface area, cumulative contour, item size) across the exemplars during habituation to discourage attention to these other dimensions and to highlight the constant dimension of number (e.g. Xu & Spelke, 2000). Although structuring the task in this way would intuitively seem to provide infants with much evidence that number is indeed the relevant dimension - one that should be the primary dimension for category representation - the Signal Clarity Hypothesis proposes that structuring the task in this way may in fact generate summary representations that are noisy and less easily discriminated.

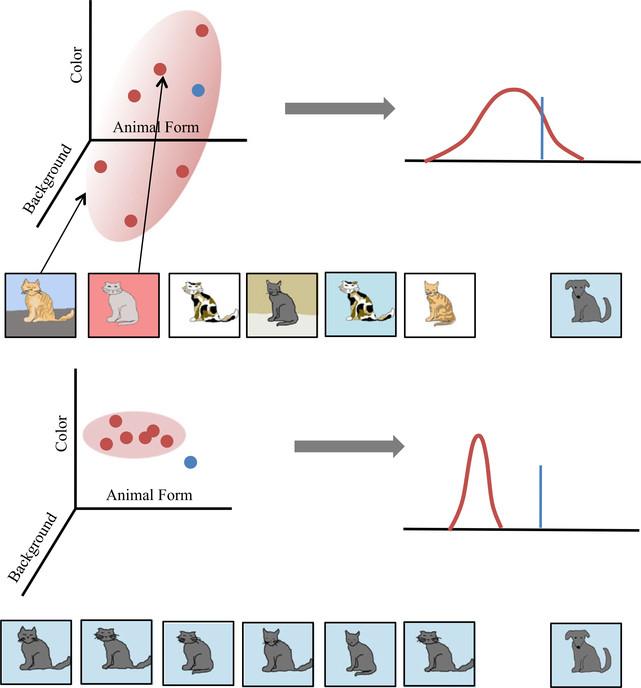
According to the Signal Clarity Hypothesis proposed by Cantrell and Smith (2013), a summary representation formed across a series of displays will vary as a function of two main factors: (1) the dimensions that are extractable and salient for each display in the series and (2) the variability of these dimensions across exemplars. This means that for any class of stimuli, the representation of a dimension will be stronger if that dimension is easy to extract from each individual display in the habituation series and if there is low variability across the exemplars in the series. When there is high variability across exemplars - such as when the exemplars from some category vary in color, background size, or in the feature details - a wide tuning function of the series is created, one that may be less easily discriminated from instances of other categories (see Quinn, 1987; Eimas, Quinn & Cowan, 1994). When there is low variability across the series, a narrower tuning function is formed. Figure 1 illustrates this idea. Further, if the exemplars share values on multiple and therefore redundant dimensions, this should increase the precision of the summary representations as well, as human learners are highly sensitive to correlated properties and dimensions (e.g. Medin, Altom, Edelson & Freko, 1982).

Figure 1.

Each exemplar in a series presented in an habituation task may be represented as a single instance in a stimulus that varies by several dimensions. When there is high variation in these dimensions across the exemplars, the points in the space are widely distributed (depicted by the red points) and a broad summary representation is formed (top). When there is low variation and redundancy in dimensions, a narrow tuning curve is generated (bottom)-one that may be more easily discriminated from a novel exemplar (depicted by the blue point)

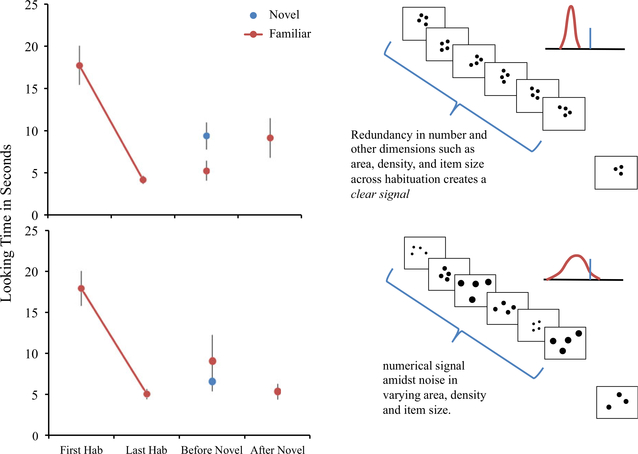
From this hypothesis, task structures that present the dimension of number amidst changing dimensions of surface area, item size, and density create a context for the formation of a less precise representation (such as in Figure 1, 3 (bottom panel), and 4; see also Suanda, Tompson & Brannon, 2008) which would be expected to lead to poorer discrimination (i.e. requiring larger ratios of difference for success). In contrast, task structures that present a numerical signal in reduced noise contexts by stabilizing the surrounding dimensions and creating redundancy and regularity across the displays by minimizing variation on dimensions such as surface area, density, and item size should lead to more precise representations and increased precision and better discrimination. This proposal fits the current documented success of infants discriminating 2 versus 3, which has occurred when number was correlated with area and cumulative contour (that is, they were held constant across habituation trials; Cordes & Brannon, 2009a; see also Clearfield, 2004; Wynn, 1996). This proposal also provides an explanation for documented infant failures in discriminating 1 versus 2, 2 versus 4 and 3 versus 6 (Cordes & Brannon, 2009b; Xu, 2003; Xu et al., 2005): in all of these studies, number was presented in a context in which the number was held constant while other stimulus dimensions varied during habituation. Further, the hypothesis is not specific to number; it offers an account for the variability in surface area discrimination - discriminations which have varied depending on whether number and item size were constant across habituation (Cordes & Brannon, 2008; Brannon et al., 2004; Brannon et al., 2006; Hespos et al., 2012) and provides testable predictions for variable precision in large quantity discrimination as well.

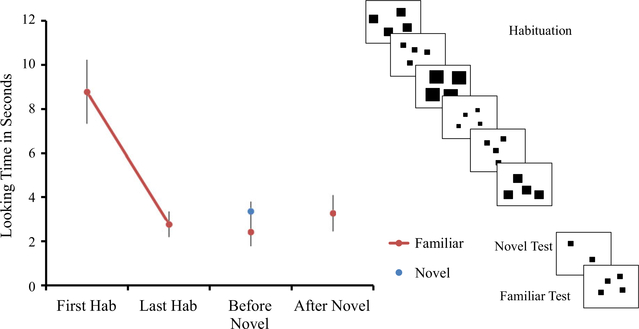
Figure 3.

Looking time on the First Habituation, Last Habituation and first pair of test trials (Novel and Familiar) in Experiment 2.

Here we directly test whether precision and successful discrimination of quantity stimuli can be, in part, predicted by the principles of the Signal Clarity Hypothesis. Due to theoretical interest (Cordes & Brannon, 2009b; Xu, 2003; Vanmarle, in press), we chose to test the hypothesis in four experiments that compare small (< 4) and large quantities (> 4 such as in comparisons of 2 versus 4 and 3 versus 4) and that either present a clear signal with all dimensions stable and redundant across habituation (Experiments 1 and 3) or in a noisy context with area, item size, and density changing across the habituation trials displays (Experiments 2 and 4). In all experiments, number and surface area (as well as the cumulative contour) changed together from habituation to testing, meaning that any of these dimensions could be used for successful discrimination at test. We allowed this correlation in useable cues for two reasons. First, it is impossible to control continuous extent dimensions in numerical tasks that create a clear signal - there will always be some, albeit small at times, magnitude of change in some other dimension when number changes from habituation to testing. However, it is currently not clear what ratio of change infants need to robustly discriminate area or contour. Here we focus on area in describing the stimuli; however, the cumulative contour is also reported in Tables 1 and 2. As previously noted, infants have at times discriminated a 2-fold difference, but have also required up to a 4-fold difference in area. In Experiments 1, 2 and 4, cumulative area changed at approximately a 1:2 ratio (2-fold and 1.9-fold), and in Experiment 3 (to be more conservative for a strong test of the Signal Clarity Hypothesis) cumulative area changed by approximately a 2:3 ratio (1.56 fold) - all ratios at the cusp, if not below, what has been shown to be robustly discriminable by young infants (Brannon et al., 2004; Brannon et al., 2006; Cordes & Brannon, 2008; Hespos et al., 2012). Second, and importantly, the argument here is not about whether number or some other dimension is being used in the task; rather, the prediction is about the precision of discrimination for any of these dimensions as influenced by Signal Clarity.

Table 1.

Dimensions, averages, and ratio of change for stimuli presented during habituation and testing for (A) Experiment 1 and (B) Experiment 2

Number	Total surface area	Total contour	Stimulus label
A. Experiment 1: 2 vs. 4 clear signal
Habituation
2	32	32	A
2	32	32	B
2	32	32	C
2	32	32	D
2	32	32	E
2	32	32	F
4	64	64	A
4	64	64	B
4	64	64	C
4	64	64	D
4	64	64	E
4	64	64	F
Testing
2	32	32	Randomly drawn from G, H, and I
4	64	64
B. Experiment 2: 2 vs. 4 noisy signal
Habituation
2	23.2	27.2	A
2	32	32	B
2	44.2	37.6	C
2	60.9	44.2	D
2	84.1	51.9	E
2	116.06	60.9	F
Average	60.1	42.3
4	46.4	54.5	A
4	64	64	B
4	88.3	75.2	C
4	121.9	88.3	D
4	168.2	103.8	E
4	232.1	121.9	F
Average	120.15	84.6
Testing
2	60.9	44.2	Randomly drawn from G, H, and I
4	121.9	88.3

Infants in both Experiments 1 and 2 were habituated to either 2 or 4 then presented both test stimulus displays during testing. All dimensions are in cm². For Experiment 1, the change in total surface area from habituation to testing was 2-fold; the change in total contour from habituation to testing was 2-fold. For Experiment 2, the change in average total surface area from habituation to test was 2 fold; the change in average total contour from habituation to testing:

2 → 4, 2.1-fold

4 → 2, 1.9-fold

Table 2.

Dimensions, averages, and ratio of change for stimuli presented during habituation and testing for (A) Experiment 3 and (B) Experiment 4

Number	Total surface area	Total contour	Stimulus label
A. Experiment 3: 3 vs. 4 clear signal
Habituation
3	14.7	23.55	A
3	14.7	23.55	B
3	14.7	23.55	C
3	14.7	23.55	D
3	14.7	23.55	E
3	14.7	23.55	F
4	22.92	33.92	A
4	22.92	33.92	B
4	22.92	33.92	C
4	22.92	33.92	D
4	22.92	33.92	E
4	22.92	33.92	F
Testing
3	14.7	23.55	Randomly drawn from A–F
4	22.92	33.92
B. Experiment 4: 3 vs. 4 noisy signal
Habituation
3	8.5	23.9	A
3	12.5	28.9	B
3	15.9	32.7	C
3	21.2	37.7	D
3	30.5	45.2	E
3	43.6	54	F
Average	22	37.1
4	10.2	22.6	A
4	12.6	25.1	B
4	16.6	28.9	C
4	26.42	36.4	D
4	36.32	42.7	E
4	50.27	50.27	F
Average	25.4	34.3
Testing
3	12.47		Randomly drawn from A–F
4	36.32

Infants in both Experiments 3 and 4 were habituated to either 3 or 4 then presented both test stimulus displays during testing. For Experiment 3, the change in total surface area from habituation to testing was 1.56-fold; the change in total contour from habituation to testing was 1.44-fold. For Experiment 4 the change in average total surface area from habituation to testing was as follows:

3 → 4, 1.77-fold

4 → 3, 2.04-fold

Average change: 1.9-fold

The change in average total contour from habituation to testing for Experiment 4 was as follows:

3 → 4, 1.18-fold

4 → 3, 1.15-fold

Average change: 1.1-fold

The first two experiments test infants in a 2 versus 4 numerical comparison presented as a clear signal (Experiment 1) and as a noisy signal (Experiment 2). Experiments 3 and 4 push the idea further, asking whether success at even smaller ratios of change (3:4 in number) can be predicted by principles of Signal Clarity. Nine-month-olds were tested because this is an age prior to which both success and failure have been observed in 2 versus 4 comparisons (e.g. Cordes & Brannon, 2009b; Wynn, Bloom & Chiang, 2002) and thus predicting success and failure would be notable. It is also an age at which it is currently believed that a 3:4 ratio is not discriminable (see Mou & vanMarle, 2014, for a review).

Experiment 1: 2 versus 4 with a clear signal

Method

Participants

Twenty 9-month-olds were included in the final sample for the study (mean age = 9.2 months, range = 8.6–9.7 months). An additional five infants were tested but were excluded from the final sample (four due to fussiness, one due to premature birth). Infants were recruited and tested in a laboratory at a university in the northeastern US.

Stimuli

Stimuli were black squares on a white background. The white background was a 30 × 38 cm (height × width) screen. The stimulus displays were of either 2 or 4 items. The squares in all the displays were the same size − 4 × 4 cm with an individual surface area of 16 cm². Thus the cumulative area for the 2-item display was 32 cm² and for the 4-item display the total area was 64 cm², making the 2-item and 4-item stimuli sets differ from one another in both number and area by a ratio difference of 1:2 (see Table 1 for details). Six different configuration displays were created for the habituation phase and three different test displays for each stimulus set were created and randomly drawn from for each infant’s testing. The inter-item spacing of the items (edge-to-edge) was not specifically maintained constant but was comparable across the displays during habituation within each item set.

Procedure

Infants were seated in a highchair or a caregiver’ s lap approximately 70 cm from the screen in a dimly lit room. A small camera placed above the screen recorded the infant’ s face and was used for online and offline coding of looking to the screen. Each infant was randomly assigned to one of the habituation conditions (2-item or 4-item condition). Infants were presented displays from one condition set (e.g. 4-item) until habituation was reached or until 16 trials were completed at which time infants entered a testing phase. Habituation was defined as a 50% reduction from the average of the first three consecutive trials (that summed to at least 12 seconds total) to the last three averaged trials (as per Cordes & Brannon, 2008; Xu & Spelke, 2000). The habituation trials were randomized with the only constraint being that infants could not see the same display twice in a row. A trial began once the infant looked at the screen and continued until the infant looked away for 2 consecutive seconds or until the infant had looked a total of 60 seconds. Each infant’ s looking was recorded by an online coder hidden from the infant’s view and blind to the stimulus presentation. The coder recorded looking by holding a button down when the infant looked at the screen and releasing the button when the infant looked away. The experiment was managed with a customized RealBasic program, which kept track of infant looking across trials and automatically terminated habituation and entered testing based on the stated habituation criteria.

Once infants reached habituation, testing began. Infants were shown a total of six displays, three novel and three familiar. The familiar stimuli were displays created for the testing phase and were a different configuration from any display seen during habituation (but were the same number and surface area as seen during habituation). The novel stimuli were created for the test trial phase and were the number and area not seen during habituation. All infants saw both novel and familiar displays in alternation during testing; half of the infants saw the novel display first (Novel First Order), while half saw the familiar display before the novel (Familiar First Order).

Data coding and analyses

After the experimental session, videos were coded offline by four independent coders using the Preferential Looking Coder (Libertus, 2008). The looking times with the highest inter-reliability matching between at least two of the offline coders (looking times within 550 ms of each other for total trial looking) were used in the analyses. Inter-reliability was at 99% for all infants and trials included in the analyses and there was a low average of inter-coder difference (.5 s on average per trial). One test trial from one infant was identified as an outlier, defined as a looking time that exceeded 3 standard deviations from the group average, and was replaced by the next longest looking time within the sample (as per Cordes & Brannon, 2009b).

Results and discussion

We first asked whether infants habituated to the stimuli. A paired samples t-test showed a significant decrease from the first habituation (M = 9.7 s) to the last habituation trial (M = 2.1 s), t(19)= 5.94, p < .001; thus, infants as a group habituated. Fourteen of the 20 infants reached habituation and the infants who reached habituation did so after an average of 8.1 trials (11/20 reached habituation within 8 trials). A difference score was calculated for each infant by subtracting the looking time to the last habituation trial from the average looking time on the three novel test trials; an independent samples t-test comparing these difference scores between habituators and non-habituators showed no differences between the two groups of infants (t(18) = .304 p = .78) and thus all infants regardless of habituation were included in final analyses. The difference scores were then analyzed in a 2 (Gender) × 2 (Test Order) × 2 (Habituation Condition) ANOVA and no significant main effects or interactions were found.

The main question was whether infants would show an increase in looking to the novel test stimuli after habituation. A two-tailed paired samples t-test between the looking time on the last habituation (M = 2.1 s) and the average looking time to the three novel test stimuli (M = 3.8 s) showed a significant increase, t(19) = 3.05 p = .007. A paired samples t-test between the last habituation trial and the average of the familiar test trials (M = 3.8 s) also showed a significant increase, t(19) = 3.46, p = .003. Thus, infants showed dishabituation to both the novel and familiar stimuli. There are three possible reasons for this result. One possibility is that the observed increase in looking to both test stimuli (Novel and Familiar) is a Type 2 error (see Oakes, 2010). The second possibility is that infants in fact noticed that the displays - both novel and familiar - were different in configuration from all others they had viewed during habituation. The third possibility - and the one that is most likely in our view - is that infants noticed the change in the novel stimulus first and that the increase in looking to the familiar is due to arousal or a rebound after seeing the novel (Oakes, 2010). This third possibility would specifically predict that increased looking to the familiar stimulus would only be observed for infants who saw the familiar after having viewed the novel.

To address this possibility, the first pair of test trials (Novel 1 and Familiar 1) was examined more closely. A two-tailed paired samples t-test between the last habituation (M = 2.1 s) and first novel test trial (M = 6.1 s) confirmed that infants dishabituated to the novel stimulus in the first test pair, t(19) = 3.07, p = .006, indicating that as expected infants showed an increase in looking to the novel test stimulus. Further, a significant majority of infants (15/20, 75%) showed this increase in looking (Binomial, p < .05). A paired samples i-test, however, also showed a significant increase in looking from the last habituation to the first familiar test trial, M = 3.6 s, t(19) = 2.46,p = .024); however, this dishabituation effect was observed in only a statistically non-significant majority of infants (12/20, 60%, Binomial, p > .05) and analyses showed that it was only those infants who saw the familiar test stimulus after seeing the novel test stimulus who showed a significant increase in looking to the familiar (last habituation M = 2.0 s versus first familiar M = 4.2 s, t(9) = 2.34 p = .044). Those who were presented the familiar test stimulus first (that is, prior to the first novel stimulus) did not show an increased looking time: habituation (M = 2.2) versus first familiar test stimulus (M = 3.0 s), t(9) = 1.03, p = .33.

This pattern of looking can be seen clearly in Figure 2: looking time increased from the last habituation to the first novel test trial across all infants, and looking time to the familiar test stimulus also increased significantly after having seen the novel. Despite the increased looking to the familiar stimulus observed in the Novel First Order, there was a marginally significant difference between first novel and first familiar test trials, t(19) = 1.94, p = .07 – even when collapsing across the test orders.

Figure 2.

Looking time on the First Habituation, Last Habituation and first pair of test trials (Novel and Familiar) in Experiment 1. Half of the infants saw the familiar stimulus first; half saw the familiar stimulus second (after first seeing the novel). Average looking times of the infants in each order are shown in the graph. The novel looking time is the novel trial average across all infants - those who saw it first as well as second in the testing phase.

Overall, the results from Experiment 1 suggest that infants successfully discriminated a set of 2 from a set of 4 items when the noise was reduced in the stimulus signal across habituation trials. This is different from previous results in which infants in a 2 versus 4 comparison failed when all variables changed throughout habituation (Cordes & Brannon, 2009b). One possibility, clearly, is that infants ignored number and only used correlated surface area to discriminate habituated and test stimuli. If this were the case, then the results tell us at the very least that infants should be able to succeed in a 1:2 surface area change when the signal is clear and presented amidst stable dimensions (in contrast to failure with this same surface area ratio when the signal was noisy, Cordes & Brannon, 2008). Alternatively, the rather large 1:2 ratio change in multiple dimensions (both number and area) may have driven discrimination; that is, it is possible that there is an additive effect as infants combined the differences of both the number and area. If this is the case, then Signal Clarity may not be playing a key role and infants should succeed in any task in which number + area change together.

To address these alternative possibilities for the success observed in Experiment 1, in Experiment 2 infants were presented a noisy numerical signal: surface area varied across the habituation trials while number remained constant. (Note, we could presumably create the same noise in a surface area signal by varying number throughout habituation.) The novel stimulus at test involved a novel number and a novel area - just as in Experiment 1. The novel test stimulus’ area was a 2-fold difference on average from the surface areas viewed during habituation and the novel stimulus’ area was in fact different from all the stimuli seen in the habituation phase. Thus, like in Experiment 1, infants could use the dimension of number to discriminate, or they could use the change in number + the change in area. The prediction here, however, was that if a noisy signal is in fact more difficult to represent and if it creates a wider tuning signal that may overlap with other signals, then - despite multiple dimensions of change from habituation to test - infants should not show robust discrimination.

Experiment 2: 2 versus 4 with a noisy signal

Method

Participants

Twenty nine-month-old infants (14 males, mean age = 9.03 months, range = 8.6–9.6 months) were recruited and tested. Seven additional infants were tested but were excluded from the final sample (six due to fussiness and one due to parental interference). Infants were recruited and tested in the same laboratory as those in Experiment 1.

Stimuli

Stimuli were similar to those used in Experiment 1; they were of black squares on a white background, and the white background was a 30 × 38 cm (height × width) screen. The stimulus displays were of either 2 items or 4 items and six displays were created for each stimulus set. Unlike Experiment 1, however, the habituation displays contained different surface areas and varied approximately 5-fold across habituation trials to create a noisy context for the dimension of number. Thus, stimuli were very similar to those used in previous studies investigating numerical discrimination (studies that attempt to dissociate number from other dimensions across habituation; e.g. Xu & Spelke, 2000). The individual item sizes for both the 2-item and 4-item displays varied between 11.6 cm² and 57.8 cm² (individual item size side lengths were 3.4 cm, 4 cm, 4.7 cm, 5.5 cm, 6.5 cm, and 7.6 cm). Therefore, for the 2-item displays, the cumulative surface area of the displays varied between 23.2 cm² and 116.1 cm², with an average cumulative surface area across the displays being 60.1 cm². The 4-item displays ranged between 46.4 cm² and 232.1 cm² and the average surface area across all the displays was thus 120.1 cm² (approximately double that of the 2-item displays). Details are shown in Table 1, Panel B.

Test displays were the same for infants regardless of habituation condition (i.e. whether infants were shown 2 versus 4 items during habituation), and each served as either the novel or familiar test stimulus, depending on the habituation condition. Three different test display configurations were made for each item set (2 and 4) and were randomly drawn and presented to the infants during test in alternation. The items in the test displays always had side lengths of 5.5 cm with individual item sizes of 30.5 cm². Thus the 2-item display had a total surface area of 60.9 cm ² and the 4-item display had a surface area of 120.1 cm². The familiar display was of a surface area that infants had seen during habituation and the novel display was different in number by 2-fold and was also different from the average surface area of habituation by 2-fold - comparable to Experiment 1 (see Table 1B). Because item size varied across the displays, the edge-to-edge distance for the items also varied and thus density (just as surface area) varied more across the displays in Experiment 2 than in Experiment 1.

Procedure

The procedure was identical to Experiment 1. Infants were randomly assigned to one of the two habituation conditions − 2-item or 4-item. Habituation in Experiment 2 was defined in the same way as in Experiment 1. Once habituation was reached, infants entered a testing phase in which they saw a novel and a familiar trial. Half the infants saw the novel trial first; half of the infants saw the familiar first - just as in previous experiments.

Coding and data analyses

Intercoder reliability for all of the trials across all infants for the trials included in the analyses was high, r = .95, p < .001, and the difference between coders for the trials was low - .4s on average. One trial’s looking time met the outlier criterion and was replaced.

Results and discussion

Results are shown in Figure 3; infant looking times showed a significant decrease from the first habituation trial (M = 8.8 s) to the last habituation trial (M = 2.6 s), t(19) = 4.43, p < .0001. A majority of infants habituated (13/20, 65%) and those who habituated did so on average in 8.6 trials (10 infants habituated within 8 trials). A 2 × 2 × 2 ANOVA showed no main effects or interactions of Gender, Habituation Condition, and Test Order on the difference scores (average of novel trials — last habituation).

The main question was whether infants would show an increase in looking from habituation to test as infants did in Experiment 1. Infants showed no significant increase from the last habituation to the average of the novel test trials (M = 3.2 s), t(19)= 1.28, p = .22, nor to the average of the familiar test trials (M = 3.1 s), <(19) = .94, p = .36, and this was true even when analyzing only the first pair of novel and familiar trials (Novel 1 and Familiar 1); the difference between the last habituation and first novel test trial (M = 3.4 s) did not reach significance, t(19) = .80, p = .43, nor did the difference between the last habituation and first familiar test trial (M = 2.9 s), t(19) = .095, p = .93. There was also no difference in looking time between novel and familiar test trials in the first pair, t(19) = .92, p = .37.

The results from Experiment 2, thus, yielded a null result - indicating that infants as a group did not demonstrate robust discrimination of the stimuli sets when the number was presented in a noisy context - despite the fact that the stimuli differed numerically as well as in surface area on average by the same ratio as Experiment 1 (1:2 ratio). We also directly compared Experiments 1 and 2. A two-tailed independent samples t-test yielded a significant difference between the difference scores for infants in the two experiments, t (38) = 2.27, p = .029, indicating that infants in Experiment 1 not only showed a significant increase in looking from habituation to novel testing, but their average increase was greater - with a mean difference of 4 s between the last habituation and first novel - than the average increase shown by infants in Experiment 2 (M = 0.6 s). Thus, Experiment 2 rules out the possibility that infants succeeded in Experiment 1 solely through attention to area or by relying on the change in multiple dimensions. It should also be noted that although the Signal Clarity Hypothesis predicts that discrimination is a function of both the precision of the representation and the ratio of difference between the to-be-compared stimuli, the results from Experiment 2 suggest that a 2-fold difference in number + area is not large enough to overcome the noise introduced by the 5-fold changing area during habituation. Future work may reveal that less noise or slightly larger ratios of difference should lead to discrimination - an idea outlined in the General Discussion.

The next two experiments were conducted to push the principles of Signal Clarity further. The ratio of difference between stimuli was lowered to a threshold previously believed not to be discriminable by infants at this age − a 3 versus 4 numerical comparison with a correlated 2:3 area change. Few studies have tested a 3:4 numerical ratio (but see Strauss & Curtis, 1981; Van Loosbroek & Smitsman, 1990); even fewer have tested a 2:3 area change in young infants and these have shown failure (Brannon et al., 2004; Brannon et al., 2006), and this area change is smaller than previous studies have found infants are able to discriminate.²

Experiment 3: 3 versus 4 with a clear signal

Method

Participants

Twenty-three 9-month-old infants (16 males, mean age = 9.4 months, range = 9.0–9.9 months) were recruited and tested in a laboratory in the Midwest US. Two additional infants were recruited and tested but were excluded from the final sample (one due to fussiness and one due to equipment failure).

Stimuli

Stimuli were black dots on a white background. The background on which the dots were displayed was a screen of 43 × 33 cm (height × width). The stimulus displays were of either 3 items or 4 items. There were six different display configurations for each item set condition. Surface area and contour measurements for the stimuli are reported in Table 2A. Density (average edge- to-edge distance) was maintained approximately equal across all displays. Importantly, the 3-item and 4-item stimuli sets were different from one another in number by 1.5-fold in number and 1.56-fold in surface area. The goal here was not to control for all dimensions; as already noted, it is in fact impossible to control all dimensions in one study without making a signal noisy. Thus our concern was not to eliminate dimensional correlation with number, but, rather, was to allow dimensions only to change by a ratio that was below the currently believed threshold of discrimination in quantity studies that have attempted to isolate other dimensions in a noisy-signal design (by removing one or more correlated dimensions, e.g. Xu & Spelke, 2000).

Procedure

The procedure was identical to Experiments 1 and 2 except for the following. Infants were seated in a caregiver’s lap approximately 70 cm from the screen. The caregiver was instructed to look down during the session and to hold the infant comfortably but to sit as still as possible and not to interact with the infant verbally or physically shift the infant during the trials. Each trial (in habituation and testing) began with an animated attractor video. Attractors were randomly drawn from a pool of 12 animated figures (e.g. a dancing teddy bear, a jumping stuffed monkey) accompanied by different rhythmic sounds (e.g. a ringing bell, spring sound, kazoo). Once the infant looked toward the screen the attractor was replaced with a stimulus. If the infant was not looking at the start of a trial, or if the infant looked less than 0.5 seconds, an attractor was presented and the trial was repeated (with an identical stimulus display). This occurred on less than 0.5% of all trials across all infants. All infants completed the session without stopping or taking breaks. Each infant was randomly assigned to one of the habituation conditions (3-item or 4-item condition). Looking time was recorded via a customized program in Eprime. The familiar stimulus was a display randomly drawn from the same set of 6 from which the habituation displays were drawn. The novel stimulus was randomly pulled from the not- seen stimulus set.

Coding

After the experimental session, videos were slowed and looking time was coded offline in OpenShapa by two independent coders for the trials included in the analyses. Intercoder reliability for 35% of the trials was highly correlated, r = .99, p < .001; intercoder differences were low - on average, .3 s per trial. Offline coding was used in all looking times analyses. One outlier trial across all infants and trials was replaced using the same criteria established in Experiment 1.

Results and discussion

There was a significant decrease from the first habituation (M = 17.8 s) to the last habituation trial (M = 4.2 s), t(22) = 3.8, p < .001; thus, infants as a group habituated. Twenty of the 23 infants reached habituation and did so in an average of 8.3 trials (15 infants habituated within 8 trials). Again, a 2 (Gender) × 2 (Habituation Condition) × 2 (Test Order) ANOVA was first conducted on difference scores, which yielded no significant main effects or interactions (all ps > .05).

The main question was, again, whether infants would show evidence of discrimination through an increase in looking to the novel stimulus after habituation. A twotailed paired samples t-test comparing the last habituation trial to the average of the three novel test trials (M = 6.3 s) showed a significant increase in looking, t(22) = 2.94, p = .008; again, as in Experiment 1, infants also showed a significant increase in looking to the average of the three familiar test trials (M = 6.3 s), t(22) = 2.97, p = .007.

Further analyses again showed that the increase in looking to the familiar was due to arousal after having viewed the novel stimulus. There was a significant increase in looking from habituation to the first novel test trial across all infants (M = 9.4 s), t(22) = 3.38, p = .003, and a significant majority of infants (16/23, 70%) showed this increase (Binomial, p < .05). The increase in looking to the familiar test stimulus - although observed on the first test trial pair, t(22) = 2.52, p = .02 - was driven by the infants in the Novel First Order condition. Infants who saw the novel stimulus first at test showed a significant increase in looking to the familiar test stimulus after seeing the novel test stimulus: (last habituation M = 4.3 vs. familiar M = 9.1 s), t(10) = 2.33, p = .04, but infants who saw the familiar test stimulus before seeing the novel test stimulus did not increase looking to the familiar test stimulus (last habituation M = 4.2 s vs. familiar M = 5.3 s), t(11) = 1.23, p = .24. There was no significant difference between the novel and familiar test trials when collapsing over the different test orders. The results (looking time on the first habitutation, last habituation, and first block of test trials) from Experiment 3 are depicted in Figure 4 (top).

Figure 4.

Mean looking time during habituation and first block of novel and familiar test trials for Experiment 3 (top) and Experiment 4 (bottom).

The results provide evidence that infants successfully detected the difference in stimuli that varied in number by a 3:4 ratio change and in surface area by a 2:3 ratio change - quantity changes believed to be below what is typically discriminable to infants of this age - when the signal was clear due to redundancy in these dimensions across habituation. This suggests that increased Signal Clarity improves precision. Although we suspect - given the results of Experiments 1 and 2 - that infants were not relying on surface area changes or on the change in multiple dimensions, there is still the possibility that infants discriminated sets of 3 and 4 based on more gestalt or holistic differences between the displays - differences that may be more salient between 3 and 4 than between 2 and 4 (see Mandler & Shebo, 1982). If infants used configural information (and/or the change in surface area) to succeed in Experiment 3, then such success should occur regardless of whether the numerical signal is noisy or clear. However, if success in Experiment 3 can be attributed to increased precision resulting from the redundant dimensions in habituation, then infants are expected to not show robust discrimination when the numerical signal is presented amidst noise. In Experiment 4 we directly tested this prediction. Infants in the final experiment were presented a comparison of 3 versus 4 items in which number was presented as a noisy signal.

Experiment 4: 3 versus 4 with a noisy signal

Method

Participants

Twenty-three 9-month-old infants (11 males, mean age = 9.4 months, range = 8.8–10.1 months) were recruited and tested. Again, two additional infants were recruited and tested but were excluded from the final sample (one due to fussiness and one due to experimenter error).

Stimuli

Stimuli were black dots on a white background. The background, as in Experiment 3, was a 43 × 33 cm (height × width) screen. The stimulus displays were of either 3 items or 4 items. Six displays were created for each stimulus set; however, unlike in Experiment 3, all the displays contained different surface areas (which meant that they all contained different item sizes, contours, and densities). Importantly, surface area varied approximately 5-fold across habituation trials, providing a noisy signal. Surface area and contour measurements for the stimuli are reported in Table 2B.

The test displays were the same for infants regardless of habituation condition (i.e. whether infants were shown 3 versus 4 items during habituation), and each served as either the novel or familiar test stimulus, depending on the habituation condition. The test displays were from the set of 6 created for each condition; infants saw three novel and three familiar displays, alternating across test trials. The cumulative area of the 4-item test display was 36.32 cm² (individual diameter 3.4 cm) and the cumulative surface area of the 3-item display was 12.47 cm² (diameter 2.3 cm). Thus, the familiar display was one that infants had seen during habituation and the novel display was different in number and was also different from the average surface area of habituation by 1.9-fold. We intended this to be comparable to Experiment 3, in which infants could have used area change (in addition to number or the area change alone) to make the discrimination from habituation to test. The change in surface area was in fact greater in Experiment 4 than in Experiment 3 (1.9-fold versus 1.56-fold increase in Experiment 2); thus failure in this experiment would be a strong demonstration of the importance of Signal Clarity in numerical discriminations.

Procedure

Infants were randomly assigned to one of the two habituation conditions − 3-item or 4-item. Infants were habituated to the item sets and displays were randomly ordered during the habituation phase with one constraint: in each condition infants were shown all six different surface areas before repeating any display. This ensured that infants indeed viewed a wide range of surface areas rather than potentially seeing the same stimulus twice, which would have reduced the noise in the signal. Habituation in Experiment 4 was defined in the same way as in the previous experiments. Once habituation was reached, infants entered a testing phase in which they saw a novel and a familiar trial. Half the infants saw the novel trial first; half of the infants saw the familiar first - just as in previous experiments. All other aspects of the procedure were the same as in Experiment 3

Coding and data analyses

Inter-coder reliability for 30% of the trials - evaluated in the same way as in Experiment 3 was high, r = .99, p < .001, with an average of .6 s difference between the two offline coders per trial. One trial’s looking time met the outlier criterion and was replaced.

Results and discussion

Results are shown in Figure 4 (bottom); infant looking times showed a significant decrease from the first habituation trial (M = 17.9 s) to the last habituation trial (M = 5.0 s), t(22) = 6.45, p < .001. Twenty of the 23 infants habituated and did so on average in 9.8 trials (9 infants habituated within 8 trials). A 2 × 2 × 2 ANOVA showed no main effects or interactions of Gender, Habituation Condition, or Test Order on the difference scores.

The main question was whether infants would show an increase in looking from habituation to test as infants did in Experiments 1 and 3 - which would indicate discrimination of the stimuli. Infants, in fact, showed no significant increase in looking from the last habituation trial (M = 5.0 s) to the novel test trials (M = 6.6 s) nor to the familiar test trials (M = 6.4 s). Further, no significant increases in looking were found when analyzing only the first pair of test trials, with no difference between the last habituation and first novel stimulus (M = 6.6 s), t(22) = 1.14, p = .27, nor between the looking time on the last habituation and first familiar stimulus (M = 7.2 s), t(22) = 1.26, p = .22; furthermore, there was no difference in looking between the first novel and familiar test trials, t(22) = .337, p = .76.

The results from Experiment 4 thus yielded a null result - infants as a group did not demonstrate discrimination of the stimuli sets - despite the fact that the stimuli displays presented item sets that differed numerically by the same ratio as that of Experiment 3 (3:4 ratio), differed by almost a 1:2 surface area (a greater ratio than in Experiment 3), and presented similar differences in configural information. Both Experiments 3 and 4 presented infants with a number and surface area change (as well as a potential configuration difference); yet infants only showed evidence of discrimination in Experiment 3 when the signal for the dimension of number was clear with all surrounding dimensions stable and constant. Further analyses across the two experiments supported this conclusion. A two-tailed independent samples t-test yielded a marginally significant difference between the difference scores for infants in the two experiments, t (44) = 1.825, p = .075, indicating that infants in Experiment 3 not only showed an increase in looking from habituation to novel testing, but their average increase was greater than the average increase shown by infants in Experiment 4.

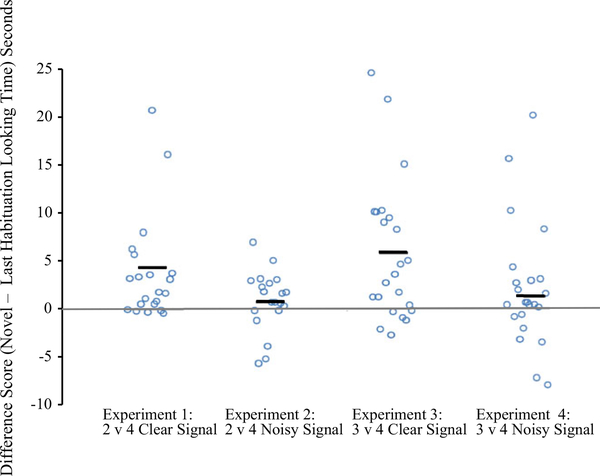
Individual difference scores for all of the experiments are graphed in Figure 5. As can be seen in this figure, when comparing the analogous experiments (Experiments 1 and 2 and Experiments 3 and 4) overall more infants showed a positive difference score in the Clear Signal experiments than in their Noisy Signal counterparts - though there are clearly individual differences.

Figure 5.

Individual difference scores for the four experiments. Experiments 1 and 3 presented a numerical and surface area change in a clear signal context; Experiments 2 and 4 presented the same or greater changes in a noisy context.

In sum, the results across the four experiments support the hypothesis that Signal Clarity plays a role in infant discrimination. Infants’ lack of discrimination in Experiments 2 and 4 suggests that an increase in surface area alone cannot account for the success in Experiments 1 and 3, nor can increases in multiple dimensions (area + number change); it is the clarity of the signal that supported infants’ successful comparison of the quantities in Experiments 1 and 3.

General discussion

Previous research has shown variable precision for infant numerical comparisons - at times infants have successfully compared numerosities at a 2:3 ratio difference, but at other times they have needed a 1:2 or even a 1:4 ratio difference for successful discrimination. One hypothesis that dominates current thinking is the two-systems approach and the accompanying systems-divide hypothesis; this hypothesis does not, however, explain all the data, nor does the alternative explanation that infants rely solely on continuous extent variables predict all previous data. In four experiments, we provide evidence that the principles of the Signal Clarity Hypothesis may account for the variation - at least in the success and failure of comparisons involving small and large sets. Infants in Experiments 1 and 3 successfully discriminated comparisons that involved small and large sets when the signal was clear. Further, they did so when the ratio of change for both number and continuous extent was extremely small (1.56-fold area change accompanying a 1.33-fold number change in Experiment 3) but did not do so when noise was introduced into the signal (Experiments 2 and 4) - even when the number change was the same (2 vs. 4 for Experiments 1 and 2 and 3 vs. 4 in Experiments 3 and 4) and when the accompanying area change was comparable if not larger than those presented in the clear signal experiments. These results provide support for the idea that precision in quantity discrimination is determined in part by the regularities and redundancy across visual displays during the habituation procedure used to measure number discrimination.

The Signal Clarity Hypothesis is not only supported by the four experiments presented in this paper, it also aligns with results from previous studies. Instances in which infants have shown more precise discrimination in previous research come from studies that have provided redundant information to the infant across habituation (e.g. Suanda et al., 2008; Cordes & Brannon, 2009b; Clearfield, 2006). Researchers have previously suggested that redundant information within and across modalities may make numeric representation more precise (Jordan & Brannon, 2006; Baker, Mahamane & Jordan, 2014). However, of theoretical interest, within-modality redundancy may in fact account for many of the previously observed successes in infants’ small set comparisons: in studies in which infants have successfully discriminated small ratios of change (e.g. 2 versus 3 items), the dimensions of surface area, item size, and contour were stable and correlated to number across habituation. Instances when infants have failed to discriminate larger ratio changes (1:2; e.g. 2 versus 4 or 3 versus 6) have presented the numerical signal amidst changing dimensions (changing surface area, item size, cumulative contour; e.g. Cordes & Brannon, 2009b; Xu et al., 2005; Xu, 2003; see also Wood & Spelke, 2005). Further, these principles and their predictions also align to the variation observed in continuous extent discrimination. Although there is relatively less work investigating cumulative contour, density, and item size discrimination, the research focused on infants’ surface area representation has also shown that comparisons are more precise when these sorts of surrounding dimensions are stable and - like the results from numerical comparisons - that when these dimensions vary over habituation, larger ratios of change are needed for discrimination (Brannon et al., 2004; Cordes & Brannon, 2008).

Thus, the Signal Clarity Hypothesis opens new questions and redirects research focus. Among the questions are, how much and in what dimensions does noise become introduced to a signal? Interestingly, the pattern of discrimination of larger sets has been relatively more predictable across studies (see Cantrell & Smith, 2013, for a review). That is, in previous work infants have shown less variation in their successful discrimination of 1:2 ratio differences of large sets even when the numerical signal has been presented amidst changing surface areas, cumulative contours, and item sizes. Such results suggest that the amount of noise needed to disrupt a signal must interact with other dimensions. Number may be less easily disrupted (with the same variations in area, for example) at larger set sizes. This could mean that the salience of dimensions shifts with set size (see Cantrell, Kuwabara & Smith, 2015) and that the dimensions being used at smaller sets may be those that are more easily disrupted by variations in surface area number. The dimension(s) that are more salient at larger set sizes may have greater resistance to noise introduced through area. Likewise, number at these higher set sizes may be more easily disrupted by variations in some other dimension (not area - the dimension most commonly focused on and varied across habituation - but perhaps density or contour). Systematic study of the noise and the dimensional variation that may make precise representations of number difficult to form would lead to a better understanding of how these dimensions interact and of the limits on infant numerical competence.

A further question is how the distribution of noise affects representation. In the current study, noise was introduced by varying area 5-fold over six different area values (as in Xu & Spelke, 2000). However, the infant representations that are being formed over the course of habituation in these tasks, from the framework of statistical learning and the Signal Clarity Hypothesis, occurs through unsupervised learning of the category; therefore, as theories of categorical learning have proposed, representation should also vary with the distribution of instances, not just the average of a dimension (e.g. Nosofsky, 1988). Thus, although in the current study the instances were fairly evenly distributed over a 5-fold range (and the novel stimulus was pulled from the extreme end of that distribution - either the high or low end, see Stimuli section of Experiment 3), we predict that discrimination will change as the distribution of variation changes: if it is bimodal, or if the frequency of instances presented to the infant is skewed, the formed representation, and thus discrimination, will be different. Similarly, because working memory is still very fragile and is undergoing significant developmental changes this early in infancy (Oakes & Luck, 2014), the time point at which some instance occurs in a series of sequentially presented displays will likely also play a role in its influence in the distribution and in the subsequent representation and precision by which the series’ representation is discriminated from a new instance from another category.

Another question is how the Signal Clarity Hypothesis may fit within recent findings using procedures that do not depend on infants’ accumulation of visual representations. For example, in a recent study, Starr, Libertus and Brannon (2013) found that infants successfully discriminated 2 vs. 4 (as well as 1 vs. 2) in a change detection task but failed to discriminate 2 vs. 3 - a pattern that differs from previous findings in habituation studies. Although the representation and discrimination of stimuli in both habituation and the change detection task depend on extracting dimensions at the individual stimulus level, change detection - unlike habituation - does not depend on the accumulation of these signals across multiple displays. In the change detection task, successful discrimination may occur if there is detection of a difference between two individual stimuli that are sequentially presented for very short periods of time (on the order of hundreds of milliseconds; see Ross-Sheehy, Oakes & Luck, 2003). The representations being compared in each task are therefore different: in habituation, a summary representation formed over multiple stimuli at a relatively longer time scale is compared to a single novel stimulus; however, in the change detection task, rapidly formed representations of individual stimuli are compared. According to the principles of Signal Clarity, it should be possible to manipulate individual stimulus properties to produce variability in the ratio of discrimination in the change detection task. Understanding how manipulation of various dimensions shifts the threshold of discrimination in the change detection task will inform us about what dimensions may be represented at the individual stimulus level and will have implications for predictions made in tasks that require infants to accumulate signals over multiple stimuli such as habituation (however, see Posid & Cordes, in press, for an alternative view).

Lastly, the Signal Clarity Hypothesis may fit within either of the current and opposing positions about early number discrimination. That is, it may be taken as a way by which representations in the ANS are made clearer and more easily compared to small set representations (thus aligning with a two-systems hypothesis). Alternatively, the Signal Clarity Hypothesis may stand on its own without the need to implicate two systems per se. As the hypothesis proposes, the dimensions that are salient and easily extracted from a series of displays will depend on the nature and degree of variation across the displays. Further, because the dimensions that may covary with number are not linearly related to number, set size itself may be a factor. For example, as set size increases in an array of items, the saliency of number or area may change and so would the ability to make these different dimensions more precise (i.e. if a dimension is more salient, it may be less easily disrupted by noise). This idea may help explain why discrimination of larger set sizes is more stable; number - or another dimension that varies less across habituation in these tasks for larger sets than for smaller sets - may be more readily represented and less disrupted by the variation in a less salient dimension such as surface area. Understanding the relative saliency of dimensions, thus, may be about more than merely controlling and pitting dimensions against one another; rather, dimensional saliency may be studied by asking how much variation or noise each dimension can withstand and how that resistance or vulnerability to noise changes depending on the values of the other dimensions. Further, the interaction and saliency of dimensions may change over time as language is acquired; number may become less and less easily disrupted as cardinal number words are learned and mapped onto sets - ideas that are testable by asking how variation affects representation of dimensions at different ages.

In sum, the Signal Clarity Hypothesis provides a flexible framework - one that not only explains variable success but predicts it. The approach implicates basic learning processes known to be pervasive in the early infant’s system and aligns to theories of categorical learning and perceptual training and in so doing redirects future work.

Research highlights.

• Previous research shows variability in infant quantity discrimination.

• The variability has been explained by two different hypotheses, neither of which fully accounts for the findings.

• Four experiments provide evidence that a recent proposal - the Signal Clarity Hypothesis - predicts and may therefore account for this variability in discrimination tasks.