Random Walk Enzymes: Information Theory, Quantum Isomorphism and Entropy Dispersion

Abstract

Activation-induced deoxycytidine deaminase (AID) is a key enzyme in the human immune system. AID binds to and catalyzes random point mutations on the immunoglobulin (Ig) gene, leading to diversification of the Ig gene sequence by random walk motions, scanning for cytidines and turning them to uracils. The mutation patterns deposited by AID on its substrate DNA sequences can be interpreted as random binary words, and the information content of this stochastically-generated library of mutated DNA sequences can be measured by its entropy. In this paper, we derive an analytical formula for this entropy and show that the stochastic scanning + catalytic dynamics of AID is controlled by a characteristic length that depends on the diffusion coefficient of AID and the catalytic rate. Experiments showed that the deamination rates have a sequence context dependence, where mutations are generated at higher intensities on DNA sequences with higher densities of mutable sites. We derive an isomorphism between this classical system and a quantum mechanical model and use this isomorphism to explain why AID appears to focus its scanning on regions with higher concentrations of deaminable sites. Using path integral Monte Carlo simulations of the quantum isomorphic system, we demonstrate how AID’s scanning indeed depends on the context of the DNA sequence and how this affects the entropy of the library of generated mutant clones. Examining detailed features in the entropy of the experimentally-generated clone library, we provide clear evidence that the random walk of AID on its substrate DNA is focused near hot spots. The model calculations applied to the experimental data show that the observed per-site mutation frequencies display similar contextual dependences as observed in the experiments, in which hot motifs are located adjacent to several different types of hot and cold motifs.

Graphical Abstract

1. Introduction

The enzyme activation-induced deoxycytidine deaminase (AID) serves a key role in ensuring the fitness of the human immune system by generating diversity on the amino acid sequence of the antigen-binding domains of antibody proteins ¹. AID is a deaminase that catalyzes C→U mutations on single-stranded (ss) DNA ^{2–3, 4}. AID is activated during the maturation of B-cells to trigger somatic hypermutation where the variable (V) region of the immunoglobulin (Ig) gene receives point mutations resulting in random modifications of the V-gene DNA sequence ^5–7. In the switch (S) region of the Ig gene, the C→U mutations deposited by AID on IgS are also responsible for the initiation of class switch recombination (CSR) leading to further antibody diversification ⁸. Both in vitro ⁹ and in vivo ¹⁰ experiments show that AID catalytically favors trinucleotide WRC target motifs (W = A or T, R = A or G) while disfavoring SYC motifs (S = C or G, Y = C or T). AID also binds processively to ssDNA, with bound times up to several minutes ¹¹, and once bound to ssDNA AID scans its substrate bidirectionally by sliding and random short hops, searching for WRC “hot” motifs to act on. The catalytic activity of AID on WRC hot versus SYC cold motifs vary over a range of approximately 10-fold ^{3, 9}. In contrast to fast scanning DNA repair enzymes, such as DNA glycosylases ^12–13 and mismatch repair proteins ¹⁴, which remove damaged or polymerase-catalyzed misincorporated bases with a high efficiency, the scanning and enzymatic activities of AID are characterized by a very slow catalytic efficiency. In this kinetic regime, the fast scanning diffusion of AID and its low catalytic activity are counterbalanced to optimize the randomness of the mutations it produces on its substrate DNA, ensuring maximal diversity in the mutated DNA sequences.

The mutation patterns produced by AID on its substrate DNA are random. Each time AID processes a ssDNA, it produces a different set of mutations. On a nucleotide sequence, these mutation signatures can be interpreted as stochastically generated binary bit sequences, where a “0” represents no mutation and a “1” represents a site that has been mutated. The action of AID on an ensemble of DNAs all having the same nucleotide sequence (i.e. clones) generates a diverse collection of these random binary words. To ensure optimal diversity in the mutated sequences, AID must work inside a kinetic parameter space where its catalytic activity has been carefully tuned against its scanning dynamics, to produce maximal information content in the library of mutant clones it generates.

In two previous papers, we have examined mathematical models of how AID might act on ssDNA. In the first paper ¹⁵, we used extensive libraries coming from experiments where homogeneous ssDNA sequences with tandem repeats of WRC motifs were incubated with AID to derive kinetic parameters for a basic stochastic model describing both the scanning and catalytic activities of AID on ssDNA. In the second paper ¹⁶, we examined some of the peculiarities of AID’s action on inhomegenous substrates, with ssDNA sequences composed of trinucleotide repeats consisting of mixed hot and cold motifs, and illustrated some of the surprising complexities arising from mixed substrate sequences. In particular, we found that AID shows distinctively lower catalytic activity towards a hot motif in the midst of cold motifs, compared to the same hot motif amongst other hot motifs. This contextual dependence of AID’s ability to edit its substrate DNA sequence may have implications on how AID process on-target mutations within the V-gene or off-target mutations outside ^17–20.

While mathematical models that can be used to decipher the diversity of the mutation libraries generated by AID on ssDNA have been developed in our previous work ^15–16, we were unable to directly address how the scanning behavior of AID could be altered by the substrate sequence even though single-molecule studies show evidence that AID tends to “hover” around hot motifs when it scans its substrate DNA¹¹. In this paper, we will address this question in detail using an information theoretic analysis. On a target DNA sequence composed of a contiguous sequence of trinucleotide motifs, e.g. …NNC NNC NNC… , where N is any non-C nucleotide, the action of AID produces random mutations at the C sites. Using “1” to represent a mutated C and “0” an unmutated C, the action of AID on this DNA sequence generate random binary words of length L, where L is the number of trinucleotide motifs on the sequence. While the total number of possible words generated via this stochastic process is 2^L, the observed number of words is usually far fewer. The information content contained in the library can be measured by its entropy. In this paper, we present an information theoretic analysis of these mutant libraries and use it to derive insights into the origin of the contextual dependence of the observed mutations on inhomogeneous DNA target sequences with mixed hot-hot and hot-cold motifs. Combined with a mathematical analysis of how the entropy of the library is controlled by the scanning mobility of AID, this information theoretic analysis provides confirmation that the scanning of AID is in fact preferentially focused around hot motifs.

2. Libraries of Mutated DNA Sequences and Their Information Entropy

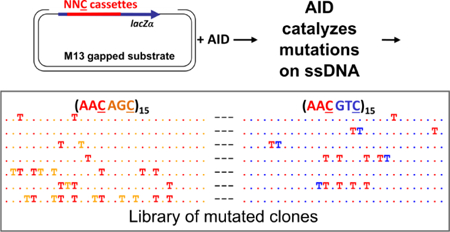
Figure 1 illustrates the experimental setup and the process by which mutant DNA sequences are generated by AID on its target DNA. A ssDNA “cassette” is inserted into a lacZα reporter gene on a gapped M13 substrate and cloned. After the clones are incubation with AID for different time intervals, the sample is quenched and the mutated clones sequenced. C→U deaminations on the mutated clones are then scored as Ts. Figure 1A shows several examples of the random binary words found in this library, with “T” mapping to “1” and “.” to “0”. Figure 1C shows histogram of C→U mutations on a (AAC AGC)₁₅-sss-(AAC GTC)₁₅ cassette across all clones in a library collected over incubation times ranging from 15 to 120 seconds, where s is a silent trinucleotide motif. The relative mutation efficiency of AID on AAC:AGC:GTC is approximately 5:3:1, and the variations in the intrinsic mutation rates of AID on these motifs are shown as a function of sequence position in Fig. 1B.

FIGURE 1.

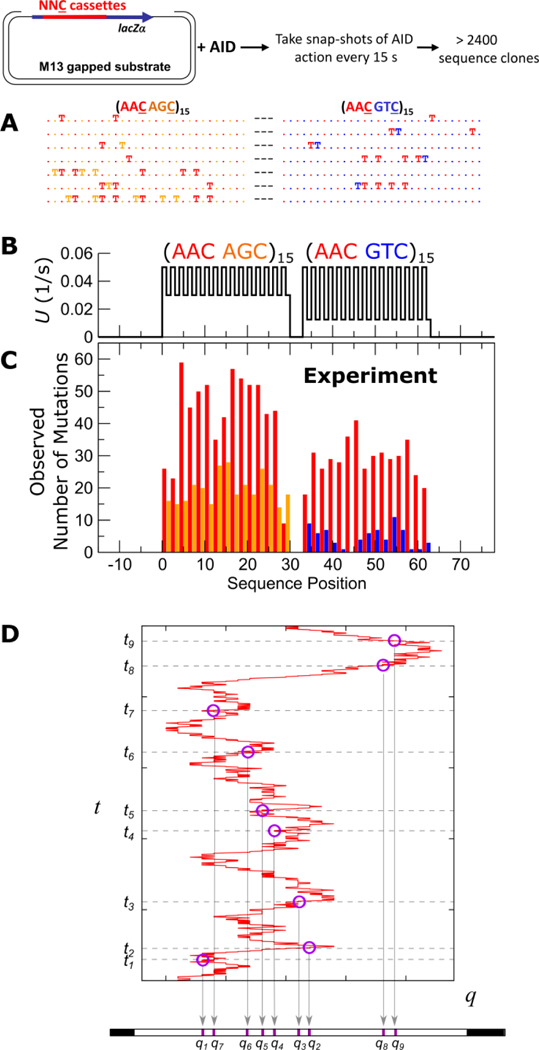
Experimental setup and results. (A) Deamination assay reports AID-catalyzed deaminations on target cassette with multiple trinucleotide motifs NNC embedded in lacZα reporter gene, and examples of mutation patterns where each “T” indicates a C→U mutation. (B) Intrinsic deamination rates for each trinucleotide motif in the (hot hot’)-(hot cold) cassette consisting of a (AAC AGC)₁₅-sss-(AAC GTC)₁₅ sequence. (C) Per-site mutation frequencies observed in experiments. The hot motifs (red) are hotter when amongst hot’ motifs (orange) than amongst cold motifs (blue). (D) A hypothetical path and a set of deamination events along this path, illustrating how the convolution between the scanning dynamics and catalysis of AID generates mutant DNA.

Figure 1D explains how each mutated clone is derived from the convolution of the scanning and enzymatic actions of AID. The red path shows a hypothetical scanning trajectory of AID along its single-stranded substrate DNA. The motif sequence is mapped onto a one-dimensional coordinate q, and the vertical axis indicates time t. Binding occurs at time 0, and then catalytic deaminations occur at times t₁, … t₉. The mutated clone resulting from this sequence of scanning + catalytic events are depicted at the bottom of Fig. 1D, where the deaminations have been deposited at positions q₁, … q₉, generating a binary word with 9 bits set to “1” while the rest remain “0”. The scanning trajectory, the number of mutations, as well as the times at which they occur are random and they are different for every clone, each generating a distinct random binary word w. The entropy of the entire library, in units of bits, is given by:

$$h=-{\sum }_{w}P\left(w\right)\times lo{g}_2\left[P\left(w\right)\right],$$ (1)

where P(w) is the normalized probability that word w shows up in the library. The entropy density, $\overline{h}\equiv h/L$, where L is the length of the word in bits, defines the information content contained in the library^21–22. The unit of $\overline{h}$ is bits of information content per bit of word length. A library with entropy density $\overline{h}=0$ contains no surprises, i.e. it holds only a single word and the library contains no useful information. On the other hand, a library with entropy density $\overline{h}=1$ contains every one of the 2^L possible words of length L, and with every word showing up with equal probability.

We now derive a formula for the entropy of the library, based on the assumptions that: (1) scanning is diffusive, (2) deamination is a Poisson process, and (3) the substrate is homogeneous, with tandem repeats of identical motifs. Using Fig. 1D as an illustration, we see that along this particular scanning trajectory, mutations are deposited at times (t₁, t₂, t₃, … t₉) when the path hits positions (q₁, q₂, q₃, … q₉). While this is just one path, there are a multitude of many other paths that could have hit the same set of positions (q₁, q₂, q₃, … q₉) at the same points in time (t₁, t₂, t₃, … t₉). The total measure of this subset of paths that cross the specific positions (q₁, q₂, q₃, … q₉) at times (t₁, t₂, t₃, … t₉), out of all possible scanning paths, is proportional to a product of eight diffusion “propagators”:

$${\mathrm{\Omega }}_9\left({\mathrm{q}}_1,{\mathrm{q}}_2,\cdots {\mathrm{q}}_9;{\mathrm{t}}_1,{\mathrm{t}}_2,\cdots {\mathrm{t}}_9\right)=K\left(q_1,q_2;t_2-t_1\right)\times K\left(q_2,q_3,t_3-t_2\right)\times \cdots K\left(q_8,q_9;t_9-t_8\right)$$ (2)

where propagator K is the Green function of a 1-dimensional diffusion equation,

$$K\left(q,q^{\prime };t^{\prime }-t\right)=\{\begin{array}{cc}{\left(4\pi D\left(t^{\prime }-t\right)\right)}^{-1/2}\text{exp}\left[-\frac{{\left(q^{\prime }-q\right)}^2}{4D\left(t^{\prime }-t\right)}\right],& t^{\prime }\ge t\\ 0,& t^{\prime }<t\end{array}$$ (3)

and D is the diffusion coefficient. Generalizing this, if there are n catalytic events occurring at times (t₁, t₂, … t_n) and at positions (q₁, q₂, … q_n), the total measure of these paths should be:

$${\mathrm{\Omega }}_n\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};{\mathrm{t}}_1,\cdots {\mathrm{t}}_{\mathrm{n}}\right)={\prod }_{i=1}^{n-1}K\left(q_i,q_{i+1};t_{i+1}-t_i\right).$$ (4)

As a stochastic process, reactions catalyzed by a processive enzyme should follow Poisson statistics. If the substrate consists of a homogeneous sequence of trinucleotide target motifs, AID will process every motif equally probably with the same catalytic efficiency. Therefore, while AID is moving around on the substrate and coming across different motifs along its scanning trajectory, deamination events anywhere on this substrate remain strictly a time-homogeneous Poisson process, and the waiting time between any two sequential deamination events i and i+1 should be weighted by an exponential distribution with a time constant equal to the reciprocal of the mean deamination rate U, i.e. U exp[−U(t_i+1−t_i)]. Applying these waiting time distributions to the probability in Eq.(4) and integrating over all event times gives the following time-ordered convolution integral:

$$\begin{gathered} {\mathrm{\Pi }}_{\mathrm{n}}\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};\mathrm{t}\right)=U^{n+1}{\int }_0^t\mathrm{d}{t}_1{\int }_{t_1}^t\mathrm{d}{t}_2\cdots {\int }_{t_n}^t\mathrm{d}{t}_n{e}^{-U{t}_1}K\left(q_1,q_2;t_2-t_1\right) e^{-U\left(t_2-t_1\right)}\times \\ \cdots \times K\left(q_{n-2},q_{n-1};t_{n-1}-t_{n-2}\right)e^{-U\left(t_n-t_{n-1}\right)}K\left(q_{n-1},q_n;t_n-t_{n-1}\right)e^{-U\left(t-t_n\right)}, \end{gathered}$$ (5)

and collecting all the exponential factors in Eq.(5) simplifies this to:

$${\mathrm{\Pi }}_{\mathrm{n}}\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};\mathrm{t}\right)=U^{n+1}{e}^{-Ut}{\int }_0^t\mathrm{d}{t}_1{\int }_{t_1}^t\mathrm{d}{t}_2\cdots {\int }_{t_n}^t\mathrm{d}{t}_n{\mathrm{\Omega }}_n\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};{\mathrm{t}}_1,\cdots {\mathrm{t}}_{\mathrm{n}}\right).$$ (6)

Eq.(6) specifies the measure for the set of all paths with n time-ordered mutations at positions (q₁, q₂, … q_n) until AID unbinds from the DNA at time t (or until the experiment is terminated after a certain incubation time). Averaging over an exponential distribution of bound times u exp(−ut) where u is the unbinding rate constant finally yields:

$${\tilde{\mathrm{\Pi }}}_{\mathrm{n}}\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};u,U\right)=u{U}^{n+1}{\int }_0^{\infty }dt e^{-\left(u+U\right)t}{\int }_0^t\mathrm{d}{t}_1{\int }_{t_1}^t\mathrm{d}{t}_2\cdots {\int }_{t_n}^t\mathrm{d}{t}_n{\mathrm{\Omega }}_n\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};{\mathrm{t}}_1,\cdots {\mathrm{t}}_{\mathrm{n}}\right).$$ (7)

Eq.(7) suggests that the effect of the enzymatic actions of AID on the scanning paths is equivalent to taking a Laplace transform with the unbinding + catalytic rate u+U as the Laplace variable, and since the integral in Eq.(7) is a convolution, the Laplace transform ${\tilde{\mathrm{\Pi }}}_{\mathrm{n}}\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};u,U\right)$ can be computed using the convolution theorem, giving:

$${\tilde{\mathrm{\Pi }}}_{\mathrm{n}}\left({\mathrm{q}}_1,\cdots {\mathrm{q}}_{\mathrm{n}};u,U\right)=\frac{u{U}^{n+1}}{{\left(u+U\right)}^2}\tilde{K}\left(q_1,q_2;u+U\right)\tilde{K}\left(q_2,q_3;u+U\right)\cdots \tilde{K}\left(q_{n-1},q_n;u+U\right),$$ (8)

where

$$\tilde{K}\left(q,q^{\prime };s\right)=\frac{1}{2\sqrt{\mathrm{s}\mathrm{D}}}{e}^{-\left|q-q^{\prime }\right|\cdot \sqrt{s/D}},$$ (9)

is the Laplace transform of the diffusion propagators $K\left(q,q^{\prime };t\right)$ in Eq.(3).

Eq.(8) gives the total measure of all paths with n time-ordered mutations deposited on the substrate at motifs (q₁, q₂, … q_n). These paths all generate the same binary word with “1” bits at positions (q₁, q₂, … q_n). But any other trajectory making the same mutations but deposited with a different time ordering will also generate the identical word. Therefore, the total probability of this word must be obtained by summing over all possible permutations $\mathcal{P}$ over $\left(q_1,q_2,\cdots q_n\right)$, yielding:

$$P\left(w\right)=\sum {\mathcal{P}}_{\left(q_1,q_2,\cdots q_n\right)\to \left(y_1,y_2,\cdots y_n\right)}{\tilde{\mathrm{\Pi }}}_{\mathrm{n}}\left(y_1,\cdots y_{\mathrm{n}};u,U\right).$$ (10)

Every $\tilde{K}$ factor, according to Eq.(9), contains an exponential function of the distance between two temporally sequential mutations, scaled by the correlation length:

$$\lambda \equiv \sqrt{D/\left(u+U\right)}.$$ (11)

On a homogeneous DNA substrate, this would be the only relevant length in the system. From experiments and previous analyses ^{9, 15}, the deamination rate U ~ 1/35 s, the unbinding rate u ~ 1/125 s and the diffusion coefficient D on a homogeneous AGC repeat cassette ~ 6.9 (motif)²/s. With these parameters, the correlation length comes out to be λ ~ 14 motifs. From Eq.(11), we see that the correlation length is a metric for the diffusion rate, and slower diffusion leads to a shorter correlation length. This also implies that extremely long words with “1”s very far apart are exponentially suppressed. In general, the length of a word should be of the order of λ. Previous experiments with AID acting on ssDNA with the IgV gene sequence suggested a correlation length consistent with this estimate ²³.

3. Stochastic Model of AID and Its Quantum Isomorphism

In a previous paper ¹⁶, we have constructed a stochastic model to describe the scanning + catalytic dynamics of AID. The diffusion of AID along its substrate is described by a scan matrix W, whose elements $W_{q{q}^{\prime }}$ give the random walk transition rates between motifs q and q’. If we represent the state of the system by a ket $|q\rangle$, which specifies the current position of AID on the substrate, then $|q^{\prime }\rangle \langle q^{\prime }|\mathbf{W}|q\rangle \langle q|$ creates a transition from state $|q\rangle \to |q^{\prime }\rangle$. The master equation that describes the diffusive scanning motions AID executes on the substrate is formally equivalent to the Bloch equation:

$$\frac{d}{dt}|\mathrm{\psi }\left(t\right)\rangle =-\mathbf{H}|\mathrm{\psi }\left(t\right)\rangle ,$$ (12)

with t corresponding to the inverse temperature 1/k_BT in a quantum statistical mechanical system, and H = W serves the function equivalent to a translational Hamiltonian. We assume W is a Toeplitz matrix, i.e. W_ij is a function of |i − j| only. As such, the random walk dynamics of AID is implicitly taken to be uniform along the entire sequence. If this was not the case, additional site-dependent energy terms must be incorporated into the Hamiltonian to ensure that the steady-state fluxes are consistent with the equilibrium distribution. We assume no energetic differences among all the sites.

When motifs on the substrate are mutable, to completely specify the state of the system, we must supplement the state descriptor by also specifying the state of each of the motifs on the sequence, indicating whether it has been mutated or not. For this purpose, we assign a spin-1/2 label σ_i to the motif at position i. If motif i has been deaminated, σ_i = |↑〉; otherwise, σ_i = |↓〉. For a sequence with L motifs, the dimensionality of the state descriptor is L + 1: one variable specifying the position of AID and L variables specifying the spin states of all motifs, i.e. $|\mathrm{\psi }\rangle =|q\rangle |{\sigma }_1\rangle |{\sigma }_2\rangle \dots |{\sigma }_L\rangle$.

To completely describe the action of AID on the substrate, we add mutation terms to the scan matrix W to construct the final Hamiltonian:

$$\mathbf{H}=-\mathbf{W}-\sum _{i=1}^L{U}_i|q_i\rangle \langle q_i|{\left[{\mathbf{\sigma }}_x\right]}_i -b\sum _{i=1}^L{\left[{\mathbf{\sigma }}_z\right]}_i$$ (13)

where U_i is AID’s catalytic rate on target motif i, [σ_x]_i and [σ_z]_i are Pauli matrices acting on the spin on motif i, and b is a sufficiently large bias to suppress reverse mutations. Starting with an initial state where all spins are down, the wavefunction $|\mathrm{\psi }\left(t\right)\rangle$ evolves according to the Block equation, flipping spins as AID traverse the substrate sequence by random walk motions. The evolution of the isomorphic quantum system under the action of the Hamiltonian in Eq.(13) is equivalent to the stochastic dynamics of AID as it scans its substrate to deposit mutations on ssDNA. Exploiting this quantum isomorphism offers two advantages. First, the isomorphic quantum system provides insights into the stochastic dynamics of the scanning and catalysis of AID. Second, it provides a straightforward simulation approach for studying a fairly complex problem, via standard path integral Monte Carlo methods ²⁴. While path integral simulations should produce the same numerical solution to the Bloch equation (12) when treated as a stochastic differential equation, we have also shown that intricate conceptual issues could arise in the proper construction of the models, and the use of path integrals helped circumvent these problems ¹⁶.

Figure 2B shows results from path integral Monte Carlo simulations of the isomorphic quantum model on a mixed (hot-hot’)-(hot-cold) cassette corresponding to the (AAC AGC)₁₅-sss-(AAC GTC)₁₅ sequence studied in the experiments summarized in Fig. 1. The mutations spectrum derived from the simulations is consistent with the experimental results, showing that the activity of the same AAC hot motif is hotter when they are amongst hot’ AGC motifs, but colder when they are amongst cold GTC motifs (see Fig. 1B, for AID’s intrinsic catalytic rates on AAC vs. AGC vs. GTC). This apparent contextual dependence of the catalytic activity of AID is peculiar, considering that in the Hamiltonian in Eq. (13), the scan matrix W is Toeplitz and contains no explicit site-dependence. The underlying assumption in the model is that there is no difference in the intrinsic random walk characteristics no matter where AID is along the substrate sequence. As a result, it is somewhat unclear why the mutation frequencies are higher on the left side of the cassette. In the simulations, we can track the footprints of AID (whereas in the experiments we cannot). Figure 2A shows the probability of where AID is found on the substrate as a function of sequence position. Clearly, while the intrinsic scanning dynamics of AID is identical on both the left and right sides of the cassette, AID lingers on the left side more than the right.

FIGURE 2.

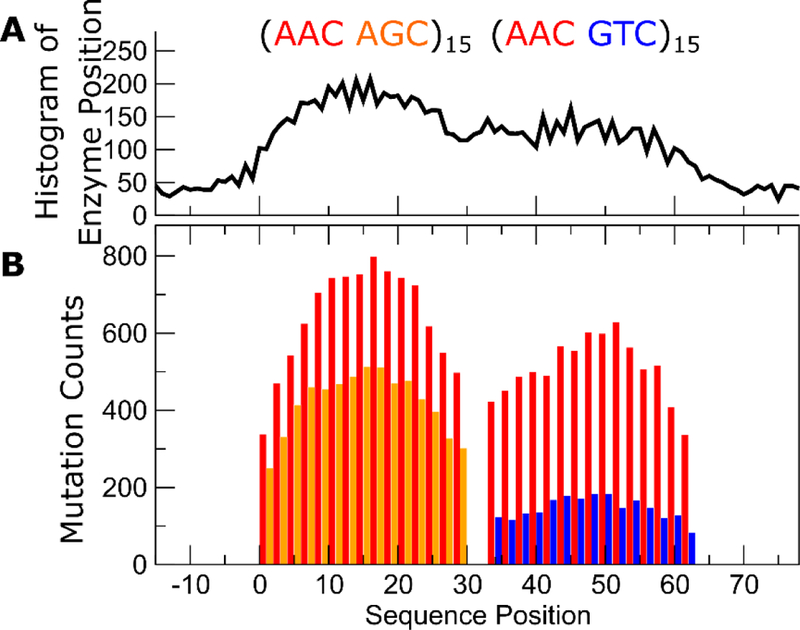
Results from Monte Carlo path integral simulations on a (hot hot’)-(hot-cold) mixed cassette. (A) Footprints of AID on the sequence. (B) Observed per-site mutation frequencies, showing similar contextual dependence observed in the experiments shown in Fig. 1.

One way to understand this contextual dependence of the deamination spectrum is to draw on the quantum isomorphism in Eq.(13). In quantum mechanics, applying a measurement to a system forces it into an eigenstate of the measurement operator. In the Hamiltonian in Eq.(13), the first term containing W disperses $|q\rangle$, because the eigenstates of a Toeplitz operator are Fourier waves. But the second term ${\sum }_{i=1}^L{U}_i|q_i\rangle \langle q_i|{\left[{\mathbf{\sigma }}_x\right]}_i$ localizes $|q\rangle$ because AID cannot deposit a mutation on motif i unless it is sitting on i. Repeated application of this term would persistently put $|q\rangle$ back into a localized state. The frequency of this is controlled by the mutation rates U_i. AID is therefore localized on hot motifs preferentially over cold ones, and the higher the density of hot motifs, the more AID will concentrate its presence in that region. The is consistent with the footprints of AID seen in Fig. 2A.

The scanning dynamics and catalysis of AID are of course completely classical. But the dynamics, however, are equivalent to the statistical mechanics of a quantum system. Because of this, we can invoke the measurement theorem in quantum mechanism to understand why AID shows a contextual dependence in its catalytic activities. From the point of view of the classical master equation, the best way to understand this phenomenon is to recognize that when AID is scanning, it cannot process mutations, and when it is catalyzing a deamination on the motif it sits on, it cannot scan. There is a competition between these two processes, one of which disperses while the other localizes. On hot sites where the catalytic rate is high, catalysis is favored, and AID is therefore preferentially localized to those sites.

4. Entropy Dispersion and Diffusion Rate

While we cannot directly observe how AID scans each clone DNA in the experiment, the experiment is in fact providing single-molecule information, albeit indirectly, about the scanning + catalytic activities of AID. The mutation pattern on each clone contains a record of the footprints of AID while it was bound to that substrate, and because AID is processive, every word in the clone library is indeed the result of a single-molecule experiment. While the clone library does not allow us to directly observe how AID scans its substrate DNA, correlations between the “1” bits in the generated random binary words do yield clues about how fast AID is scanning according to Eq.(11). And this information can be retrieved from the entropy content of the library.

To understand this, we have carried out large-scale path integral Monte Carlo simulations of the model in Eq.(13). Libraries of much larger sizes can be generated by simulations in comparison to experiment. Simulation results for a mixed (hot-hot’)-(hot-cold) cassette corresponding to the (AAC AGC)₁₅-sss-(AAC GTC)₁₅ have already been shown in Fig. 2 above. Figure 3 now shows results from simulations on another mixed (hot-hot’)-(hot-frigid)-(hot-frigid) cassette consisting of the 96-motif sequence (AAC AGC)₁₅-sss-(AAC GAC)₁₅-sss-(AAC GAC)₁₅ flanked by 15 silent motifs on both ends. The simulated library contains 30,000 clones. Figure 3B shows mutation frequencies across all clones as a function of sequence position. Similar to the contextual effects observed in both experiments and simulations for the (hot-hot’)-(hot-cold) cassette, in this (hot-hot’)-(hot-frigid)-(hot-frigid) cassette, the hot motifs are hotter when they are amongst other hot motifs. The clones are collected from samples corresponding to incubation times of 5, 10, 15, 20, 30, 45 and 60 s. The majority of these clones (45% of the library) have single mutations, but many have more than one. While the histogram in Fig. 3B counts all mutations from all clones in the library, the majority comes from clones with single mutations. But only clones with more than one mutation can form nonnull words longer than one bit, and if the mutations on a clone with multiple mutations are correlated the length of the word is also limited. Faster diffusion of AID leads to longer words, and slower diffusion to shorter ones. Figure 3A confirms that the footprints of AID are indeed concentrated on the left side of the cassette.

FIGURE 3.

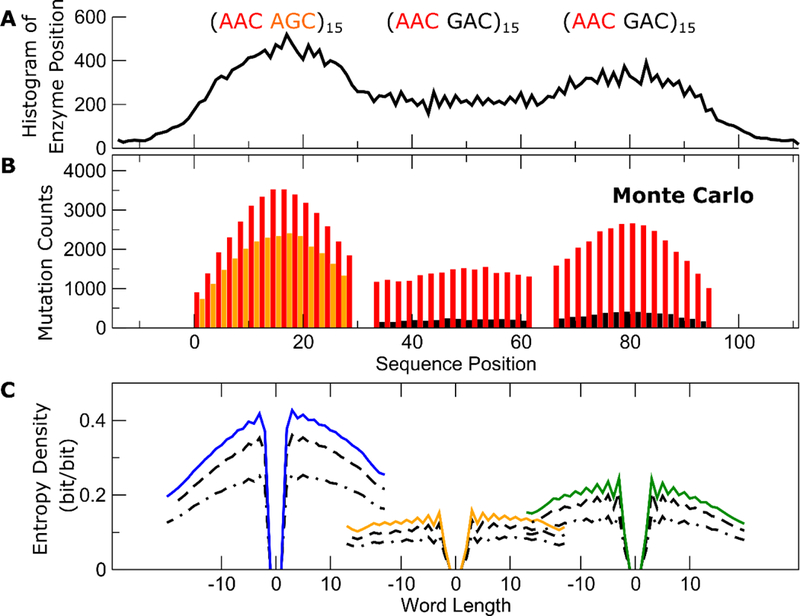
Results from Monte Carlo path integral simulations on a (hot hot’)-(hot frigid)-(hot frigid) cassette. (A) Footprints of AID on the sequence. (B) Observed per-site mutation frequencies. (C) Far left: Entropy densities of a word starting at the center of the (hot hot’) region going to the right (5’ to 3’) or the left (3’ to 5’) as a function of word length. Blue solids lines are results for a 60 s incubation time. Dashed and dotted dashed lines are for 30 s and 15 s, respectively. Middle: Orange line shows entropy densities of words staring at the center of the (hot frigid) region in the middle of the cassette for incubation times of 60 s (solid orange), 30 s (dashed) and 15 s (dotted dashed). Far right: Green line, dashed and dotted dashed line show entropy densities of words staring at the center of the (hot frigid) region on the far right of the cassette after 60 s, 30 s and 15 s, similar to the other two panels. The length of the word is shortest on the far right, indicating that AID’s diffusion is slow there. In the middle of the cassette, correlations among mutations are weak generating long words, suggesting that AID’s diffusion is fast here.

While the results in Fig. 3A and B suggest that AID may indeed be scanning around hot motifs preferentially over cold ones, determining the diffusion rate of AID requires measuring its displacements over the sequence, and ensemble average properties like those in Fig. 3A and B cannot provide direct information on the diffusion rate of AID. To extract this information from the experiments and simulations, we turn to entropy of the library. The analyses in Sect. 2 demonstrate how the entropy of the mutated clone library is related to the diffusion coefficient of AID. Figure 4 shows the entropy density, in units of bits of information per bit of word length, from the simulation reported in Fig. 3, as a function of the starting position of the word and the length of the word, going in the 5’ to 3’ direction after an incubation period of 60 s. In general, the information content of longer words tends to be lower, because the “1” bits corresponding to mutations are correlated. However, the decay of this correlation as a function of word length appears to be different on different segments on the cassette. In the region containing the (hot-hot’) motif sequence on the left, the entropy density decays faster with word length, in comparison to the middle of the cassette containing the (hot-frigid) motif sequences, where the decay is barely noticeable.

FIGURE 4.

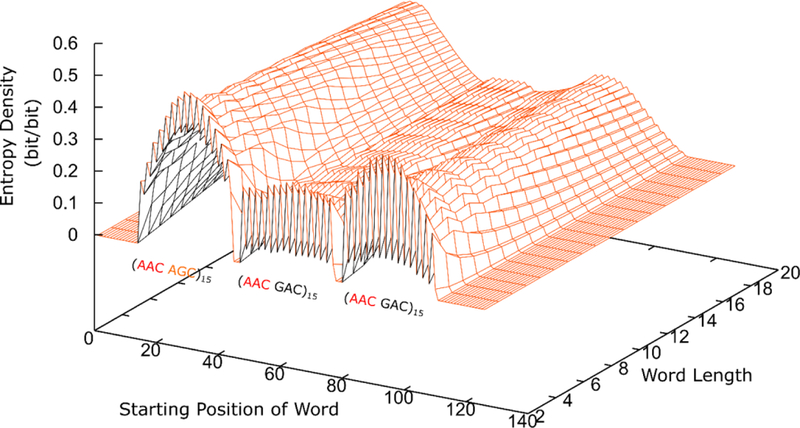
Entropy density obtained from the simulation results for the (hot hot’)-(hot frigid)-(hot frigid) cassette, in units of bits of information divided by the length of the word read in the 5’ to 3’ direction, for words of different lengths and at different starting positions along the sequence. In the middle of the cassette where the (hot frigid) cluster is, the entropy shows almost no dependence on word length, indicating that long words are preferentially generated here due to the fast diffusion of AID.

Figure 3C shows a more detailed view of how the entropy density in different regions depends on the length of the word. To specifically look at the correlation between mutations, the entropy density shown in Fig. 3C were computed using the conditional probability, given that the first bit of the word is already known. In this way, we are interrogating whether the rest of the word is sensitive to the identity of the first bit. Figure 3C shows how this entropy density decays as a function of word length, going to the right (5’ to 3’ direction) using positive values for the lengths, and going to the left (3’ to 5’ direction) using negative values for the lengths, for three different positions on the sequence, corresponding to the center of the (hot-hot’) (AAC-AGC)₁₅ cluster on the left (blue lines), the center of the (hot-frigid) (AAC-GAC)₁₅ cluster in the middle (orange lines) and the center of the other (hot-frigid) cluster on the right (green lines). The colored lines corresponding to an experiment 60 s in duration, whereas the dashed lines and the dotted dashed lines correspond to 30 and 15 s, respectively. In general, the entropy density increases with time as the mutations build up over the course of the experiment, generating words of increased diversity. But as a function of the length of the words, the entropy density always decreases as the words gets longer, once again indicative of correlations among the “1” bits. These correlations limit the diversity of longer words. As words get longer, the decay in information content as a function of the word length is a functional measure of the diffusion rate of AID.

The orange lines in the middle of the cassette in Fig. 3C show that going in either direction (5’ to 3’ or 3’ to 5’) the entropy density shows almost no decay. This is also reflected in the relatively flat region in the middle of the surface plot in Fig. 4. Based on this, we conclude that the diffusion rate of AID in the (hot-frigid) region in the middle of the cassette must be quite fast, and the random words generated in this region on the cassette are rather long. But the overall information content of the library coming from this region is also low, because the overall deamination rate is slowest here, resulting in words with mostly “0”s. On the other hand, the blue lines on the left of the cassette in Fig. 3C show that the entropy density decays much faster with word length on the left of the cassette, suggesting that AID diffuses slower in this region. There is also a slight asymmetry in the blue lines, with the decay in the 3’ to 5’ direction slightly faster than in the 5’ to 3’ direction, suggesting that diffusion on the left is somewhat slower than on the right. The overall information content originating from this region of the cassette is high, because the mutation intensity in this region is the strongest, generating words of higher diversity here. Finally, on the far right of the cassette, the word-length dependence of the green lines indicate that diffusion of AID is slower there than in the middle, but faster compared to the far left.

Figure 5 shows the same analysis now applied to experimental clone data. This experimentally obtained library consisted of just 383 clones, and the statistical quality of the data are inferior to the simulations. However, the same contextual dependence in the deamination rates are observed in the experiments as shown in Fig. 5A, where the AAC hot motifs are hotter amongst other hot motifs, compared to when they are amongst GAC frigid motifs. When examining how the entropy density decay as a function of word length, Fig. 5B reveals a similar behavior in the experiments as predicted by the Monte Carlo simulations. The diffusion rate of AID on the far left of the cassette is slowest, whereas it is fastest in the middle of the cassette.

FIGURE 5.

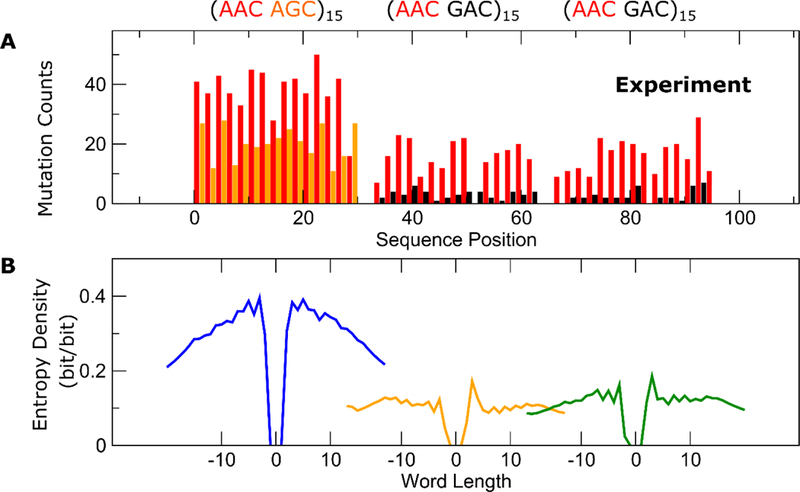
Experimental results corresponding to the cassette studied by the simulations shown in Fig. 3. (A) Per-site mutation frequencies. (B) Decay of entropy density as a function of word length, for words centered at the center of the (hot hot’) cluster on the far left (blue), the middle (orange) and the far right (green). Consistent with the simulations, the words are shortest on the far left, suggesting that AID diffusion is slowest here, while the words are longest in the middle of the cassette, indicating that AID diffusion is fastest there.

5. Conclusions

We have developed an information theoretic approach to analyze the information content contained in mutated clone libraries generated by the action of AID on ssDNA sequences. Interpreting the mutation patterns as random binary words, the scanning + catalysis dynamics of AID on its substrate DNA forms a stochastic signal source, and using the entropy as a metric we related the lengths of the randomly generated words to the diffusion constant D and the rates of AID catalysis U and unbinding u to derive a characteristic length for the library $\lambda \equiv \sqrt{D/\left(u+U\right)}$. This enables us to use the word-length dependence of the entropy in the experimental clone libraries to infer the diffusion rate of AID on different DNA substrate sequences. We found that target motifs have an elevated level of deamination activities when they are among other hot motifs. The analysis suggests that AID’s scanning is attracted to regions on the DNA sequence with a higher density of hot motifs. Exploiting an isomorphism between this system and a quantum statistical mechanical model, we show how the localization of AID to these regions can be understood by the measurement theorem in quantum mechanics. Monte Carlo path integral simulations based on this isomorphic quantum system are consistent with the experimental observables, providing validation to how the length scale of the generated mutation patterns in the clone libraries could be used to interrogate the scanning activities of AID on its substrate DNA.