Differential methylation values in differential methylation analysis

Abstract

Motivation

Both $\beta$-value and M-value have been used as metrics to measure methylation levels. The M-value is more statistically valid for the differential analysis of methylation levels. However, the $\beta$-value is much more biologically interpretable and needs to be reported when M-value method is used for conducting differential methylation analysis. There is an urgent need to know how to interpret the degree of differential methylation from the M-value. In M-value linear regression model, differential methylation M-value $\Delta$M can be easily obtained from the coefficient estimate, but it is not straightforward to get the differential methylation $\beta$-value, $\Delta \beta$ since it cannot be obtained from the coefficient alone.

Results

To fill the gap, we have built a bridge to connect the statistically sound M-value linear regression model and the biologically interpretable $\Delta \beta .$ In this article, three methods were proposed to calculate differential methylation values, $\Delta \beta$ from M-value linear regression model and compared with the $\Delta \beta$ directly obtained from $\beta$-value linear regression model. We showed that under the condition that M-value linear regression model is correct, the method M-model-coef is the best among the four methods. M-model-M-mean method works very well too. If the coefficients ${\alpha }_0,\mathrm{ }{\alpha }_2,\dots {\alpha }_p$ are not given (as ‘MethLAB’ package), the M-model-M-mean method should be used. The $\Delta \beta$ directly obtained from $\beta$-value linear regression model can give very biased results, especially when M-values are not in (−2, 2) or $\beta$-values are not in (0.2, 0.8).

Availability and implementation

The dataset for example is available at the National Center for Biotechnology Information Gene Expression Omnibus repository, GSE104778.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Changes in DNA methylation patterns play a critical role in the organ development, aging and diseases such as multiple sclerosis, diabetes, schizophrenia and cancer (Laird, 2010). Advances in the high-throughput assessment of DNA methylation have enabled quantitative profiling of DNA methylation of CpG loci throughout the genome, which is crucial to understand the role of epigenetics in regulating gene expression. The microarray-based Infinium HumanMethylation27 BeadChip, the Infinium HumanMethylation450 BeadChip and the newly developed MethylationEPIC BeadChip (Infinium) microarray (850k) (Moran et al., 2016; Sandoval et al., 2011; Thirlwell et al., 2010) are widely used commercial platforms for low-cost high-throughput methylation profiling. Both $\beta$-value and M-value have been used as metrics to measure methylation levels. $\beta$-value is defined as:

$$\beta =\frac{\max \left(methylated,\mathrm{ }0\right)}{\left(max\left(methylated,\mathrm{ }0\right)+\mathit{max}\left(unmethylated,\mathrm{ }0\right)+\alpha \right)},$$

where $methylated$ and $unmethylated$ are intensities measured by the methylated and unmethylated probes for an interrogated CpG site and a constant offset $\alpha$ (by default, $\alpha =100)$ is added to regularize $\beta$-value when both methylated and unmethylated probe intensities are low (Du et al., 2010). The standardized fraction, i.e. the M-value is defined as

$$M={\text{log}}_2\left(\frac{\beta }{1-\beta }\right).$$

While the M-value is more statistically valid for the differential analysis of methylation levels because the M-value is approximately homoscedastic (the $\beta$-value has severe heteroscedasticity outside the middle methylation range, which imposes serious challenges in applying many statistic models) (Du et al., 2010), the $\beta$-value is much more biologically interpretable, because it corresponds roughly to the percentage of a site that is methylated, which makes the $\beta$-value very attractive when modelling the underlying biological effect (Du et al., 2010).

Saadati et al. (2014) examined parametric methods, such as linear and beta regression, and nonparametric methods, such as rank-based regression. They found that the use of $\beta$-values in a beta regression setting may be of benefit, but only if the underlying distribution of the $\beta$-values is indeed the beta distribution, which requires that the methylated and unmethylated signal intensities are independently gamma distributed with the same scale parameter. Beta regression model seems very susceptible to the violation of the beta distribution assumption and may show an uncontrolled false discovery rate. By allowing for possible correlations between the methylated and unmethylated signal intensities, Weinhold et al. (2016) proposed the Ratio of Correlated Gammas (RCG) model and showed the large benefit of RCG model when the correlation is high. However, when the correlation is low (ρ = 0.2), the Type I error exceeds the nominal level of significance, 0.05 in all of their simulations. Currently, the M-value linear regression model is one of the most popular models in the analysis of DNA methylation data. In this article, we focus on M-value linear regression model.

Du et al. (2010) compared $\beta$-value and M-value approaches and demonstrated that the relationship between the $\beta$-value and M-value methods is a Log-transformation.

$$M(\beta )=lo{g}_2\left(\frac{\beta }{1-\beta }\right), \beta (M)=\frac{2^M}{1+2^M}.$$

They showed that the $\beta$-value method has severe heteroscedasticity for highly methylated or unmethylated CpG sites and recommended using the M-value method for conducting differential methylation analysis and including the $\beta$-value statistics when reporting the results to investigators.

In M-value linear regression model (see the next section for details), differential methylation value, $\Delta$M can be easily obtained from the coefficient estimate, however, it is not straightforward to get the differential methylation $\beta$-value, $\Delta \beta$ since it cannot be obtained from the coefficient alone (see the methods below). Due to this reason, some investigators usually run both M-value linear regression model and $\beta$-value linear regression model. They use the M-value linear regression model to select the CpG sites and report the p-values, but use $\beta$-value linear regression model to report differential methylation $\beta$-value, $\Delta \beta$. This can cause inconsistent results. First, the two models have different assumptions. Second, $\Delta \beta$ can be out of the [0, 1] interval (see below for details). In this article, we suggest different methods to calculate differential methylation values, $\Delta \beta$ from M-value linear regression model and compare it with the $\Delta \beta$ directly obtained from $\beta$-value linear regression model.

The outline of this article is as follows. The four different methods (three methods from the M-value linear regression model and one from $\beta$-value linear regression model) to obtain $\Delta \beta$ are presented in Section 2. In Section 3, simulations are conducted to compare the proposed methods. In Section 4, a simple method is proposed to quickly estimate $\Delta \beta$ when M-values are in (−2, 2) or $\beta$-values are in (0.2, 0.8). Examples are given in Section 5 to illustrate the proposed methods. Section 6 discusses the implications and provides concluding remarks.

2 Materials and methods

Considering the following linear regression model:

$$\begin{array}{c}{y}_i={\alpha }_0+x_{i1}{\alpha }_1+x_{i2}{\alpha }_2+\cdots +x_{ip}{\alpha }_p+{\epsilon }_i, \\ i=1,\dots ,n,\end{array}$$ (1)

where $y_i$ is the methylation value (M-value or $\beta$-value), $x_{i1}$ is the variable of interest and $x_{i2},\dots ,x_{ip}$ are the adjusting variables (confounders) for individual $i$. If M-value ($\beta$-value) is used in (1), the model is called M-value ($\beta$-value) linear regression model. The variable of interest, $x_{i1}$ and the covariates can be categorical or continuous. This model has been implemented in R package ‘MethLAB’ although the coefficient estimates for the covariates are not available (only the coefficient estimate for the variable of interest is available, this is also the case for most common methylation packages).

2.1. M-value linear regression model

The M-value linear regression model is the model (1), where M-value is used. For this model, the differential methylation value, $\Delta$M is the coefficient estimate, ${\alpha }_1$ for 1 unit increase of the variable of interest, $x_{i1}$. Given the value for each covariate $x_{ij}=x_{0j}$ (e.g. $x_{0j}$ can be chosen as the mean of $x_{ij,}\mathrm{ }i=1,\dots ,n$), $j=1,\dots ,p$, $\Delta \beta$ can be obtained by

$$\Delta \beta =\beta \left(M_0+\Delta M\right)-\beta \left(M_0\right)$$

$$=\frac{2^{(M_0+\Delta \mathrm{M})}}{1+2^{(M_0+\Delta M)}}-\frac{2^{M_0}}{1+2^{M_0}},$$ (2)

where $M_0={\alpha }_0+x_{01}{\alpha }_1+x_{02}{\alpha }_2+\cdots +x_{0p}{\alpha }_p$. This method will be called ‘M-model-coef’ method for the rest of the article.

If the coefficients ${\alpha }_0,\mathrm{ }{\alpha }_2,\dots {\alpha }_p$ are not given (as ‘MethLAB’ package (Kilaru et al. 2012)), $M_0$ can be chosen as the mean of methylation M-value, which will be called ‘M-model-M-mean’ method. $M_0$ might also be chosen as

$$M_0=M\left({\beta }_0\right)={\text{log}}_2\left(\frac{{\beta }_0}{1-{\beta }_0}\right),$$

where ${\beta }_0$ is the mean of methylation $\beta$-value. This method will be called ‘M-model-$\beta$-mean’ method.

2.2. $\mathit{\beta }$-value linear regression model

$\beta$-value linear regression model is the model (1), where $\beta$-value is used. For this model, the differential methylation value, $\Delta \beta$ is the coefficient estimate, ${\alpha }_1$ for 1 unit increase of the variable of interest, $x_{i1}$. This method will be called ‘$\beta$-model-coef’ method.

Note that the $\beta$-value has lower limit, 0 and upper limit, 1 but the right side of (1) does not have any limits. Due to this reason, the differential methylation $\beta$-value can be outside the limits if we consider many units increase of the variable of interest, $x_{i1}$.

3 Results

Simulations are conducted to compare the methods proposed in Section 2 under the condition that M-value linear regression model is correct. These simulations are not to show M-value linear regression model is better than $\beta$-value linear regression model (this work has been done by Du et al. (2010)). Linear regression model (1) with $p=1$ was used to generate the methylation M-values with sample size = 200. In the first simulation, we assume ${\beta }_0$ ($\beta$_value) = 0.05, 0.5 and 0.85 and $\Delta \beta$ = 0.1. The covariate X was generated from normal distribution with mean = 2 and standard deviation = 1. ${\alpha }_1$ and ${\alpha }_0$ were calculated by

$${\alpha }_1=\Delta M=M_0+\Delta M-M_0={\text{log}}_2\left(\frac{\Delta \beta +{\beta }_0}{1-\Delta \beta -{\beta }_0}\right)-{\text{log}}_2\left(\frac{{\beta }_0}{1-{\beta }_0}\right),$$

$${\alpha }_0=M_0-mean\left(X\right){\alpha }_1={\text{log}}_2\left(\frac{{\beta }_0}{1-{\beta }_0}\right)-2{\alpha }_1.$$

In the second simulation, we assume ${\beta }_0$ = 0.05, 0.5 and 0.75 and $\Delta \beta$ = 0.2. After M-values were generated, the β_values were calculated by

$$\beta =\frac{2^M}{1+2^M}.$$

Four methods (M-model-coef, M-model-M-mean, M-model-$\mathrm{ }\beta$-mean and $\beta$-model-coef) were performed on the generated data to estimate $\Delta \beta$ separately. We repeated 10 000 times. The bias and standard deviation (SD) were summarized in Tables 1 and 2 below.

Table 1.

$\Delta \beta$=0.1

$\beta$_value:$\mathrm{ }{\beta }_0$	M-model-coef		M-model-M-mean		M-model-$\mathrm{ }\beta$-mean		$\beta$-model-coef
	Bias	SD	Bias	SD	Bias	SD	Bias	SD
0.05	0.0002	0.0075	0.0002	0.0100	0.0640	0.0159	−0.0138	0.0094
0.5	−0.0002	0.0118	−0.0002	0.0118	−0.0002	0.0118	−0.0113	0.0103
0.85	−0.0001	0.0046	0.0001	0.0082	0.0396	0.0094	0.0581	0.0103

Table 2.

$\Delta \beta$=0.2

$\beta$_value:$\mathrm{ }{\beta }_0$	M-model-coef		M-model-M-mean		M-model-$\mathrm{ }\beta$-mean		$\beta$-model-coef
	Bias	SD	Bias	SD	Bias	SD	Bias	SD
0.05	0.0001	0.0117	0.0006	0.0216	0.1574	0.0222	−0.0532	0.0134
0.5	−0.0002	0.0106	−0.0003	0.0109	−0.0002	0.0107	−0.0297	0.0087
0.75	0.0001	0.0073	0.0005	0.0193	0.0627	0.0148	0.0577	0.0112

Based on the simulations (Tables 1 and 2), we can see the method M-model-coef is the best among the four methods. M-model-M-mean method works very well although it has a slightly larger bias and SD than M-model-coef method. It has much less bias than M-model-$\mathrm{ }\beta$-mean method (except $\beta$_value = 0.5, we will discuss this situation in the next section) and $\beta$-model-coef method. If the coefficients ${\alpha }_0,\mathrm{ }{\alpha }_2,\dots {\alpha }_p$ are not given (as ‘MethLAB’ package, Kilaru et al., 2012), M-model-M-mean should be used.

4 A simple method when M-values are in (−2, 2) or $\mathit{\beta }$-values are in (0.2, 0.8)

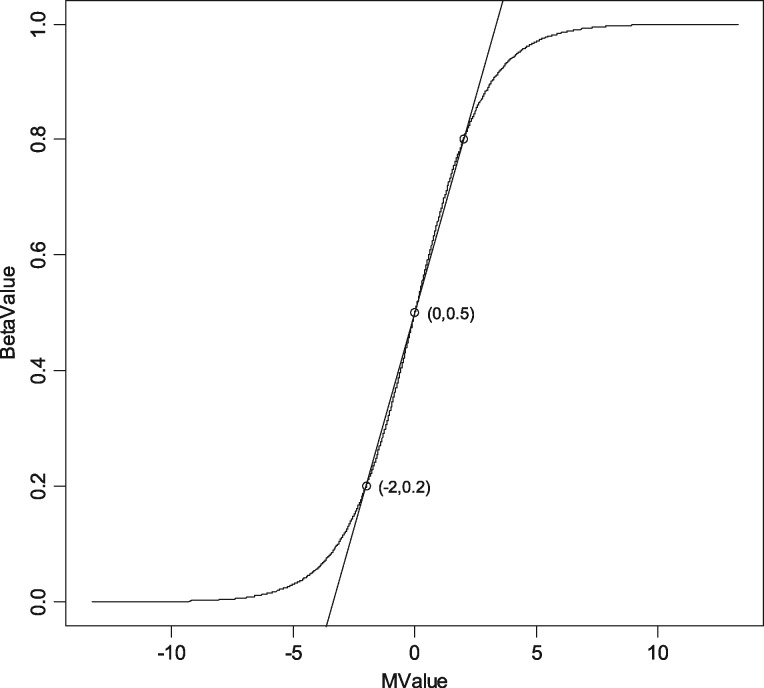
As shown in simulations above, M-model-$\mathrm{ }\beta$-mean method has a large bias, compared with M-model-coef method and M-model-M-mean method when$\mathrm{ }\beta$_value $\ne$ 0.5. However, when $\beta$_value = 0.5, M-model-$\mathrm{ }\beta$-mean method works very well. In fact, from Figure 1 above, we can see there is roughly linear relationship between M-value and $\beta$_value when M-values are in (−2, 2) or $\beta$-values are in (0.2, 0.8). Based on this approximately linear relationship, we can roughly estimate $\Delta \beta$ from the following simple formula:

$$\Delta \beta =\frac{0.6\Delta M}{4}=0.15\Delta M.$$ (3)

However, most of the methylation sites have $\beta$-values outside of (0.2, 0.8), limiting the utility and applicability of this formula.

Fig. 1.

The relationship curve between M-value and Beta-value

5 Example

In this section, we will use two real studies as examples to illustrate the methods introduced above.

The first study was to determine whether maternal, postnatal, and early childhood lead exposure can alter the differentially methylated regions (DMRs) that control the monoallelic expression of imprinted genes involved in metabolism, growth, and development (Li et al., 2016). In this study, we reported that mean blood lead concentration from birth to 78 months was associated with a significant decrease in PEG3 DMR methylation. For 1 μg/L increase of the mean blood lead concentration, $\Delta \beta$ = −0.0014117 if ‘β-model-coef’ method is used; $\Delta \beta$ = −0.0014489 if ‘M-model-coef’ method is used; $\Delta \beta$ = −0.0014491 if ‘M-model-M-mean’ method is used; $\Delta \beta$ = −0.0014495 if ‘M-model-$\mathrm{ }\beta$-mean’ method is used; $\Delta \beta$ = −0.0012782 if the simple method is used. There were no dramatic differences among all the methods in this example (note that mean $\beta$_value for PEG3 DMR methylation is 0.43, which is in (0.2, 0.8)).

The second study was to determine the association of CpG site changes with concentration of methylmercury (MeHg), major polychlorinated biphenyls (PCBs) and other organochlorine compounds (Leung et al., 2018). For this example, we only consider the association between PCB congener 105 (PCB105) and CpG site cg20619296. For 1 μg/g increase of PCB105, $\Delta \beta$ = −0.099 if ‘β-model-coef’ method is used; $\Delta \beta$ = −0.195 if ‘M-model-coef’ method is used; $\Delta \beta$ = −0.195 if ‘M-model-M-mean’ method is used; $\Delta \beta$ =−0.203 if ‘M-model-$\mathrm{ }\beta$-mean’ method is used; The simple method is not suitable for this case since the mean $\beta$_value for CpG site cg20619296 is 0.9736, which is not in (0.2, 0.8). For this example, we can see there is a large difference between ‘β-model-coef’ method and ‘M-model-coef’ method (or ‘M-model-M-mean’ method). $\Delta \beta$ given by ‘M-model-coef’ method (or ‘M-model-M-mean’ method) is almost a double of $\Delta \beta$ given by ‘β-model-coef’ method.

6 Discussion

Both $\beta$-value and M-value are commonly used to measure methylation levels. The M-value is more statistically valid for the differential analysis of methylation levels in relation to exposure x. However, the $\beta$-value is much more biologically interpretable to show how much methylation was changed. In this article, we proposed three different methods to calculate differential methylation values, $\Delta \beta$ from M-value linear regression model. Under the condition that M-value linear regression model is correct, we showed that the method M-model-coef is the best among the four methods. M-model-M-mean method works very well too. If the coefficients ${\alpha }_0,\mathrm{ }{\alpha }_2,\dots {\alpha }_p$ are not given (as ‘MethLAB’ package, Kilaru et al., 2012), the M-model-M-mean method should be used. The $\Delta \beta$ directly obtained from $\beta$-value linear regression model can give very biased results, especially when M-values are not in (−2, 2) or $\beta$-values are not in (0.2, 0.8). Note the $\beta$-value distribution across the methylome are not uniform, but more like ‘U-shape’ between 0 and 1. That means, most of the methylation sites have $\beta$-values outside of (0.2, 0.8), and the conclusion from this article can provide very valuable suggestions for better estimating the change of methylation level.