Improving protein function prediction using protein sequence and GO-term similarities

Abstract

Motivation

Most automatic functional annotation methods assign Gene Ontology (GO) terms to proteins based on annotations of highly similar proteins. We advocate that proteins that are less similar are still informative. Also, despite their simplicity and structure, GO terms seem to be hard for computers to learn, in particular the Biological Process ontology, which has the most terms (>29 000). We propose to use Label-Space Dimensionality Reduction (LSDR) techniques to exploit the redundancy of GO terms and transform them into a more compact latent representation that is easier to predict.

Results

We compare proteins using a sequence similarity profile (SSP) to a set of annotated training proteins. We introduce two new LSDR methods, one based on the structure of the GO, and one based on semantic similarity of terms. We show that these LSDR methods, as well as three existing ones, improve the Critical Assessment of Functional Annotation performance of several function prediction algorithms. Cross-validation experiments on Arabidopsis thaliana proteins pinpoint the superiority of our GO-aware LSDR over generic LSDR. Our experiments on A.thaliana proteins show that the SSP representation in combination with a kNN classifier outperforms state-of-the-art and baseline methods in terms of cross-validated F-measure.

Availability and implementation

Source code for the experiments is available at https://github.com/stamakro/SSP-LSDR.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Many algorithms have been proposed to predict Gene Ontology (GO) (Ashburner et al., 2000) terms for a protein based on defined relationships to a set of proteins already annotated with GO terms. Protein sequence is the most widely-used predictor of function. In fact, over 90% of the methods participating in the second Critical Assessment of Functional Annotation (CAFA) use sequence information (Jiang et al., 2016), by calculating either sequence similarities between proteins [e.g. ( Cozzetto et al., 2013; Gong et al., 2016; Lan et al., 2013)], or other sequence properties, such as k-mer frequencies (Cozzetto et al., 2013) and enrichment of certain sub-sequences in proteins performing a specific function (Cao and Cheng 2016). Most automatic function prediction (AFP) methods use the ‘Guilt by Association’ principle to predict annotations: assigning a GO term to a query protein if this GO term is present in proteins that are ‘similar’ to the query, by some definition of similarity. For instance, the Multi-Source-kNN (MS-kNN) method (Lan et al., 2013) applies a weighted averaging of the functions of the k proteins most similar to the query, where similarity is defined as sequence similarity, co-expression or protein–protein interaction. Other methods construct networks with proteins as nodes, where ‘similar’ proteins are connected by an edge, and annotate queries based on the functions of their neighbors in the network [e.g. (Kourmpetis et al., 2010; Youngs et al., 2013)].

An alternative view is to describe a protein with a pre-defined set of measurements (a feature vector) and use machine learning techniques to ‘learn’ which proteins perform a specific function. Choosing a meaningful feature representation for proteins is, however, not trivial. The CombFunc method (Wass et al., 2012) used different data sources to generate features, which include the lowest BLAST E-value for the query, the percent identity between the query and the top BLAST hit, the fraction of co-expressed proteins that perform a given function, etc. These features are then fed to a support vector machine (SVM) classifier. More recently, DeepGO (Kulmanov et al., 2017) used a deep neural network whose feature vectors consisted of all sub-sequences of length 3 of a protein, as well as features derived by learning an embedding of protein–protein interaction networks (Alshahrani et al., 2016).

We take a different view on defining features to represent a protein. Instead of describing the protein itself (as, e.g. DeepGO does), or extracting features from closely related proteins (BLAST hits or network-based features), we propose to use a feature representation of a protein based on its sequence similarity profile (SSP) to all annotated training proteins, known as a (dis)similarity-based representation in machine learning (Pękalska and Duin, 2002). The use of similarity-based representations of proteins in the form of an SSP was introduced by Liao and Noble for predicting protein families (Liao and Noble, 2003), but has not been used for multi-label AFP before. Although the ability to identify functional similarities decreases with decreasing sequence similarity (Wass and Sternberg, 2008), lower sequence similarity might point toward functional dissimilarity, and thus should lower the likelihood for GO terms associated with low-similarity proteins. Hence, we wanted a feature representation, like the SSP, that exploits functional relationships across all levels of similarity, and not only at high similarity, as current AFP methods do.

In addition, the CAFA benchmarks point out that especially the Biological Process ontology (BPO) is hard to predict for many species (Jiang et al., 2016). This issue is seen with many AFP algorithms and might be partly due to the nature of the GO itself. Although intuitive for humans, GO terms remain difficult to predict with automatic methods. We suspect that this is because the GO contains so many terms, that it becomes hard to differentiate between all of them. Also, GO terms are not independent of each other, due to the directed acyclic graph (DAG) structure of the GO.

A way to overcome the complexity of the GO as well as the noise in the annotations might be to reduce the number of target variables that an AFP algorithm needs to predict, by taking advantage of the redundancy imposed by the DAG. Khatri et al. used singular value decomposition (SVD) to obtain principal directions in the GO-term space and filter out noisy GO annotations of human proteins and predict novel ones (Khatri et al., 2005). Other methods inspired by text processing, use topic modeling, where GO terms are seen as words that stem from specific latent variables called topics (Masseroli et al., 2012). The topics can be interpreted as a lower-dimensional representation of functions. All the above methods use dimensionality reduction to discover new annotations for proteins that already have some GO terms annotated to them.

To (also) be able to predict annotations for proteins that do not have annotations, we propose to transform the GO terms into a lower-dimensional space using Label-Space Dimensionality Reduction (LSDR) techniques and train a machine learning method in this reduced space. Two such existing LSDR methods, namely Principal Label-Space Transformation (PLST) (Tai and Lin, 2012) and Conditional Principal Label-Space Transformation (CPLST) (Chen and Lin, 2012), are both based on an SVD of the labels. Chen and Lin showed that, when combined with linear regression, CPLST slightly outperforms PLST in predicting protein localization and protein family (Chen and Lin, 2012).

PLST and CPLST are general methods that can in principle be applied to any multi-label problem, including AFP. However, in the case of the GO, further information is available concerning the labels, namely that they are organized in a hierarchy. Exploiting this extra piece of information is likely to lead to better dimensionality reduction and, as a result, better performance. This observation was first made by Bi and Kwok, who introduced an LSDR technique that finds latent representations in which GO terms contribute to each component in a way similar to their ancestors in the DAG (Bi and Kwok, 2011).

The DAG-aware method by Bi and Kwok has three disadvantages. First, it does not take the distribution of the labels in the training set into account and projects only using information about a term’s ancestors. Second, it ignores the fact that GO terms can share information even if they are not connected by an edge in the DAG. For instance, two children of a GO term typically describe two related functions. Finally, the method uses a computationally demanding algorithm to ensure that the final predictions respect the GO hierarchy.

We address these disadvantages by introducing an LSDR method that is both GO-aware and label-distribution-aware. Then, we take the notion of GO-awareness further by combining label distributions with GO-term semantic similarity (Pesquita et al., 2009), so that similar terms are treated similarly regardless of whether they are connected in the DAG. Also, to ensure that our predictions are consistent with the GO, we simply propagate predicted annotations toward the root, which is much more efficient.

In summary, we apply dimensionality reduction schemes for the GO label-space to AFP and propose two new reduction schemes that incorporate the structure of the GO. Also, we introduce a new way to represent proteins encompassing the similarity to all other proteins, the SSP.

2 Materials and methods

2.1 Notation

Let $N_{train}$ denote the number of training proteins. These proteins are represented by a feature matrix$\mathrm{ }{\mathit{X}}_{train}\in {\mathbb{R}}^{N_{train}\times N_{feat}}$, whose i-th row contains the feature vector ${\mathit{x}}_i$ of the i-th training protein, and $N_{feat}$ is the dimensionality of the feature vector. The GO annotations of the i-th protein are represented by a binary label vector ${\mathit{y}}_i\in {\{0,\mathrm{ }1\}}^{\mathrm{ }L}$, where $y_{ij}=1$, if protein i is annotated with GO term j, and L is the number of GO terms (labels) in one of the three GO sub-ontologies. Further, ${\mathit{Y}}_{train}\in {\{0,\mathrm{ }1\}}^{N_{train}\mathrm{ }\times \mathrm{ }L}$ represents the corresponding label matrix, whose i-th row contains ${\mathit{y}}_i$.

Given a set of $N_{test}$ test proteins, represented by feature matrix ${\mathit{X}}_{test}\in {\mathbb{R}}^{N_{test}\times N_{feat}}$, we define as ${\mathit{Y}}_{test}\in {\{0,\mathrm{ }1\}}^{N_{test}\mathrm{ }\times \mathrm{ }L}$ the matrix containing the corresponding label vectors. For test protein i, the annotations predicted by an AFP algorithm are represented by the label vector ${\widehat{\mathit{y}}}_i\in {\{0,\mathrm{ }1\}}^{\mathrm{ }L}$.

2.2 Sequence similarity profile (SSP)

We represent each protein i in the dataset as a vector ${\mathit{x}}_i\in {\mathbb{R}}^{N_{train}}$ whose j-th element contains the sequence identity between i and the j-th training protein. In other words, each protein is represented by a SSP to all proteins in the training set. This profile is used as a feature representation in combination with a k nearest neighbors (kNN) classifier because it is relatively simple and efficient and does not need to be trained separately for each GO term. The posterior for each GO term l then becomes:

$$P\left(y_{il}=1\mathrm{ }|\mathrm{ }{\mathit{x}}_i\right)=\frac{\sum _{j\mathrm{ }\in \mathrm{ }{N}_k^{SSP}\left(i\right)}\left\{y_{jl}\right\}}{k}$$ (1)

where $N_k^{SSP}\left(i\right)$ represents the kNN in the training set for protein i using Euclidean distance in the SSP space.

2.3 Label-space dimensionality reduction (LSDR)

In general, the LSDR workflow can be summarized as follows:

Transform the label matrix Y into a lower-dimensional matrix $\mathit{Y}\mathrm{\text{'}}\in {\mathbb{R}}^{N_{train}\mathrm{ }\times L^{\mathrm{\text{'}}}}$, where $L^{\mathrm{\text{'}}}<L$, using a transformation matrix T, so that ${\mathit{Y}}^{\mathrm{\text{'}}}=\mathit{Y}·\mathit{T}$.

The new label vectors $\mathbf{y}\mathrm{\text{'}}\in {\mathbb{R}}^{L^{\mathrm{\text{'}}}}$ are no longer necessarily binary, so a multi-variate, multi-target regression model f is trained, so that $\mathrm{f}\left({\mathbf{x}}_{\mathrm{i}}\right)\cong \mathrm{ }{{\mathbf{y}}^{\mathrm{\text{'}}}}_{\mathrm{i}}$.

For every test vector $\mathit{x}\in {\mathbb{R}}^{N_{feat}}$, calculate its predicted latent function representation $\widehat{{\mathit{y}}^{\mathrm{\text{'}}}}=\mathrm{f}\left(\mathit{x}\right)$.

Obtain a posterior score for the test protein being annotated with each of the L GO terms using the inverse of the transformation of the first step, $\mathit{s}\mathit{c}\mathit{o}\mathit{r}\mathit{e}\left(\mathit{x}\right)=\widehat{{\mathit{y}}^{\mathrm{\text{'}}}}{\mathit{T}}^{-1}\in {\mathbb{R}}^L$. Each element of the score vector contains a value (not necessarily a probability) that reflects how certain the algorithm is about the assignment of the corresponding GO term to the protein.

LSDR is incorporated into AFP by predicting $\mathit{y}\mathrm{\text{'}}$ instead of $\mathit{y}$. After applying the inverse transformation to $\mathit{y}\mathrm{\text{'}}$ to obtain $\mathit{y}$, to ensure that the predictions respect the GO hierarchy, we transform the posterior score for a term l as follows:

$$score\left(\mathrm{ }{x}_{il}\right)=\mathrm{m}\mathrm{a}\mathrm{x}\{score\left(\mathrm{ }{x}_{il}\right),\mathrm{ }\underset{t\in \mathit{Children}\left(l\right)}{\max }\{score\left(\mathrm{ }{x}_{it}\right)\}\}$$ (2)

The scores are updated per GO level starting from the most distant terms to the root. This guarantees that the scores are consistent with the hierarchy.

We introduce three existing LSDR methods (PLST, CPLST and DAG) and two new ones (GOAT and SEM).

2.3.1. PLST

PLST (Tai and Lin, 2012) applies SVD on the label matrix Y [Equation (3)], after transforming it so that each column has zero mean:

$$\mathit{Y}=\mathit{U}\mathbf{\Sigma }{\mathit{V}}^T,\mathrm{ }\mathit{U}\in {\mathbb{R}}^{N_{train}\mathrm{ }\times N_{train}},\mathit{\Sigma }\in {\mathbb{R}}^{N_{train}\mathrm{ }\times L},\mathrm{ }\mathbf{V}\in {\mathbb{R}}^{L\mathrm{ }\times \mathrm{ }L}$$ (3)

More specifically, $\mathit{U}$ and V are unitary matrices, whose columns contain the eigenvectors of $\mathit{Y}{\mathit{Y}}^T$and ${\mathit{Y}}^T\mathit{Y}$, respectively, also known as left and right singular vectors of Y. $\mathbf{\Sigma }$ is a diagonal matrix, whose diagonal elements correspond to the singular values of Y, which are equal to the square roots of the eigenvalues of $\mathit{Y}{\mathit{Y}}^T$and ${\mathit{Y}}^T\mathit{Y}$. The transformation matrix ${\mathit{T}}_{PLST}$ consists of the columns of V corresponding to the L’ largest singular values (L’ principal right singular vectors).

2.3.2. CPLST

The CPLST (Chen and Lin, 2012) matrix ${\mathit{T}}_{CPLST}$ has as columns the L’ principal right singular vectors of the matrix ${\mathit{Y}}^T\mathit{X}{({\mathit{X}}^T\mathit{X}+\lambda \mathit{I})}^{-1}{\mathit{X}}^T\mathit{Y}$, where $\lambda$ is a regularization parameter and ${({\mathit{X}}^T\mathit{X}+\lambda \mathrm{I})}^{-1}{\mathit{X}}^T={\mathit{X}}^{+}(\lambda )$ is the left regularized pseudo-inverse of X. By incorporating the term $\mathit{X}{\mathit{X}}^{+}(\lambda )$, CPLST takes into account the distribution of the labels as well as the distributions of the features, i.e. the labels are projected onto directions where both the variance of the labels (as in the PLST) as well as the correlation between the labels and the features is large.

2.3.3. DAG

In (Bi and Kwok, 2011) a matrix ${\mathit{G}}_{anc}\in {\mathbb{R}}^{L\mathrm{ }\times \mathrm{ }L}$ is defined, such that ${G_{anc}}_{ij}=1$ if $i=j$ or $j$ is an ancestor of $i$ in the DAG defined by the GO. The labels are then transformed based on the matrix ${\mathit{T}}_{DAG}$ consisting of the L’ principal right singular vectors of ${\mathit{G}}_{anc}$. This transformation projects related GO terms toward similar directions. In their testing phase, Bi and Kwok employed an iterative algorithm to ensure that the predictions respect the GO hierarchy. Here, we obtain GO-consistent predictions by applying Equation (2).

2.3.4. GOAT

We defined a matrix $\mathit{G}\in {\mathbb{R}}^{L\mathrm{ }\times \mathrm{ }L}$ such that $G_{ij}=1$ if $i=j$ or $i$ and $j\mathrm{ }$are connected by an edge in the DAG and 0 otherwise. The labels are then transformed based on matrix ${\mathit{T}}_{GOAT}$, consisting of the L’ principal right singular vectors of $\mathit{Y}·\mathit{G}$. This transformation attempts to maintain directions of high variance in the label-space, while projecting related GO terms toward similar directions.

2.3.5. SEM

As an alternative approach to capture the similarity between GO terms, we used Resnik’s definition of semantic similarity (Resnik, 1995) to calculate a similarity score between each pair of GO terms [Equation (4)].

$$sim\left(l,\mathrm{ }{l}^{\mathrm{\text{'}}}\right)=\underset{c\mathrm{ }\in \mathrm{ }\mathit{anc}(l,\mathrm{ }{l}^{\mathrm{\text{'}}})}{\max }\{-\log \left(P\left(c\right)\right)\}$$ (4)

where $anc(l,\mathrm{ }{l}^{\mathrm{\text{'}}})$ is the set of common ancestors of GO terms $l$ and $l^{\mathrm{\text{'}}}$, and $P\left(c\right)$ is the frequency of term c in the training set. All pairwise similarities between GO terms were computed and stored in a similarity matrix $\mathit{S}\in {\mathbb{R}}^{L\mathrm{ }\times \mathrm{ }L}$. Finally, we applied LSDR using transformation matrix ${\mathit{T}}_{SEM}$ whose columns correspond to the L’ principal right singular vectors of $\mathit{Y}·\mathit{S}$.

2.4 Baseline methods, evaluation and datasets

We compared SSP to three baseline methods. Two are based on BLAST hits, TRANSFERBLAST and CAFABLAST, and the third is the sequence-based part of MS-kNN (Lan et al., 2013). MS-kNN performed best in most CAFA2 benchmarks, using sequence information only for all species but human. Details of these methods are provided in Supplementary Material (SM1). We studied the effects of LSDR on SSP, TRANSFERBLAST and MS-kNN.

We compared the methods using the protein-centric F-measure ($F_p$), Area under the Precision-Recall Curve (${AUPRC}_p$) and Semantic Distance (${SD}_p$) and the term-centric F-measure ($F_t$) and Area under the ROC curve (${AUROC}_t$). Definitions of these metrics can be found in Supplementary Material SM2.

We tested the methods on three different datasets: the targets of CAFA2 from the nine species with the most target proteins (Supplementary Material SM3), the preliminary CAFA3 Arabidopsis thaliana targets released by the organizers (Supplementary Material SM4), and the dataset containing all A.thaliana proteins with experimental and/or computational annotations (cross-validation dataset, Supplementary Material SM5). In all cases we trained and tested all methods only on the target species (intra-proteome annotation), as motivated in Supplementary Material SM6 and Supplementary Figure S16. The parameters of all algorithms were optimized for each dataset using cross-validation (Supplementary Material SM7).

3 Results

3.1 LSDR improves CAFA performance

We evaluated the effect of the five LSDR techniques on SSP, MS-kNN and TRANSFERBLAST (Table 1 and Supplementary Figs S1–S5, Supplementary Material SM3) using 860 proteins from the CAFA2 data. LSDR improves the performance of all three algorithms for all metrics except for $F_t$, where the improvement is evident only for TRANSFERBLAST. GO-aware LSDR techniques achieve slightly better performance on ${SD}_p$, a metric that rewards more meaningful predictions and punishes shallow annotations, with SEM achieving the best ${SD}_p$ for all the methods, although the differences are small.

Table 1.

CAFA2 performance (rounded to two decimal places) of the tested algorithms (rows) on the 860 targets based on five different evaluation metrics (columns), as well as the 95% confidence intervals after 1000 bootstraps

LSDR	AFP method	${\mathrm{F}}_{\mathrm{p}}$↑	${\mathrm{A}\mathrm{U}\mathrm{P}\mathrm{R}\mathrm{C}}_{\mathrm{p}}$↑	${\mathrm{S}\mathrm{D}}_{\mathrm{p}}$↓	${\mathrm{F}}_{\mathrm{t}}$↑	${\mathrm{A}\mathrm{U}\mathrm{R}\mathrm{O}\mathrm{C}}_{\mathrm{t}}$↑
—	CAFABLAST	0.14 [0.129, 0.144]	0.15 [0.144, 0.159]	27.36 [29.05, 39.02]	0.04 [0.043, 0.047]	0.75 [0.723, 0.746]
None	SSP	0.27 [0.263, 0.280]	0.29 [0.287, 0.306]	25.07 [27.01, 34.70]	0.04 [0.038, 0.044]	0.55 [0.548, 0.564]
	MS-kNN	0.27 [0.263, 0.279]	0.31 [0.300, 0.321]	25.05 [27.16, 34.93]	0.03 [0.036, 0.040]	0.55 [0.548, 0.563]
	TRANSFERBLAST	0.15 [0.138, 0.156]	0.06 [0.060, 0.072]	37.64 [39.83, 50.89]	0.02 [0.025, 0.027]	0.50 [0.502, 0.507]
PLST	SSP	0.28 [0.272, 0.289]	0.33 [0.317, 0.336]	24.90 [27.04, 34.78]	0.03 [0.038, 0.043]	0.77 [0.737, 0.764]
	MS-kNN	0.29 [0.277, 0.294]	0.33 [0.320, 0.341]	24.72 [26.83, 34.42]	0.03 [0.034, 0.039]	0.77 [0.744, 0.768]
	TRANSFERBLAST	0.24 [0.233, 0.251]	0.30 [0.292, 0.310]	26.98 [29.18, 38.01]	0.04 [0.041, 0.046]	0.75 [0.715, 0.738]
CPLST	SSP	0.28 [0.273, 0.289]	0.33 [0.317, 0.336]	24.87 [27.06, 34.76]	0.04 [0.040, 0.045]	0.77 [0.742, 0.768]
	MS-kNN	0.29 [0.277, 0.293]	0.33 [0.320, 0.341]	24.72 [26.85, 34.45]	0.03 [0.034, 0.039]	0.77 [0.745, 0.769]
	TRANSFERBLAST	0.24 [0.237, 0.253]	0.30 [0.290, 0.310]	27.11 [28.91, 38.78]	0.04 [0.044, 0.048]	0.77 [0.739, 0.764]
DAG	SSP	0.27 [0.265, 0.282]	0.32 [0.311, 0.330]	25.15 [27.13, 34.81]	0.03 [0.032, 0.037]	0.76 [0.734, 0.757]
	MS-kNN	0.28 [0.275, 0.291]	0.33 [0.319, 0.339]	24.76 [26.93, 34.54]	0.03 [0.031, 0.036]	0.77 [0.741, 0.763]
	TRANSFERBLAST	0.20 [0.190, 0.204]	0.24 [0.230, 0.251]	26.92 [28.95, 38.01]	0.02 [0.025, 0.030]	0.77 [0.740, 0.762]
GOAT	SSP	0.28 [0.272, 0.289]	0.33 [0.317, 0.336]	24.90 [27.04, 34.80]	0.03 [0.038, 0.043]	0.77 [0.737, 0.763]
	MS-kNN	0.29 [0.277, 0.293]	0.33 [0.320, 0.341]	24.71 [26.83, 34.44]	0.03 [0.034, 0.039]	0.77 [0.739, 0.762]
	TRANSFERBLAST	0.24 [0.229, 0.247]	0.30 [0.289, 0.309]	26.97 [29.16, 37.99]	0.04 [0.041, 0.046]	0.75 [0.723, 0.746]
SEM	SSP	0.28 [0.277, 0.293]	0.33 [0.321, 0.341]	24.68 [26.62, 34.34]	0.04 [0.043, 0.047]	0.77 [0.739, 0.765]
	MS-kNN	0.29 [0.277, 0.293]	0.33 [0.321, 0.341]	24.65 [26.56, 34.27]	0.03 [0.038, 0.043]	0.77 [0.747, 0.770]
	TRANSFERBLAST	0.28 [0.275, 0.290]	0.33 [0.318, 0.337]	24.76 [26.80, 34.37]	0.04 [0.042, 0.048]	0.77 [0.747, 0.769]

Note: The top performances for each metric are shown in bold. An upwards-pointing arrow next to the metric means that higher values are better and a downwards-pointing arrow that lower values are better.

We also tested our methods on the preliminary CAFA3 dataset for Arabidopsis, which is the species with the most targets in this test set (137) (Supplementary Material SM4, Supplementary Figs S6–S10 and Table S1). The results follow a pattern similar to that of CAFA2, with LSDR considerably improving ${SD}_p$ and ${AUROC}_t$ for all three algorithms. For most cases, any AFP algorithm combined with LSDR performs at least on par with, if not better, than the standalone AFP algorithm. It should be noted that SSP—with or without LSDR—achieves much better $F_p$ and ${AUPRC}_p$ than the baselines in this plant-only dataset, while doing slightly worse than MS-kNN on ${SD}_p$.

3.2 Similar cross-validation and CAFA performances

To better compare LSDR methods among each other, we used a larger dataset containing 7834 A.thaliana proteins with experimental or computational BPO annotations and repeated the evaluation using cross-validation (Supplementary Material SM5, Supplementary Figs S11–S15 and Table S2). SSP is the top-performing non-LSDR method in this dataset based on three out of the five evaluation metrics ($F_p$, ${AUPRC}_p$ and $F_t$) and is on par with the best method based on ${SD}_p$. CAFABLAST achieved the top ${AUROC}_t$ with SSP ranking second. Similar to the CAFA2/3 experiments, the use of LSDR, and especially GO-aware LSDR, also gives a performance boost on this A.thaliana experiment, with the exception of $F_t$.

Supplementary Table S4 (Supplementary Material SM5) shows the best performance achieved in each of the three datasets (CAFA2/3, A.thaliana) regardless of the AFP method. The F-measure and the AUPRC are affected most by the fraction of positive examples in each class (Powers, 2011), which varies a lot among the datasets. Therefore, comparing the values of these metrics is not straightforward. The same holds for ${SD}_p$, as the Information Content (IC) of terms also changes per dataset. The ${AUROC}_t$ is the only metric that allows for a fairer comparison. Based on that, CAFA2 and CAFA3 performances are similar to that in the cross-validation dataset as obtained with cross-validation (0.77, 0.7 and 0.73, respectively).

3.3 Ranking of methods robust to evaluation set-up

Since a direct comparison of the performances of methods across datasets is not trivial, we investigated how sensitive the relative ranking of methods was to different evaluation schemes. We calculated the rank correlation between the performances of all AFP-LSDR combinations across the three different datasets (Supplementary Material SM8, Supplementary Figs S17–S21). For all metrics except for $F_t$, the correlations were positive, although not always statistically significant. The CAFA3 and cross-validation datasets demonstrate the highest similarity, as they contain proteins from the same species. Furthermore, in our CAFA2 results there were a lot of ties which were not observed in the other two datasets and that is bound to have a negative effect on the rank correlations.

Since the CAFA3 dataset (containing only experimental annotations) and the cross-validation dataset (containing in addition computational annotations) gave a similar ranking of the methods, we tested what happens if even more annotations were used. We additionally included IEA annotations obtained from UniProt keywords in our cross-validation dataset. Adding these annotations increased the performance of all methods. The increases were statistically significant for three out of the five metrics (Supplementary Material SM9) but the relative ranking of the methods was not affected (rank correlations >0.7, Supplementary Material SM9), again supporting that LSDR improves AFP.

3.4 Tuning of LSDR parameters

For all methods and datasets, parameters were tuned to optimize for ${AUPRC}_p$. We repeated the cross-validation experiments on A.thaliana while optimizing the parameters for term-centric criteria and the ranking of the methods remained similar (Supplementary Table S5, Supplementary Material SM10). Again, $F_t$ was an exception to that pattern. The optimal values for parameter k of the standalone SSP and MS-kNN are similar to their LSDR variants (Supplementary Table S3, Supplementary Material SM5). The optimal number of dimensions of the reduced label-space (L’) was found to be either 500 or 1000, reducing the number of labels at least 2-fold (Supplementary Table S3, Supplementary Material SM5), indicating a minimum required number of dimensions to encapsulate the expressiveness of the GO terms.

3.5 LSDR useful regardless of term informativeness

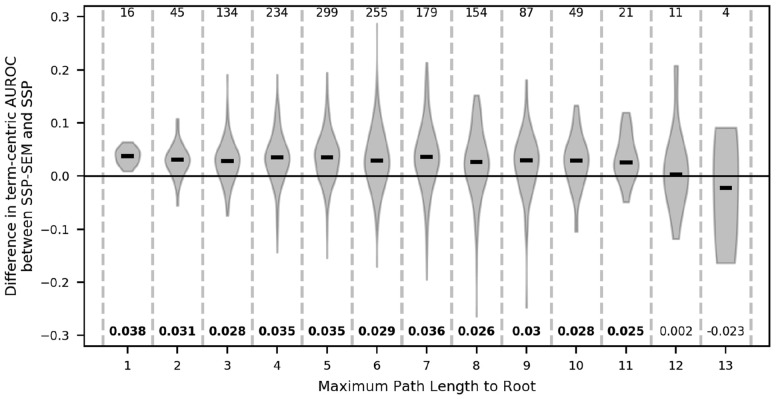
We were interested in whether the improvement of SSP-SEM in ${SD}_p$ was because SSP-SEM performed better than SSP at more informative GO terms. We used the maximum path length to the ontology root as a proxy for the informativeness of a term. Figure 1 shows the distribution of the differences in ${AUROC}_t$’s between SSP-SEM and SSP for different path lengths of the individual terms (term informativeness). The variance is relatively large at all levels. Nevertheless, SSP-SEM does perform significantly better than SSP for levels 1–11 (FDR < 0.05, Bonferroni-adjusted Wilcoxon rank-sum test) with the improvement being consistently around 0.03. The differences are not significant for levels 12 and 13 (FDR = 1.0, Bonferroni-adjusted Wilcoxon rank-sum test), but these levels also contain only a few terms. From this we conclude that LSDR is on average useful regardless of the informativeness of the terms. Although intuitive, path length does not accurately capture the IC for a term. Therefore, we also checked how SSP-SEM performs with respect to SSP when ranking terms based on Resnik IC (Supplementary Fig. S22, Supplementary Material SM11). From that, the same conclusions can be drawn, i.e. the improvement is not depending on the IC of a term.

Fig. 1.

Differences in term-centric ${\mathrm{A}\mathrm{U}\mathrm{R}\mathrm{O}\mathrm{C}}_{\mathrm{t}}\mathrm{ }$performance of SSP-SEM with respect to SSP as a function of term specificity. At every path length from the ontology root (x axis), the distribution of the difference in ${AUROC}_t$ for all terms having that length is plotted using a violin plot. The medians of these differences are designated by the black stripes. The difference between the two medians is shown below the distribution and is marked in boldface if that difference is significant with an FDR of 0.05. The black horizontal line at y=0.0 indicates no difference in performance. The numbers on top of the figure denote the number GO terms with that particular path length

3.6 LSDR captures GO term correlations

LSDR reduces the number of dimensions in the label-space by exploiting the correlations between the GO terms, which potentially improves the power of the term-specific predictors (they can be learned from more examples in the created meta-terms). A schematic explanation of this is given in Supplementary Figure S23 (Supplementary Material SM12). The predictions in the reduced label-space do, however, not guarantee to comply with the GO hierarchy. In the cross-validation dataset, the posterior scores need to be corrected with Equation (2) for 57–70% of the cases depending on the LSDR method (Supplementary Material SM13). Nevertheless, after this correction, LSDR improves the performance of all AFP methods. Interestingly, all LSDR methods generate a similar fraction of inconsistent parent–child pairs, but GO-aware ones have a higher total fraction of inconsistencies (Supplementary Table S6, Supplementary Material SM13). This implies that GO-aware LSDR methods tend to produce more confident predictions for the more specific terms than for the generic ones (Supplementary Table S7, Supplementary Material SM13). Also, GO-aware LSDR can identify GO-term correlations, which cannot be done by generic methods (Supplementary Tables S8–S9, Supplementary Material SM14).

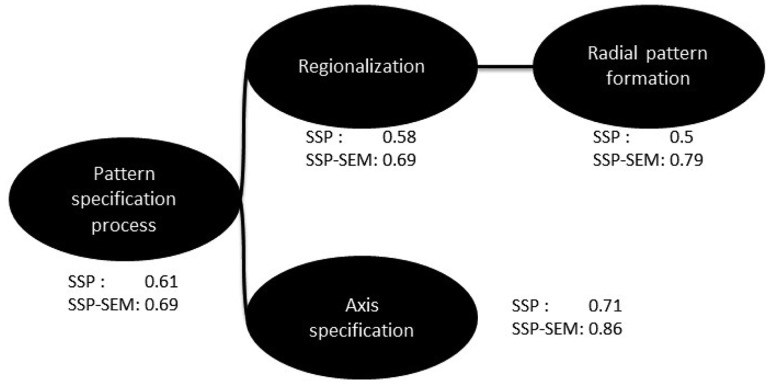
As an example, consider GO term GO: 0009798 (axis specification), which can be predicted reasonably well by both SSP and SSP-SEM, having an ${AUROC}_t$ of 0.71 and 0.86, respectively (averaged across the 3-folds). A term related to that is GO: 0009956 (radial pattern formation). The two terms share a common ancestor namely GO: 0007389 (pattern specification process) (Fig. 2), which is a parent of the former and a grandparent of the latter. SSP, which essentially treats each term independently, achieves random performance on GO: 0009956 (${AUROC}_t$ 0.499). However, SSP-SEM performance was 0.79 for this term, as it could exploit the semantic similarity of the term with GO: 0009798.

Fig. 2.

Example subgraph of the BPO. SSP achieves reasonable performance for term ‘axis specification’, but its performance is much worse on the other branch of this subgraph. SEM can exploit the similarity of the terms in the right branch to that on the left and achieve reasonable performance for both branches

3.7 SSP selects more informative proteins in Arabidopsis

The optimal value of parameter k, as chosen with a double cross-validation loop, was 1 for both SSP and MS-kNN (Supplementary Material SM5, Supplementary Table S3), which means that both methods predict annotations for a protein based on the single most similar training protein. On average, over the three outer folds in our cross-validation experiment, the training protein that is most similar to the test protein based on the SSP, $N_1^{SSP}\left(i\right)$, is different from the protein with the highest sequence similarity, $N_1^{seq}\left(i\right)$, in 61.6% of the cases. Importantly, we found that in all three folds, when $N_1^{SSP}\left(i\right)\ne N_1^{seq}\left(i\right)$, the Jaccard similarity of the GO annotations of $i$ and $N_1^{SSP}\left(i\right)$ was significantly larger than the Jaccard similarity of the GO annotations of $i$ and $N_1^{seq}\left(i\right)$ (P-values = ${10}^{-70},\mathrm{ }{10}^{-78},\mathrm{ }{10}^{-18}$ Wilcoxon rank-sum test for each fold, Supplementary Fig. S24, Supplementary Material SM15). In other words, the SSP representation selects more informative proteins than the MS-kNN to predict functional annotations in this large plant dataset.

As an example, consider query protein Q9SL78, whose best BLAST hit in Arabidopsis is P33207. These two proteins have 48% sequence identity and a BLAST E-value in the order of ${10}^{-74}$. However, their Jaccard semantic similarity in the BPO is 0.0. They are also dissimilar in the other two GO branches, as they are involved in different reactions and are present in different cell compartments. On the other hand, SSP chose Q5EAE9 as the nearest neighbor of Q9SL78. These two proteins have exactly the same GO annotations: GO: 0016567 and GO: 0043161, and they both belong to the ATL subfamily of the RING-type zinc finger family. However, they have lower sequence similarity than the query and P33207 (39%). Their profile similarity was more similar, though. Importantly, they are both roughly equally similar (∼40%) to all the remaining members of the ATL subfamily, 30 of which were present in the training set in this case. As shown in Supplementary Figure S25 (Supplementary Material SM16), the proteins are similar on a specific part of their sequence, which corresponds to a zinc finger domain. Because SSP looks at the similarity to all proteins and not the most similar one, and because many members of the same subfamily were available in the training set, SSP was able to identify the correct protein in this case.

4 Discussion

We presented new AFP methods that exploit the similarities between GO terms (LSDR techniques) and between proteins (SSP representation) to predict GO annotations for new, unannotated proteins. We benchmarked the new methods to MS-kNN (Lan et al., 2013), one of the top-performing methods in CAFA2, as well as to BLAST-based baseline methods, under different evaluation set-ups and metrics. We showed that LSDR remarkably improves CAFA performance of all tested methods in predicting BPO annotations and that SSP outperforms the baselines in A.thaliana.

4.1 LSDR

AFP is a special case of multi-label learning due to the additional constraint that the labels are by definition organized in a DAG structure. This is also known as structured output learning (Tsochantaridis et al., 2004). Several solutions have been proposed to tackle this problem.

Vens et al. train a separate binary decision tree classifier for every GO term, but they use as training examples only the proteins that are annotated with all the parents of the term (Vens et al., 2008). This might lead to problems due to lack of negative examples in tree-shaped sub-branches of the DAG (where each node has exactly one parent). Other work by Zhang et al. trains independent binary predictors for each label and then attempts to reconcile conflicting predictions by solving a regression problem from the outputs of the predictors to the true labels using an L2 penalization of predictions that do not respect the hierarchy (Zhang et al., 2017). Recently, it was proposed to train a multi-label classifier for every level of the GO (i.e. first on all terms of distance 1 to the root, then all terms of distance 2 and so on) (Cerri et al., 2016; Rifaioglu et al., 2017). This approach suffers from the lack of negative examples as well. A simpler and faster approach, which was also used here, is to force the posterior probability of a label to be greater or equal to the maximum posterior probability of all its descendants (Kulmanov et al., 2017).

The machine learning community has produced many interesting methods on how to reduce the number of target variables in a multi-label problem (LSDR), e.g. Zitnik and Zupan used LSDR implicitly to integrate several data sources for AFP (Žitnik and Zupan, 2015). Each data source (including the label matrix Y) is represented by a lower-dimensional representation, whose dimensionality is a parameter of the algorithm. This method has high computational demands as it requires solving an optimization task during training as well as one more for every query protein (Žitnik and Zupan, 2015).

The first DAG-aware LSDR work applied to AFP was by Bi and Kwok and was tested on a yeast dataset (Bi and Kwok, 2011). Recently, a study by Yu et al. learned a lower-dimensional embedding of the DAG structure and used it to reduce the dimensionality of the label-space (Yu et al., 2017). They then used semantic similarity in the reduced space to infer new functions for already annotated proteins. Our GOAT approach combines the benefits of the work of Bi and Kwok and those of PLST (Tai and Lin, 2012), by finding projections where the variance in the label-space is high, but also making sure that terms connected by an edge in the DAG are ‘pushed’ toward similar directions.

These techniques ignore the fact that terms not connected by an edge might still represent related functions. For instance, GO: 0036367 (light adaptation) and GO: 0009644 (response to high light intensity) are not connected by an edge, but are semantically related and they are both children of GO: 0009416 (response to light stimulus). GO term semantic similarity was used by Argot2 to cluster similar GO terms into groups and then to perform predictions per group (Falda et al., 2012). It has also been used to transform the label-space by Zhang and Dai (Zhang and Dai, 2012). However, their transformation does not reduce the dimensionality of the label vectors.

We developed SEM, an LSDR technique that uses semantic similarity of GO terms as well as annotation patterns of proteins to reduce the number of target variables. SEM creates an annotation matrix similar to that of Zhang and Dai, but then reduces its dimensionality with SVD to create a more compact and less noisy functional representation. This method projects semantically similar terms toward similar directions in the reduced label-space, even if they are not connected by an edge in the DAG. Although even GO-unaware methods were able to capture similarities between terms that are connected by an edge, SEM captured similarities between non-connected, but related terms much better than any other method (Supplementary Material SM14).

The use of all LSDR techniques showed consistent improvements on the performance of all tested AFP methods in predicting experimental annotations from CAFA2 and CAFA3. These small datasets do not show significant differences among the different LSDR techniques. However, SEM combined with SSP achieved the best performance in terms of protein-centric SD and term-centric AUROC, while it performed on par with the best-performing methods under most of the other evaluation metrics in the much larger cross-validation dataset.

Finally, LSDR is ‘blurring’ and simplifying the GO-term space, which is expected to have a negative effect on term-centric performance. This effect was partially observed for the term-centric F-measure, but not for the AUROC, where three methods combined with different LSDR techniques performed consistently better than the same methods without LSDR across all levels of the GO DAG.

In terms of complexity, all LSDR techniques rely on SVD, which takes $O\left(L^3\right)$, so they are fairly efficient. In the training phase, PLST requires only computing the SVD of a matrix. The other methods include an extra matrix multiplication step. The most computationally demanding method is CPLST, which also computes the pseudo-inverse of the feature matrix. The training time of LSDR techniques on the cross-validation dataset never exceeds a few minutes on a single-core machine. In the testing phase, only one matrix multiplication is required ($O\left(L\right)$), contrary to more complicated methods that solve optimization problems (Bi and Kwok, 2011; Hsu et al., 2009; Žitnik and Zupan, 2015).

Finally, all LSDR techniques tested reduce the number of target variables by at least 2-fold with either no significant loss or even gain in performance. This hints at the fact that the inherent dimensionality of a GO annotations matrix is lower than the actual number of GO terms present, which can be expected as the DAG structure enforces constraints on the annotations. It also means that the training time of more complex AFP methods can be reduced without loss of performance by applying LSDR first.

4.2 Sequence similarity profile

The rationale of SSP and MS-kNN is similar. The difference is that MS-kNN finds neighbors based on pairwise similarities, whereas SSP identifies the training proteins based on a similarity profile including all training proteins. We believe that the latter approach can be more informative, as functions can be conserved at medium levels of sequence similarity (Wass and Sternberg, 2008) and really low similarities might indicate low functional similarities. SSP is expected to be particularly useful in species in which the majority of proteins are members of expanded protein families, such as in plants (Lockton and Gaut, 2005). In such cases, SSP can identify the shared similarity between the query and all members of the family, even if that similarity is not particularly high. Indeed, the proteins chosen by SSP had on average more similar annotations (based on Jaccard similarity) to the queries than those by MS-kNN, also explaining the difference in F-measures between the two methods in our two Arabidopsis (cross-validation and CAFA3) datasets. The two methods performed similarly in the CAFA2 dataset, hinting indeed toward the usefulness of SSP when there are many genes from the same family.

The notion of using distances or similarities as a feature representation of objects is not new (Pękalska and Duin, 2002). In bioinformatics, the similarity-based representation of proteins is a simple way to convert arbitrary-length sequences to fixed-length vectors. It has been used for predicting protein families (Liao and Noble, 2003), antimicrobial peptides (Ng et al., 2015) and allergen sequences (Muh et al., 2009), as well as protein–protein interactions (Zaki et al., 2009). In addition, Li et al. used this representation along with other sequence features to predict functional annotations of viral proteins (Li et al., 2007). Each function was treated as a separate binary classification problem.

All these studies made use of SVMs. The reason the kNN classifier was employed in this work is its simplicity and efficiency. In the other application domains, the classification task was binary, i.e. only discriminating between two classes. In the case of AFP, we are dealing with thousands of target classes, which would require training one SVM per class. On the contrary, kNN is inherently multi-label and can still capture non-linear relationships in the data and have reasonable performance in diverse problems (Munisami et al., 2015; Saini et al., 2013).

From our parameter tuning, a very small value for k (1–3), the number of neighboring proteins to consider, was shown to give best performances, both for SSP and MS-kNN. This result is contradictory to the original MS-kNN study in which k was set to 20 (Lan et al., 2013), as well as the work by Yu et al. which predicted novel annotations for a partially annotated protein using the 250 or 500 most semantically similar proteins to the query (Yu et al., 2016). Neither of these studies reported tuning of k, using cross-validation or a similar procedure, but rather they set k manually. Another reason for this difference might be the fact that MS-kNN was tested on human proteins (Lan et al., 2013) and the semantic similarity approach on human and mouse proteins (Yu et al., 2016). As the annotations for those species are much denser than for A.thaliana, we expect that including more neighbors would tend to reinforce the predictions of true annotations. In A.thaliana, many more annotations are missing, so true annotations might be given a low score if k is large, because they are present in only one neighbor. Perhaps this, currently, is an artifact of the fact that the other neighbors have not acquired this annotation yet.

A disadvantage of using a similarity representation is the fact that it suffers from the curse of dimensionality (Köppen, 2000), since there are as many features as training examples. As a result, methods that use this representation are more susceptible to overfitting, especially if a complex classifier is used. For binary classification tasks, several methods have been proposed for prototypes selection, i.e. identification of a small number of proteins that are representative of the training set in order to use the similarities to only these prototypes as features (Pękalska and Duin, 2002). In AFP, we are dealing with thousands of target classes (GO terms) instead of two and different proteins are likely to be informative for different terms. This makes prototype selection more complicated and increases the computational burden during training significantly, so we did not explore this option further. However, we did attempt randomly selecting a smaller number of prototypes (Pękalska et al., 2006), leading to a significant deterioration in performance (Supplementary Figs S26–S30, Supplementary Material SM17).

4.3 Importance of proper evaluation

Finding proper evaluation practices for AFP remains an open problem (Jiang et al., 2016). In this paper, we were interested in predicting annotations for completely unannotated proteins; No-Knowledge evaluation (Radivojac et al., 2013). The CAFA challenges (Jiang et al., 2016; Radivojac et al., 2013) provide a unified comparison framework, where target proteins are made available at a certain time point and participants have a few months to submit their predictions on these targets. The evaluation takes place based on the subset of the targets that have accumulated experimental annotations during a pre-defined period of time after the submission deadline.

Experiments have shown that cross-validation performance is not an informative predictor of performance in the CAFA challenges (Kahanda et al., 2015). However, it remains unclear whether cross-validation or CAFA-like experiments are more informative concerning the performance of a certain method in practice, as both of them have their own limitations. First of all, both tactics suffer from the incompleteness of annotations, which leads to potentially correct predictions of a classifier to be perceived as false positives, if the corresponding annotation has not yet been confirmed by other means. Indeed, we showed that the performance of all methods increases when annotations are more complete, i.e. in our case when we included IEA annotations. CAFA challenges are expected to suffer more from this, as they deal with only newly-derived annotations, whereas in cross-validation the test set consists of randomly selected proteins, regardless of when they received their annotations. These annotations are expected to be ‘more complete’ on average. Also, this leads to a larger number of GO terms being available for evaluation with cross-validation.

A disadvantage of cross-validation is that stratification (i.e. maintaining an equal fraction of positive and negative examples per label across all folds) becomes virtually impossible because of the vast number of labels. As a consequence, some rare terms are left with only a handful or no positive examples. To deal with the lack of examples and its effect on performance estimation, we ignored terms that contained <0.1% positive examples in the test set.

Furthermore, we used the inner cross-validation loops to select the optimal parameter set of the tested predictors, using the mean protein-centric AUPRC as a performance criterion. However, due to the aforementioned issues, the AUPRC in different folds was calculated using not always the same target variables or the same target variables but with considerably different priors, which can be very misleading (Boyd et al., 2012). The different term frequencies also lead to differences in the calculation of term IC among folds. The impact of these differences needs to be investigated further, but we found that optimizing for a term-centric metric give a significantly similar ranking of the methods. We also found similarities between the ranking of methods in CAFA and cross-validation experiments.

The choice of evaluation metrics is another open problem (Jiang et al., 2016), as the ranking of methods can vary based on the choice of evaluation metric (Jiang et al., 2016; Radivojac et al., 2013). The short-comings of precision, recall and F-measure are well-known. They depend heavily on the class prior, which is different for each GO term and whose true value is not known in this case and can only be roughly estimated based on GO-term frequencies in the training set (Jain et al., 2017). Moreover, they can give a seemingly high performance for a method that restricts itself in general predictions, near the ontology root. SD (Clark and Radivojac, 2013) was designed to address these limitations, but it still relies on the calculation of IC of terms, which (again) needs to be estimated from the training data and can change significantly from dataset to dataset. Nevertheless, we showed that LSDR is on average useful across all levels of the GO hierarchy, i.e. independent of term frequency or IC. We also observed that term-centric F-measure behaved differently from the other four (both protein- and term-centric) metrics.

4.4 Conclusion

We used similarity in GO-terms space as well as in protein sequence space to build new AFP algorithms. These algorithms improve CAFA and cross-validation performances. Consequently, we combined known concepts from machine learning and bioinformatics into new function prediction methods with encouraging results. Taken together, this shows that AFP can benefit greatly from borrowing ideas from related fields.

Funding

This work was supported by Keygene, a crop innovation company in the Netherlands.

Conflict of Interest: none declared.