Deep learning for FTIR histology: leveraging spatial and spectral features with convolutional neural networks

Abstract

Current methods for cancer detection rely on tissue biopsy, chemical labeling/staining, and examination of the tissue by a pathologist. Though these methods continue to remain the gold standard, they are non-quantitative and susceptible to human error. Fourier transform infrared (FTIR) spectroscopic imaging has shown potential as a quantitative alternative to traditional histology. However, identification of histological components requires reliable classification based on molecular spectra, which are susceptible to artifacts introduced by noise and scattering. Several tissue types, particularly in heterogeneous tissue regions, tend to confound traditional classification methods. Convolutional neural networks (CNNs) are the current state-of-the-art in image classification, providing the ability to learn spatial characteristics of images. In this paper, we demonstrate that CNNs with architectures designed to process both spectral and spatial information can significantly improve classifier performance over per-pixel spectral classification. We report classification results after applying CNNs to data from tissue microarrays (TMAs) to identify six major cellular and acellular constituents of tissue, namely adipocytes, blood, collagen, epithelium, necrosis, and myofibroblasts. Experimental results show that the use of spatial information in addition to the spectral information brings significant improvements in the classifier performance and allows classification of cellular subtypes, such as adipocytes, that exhibit minimal chemical information but have distinct spatial characteristics. This work demonstrates the application and efficiency of deep learning algorithms in improving the diagnostic techniques in clinical and research activities related to cancer.

1. Introduction

Histopathology is the gold standard for cancer diagnosis and determining initial directions for treatment. Standard steps consist of biopsy collection, tissue preparation and sectioning, chemical staining, and analysis by expert pathologists. Typical stains include hematoxylin and eosin (H&E), Masson’s trichrome, and immunohistochemical labels such as cytokeratin for epithelial cells (Fig. 1). The high level of morphological detail present in stained biopsies enables pathologists to determine the presence of cancer, as well as characteristics of tumor such as grade and extent. However, these examinations are performed manually and can be time-consuming and susceptible to human error, which can delay effective treatment. Furthermore, staining techniques are difficult to quantify, with clinical settings relying on various protocols and imaging systems for analysis. Nevertheless, the manual assessment of stained tissue by pathologists is the standard in cancer diagnosis and is heavily relied upon in clinical assessment.¹

Fig. 1.

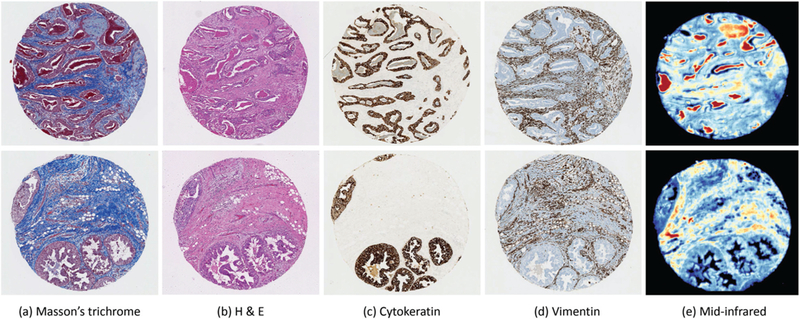
Chemically stained (a–d) and mid-infrared (e) images of two breast biopsy cores. Individual cores from two separate patients are shown with tissue stained with Massson’s trichrome (a) and H & E (b), as well as immunohistochemical labels for cytokeratin (c) and vimentin (d). Colormapped mid-infrared images of the corresponding two cores are shown (e), where color indicates the magnitude of the absorbance spectrum in arbitrary units at 1650 cm⁻¹.

IR spectroscopic imaging is an attractive tool since it can extract molecular microstructure and spatial information in a non-destructive manner.^2–5 Absorption spectra provide molecular fingerprints for each pixel, which translates to key cellular biomolecules, such as proteins, lipids, DNA, collagen, glycogen, and carbohydrates. Numerous studies have shown that FTIR microscopy can be used to distinguish different histological entities across a wide variety of tissue types, including colon,^6–9 prostate,^2,10–13 lung,^14,15 breast,^16,17 cervex,¹⁸ brain,¹⁹ and kidney.²⁰ Methods have also been proposed to digitally apply standard histological stains to tissue samples.²¹

Tissue classification is achieved in most IR imaging studies using pixel-level methods, including unsupervised techniques such as K-means clustering²² or hierarchical cluster analysis (HCA),²³ and supervised techniques such as Bayesian classification^10,14,24 random forests,^14,15,25 artificial neural networks (ANNs),^14,26 kernel classifiers such as support vector machines (SVMs)¹⁴ and linear discriminant classifiers.²⁷ FTIR spectroscopic data contains an abundance of spatial information that is often unused due to difficulty identifying useful features. Spatial information has been utilized in multi-modal applications involving FTIR and traditional histology²⁸ since spatial features are more clearly understood in standard color images. Spatial information has also been used as a post-classification step on the classified output.²⁹ However, these approaches are sequential to spectral analysis and do not take advantage of the spectral–spatial relationships within the IR data set.

While spatial information is being increasingly appreciated in IR imaging,³⁰ deep learning methods have been successfully applied to a variety of other image analysis problems. Increases in processing power, inexpensive storage, and access to parallel computing (such as GPUs) allow traditional laboratories to use deep learning for image classification problems. Convolutional neural networks (CNNs) have been shown to outperform many other techniques for 2D image analysis,^31,32 since they exploit spatial features by enforcing local patterns within the image. The major benefit of CNNs is their ability to identify spatial features optimized on the training data. In addition to extracting spatial correlations between pixels, CNNs can be implemented for hyperspectral images, extracting correlations across the entire spectrum for a given pixel.^33,34 CNNs have therefore become an effective machine learning tool for image classification tasks.^35,36 Unlike many other classification techniques that depend on complex hand-crafted features as input, CNNs automatically learn and hierarchically construct a unique set of high-level features optimized for a given task. While a traditional ANN is often used for the final classification phase, any classifier can be applied to the extracted CNN features.^37–40

More traditional artificial neural network (ANN) architectures have been used for classification and regression problems in vibrational spectroscopic imaging. However, they exhibit poor performance on independent testing data⁴¹ due to overfitting from the large number of available parameters in a hyperspectral image. The use of local connectivity patterns between neurons of adjacents layers and weight sharing schemes make CNNs far more robust. CNNs have been extensively used in remote sensing⁴² and, more recently, one-dimensional CNNs have been used to identify important spectral features in vibrational spectroscopic data.⁴³ To the best of our knowledge, CNNs have not been used for classification of IR spectroscopic imaging.

In this paper, we assess the ability of CNNs to solve IR spectroscopic image classification problems on both standard-definition (SD) at 6.25 μm per pixel and high-definition (HD) at 1.1 μm per pixel. We seek to assess whether deep learning achieves significantly better performance than traditional classifiers due to the use of spatial features. This is of particular interest in HD images, where high-frequency spatial features are more accessible.

2. Materials and methods

Tissue samples were imaged using FTIR spectroscopy and annotated based on adjacent histological evaluation. The FTIR images were pre-processed using standard protocols and a variety of traditional classifiers were extensively tested using per-pixel spectral data, such as k-nearest neighbor (KNN), support vector machines (SVM) with linear and radial basis function (RBF) kernels, decision tree classifier (DT), random forest (RF), neural networks (NN), adaptive boosting classifier (AdaBoost), naive Bayes (NB), and a quadratic discriminant analysis (QDA) classifier. The classification results identified a SVM using a RBF kernel as the optimal spectral-based classifier for this data set as it achieved the best overall classification accuracy. We then designed a new classifier incorporating spatial information using a CNN.

2.1. Tissue microarrays

Four serial sections of formalin fixed paraffin embedded breast tissue microarray (TMA) cores were obtained from Biomax US, Rockville, MD (TMA IDs: BR1003, BR2085b, BR961, and BR1001). Adjacent tissue sections were cut at 4 μm and placed on glass slides for chemical staining and barium fluoride (BaF2) slides for FTIR imaging. The TMAs used in this study consisted of 504 breast tissue cores (with 1 mm diameter) from different patients. The cores contained breast tissue that had been diagnosed as normal, hyperplasia, dysplasia and cancer. The sectioned tissues underwent hematoxylin and eosin (H&E), Masson’s trichrome, cytokeratin, and vimentin staining. Histological sections were examined by experienced pathologists to identify cell types within the tissues. Cell types were identified for training and classification from all disease states.

2.2. Data collection

FTIR chemical images for the SD dataset were acquired in trans-mission mode using a PerkinElmer Spotlight FTIR spectrometer and microscope with a 16-element linear array detector at a nominal pixel size of 6.25 μm × 6.25 μm. Before imaging, a background image was acquired as a single tile from an area of the slide that had been identified as being tissue free. Each core in the TMA was imaged using 4 co-additions with a spectral resolution of 4 cm⁻¹. Chemical images were truncated to the spectral range 750 to 4000 cm⁻¹. A background scan was performed with 128 co-additions and ratioed to the single beam data to remove spectral contributions from the substrate, atmosphere, and globar source. Light microscope images of the chemically stained sections were acquired of the whole slide using an Aperio Scanscope system.

The HD dataset consisted of TMA BR961, which was imaged using the Agilent Stingray imaging system comprised of a 680-IR spectrometer coupled to a 620-IR imaging microscope with 0.62 numerical aperture averaged with 32 co-additions. The spectral resolution was 4 cm⁻¹ with a pixel size of 1.1 μm and a truncated spectral range of 1000 to 3801 cm⁻¹. The dataset contained 96 cores from separate patients with cases of normal, hyperplasia, dysplasia and malignant tumors.

2.3. Data pre-processing

The community has established a set of common pre-processing protocols that have been shown to be effective for biological samples.⁴⁴ In this work we apply the following pre-processing steps using in house implemented software:⁴⁵

1. Baseline correction –

Scattering through the specimen is mitigated by applying piece-wise linear (rubber band) baseline correction.⁴⁴

2. Normalization –

Normalization is performed by dividin the baseline corrected spectra by Amide I absorbance at ≈1650 cm⁻¹.

3. Dimensionality reduction –

We apply principal component analysis (PCA), keeping 16 principal components, which captures 90.03% and 96.86% of the spectral variance for SD and HD data, respectively.

2.4. Convolutional neural network (CNN) architecture

A typical CNN is composed of alternatively stacked convolutional and pooling layers followed by fully connected ANN. The cascading layers allow for hierarchical feature learning, where feature abstraction increases with layer depth. In general, increasing the depth of the network allows for learning more discriminative and semantic information.^35,46,47 The increase in the number of convolution and pooling layer duets offers the benefits of learning higher level abstract features from the data and provides translation invariance. The use of small convolution and pooling reduces the number of internal para-meters, allowing for increased depth.

The input and output of each CNN layer is referred to as a feature map. Since our input is a hyperspectral datacube, each feature map is a 2D array containing an image representing a single principal component. Typically, CNNs are composed of multiple stages, where each stage consists of 3 layers: (1) the convolution layer, (2) a non-linearity or activation layer, and (3) a pooling layer. Multiple stacks of these 3 layers are then followed by a fully connected classification module.

Each convolutional layer calculates the convolution of the input with a set of filters that are trained to detect particular features. The convolution layer is followed by an element-wise nonlinear activation operation. The convolution and activation layer weights and biases are calculated during training. The activity of the j^th feature map in the l^th layer is computed as:⁴⁸

$${\mathit{F}}_j^l=g\left(\sum _i^{N_f}\left({\mathit{W}}_{i,j}^l\ast {\mathit{F}}_j^{l-1}+{\mathit{b}}_j^l\right)\right),$$

where N_f denotes the number of feature maps in the (l − 1)^th layer, ${\mathit{F}}_j^{l-1}\in {ℝ}^{m\times n}$ is the i^th feature map in the (l − 1)^th layer that connects to feature map ${\mathit{F}}_{\text{j}}^{\mathrm{l}}$ in the l^th layer, ${\mathit{W}}_{i,j}^l\in {ℝ}^{k\times k}$ is the convolutional kernel (of size k) for ${\mathit{F}}_{\text{i}}^{\text{l-1}}$, ${\mathit{b}}_{\text{j}}^{\mathrm{l}}$ is the bias, g(·) is a non-linear activation function such as tanh or a rectified linear unit (ReLu), and * denotes the discrete convolution operator.

The convolutional layer is often followed by a pooling layer, with max pooling used as the most common pooling algorithm. Max pooling computes the maximum in a local window of the input feature map. By using a stride larger than 1, this results in subsampling of the input feature map, which in turn reduces the number of parameters and therefore the computational complexity.⁴⁹ A 2 × 2 pooling filter is the most common, which reduces the spatial dimensions of the output by half. The pooling layer is used to increase the robustness to small variations in the location of features detected by the convolutional layer.

The last module of a CNN typically consists of several fully connected layers, similar to a traditional ANN. The extracted high-level features are flattened to a fixed-dimensional vector. The feature vector learned by the l-th fully connected layer can be expressed as:

$${\mathit{F}}^l=g({\mathit{W}}^l{f}^{l-1}+{\mathit{b}}^l),$$

where W^l is the weight matrix connecting the (l − 1)^th layer and the l^th fully connected layer, f^l−1 is the feature vector in the (l − 1)^th layer, and b^l is the bias vector of the l^th layer.

The output layer consists of a softmax activation function used to compute the predictive probabilities for each class:

$${\text{softmax}}_c(\mathit{F})=p(y=c|\mathit{F})=\frac{e^{({\mathit{W}}_c{}^{\text{T}}\mathit{F}+{\mathit{b}}_c)}}{\sum _{j=1}^{N_c}{e}^{\left({\mathit{W}}_j^{\text{T}}\mathit{F}+{\mathit{b}}_j\right)}},$$

where y is the desired output label, f is the input vector, w is the weight matrix, b are the bias vectors, and N_c is the number of classes.

Supervised training of CNNs is performed using a form of stochastic gradient descent that minimizes the difference between the ground truth labels and the network prediction.⁵⁰ If the output layer consists of a softmax activation then the loss function is given by the cross-entropy loss:

$$L_i=-\log (p(y_i|{\mathit{F}}_i))$$

where L_i is the loss for sample i. The full loss for the dataset is the mean of L_i over all training examples as $L=\frac{1}{N}\sum _{i=1}^N{L}_i$, where N is the number of samples. During the training phase all the coefficients of all the filters in all layers are updated simultaneously during each iteration. Backpropagation^32,51 is used to compute the gradients.

2.5. CNNs for FTIR histological classification

The goal of tissue classification in histological samples is to generate a chemical map that can be used by a pathologist to identify the spatial distribution of tissue types within the sample. Previous work relies primarily on the vibrational spectrum to perform this labeling. Let X represent the hyperspectral image, such as a TMA data cube. Then $\mathit{X}\in {ℝ}^{m\times n\times b}$, where m is the number of rows, n is the number of columns, and b is the number of bands or spectral components. In general, a CNN takes an image as input and outputs the desired chemical map. In order to comply with the specific nature of CNNs, we decompose the acquired data X into patches containing spectral and spatial information for each pixel (Fig. 2).

Fig. 2.

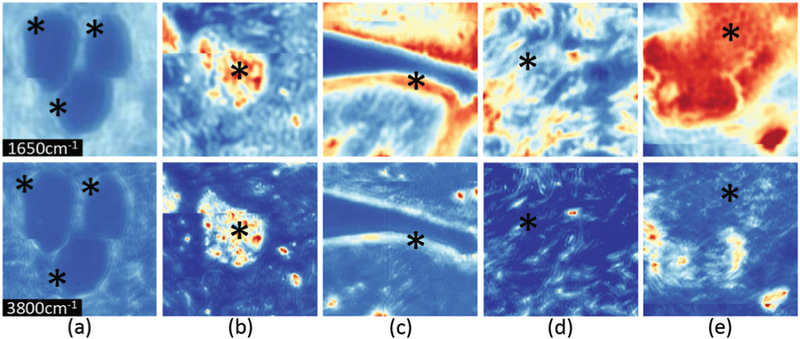
Spatial visual differences between different cell types. Cropped regions around pixels from HD cores (top row – band 1650 cm⁻¹, bottom row – band 3800 cm⁻¹) consisting of (a) adipocytes, (b) blood, (c) epithelium, (d) collagen, and (e) necrosis.

Let p_i be a pixel of X. We crop a volume of size s × s × b centered at p_i. Each pixel patch is a 3D volume – or tensor – containing all spatial and spectral information in the local neighborhood of p_i. We construct the training set using the label l_i of p_i and the patch P_i containing the local neighborhood of p_i. Given t training samples, the training set is given by T = {(P_il_i)}, for i = [1,…,t]. The set T is provided as input to the CNN training algorithm, which hierarchically builds high-level features that encode spectral and spatial characteristics of each pixel. An overview of the CNN architecture used for classification of HD data is shown in Fig. 3. The same architecture without batch normalization (BN) and input size of 17 × 17 × 16 is used for SD data.

Fig. 3.

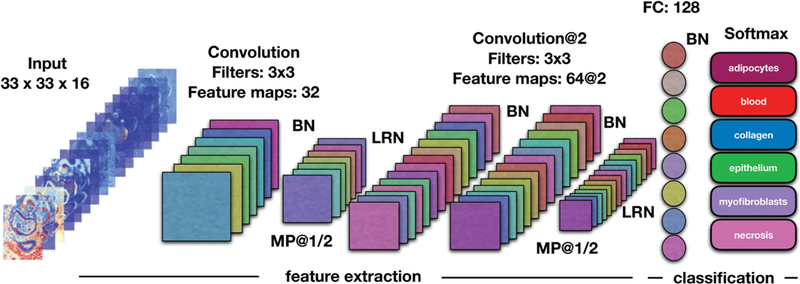
Schematic presentation of the CNN architecture used for classification of HD data. A spatial region of size 33 × 33 is cropped around each pixel. Data cubes of size 33 × 33 × 16 are fed into one convolution layer. Each input is convolved with filters of size 3 × 3 outputing 32 feature maps. The following layer is a max pooling layer, which reduces the spatial dimensions by half. Feature extraction continues with two more convolution layers consisting of 64 feature maps each. After another max pooling layer, the extracted features are vectorized and fed to a fully connected layer with 128 units. The last layer, softmax, consisting of 6 units (number of classes) outputs a vector of class probabilities. At the end, maximum probability is used to map each input pixel to its corresponding class labels. Legend: BN – batch normalization, LRN – local response normalization, MP – maximum pooling layer, FC – fully connected layer.

A convolution and max pooling based set of layers are introduced, followed by fully connected layers. In particular, one convolution layer consisting of 32 feature maps is followed by a max pooling layer with a kernel size of 2 × 2. This reduces the spatial dimension of the images by a factor of 2. The max pooling layer is followed by two additional convolution layers consisting of 64 feature maps each. An additional max pooling layer, with a kernel size of 2 × 2, is introduced followed by a fully connected layer of 128 units. The strides size is fixed as 1. For all convolution layers, we use kernels of size 3 × 3. The network ends with a softmax layer of size equal to the number of classes so that the final output is a vector of class probabilities for each pixel.

2.5.1. Software.

All data pre-processing was performed using our open-source SIproc software,⁴⁵ implemented in C++ and CUDA. Training and testing was performed in Python using open-source software packages. The Scikit-learn package⁵² was used for traditional classifiers (SVM, Random Forests, etc.) and TensorFlow, leveraging the TFlearn interface,⁵³ was used to design and implement CNNs.

2.5.2. Implementation hyperparameters.

The choice of hyperparameters is crucial when designing a deep learning architecture, significantly influencing overall accuracy and convergence speed. Through extensive experimentation on our training set, we chose the following hyperparameters:

1. Optimization method –

We used an Adadelta⁵⁴ adaptive learning rate method with a learning rate of r = 0.1. Adadelta adapts the learning rate over time, removing the need to manually tune for our application.

2. Regularization of the weights –

We used ℓ2 optimization combined with dropout⁵⁵ to minimize overfitting. Dropout keeps the activation of a fraction of hidden nodes and it randomly turns off the activation of the rest of the nodes in the layer based on a keep probability threshold. The keep probability is set to 0.5 and 1 in training and testing modes, respectively.

3. Batch normalization –

During training, the distribution of each CNN layer changes as the parameters of the previous layers change. This shift of the hidden unit values (otherwise known as internal covariate shift) complicates and slows down the training of deep neural networks. We address this problem by normalizing layer inputs using batch normalization.⁵⁶ Batch normalization allows the use of higher learning rates, reduces the need for careful initialization of training para-meters, it acts as a regularizer (sometimes eliminating the need for dropout), and provides faster convergence and higher accuracy rates.

4. Local response normalization –

This sort of response nor-malization implements the concept of lateral inhibition (capacity of an excited neuron to subdue its neighbors) from neurobiology. The output of the nonlinear activation function can result in unbounded activations. Local response normali-zation (LRN) is used to normalize these activations.³⁵ LRN helps to detect high frequency features with a large response and thus it promotes some sort of inhibition. By normalizing around the local neighborhood of a unit/neuron, LRN increases the sensitivity of the neuron compared to its neigh-bors and thus boosts the neurons with relatively larger activations.

5. Non-linearity –

We use the softplus nonlinear activation function:⁵⁷

$$\text{softplus}(x)=\ln (1+e^x),$$

where x is the output of each unit at a particular layer. Softplus is smooth and differentiable (near 0) and provided better convergence than the popular rectified linear unit (ReLU), likely because the ReLU hard saturation at 0 can hurt optimization by blocking gradient backpropagation.⁵⁸

6. Weight initialization –

We initialize the weights with random values from a normal distribution with a 0 mean and standard deviation of 0.02.

7. Batch size –

We chose a batch size of 128 and applied a mini-batch training strategy in order to reduce loss fluctuation. This batch size facilitated training with our system memory (250 GB), and higher-memory systems could benefit from larger batches.

8. Training epochs –

We train our network for 8 epochs, terminating training when validation accuracy began to decline.

9. Data shuffling –

We introduced data shuffling, applying random orderings for each epoch, in order to break any predefined data structure in the training set.

3. Results

Given our goal of establishing spatial features as a particularly useful metric in FTIR image classification, we use multiple metrics for assessing various goals for end users. Receiver operating characteristic (ROC) curves characterize the relationship between specificity and sensitivity, allowing clinicians to set acceptable false-positive versus true-positive rates. Alternatively, overall accuracy (OA) may be more useful for multi-class characterization, provided that the validation data is either balanced or weighted based on importance. The confusion matrix provides a quantitative measure of classifier performance robustness to multi-class labels and unbalanced datasets.

Several machine learning algorithms were evaluated to find the highest performing per-pixel classifier. In particular, we tested spectral-based classification algorithms such as KNN, SVM with linear and RBF kernels, DT, RF, NN, AdaBoost, NB, and a QDA classifier. The overall accuracies obtained after applying the above mentioned classification algorithms to SD and HD data are shown in Table 1. Notice that the RBF SVM outperforms all other spectral-based classifiers in terms of the overall accuracy.

Table 1.

Overall accuracy comparison (in percentage) between different spectral-based classifiers. Legend: k-nearest neighbor (KNN), support vector machine (SVM), radial basis function (RBF), decision tree (DT), random forest (RF), neural net (NN), adaptive boosting (AdaBoost), naive Bayes (NB), quadratic discriminant analysis (QDA)

	KNN	Linear SVM	RBF SVM	DT	RF	NN	AdaBoost	NB	QDA
SD	52.43	53.99	56.83	46.47	46.76	45.36	50.26	47.90	47.09
HD	64.75	63.93	76.28	61.38	69.28	66.22	62.50	73.90	67.96

Classifier performance is based on the results obtained from 10 different experiments with randomly selected training pixels. Experiments were executed on an Nvidia P100 GPU. The CNN framework was implemented in python using TFLearn,⁵³ which is a higher-level API for TensorFlow.⁵⁹ Comparisons for per-pixel classifiers were implemented using the Scikit-learn machine learning Python library.⁵²

3.1. Standard definition (SD) datasets

IR chemical images of breast tissue cores were compared to H&E, Masson’s trichrome, cytokeratin, and vimentin stained sections, and regions of adipocytes, blood, collagen, epithelium, myofibroblasts, and necrosis were identified. After applying PCA, the dimensions of the training set were 2800 × 6800 × 16, whereas the testing set consisted of a datacube of size 3400 × 6800 × 16. Separating the cores into training and testing samples from different slides ensures complete independence between training and testing sets and assesses the ability of the classifiers to generalize to data acquired under conditions that may vary in a standard laboratory setting. Table 2 shows the number of annotated pixels per class for the training and testing sets, indicating a high inbalance in the number of available annotations for different tissue types. The unbalanced number of training samples is common in histological data and a known challenge in training CNNs as the network can become biased towards classes with larger training samples. In order to minimize bias, we stack copies of underrepresented classes to balance training data. For example, we use 100 000 pixels for each class to train the CNN.

Table 2.

Description of the available annotations for the training and testing SD datasets. BR1003 and BR2005b are used for training while BR961 and BR1001 are used for testing. Note that the per-pixel labels are highly unbalanced, which is common in histological images

Classes	# of annotated pixels per class
	Train	Test
Adipocytes	10 261	9864
Blood	1072	1158
Collagen	102 350	80 318
Epithelium	38 646	73 264
Myofibroblasts	17 655	154 389
Necrosis	13 653	51 555
Total	183 637	370 548

The Python implementation of the SVM in Scikit-learn⁵² is based on the libsvm library. The time complexity for the training (fitting) is more than quadratic with the number of samples. SVMs are discriminative classifiers formally defined by a separating hyperplane. Given labeled training samples, the SVM algorithm finds the “optimal” multidimensional hyperplane that best separates the classes. We use the one-vs.-the-rest multiclass strategy for the SVM classifier, which consists in fitting one classifier per class, i.e. for each classifier the class is fitted against all other classes. This strategy is more computationally efficient, given the size of our data, and proves to be more stable, accurate, and reproducible.

An SVM classifier was constructed using the pixels from the training set summarized in Table 2. In particular, SVM was trained using 10 000 samples for each class in order to balance the number of samples per class. A greater or lower number of samples per class did not show any significant improvements in the overall accuracy. A Gaussian RBF kernel was used and after extensive experimentation a penalty parameter of C = 1.0 and a kernel coefficient of $\gamma =\frac{1}{n_{\text{features}}}$ was used, where in our application n_features = 16. The number of support vectors is automatically determined by the Scikit-learn implementation.

Table 3 summarizes the per class accuracy values and the overall accuracy obtained after classifying the SD datasets, while Table 4 provides the sensitivity and specificity for each class at the optimal threshold selected for the final multi-class classifier. CNN achieves higher classification accuracy for all other classes except epithelium. It is well known that collagen and epithelium can be easily correctly classified using the spectral information only. CNN overcomes SVM in AUC values for all classes (Fig. 5). In terms of the overall accuracy CNN achieves a significant ≈23% improvement. This is mostly due to the ability of CNN to classify with higher accuracy adipocytes, myofibroblasts, and necrosis. The high overall accuracy achieved by CNN implies that a per pixel classification map can be produced with an image quality that is comparable to existing diagnostic tools.

Table 3.

Per class and overall accuracy (OA) for a support vector machine (SVM) classifier and the proposed CNN applied to SD data (6.25 μm per pixel)

Class/method	SVM	CNN
Adipocytes	75.35 ± 0.58	89.38 ± 3.35
Blood	61.14 ± 0.3	68.83 ± 1.57
Collagen	94.26 ± 0.26	95.79 ± 0.28
Epithelium	90.65 ± 0.09	82.98 ± 0.75
Myofibroblasts	10.8 ± 0.58	64.57 ± 3.08
Necrosis	81.61 ± 0.35	91.89 ± 1.13
OA (%)	SVM: 56.41 ± 0.27	CNN: 79.45 ± 1.25

Table 4.

Sensitivity/specificity values for each histological class for a SVM classifier and the proposed CNN applied to SD data

Class/method	SVM	CNN
Adipocytes	75.47/91.08	93.20/88.97
Blood	60.97/98.98	70.64/99.12
Collagen	94.11/86.49	95.89/96.89
Epithelium	90.72/77.53	82.88/94.62
Myofibroblasts	11.41/99.57	61.95/96.07
Necrosis	82.02/94.49	90.63/98.79

Fig. 5.

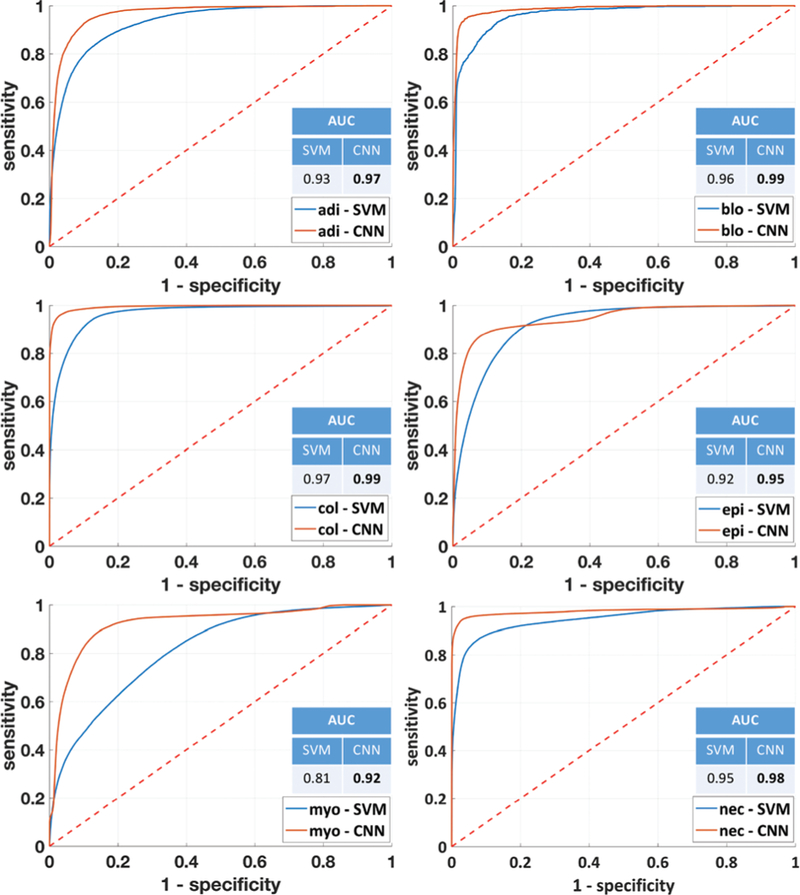
ROC curves and AUC values for each individual class obtained using both SVM and CNN to classify SD data. For the CNN, ROC curves are computed by training the classifiers for each class, where elements of that class have the target value 1 and elements outside of that class have the target value 0. The ROC value for the SVM is obtained by calculating the posterior probability based on the percentage of individual votes. While the CNN provides a significant improvement for most classes, the increased differentiation between adipocytes, myofibroblasts, and collagen stands out due to the prevalence of both in breast biopsies.

Fig. 4 shows 3D plots of the confusion matrices for the six-class system using SVM and CNN classifiers. Correctness of classification rates per class are shown by the diagonal bars. Notice that the confusion matrix for CNN shows significantly higher bars for adipocytes, myofibroblasts, and necrosis classes. Furthermore, the CNN confusion matrix is more sparse, which indicates less mixing between different classes.

Fig. 4.

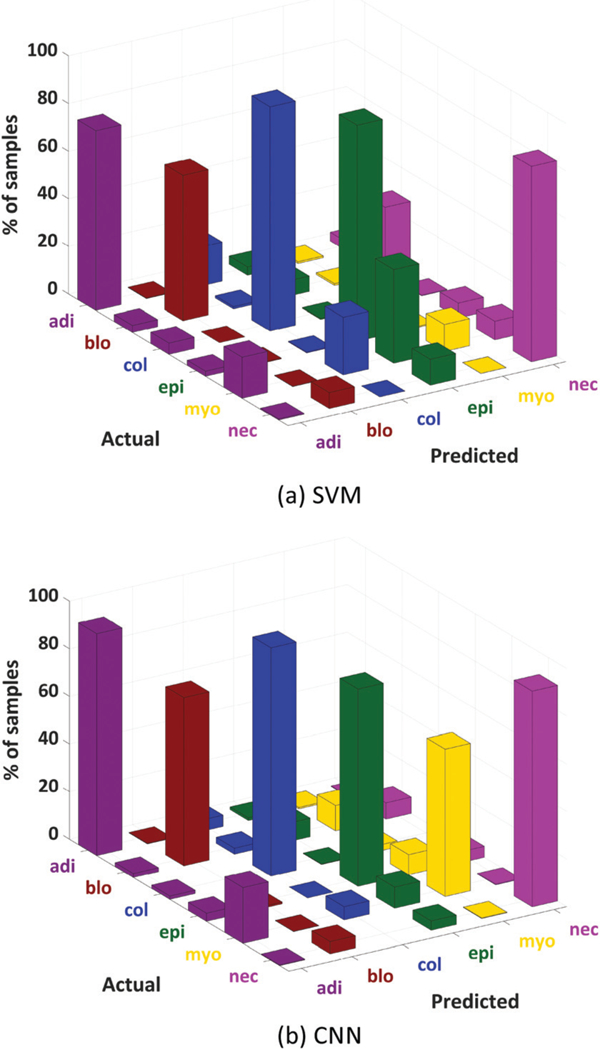
Three-dimensional plots of the confusion matrices for SVM (a) and the proposed CNN (b) on SD data. We see particularly large improvements in adipocyte classification as well as increased differentiation between collagen and myofibroblasts. Both of these results are likely due to the inclusion of spatial features.

The output of SVMs does not consist of probability estimates but rather of per-class scores for each sample. Probability estimates for binary and multi-class classification are obtained in the Scikit-learn implementation⁵² using Platt scaling and cross-validation on the training data.^60,61 The output of CNN is a vector of probabilities for each pixel, which represents an estimation of the probability that a pixel belongs to a particular class. The adjustment of the class probability threshold allows for the visualization of the trade off between true positives and false positives using ROC curves. The performance of the classifiers in terms of sensitivity and speci-ficity of the model for classification of the independent test set is shown in Fig. 5. The CNN ROC curves appear better than SVM for most classes. This is particularly noticeable in the case of adipocytes, myofibroblasts and necrosis, likely because of the additional consideration of spatial features from the CNN.

3.2. High definition (HD) datasets

Given the exceedingly long acquisition and analysis times, we employed one half of a TMA for training and the other half for validation. While the actual results are likely to be slightly worse for an independent dataset, we emphasize the comparison with SVM here and the general trend should still hold. Table 5 shows the number of annotated pixels per class for the training and testing sets. The high class imbalance between different tissue types is also present here. In order to balance the number of pixels per class in the training set we repeat the pixels of underrepresented classes as in the case of SD data. We use 100 000 pixels for each class for the training of the CNN.

Table 5.

Description of the pixels used for training and testing on HD data. Left and right halves of TMA BR961 are used for training and testing, respectively

Classes	# of annotated pixels per class
	Train	Test
Adipocytes	133 171	33 724
Blood	8574	5608
Collagen	443 587	650 589
Epithelium	582 621	463 579
Myofibroblasts	1 044 708	1 069 940
Necrosis	532 820	268 103
Total	3 745 481	2 491 543

Table 6 shows the per class accuracies and the overall accuracy obtained after classifying the HD dataset, while Table 7 shows the sensitivity and specificity for each class in the final classifier. CNN achieves higher classification accuracy for all classes. The higher class accuracy obtained via CNN is noticeable especially for adipocytes, myofibroblasts, and necrosis. CNN also overcomes SVM in AUC values for most classes except blood and collagen for which they achieve same value. In terms of the overall accuracy CNN achieves about 16% improvement.

Table 6.

Per class and overall accuracy (OA) for a support vector machine (SVM) classifier and the proposed CNN applied to HD data (6.25 μm per pixel)

Class/method	SVM	CNN
Adipocytes	37.44 ± 1.86	88.35 ± 4.85
Blood	83.62 ± 0.43	89.15 ± 3.13
Collagen	97.51 ± 0.07	98.92 ± 0.6
Epithelium	90.80 ± 0.31	91.20 ± 1.56
Myofibroblasts	60.51 ± 0.43	90.25 ± 4.28
Necrosis	67.32 ± 0.74	92.03 ± 1.02
OA (%)	SVM: 76.28 ± 0.12	CNN: 92.85 ± 2.12

Table 7.

Sensitivity/specificity values for each histological class for a SVM classifier and the proposed CNN applied to HD data

Class/method	SVM	CNN
Adipocytes	38.69/98.92	91.86/99.58
Blood	84.04/99.48	87.50/99.98
Collagen	97.49/94.10	98.22/98.54
Epithelium	90.91/80.66	90.90/96.41
Myofibroblasts	60.30/97.14	93.39/97.29
Necrosis	66.68/99.40	91.89/99.97

A confusion matrix was constructed for the independent testing set (Fig. 6). The sparsity of the CNN confusion matrix reveals that CNN is better at discriminating between different classes. The diagonal bars are higher for CNN especially in the case of adipocytes, necrosis, and myofibroblasts.

Fig. 6.

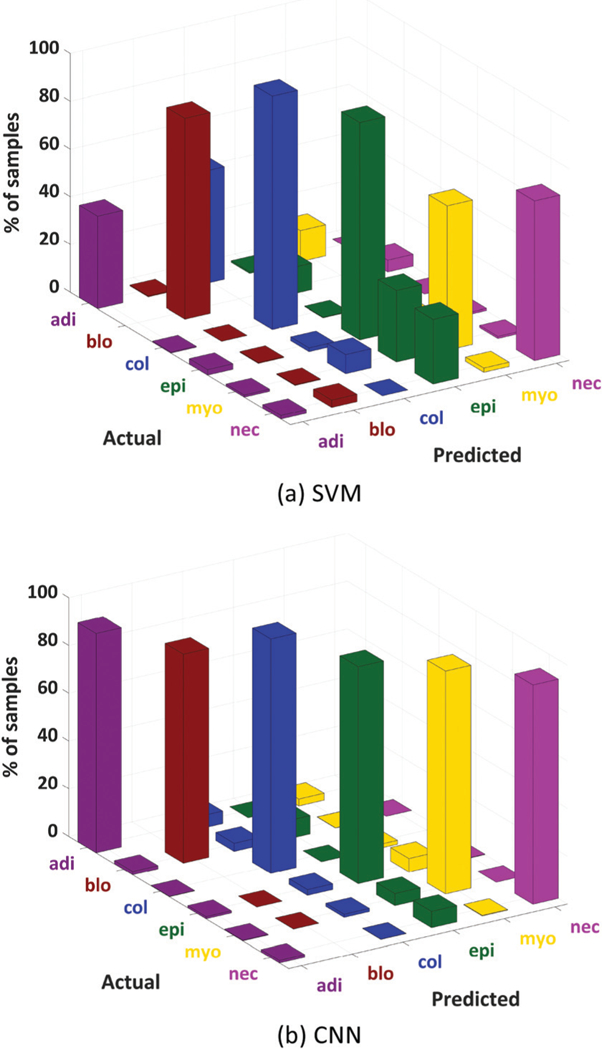
3D plot of confusion matrices obtained for all independent test pixels in the HD (1.1 μm) microarray image data using SVM (a) and CNN (b) classifiers.

The performance of the classifiers in terms of sensitivity and specificity is shown in Fig. 7, where a significant improvement in ROC curves and AUC metrics can be noticed. Visual inspection of the validation TMA shows a strong spatial correlation between the CNN classified false-color results and the corresponding adjacent H&E histology (Fig. 8).

Fig. 7.

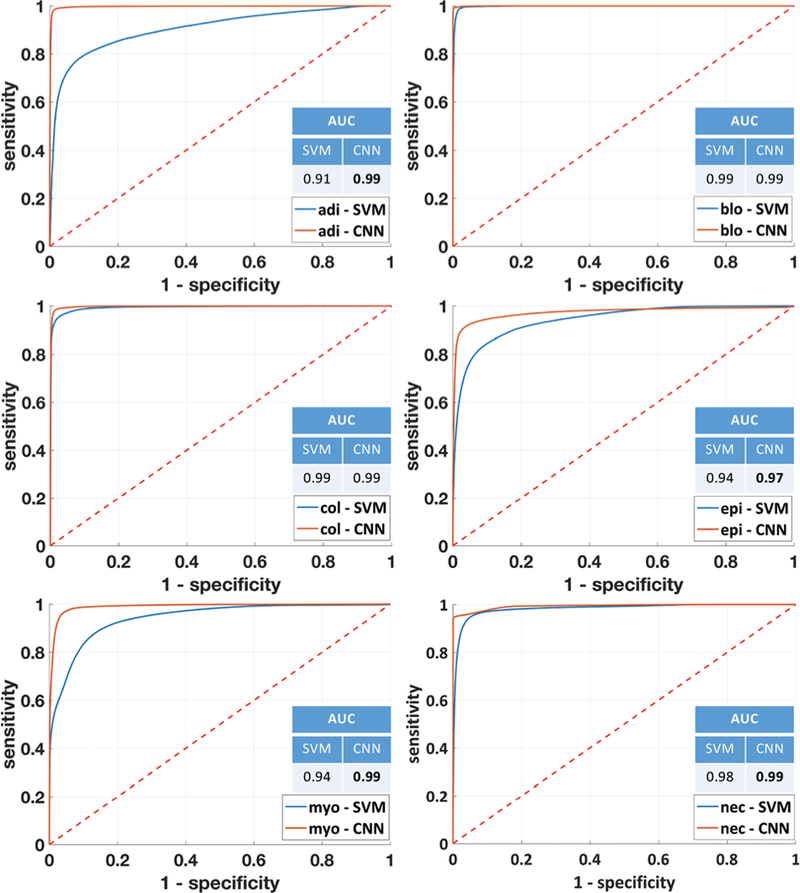
ROC curves and AUC values for each individual class for SVM and CNN classifiers applied to HD data.

Fig. 8.

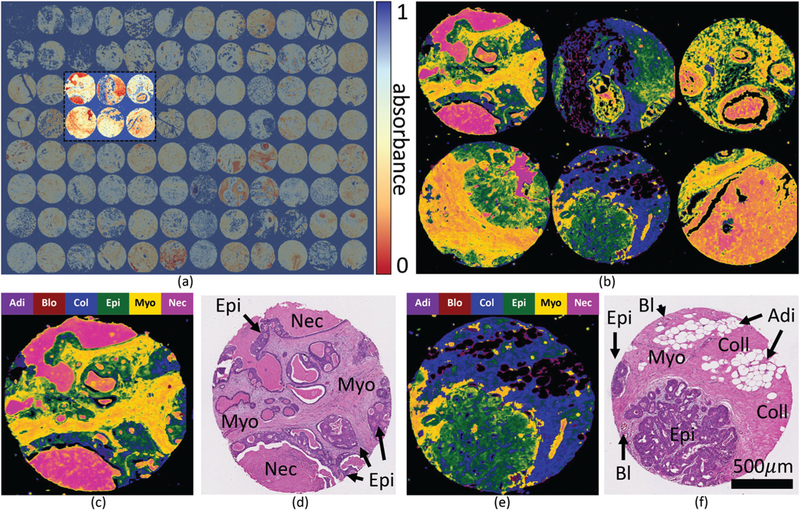
HD classification using a convolutional neural network with both spectral and spatial features. (a) FTIR validation microarray (11 557 × 17 000 pixels) showing the Amide I (1650 cm⁻¹) absorption band. (b) Classified cores labeled using a false-color overlay on the Amide I absorbance band. Individual classified cores are shown in false-color (c and e) with corresponding images H&E stained adjacent sections (d and f ). H&E images are labeled with cell types of interest, annotated using additional immunohistochemical stains of adjacent sections.

We have also applied a CNN architecture without using spatial information. In this implementation, only the pixel spectral information is used. The overall accuracy results are summarized in Table 8. We can observe that CNN with spatial information outperforms the spectral-based classifiers, such as SVM and spectral CNN, for both SD and HD data. This confirms that the use of spatial information in combination with the spectral information is indeed crucial for improving the classification accuracy.

Table 8.

Overall accuracy comparison (in percentage) between an SVM classifier, CNN without spatial information (spectral only), and CNN with spatial information applied to the SD and HD data

	SVM	CNN (spectral)	CNN
SD	56.41	62.52	79.45
HD	76.28	79.54	92.85

Care must be taken in constructing the ground truth, since tissue is labeled using adjacent sections that may not perfectly align with FTIR images. In addition, the effects of scattering and noise may confound analysis. Spectra-only based classification methods assume that individual spectra are independent. In the case of FTIR images, this is almost certainly not the case. Machine-learning models, such as CNNs can take advantage of the spatial dependence of individual spectra in order to improve classifier performance.

4. Discussion

The accurate differentiation of cell types in breast tissue is of critical importance for accurate diagnosis and staging of breast cancer. FTIR chemical imaging has the potential to provide additional information to augment diagnosis techniques, leading to improved patient treatment and care. While there have been significant advances in both FTIR instrumentation and spectral computation, appropriate assessment of classification quality has been lacking. An assessment is critical to ensure that classifiers are operating correctly and that spectral and spatial information is being assigned to the appropriate cell type. This is especially important going forward due to the increasing evidence that the different compartments within tissues may hold novel spectral biomarkers of diagnostic or prognostic value, such as the stroma region in breast cancer. FTIR imaging is a rapidly emerging tool that has potentially significant applications in histopathology due to its ability to add novel biochemical information in an objective, automated, and non-destructive fashion. This biochemical information derived from different cell types may provide a new route to identify biomarkers that can enable a better prediction of those breast cancers that will be lethal and will undergo metastases to other organs.

Due to the ability to learn complex features directly from the data, CNNs can also be used as feature extractors only. The extracted features can then be passed as input to other machine learning classification models. In many studies, it has been shown that the features extracted using CNNs can significantly improve the capabilities of SVMs and KNNs as opposed to running these algorithms on the raw data.^37–40 These studies demonstrate that CNNs are powerful feature extraction tools and thus can be combined with other machine learning models that are better at classification but cannot learn invariant and complicated features.

We investigated the potential of FTIR chemical imaging and CNNs for classification of tissue types of importance in breast histopathology. We demonstrated that CNNs can be trained with FTIR chemical images in order to accurately discriminate between six histological classes. Compared to the commonly used SVM approach, we were able to demonstrate that CNNs offer at least as accurate an approach when considering spectral data alone, and an improved approach when including spatial information. As a consequence, cell type differentiation can be improved by using chemical and spatial information in a quantitative and objective manner and does not require manual intervention to generate and interpret images. The results show that exploiting the spatial information in combination with a small number of PCA components can provide better classification performance, thus utilizing the full information content of the IR imaging data set. The selection of the number of principal components used depends on the data and the selecting criterion used, such as the percentage of the total variance retained. The percentage of the total variance captured and hence the number of principal components kept vary in different studies.^62–65 However, for FTIR data usually 90–99% of the variance is kept.²²

Training and testing on separate TMAs introduces several challenges to tissue classification in FTIR imaging. The measured spectra of different tissue types from different TMAs is affected by the noise level, the substrate used, differences in tissue thickness, and variations in focus across the imaged TMA. However, training and testing must be performed on separate TMAs in order to demonstrate the potential of a classification method for application in real settings for disease diagnosis and to test its ability to generalize to new datasets. Here, we have shown that the proposed CNN classifier can significantly outperform SVM in terms of overall accuracy for different training and testing TMAs of SD data. This has to be further tested on HD data for which the variations on different TMAs can be significantly increased due to higher data acquisition times.

5. Conclusion

We describe a deep learning method for classification of IR imaging data for tissue histology. As far as we are aware, this is the first application of deep convolutional neural networks applied to FTIR imagery, as well as the first application of deep CNNs to HDIR images, where spatial features could be of high benefit to classification. As opposed to previous spec-tral-based approaches, the integrated inclusion of spatial data offers an avenue for even higher performing classifiers. Thus, FTIR imaging coupled with CNNs can provide an accurate and potentially rewarding avenue for automated and objective analysis in digital pathology. Future studies of FTIR image classification using the techniques described here with a large number of patients are required to assess the full potential of deep learning for routine classification of cell types in tissue.