Spatial-temporal Analysis of Cancer Risk in Epidemiologic Studies with Residential Histories

Abstract

Exploring spatial-temporal patterns of disease incidence identifies areas of significantly elevated risk and can lead to discoveries of disease risk factors. One popular way to investigate patterns in risk over space and time is spatial-temporal cluster detection analysis. The identification of significant clusters may lead to etiological hypotheses to explain the pattern of elevated risk and to additional epidemiologic studies to explore these hypotheses. Several methodological issues and data challenges that arise in space-time cluster analysis of chronic diseases, such as cancer, include poor spatial precision of residence locations, long disease latencies, and adjustment for known risk factors. This paper reviews the key challenges faced when performing cluster analyses of chronic diseases and presents a spatial-temporal analysis of non-Hodgkin lymphoma (NHL) risk addressing these challenges. Residential histories, collected as part of a population-based case-control study of NHL (the National Cancer Institute [NCI]-Surveillance, Epidemiology, and End Results [SEER] NHL study) in four SEER centers (Detroit metropolitan area, Los Angeles, California, Seattle metropolitan area, and Iowa) were geocoded. In this analysis, we explored previously detected spatial-temporal clusters and adjusted for exposure to polychlorinated biphenyls (PCBs) and genetic polymorphisms in four genes, previously found to be associated with NHL, using a generalized additive model framework. We found that the genetic factors and PCB exposure did not fully explain previously detected areas of elevated risk.

Introduction

Exploring spatial-temporal patterns of disease incidence has proven to be beneficial for identifying areas of significantly elevated risk and discovering significant factors associated with risk. Particularly for cancer, there is a long history of research analyzing geographic patterns in disease incidence and mortality with the objective of discovering environmental determinants of disease (Fraumeni and Blot 1977). Examples of risk factors revealed by analytic epidemiologic studies that followed upon observations of geographic patterns of cancer include exposure to asbestos from shipyard as a risk factor for lung cancer among men along the southeastern United States seaboard (Blot et al. 1979) and chronic use of snuff as a risk factor for oral and pharyngeal cancer among women in the southern United States (Winn et al. 1981).

While there have been success stories in pursuing leads from analyzing geographic patterns of disease, most early studies of spatial patterns of cancer were ecological studies, using data on disease and the population at risk aggregated to areal units, such as counties. Ecological studies have a number of inherent analytic challenges (Beale et al. 2010) that limit their role in etiologic research. These challenges include spatial inaccuracy of data, exposure misclassification, and ecological bias (Elliott and Savitz 2008; Wakefield and Elliott 1999). In addition, analyses in ecological studies are usually based on administrative geographic boundaries that are not inherently meaningful for studying disease. These studies lack information on residential history and risk factors for individuals. Furthermore, environmental exposure data of interest typically will have been collected on different spatial scales.

For establishing causal factors in chronic diseases, studies should collect individual-level data (Elliott and Savitz 2008). In public health research, individual-level data are the foundation of case-control and cohort studies. Often, these epidemiologic studies contain spatial information at the individual level through residential addresses, which may include the address at time of diagnosis for a case or time of study enrollment for controls or cohort subjects. Increasingly, residential histories over long periods of a participant’s lifetime are available (collected directly from participants), hence, it is possible to consider residential mobility and disease latency when analyzing disease patterns. In addition, with the increasing accessibility of geographic information systems and geocoding technology, it is possible to analyze epidemiologic data at a finer spatial scale than in the past.

One approach to analyzing geographic patterns in disease that makes use of individual-level data is the detection of spatial clusters, i.e., areas of significantly elevated risk. The identification of clusters in space and time can lead to the development of hypotheses to explain the pattern of elevated risk and reveal important clues about disease etiology. We note the distinction in goals between detecting an individual cluster (or clusters) and approaches to describe general clustering of disease, the general tendency for cases to occur nearer other cases than one might expect under equal risk (Besag and Newell 1991; Waller and Gotway 2004). The incorporation of temporal data further refines the analysis by linking cases that are coincident in both time and space.

Our discussion focuses on cluster detection for individual-level epidemiologic studies with residential histories. In the remainder of this paper, we discuss the challenges that epidemiologic studies with residential histories present for existing approaches in cluster detection, and then present a spatial-temporal analysis of non-Hodgkin lymphoma (NHL) risk addressing these challenges through a statistical analysis approach that evaluates residential histories and adjusts for known risk factors. Our motivating interest centers on evaluation of whether or not previously detected areas of significantly elevated NHL risk in a case-control study could be explained by adjusting for additional environmental and genetic risk factors.

Cluster analysis approaches for epidemiologic studies with residential histories

There are several existing methods for spatial cluster detection within individual-level data. Among the most commonly used methods are local scan statistics (Kulldorff 1997; Kulldorff 2006), kernel density ratio estimation (Bithell 1990; Kelsall and Diggle 1995), Q-statistics (Jacquez et al. 2005), and generalized additive models (Kelsall and Diggle 1998; Vieira et al. 2005; Webster et al. 2006), and we limit our discussion to these methods. Few cluster detection methods are designed to fully evaluate the multidimensional, spatial and temporal data that are increasingly available within epidemiologic studies. To improve the power to detect unexplained clusters when exploring spatio-temporal patterns of disease in individual-level data, analysis approaches should explicitly consider residential patterns that change over time due to migration and adjust for known risk factors.

In many cluster studies, the residential locations of study subjects at time of diagnosis are typically the only address information available and are assumed to be a reasonable surrogate for unmeasured environmental exposures, defined broadly to include lifestyle factors as well as pollutants. Due to residential mobility, the residence at time of diagnosis of disease may not accurately reflect the most relevant environmental exposures for diseases with long latencies, such as cancer. We define latency as the number of years between exposure to a relevant risk factor and the diagnosis of disease. For diseases with long latencies, migration must be considered. Researchers in public health and geography (Jacquez et al. 2005; Vieira et al. 2005; Sabel et al. 2009) have recognized the importance of migration when studying patterns and etiology of disease. Ignoring migration when studying health outcomes with long latencies can lead to exposure misclassification, diminished study power, and biased risk estimates (Tong 2000). Migration bias can occur when there is differential migration related to a factor of interest among study population groups (Tong 2000). The factor of interest is typically space in a cluster detection study.

Among existing methods, only Q-statistics were designed to adjust for migration. Q-statistics can consider the entire residential history of study subjects, but requires an a priori knowledge of the number of nearest neighbor subjects to use in defining the relevant cluster size when searching over space for clusters. Unfortunately, one often does not know which number of nearest neighbors is relevant for a particular study. The local scan statistics and the kernel density ratios were designed to model only one relevant location for each study subject. Analyses with these methods typically use the residential address at the time of diagnosis, which makes the implicit assumption that individuals do not migrate (at least between the time of the relevant exposure and the diagnosis of disease) or that the latency between causal exposures and diagnosis of disease is negligible (Jacquez 2004). Generalized additive models (GAMs) have the potential to model several residential locations in a residential history, but studies to date using GAMs have either assumed one latency period with little empirical justification or have included all historical residential locations for each subject in one statistical model, violating the model assumption of independent observations with potentially biased model parameters (Vieira et al. 2005; Webster et al. 2006). Vieira et al. (2008) explored latency while estimating disease risk spatially using GAMs in overlapping time periods, but included multiple addresses per subject in each time period. An adjustment is needed to include several records for a subject in a GAM, or the data must be structured in a way to include only one record per subject in order to have an unbiased model.

As the goal of cluster detection is hypothesis generation through identification of geographic areas of unusually high risk, any known risk factor that could explain a detected cluster should be adjusted for in the analysis. Any cluster observed after adjustment for known risk factors could be potentially explained by a yet unknown spatially- or temporally-patterned risk factor. Local scan statistics and kernel density methods do not allow for simple adjustment for risk factors with individual-level data. With Q-statistics, adjustment for risk factors is done separately from cluster detection. In contrast, generalized additive models (GAMs) can adjust for risk factors and test for clusters within a unified statistical framework. We next present an investigation of areas of significantly elevated NHL risk illustrating a GAM-based approach that simultaneously adjusts for risk factors, considers latency periods, and tests for significant clusters in one unified statistical framework.

Spatial-temporal analysis of non-Hodgkin lymphoma risk

Study population

Since 1975 in the United States, the annual age-adjusted incidence rate of NHL increased more than 75 percent from 11.1 to 19.8 per 100,000 person-years (Ries et al. 2003). The cause for this increase is largely undetermined and little is known about the etiology of NHL, except for established risk factors that include certain viral infections, immune suppression, and a family history of hematolymphoproliferative cancers (Chatterjee et al. 2004). Incidence of NHL increases with age, is higher in men, and is 40–70% higher in whites compared to blacks (Jemal et al. 2004). NHL incidence has also been associated with specific genetic polymorphisms (Morton et al. 2008) and environmental risk factors including pesticides (Zahm et al. 1990), insecticides such as chlordane (Colt et al. 2006), and polychlorinated biphenyls (PCBs) (Colt et al. 2005). Taken together, the established risk factors account only for a small proportion of the total annual NHL cases.

A previous analysis of NHL risk in the National Cancer Institute (NCI) Surveillance, Epidemiology, and End Results (SEER) NHL study, a population-based case-control study of NHL at four SEER centers (Detroit, Los Angeles, Seattle, and Iowa), revealed unexplained areas of significant risk in Detroit, Los Angeles, and Iowa after adjusting for the risk factors age, race, gender, education, and home treatment for termites before 1988, a surrogate for exposure to chlordane (Wheeler et al. 2011). The analysis also explored the latency period that may be relevant for environmental exposures for NHL and found that a lag time of 20 years before diagnosis was most associated with risk of NHL. Here, we perform an analysis of NHL risk in the NCI-SEER study to adjust for additional risk factors of exposure to PCBs and presence of specific genetic polymorphisms available for a subset of subjects to ascertain whether or not they explain the previously detected areas of elevated risk.

Details of the NCI-SEER study have been reported previously (Chatterjee et al. 2004; Morton et al. 2008; Wheeler et al. 2011). NHL cases aged 20 to 74 years were identified between July 1, 1998 and June 30, 2000. Participants provided lifetime residential histories that were then matched to geographic address databases. In addition to demographic data and select risk factors available for all subjects, carpet dust samples from used vacuum cleaner bags were collected in homes to measure residential exposure to PCBs for 58% of cases and 56% of controls, and genotyping was conducted from DNA samples for 89% of cases and 93% of controls. Details on the collection and analysis of the dust samples are available in Colt et al. (2005). Based on the previous findings of a significant association between NHL incidence and residential levels of PCB congener 180 (Colt et al. 2005; Morton et al. 2005), we used concentrations of this PCB in our analysis. We used a binary measure of PCB 180 exposure, defined as 1 if PCB 180 was >=44.4ng/g in dust, where this level was the lower bound for the highest category of exposure in Morton et al. (2008). Based on findings of increased risk of NHL with genetic polymorphisms for the genes FCGR2A, RAG1, TNF, and XRCC1 (Morton et al. 2008), we included these in our analysis.

To be consistent with the analysis of Wheeler et al. (2011) while exploring the elevated areas of NHL risk, this analysis included only study participants with a complete 20-year residential history within one of the three study centers that contained areas of significantly elevated risk. A total of 671 cases (67 percent) and 516 controls (68 percent) met this criterion. Among these subjects, there were 521 cases and 404 controls with complete genetic data and 305 cases and 212 controls with complete genetic and PCB data.

GAM analysis with lag times

We used GAMs (Hastie and Tibshirani 1990) to model spatially the probability that an individual was diagnosed with NHL. The methods are further detailed in Wheeler et al. (2011). Given the coordinates(s₁, s₂) for residential locations(s) at a particular time t, the odds of being a case are modeled as

$$\text{logit}[p(s_1,s_2)]=\alpha +{\beta }^{\prime }x+Z_t(s_1,s_2),$$ (1)

where the left-hand side of the equation is the log of the disease odds at location s, α is an intercept, β is a vector of regression coefficients, x is a vector of covariates observed at location s, and Z_t (s₁, s₂) is a function of the residential locations at a particular time point. This function provides spatial smoothing of the locations and models spatial variation not explained by the covariates. The spatially smoothed term may be considered a surrogate for unmeasured environmental factors at a specified time. The technique of smoothing over residential locations is used to measure the density of cases relative to controls over space. This approach models cases and controls as a marked heterogeneous Poisson point process with intensity $\lambda (s)={\lambda }_1(s)+{\lambda }_0(s)$, where ${\lambda }_1(s)$ denotes the intensity of cases and ${\lambda }_0(s)$ the intensity of controls.

Within this framework, we can evaluate several lag times in years before diagnosis, for example 20 years and 10 years, through Z_t and select the one that best explains the risk of disease. Analysis of deviance (ANODEV) may be used to evaluate the significance of the lag times by testing differences in deviances between nested models, with and without Z_t. The difference in deviances for two nested models approximately follows a chi-square distribution with an associated p-value. A significantly lower deviance from a model with a lag time of k years indicates that using the smoothed pattern of residential locations from k years before diagnosis significantly explained overall disease risk. This model specification does not consider the duration spent at each residence but rather the pattern of residences at any time t.

For the form of the spatial smoothing function, we used loess, or locally weighted scatterplot smoothing (Cleveland 1979), and smoothed over both spatial dimensions. The smoothing function has a span parameter that controls the amount of smoothing. The span parameter must be estimated, and we selected the span that minimized the Akaike Information Criterion (Akaike 1973) over a large range of span values. We estimated the GAM model parameters in the statistical analysis software R (R Development Core Team 2010) using the gam package, version 1.03.

To assess the variation in risk of disease over space, we plotted the local odds ratios (ORs) using the model specified in equation (1). To produce a map of local ORs, we first estimated all parameters for the model expressed in equation (1) using the study data. We then predicted the log odds over a rectangular grid placed over the study area using the estimated model parameters. To provide an interpretable odds ratio map, we used the entire study population as the reference and divided the odds from the spatial model at each grid point by the odds from the null model.

For inference on clusters, we identified areas of significantly elevated risk using Monte Carlo randomization. This procedure compares the observed local odds ratios to distributions of local odds ratios under the null hypothesis that case status does not depend on location (Waller and Gotway 2004). We used 999 Monte Carlo samples to build the permutation distribution of odds ratios at each grid location, using the optimal span from the observed data for the permutations. We identified areas of significantly elevated risk as those areas that had an observed odds ratio in the upper 2.5% of the ranked permutation distribution of odds ratios. Similarly, we identified areas of significantly lowered risk of disease as those having an observed odds ratio in the lower 2.5% of the ranked permutation distribution. Clusters of either elevated or lowered risk are significant at the 0.05 level (assuming a two-tailed distribution). We mapped the local ORs and highlighted the significant areas of risk for disease simultaneously.

We applied the approach described above in the three study centers (Detroit, Iowa, Los Angeles) in the NCI-SEER NHL study where clusters were previously detected (Wheeler et al. 2011). In the previous adjusted models, the most significant lag time was 20 years in Detroit (p = 0.07), Iowa (p = 0.14), and Los Angeles (p = 0.03) and clusters of elevated risk were detected at a time lag of 20 years in all three study areas; therefore, we focused on this time lag in our analysis. We fitted separate models for each center. We fitted crude models; models adjusted for the core covariates age at enrollment, gender, race, education, and home treatment for termites before 1988; and models additionally adjusted for PCB 180 and genetic polymorphisms for the four previously mentioned genes. The covariates did not vary over time in the models. We fitted the models for three sets of data for each center. We used a set of all subjects with complete residential histories and for whom missing values for PCB 180 and genetic risk factors were coded with a missing indicator, a set of subjects with complete genetic data, and a set with complete genetic and PCB data.

Results

The analyses from all three subsets of study subjects showed that adjusting for PCB 180 and the four genetic factors made little difference in Detroit, Iowa, and Los Angeles at a lag time of 20 years before diagnosis in terms of the significance of the spatial term in the models and the presence of significantly elevated or lowered areas of NHL risk (Table 1). The only change in significant clusters due to adjusting for the genetic factors and PCB 180 occurred in Detroit with the model that included those with complete genetic and PCB data, where an area of significantly lowered risk was explained by these factors. Adjusting for the core covariates was adequate to detect an area of significantly elevated risk that was not found by the crude model in Los Angeles in the genetic and PCB subset of data.

Table 1.

Sample size, estimated span parameter, approximate p-value for the spatial term, and presence of significantly elevated or lowered risk areas of NHL for crude and adjusted models for several sets of data for three centers. For each center, the first set is all subjects with complete 20-year residential histories and uses missing indicator coding for the genetic factors and PCB exposure, the second set is only subjects with complete genetic data, and the third set is only subjects with complete genetic and PCB data. The core covariate adjusted model includes age, gender, race, education, and home treatment for chlordane before 1988. The other adjusted models also include genetic polymorphisms in four genes, as well as exposure to PCB 180 in some models.

Model	Cases	Controls	Total	Span	p- value	High- Risk Cluster	Low- Risk Cluster
Detroit - Missing indicator	214	144	358
Crude				0.600	0.071	Yes	Yes
Core covariates				0.600	0.072	Yes	Yes
Core + genes and PCB 180				0.600	0.093	Yes	Yes
Detroit - Genes subset	128	91	219
Crude				0.625	0.051	Yes	Yes
Core covariates				0.625	0.093	Yes	Yes
Core + genes				0.625	0.086	Yes	Yes
Detroit - Genes + PCB subset	65	41	106
Crude				0.700	0.022	Yes	Yes
Core covariates				0.700	0.021	Yes	Yes
Core + genes and PCB 180				0.700	0.019	Yes	No
Iowa - Missing indicator	267	211	478
Crude				0.625	0.211	Yes	No
Core covariates				0.625	0.144	Yes	No
Core + genes and PCB 180				0.625	0.204	Yes	No
Iowa - Genes subset	233	186	419
Crude				0.625	0.337	Yes	No
Core covariates				0.625	0.225	Yes	No
Core + genes				0.625	0.318	Yes	No
Iowa - Genes + PCB subset	133	109	242
Crude				0.600	0.378	No	No
Core covariates				0.600	0.346	No	No
Core + genes and PCB 180				0.600	0.422	No	No
Los Angeles - Missing indicator	190	161	351
Crude				0.275	0.003	Yes	Yes
Adjusted				0.275	0.029	Yes	Yes
Adjusted + Genes, PCB 180				0.275	0.024	Yes	Yes
Los Angeles - Genes subset	160	127	287
Crude				0.375	0.001	Yes	Yes
Core covariates				0.375	0.009	Yes	Yes
Core + genes				0.375	0.009	Yes	Yes
Los Angeles - Genes + PCB subset	107	62	169
Crude				0.500	0.132	No	Yes
Core covariates				0.500	0.057	Yes	Yes
Core + genes and PCB 180				0.425	0.038	Yes	Yes

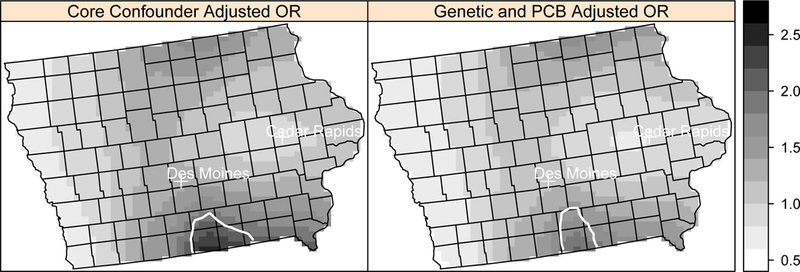
The locations of the areas of significantly elevated and lowered NHL risk remained the same across adjusted models, although the shape of the detected areas changed slightly for some models. In Detroit, the delineation of the area of significant elevated risk (in southeast Oakland County) was consistent when adjusting for the core covariates and additionally for the genetic factors, and PCB exposure (Figure 1). In Los Angeles, an area of elevated risk (West Hollywood) decreased slightly in size after adjusting for PCB exposure and the genetic factors (Figure 2). The other region of elevated risk contains sparsely populated areas. The area of significantly elevated risk in Iowa, including parts of Wayne County and Appanoose County, also decreased in size after adjusting for PCB exposure and the genetic polymorphisms (Figure 3). The risk overall decreased in Iowa after adjusting for the additional genetic and PCB risk factors, and the approximate p-values for the spatial term increased with the adjustment in each of the three sets of data.

Figure 1.

Local odds ratios (OR, scale at right) for NHL adjusted for the core covariates (age, gender, race, education, home termite treatment) and additionally for four genetic polymorphisms and PCB 180 exposure at a residential lag time of 20 years in the Detroit study area using the model with missing variable coding. Areas of statistically significant elevated odds ratios are identified with a solid white line and statistically significant lowered odds ratios are identified with a dashed black line.

Figure 2.

Local odds ratios (OR, scale at right) for NHL adjusted for the core confounders and additionally for four genetic polymorphisms and PCB 180 at a residential lag time of 20 years in the Los Angeles study area using the model with missing variable coding. Areas of statistically significant elevated odds ratios are identified with a solid white line and statistically significant lowered odds ratios are identified with a dashed black line.

Figure 3.

Local odds ratios (OR, scale at right) for NHL adjusted for the core confounders and additionally for four genetic polymorphisms and PCB 180 at a residential lag time of 20 years in Iowa using the model with missing variable coding. Areas of statistically significant elevated odds ratios are identified with a solid white line.

Our study demonstrates the importance of adjusting for suspected risk factors, including genetic and environmental risk factors, and considering residential histories when performing a spatial analysis of disease. Even if such adjustments do not fully explain observed patterns, they refine the hypotheses generated by the analyses. Our study also highlights the potential heterogeneity in risk factors for NHL incidence across different geographic areas. Additional efforts are required to identify risk factors that may explain areas of significant risk in Detroit, Iowa, and Los Angeles.

Conclusions

In this paper, we first reviewed the challenges encountered when performing spatial cluster analysis of chronic diseases and then presented an analysis that addressed these challenges. We investigated previously detected areas of significantly elevated risk of non-Hodgkin lymphoma in a case-control study to see if PCB exposure and genetic risk factors could explain the clusters. We found that adjusting for genetic factors and PCB 180 levels in homes did not explain significantly elevated risk areas in Detroit, Iowa, and Los Angeles, but did explain an area of significantly lowered risk in Detroit in one model. Our analysis demonstrates an approach to spatial-temporal analysis of disease for epidemiologic studies with individual-level suspected risk factors and residential histories. Our approach is based on the well-established generalized additive model, which provides a unified statistical framework for adjusting for risk factors, estimating disease risk spatially, and assessing significance of elevated risk for individual-level epidemiologic studies. A strength of our approach is that it is straightforward to evaluate several latency periods within an unbiased model. This approach can be extended in the future to include several latency periods as covariates in one model to represent multiple locations of exposure at different time points. It should also be possible to include duration at each residence in a model. A limitation of this approach is that a latency period not considered in the model may be the most relevant for a particular disease. The selection of latency period candidates to evaluate in an exploratory analysis may be somewhat arbitrary. In addition, not all available residential locations would typically be evaluated in the current approach. Extending existing approaches to include all address information is an area for methodological development in the future. Another limitation, common to all cluster detection approaches, is that detection of a cluster only identifies a location of potential exposure, but does not identify the nature of any exposure. In summary, our application of this approach serves as an illustrative example for those interested in performing space-time cluster analysis of chronic diseases with suspected latencies and limited risk factor information to assist in the generation of new hypotheses about potential risk factors. The approach is especially applicable to other chronic diseases with suspected environmental causes.