Abstract
There are no practical and effective mechanisms to share high-dimensional data including sensitive information in various fields like health financial intelligence or socioeconomics without compromising either the utility of the data or exposing private personal or secure organizational information. Excessive scrambling or encoding of the information makes it less useful for modelling or analytical processing. Insufficient preprocessing may compromise sensitive information and introduce a substantial risk for re-identification of individuals by various stratification techniques. To address this problem, we developed a novel statistical obfuscation method (DataSifter) for on-the-fly de-identification of structured and unstructured sensitive high-dimensional data such as clinical data from electronic health records (EHR). DataSifter provides complete administrative control over the balance between risk of data re-identification and preservation of the data information. Simulation results suggest that DataSifter can provide privacy protection while maintaining data utility for different types of outcomes of interest. The application of DataSifter on a large autism dataset provides a realistic demonstration of its promise practical applications.
Keywords: Data sharing, personal privacy, information protection, Big Data, statistical method
Introduction
Recently, David Donoho predicted that by 2060 we will enter an Open Science era, where data and code sharing will become a trend in scientific publications [1]. However, without privacy protections, sharing sensitive data may result in excessive information disclosure. Currently, there are no generic, practical, and effective mechanisms to share high-dimensional data in aggregate without compromising participant confidentiality, exposing personal information, or undermining individual rights. Examples of such delicate information include clinical data, electronic health records (EHR), banking and investment, student learning analytics, and government data including income tax and socioeconomic data. Cohort stratification approaches for large multi-source data archives may be used by various actors to re-identify specific cases.
For example, a malicious adversary might be interested in linking de-identified hospital EHR with voter registration database using shared demographic variables. Without deliberate obfuscation, re-identification can be easily achieved. As early as 1997, Latanya Sweeney showed that one might identify 90% of the US population when information for date of birth, postal code, and gender is known [2–5]. In 2007, Netflix published its de-identified user data for its famous contest to improve the recommendation system. Deanonymization can be easily realized when linking the Netflix data with the International Movie DataBase (IMDB) dataset that contains user information [6]. However, to advance our understanding of a number of natural phenomena, including benign and pathological human conditions, and provide massive volumes of information for scientific discoveries, it is useful to share, release, and aggregate data.
Some existing techniques are able to provide privacy-preserving solutions for specific types of data sharing. Differential Privacy (DP) is a mathematical definition of this privacy loss, providing statistical properties about the behaviour of a mechanism for answering privacy-preserving queries [7–10]. DP ensures that similar datasets can behave approximately when similar information is requested by differentially private algorithms. To promote data sharing, Mohammed et al. [11] proposed the DiffGen algorithm to publish differentially private anonymized data. They partitioned the raw data into subgroups and introduced Laplacian noise to the group counts. Model-free Probably Approximately Correct (PAC) learning provides another solution for low-dimensional synthetic data sharing [12]. Several model-based sampling inference techniques have also been proposed for medium-sized data sharing, including Zhang et al. [13] and Chan et al. [14] Bayesian frameworks and clustering techniques may also be employed to derive noisy conditional distributions or marginal tables and approximate the overall data joint distribution. Such methods provide good asymptotic properties on the errors introduced to the original data. However, most rely on low-dimensional evaluation datasets (e.g. less than 24 features), and when the data dimensionality increases such methods may become computationally intractable. Additionally, the conditional distributions and marginal tables were derived using specific models; thus the ultimate utility of the synthetically generated datasets was highly dependent on the adequateness of the a priori selected models.
Data encryption provides another strategy for data sharing [15–17]. Fully homomorphic encryption transfers plain text (raw data) into cipher text that is not humanly parseable unless decrypted with a specific decryption key [18–21]. Homomorphic encryption allows users to operate, process, or analyse the encrypted data without having access to the decoding key. However, the operations on encrypted data are limited as they are designed ahead of time, Thus, general model fitting on encrypted EHR data is difficult to conduct in practice.
The proposed statistical obfuscation technique (DataSifter) combines introducing artificial random missingness with partial alterations using data swapping within subjects’ neighbourhoods. These furtive operations have minimal impact on the joint distribution of the obfuscated (sifted) output data as the controlled rate of missingness is introduced completely at random and nearest neighbourhoods tend to have consistent distributions. In terms of the overall distribution of the data features, the DataSifter algorithm attempts to preserve the total energy, i.e. information content, of the original data. At the same time, the method sufficiently obfuscates the individual cases to provide privacy protection and mitigate the risks of re-identification. There are several user-controlled parameters that allow the data governor the flexibility to control the level of obfuscation, trading privacy protection and preservation of signal energy.
Methods
The core of the DataSifter is an iterative statistical computing approach that provides the data-governors controlled manipulation of the trade-off between sensitive information obfuscation and preservation of the joint distribution. The DataSifter is designed to satisfy data requests from pilot study investigators focused on specific target populations. These pilot studies may not necessarily be driven by specific research questions or a priori hypotheses. Thus, this technique is generally query-free. Iteratively, the DataSifter stochastically identifies candidate entries, cases as well as features, and subsequently selects, nullifies, and imputes the chosen elements. This statistical-obfuscation process relies heavily on non-parametric multivariate imputation to preserve the information content of the complex data.
The DataSifter is designed to process various types of data elements. The method can handle multiple numerical or categorical features, as well as one unstructured feature, e.g. rich text. However, the method cannot be applied to features with a single constant value or categorical features with probabilities of some categories close to 0.
At each step, the algorithm generates instances of complete datasets that in aggregate closely resemble the intrinsic characteristics of the original cohort; however, at an individual level, the rows of data are substantially obfuscated. This procedure drastically reduces the risk for subject re-identification by stratification, as meta-data for all subjects is randomly and repeatedly encoded. Probabilistic (re)sampling, distance metrics and imputation methods play essential roles in the proposed DataSifter obfuscation approach.
In regard to the designed data requests, the main assumptions of the DataSifter technique include: (A1) Incomplete observations are driven by missing at random (MAR) or missing completely at random (MCAR) mechanisms [22]; (A2) The utility of each feature is equally important; (A3) Large random samples of the original data preserves the overall joint distribution. These assumptions are standard and allow us to manage the data or quantify data utility. (A1) allows accurate imputations (A2) is essential in calculating subject-pair distances, and (A3) promotes subject-wise parallelization.
We use the following framework to form the DataSifter algorithm. Three sources of obfuscation have been applied to the data during the DataSifter technique: (1) initial data imputation (in the preprocessing step), (2) artificially create and impute missingness (in the imputation step), and (3) swapping data values in the neighbourhood (in the obfuscation step). Here we define all the mappings that have been employed for obfuscation.
Notation
Define as the counterfactual complete sensitive dataset for Sifting consisting m features and n cases. Let us use 1 ≤ j ≤ m to denote features and 1 ≤ i ≤ n to denote cases:
In the above expression, Xi,j denotes the i-th subject’s j-th feature value.
We define the utility information embedded in a dataset as the knowledge about the joint distribution of the holistic data including all variables. By DataSifting preservation of utility, we mean the relative conservation of the signal energy that suggests small deviation of the sifted-data joint distribution from the original (raw) data joint distribution. Clearly, this does not hold true for large obfuscation levels (e.g. as η → 1).
Define Fj as the distribution of the j-th variable (feature) in the dataset:
Missing data are pervasive in almost all real-world datasets. We define the hypothetical complete j-th feature as
where Xj,mis denotes a vector containing the actual values of the missing data portion. What we observe is denoted as Xj = (Xj,obs, Nj), here Nj represents the missing cells. The length of Xj,obs is nj and the length of Nj is m − nj.
Initial data imputation
This obfuscation happens in the data preprocessing step, we aim to impute the missing cells in the origin data using missForest [23]. We define the imputation method as a mapping from the observed incomplete dataset to a complete dataset with imputed values following estimated conditional distributions:
Here are the conditional distributions of Xi,j given all other features in the dataset. missForest uses an iterative approach with random forest models to approximate the true fj.
Then, we impute the missing data with G to obtain , where , where follows the same distribution as Xi,j.
Artificially create and impute missing
During the imputation step, we introduce artificially missing observations and subsequently employ data imputation to re-generate complete instances (chains) of the dataset. Similar to initial imputation we apply MF(·) to approach the true conditional distributions of the features.
We first randomly introduce missingness to the dataset after preprocessing step:
The new data would possess an MCAR missing mechanism. The corresponding complete data chains following the imputation is denoted by
where are obtained by MF(·). Assuming we have obtained the true conditional models for all the imputations, the above two sources of obfuscation would not alter the joint distribution of all features.
Neighbourhood data-element swapping
To further guarantee the obfuscate has been applied to each record, we swap the data values in the neighbourhood without substantially altering the joint feature distribution. We need to determine the neighbours for each record in the dataset. First, we calculate the distance matrix for all cases:
Here Di,j = Dj,i ∀i, j. Di,j is the distance between the i-th case and the j-th case. Then, define aij = I(Di,j < min(D′) + sd(D′)) here D′ = {Di,j|i ≤ j}. We use the hard threshold min(D′) + sd(D′) to restrict the neighbourhood. Hence, the neighbourhood matrix is defined as
Next, we define an index set that contains all the possible neighbours for j-th case, Ωj = {(i, j)|aij = 1}, j = 1, …, m. The swapping procedure can be represented by a set that contains all the mapping functions to be performed on :
where the notation suggests using the element to replace x11, noting that here depends on both the column and the row indices.
Finally, we define one random function that picking a specific neighbourhood from the neighbour set generated above as Ωj:
where each pair of (ij, j) ∈ Ωj, j = 1, … m.
We define another function that picks k4% of the replacement to execute, it’s also a function that mapping to the map function set, shown as below:
where , subject to the following identity:
A specific R-implementation of the DataSifter method is available in the DataSifter package, method dataSifter(). Detailed description and code are available in our GitHub repository (https://github.com/SOCR/DataSifter).
User-controlled parameters
Sifting different data archives requires customized parameter management. Five specific parameters mediate the balance between protection of sensitive information and signal energy preservation:
k0: A binary parameter indicating whether or not to obfuscate the unstructured feature, if any.
k1: The per cent of artificial missing data values that should be synthetically introduced prior to each imputation iteration. Missingness is stochastically introduced to all data elements. The range of this parameter can be between 0% and 40% of the total number of cells. We set an upper bound of 40% missingness in order to keep the remaining dataset is still informative. However, this range can be expanded.
k2: The number of times to repeat the introduction-of-missing-and-imputation step. Five options are available from 0 to 4.
k3: The fraction of structured features to be obfuscated in all the cases. Available options can vary between 0% and 100%.
k4: The fraction of closest subjects to be considered as neighbours of a given subject. This implies that the top k4% of the closest-distance subjects of a given subject can be considered as candidates for its neighbours. Then, the final neighbouring status of any subject is determined by an additional hard cut off.
As a reference, Table 1 illustrates some example combinations of ki parameters to show the trade-offs between privacy protection and obfuscation. The level of obfuscation spans the range from raw data (no obfuscation) to synthetically simulated data (complete obfuscation). Our highest level of obfuscation, i.e. ‘indep’, refers to the synthetic dataset sample from the joint empirical distributions of all the features.
Table 1.
DataSifter k parameter vector mapping determining the level of obfuscation.
| Obfuscation level | k0 | k1 | k2 | k3 | k4 |
|---|---|---|---|---|---|
| None | 0 | 0 | 0 | 0 | 0 |
| Small | 0 | 0.05 | 1 | 0,1 | 0.01 |
| Medium | 1 | 0.25 | 2 | 0.6 | 0.05 |
| Large | 1 | 0,4 | 5 | 0,8 | 0.2 |
| Indep | Output synthetic data with independent features | ||||
Preprocessing
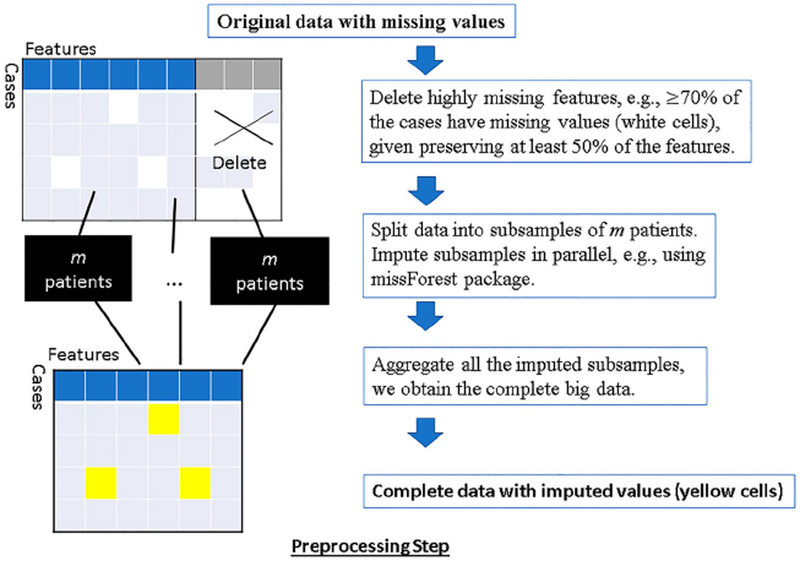
The preprocessing steps of the original data might vary for different datasets. Figure 1 illustrates the procedures included in the default DataSifter preprocessing step. These may be tailored to the specific characteristics of the study. The overall goal is to delete uninformative features and impute originally missing values. Uninformative features are features that either represent constant values or have excessive levels of missingness. DataSifter produces a complete dataset after the preprocessing step. For ease of notation in the rest of the manuscript we denote the number of subjects in the dataset as n, the number of informative features filtered by the preprocessing step as p, and the number of subjects per batch during the parallel process as M. Alternative preprocessing methods are possible as long as the aims are met.
Figure 1.
Flow chart for preprocessing step.
Imputation step
Following the data preprocessing, the DataSifter continues with an iterative imputation and obfuscation. During the imputation step, the DataSifter algorithm first introduces random artificial missing values to the complete dataset, which synthetically provides privacy protection. The artificial missingness obeys missing completely at random (MCAR) requirements as the missingness is introduced stochastically for the case and features indices [22]. Assume we have n entries of data and denote the full data as Y = (Yobs, Ymis), where Yobs represents the observed part and Ymis the missing part. Let R denote the missing indicator with Ri = I(Yi ∈ Ymis) for i = 1, 2,.., n. Because the MCAR assumption is satisfied, we have the following relationship:
This relationship between observed and missing values guarantees that the fully observed data represents a random sample of the complete data. Accurate imputations of the missing values based on the observed values can be obtained with non-parametric imputation methods [23]. Thus, as described above, our specific introduction of missing data has limited effect in altering the joint distribution of the data during the imputation process. To impute the missing values, we use the non-parametric imputation method missForest [23], albeit many alternative strategies are also possible. As an iterative non-parametric imputation method of mixed data types, missForest fits a random forest model using the observed data as training data and provide predictions for the missing cells. Hence, the random forest model for imputing a specific column uses all other variables in the dataset as predictors. In each iteration, the imputation of the entire dataset starts in the column with the least missing values and ends in the column with most missing values. When the newly imputed data matrix tends to diverge with the previous matrix then the algorithm stops. We choose missForest algorithm, rather than other model-based multiple imputation methods, for the following reasons [23]: (1) missForest employs random forest imputation that can cope with complex EHR data, which typically involves mixed-type data, complex interactions, and non-linear relations; (2) it relies on limited modelling assumptions; and (3) it is relatively efficient for large-scale and high-dimensional data.
Following the imputation step, the outputted ‘sifted’ dataset, Xwork, has the following properties: (1) individual cases are manipulated, yet complete, protecting individual privacy, since hackers cannot distinguish ‘true’ values from imputed values that are in the same format; (2) subjects with introduced missingness can still play an important role in the analysis after the imputation.
Obfuscation step
During the obfuscation step, the DataSifter repeatedly selects and swaps structured data feature values based on the closest neighbours to ensure a balance between data privacy and preservation of the feature distributions. The algorithm relies on distance metrics to determine neighbourhoods for all cases [24,25], and swaps feature values between closely adjacent neighbouring pairs. We compute pair-wise distances between all cases using a weighted distance measure: (1) Euclidean distances for normalized numerical features, and (2) Gower’s distance for categorical features [24]. To obtain the distance matrix, we divide the current dataset outputted by the imputation step into three subsets and re-index the elements as a numerical subset , categorical dataset , and the unstructured feature Xunstr, where we have l numerical features, p-1-l categorical features and one unstructured feature. For Xnum, we apply a map algorithm f, which calculates the Euclidean distance for every pair of cases and maps the input data metric to the target distance metric, and f: Rn×l → Rn×n is defined as below. For X = (x1, x2, …, xn)T, f(X) = DE = (eij), where ∀i, j:
And we can utilize f to obtain f (Xnum) = DE (eij)n×n.
For the categorical subset, we define a mapping=algorithm g which calculates the distance for categorical features via Gower’s rule. For X = (x1, x2, …, xn)T, X ∈ Rn×p, g(X) = DG = {gij}. For ∀i, j:
where gijs is an indicator function related to the s-th feature, which is defined as
Under Gower’s rule, we calculate the distance by the weighted dissimilarities of categorical features. Similarly, for , we attain DG = (gij)n×n g(Xcat). Under assumption (A2), we define the complete paired-distances metric as a weighted version,
where l/p and (p − 1 − l)/p represents the weights for the Euclidean and Gower distances, respectively. Two criteria are used to determine the neighbouring status for subject pairs: (1) closest k4 × n neighbours regarding the pair distances; and (2) a hard cut off. In the distance matrix D, for each i, we rank the paired distances dij as . Then, we find the maximum distance of the top k4% (percent) , where floor(k4 × n) rounds to the lower integer the percentage of cases to select within the closest neighbours. We use the cutoff to identify the potential neighbours of the i-th individual:
In addition, we set up a criterion to narrow the neighbourhood. Let
where inf {dij} refers to the minimum pair-wise distance between cases and sd{dij}refers to the standard deviation of all the dij’s in D. We only preserve the neighbours that satisfy dij ≤ c. The final set of neighbours, i.e. neighborfinal, is defined as follows:
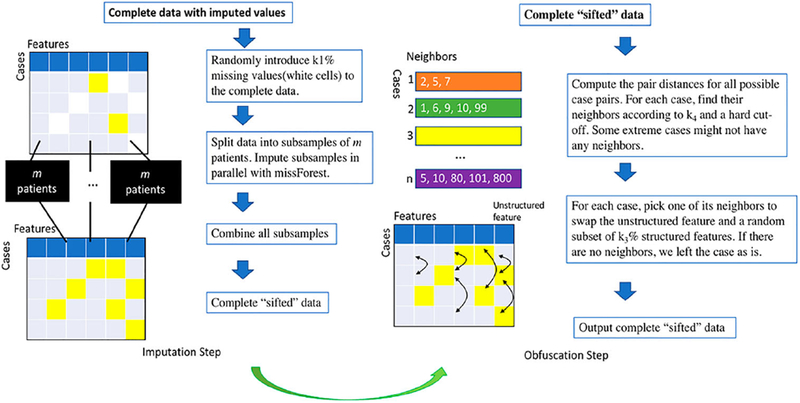
For extreme subjects that have no neighbours selected by the above process, we do not apply the obfuscation step. One subject could have multiple neighbours. For every subject, a neighbouring subject is randomly selected as its swapping partner. We randomly swap a subset of randomly chosen features among each swapping pair. A detailed flow chart illustrating the imputation and obfuscation steps can be found in Figure 2.
Figure 2.
Flow chart for imputation and obfuscation steps.
Pseudo code
In this section, we define Xstr as the structured feature subset of current data, which consists of Xnum and Xcat. Also, Rand(X, r) is a function that randomly picks r elements in X.
Input:
The dataset after preprocessing with n cases and p features. There are one unstructured and p − 1 structured features in the dataset. After the preprocessing step, p is less or equal to the number of features in the original dataset. Each is a column vector, .
The categorical level of obfuscation L = {‘none’, ‘small’, ‘medium’, ‘large’, ‘indep’}, or alternatively a specific parameter vector (k0, k1, k2, k3, k4).
Special cases:
If L = ‘none’, the output is Xwork and if L = ‘indep’, the output is denoted by Xnew. Each feature in Xnew is a synthetic sample from the empirical distribution of the corresponding feature in Xwork.
| Core Algorithm: |
| For i in 1: k2 do |
| Introduce k1 % × n × (p − 1) missing values to Xstr. |
| Impute missingness (e.g. via missForest) and update Xwork. |
| End for |
| If k0 = 1 do |
| For i = 1 : n |
| (i, j) = Rand(neighbor*(i), 1) |
| Swap the unstructured value for the pair (i, j) in Xwork. |
| End for |
| End If |
| For i = 1 : n |
| j = Rand(neighbor*(i), 1); |
| Zi = Rand |
| For t ∈ Zi do |
| Swap Xstr[i, t] with Xstr[j, t] |
| End for |
| End for |
Simulation experiment design
We present three different simulation studies to demonstrate the performance of the DataSifter algorithm and assess its capability to (1) obfuscate and guard against stratification attempts for re-identification and (2) manage the overall data structure and preserve useful information in the resulting ‘sifted’ data. In all experiments, we use a sample size of n = 1000 subjects.
In the first simulation, a binary outcome (y) and five covariates (xi, i = 1, …, 5) were simulated; X1 to X4 were independently generated by normal distributions with the following distribution specifications:
The binary variable X5 was directly dependent on X1 and X2:
The binary outcome variable was generated as follows:
where the residuals were independent and identically distributed (iid) and ϵi ~ N(0, 1) and i = 1,.., n. Missingness for X1 and X2 was then introduced based on X5 to meet the missing-at-random (MAR) criteria, which mimicked the real data situation. Denote Xi,1mis = I(Xi1 = NA) and Xi,2mis = I(Xi2 = NA), where i is the subject indicator. Missingness was introduced using the following probabilities:
As mentioned in the Imputation section, we can impute the original missing values in the dataset prior to applying the subsequent DataSifter algorithmic steps. However, to handle the original missingness, we have to consider MAR missingness.
The second simulation demonstrates an example of count outcomes. A Poisson model was used to generate the data:
where
with iid residuals (i.e. ϵi ~ N(0, 1)). The covariates xi, i = 1, …, 4 were generated using uniform distributions. We constructed x5 based on x1 and x2 and used a similar strategy as in the first binary simulation to introduce missingness.
The third simulation involves continuous outcomes, where the response y is generated by a similar linear model as in the first experiment; however, it uses an identity link yielding a continuous outcome:
Again, the residuals were iid and, ϵi ~ N(0, 1). All covariates were generated from uniform distributions and the missing patterns were stochastically determined as in the first binary experiment.
For all simulation studies, we focused on verifying whether the ‘sifted’ output datasets preserve a certain level of the energy that was present in the original true signals, relative to null signals. In addition, we examined the trade-offs between the level of obfuscation and the residual value (utility) of the resulting ‘sifted’ data as a measure of the algorithm’s performance. To make all three simulations more realistic, we augmented the original outcome and the (real) five covariates, with 20 additional null features that acted as decoy or ‘noisy’ control features. All 20 null features were uniformly distributed with various ranges and were independent of the outcome.
Datasifter validation
For each simulation, we derived 30 ‘sifted’ datasets under a range of privacy levels, from ‘none’ to ‘indep’ levels of obfuscation. To assess the privacy protection ability, we measured the Percent of Identical Feature Values (PIFV) between the ‘sifted’ outcome and the original data for all the cases under each obfuscation level, i.e. we compared each subject’s original and ‘sifted’ records and measured the ratio between the number of identical values over the total number of features. For determine utility preservation, we used regularized linear models, with an elastic net regularization term, to identify the salient variables. Internal 10-fold statistical cross-validation was used to validate the results of the elastic net feature selection. X denotes the covariate matrix (subjects × features = 1,000 × 25), y is the outcome, and β as the elastic net parameter estimates obtained by optimizing the following objective function:
where α is the parameter to determining the blend of the LASSO and Ridge contributions to the penalty, and λ is the regularization penalty parameter [26]. In our experiments, we used α = 0.8 giving a slight dominance to the LASSO penalty.
A regularization parameter tuning procedure was also performed, using misclassification error rate for binary simulation, deviance for count simulation, and mean squared error for continuous simulation. The largest λ value, which is within one standard error of the minimum cross-validated error, was selected as the optimal parameter [26]. When the estimated coefficient was different from zero, we considered this evidence that the corresponding feature represented a ‘true’ predictor. On the other hand, zero coefficient estimates corresponded to ‘false’ predictors. Recall that in all simulations, there were five true predictors and 20 null variables. The true positives (number of true features identified) and the false positives (number of null features identifies as true predictors) were recorded for all experiments and each privacy level.
Results
Protection of sensitive information (privacy)
The privacy protection power relies heavily on the user-defined privacy level and the intrinsic information structure. Overall DataSifter performed very well. Our results showed that for high privacy levels, the Percent of Identical Feature Values (PIFVs) was close to 0% for all numerical features. For datasets including categorical features, the algorithm provided PIFVs similar to the lowest PIFV between any pair of different subjects in the original dataset. The overall privacy protection performance of the DataSifter was excellent.
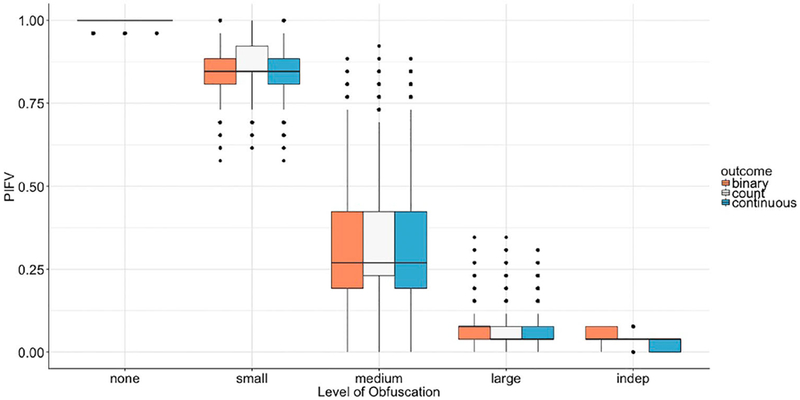
Based on the overall simulation performance, a default recommended privacy level may be set at ‘medium’. However, this is also subject to the sensitivity of the data, the specific characteristics of the data, and the trustworthiness of the requestor. Figure 3 illustrates the relationship between PIFVs for synthetic datasets and user-defined privacy levels. The outcome labels ‘binary’, ‘count’, and ‘continuous’ refer to the first experiment, second experiment, and third experiments, respectively. As expected, the graph shows that the preservation of sensitive information is better protected when the privacy level is higher. For all three simulations, the DataSifter had similar performance in terms of PIFV. The outliers in the ‘none’ level resulted from the imputation of originally missing values. When the obfuscation was set at ‘medium’ level, the variance of the PIFV was the largest as the levels of obfuscation might differ among individuals when using random sampling. ‘Small’ level of obfuscation manipulated less of the data, with a limited range around the neighbourhood of each case. Hence, it generated smaller PIFV variances among individuals. On the other hand, ‘large’ obfuscation level had a small variance for PIVF as it changed most of the features for all cases. Under the ‘large’ obfuscation setting, PIFV was around 25% for all three experiments, which provided reliable protection for patient privacy. Under the ‘medium’ level, around 75% of the cases had more than 50% of their data elements different from their original (true) counterparts. The synthetic data under ‘indep’ changed almost all the feature values for every subject. Remember that these five original obfuscation levels represent simple examples of specifying the 5D Data-Sifter-control parameter vector k.
Figure 3.
Boxplots of percent of identical feature values (PIFV) under different privacy levels. Binary outcome refers to the first experiment; count refers to the second experiment; continuous refers to the third experiment. Each box represents 30 different ‘sifted’ data or 30,000 ‘sifted’ cases.
Preserving utility information of the original dataset
Next, we assessed the DataSifter algorithm’s integrity, in terms of its ability to maintain utility information, i.e. preserve the energy or all features’ joint distribution of the original data. A detailed explanation can be found in the Methods section. Our results suggest that up to moderate obfuscation levels, the algorithm maintains a fair amount of information (data energy). However, as expected, this ability fades away for larger obfuscation levels. Also, different k parameter vectors have varying effects on the overall utility preservation.
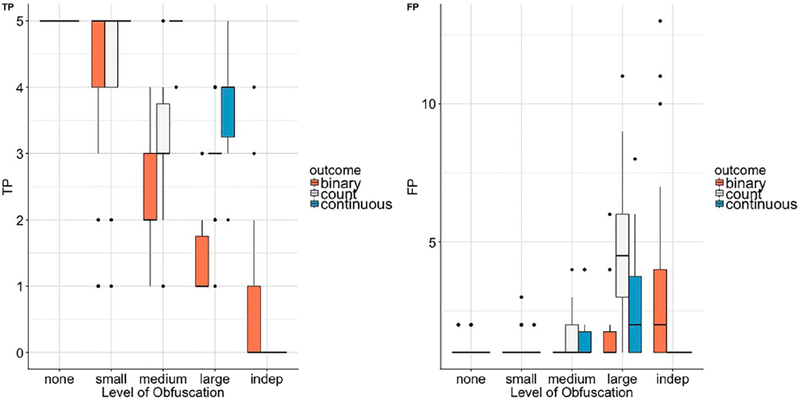
The results illustrating the DataSifter ability to conserve the data energy are presented in Figure 4. We report the true positive (TP) and false positive (FP) number of feature selections for the three simulation experiments. These results showed that the DataSifter is able to preserve the signal energy in the original data. As expected, and in contrast to the privacy preservation ability, the performance of the technique to maintain data utility is better under low obfuscation levels. Different outcome types also affect the utility preservation. The simulations show that information energy preservation in the continuous outcome case is slightly better, compared to binary and count outcomes.
Figure 4.
Logistic model with elastic net signal capturing ability. TP is the number of true signals (total true predictors = 5) captured by the model. FP is the number of null signals that the model has falsely selected (total null signals = 20).
In the continuous outcome simulation, for obfuscation levels below ‘large’, regularization and variable selection via elastic net successfully identified all five important predictors in almost all ‘sifted’ datasets, and the number of false positives was mostly 0. In addition, the variations of TPs and FPs among different privacy levels was the smallest among the three simulation experiments. The count outcome simulation performed similarly well; under ‘medium’ obfuscation, elastic net was able to select 3 out of 5 features over 75% of the times. Count outcome simulation was not always stable. For instance, some datasets undergoing extreme ‘sifting’ had 0 true features selected; however, the algorithm also kept low the false negative rate.
The binary outcome simulation demonstrated the least utility preservation as it had the highest false positive rates and the largest variability among all settings. Based on Figure 4, there is almost no true signal, or false signal, captured in the synthetic ‘indep’ setting, which results from the elimination of the correlations among features. The extreme ‘indep’ case aims to achieve maximum protection for patient privacy. As a consequence, the resulting ‘sifted’ data provides little utility.
Clinical data application: using DataSifter to obfuscate the ABIDE data
We demonstrate the functionality of the DataSifter on the Autism Brain Imaging Data Exchange (ABIDE) dataset. The ABIDE dataset represents a multi-institutional effort for aggregating and sharing the imaging, clinical and phenotypic data of 1,112 volunteers (see [27] and http://fcon_1000.projects.nitrc.org/indi/abide for details). The data includes resting-state functional magnetic resonance imaging (rs-fMRI) structural MRI, and phenotypic information of 539 patients (autism spectrum disorder) and 573 age-matched asymptomatic controls. In our study, we selected a subsample of 1,098 patients including 528 autism spectrum disorder (ASD) and 570 controls. The dataset has 500 structural MRI biomarkers and phenotypical information such as age, sex and IQ. It is a very challenging case-study due to the heterogeneity of the data, format of the data elements, and the complexity of mental health phenotypes. We use the ABIDE data to showcase the performance of the DataSifter technique on a convoluted multiplex study.
The ABIDE dataset comprises 1,098 patients and 506 features. We included one unstructured feature, ‘image data file name’ (‘Data’), in the dataset to demonstrate the DataSifter ability to obfuscate unstructured text elements. Resembling the simulation experiments, we built a dataSifter() function that has five different levels of obfuscation to demonstrate the obfuscation utility trade-off. Obfuscation was assessed using PIFV as the simulation studies. We applied random forest [28] to predict the target binary outcome autism spectrum disorder (ASD) status (ASD vs. control) as a proxy of the algorithm’s utility to maintain the energy of the original dataset into the ‘sifted’ output. Predictions of the ASD status was conducted with the randomForest package.
When specifying the parameters in the dataSifter() function, level of obfuscation can be set by level. Here we used five different obfuscation levels. The level of obfuscation can be alternatively specified using a set of k combinations as function arguments, which creates a flexible way to manage obfuscation levels. In general, low values of the user-controlled parameters k0–k4 result in ‘small’ obfuscation levels. However, even if the relationship between the user-controlled parameters and the obfuscation level is generally monotonic(i.e. an increase in the parameters is associated to higher obfuscation), the relationship is not necessarily linear. For example, our obfuscation level ‘small’ is obtained by setting the user-controlled parameters in the dataSifter() function as follows: k0 = 0, k1 = 0.05, k2 = 1, k3 = 0.1, k4 = 0.01.
In this example, the name of the unstructured feature was ‘Data’. In general, when there are no text variables, the set of unstructured.names can be left to default (i.e. NULL). Explicit sensitive information like the subject ID, i.e. subjID column, needs to be removed from the original dataset in advance. The batch size for the algorithm is defined by the parameter batchsubj. As mentioned in the Methods section, the DataSifter algorithm operated on batches to provide scalability and alleviate the computational complexity. We recommend using a relatively small batchsubj and a large number of cores for datasets with a huge number of cases (e.g. hundreds of thousands). The maximum number of iterations for the missForest imputation algorithm is set to 1 to minimize the computational cost determined by imputing a large number of features. An example call to the dataSifter function is illustrated below:
We obtained five ‘sifted’ output datasets corresponding to different obfuscation levels: no (‘none’ obfuscation), s (‘small’ obfucation), m (‘medium’ obfuscation), l (‘large’ obfuscation), and i (‘indep’ synthetic data from empirical distributions of each feature). We then inspected the obfuscations made to the original dataset. As an example, Table 2 shows the impact of the 5 different obfuscation levels on 10 selected features from a randomly selected case, the 22-nd subject, in the ABIDE data. Note that subject order was not changed in the DataSifter process. The last feature ‘curv_ind_ctx_lh_S_interm_prim.Jensen’ is missing for the 22-nd subject.
Table 2.
Compare original and ‘sifted’ data for the 22-nd subject.
| Data | Output | Sex | Age | Acquisition Plane | IQ | thick_std_ctx.lh.cuneus | curv_ind_ctx_lh_G_front_inf.Triangul | gaus_curv_ctx.lh.medialorbitofrontal | curv_ind_ctx_lh_S_interm_prim.Jensen | |
|---|---|---|---|---|---|---|---|---|---|---|
| original | 0887.nii | Autism | M | 31.72 | Sagittal | 131 | 0.475 | 2.1 | 0.315 | NA |
| none | 0887.nii | Autism | M | 31.72 | Sagittal | 131 | 0.475 | 2.1 | 0.315 | 0.51 |
| small | 0717.nii | Autism | M | 31.72 | Sagittal | 131 | 0.475 | 2.1 | 0.315 | 0.4589 |
| medium | 0887.nii | Autism | M | 31.72 | Sagittal | 111 | 0.548 | 2.85 | 0.315 | 0.463 |
| large | 0887.nii | Control | M | 18.21 | Sagittal | 104 | 0.5347 | 3.198 | 0.1625 | 0.4524 |
| indep | 1004.nii | Control | M | 15.4 | Coronal | 104.4 | 0.4842 | 3.383 | 0.1079 | 1.002 |
Compared to the original dataset, the results of the following obfuscation levels indicate: none – only imputed the missing value; s – incorporated 2 ‘sifted’ features, m – had 4 features that differed from their original value; l had 7 out of 10 ‘sifted’ features including the outcome ‘researchGroup’; and i had all features differ from the original except subjct-Sex. Moreover, for ‘none’ to ‘medium’ obfuscation, the values were relatively close to the original value in the example. Overall, Table 2 shows a ladder in obfuscation ability for different levels.
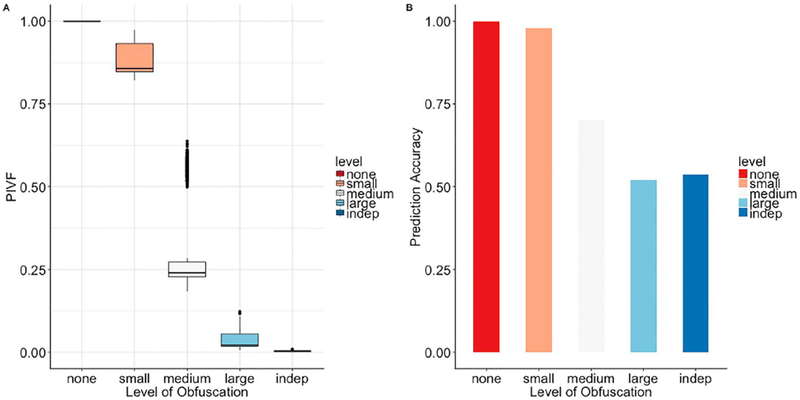
Boxplots for PIFV were then plotted in Figure 5(A) to illustrate the overall obfuscation effect. As expected, PIFV decreases with the level of obfuscation. Comparing the application with the simulation experiments, the algorithm works better with a larger number of features. Under ‘medium’ obfuscation level, the algorithm achieved 50% and 25% PIVF for the binary simulation data and ABIDE data, respectively.
Figure 5.
Boxplots of PIFVs for ABIDE under different levels of DataSifter obfuscations. Each box represents 1098 subjects among the ABIDE sub-cohort.
To assess the utility information, we used the ‘sifted’ datasets as training sets to fit random forest. These trained models provided predicted values for 632 complete cases in the original ABIDE data. The random forest built using no dataset predicted all outcomes correctly. s, m, l and i datasets were able to provide predictions with 98%, 70%, 52% and 54% accuracy, respectively. The prediction accuracy of all the datasets are illustrated in Figure 5(B). Again, this result demonstrated the trade-off between utility and the user-controlled privacy levels.
Parallel computing and CPU time
We used R to implement the proposed DataSifter algorithm. Parallel processing was employed to deal with datasets with a large number of subjects. To optimize the performance, we randomly divided the complete dataset by cases into batches. By default, we binned cases into batches of 1000, with the remaining patients added to the last batch. After splitting the data into manageable bundles, we did parallel computing introducing missing values and imputing them back iteratively using missForest. For extremely large datasets and efficient timely calculations, we recommend applying the DataSifter algorithm on Cloud servers where each code, or node, may be assigned a batch of cases. The current DataSifter implementation (V.0.1.4), takes about 2 h to complete the entire DataSifter protocol using 4392×503 EHR data archive. The relative CPU times for each step in the DataSifter are listed in Table 3.
Table 3.
CPU time for each step in DataSifter.
| Function | Function definition | CPU time average (s) | CPU time minimum (s) | CPU time maximum (s) | Number of evaluations performed | Dimension of data (row × column) |
|---|---|---|---|---|---|---|
| thinning | Delete features inthe original datawhen missing is significant | 9.10 | 8.90 | 9.70 | 50 | 1098×2143 |
| sep | Separate the original data by row and construct batches. | 0.07 | 0.06 | 0.21 | 50 | 4392 × 503 |
| firstImp | IImpute the data batches in parallel | 770.00 | 748.70 | 779.40 | 10 | 4392 × 503 |
| Subjdist | Calculate the subject pair distances. | 27.50 | 27.20 | 27.90 | 50 | 4392 × 503 |
| dataSifter (swap unstructured) | Swap unstructured variables with neighbours | 718.90 | 718.60 | 719.20 | 10 | 4395 × 503 |
| DataSifter (imputation step) | IIntroduce artifical missing and impute | 4621.10 | 4598.70 | 4640.80 | 10 | 4394 × 503 |
| dataSifter (swap structured) | Swap structured variables with neighbours | 752.50 | 752.20 | 753.30 | 10 | 4393 × 503 |
| Total | DataSifter procedure | 1.91 h |
Discussion and conclusion
Researchers interested in examining specific healthcare, biomedical, or translational characteristics of multivariate clinical phenomena frequently need to fit models, estimate parameters, train machine learning algorithms, or generate forecasting models. Large realistic datasets are required for all these tasks. There is an urgent need to develop effective, reliable, efficient, and robust mechanisms to support FAIR data sharing and open-scientific discovery [29]. The amount of data collected far exceeds our ability to interpret it. The main barriers for data sharing remain to be data-ownership and the need to protect sensitive information. The DataSifter method aims to balance data obfuscation, scrambling, or encoding and preserving the information content to facilitate useful downstream modelling, analytics and interpretation. The DataSifter represents a statistical obfuscation technique that reduces the risk of data re-identification at the same time it preserves the core data information. Our experiments with real and simulated data using multiple user-defined privacy levels, confirm the algorithm’s ability to protect privacy while maintaining data utility.
According to the simulation experiments results, under a careful set-up for user-defined privacy levels, DataSifter can successfully provide privacy protection while maintaining data utility. The clear negative relationship between the level of obfuscation and the proportion of PIFVs indicates that a high user-specified privacy level does provide increased privacy protection for sensitive information. Using DataSifter under ‘large’ or ‘indep’ settings, patient privacy was highly protected. Data re-identification was almost impossible by stratification filtering of the targeted patients via known feature values. This is due to the method’s inability to distinguish between real, imputed, or obfuscated values within each real feature, and the relatively small proportion of untouched data elements. Of course, caution needs to be exercised, as multiple queries resulting in repeated ‘sifted’ data instances may expose the overlapping ‘true’ values especially for low levels of obfuscation. However, the large proportion of ‘sifted’ elements protects sensitive information and may allow data users to request a small number of data queries. The application of DataSifter on ABIDE provided a realistic demonstration of how to employ the proposed algorithm on EHR. Also, the application confirmed DataSifter’s ability to handle high-dimensional data. The excellent prediction performances on the ‘medium’ obfuscation level suggested similar data utility between original and ‘sifted’ data.
In practice, to guarantee a great performance, data users should calibrate the obfuscation parameter values and choose an egalitarian strategy for counterbalancing risk vs. value. This decision may be based on specific criteria about access level, research needs, information sensitivity, etc. To stimulate innovative pilot studies, one may dial up the level of data protection. For more established investigators, data governors may balance the preservation of information content and sensitive-information protection by sharing a less obfuscated dataset.
Although with promising performance, several improvements and extensions could be made in future studies for the algorithm and R package. The major computational limitation is scalability, when the dataset is extremely large with many features (e.g. cases ~ 10–100 K and features ~ 1–10 K). In this scenario, the imputation with missForest can be inefficient. Parallelizing the missForest algorithm by features or using more efficient computational language like C++ might alleviate this problem. Another challenge is represented by the obfuscation of longitudinal data, which must be performed without breaking the correlations among time-varying features, which the current version of DataSifter is unable to do.
In addition, some of the records might not be changed after the DataSifter algorithm, however at sufficient levels of obfuscation, all cases, or records, in the sifted output will be distinct from their raw data counterparts. Any one of the following three steps will almost certainly alter a data cell element: (1) imputation for originally missing cells; (2) introducing artificially missing and imputed cells; and (3) obfuscating using swapping with a close neighbour. Thus, if a record is unchanged during the DataSifter process, none of these three processes took place. Assume we have a dataset with n records (rows) and m features (columns); #1 would not occur if the raw record is complete, the probability of #2 not occurring in a given record is , and the probability of #3 not occurring would be high only for outliers, as they would have few or no neighbours. Overall, a record without originally missing cells would have chance of remaining unchanged following the sifting process. However, if we force the swapping for complete cases and outliers, the overall joint distribution of the sifted result may be quite different from the original data. We are still investigating options to identify these rare complete cases and implement special obfuscation steps before the DataSifter algorithm processes the entire datasets. The goal is to introduce a special obfuscation strategy for rare cases preserving their uniqueness within the sifted result.
The DataSifter method is query independent; that is, it was designed to solve general data-access requests without an apriori specific research question. In general, it can be difficult to select an appropriate obfuscation level for discovery studies where the outcome of the dataset is unknown. Also, attaining asymptotic performances for the introduced noise can be challenging. The DataSifter relies on non-parametric techniques to introduce noise to a large proportion of data values. It provides model-free robustness, but the noise is hard to quantify without some modelling-based assumptions. For example, the imputation errors from missForest, i.e. the prediction errors from random forest imputation, do not have asymptotic properties. Future directions for DataSifter improvements would include specific handling of diverse outcomes and data types. When the data user has clear apriori study goals and a targeted outcome, model-based imputation and obfuscation methods can be applied for the algorithm.
The DataSifter approach represents an effective strategy for publishing a synthetic version of high-dimensional data (≥ 30 features) like the information contained in Electronic Health and Medical Records (EHR/EMR), insurance claims warehouses, government organizations, etc. This process facilitates data sharing, which in turn promotes innovation and evidence-based decision-making without compromising the risk of individual re-identification.
Acknowledgements
The authors are deeply indebted to the journal reviews and editors for their insightful comments and constructive critiques. Many colleagues at the Statistics Online Computational Resource (SOCR), Big Data Discovery Science (BDDS) and the Michigan Institute for Data Science provided valuable input. The DataSifter technology is patented (62/540,184 Date: 08/02/2017).
Funding
This research was partially funded by the National Science Foundation (NSF grants 1734853, 1636840, 1416953, 0716055 and 1023115), the National Institutes of Health (NIH grants P20 NR015331, U54 EB020406, P50 NS091856, P30 DK089503, P30AG053760, UL1TR002240), the Elsie Andresen Fiske Research Fund, and the Michigan Institute for Data Science.
Footnotes
Disclosure statement
No potential conflict of interest was reported by the authors.
References
- [1].Donoho D 50 years of data science. J Comput Graph Stat. 2017;26(4):745–766. [Google Scholar]
- [2].Golle P Revisiting the uniqueness of simple demographics in the US population. Proceedings of the 5th ACM Workshop on Privacy in Electronic Society. ACM; 2006. [Google Scholar]
- [3].Sweeney L Weaving technology and policy together to maintain confidentiality. J Law Med Ethics. 1997;25(2–3):98–110. [DOI] [PubMed] [Google Scholar]
- [4].Sweeney L Simple demographics often identify people uniquely. Health (San Francisco). 2000;671:1–34. [Google Scholar]
- [5].Aggarwal G, et al. Approximation algorithms for k-anonymity. J Privacy Technol. 2005:1–18. http://ilpubs.stanford.edu:8090/645/1/2004-24.pdf. [Google Scholar]
- [6].Harper FM, Konstan JA. The movielens datasets: history and context. ACM Trans Interact Intell Syst. 2016;5(4):19. [Google Scholar]
- [7].Dwork C, Roth A. The algorithmic foundations of differential privacy. Found Trends Theoret Comput Sci. 2014;9(3–4):211–407. [Google Scholar]
- [8].Dwork C Differential privacy: a survey of results. International Conference on Theory and Applications of Models of Computation. Springer; 2008. [Google Scholar]
- [9].Dinur I, Nissim K. Revealing information while preserving privacy. Proceedings of the Twenty-second ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems. ACM; 2003. [Google Scholar]
- [10].Dwork C, et al. Calibrating noise to sensitivity in private data analysis. Theory of Cryptography Conference. Springer; 2006. [Google Scholar]
- [11].Mohammed N, et al. Differentially private data release for data mining. Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM; 2011. [Google Scholar]
- [12].Raskhodnikova S, et al. What can we learn privately. Proceedings of the 54th Annual Symposium on Foundations of Computer Science 2008. [Google Scholar]
- [13].Zhang J, et al. Privbayes: private data release via Bayesian networks. ACM Trans Database Syst. 2017;42(4):25. [Google Scholar]
- [14].Chen R, et al. Differentially private high-dimensional data publication via sampling-based inference. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM; 2015. [Google Scholar]
- [15].Bhanot R, Hans R. A review and comparative analysis of various encryption algorithms. Int J Secur Appl. 2015;9(4):289–306. [Google Scholar]
- [16].Stallings W, et al. Computer security principles and practice. Upper Saddle River (NJ): Pearson Education; 2012. [Google Scholar]
- [17].Suo H, et al. Security in the internet of things: a review. 2012 International Conference on Computer Science and Electronics Engineering (ICCSEE). IEEE; 2012. [Google Scholar]
- [18].Gentry C A fully homomorphic encryption scheme. Palo Alto (CA): Stanford University; 2009. [Google Scholar]
- [19].Gentry C, Halevi S. Implementing gentry’s fully-homomorphic encryption scheme. Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer; 2011. [Google Scholar]
- [20].Gentry C, Sahai A, Waters B. Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-basedAdvances in cryptology – CRYPTO 2013. Santa Barbara (CA): Springer; 2013. p. 75–92. [Google Scholar]
- [21].Van Dijk M, et al. Fully homomorphic encryption over the integers. Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer; 2010. [Google Scholar]
- [22].Little RJ. A test of missing completely at random for multivariate data with missing values. J Am Stat Assoc. 1988;83(404):1198–1202. [Google Scholar]
- [23].Stekhoven DJ, Bühlmann P. Missforest—non-parametric missing value imputation for mixed-type data. Bioinformatics. 2011;28(1):112–118. [DOI] [PubMed] [Google Scholar]
- [24].Gower JC. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika. 1966;53(3–4):325–338. [Google Scholar]
- [25].Gower JC. Properties of Euclidean and non-Euclidean distance matrices. Linear Algebra Appl. 1985;67:81–97. [Google Scholar]
- [26].Haggag MM. Adjusting the penalized term for the regularized regression models. Afr Stat. 2018;13(2):1609–1630. [Google Scholar]
- [27].Di Martino A, et al. The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Mol Psychiatry. 2014;19(6):659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Liaw A, Wiener M. Classification and regression by randomForest. R News. 2002;2(3):18–22. [Google Scholar]
- [29].Wilkinson MD, et al. The FAIR guiding principles for scientific data management and stew-ardship. Sci Data. 2016;3:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]