Automatic Needle Segmentation and Localization in MRI with 3D Convolutional Neural Networks: Application to MRI-targeted Prostate Biopsy

Abstract

Image-guidance improves tissue sampling during biopsy by allowing the physician to visualize the tip and trajectory of the biopsy needle relative to the target in MRI, CT, ultrasound, or other relevant imagery. This paper reports a system for fast automatic needle tip and trajectory localization and visualization in MRI that has been developed and tested in the context of an active clinical research program in prostate biopsy. To the best of our knowledge, this is the first reported system for this clinical application, and also the first reported system that leverages deep neural networks for segmentation and localization of needles in MRI across biomedical applications. Needle tip and trajectory were annotated on 583 T2-weighted intra-procedural MRI scans acquired after needle insertion for 71 patients who underwent transperenial MRI-targeted biopsy procedure at our institution. The images were divided into two independent training-validation and test sets at the patient level. A deep 3-dimensional fully convolutional neural network model was developed, trained and deployed on these samples. The accuracy of the proposed method, as tested on previously unseen data, was 2.80 mm average in needle tip detection, and 0.98ᵒ in needle trajectory angle. An observer study was designed in which independent annotations by a second observer, blinded to the original observer, were compared to the output of the proposed method. The resultant error was comparable to the measured inter-observer concordance, reinforcing the clinical acceptability of the proposed method. The proposed system has the potential for deployment in clinical routine.

I. Introduction

PROSTATE cancer is the most frequently diagnosed non-cutaneous male malignancy and the second leading cause of cancer-related mortality among men in the United States and Europe [1], [2]. It is a heterogeneous disease with a wide range of possible ramifications for an individual diagnosed with it; the 5-year survival rate can be as low as 30% for metastatic disease and as high as 100% for localized disease[3], [4]. When screening indicates the possibility of prostate cancer in an individual, the standard of care includes non-targeted systematic (sextant) biopsies of the entire organ under the guidance of transrectal ultrasound (TRUS). These biopsies randomly sample a very small part of the gland and the results sometimes miss the most aggressive tumor within the gland[5]–[7]. MRI has demonstrated value in not just detecting and localizing the cancer, but also in guiding biopsy needles to the suspicious targets [8]. In particular, biopsies with intra-operative MRI guidance require significantly fewer cores than with the standard TRUS approach and reveal a significantly higher percent of cancer involvement per biopsy core [9]–[12].

Accurately placing needles in suspicious target tissue is critical for the success of a biopsy procedure. An intra-operative MRI allows the physician to check the position and trajectory of the needle relative to the suspicious target in a three-dimensional (3D) stack of cross-sectional images and to make needed adjustments. Physicians achieve targeting accuracy in the range of 3–6 mm for MRI-guided prostate biopsy, which is adequate for the task since clinically significant prostate cancer lesions are typically larger than 0.5 mL in volume or9.8 mm in diameter (assuming spherical lesions) [13]–[15]. Automatic localization of the needle tip and trajectory can aid the physician by providing rapid 3D visualization that reduces their cognitive load and the duration of the procedure. In addition, for the realization of robot-guided percutaneous needle placement procedures, accurate and automatic needle localization is a necessary part of the feedback loop [16].

While MRI is the imaging modality of choice for identifying suspicious biopsy targets because of its ability to provide superior soft tissue contrast, it poses two types of challenges in the needle localization task. The first challenge is that parts of a needle may appear substantially different from others in an MRI scan while also being difficult to distinguish from surrounding tissue [17]. This variability in grayscale appearance of needles confounds automatic segmentation algorithms and is addressed in this work. Today, aside from the proposed work, there are no automatic solutions for the segmentation of needles from MRI images [18], [19]. Even manual segmentation from MRI is tedious and error-prone, and to the best of our knowledge, not attempted in clinical or research programs. The second challenge, while not addressed in this paper, is worth noting; an MRI does not directly show the geometric location of a needle. Instead, the needle is detected through a loss of signal due to the susceptibility artifact that occurs at the interfaces of materials with substantially different magnetic resonance properties, and is commonly referred to as the needle artifact. Studies report a displacement between the actual needle tip and the needle tip artifact [18]. For brevity the term needle is used instead of needle artifact in this paper. Needle trajectory is defined as the set of points connecting the center of the artifact across a stack of axial cross-sections. The needle tip is the center of needle artifact at the most distal plane.

Several approaches have been suggested in the literature for segmentation and localization of needle-like i.e. elongated tubular objects in medical images. Segmentation of tortuous and branched structures, such as blood vessels [20], [21], white matter tracts [22], [23] or nerves [24] are the targets of many reported methods. Other methods target straight or bent catheters [25]–[27]. Based on the clinical application, the proposed techniques have been applied to different image modalities including ultrasound [27]–[29], computed tomography [30], [31], and MRI [25], [26] for the purpose of localization after insertion or real-time guidance during insertion. Many attempts have been made to incorporate hand crafted and kernel-based methods to segment and localize the objects which can be considered as line detection algorithms. The reported methods are based on 3D Hough transforms [27],[28], on model based and raycasting-based search [25], [26], orthogonal 2-dimensional projections [29], generalized radon transforms [32], and random sample consensus (RANSAC)[33].

Deep convolutional neural networks (CNNs) use the power of representation learning for complex pattern recognition tasks [34]. Deep model representations are learned through multiple levels of abstraction in a supervised training scheme, as opposed to hand-crafting of features. CNNs have been extensively used in medical image analysis and have outperformed conventional methods for many tasks [35]. For instance, CNNs have been shown to achieve outstanding performance for segmentation [36], localization [37], cancer diagnosis [38], quality assessment [39], and vessel segmentation [40].

In this paper, we propose a CNN-based system for automatic segmentation and localization of biopsy needles in MRI images. The proposed system uses CNNs to extract hierarchical representations from MRI to segment needles for the purpose of tip and trajectory localization. An asymmetric 3D fully convolutional neural network with in-plane pooling and up-sampling layers was designed to handle the anisotropic nature of the needle MR images. The proposed asymmetry in the network design is computationally efficient and allows the whole volumetric MR images to be used for the process of training. A large dataset of MRI acquired in transperineal prostate biopsy procedures was used for developing the system; 583 volumetric T2-weighted MRI from 71 biopsy procedures (on 71 distinct patients) were used to design, optimize, train and test the deep learning models.

The performance of CNNs and other supervised machine learning methods is measured against that of experienced humans, which is known to be variable for medical image analysis tasks; observer studies are used to establish ranges for human performance, against which automated CNNs can be rated. An observer study was conducted to compare the quality of the predictions against a second observer.

To promote further research and facilitate reproduction of the results, the resultant trained deep learning model is publicly available via DeepInfer [41], an open-source deployment platform for trained models. To the best of our knowledge, we are the first and only group to attempt fully automatic segmentation and localization of needles in MRI. Since there are no prior assumptions regarding the prostate images, the proposed method can be generalized and adopted in other clinical procedures for needle segmentation and localization in MRI.

The rest of the paper is organized as follows: in Section II we describe the methods for this study including the clinical workflow of in-gantry MRI-targeted prostate biopsy and details of the proposed deep learning system. Section III and IV cover the experimental setup and results, respectively, of applying the proposed system to the MRI-targeted biopsy procedure. Section V presents a discussion and our conclusions from this study.

II. Methods

A. MRI-Targeted Biopsy Clinical Workflow

The general workflow of an in-gantry transperineal MRI-targeted prostate biopsy involves imaging in two stages: a) the preoperative stage during which multiparametric MRI consisting of T1, T2, diffusion weighted, and dynamic contrast enhanced images are acquired and the cancer suspicious targets are marked, and b) the intraoperative stage during which the patient is immobilized on the table top inside the gantry of the MRI scanner and tissue samples are acquired transperineally with a biopsy needle under intraoperative MRI guidance. At the beginning of the intra-operative stage, anesthesia is administered to the patient and a grid template affixed to his perineum to facilitate targeted sampling. Intra-operative MR images are acquired as needed to optimize the skin entry point and depth for each needle insertion. One or more biopsy samples are taken for each target, depending on the sample quality. Samples are sent for histological analysis, and the institutional post-operative care protocol is followed for the patient. At our site, almost 600 such procedures have been performed under intravenous conscious sedation; one to five biopsy samples are obtained using an off-the-shelf 18-gauge side-cutting MR-compatible core biopsy needle and the patient discharged, on an average, two hours later [10], [42], [43].

B. Data

The data used in this study consists of 583 intraprocedural MRI scans obtained from 71 patients who underwent transperineal MRI-guided biopsy between December 2010 and September 2015. This retrospective study was HIPAA compliant and institutional review board approval (IRB) and informed consent was obtained. The patients in this cohort had prostate MRI lesions suspicious for new cancer, recurrent cancer after prior therapy, or lesions suspicious for higher grade cancer than their initial diagnosis. Each of the intraprocedural MRI scans is an axial fast spin echo (FSE) T2-weighted volume of size range 256–320 204–320 18–30 voxels, with voxel spacing in the range×of 0.53–0.×94 mm in-plane and slice thickness of 3.6–4.8 mm. The acquisition parameters for the FSE sequence were set as follows: repetition time (TR) is 3000 ms, echo time (TE) is 106 ms, and flip angel (FA) is 120 degrees [10]. The imaging time is about one minute and is performed after needle insertion to visualize it relative to the target. These scans were acquired on either a conventional wide-bore, 3T MR scanner (Verio, Siemens Healthcare, Erlangen, Germany) or a ceiling-mounted version of it (IMRIS/Siemens Verio; IMRIS, Minnetonka, Minn).

C. Data Annotation

A custom needle annotation software tool was used by an expert human rater to interactively mark the needle trajectory and tip on each of the 583 MRI [25]. These annotations are also referred to as ground truth. In these images, a needle can be identified by the dark susceptibility artifact around its shaft, as seen in Figure 1(c) and (d). The annotation tool allowed the human rater to place several control points ranging from the tip of the needle to its base. Those control points were then used to fit a Bézier curve which represents a trajectory of the needle artifact. Thus the manual needle trajectory relies only on the observer input (and not on the underlying gray scale values). Ground truth needle segmentation label maps were then generated by creating a 4 mm diameter cylinder around the Bézier curve to cover the hypointense artifact that surrounds the needle shafts, as seen in Figure 1(e).

Fig. 1.

Transperineal in-gantry MRI-targeted prostate biopsy procedure: (a) The patient is placed in the supine position in the MRI gantry, and his legs are elevated to allow for transperineal access. The skin of the perineum is prepared and draped in a sterile manner, and the needle guidance template is positioned.(b), (c) and (d): Axial, sagittal and coronal views of intraprocedural T2-W MRI with needle tip marked by white arrow. (e) 3D rendering of the needle (blue), segmented by our method, and visualized relative to the prostate gland (purple), and an MRI cross-section that is orthogonal to the plane containing the needle tip.

It should be noted that even for experienced human observers, there can be ambiguity in picking the axial plane containing the needle tip due to the large slice thickness and partial volume effects. In addition, there are cases, as shown in Figure 2, where the needle susceptibility artifact consists of two hypointense regions separated by a hyperintense one (instead of a single hypointese region). The human observer followed the needle carefully across several slices to ensure the integrity of the annotation.

Fig. 2.

(a) and (b): Examples of needle induced susceptibility artifacts in MRI where instead of a single hypointense (dark) region, there are two hypointense regions separated by a hyperintense (bright) region. In such cases, the human expert followed the needle carefully across several slices to ensure the integrity of the annotation. The arrow marks the needle identified by the expert.

The annotated images were split at the patient level into 70% training/cross-validation for algorithm development and 30% for final testing (Table I).

Table I.

Number of Patients and Needle MRIS for Training/Validation and Test Sets.

set	training & validation		test
	# patients	# images	# patients	# images
size	50	410	21	173

D. Data Preprocessing

Prior to training the CNN models, the data was preprocessed in four steps: resampling, cropping, padding, and intensity normalization, as follows.

Resampling:

First, the data was resampled to a common resolution of 0.88 × 0.88 × 3.6 mm. The MR images and ground truth segmentation maps were resampled with linear and nearest neighbor interpolation methods respectively. SimpleITK implementation of the interpolation methods were used for image resampling [44].

Cropping:

Second, to constrain the search area for the needle tip, each MR image was cropped to a cube of size 165.4×165.4×165.6 mm (188×188×46 voxels) around the center of the prostate gland. The size of the box was chosen to be large enough to easily accommodate the size of the largest expected diseased gland, and small enough to fit in the GPU memory for efficient processing. Even though a very coarsely selected bounding box that contains the prostate gland is sufficient for this step, we used a separate deep network, a customized variant of 2D U-Net architecture, that was readily available to us to perform the segmentation automatically[41]¹.

Padding:

Third, the borders of the cropped volume were padded by 50 mm (14 pixels) in the z direction. The zero padding in the z direction is required to accommodate the reduction in spatial dimension of the output of 3D convolutional filters. As a result of convolution operation, for in-plane directions (x and y) the output of the final layer of the network (green box in Figure 3) will be 88 pixels smaller than the input image (blue box in Figure 3).

Fig. 3.

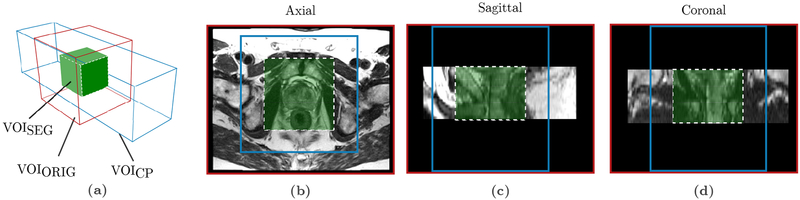
Original, cropped and padded, and segmentation volumes of interests (VOIs) (a) The original grayscale volume (VOI_ORIG, red box) is cropped in x and y directions and padded in the z direction to a volume of size 164.5 × 164.5 × 165.6 mm (188 × 188 × 46 voxels) centered on the prostate gland (VOI_CP, blue box). VOI_C is used as the network input. The network output segmentation map is of size 88 × 88 × 64.8 mm (100 × 100 × 18 voxels) (VOI_SEG, green box). The adjusted voxel spacing for the volumes is 0.88 × 0.88 × 3.6 mm. (b), (c), (d) show axial, sagittal and coronal views respectively of a patient case overlayed with the boundaries of the volumes VOI_ORIG, VOI_CP and VOI_SEG.

Intensity Normalization:

Fourth, to reduce the heterogeneity of the grayscale distribution in the data, intensities were truncated and re-scaled to the range between 0.1% and 99% quantiles of the intensity histogram and then normalized to the range of [0, 1].

E. Convolutional Neural Networks

In this work a binary classification model based on CNNs is proposed for needle segmentation and localization in prostate MR images. The deep network architecture is composed of sequential convolutional layers l ϵ[1, L]. At each convolutional layer l, the input feature map (image) is convolved by a set of K kernels W_l = {W ¹, …, W ^K} and biases b_l = {b¹ …, b^K to generate a new feature map. A non-linear activation function f is then applied to this feature map to generate the output Y_l which is the input for the next layer. The nth feature map of the output of the l^th layer can be expressed by:

$$Y_l^n=f\left(\sum _{k=1}^K{W}_l^{n,k}*Y_{l-1}^k+b_l^n\right),$$ (1)

The concatenation of the feature maps at each layer provides a combination of patterns to the network, which become increasingly complex for deeper layers. Training of the CNN is usually done through several iterations of stochastic gradient descent (SGD), in which several samples of training data (a batch) is processed by the network. At each iteration, based on the calculated loss the network parameters (kernel weights and biases) are optimized by SGD in order to decrease the loss.

Medical image segmentation can be formulated as a pixel-level classification problem which can be solved by convolutional neural networks. Leveraging the volumetric nature of the data through the inter-slice dependence of 2D slices is a key factor in 3D biomedical image classification and segmentation problems. Representation learning for segmentation in 3D has been done in different ways: directly by the use of 3D convolutional filters, multi-view CNNs with 2D images, and recurrent architectures [35]. 3D convolutional filters can be used in 3D architectures known as fully convolutional neural networks (FCNs) or through patch-based sliding-window methods [45].

The use of FCNs for image segmentation allows for endto-end learning, with each pixel of the input image being mapped by the FCN to the output segmentation map. This class of neural networks has shown great success for the task of semantic segmentation [46]. During training, the FCN aims to learn representations based on local information. Although patch-based methods have shown promising results in segmentation tasks [36], FCNs have the advantage of reduction in the computational overhead of sliding-window-based computation. The efficiency of FCNs in prediction time makes them better suited for procedures such as intera-operative imaging where time is an important factor. One drawback of 3D FCNs is the memory constraint of the graphical processing units (GPUs) to hold the large parameters during the optimization process which limits the input size, number of model parameters and number of mini-batches in stochastic gradient descent iterations. In addition to CNNs, recurrent neural networks (RNNs) have also been successfully used for segmentation tasks by feeding prior information from adjacent locations such as nearby slices or nearby patches into the classifier [47].

The CNN proposed in this paper is a 3D FCN. FCNs for segmentation usually consist of an encoder (contracting) path and a decoder (expanding) path [48], [49]. The encoder path consists of repeated convolutional layers followed by activation functions with max-pooling layers on selected feature maps. The encoder path decreases the resolution of the feature maps by computing the maximum of small patches of units of the feature maps. However, good resolution is critical for accurate segmentation, therefore in the decoder path, up-sampling is performed to restore the initial resolution, but the feature maps are concatenated to keep the computation and memory requirements tractable. As a result of multiple convolutional layers and max-pooling operations the feature maps are reduced and the intermediate layers of an FCN become successively smaller. Therefore, following the convolutions, an FCN uses inverse convolutions (or backward convolutions) to up-sample the intermediate layers until the input resolution is matched [46], [50]. FCNs with skip-connections are able to combine high level abstract features with low level high resolution features which has been shown to be successful in segmentation tasks [45].

F. Network Architecture

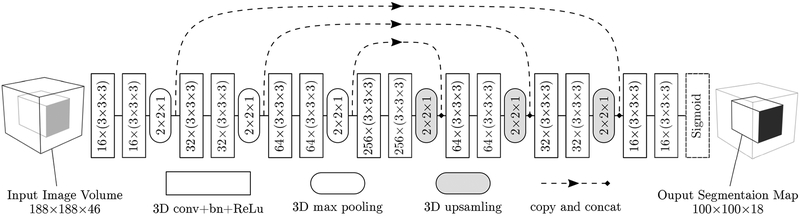
We present a fully automatic approach for needle localization by segmentation in prostate MRI based on a 14-layers deep anisotropic 3D FCN with skip-connections (Figure 4). The network architecture is inspired by the 3D U-Net model[45]. We improved the network architecture to efficiently handle the anisotropic nature of MRI volumes and for the specific problem of needle segmentation in MRI. Due to the time constraints in intraoperative imaging, MRIs taken during the interventional procedure often have thick slices but high resolution in the axial plane which leads to anisotropic voxels. Pooling and up-sampling were only applied to the in-plane axes (x and y) to handle the anisotropic nature of the needle MRI. The proposed asymmetry in the network design is computationally efficient and allows the whole volumetric MRI to be used for training.

Fig. 4.

Schematic overview of the anisotropic 3D fully convolutional neural network for needle segmentation and localization in MRI. Network architecture consisting of 14 convolutional layers, 3 max-pooling and 3 up-sampling layers. Convolutional layers were applied without padding while max-pooling layers halved the size of their inputs only in in-plane directions. The parameters including the kernel sizes and number of kernels are explained in each corresponding box. Shortcut connections insures combination of low-level and high-level features. The input to the network is the 3D volume image with the prostate gland at the center (188 × 188 × 46) and the output segmentation map has the size of 100 × 100 × 18.

As illustrated in Figure 4, the proposed network consists of 14 convolution layers. Each convolution layer has a kernel size of (3 × 3 × 3) with stride of size 1 in all three dimensions. Since the input of the proposed network is a T2-weighted MRI, the number of channels for the first layer is equal to one. After each convolutional layer, a rectified linear unit (ReLu) f(x) = max(0, x) is used as the nonlinear activation function except for the last layer [51] where a sigmoid function S(x) = e^x(e^x + 1)⁻¹ is used to map the output to a class probability between 0 and 1. There are 3 max-pooling and 3 up-sampling layers of size (2 × 2 × 1) in the encoder and decoder paths respectively. The network has a total of 3,231,233 trainable parameters. The input to the network is the 3D volume image with the prostate gland at the center (188 × 188 × 46) and the output segmentation map size is 100 ×100 ×18 which corresponds to a receptive field of size 88 × 88 × 65 mm.

G. Training

During training of the proposed network, we aimed to minimize a loss function that measures the quality of the segmentation on the training examples. This loss Ꮭ_t over N training volumes can be defined as:

$${\mathcal{L}}_t=-\frac{1}{N}\sum _{n=1}^N\left(\frac{2\left|X_n\cap Y_n\right|}{\left|X_n\right|+\left|Y_n\right|+s}\right),$$ (2)

where X_n is the output segmentation map, Y_n is the ground truth obtained from expert manual segmentation for the n^th training volume, and s (set to 5), is the smoothing coefficient which prevents the denominator from being zero. This loss function has demonstrated utility in image segmentation problems where there is a heavy imbalance between the classes, as in our case where most of the data is considered background[52].

We used a SGD algorithm with the Adam update rule [53] which was implemented in the Keras framework [54]. During the training we used a mini-batch of 4 image volumes. The initial learning rate was set to 0.001. Learning rate was reduced by a factor of 0.8 if the average of validation Dice score did not improve by 10⁻⁵ in five epochs. The parameters of the convolutional layers were initialized randomly from a Gaussian distribution using the He method [55]. To prevent overfitting, in addition to the batch-normalization [56], we used drop-out with 0.1 probability as well as L₂ regularization with λ₂ = 10⁻⁵ penalty on convolutional layers except the last one. Training was performed on 410 MRI scans from 50 patients using five-fold cross validation with splitting at the patient level. Each training sample was a 3D patch (also referred to as input volume or VOI_CP) of size 188 × 188 × 46 voxel. Data augmentation was performed by flipping the 3D volumes horizontally (left to right), which doubled the amount of training examples [57]. Cross-validation was used to optimize and tune the hyperparameters including CNN architecture, training scheme, and finding the best epoch (model checkpoint) for the test-time deployment. For each cross-validation fold, we used 100 as the maximum number of epochs for training and an early stopping policy by monitoring validation performance. This resulted in five trained models, one from each of the cross-validation folds, that are aggregated later with the ensembling method (described in Section III-C) for test-time prediction.

III. Experimental Setup

A. Observer Study

We designed an observer study in which a second observer, blinded to the annotations by the first observer (the ground truth), segmented the needle trajectory on the test set (n = 173 images) using the same annotations tools as the first observer. We compared the performance of both the proposed automatic system and the second observer with the first observer (ground truth).

B. Evaluation Metrics

We evaluated the accuracy of the system by measuring how well it localizes the tip of the needle, and how well it segments the entire trajectory of the needle. In addition to measuring the tip and angular deviation errors which are commonly used to quantify targeting accuracy of percutaneous needle insertion procedures [28], we report the number of axial planes contained in the tip error because of the high anisotropy of the data set. We used the Hausdorff distance to measure the quality of the segmentation of the entire length of needle (beyond the tip error) [25], [26].

• Tip deviation error ᐃP : The ground truth needle tip position was determined as the center of the needle artifact in the most distal plane of the needle segmentation image P (x, y, z). Tip deviation ᐃP is quantified as the 3D Euclidean distance between the prediction $\widehat{P}$ and manually specified ground truth P in millimeters.

• Tip axial plane detection error ᐃA: The tip plane detection error is the absolute value of the distance between the ground truth axial plane index A containing the needle tip and the predicted axial plane index  in voxels.

• Hausdorff Distance HD: Trajectory accuracy was calculated by measuring the directed Hausdorff distance between two N-D sets of predicted $\widehat{X}$ and ground truth X needles defined with

  $$d_{\text{H}}(X,\widehat{X})=\max \{\underset{x\in X}{\sup }\underset{\widehat{x}\in \widehat{X}}{\inf }d(x,\widehat{x}),\underset{\widehat{x}\in \widehat{X}}{\sup }\underset{x\in X}{\inf }d(x,\widehat{x})\},$$ (3)

  where sup represents the supremum and in f the infimum, and x and $\widehat{x}$ are points from X and $\widehat{X}$ respectively.

• Angular deviation error ᐃθ : The true needle direction θ was defined as the angle between the needle shaft and the axial plane. The angular deviation between the ground truth needle direction θ and the predicted needle direction $\widehat{\theta }$ quantifies the accuracy of needle direction prediction $(\Delta \theta =|\theta -\widehat{\theta }|)$.

C. Test-time Augmentation

Test-time augmentation seeks to improve classification by analyzing multiple augmentations or variants of the same image and averaging out the results. Recently, it has been used to improve pulmonary nodule classification from CT [58], detection of lacunes from MRI [57], and prostate cancer diagnosis from MRI [59]. We performed test-time augmentation by flipping 3D volumes horizontally which doubles the test data.

We conducted experiments to quantify the impact of training-time and test-time augmentation and performed analysis to measure the statistical significance of the results. Paired comparison of needle tip localization errors for unequal cases was performed using Wilcoxon signed-rank test (two-tailed). For reporting statistical analysis results, statistical significance was set at 0.05.

D. Ensembling

As reported in Section II-G, cross-validation resulted in five trained models. Combined with test-time augmentation, this results in 10 segmentation maps for each test case, i.e. for each of the five trained models, there is one prediction for the test image, and one for its flipped variant. To obtain the final binary prediction, we used an iterative ensembling or voting mechanism to aggregate the results of 10 predictions at the voxel level (Algorithm 1).

The input to the algorithm is S, the sum image of all predictions. In an iterative procedure, the binary segmentation map B, is generated by thresholding S using τ. τ is initialized at the value of majority votes $\tau =\lceil \frac{n}{2}\rceil$, where n is the number of predictions. v is a constant that represents the minimum size of a needle which was measured at 100 voxels over the 410 needles in the training set. An iterative procedure reduces τ until a needle is found.

Finally, to obtain the needle tip and trajectory the binary segmentation map is converted to 3D points in space by getting the center of the bounding box of the needle in each axial slice. The most distal point in the z-axis is considered the needle tip.

Algorithm 1.

Overview of the ensembling algorithm

$$\begin{array}{l}\text{Require}:\text{\hspace{0.17em}S,\hspace{0.17em}the sum image of n predictions}\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1:\hspace{0.17em} Constant:\hspace{0.17em}}\nu =100,\text{min number of voxels in a needle}\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2:\hspace{0.17em} Initialize:\hspace{0.17em}}\tau =\lceil \frac{n}{2}\rceil ,\text{min vote threshold}\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}3:\hspace{0.17em} Initialize:\hspace{0.17em}}B=0,\text{output segmentation image, same shape\hspace{0.17em}as\hspace{0.17em}}S\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}4: \hspace{0.17em}}\text{\hspace{0.17em}repeat}\\ 5:\text{for}\text{\hspace{0.17em}voxels}[i]\in S\text{and}b[i]\in Bdo\\ 6:ifs[i]\ge \tau then\\ 7:b[i]\leftarrow 1\left\{\text{voxel is needle}\right\}\\ 8:else\\ 9:b[i]\leftarrow 0\left\{\text{voxel is not needle}\right\}\\ 10:end\hspace{0.17em}if\\ \text{\hspace{0.17em}11:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\mathrm{end}\hspace{0.17em}for\\ 12:\tau \leftarrow \tau -1\left\{\text{relax threshold if no needle found}\right\}\\ \text{\hspace{0.17em}13:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}c\leftarrow {\sum }_{b[j]\in B}b\left[j\right]\left\{c\text{\hspace{0.17em}is total number of needle voxels}\right\}\\ 14:untilc\ge \nu \text{\hspace{0.17em}or\hspace{0.17em}}\tau =0\end{array}$$

E. Implementation and Deployment

The proposed algorithm for needle localization and segmentation was implemented in Keras V2.0 [54] with Tensorflow back-end [60] and trained on an Nvidia GTX Titan X GPU with 12 GB of memory, hosted on a machine running Ubuntu14.04 operating system on a 3.4 GHz Intel(R) Core(TM) i7–6800K CPU with 64 GB of memory. Training of large volumetric 3D networks was enabled and accelerated by the efficient cudNN² implementation of deep neural network layers. The trained models were deployed in the open-source DeepInfer toolkit and are publicly available for download and use from the DeepInfer model repository³.

IV. Results

We tested the proposed method on a previously unseen test set of 173 MRI volumes from 21 patients. Figure 5 visually illustrates the localization of a single needle and the corresponding measured quality metrics in an example that is representative of the results of the proposed system. In the rest of this section, we present quantitative results of the performance of the proposed system against the ground truth, and also that of a second observer against the ground truth.

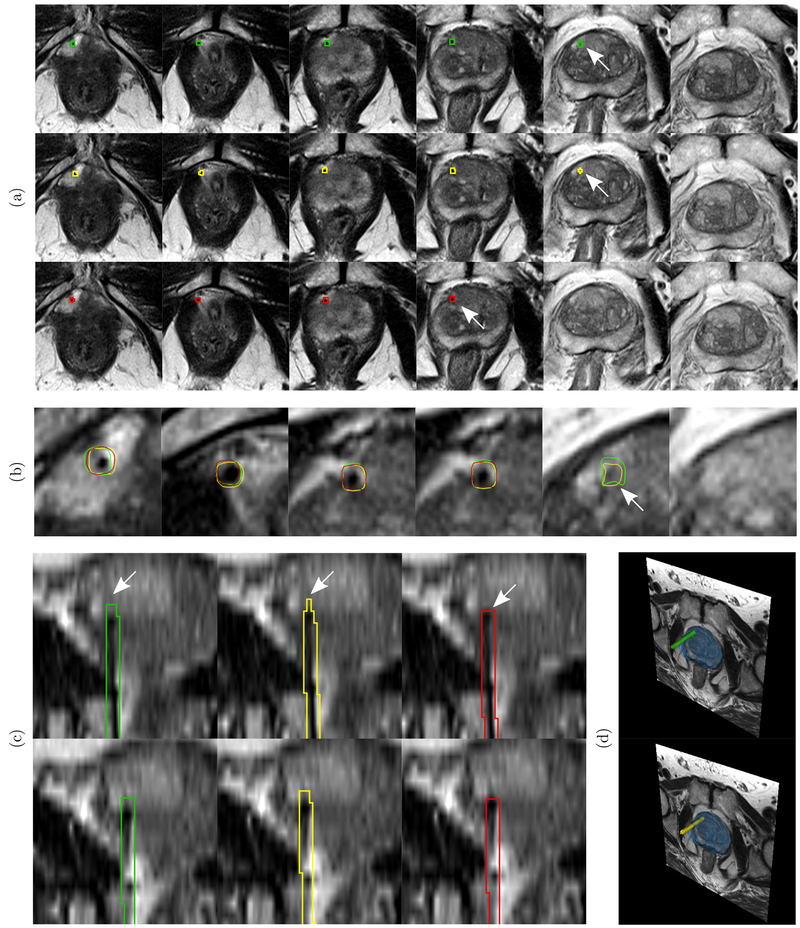
Fig. 5.

An example test case to illustrate the localization results of the proposed system. Green, yellow, and red contours show the needle segmentation boundaries of the ground truth, the proposed system, and the second observer respectively. The arrows mark the needle tips. (a) First row shows the needle trajectory segmentation and tip localization (arrow) of ground truth in axial slices. The second row shows the results of needle tip and trajectory localization by the proposed system. The third row shows the needle tip and trajectory localization by the second observer. (b) Zoomed view of slices in (a) with overlapping cross sections of 3D needle models of ground truth, second observer, and CNN prediction. (c) Coronal views of different sections of the needle respectively.(d) 3D rendering of the needle relative to the prostate gland (blue) and cross-section of the axial plane of the MRI with 3D models of ground truth and CNN predicted needles. For the proposed CNN, the measured needle tip localization error (ᐃP), tip axial plane detection error (ᐃA), Hausdorff distance (HD), and angular deviation error (ᐃθ) are 1.76 mm, 0 voxels, 1.24 mm, and 0.30° respectively. The needle tip localization error 1.76 mm lies within the range of median and mean of the test cases which are 0.88 mm and 2.80 mm respectively (Table II). The tip axial plane error is 0 voxels which is representative of 65% of the test cases (Figure 7). The Hausdorff distance 1.24 mm is same as the median of the test cases (Table III). The angular deviation error 0.30° is better than both mean and median of the test cases (Table IV). For the second observer, the tip localization error (ᐃP), tip axial plane detection error (ᐃA), Hausdorff distance (HD), and angular deviation error (ᐃθ) are 4.48 mm, 1 voxel, 3.7 mm, and 0.56° respectively.

A. Tip Localization

The average tip localization errors for the proposed automatic system and the second observer relative to the ground truth are presented in Table II. Corresponding box plots are presented in Figure 6.

Table II.

Needle TIP Localization Error (MM) for Test Cases for Proposed CNN Method and the Second Observer^*.

	$\overline{\Delta P}$	σᐃP	RMS(ΔP)	M(ΔP)
CNN	2.80	3.59	4.54	0.88
Second observer	2.89	4.05	4.98	0.88

^*$\overline{\Delta P}$, _σᐃP, RMS(ᐃP) and M(ᐃP) are the mean, standard deviation, root mean square, and median of the needle tip deviation, respectively. First row indicates the error of the CNN against ground truth, and second row indicates error of the second observer against ground truth.

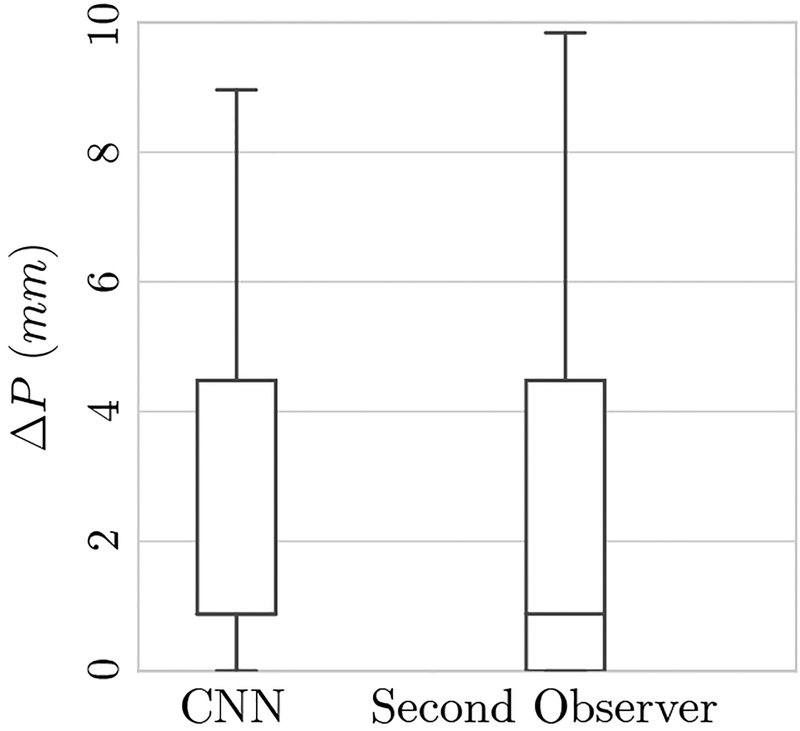
Fig. 6.

Box plots of the needle tip deviation error in millimeters for the test cases. Distances of automatic (CNN) and second observer are shown which are comparable. The median tip localization error for both CNN and second observer is 0.88 mm (1 pixel in transaxial plane).

The median needle tip deviation for both the CNN and the second observer was 0.88 mm (1 pixel in the transaxial plane). Perfect matching of the predicted needle tip (0 mm deviation) was achieved for 32 (18% of test images) and 46 needles (27% of test images) for the CNN and second observer, respectively.

B. Tip Axial Plane Detection

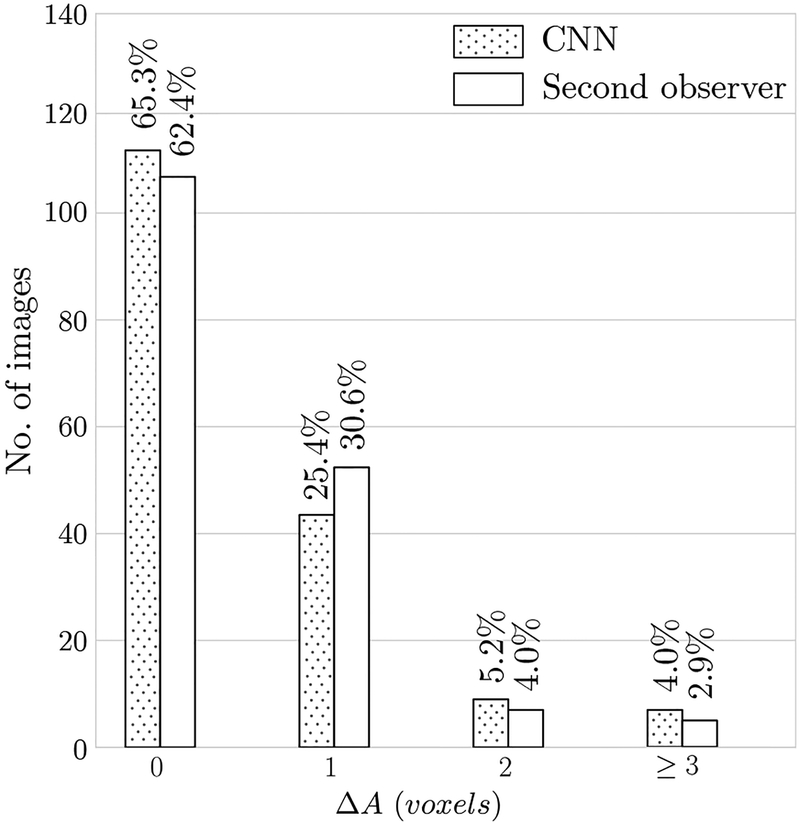
The bar chart in Figure 7 summarizes the accuracy results for needle tip axial plane detection. For 113 images (65%) the algorithm detected the correct axial slice (ᐃA = 0) containing the needle tip which is comparable to the agreement between the two observers (108 cases (62%)). The algorithm missed the needle tip by one slice (ᐃA = 1) on 44 images (25%), by two slices (ᐃA = 2) for 9 images (5%) and by three or more slices (ᐃA ≥ 3) for 7 images (4%). The bar chart shows that the performance of the CNN and the second observer are in the same range.

Fig. 7.

Bar charts of needle tip axial plane localization error (ᐃA). Needle tip axial plane distance error of the automatic (CNN) method and second observer are shown. The results of the automatic CNN method are comparable with the second-observer.

C. Trajectory Localization

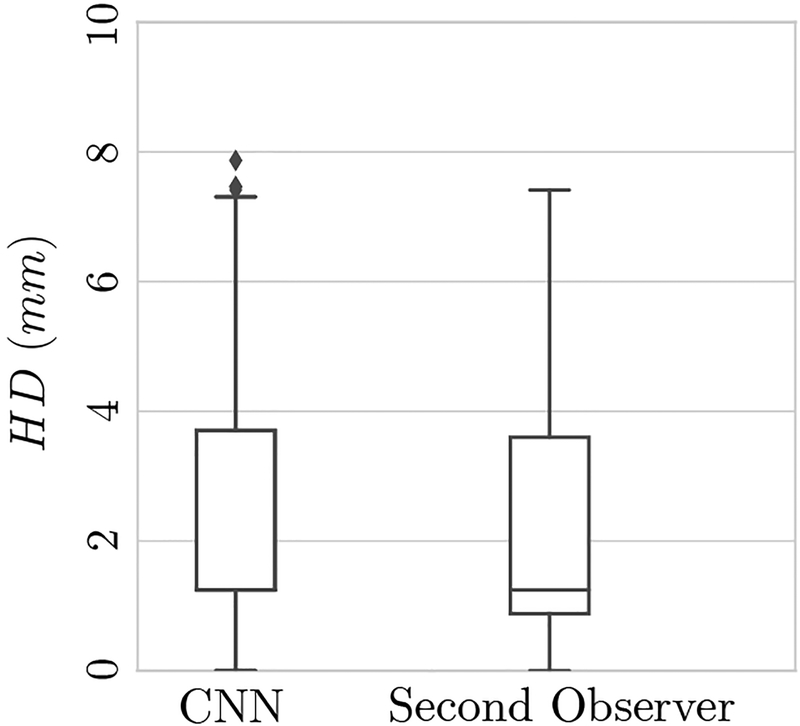
Table III presents the results of needle trajectory localization error in terms of directional Hausdorff distance (HD) for the test cases for both the CNN and the second observer. Trajectory localization errors are summarized as the mean, standard deviation, root mean square, and median of the error. Corresponding box plots are presented in Figure 8.

Table III.

Trajectory Localization Error Averaged Over Test Cases for Proposed CNN Method and the Second Observer^* (Units are in Millimetres).

	$\overline{HD}$	σHD	RMS(HD)	M(HD)
CNN	3.00	3.15	4.35	1.24
Second observer	2.29	2.82	3.63	1.24

^*$\overline{HD}$, _σHD, RMS(HD), and M(HD) are the mean, standard deviation, root mean square, and median of the needle trajectory localization Hausdorff distance, respectively.

Fig. 8.

Box plots of Hausdorff distance (HD) in millimeters for test cases. The median HD distance for both the CNN and the second observer is 1.24 mm.

D. Needle Direction

Table IV presents the needle direction error in terms of angular deviation (ᐃθ) for the test cases for both the CNN and the second observer. Needle angular deviation errors are summarized as the mean, standard deviation, root mean square, and median of the error.

Table IV.

Needle Direction Error Quantified as the Deviation Angle Averaged Over Test Cases for Proposed CNN Method and the Second Observer^* (Units are in Degrees).

	$\overline{\Delta \theta }$	σᐃθ	RMS(Δθ)	M(Δθ)
CNN	0.98	1.1	1.47	0.68
Second observer	0.97	1.04	1.43	0.75

^*$\overline{\Delta \theta }$, _σᐃθ, RMS(ᐃθ), and M(ᐃθ) are the mean, standard deviation, root mean square, and median of the needle deviation angle, respectively.

E. Data Augmentation

Table V summarizes the impact of training-time and test-time augmentation on system performance as measured by the mean and standard deviation of the needle tip localization error in millimeters. The bottom right cell indicates best per formance when both training-time and test-time augmentation are used. While both training and test-time augmentation did demonstrate smaller averages of needle tip deviation errors and fewer number of failures, we did not find improvements to be statistically significant.

Table V.

Impact of Training-Time and Test-Time Augmentation on Performance^*.

	$\overline{\Delta P}\pm {\sigma }_{\Delta P}$
	TRAINING-TIME AUGMENTATION
	Without	With
Without TEST-TIME AUG.	4.92 ± 13.22	3.07 ± 3.70†
With TEST-TIME AUG.	3.93 ± 8.83	2.80 ± 3.59

^*This table quantifies the system performance as measured by the mean and standard deviation of the needle tip localization error in millimeters.

^†This model failed to segment one needle out of 173 in the test set. All other models did not miss any needles.

F. Execution Time

The execution time of the proposed system was measured for inference on the test set of 173 volumes in the same environment that was described in Section III-E. The average localization time using the proposed system was 29 seconds. This includes preprocessing, running five models on the original MRI volume and the flipped version, ensembling, and resampling back to the original spatial resolution of the input image. In comparison, the second observer annotated a needle in 52 seconds on average.

V. Discussion and Conclusion

Automatic localization of needle tip and visualization of needle trajectories relative to the target can aid interventionalists in percutaneous needle placement procedures. Furthermore, accurate needle tip and trajectory localization is necessary for robot-guided needle placement. To the best of our knowledge, this is the first report of a fully automatic system for biopsy needle segmentation and localization in MRI with deep convolutional neural networks. A fairly large dataset of 583 MRI volumes from 71 patients suspected of prostate cancer was used to design, optimize, and test the proposed system. The system achieves human expert level performance for MRI-targeted prostate biopsy procedures. The results on an unseen test set show a mean accuracy error of 2.8 mm in detection of needle tip, 96% detection of axial tip plane within 2 slices, mean Hausdorff distance of 3 mm in needle trajectory, and a mean 0.98° error in needle trajectory angle, all of which lie within the range of agreement between human experts as shown by an observer study.

Our results support the findings of other studies in using 3D fully convolutional neural networks including 3D U-Net and its variants, for biomedical image segmentation to achieve promising results [35]. Additionally, the deployed trained model segments and localizes a needle in a 3D MRI volume in 29 seconds which makes it viable for adoption in the clinical workflow of MRI-targeted prostate biopsy procedures. The results of experiments to quantify the effect of data augmentation demonstrated smaller averages of needle tip deviation errors. However, unlike Ghafoorian et al. [57], we did not find the improvements to be statistically significant. Further analysis on larger test sets is required to statistically assess the effect of data augmentation for the needle segmentation problem. By preserving the ratio between in-plane resolution and slice thickness with anisotropic max-pooling and down sampling, we were able to train and deploy our model with whole 3D MRI volumes as inputs to the networks.

CNNs tend to be sensitive to the variations in MRI acquisition protocols. Variations in parameters during the acquisition of the MRI volumes result in different appearances of tissue and needle artifact [61]. Although we used a fairly large dataset of 583 MRI volumes in our experiments, and these MRI were acquired on two different MRI scanners, they were all obtained in a single institution using substantially similar MRI protocols. Therefore it is a reasonable conclusion that the performance of the trained models will degrade when applied to data acquired using substantially different MRI parameters. Domain adaptation and transfer learning techniques can be used to address this issue [61]. Moreover, due to the large slice thickness of 3.6 mm and partial volume effect, in many cases there is ambiguity in identifying the correct axial plane containing the needle tip. In this study we used the first observer as the gold standard and compared the second observer and the proposed method with it. Ideally, we would have had multiple observers and used majority voting for needle segmentation and tip localization.

We plan to incorporate the proposed automatic localization method in the workflow of the transperenial in-gantry MRI-targeted prostate biopsies under a prospective study approved by the institutional ethics board. In order to do this, we will design a study to determine how the needle trajectory should be presented to the interventionalist to help them make the most efficacious decisions – e.g. should the insertion point or angle of a suboptimal trajectory be changed – during the procedure. In addition, we plan to transfer the framework and proposed methodology to other types of image-guided procedures which involve needle detection and localization.

In conclusion, 3D convolutional neural networks, designed with some attention to domain knowledge, can effectively segment and localize needles from in-gantry MRI-targeted prostate biopsy images. The results of this study suggest that our proposed system can be used to detect and localize biopsy needles in MRI within the range of clinical acceptance and human-expert performance.