Sampling frequency influences sample entropy of kinematics during walking

Abstract

Sample entropy (SaEn) has been used to assess the regularity of lower limb joint angles during walking. However, changing sampling frequency and the number of included strides can potentially affect the outcome. The present study investigated the effect of sample frequency and the number of included strides on the calculations of SaEn in joint angle signals recorded during treadmill walking. Eleven subjects walked at their preferred walking speed for 10 minutes, and SaEn was calculated on sagittal plane hip, knee and ankle angle signals extracted from 50, 100, 200, 300 and 400 strides at sampling frequencies of 60, 120, 240 and 480Hz. Increase in sampling frequency decreased the SaEn significantly for the three joints. The number of included strides had no effect on the SaEn calculated on the hip joint angle and only limited effect on the SaEn calculated on the knee and ankle joint signals. The present study suggests that the number of data points within each stride to a greater extent determines the size of the SaEn compared to the number of strides and emphasizes the use of a fixed number of data points within each stride when applying SaEn to lower limb joint angles during walking.

GRAPHICAL ABSTRACT

Introduction

The concept of information entropy was first introduced by Claude Shannon in 1948 as a method of quantifying the amount of information in communication [16]. The original idea was based on the probability of information coming from various sources and later became the foundation for various versions of entropy measures used to quantify predictability (e.g. approximate entropy, sample entropy (SaEn), fuzzy entropy). SaEn was introduced by Richmann and Moorman [14] and is the most used version in biomechanical research to quantify predictability. It has been used to investigate standing [9] and sitting [17] balance, gait impairment in various individuals [2,19,22,13], sport performance [12], and force production [18,4].

Compared to other widely used nonlinear methods applied to gait data (e.g. the largest Lyapunov exponent, correlation dimension and detrended fluctuation analysis), SaEn has gained increasing interest in the last two decades [24]. While the aforementioned methods have been associated with both methodological and interpretational challenges, the computation and interpretation of SaEn is relative straight forward [5,7,8,24]. We have previously shown that when applied appropriately, SaEn constitutes a valuable tool for characterizing the dynamics of human movements in terms of predictability [24,23]. In gait analysis, SaEn has been used on various types of discrete and continuous data such as stride-to-stride time intervals [2,21], stride length and step width fluctuations [21], joint angles [22,1,13,19], and trunk accelerations [11,10,15]. Although deterministic in nature, stride characteristics exhibit a stochastic behavior in contrast to the pseudo-periodic behavior of joint angles and trunk accelerations. Furthermore, the stride characteristic variables are discrete variables and the joint angles and trunk acceleration signals are continuous variables. This difference could have important methodological implications.

During treadmill walking, stride time intervals and joint angles can be extracted from motion capture based kinematic data. Altering the sampling frequency will increase the detail level for both variables. For the stride time interval, changing the sampling frequency from 60Hz to 240Hz will change the detection level from 0.0167 second to 0.0042 seconds. Equally, this change in sampling frequency will increase the number of data points fourfold within each stride for the joint angle signals. We have previously shown that data length affects the outcome of SaEn analysis when using stride-to-stride time intervals [24,23]. However, it is unknown how changing the number of data points within each stride will affect the SaEn calculated on cyclic data like joint angles. Furthermore, since the use of SaEn in joint angle data should aim at investigating the regularity within the stride-to-stride fluctuations and not just within a single stride, it is equally important to investigate the effect of changing the number of included strides. Thus, the purpose of the present study was to investigate the effect of sample frequency and the number of included strides on the calculations of sample entropy in joint angle signals recorded during treadmill walking.

Methods

Subjects

Eleven healthy subjects (8 males) with mean (SD) age of 24 years (3), body mass of 74.7 kg (12.4) and body height of 174.2 cm (6.9) were recruited for the present study. All subjects were without lower limb injuries and neurological disorders that could affect the gait pattern. Informed consent was obtained from all individual participants included in the study. The study was approved by the Institutional Review Board of the University of Nebraska Medical Center and the study was carried out in accordance with the approved guidelines.

Experimental setup

A 12 high-speed camera system operating at 480Hz (Motion Analysis Corp., Santa Rosa, CA) recorded the three-dimensional position of 27 reflective markers placed bilaterally on: 1) anterior superior iliac spines, 2) posterior superior iliac spines, 3) greater trochanters, 4) midlateral thighs, 5) lower front thighs, 6) lateral knees, 7) tibial tubercles, 8) lower lateral shanks, 9) lateral ankles, 10) top of the second metatarsophalangeal (MTP) joints, 11) posterior heels, 12) lateral fifth MTPs, and 13) lateral calcanei. An additional single marker was placed on the sacrum. The subjects were walking at their preferred walking speed (PWS) on a treadmill (AMTI force-sensing tandem treadmill). Prior to the data collection, the preferred walking speed of the subjects were established by increasing and decreasing the speed of the treadmill above and below what the subjects reported as being comfortable. The average speed was 1.17 ± 0.23 m/s. The subject walked for 10 minutes during which data was collected.

Data analysis

Sagittal hip, knee and ankle joint angles were extracted from the kinematic data using Visual 3D (c-Motion, Inc., Germantown, MD). The joint angles from 400, 300, 200, 100 and 50 consecutive strides were extracted. For each data length, the original time series with a sampling frequency of 480Hz were additionally down sampled to 240, 120 and 60Hz. SaEn was calculated from the joint angle time series based on the algorithm presented by Richman and Moorman [14] and defined as the negative logarithm for the conditional probability that a series of data points within a certain distance, m, would be repeated within the distance m+1 (equation 1).

$$SaEn(m,r,N)=-\ln \left[\frac{A^{m+1}(r)}{B^m(r)}\right]$$ Equation 1

Where N is the number of data points in the time series, A is the number of similar vector lengths (m+1) falling within a relative tolerance limit (r times standard deviation of the time series) and B is the number of similar vector lengths (m) falling within the tolerance limit [24]. To investigate the effect of parameter choice, SaEn calculations were performed with m = 2 and 3 and r = 0.1, 0.15, 0.2, 0.25 and 0.3. The results from the analysis using m=2 and r=0.2 is presented below and remaining results are presented in a supplementary material available at the University of Nebraska, Omaha Digital Commons (https://digitalcommons.unomaha.edu).

Statistics

The applied statistical models assumed independency of observation, normal distribution of the residuals and homogeneity of variances (homoscedasticity). The normal distribution was confirmed by the Shapiro-Wilk test and the homogeneity was confirmed by the Brown-Forsythe test. To investigate if there was an overall effect of sampling frequ6ency and number of included strides on the SaEn calculated on each of the three joint angles, a two-way ANOVA for repeated measures was applied to each joint angle with sampling frequency and number of included strides as independent variables. In case of an overall significant effect of the independent variables or the interaction (sampling frequency x strides), a Holm Sidak post hoc test was applied to investigate differences in sampling frequency and number of strides. To investigate if there was an overall effect of joint on the SaEn, a one-way ANOVA for repeated measures was applied to the SaEn calculated from 400 strides with a sampling rate of 480Hz. This combination of sampling frequency and number of strides was chosen to include as much information as possible in the comparison. In case of an overall significant effect of joint, a Holm Sidak post hoc test was applied to investigate between joint differences. Level of significance was set at 0.05. All statistical analyses were performed in Sigmaplot (Systat Software, Inc. 2014, version 13.0, Germany).

Results

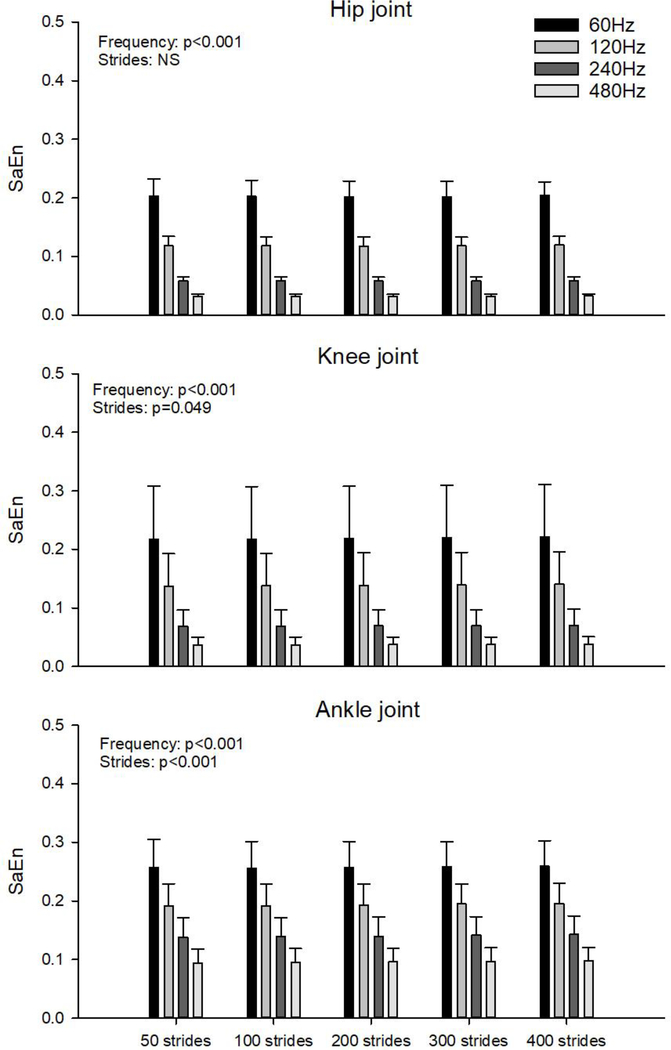
There was an overall significant effect of sampling frequency on the SaEn for the hip joint angle (p < 0.001) (figure 1). The post hoc tests revealed that with each increase in sampling frequency, the SaEn decreased significantly (p < 0.001 for all comparisons). There was an overall significant effect sampling frequency (p < 0.001) and of the number of included strides (p = 0.049) on the SaEn for the knee joint angle (figure 1). The SaEn decreased significantly with each increase in sampling frequency. In contrast, the post hoc test revealed no differences in SaEn between the different numbers of strides. There was an overall significant effect of both sampling frequency (p < 0.001) and of the number of strides included (p < 0.001) on the SaEn for the ankle joint angle (figure 1). The post hoc tests revealed that with each increase in sampling frequency the SaEn decreased significantly (p < 0.001 for all comparisons). Furthermore, SaEn calculated from 50 and 100 strides was significantly lower compared to SaEn calculated from 300 and 400 strides. Additionally, SaEn calculated from 200 strides was significantly lower compared to SaEn calculated from 400 strides.

Figure 1:

SaEn calculated on the hip joint angle (top graph), knee joint angle (middle graph) and ankle joint angle (bottom graph) for time series including 50, 100, 200, 300 and 400 strides and sampled at 60, 120, 240 and 480 Hz.

When comparing SaEn from the three joints calculated from 400 strides at 480 Hz (figure 1), there was an overall significant effect of joint (p < 0.001). The post hoc test revealed the SaEn from the ankle joint was significantly higher compared to the SaEn of the two more proximal joints (p < 0.001 in both cases). There was no significant difference between the SaEn from the knee and hip joint angles.

The results presented in the supplementary material indicated the same overall tendency as presented above. For all input parameter combinations, there was a significant effect of sampling frequency with SaEn decreasing considerable with increase in sampling frequency. However, the observed overall effect of the number of included strides resulted in relative small absolute changes in the SaEn.

Discussion

The present study aimed at investigating the effect of sample frequency and the number of included strides when quantifying regularity using SaEn on lower limb joint angles during walking. The main result was that while SaEn decreased considerably when sampling frequency was increased, changing the number of included strides seemed to have limited effect of the SaEn. These effects did not differ substantially between the three joints investigated in the present study.

We have previously observed considerable effects of changes in input parameters when using SaEn to quantify regularity in step-to-step time characteristics during walking [24,23]. Especially, time series including less than 200 steps exhibited low parameter consistency [24]. In contrast, the number of included strides had limited effect on the SaEn in the present study. Assuming that the average stride time was 1 second, the lowest number of data points in the present study was (60Hz x 50 strides x 1 second) 3000. Increasing the number of strides to 400 but keeping the same sampling frequency resulted in (60Hz x 400 strides x 1 second) 24000 data points, just as keeping the number of strides at 50 and increasing the sampling frequency to 480Hz did (480Hz x 50 strides x 1 second). While the first example had limited effect of the SaEn, the other decreased the SaEn substantially. These two examples of increasing the total number of data points resulted in two different changes in SaEn. This illustrates that the number of data points within each stride affects SaEn to a greater extent than the number of strides. It could be speculated that the decrease in SaEn with increase in sampling frequency could be related to the nature of the algorithm. Since an increase in sampling frequency does not change the standard deviation of the investigated time series, the applied critical limit will not change. However, as the sampling frequency increases the spatial distance between adjacent data points will decrease which will increase the number of vectors within each stride cycle. This will increase the likelihood of identifying vectors of m+1 that falls within vectors of m in subsequent strides. In contrast, increasing the number of included stride cycles without increasing the sampling frequency will not increase the number of vectors within each stride cycle and the likelihood of identifying similar vectors will not change significantly.

The present study suggests that data from various populations can be compared even if the number strides is not the same as long as the number of data points within each stride is kept the same. This supports the use of SaEn on joint angles during walking in patients groups or frail individuals incapable to complete long recording sessions which is needed when assessing regularity in stride-to-stride time intervals [24,23]. Some of the previous studies applying SaEn to lower limb joint angles recorded during walking have used a range of sampling frequencies from 60Hz [22] to 200Hz [19]. In light of the results from the present study, SaEn values from studies with different sampling frequencies should not be compared directly. However, the present study cannot recommend the use of a specific sampling frequency. Therefore, the sampling frequency of future studies should be determined a priori based on the research design and appropriate power spectral analysis.

Our previous studies have revealed some input parameter inconsistency when applying SaEn to stride-to-stride time interval time series with the same range of input parameters as in the present study [24,23]. The present study observed an acceptable input parameters consistency across the different sampling frequencies and numbers of included strides. Thus, regardless of the choice of input parameters the SaEn changed in a similar manner across sampling frequencies and number of strides. Additionally, the between-joint differences in SaEn did not differ across different input parameters.

While the present study elucidates important methodological aspects of applying SaEn to lower limb joint angles recorded during walking, it also indicates potential differences in these methodological aspects when comparing SaEn applied to continuous time series (e.g. joint angles, center of mass trajectories) compared to time series including discrete events (e.g. stride-to-stride time interval time series). Thus, future studies should investigate this topic further.

SaEn is one of several nonlinear methods, which has received increasing interest in both basic and applied gait research in recent years. While methods like detrended fluctuation analysis, the largest Lyapunov exponent and correlation dimension offers quantification various characteristics of the dynamics of human locomotion, the implementation and interpretation possess inherent challenges which has let to inconsistent observations and conclusions in the literature [5,6,3,8,20]. The interpretation and calculation of SaEn is relative straight-forward once a few methodological aspect related to the input parameter consistency are accounted for [24,23]. In light of the present study, we do not believe that the methodological constraints mentioned should prevent the application of SaEn to continuous cyclic signals recorded during human locomotion.

In conclusion, the present study observed that while increasing the sampling frequency significantly reduced the SaEn of joint angle trajectories during walking increasing the number of included stride cycles had limited effect. Based on these observations, we recommend that when SaEn is applied to lower limb joint angles recorded during walking, the number of data points within each stride is fixed across all subjects even if the number of recorded strides differs. This could be done by keeping the sampling frequency fixed and the walking speed fixed across subjects. Alternatively, the recorded time series are resampled to a fixed number of data points within each stride.

Biography

Peter C. Raffalt is a Postdoctoral Researcher at the Julius Wolff Institute for Biomechanics and Musculoskeletal Regeneration, Charité - Universitätsmedizin Berlin in Germany. His research covers human movement variability.

John McCamley received his PhD in Bioengineering from the University of Bologna in 2013. He is currently director of the Human Movement Laboratory, MORE Foundation Phoenix, Arizona.

William Denton is a laboratory technician in the Center for Human Movement Variability (MOVCENTR), Department of Biomechanics at the University of Nebraska at Omaha. He has degrees in Biological Systems Engineering and Biomechanics.

Jennifer M. Yentes is an Assistant Professor in the Center for Human Movement Variability (MOVCENTR), Department of Biomechanics at the University of Nebraska at Omaha. Her research covers human movement variability.