A Nondimensional Model Reveals Alterations in Nuclear Mechanics upon Hepatitis C Virus Replication

Abstract

Morphology of the nucleus is an important regulator of gene expression. Nuclear morphology is in turn a function of the forces acting on it and the mechanical properties of the nuclear envelope. Here, we present a two-parameter, nondimensional mechanical model of the nucleus that reveals a relationship among nuclear shape parameters, such as projected area, surface area, and volume. Our model fits the morphology of individual nuclei and predicts the ratio between forces and modulus in each nucleus. We analyzed the changes in nuclear morphology of liver cells due to hepatitis C virus (HCV) infection using this model. The model predicted a decrease in the elastic modulus of the nuclear envelope and an increase in the pre-tension in cortical actin as the causes for the change in nuclear morphology. These predictions were validated biomechanically by showing that liver cells expressing HCV proteins possessed enhanced cellular stiffness and reduced nuclear stiffness. Concomitantly, cells expressing HCV proteins showed downregulation of lamin-A,C and upregulation of β-actin, corroborating the predictions of the model. Our modeling assumptions are broadly applicable to adherent, monolayer cell cultures, making the model amenable to investigate changes in nuclear mechanics due to other stimuli by merely measuring nuclear morphology. Toward this, we present two techniques, graphical and numerical, to use our model for predicting physical changes in the nucleus.

Introduction

It is known that cell function and cell fate are regulated by mechanical properties of the nucleus (1, 2, 3) and its morphological changes brought about by forces acting on it (4). Cancer (5, 6), laminopathies (7, 8, 9, 10), and other diseases are known to effect such modifications in nuclei. Alterations in nuclear morphology are caused by a variety of molecular mechanisms, such as changes in the structural members of the nuclear envelope like lamins (11), differential regulation of the cytoskeleton (12), modifications in chromatin (13), and variations in osmotic pressure between the nucleoplasm and cytoplasm (14, 15). Various models have been proposed to simulate the changes in nuclear morphology due to molecular perturbations during cell spreading (16) and migration of cells through constrictions (1). In contrast, here, we propose a model for predicting the molecular mechanisms driving shape changes of the nucleus by merely analyzing the differences in nuclear morphology.

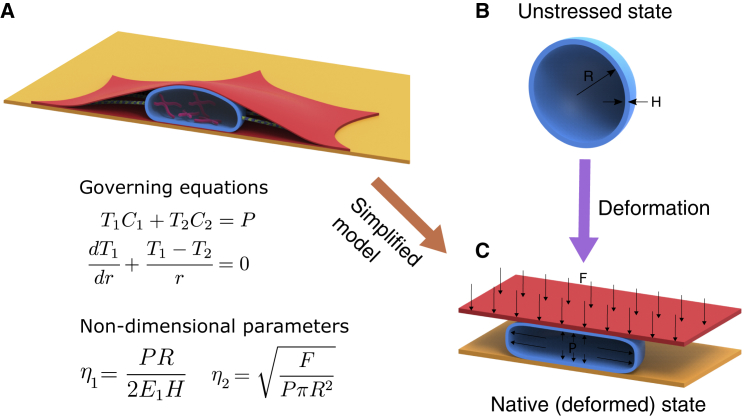
Nuclear morphology was described using a two-parameter, nondimensional mechanical model that consists of compression by cortical actin and net expansion by osmotic pressure, chromatin, and microtubules. Fig. 1 illustrates these two competing forces acting on a nucleus in monolayer cell culture as in (14). As shown in the figure, compressive force by cortical actin can be approximated as planar pressure pushing the nucleus down. This is akin to pressing an inflated sphere with a flat plate. Incidentally, the deformation analysis of such an elastic sphere was reported in (17) using an axisymmetric model that led to a pair of ordinary differential equations. The solutions to these equations depend only on two nondimensional parameters: 1) η₁ = PR/2E₁H, the ratio between the expanding pressure, P, to the elastic modulus, E₁, of the nuclear envelope of radius, R, and thickness, H, in the unloaded state (Fig. 1 B); and 2) ${\eta }_2=\sqrt{F/P\pi R^2}$, the ratio between the compressive force, F, to P. To estimate η₁ and η₂ corresponding to individual, experimentally measured nuclear morphological features, we first calculated three parameters to characterize nuclei individually: 1) projected area (A_p), 2) surface area (A_s), and 3) volume (V). Next, we normalized these parameters using R to define a_p = A_p/R², a_s = A_s/R², and v = V/R³. Our model enables expressing η₁ and η₂ in terms of a_p, a_s, and v. The three normalized parameters were then used to fit the model and thereby obtain η₁ and η₂. Differences in η₁ and η₂ between control and treated cells can reveal the molecular mechanisms causing the differences in nuclear morphology.

Figure 1.

A mechanical model for nuclear morphology. (A) Nuclear envelope (blue) is shaped by forces from the nucleoplasm and cytoplasm. These forces are mainly due to cortical actin (red), microtubules (green), chromatin (pink), and an osmotic pressure difference between the nucleoplasm and cytoplasm. (B) In the absence of forces, the nucleus is assumed to be a spherical membrane of radius R and thickness H. (C) The net contribution from osmotic pressure, microtubules, and chromatin is assumed to be an inflating pressure P. The force due to cortical actin, F, is assumed to be originating from a flat plate that is pushing down on the nucleus. The equations of equilibrium of the membrane in the normal and tangential directions are shown. T₁ and T₂ are the forces per unit length in the principal directions, and C₁ and C₂ are the principal curvatures. The solutions to the equations depend only on two nondimensional parameters, η₁ and η₂. To see this figure in color, go online.

We used hepatitis C virus (HCV) because some of our previous results showed that viral replication requires nuclear proteins such as La, PTB, and HuR (18, 19, 20, 21) to relocalize into cytoplasm during infection, which suggested alterations to the nucleus in HCV-infected liver cells. HCV is a cytoplasmic RNA virus, and the entire life cycle of this virus is completed inside the cytoplasm, including the viral genome replication. Hence, our findings suggesting a role for the nucleus in HCV life cycle were intriguing. These findings were independently supported by results from the literature. HCV proteins, NS5B and NS3, were shown to move into the nucleus (22). The viral protein core was shown to interact with the transcription factor RXRA and could influence the transcription of infected cells (23). We anticipated that the invasion of viral proteins into the nucleus might be important during the chronic phase of infection and therefore may influence the pathogenic fate of the infected cell (22, 24). Hence, we used HCV replicon cells that constitutively harbor HCV replicon RNA and thereby mimic a chronic HCV infection as our model system (25). Huh7 cells were used as control.

We observed that the size of the nuclei of HCV replicon cells was larger than those of control cells. By comparing η₁ and η₂ between Huh7 and HCV replicon cells, we predicted alterations in E₁ and F. These predictions from the model were experimentally verified using atomic force microscopy (AFM), western blot, and immunofluorescence assay. By using AFM, we measured nuclear and cell stiffness. Nuclear stiffness can be used as an indicator of E₁ and cell stiffness as an indicator of F. This is because nuclear stiffness increases with expression of lamin-A,C (26), which in turn is known to be a major elastic component of the nuclear envelope (27). Additionally, pre-tension in cortical actin is known to correlate with cell stiffness (28). Differential expression of lamin-A,C and β-actin measured using western blot and immunofluorescence assay independently reinforced the predictions from our model as well as AFM measurements.

An important biologically relevant finding of this work is that HCV proteins downregulate lamin-A,C and upregulate β-actin. This finding is supported by morphological and biomechanical measurements with the help of the aforementioned two-parameter model. Thus, we show consistency in the results of three different experiments, namely, biochemical assays, AFM stiffness measurements, and morphological parameters.

• 1)Biochemical assays showed downregulation of lamin-A,C and upregulation of β-actin in HCV replicon cells as compared to Huh7 cells. Based on the reported literature, we associate these two changes to reduced elastic modulus of the nuclear membrane and enhanced cortical actin force acting on the nucleus. The two changes correspond to smaller E₁ and larger F in replicon cells than those in the control.
• 2)F-d characteristics from AFM measurements on replicon and control cells, with and without disruption of actin, were found to be consistent with the observed trends in E₁ and F. That is, HCV replicon cells showed higher stiffness than control cells when actin was intact. This supports the increased pre-tension in cortical actin in HCV replicon cells. On the other hand, upon disruption of actin using cytochalasin D, indentation using AFM is indicative of elastic modulus of the nuclear membrane. In this case, replicon cells showed lower stiffness than control cells.
• 3)Nuclei of replicon cells have larger volume, surface area, and projected area than control cells. The increase in size of the nucleus of replicon cells was rescued with overexpression of lamin-A.

These experimental results are tied together with the help of a simplified elastic model of the nucleus of an adherent cell. It is worth mentioning that three morphological parameters (a_p, a_s, and v) are adequate to establish relative changes in the elastic modulus of nuclei and force acting on them, which in turn are related to changes in lamin-A,C and actin. Its significance lies in the fact that the volume and area of individual nuclei are easily quantified experimentally and computationally. This simple and direct biomechanical assay of extracting physical properties of nuclei of a large population is an overarching contribution of this work.

Materials and Methods

Measuring the morphology of the nucleus

Huh7 cells and HCV replicon cells (Huh7 cells constitutively harbouring HCV replicon RNA) were cultured at 37°C in Dulbecco’s modified Eagle medium (DMEM) with 10% fetal bovine serum (FBS). Cells were regularly passaged at around 80% confluence. For the measuring nuclear morphology, cells were seeded at low concentrations (around 100 k cells in a 35-mm petri dish) and allowed to attach overnight. 16 h after seeding, the cells were fixed using 4% paraformaldehyde and stained for nucleus and actin using SYTOX green and Rhodamine Phalloidin, respectively. Confocal z-stacks of the stained cells were taken on a Leica Microsystems (Buffalo Grove, IL) TCS SP5 II confocal microscope. An oil-immersion objective lens with a magnification of 40× and a numerical aperture of 1.3 was used. Z-stack images were taken at a pixel size of 378 nm in the lateral directions and z-step size of 500 nm. The morphology of the nucleus was obtained from these confocal stacks using a three-dimensional (3D) image processing technique.

The lateral location of individual nuclei was identified from the maximal-intensity projection of the confocal stacks using a two-dimensional (2D) image processing algorithm (29). In this technique, an approximate initial boundary is converged to the actual boundary of the nucleus by an active contour method (30) (Fig. S2, A–C). A region slightly larger than the 2D boundary, five pixels on each side, was cropped from the confocal stack and processed individually for obtaining the boundary surface of the nucleus. Our algorithm is an extension of the method in (29) for 2D images to 3D. We first binarized the cropped volume using Otsu’s threshold (31), estimated the boundary surface of the thresholded region, and further dilated the boundary surface to get a smooth, outer-boundary surface of the nucleus. Next, we enhanced the contrast of the original, cropped stack by rescaling the pixel intensities between 70 and 130% of Otsu’s threshold. By using the outer boundary along with the contrast-enhanced stack in a 3D active contour algorithm, we were able to obtain the actual boundary of the nucleus (Fig. S2, D and E; Video S1).

Video S1. Obtaining 3D Nuclear Morphology from Confocal Images by Image Processing

The approximate boundary surface converging to the actual boundary of the nucleus. Cross-sectional views on three orthogonal planes of the confocal stack with the converging boundary and an isometric view of the boundary surface are shown.

Nondimensional, mechanical model for the nucleus

Nuclear morphology is a consequence of mechanical equilibrium between the forces acting on the nuclear envelope and the stresses generated inside it. Stresses in the nuclear envelope are in turn a function of the forces acting on it and its mechanical properties. Therefore, information about these forces and mechanical properties is contained in the morphology of the nucleus. For a given shape of the nucleus, we estimated the forces acting on the nuclear envelope and its mechanical properties.

We assumed that in its native state under mechanical equilibrium, there are predominantly two forces acting on the nuclear envelope: 1) a uniform pressure that inflates the nucleus and 2) a downward force from cortical actin that compresses the nucleus (Fig. 1 C). These forces are qualitatively similar to those in (14). In that study, the authors assumed that the inflating pressure is the net result of the osmotic pressure due to the difference in solute concentration between the nucleoplasm and cytoplasm and a compressive force from the microtubules. However, some previous studies have argued that the osmotic pressure is due to a difference in concentration of macromolecules, not solutes, across the nuclear envelope (15, 32). In another study, additional forces on the nuclear envelope due to chromatin were assumed (1). As the origin of pressure is unimportant in our study, we combined all contributions from the osmotic pressure, microtubules, and chromatin into a single inflating pressure.

The force due to cortical actin is assumed to be arising from a flat plate pushing down on the nucleus (Fig. 1 C) as in (14). Because we considered the steady-state morphology of the nuclear envelope, we neglected the effects due to viscosity. Viscosity would affect the rate of convergence of the changing morphology but not the final morphology (14). The nuclear envelope was hence assumed to be a hyperelastic membrane that is spherical in the unloaded state (1, 14, 33). Its bending was neglected because the nuclear envelope is relatively thin, on the order of 100 nm, as compared to the size of the nucleus, which is around 10 μm in diameter. We assumed the nuclear envelope to be made of an incompressible Mooney-Rivlin material. Unlike in some previous studies (1, 14), we did not choose a neo-Hookean model because it exhibits instabilities at large strains (34). The instability refers to the drop in pressure at large strains (>38%) when a spherical, neo-Hookean membrane is inflated (34).

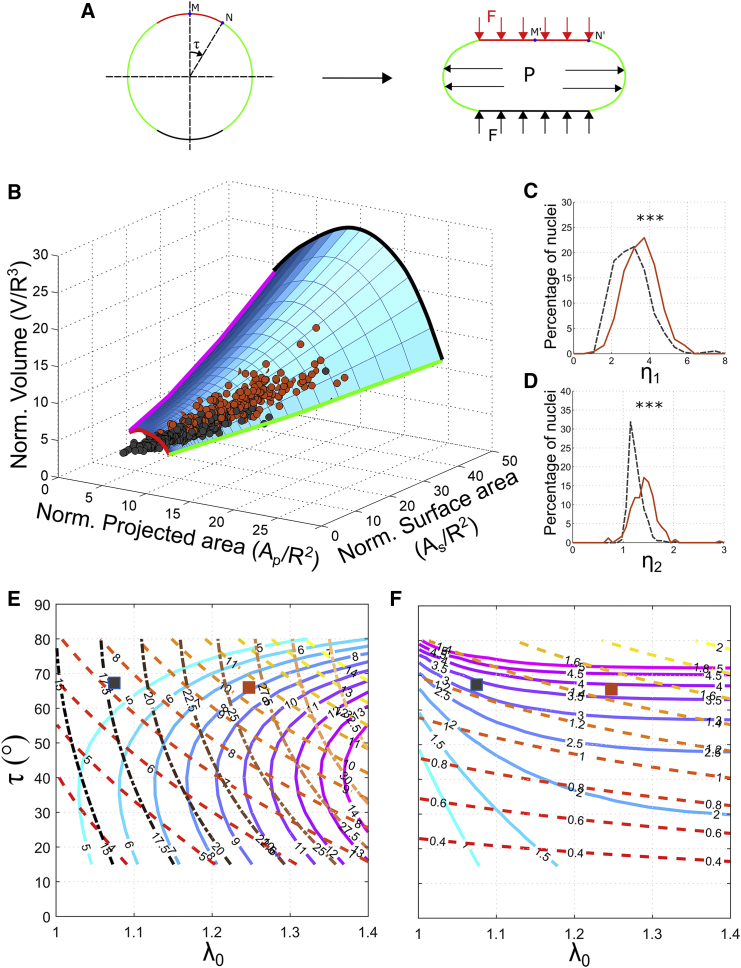
Because the initial geometry, forces, and boundary conditions are axisymmetric, we used an analytical formulation developed for mechanical equilibrium of axisymmetric membranes (17). When the governing ordinary differential equations for mechanical equilibrium were expressed in terms of the principal strains (see Supporting Materials and Methods), we obtained the two nondimensional parameters that govern the deformation, namely 1) η₁ = PR/2E₁H and 2) ${\eta }_2=\sqrt{F/P\pi R^2}$. Whereas η₁ appears in the equation for force equilibrium, η₂ appears in the boundary condition (see Supporting Materials and Methods). To solve the governing differential equations, we require two other parameters: 1) λ₀, the stretch at the apex point of the nucleus in the deformed state (point M′ in Fig. 3 A) and 2) τ, half of the angle subtended by the region of contact between cortical actin and the nuclear envelope in the undeformed state (Fig. 3 A). However, as there are only two independent parameters, by specifying either of them, the other two can be determined (see Supporting Materials and Methods). In our simulations, we have specified λ₀ and τ and estimated η₁ and η₂ (Fig. 3 F).

Figure 3.

Nondimensional mechanical model of nuclear morphology. (A) The spherical nuclear envelope is deformed by two forces: 1) an inflating pressure P and 2) a force F due to cortical actin. The force from cortical actin is assumed to be arising from a flat plate that is pushing down on the nucleus. Contact between actin and the nuclear envelope in the deformed state is along the red, horizontal line on the top of the nucleus. The corresponding region in the undeformed configuration is also marked in red. Points N and N′ are the boundary of the contact region in the undeformed and deformed configurations, respectively. The angle subtended by N with the axis of symmetry is the contact angle τ. The stretch at the apex point of the nucleus, M′, is λ₀. (B) Blue surface represents a relationship among the normalized projected area, surface area, and volume of individual nuclei as predicted by the model. Black and red dots are the experimentally measured morphologies of the nuclei of Huh7 and HCV replicon cells, respectively. Almost all individual nuclei lie on the surface predicted by the model. The different boundaries of the surface are marked. Red and black curves are the lower and higher limits, respectively, of the initial stretch λ₀. Magenta and green curves are the lower and higher limits, respectively, of the contact angle τ. Probability distributions of the nondimensional parameters η₁ (C) and η₂ (D) obtained from the experimentally measured nuclear morphologies are shown in Fig. 2. η₁ and η₂ are significantly larger for HCV replicon cells (red, solid lines) in comparison to Huh7 cells (black, dashed lines). ^∗∗∗p < 0.001 by two-tailed Kolmogorov-Smirnov test. (E) Shown are contour curves of normalized volume (solid lines colored blue to magenta), normalized projected area (dashed lines colored red to yellow), and normalized surface area (dash-dot lines colored dark to light brown) as a function of λ₀ and τ. (F) Shown are contour curves of η₁ (solid lines colored blue to magenta) and η₂ (dashed lines colored red to yellow) as a function of λ₀ and τ. By using these contour plots, η₁ and η₂ for any nuclei can be obtained as follows. From the volume, projected area, and surface area of a nucleus, calculate the normalized volume, projected area, and surface area using Eq. 2 by assuming R. From these normalized nuclear shape parameters, obtain λ₀ and τ using the contour plot in (E). η₁ and η₂ can now be obtained from λ₀ and τ using the contour plot in (F). To illustrate the method, we have plotted the mean nuclear morphology of Huh7 (black square) and HCV replicon (red square) cells on (E and F). To see this figure in color, go online.

For given λ₀ and τ, we first calculated η₁ and η₂ and then numerically integrated the governing equations to obtain the principal strains. From the principal strains, we obtained normalized nuclear morphology, which is the deformed shape when a spherical membrane of unit radius is deformed by η₁ and η₂. The normalized nuclear morphology was characterized by normalized nuclear shape parameters, namely, projected area (a_p), surface area (a_s), and volume (v), defined earlier. To obtain the actual nuclear morphology, we scaled the normalized nuclear morphology by R. The normalized nuclear shape parameters are related to the actual nuclear shape parameters through scaling relations.

$$A_p=R^2{a}_p,A_s=R^2{a}_s\text{and}V=R^{3}v.$$ (1)

To obtain η₁ and η₂corresponding to experimentally measured nuclei, we first normalized its nuclear shape parameters,

$${\hat{a}}_p=\frac{{\hat{A}}_p}{R^2},{\hat{a}}_s=\frac{{\hat{A}}_s}{R^2}\text{and}\hat{v}=\frac{\hat{V}}{R^3},$$ (2)

where ˆ denotes experimentally measured values. We have assumed that our control and HCV-infected cells are descendant from a single clone, and hence we have assumed the same R for all nuclei. η₁ and η₂ corresponding to each nucleus were then obtained using a least-squares minimization by solving the following problem:

$$\underset{{\eta }_1,{\eta }_2}{\text{Min}}{\left(\frac{a_p-{\hat{a}}_p}{{\hat{a}}_p}\right)}^2+{\left(\frac{a_s-{\hat{a}}_s}{{\hat{a}}_s}\right)}^2+{\left(\frac{v-\hat{v}}{\hat{v}}\right)}^2.$$ (3)

Measuring cell and nuclear stiffness using AFM

Cells were maintained in DMEM with 10% FBS at 37°C. For AFM measurements, cells were trypsinized and allowed to attach overnight before the experiment. The growth medium was removed before taking the measurements, and the cells were washed with Hanks’ balanced salt solution (HBSS) buffer. Cells were kept in HBSS buffer during the experiment because the color of the growth medium can affect the laser light-path. For depolymerizing actin and microtubule during nuclear stiffness measurements, the cells were incubated with growth medium containing cytochalasin D and nocodazole at concentrations of 3.6 and 6 μM, respectively, for 2 h before the measurements. The drugs were added at the same concentrations in the HBSS buffer used during measurement to avoid polymerization of actin and microtubule during the measurements.

The apparent modulus of elasticity of the cells was measured using an Atomic Force Microscope (XE Bio from Park Systems, Suwon, South Korea). We have used a V-shaped cantilever with a spherical bead of diameter 5.2 μm made of silicon dioxide attached to its bottom (AppNano HYDRA6V-200NG-TL; AppNano, Mountain View, CA). The stiffness of the cantilever was measured using a thermal tuning method available with the AFM and was found to be 0.041 N/m. The relation between the deformation of the cantilever and the voltage on the photodetector (A-B sensitivity) was calibrated by indenting the cantilever on the petri dish. The calibration was done whenever the laser position on the cantilever was adjusted. We have used a cantilever speed of 0.8 μm/s while approaching as well as while retracting from the cell.

Both Huh7 and HCV replicon cells were first imaged in the contact mode using a small contact force (0.7 nN). The position of the nucleus was identified from the topography image. Multiple force-displacement (F-d) curves over a 4 × 4 grid on a small region (5 × 5 μm) above the nucleus were obtained. Each of these curves were analyzed to obtain the apparent modulus of elasticity of the cell and the point of contact between the cantilever tip and the cell (35). The highest point among the contact points was chosen as the apex of the nucleus, and the corresponding modulus was chosen as the elastic modulus of the cell (Fig. S6 C). In the case of cells with actin and microtubules depolymerized, the cells were almost rounded up and the position of the nucleus could be identified from optical imaging. Hence, in this case, we positioned the cantilever on top of the nucleus (identified from the optical image) and obtained F-d curves on a 4 × 4 grid on a 5 × 5 μm region. The elastic modulus corresponding to the highest contact point is designated as the modulus of the cell.

For obtaining the elastic modulus and the point of contact from the F-d curves, we have used the Hertzian contact model. First, the approach region of the F-d curve when the cantilever is not in contact with the cell is identified, and the force in this region is corrected to zero. In this region, the F-d curve is linear and almost flat (blue curve in Fig. S6 B). A straight line is fitted to this region, and this line is subtracted from the F-d curve to correct for the baseline force (black curve in Fig. S6 B). The elastic modulus and contact point are now obtained from the baseline-corrected F-d curve by fitting a Hertzian contact model for the region between 0.2 and 1 nN. The Hertzian contact model gives the relation between the force and indentation as

$$F=\frac{4\pi E}{3\left(1-{\upsilon }^2\right)}\sqrt{R}{\delta }^{3/2},$$ (4)

where E is the apparent elastic modulus of the cell, ν is the Poisson’s ratio (assumed to be 0.5), R is the radius of the indenter, and δ is the indentation depth. The cell is assumed to be semi-infinite, and the indenter is assumed to be rigid. The Hertzian contact model relation can be rewritten as

$$F^{2/3}={\left(\frac{4\pi E}{3\left(1-{\upsilon }^2\right)}\sqrt{R}\right)}^{2/3}\delta .$$ (5)

The indentation depth can be written in terms of the contact point as

$$F^{2/3}={\left(\frac{4\pi E}{3\left(1-{\upsilon }^2\right)}\sqrt{R}\right)}^{2/3}\left(s_0-s\right),$$ (6)

where s is the separation (displacement + deformation of the cantilever), and s₀ is the separation at contact. By fitting a straight line to the F^2/3-s curve, we can obtain the elastic modulus from the slope and the point of contact from the intercept. The model fit is the red curve, and the contact point is the red marker in Fig. S6 B.

Western blot analysis

Cells were lysed in Radioimmuno precipitation assay (RIPA) buffer and quantified using Bradford reagent (Bio-Rad Laboratories, Hercules, CA). Equal amounts of protein were loaded on to a sodium dodecyl sulfate-polyacrylamide electrophoresis gel and resolved. Proteins separated on the gel were transferred to a nitrocellulose membrane (Pall Biosciences, Port Washington, NY). Various antibodies (anti-lamin-A,C, #2032, Cell Science Technologies, Danvers, MA; anti-NS5B, cat#ab35586, Abcam, Cambridge, UK; anti-GAPDH, NB100-56875, Novus Biologicals, Centennial, CO) were used to probe for proteins. This was followed by horseradish peroxidase-conjugated secondary antibody (goat-raised anti-rabbit and goat-raised anti-mouse; Sigma-Aldrich, St. Louis, MO). β-actin was probed using horseradish peroxidase-conjugated monoclonal anti-β-actin antibody (cat#A3854, Sigma-Aldrich). The protein antibody complexes were then analyzed by chemiluminescence using Immobilon Western systems (MilliporeSigma, Billerica, MA).

Overexpressing lamin-A in HCV replicon cells and measuring the morphology

HCV replicon cells were seeded at 80% confluency in 35-mm dishes. A green fluorescent protein (GFP)-conjugated lamin-A construct was used to overexpress lamin-A in HCV replicon cells. 2 μg of lamin-A,C-GFP was transfected in Opti-MEM (Invitrogen, Carlsbad, CA; Life Technologies, Carlsbad, CA) using Lipofectamine-2000 (Invitrogen; Life Technologies). The transfection medium was replaced with culture medium (DMEM containing 10% FBS) 5 h post-transfection. The transfected cells were trypsinized 24 h post-transfection and seeded at low density (∼200,000 cells) into 35-mm dishes. The reseeded cells were fixed using 4% paraformaldehyde 48 h post-transfection. Confocal z-stacks of the stained cells were taken on a Leica Microsystems TCS SP5 II confocal microscope. An oil-immersion objective lens with a magnification of 40× and a numerical aperture of 1.3 was used. Z-stack images were taken at a pixel size of 378 nm in the lateral directions and a z-step size of 500 nm. The cells overexpressing lamin-A were identified using the GFP signal (Fig. 5 F), and their morphology was compared with those not having a GFP signal (Fig. 5, G–I)

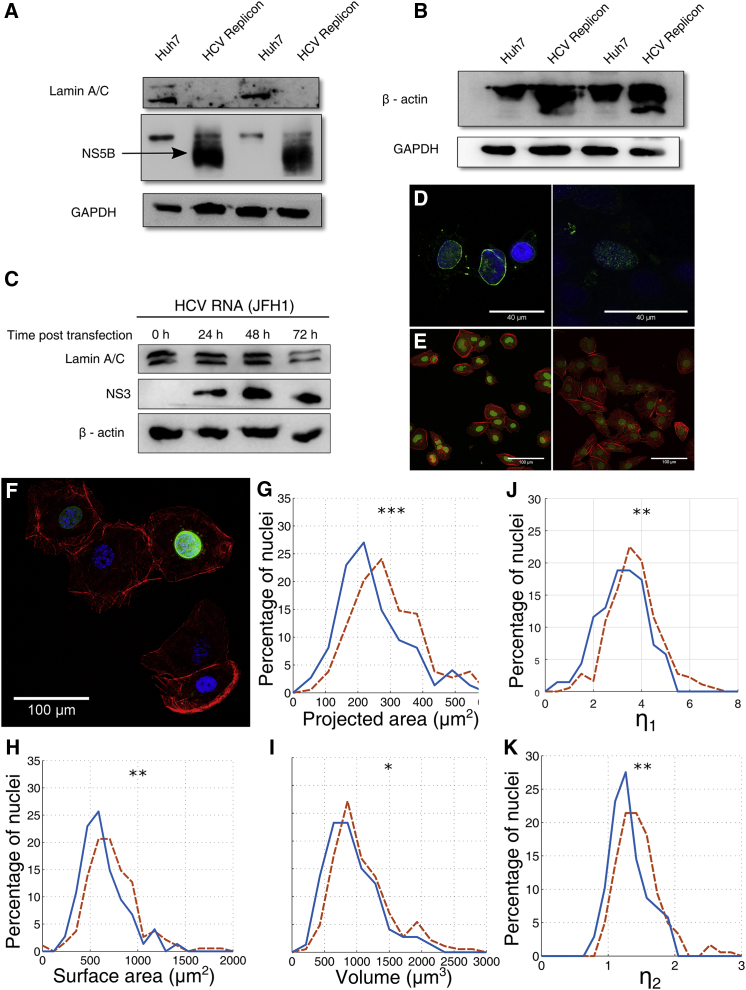
Figure 5.

Downregulation of lamin-A,C by HCV. (A) Lamin-A,C levels in HCV replicon cells and (B) β-actin levels in HCV replicon cells are shown. (C) Shown is the change in lamin-A,C level with time for Huh7 cells transfected with HCV RNA. (D) Immunofluorescence of Huh7 cells (left) and Huh7 cells transfected with HCV RNA (right) was performed. Nucleus is stained in blue by DAPI and lamin-A,C in green. (E) Shown is the immunofluorescence of Huh7 cells (left) and HCV replicon cells (right) stained for nucleus in green and actin in red. (F) HCV replicon cells were transfected with lamin-A-GFP overexpression construct. Nucleus is stained in blue, actin in red, and lamin-A-GFP in green. Shown are the probability distributions of the projected area (G), surface area (H), and volume (I) of the nuclei of HCV replicon (red, dashed lines, n = 192) and HCV replicon cells expressing lamin-A,C-GFP (blue, solid lines, n = 74). Probability distributions of the nondimensional parameters η₁ (J) and η₂ (K) were obtained from the nuclear morphologies in (G–I). η₁ and η₂ are significantly larger for HCV replicon cells (red, dashed lines) in comparison to those overexpressing lamin-A (blue, solid lines). ^∗p < 0.05, ^∗∗p < 0.01, and ^∗∗∗p < 0.001 by two-tailed Kolmogrov-Smirnov test. To see this figure in color, go online.

Measuring the DNA content and chromatin condensation

Huh7 and HCV replicon cells were seeded at 80% confluency in 35-mm dishes and allowed to grow for 24 h. Huh7 cells were treated with 6 μM nocodazole for 24 h and were used as positive control. Nocodazole will depolymerize microtubule and arrest the cell at G2/M, thereby increasing the DNA content per cell. After 48 h from seeding, cells were collected by trypsinization for measuring the DNA content. The number of cells were estimated using a hemocytometer. Total DNA content was measured using Quant-iT PicoGreen double-stranded DNA Assay Kit from Invitrogen. DNA content per cell was then estimated by dividing the total DNA content by the number of cells.

For estimating the chromatin condensation, confocal images of Huh7 and HCV replicon cells stained with 4',6-diamidino-2-phenylindole (DAPI) were obtained. Chromatin condensation parameter, a previously reported measure for DNA condensation (36, 37), was then calculated from these confocal images.

Results

HCV proteins alter the morphology of the nucleus

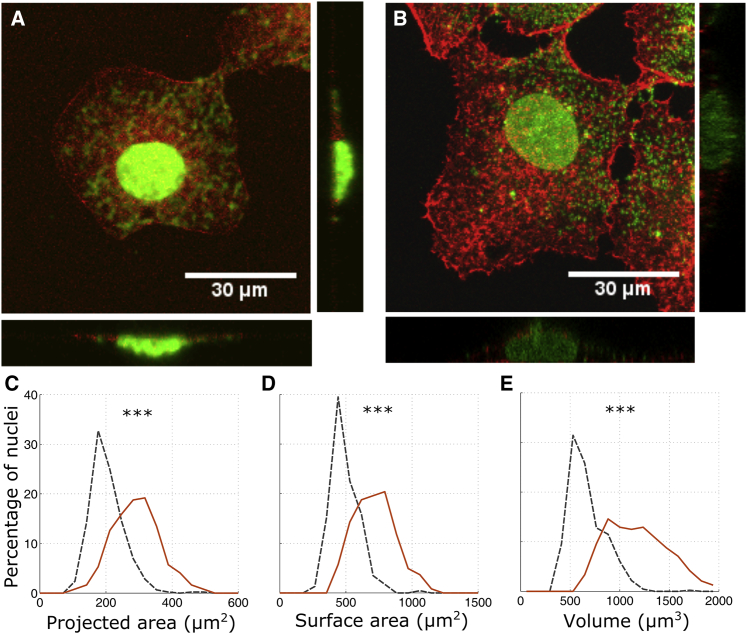
We measured the morphology of the nuclei of Huh7 and HCV replicon cells from confocal images. We obtained the boundary surface of the nucleus from confocal images using a 3D image processing algorithm (Video S1). From the boundary surface, nuclear shape parameters, such as projected area, surface area, and volume were calculated. The nuclear shape parameters of Huh7 and HCV replicon cells are shown in Fig. 2, C–E. As seen in Fig. 2, HCV replicon cells show increased projected area, surface area, and the volume of the nucleus. The mean projected area of the nuclei in HCV replicon cells is equal to 312 μm², whereas that of its control cell line (Huh7) is 220 μm². The mean projected area of HCV replicon cells is ∼42% higher than that of the control cells. Nuclei of HCV replicon cells have a mean surface area of 768 μm², which is 44% higher than the mean surface area of control cells (534 μm²). The mean volume of the nucleus of HCV replicon cells (1.218 × 10³ μm³) is 88% larger than that of control cells (0.667 × 10³ μm³).

Figure 2.

Morphology of the nuclei of Huh7 and HCV replicon cells. Shown are confocal images of Huh7 (A) and HCV replicon cells (B) stained for actin in red and nucleus in green. Shown is the probability distribution of projected area (C), surface area (D), and volume (E) of the nuclei of Huh7 (black, dashed lines, n = 461) and HCV replicon cells (red, solid lines, n = 246). Nuclei of HCV replicon cells have larger projected area, surface area, and volume in comparison to the nuclei of Huh7 cells. ^∗∗∗ indicates p < 0.001 by two-tailed Kolmogrov-Smirnov test. To see this figure in color, go online.

By using the model, we obtained η₁ and η₂ corresponding to individual nuclei. The differences in η₁ and η₂ between Huh7 and HCV replicon cells were used to identify the mechanisms responsible for the changes in nuclear morphology.

Two-parameter, nondimensional mechanical model

In our computations, we systematically varied λ₀ and τ to obtain the corresponding normalized projected area (a_p), surface area (a_s), and volume (v) corresponding to each of them. These normalized nuclear shape parameters form a surface in a_p-a_s-v space. This surface (blue surface in Fig. 3 B) represents a relation among a_p, a_s, and v as predicted by the model. The bounds of the surface (blue surface in Fig. 3 B) are due to limits on the simulation parameters. Because the nuclear envelope is assumed to be a membrane, it cannot resist compression. This sets a lower bound on λ₀ (red boundary, λ₀ = 1.001). Even though there is no upper bound for λ₀, we have simulated only up to λ₀ = 1.4, which was enough to contain all experimentally measured nuclear morphologies (black curve). The lower and higher limits of τ are 0 and 90°, respectively. However, we have simulated from τ = 15° (magenta curve) to τ = 80° (green curve).

By assuming R = 5.5 μm, we obtained ${\hat{a}}_p$, ${\hat{a}}_s$, and $\hat{v}$ (Eq. 2) for all experimentally measured nuclear morphologies (Fig. 2, C–E). ${\hat{a}}_p$, ${\hat{a}}_s$, and $\hat{v}$ from individual, experimentally measured nuclei (black dots are Huh7 cells, and red dots are HCV replicon cells in Fig. 3 B) lie on the surface predicted by the model (Fig. 3 B; Video S2). Because the nuclei in this study have a low aspect ratio (Fig. 2, A and B, height to diameter around 0.18), they lie on the model surface in regions of large τ (between 55 and 75°). The nuclear morphologies would lie on the surface even if we change the radius in the unstressed state (R = 5 and 6 μm are shown in Fig. S5). At low values of R, more points will lie on the surface. However, many nuclei (larger ${\hat{a}}_p$, ${\hat{a}}_s$, and $\hat{v}$) will have large strains (λ > 2). At high values of R, many nuclei were below the lower bound on λ₀ (red boundary of the blue surface in Figs. 3 D and S5 D). Hence, we used an intermediate value of R = 5.5 μm, wherein large number of nuclei (85% of Huh7 nuclei and 99% of HCV replicon nuclei) lie on the surface predicted by the model (Fig. 3 B), and the principal strains are not very large (λ > 2). The nuclear morphology of HeLa cells obtained from (38) also lies on the surface predicted by our model (see Video S3).

Video S2. Model Explains the Variability in the Morphology of the Nuclei of Huh7 and HCV Replicon Cells

Nuclear morphological parameters of Huh7 (black) and HCV replicon (red) cells plotted over the surface (blue) predicted by the model. Axes represent the normalized projected area (red), surface area (green) and volume (blue) of the nuclei.

Video S3. Model Explains the Variability in the Morphology of the Nuclei of HeLa Cells

Nuclear morphological parameters of HeLa cells (red) obtained from (38) plotted over the surface (blue) predicted by the model. Axes represent the normalized projected area (red), surface area (green) and volume (blue) of the nuclei.

We fitted the model to ${\hat{a}}_p$, ${\hat{a}}_s$, and $\hat{v}$ of Huh7 and HCV replicon cells, using Eq. 3, and obtained η₁ and η₂. Only those fits with relative errors <0.05 (relative error in volume is defined as ${\text{err}}_v=\left|\left(v-v^{\prime }\right)/v^{\prime }\right|$ and similarly for projected area and surface area) for each of the normalized shape parameters are plotted in Fig. 3 C. With an upper limit in error of 5%, we were able to fit around 85% of Huh7 nuclei and 99% of HCV replicon nuclei. We observed that both η₁ and η₂ are significantly larger for HCV replicon cells in comparison to Huh7 cells (p < 0.001 using two-tailed Kolmogrov-Smirnov test). The mean value of η₁ is 3.33 for Huh7 cells and 3.81 for HCV replicon cells. The mean value of η₂ is 1.29 for Huh7 cells and 1.45 for HCV replicon cells. An increase in η₁ suggests that the nuclear envelope of HCV replicon cells have a lower elastic modulus in comparison to Huh7 cells. An increase in η₂ suggests that the pre-tension in cortical actin is higher in HCV replicon cells in comparison to Huh7 cells. These predictions do not change for R = 5 and 6 μm (Fig. S5). Furthermore, η₁ and η₂ are similar to those estimated from individual values of the forces, material properties, and initial geometry in (14): PR/μH = 3.9 and $\sqrt{F/P\pi R^2}=1.2$.

The values of η₁ and η₂ can be approximately estimated using a graphical method instead of solving the minimization problem in Eq. 3. λ₀ and τ corresponding to a nuclear morphology can be obtained by locating ${\hat{a}}_p$, ${\hat{a}}_s$, and $\hat{v}$ on the contour plot shown in Fig. 3 E. η₁ and η₂ can then be obtained from the corresponding point in the contour plot shown in Fig. 3 F. η₁ and η₂ for the mean nuclear morphology of Huh7 and HCV replicon cells were obtained using this technique (Fig. 3, E and F). Alternatively, these steps can be done numerically using the MATLAB (The MathWorks, Natick, MA) codes provided with the Supporting Materials and Methods.

Because we have modeled the nuclear envelope as a solid membrane, we need to assume a stress-free reference configuration to compute the strains. However, we cannot observe this configuration because we can never isolate the nuclear envelope from all forces, such as osmotic pressure and force from chromatin. We can avoid assuming an unstressed state if we consider the nucleus as a liquid cortex (nuclear envelope) enclosing a liquid (nucleoplasm). Such models have been previously proposed for simulating cells being aspirated into a micropipette (39, 40). In these models, the tension in the liquid cortex (force per unit length) comprises a term akin to surface tension and a term proportional to the strain rate. Because nuclear deformation in spread cells is known to be very slow, we may neglect the strain rate. Hence, by taking only the surface tension, force equilibrium in the direction normal to the nuclear envelope is then given by

$$\sigma C_1+\sigma C_2=P,$$ (7)

where σ is the surface tension, C₁ and C₂ are the principal curvatures, and P is the pressure. By rearranging this equation, we get that the mean curvature of the surface is a constant:

$$\frac{C_1+C_2}{2}=\frac{P}{2\sigma }.$$ (8)

To check whether this is true for our data, we calculated the mean curvature of the nuclei of Huh7 and HCV replicon cells. We observed substantial variability in the mean curvature along the nuclear surface (Fig. S7). Hence, we concluded that a liquid-shell model subject to tension force might not be apt for our data.

HCV proteins increase cell stiffness and decrease nuclear stiffness

Cell stiffness

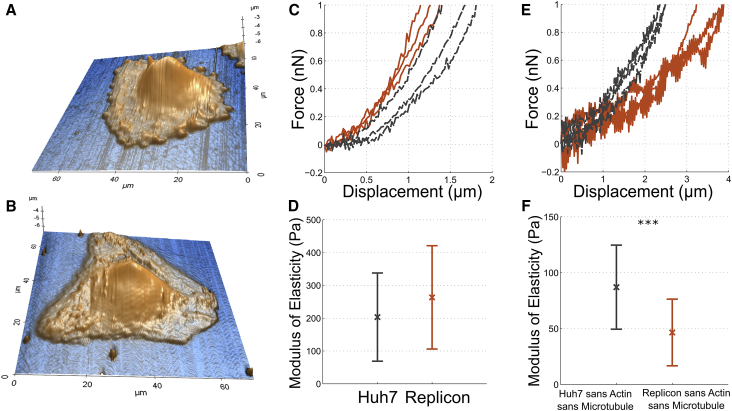
The stiffness of adherent cells, measured using AFM, is due to pre-tension in cortical actin, microtubules, and the nucleus. However, the major contributing factor is the pre-tension in cortical actin (up to 50%) (28). Hence, we used cell stiffness measured using AFM as an indicator of the change in pre-tension in cortical actin. For comparing the cell stiffness between Huh7 and HCV replicon cells, we used the apparent modulus of elasticity obtained by fitting a suitable contact model to the F-d curves (41) (Fig. S6; Supporting Materials and Methods). The elastic modulus of HCV replicon cells (263 ± 157 Pa) was found to be higher than that of Huh7 cells (203 ± 134 Pa) (Fig. 4 E), but the increase was not statistically significant. The mean stiffness of HCV replicon cells was around 25% higher than that of Huh7 cells. The increase in stiffness suggests higher pre-tension in actin in HCV replicon cells in comparison to Huh7 cells.

Figure 4.

Mechanical characterization of Huh7 and HCV replicon cells using AFM. Shown is the topography of Huh7 (A) and HCV replicon cells (B) by contact mode imaging. Sample F-d curves (C) and apparent elastic modulus (D) of Huh7 (black, dashed lines, n = 21) and HCV replicon (red, solid lines, n = 23) cells are shown. Sample F-d curves (E) and apparent modulus of elasticity (F) of Huh7 cells (black, dashed lines, n = 34) and HCV replicon cells (red, solid lines, n = 20) with actin and microtubule depolymerized. ^∗∗∗p < 0.001 by one-tailed Student’s t-test. To see this figure in color, go online.

Nuclear stiffness

A recent study has shown that the nucleus becomes the major load-bearing member when the actin and microtubules are depolymerized. The authors observed that when indenting using an AFM tip, the nuclear deformation increased from 5 to 30% upon depolymerization of the actin cytoskeleton and microtubules (42). This suggests that we can obtain the stiffness of the nucleus by measuring the cell stiffness after depolymerizing the actin cytoskeleton and microtubules. Hence, we used cytochalasin D and nocodazole to depolymerize actin and microtubule, respectively, and measured the stiffness using AFM. The stiffness of the nuclei of HCV replicon cells was significantly lower (p < 0.001) than that of Huh7 cells (Fig. 4 F). Nuclei of HCV replicon cells had a mean apparent elastic modulus of 49 ± 26 Pa, whereas those of Huh7 cells was 87 ± 37 Pa. The reduction in nuclear stiffness is around 43%.

Our results suggest that HCV proteins marginally increase the stiffness of the cells but significantly reduce the stiffness of the nuclei. The stiffness of the cells was measured right above the nucleus (see Fig. S6; Supporting Materials and Methods), and hence the measured stiffness will have contributions from the cortical actin as well as the nucleus. Hence, the increase of prestress in actin could be masked by a reduction in stiffness of the nucleus. This could be the reason why we do not see a significant increase in the stiffness of HCV replicon cells in comparison to Huh7 cells.

Hepatitis C viral proteins downregulate lamin-A,C and upregulate actin

Downregulation of lamin-A,C

We measured the expression levels of lamin-A,C and β-actin for biochemical confirmation of the predictions from the computational model. We observed that HCV downregulates lamin-A,C in Huh7 cells. The downregulation of lamin-A,C was observed in HCV replicon cells as well as those transfected with full-length HCV RNA. The downregulation of lamin-A,C was confirmed by western blot (Fig. 5, A and C) as well as immunofluorescence assay (Fig. 5 D). In Huh7 cells, lamin-A,C is localized at the nuclear periphery, whereas in Huh7 cells transfected with HCV RNA, the levels of lamin-A,C were downregulated and did not localize to the nuclear periphery (Fig. 5 D). However, there was no difference in the expression level of lamin-B1 between Huh7 and HCV replicon cells (Fig. S1 G). We further checked the levels of lamin-A,C in Coxsackie virus B3, which is another single-stranded positive-sense RNA virus. However, upon Coxsackie viral infection, lamin-A,C levels were not downregulated (Fig. S1 H). Hence, lamin-A,C downregulation may be a specific strategy of HCV and not a general mechanism of cytoplasmic RNA viruses.

To establish the causal relationship between the changes in nuclear mechanics and the downregulation of lamin-A,C, we overexpressed lamin-A in HCV replicon cells and measured the effect on nuclear morphology. We used a lamin-A-GFP construct so that the cells that were overexpressing lamin-A could be identified by fluorescence imaging (Fig. 5 F). We observed that the nuclei of HCV replicon cells overexpressing lamin-A had a lower projected area, surface area, and volume as compared to the nuclei of HCV replicon cells (Fig. 5, G–I). The mean projected area of the nuclei of HCV replicon cells overexpressing lamin-A was 271 μm², whereas that of the nuclei of HCV replicon cells was 330 μm². The mean surface area of the nuclei of HCV replicon cells overexpressing lamin-A was 686 μm², whereas that of the nuclei of HCV replicon cells was 805 μm². The mean volume of the nuclei of HCV replicon cells overexpressing lamin-A was 1048 μm³, whereas that of the nuclei of HCV replicon cells was 1255 μm³. Rescue of nuclear morphology upon overexpressing lamin-A confirms that the changes in nuclear mechanics in HCV replicon cells are due to downregulation of lamin-A,C.

Upregulation of actin

HCV replicon cells showed a higher expression of β-actin in comparison to Huh7 cells. This was confirmed both by western blot (Fig. 5 B) as well as immunofluorescence assay (Fig. 5 E). However, β-actin upregulation was not observed under HCV RNA transfection (Fig. 5 C). This could be because the upregulation of β-actin is a long-term effect of HCV nonstructural proteins and is hence not observed in a short-term, transient transfection of HCV RNA. In contrast, we did not observe any significant difference in the expression of microtubules between Huh7 and HCV replicon cells (Fig. S1, A and B).

Interplay between lamin-A,C and E₁

Because overexpressing lamin-A increases the modulus of the nuclear envelope, the model predicts that η₁ will be lower for HCV replicon cells overexpressing lamin-A in comparison to HCV replicon cells. To validate this, we calculated η₁ and η₂ from the nuclear morphology of HCV replicon cells and those overexpressing lamin-A. We observed that the HCV replicon cells overexpressing lamin-A (mean value of η₁ = 3.45) have significantly lower η₁ in comparison to HCV replicon cells (mean value of η₁ = 3.97). The reduction in the size of the nucleus and η₁ upon overexpressing lamin-A further validates our model. Interestingly, η₂ is also lower in HCV replicon cells overexpressing lamin-A in comparison to HCV replicon cells.

Even though our experimental results using AFM, western blot, and immunofluorescence assay confirm a decrease in the modulus of the nuclear envelope and an increase in the pre-tension in cortical actin, the possibility of changes in the inflating pressure cannot be discounted. Depolymerization of microtubules can increase the net inflating pressure (14) and hence increase η₁. However, we have not observed any difference in the expression of microtubules between Huh7 and HCV replicon cells (Fig. S1, E and F). Another factor that can increase the inflating pressure is an increase in DNA content or decondensation of chromatin. We measured the relative DNA content between Huh7 and HCV replicon cells and observed that it has doubled in HCV replicon cells in comparison to Huh7 cells (Fig. S1 A). This observation corroborates with a previous report that showed cell cycle arrest at the G2 phase in HCV-infected cells (43). Chromatin condensation was not significantly different between these cells (Fig. S1 D). The increase in DNA content suggests that HCV replicon cells have a higher inflating pressure in comparison to Huh7 cells. The increase in inflating pressure, however, does not change our conclusions about an increase in F and a decrease in E₁.

Discussion

It is pertinent to note another contemporary viewpoint that there is no elastic energy stored in the nuclear envelope (44, 45), unlike our model. In the alternative model, the increase in nuclear size during cell spreading is due to unfolding of the wrinkles in the nuclear envelope. Furthermore, it is considered that the nucleus is shaped by a stress transmitted to the nuclear envelope by the movement of the cell boundary (16). In contrast, our model and data support the latter viewpoint that elastic energy is stored in the nucleus by stretching the nuclear envelope (1, 14, 46).

We presented a nondimensional, two-parameter elastic model that gives morphological parameters (volume, surface area, and projected area) of the nucleus in its native adherent state in terms of net inflation pressure and force because of cortical actin. There exists a relationship among the three morphological parameters, which is depicted as a surface in Fig. 3 B. Experimentally measured volume, surface area, and projected area of individual nuclei lie on this surface. This applies to our data and those reported in (38). Every point on the surface is associated with two nondimensional parameters expressed in terms of the inflation pressure and force because of cortical actin as well as elastic modulus, radius, and thickness of the nuclear envelope. For known values of the radius and thickness of the nuclear envelope, the first nondimensional parameter gives the ratio of inflation pressure/elastic modulus, and the second gives the ratio of the force due to cortical actin and the inflation pressure as per equations shown in Fig. 1 (see also Eqs. S30 and S36). The two nondimensional parameters together also give the ratio of cortical actin force/modulus of the nuclear envelope.

It may be noted that the nondimensional nuclear parameters can be approximately estimated using a graphical method or a numerical method (see Supporting Materials and Methods for the numerical method). Hence, our model can be used to study the effect of stimuli on the nuclear envelope and cytoskeleton by just measuring the nuclear morphology. For example, a recent study (47) showed that increased substrate stiffness concomitantly increased the expression of lamin-A,C and myosin in mesenchymal stem cells, thereby increasing the modulus of the nuclear envelope and the pre-tension in actin cytoskeleton. Using our model, these results could be inferred from the nuclear morphology by a decrease in η₁ and an increase in η₂ (see equations in Fig. 1).

Our model is axisymmetric and, hence, does not consider the eccentricity of the nucleus. For the cells used in this study, the eccentricity of the nucleus is around 0.6–0.7, which translates to a low aspect ratio (major axis/minor axis) of 1.25–1.4. Our model may not be applicable to cells with elongated nuclei (aspect ratio >2) such as fibroblasts. However, because the model predicts a relationship among the projected area, surface area, and volume of individual nuclei (blue surface in Fig. 3 B), it can be used to verify the applicability of our model to nuclei of any cell type. MATLAB codes (The MathWorks) and modeling data for plotting individual nuclear morphology over the model surface are provided for verification (see Supporting Materials and Methods).

The inflating pressure in our equations is the net effect of the osmotic pressure and forces from chromatin and microtubules. Therefore, an indication of change in pressure (increase in η₁ and decrease in η₂ or vice versa) cannot be attributed to any of these without further experimental measurements.

The force exerted by cortical actin on the nucleus is a function of the pre-tension in cortical actin and the contact area between the nuclear envelope and cortical actin. The contact area in turn depends on the inflating pressure. Thus, the contact force is not independent of the inflating pressure. Hence, there could be a relation between η₁ and η₂. We have observed a positive correlation between η₁ and η₂ for Huh7 and HCV replicon cells. Pearson’s correlation coefficient for Huh7 cells was 0.96, and that for HCV replicon cells was 0.88. However, a part of this correlation could be due to dependencies between the parameters in η₁ and η₂ arising from biochemical mechanisms. For example, expression of lamin-A,C (E₁) is known to increase with pre-tension in cortical actin (F) in mesenchymal stem cells (47).

We showed the applicability of our two-parameter model in the case of HCV replicon cells in which lamin-A,C is downregulated and cortical actin is upregulated. It is interesting that HCV, which is a cytoplasmic RNA virus, affects nuclear mechanics. DNA viruses such as herpes simplex virus (48), human immunodeficiency virus (49), and Simian Virus 40 (50) are known to alter nuclear mechanics by disrupting the nuclear lamina through the downregulation of lamin-A,C or B. The replication complexes of these viruses are assembled inside the nucleus. They need to enter the nucleus and export the viral particles produced to the cytoplasm. The nuclear lamina forms a barrier to these transports, and hence these viruses need to disassemble the nuclear lamina. But such considerations are absent in the case of RNA viruses such as HCV because their entire life cycle is confined to the cytoplasm. However, our study shows that HCV is disrupting the nuclear lamina by downregulating lamin-A,C and thereby deregulating important functions of the nucleus. Apart from its role in gene regulation, lamins are shown to be mechanosensors (51). They are known to translate mechanical stimuli from the exterior of the cell into the appropriate changes in gene expression by forming a mechanical signaling pathway through the cytoskeleton and linker of nucleoskeleton to cytoskeleton to the interior of the nucleus (52). Hence, by disrupting the nuclear lamina, HCV could be impairing the mechanobiological homeostasis of liver cells.

In summary, we have related morphological, biochemical, and biomechanical measurements to the physical properties of the nucleus and the cell through a mechanical model. The model predicts a relationship among the projected area, surface area, and volume of individual nuclei. These morphological parameters can be easily obtained by confocal imaging and the relationship can then be used to ascertain the applicability of our model to any cell type. Once the model is found to be suitable, the nondimensional parameters corresponding to individual nuclei can be estimated. The changes in the nondimensional parameters due to a stimulus suggest perturbations in the nuclear envelope and cytoskeleton, which can then be used to guide further experimental studies. We have used this technique in liver cells and discovered alterations in nuclear mechanics due to HCV.

Author Contributions

S.B. formulated the nondimensional model and performed the computations. S.B., S.D., and G.K.A. designed the experiments. S.B., S.S.M., G.S., S.R.R., and U.B.R. performed the experiments. S.B. developed the codes for image processing and AFM analysis, S.B., G.S., S.D., and G.K.A. analyzed and interpreted the data. S.B., G.S., S.D., and G.K.A. wrote the article.

Editor: Sean Sun.