Ab Initio Derivation of the FRET Equations Resolves Old Puzzles and Suggests Measurement Strategies

Abstract

Quantitative imaging methods based on Förster resonance energy transfer (FRET) rely on the determination of an apparent FRET efficiency (E_app), as well as donor and acceptor concentrations, to uncover the identity and relative abundance of the supramolecular (or quaternary) structures of associating macromolecules. Theoretical work has provided “structure-based” relationships between E_app distributions and the quaternary structure models that underlie them. By contrast, the body of work that predicates the “signal-based” dependence of E_app on directly measurable quantities (i.e., fluorescence emission of donors and acceptors) relies largely on plausibility arguments, one of which is the seemingly obvious assumption that the fraction of fluorescent molecules in the ground state pretty nearly equals the total concentration of molecules. In this work, we use the kinetic models of fluorescence in the presence and absence of FRET to rigorously derive useful relationships between E_app and measurable fluorescence signals. Analysis of these relationships reveals a few anticipated results and some unexpected explanations for known experimental FRET puzzles, and it provides theoretical foundations for optimizing measurement strategies.

Introduction

Förster resonance energy transfer (FRET) (1, 2, 3) is, without doubt, a very useful physical phenomenon that enjoys broad popularity among researchers in various science areas (4, 5, 6, 7, 8). Defined as the transfer of energy from an excited fluorescent tag to an unexcited one, FRET has become an indispensable tool in a gamut of applications ranging from estimation of intramolecular distances within a protein or DNA molecule (2, 9), through probing the structure of molecular complexes (10, 11, 12, 13), to the determination of the proportion of complexes with different size and their dissociation constants in living cells (11, 14). Fully quantitative analysis has been facilitated by the use of the kinetic theory of FRET (15, 16) as well as the availability of multiphoton microscopy with spatial and spectral resolution (7, 10, 12, 17, 18).

A relevant quantity in FRET is the efficiency of energy transfer (E), which depends on the sixth power of the ratio between the Förster distance, R₀, and the distance between the chromophores of the fluorescent tags (1, 19, 20). Customarily, E is connected to the lifetimes of the excited state of the donor in the presence (τ^DA) and absence (τ^D) of acceptors in fluorescence lifetime imaging (FLIM), as well as to the fluorescence emitted by the donor in the presence (F^DA) and absence (F^D) of acceptors in steady-state intensity-based measurements (17, 20, 21).

In many FRET experiments, F^DA or τ^DA are measured separately from F^D or τ^D, although preferably they should be measured from the same sample after FRET is somehow abolished, such as by inducing separation of the molecular complexes. The latter is rarely, if ever, possible, and several methods have been devised that provide different degrees of approximation to the true values of F^D and τ^D and therefore of E. Such methods rely on various corrections (for example, for spectral bleedthrough) or on photobleaching of the acceptor through its repeated excitation to obtain approximate values for F^D, as reviewed by Erijman and Jovin (22). Alternatively, one avoids use of corrections or additional measurements altogether by using spectral resolution to quantify a reduction in the donor emission as well as acceptor-sensitized emission simultaneously, thereby separating the donor and acceptor signals upon a single sample scan (10, 23, 24, 25). This latter approach has led to the introduction of different variants of FRET-based imaging, including FRET spectrometry (12, 14, 26), simultaneous unmixing of excitation and emission spectra (27), fully quantitative spectral imaging (11, 13) and, more recently and only theoretically for now, FRET-induced color contrast shift spectrometry (28).

It is generally recognized that, when a single excitation wavelength is used, it is possible to determine the FRET efficiency and the donor concentration but not the acceptor concentration (11, 12, 14, 28). Experimentally determined distributions of apparent FRET efficiencies (E_app) comprise one or more peaks, each of which can be simulated using a certain proportion of donor and acceptor molecules within a complex with a certain size and geometry (20, 29). The model that correctly predicts the number and position of each peak in the E_app histogram is taken as the quaternary structure of the protein of interest. This method is known as “FRET spectrometry.” When employing a second excitation wavelength, it also provides the acceptor concentration in addition to E_app and donor concentration (7, 11, 12, 14, 17), which could be used to monitor any dependence of the molecular complex size or geometry on concentration (12, 14).

The relationships between the experimentally determined E_app and the theoretical models incorporating the geometry and size of the complex as well as the different possible proportions of donors and acceptors within each complex are termed in this work “structure-based relationships” and are based on the well-tested (16, 30) kinetic theory of FRET (15) or Monte Carlo simulations (31, 32). By contrast, “signal-based relationships,” which allow one to compute E_app from donor and acceptor signals without making arbitrary assumptions about the probabilities of finding molecules in excited or ground states, have not been rigorously derived from the kinetic model of FRET until now. The work presented in this report starts from suitable kinetic models for fluorescent molecules in the presence and absence of FRET to derive expressions for E_app as well as donor and acceptor concentrations from fluorescence emission of acceptors and donors, some of which have been introduced and used but not rigorously derived in previous publications (10, 15, 20). It is shown that some of the assumptions that were implicit in some of the signal-based relationships used by all of us in the FRET community are not automatically valid and could lead to systematic errors if not carefully considered in the context of the experimental protocol used. Detailed analysis of those assumptions allows us to provide long-sought explanations for known experimental puzzles. In addition, this work provides the theoretical basis for identifying and refining the experimental conditions for quantitative FRET methods based on intensity measurements with no temporal resolution. Finally, a possibility is also suggested for using temporally resolved measurements for computing E_app distributions needed in FRET spectrometry analysis.

It should be mentioned that the present theory is general and therefore compatible with both hetero- and homo-FRET analyses, provided that a quantity directly related to the efficiency of energy transfer may be computed in each case. Nevertheless, the methods by which the experimental quantities are extracted from homo-FRET experiments (33, 34) are different from those used for hetero-FRET and thus may introduce certain restrictions in using this theory.

Methods

The kinetic equations of fluorescence and FRET

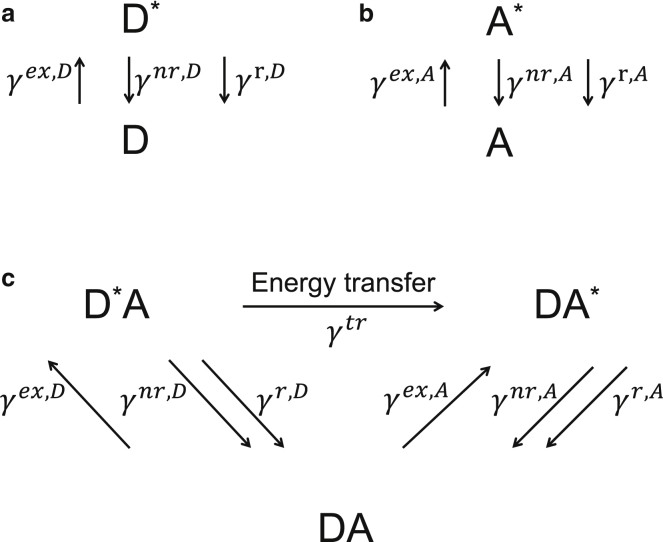
The relationships between the different rates of excited-state depopulation (or de-excitation) and the probabilities of fluorescent molecules to be in their excited states are obtained from the simple kinetic models presented in Fig. 1. According to these models, for donors in the absence of acceptors (Fig. 1 a), the rate of change of the probability $\left(p_{D^{\ast }}\right)$ to find a donor in an excited state (D^∗) is

$${\gamma }^{ex,D}{p}_D-\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)p_{D^{\ast }}=\frac{d{p}_{D^{\ast }}}{dt},$$ (1a)

where p_D is the probability to find a donor in its ground state and γ^{ex, D} is the rate of excitation of donors initially in their ground state (D), whereas γ^{nr, D} and γ^{r, D} are the rates of donor excited-state depopulation through nonradiative (e.g., internal conversion) and radiative (i.e., emission of a photon) processes, respectively. Similarly, for acceptors in the absence of donors (Fig. 1 b) the rate of change of the probability to find the j-th acceptor in an excited state $\left(p_{A^{\ast },j}\right)$ is

$${\gamma }^{ex,A}{p}_{A,j}-\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)p_{A^{\ast },j}=\frac{d{p}_{A^{\ast },j}}{dt},$$ (1b)

where p_{A, j} is the probability to find the j-th acceptor in its ground state and γ^{ex, A} is the rate of excitation of acceptors in their ground state (A), whereas γ^{nr, A} and γ^{r, A} are the rates of acceptor excitation loss through nonradiative and radiative processes, respectively.

Figure 1.

Kinetic models of fluorescence and FRET for (a) donors, D, in the absence of acceptors, A, and (b) acceptors in the absence of donors, as well as (c) donors and acceptors in the presence of each other (i.e., FRET). Asterisk denotes excited species. All other symbols are defined in the text.

For single donors associated with n acceptors, if the acceptors are excited both directly by light and through energy transfer from the donor, the kinetic model of FRET (Fig. 1 c) gives

$${\gamma }^{ex,D}{p}_{Da}-\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)p_{D^{\ast }a}-\sum _{j=1}^n{\gamma }_j^{tr}\left(1-p_{A^{\ast }d,j}\right)p_{D^{\ast }a}=\frac{d{p}_{D^{\ast }a}}{dt},$$ (1c)

$${\gamma }^{ex,A}\left(1-p_{A^{\ast }d,j}\right)+{\gamma }_j^{tr}\left(1-p_{A^{\ast }d,j}\right)p_{D^{\ast }a}-\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)p_{A^{\ast }d,j}=\frac{d{p}_{A^{\ast }d,j}}{dt},$$ (1d)

where ${\gamma }_j^{tr}$ is the rate of energy transfer to each of the n acceptors, whereas p_Da, $p_{D^{\ast }a}$, p_{Ad, j}, and $p_{A^{\ast }d,j}$ are the probabilities to find donors and acceptors in their unexcited or excited states in the presence of each other. These probabilities obey the relations $p_{Da}+p_{D^{\ast }a}=1$ and $p_{Ad,j}+p_{A^{\ast }d,j}=1$. For single-photon excitation, the excitation rates of donors and acceptors depend on the light irradiance, I (in W/m²), and the wavelength-dependent extinction coefficient of each fluorescent species, ε^X(λ_ex), according to the expression

$${\gamma }^{ex,X}=I{\mathcal{E}}^X\left({\lambda }_{ex}\right),$$ (2)

where X stands for A or D and ${\mathcal{E}}^X={\epsilon }^X\left({\lambda }_{ex}\right)\ln \left(10\right){\lambda }_{ex}{\left(hc{N}_A\right)}^{-1}={\sigma }^X{\lambda }_{ex}{\left(hc\right)}^{-1}$, with λ_ex being the excitation wavelength, σ the absorption cross-section, h Plank’s constant, c the speed of light, and N_A Avogadro’s number. An instrumental multiplicative factor also may be incorporated to account for changes introduced by the optics, but this almost invariably leads to a change in the excitation light intensity at the position of the sample, and so it can be safely absorbed into I for simplicity.

As is well known, for two-photon excitation, the extinction coefficient depends on the second power of the light intensity. We are not going to consider that particular fact herein because from the point of view of this research, the effect of two-photon excitation is only to change the value of the excitation rate and not the kinetics behavior.

Particular forms for long integration time of fluorescence

In this section, we will derive particular cases of the (1a), (1b), (1c), (1d) that are relevant in experimental situations in which the fluorescence is not temporally resolved, i.e., the integration time of the detector (t − t₀) is much longer than the decay time of the fluorescent molecules. We will treat two situations that are encountered practically: CW excitation—used in, e.g., confocal microscopy—and pulsed excitation, which is used in two-photon excitation.

Taking Eq. 2 into account and integrating (1a), (1b), (1c), (1d) with respect to time, we have

$${\mathcal{E}}^D{\mathit{\Pi }}_D-\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }}=\underset{p_{D^{\ast }}\left(t_0\right)}{\overset{p_{D^{\ast }}\left(t\right)}{\int }}d{p}_{D^{\ast }},$$ (3a)

$${\mathcal{E}}^A{\mathit{\Pi }}_A-\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }}=\underset{p_{A^{\ast }}\left(t_0\right)}{\overset{p_{A^{\ast }}\left(t\right)}{\int }}d{p}_{A^{\ast }},$$ (3b)

$${\mathcal{E}}^D{\mathit{\Pi }}_{Da}-\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}-\sum _{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j}=\underset{p_{D^{\ast }a}\left(t_0\right)}{\overset{p_{D^{\ast }a}\left(t\right)}{\int }}d{p}_{D^{\ast }a},$$ (3c)

$${\mathcal{E}}^A{\mathit{\Pi }}_{Ad,j}+{\gamma }_j^{tr}{P}_{D^{\ast }A,j}-\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }d,j}=\underset{p_{A^{\ast }d}\left(t_0\right)}{\overset{p_{A^{\ast }d}\left(t\right)}{\int }}d{p}_{A^{\ast }d,j},$$ (3d)

where we have used the following notations for the various integrals: ${\mathit{\Pi }}_D={\int }_{t_0}^t{p}_{D}I\left(t\right)dt$, $P_{D^{\ast }}={\int }_{t_0}^t{p}_{D^{\ast }}dt$, ${\mathit{\Pi }}_A={\int }_{t_0}^t{p}_{A}I\left(t\right)dt$, $P_{A^{\ast }}={\int }_{t_0}^t{p}_{A^{\ast }}dt$, ${\mathit{\Pi }}_{Da}={\int }_{t_0}^t{p}_{Da}I\left(t\right)dt$, $P_{D^{\ast }a}={\int }_{t_0}^t{p}_{D^{\ast }a}dt$, ${\mathit{\Pi }}_{Ad,j}={\int }_{t_0}^t{p}_{Ad,j}I\left(t\right)dt$, $P_{A^{\ast }d}={\int }_{t_0}^t{p}_{A^{\ast }d}dt$, and $P_{D^{\ast }A,j}={\int }_{t_0}^t{p}_{D^{\ast }a}{p}_{Ad,j}dt$.

The probability of finding donors or acceptors in their excited states is always less than unity, whereas the excitation and de-excitation rates are all greater than 10⁴ s⁻¹ (with de-excitation rates being some three to five orders of magnitude higher). As a result, for integration times of 1 μs or greater, the values of the integrals on the left-hand side of (1a), (1b), (1c), (1d) far exceed the values of the integrals on the right-hand side, which are always ≤1. This applies both to the case of steady-state intensity measurements employing CW light sources, in which the probabilities are constant, and to measurements employing ultrashort light pulses that change the excited-state probabilities from zero to some higher value and then back to zero. In either case, the integrals on the right-hand side of (1a), (1b), (1c), (1d) vanish, and we have

$${\mathcal{E}}^D{\mathit{\Pi }}_D=\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }},$$ (4a)

$${\mathcal{E}}^A{\mathit{\Pi }}_A=\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }},$$ (4b)

$${\mathcal{E}}^D{\mathit{\Pi }}_{Da}=\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}+\sum _{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j},$$ (4c)

$${\mathcal{E}}^A{\mathit{\Pi }}_{Ad,j}+{\gamma }_j^{tr}{P}_{D^{\ast }A,j}=\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }d,j}.$$ (4d)

CW excitation and long integration time of fluorescence

If continuous wave (CW) lasers are used, the light intensity, I, is constant on timescales larger than those corresponding to the statistical fluctuations of the photons of light, and (1a), (1b), (1c), (1d) become

$${\mathcal{E}}^{D}I{P}_D=\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }},$$ (5a)

$${\mathcal{E}}^{A}I{P}_A=\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }},$$ (5b)

$${\mathcal{E}}^{D}I{P}_{Da}=\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}+\sum _{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j},$$ (5c)

$${\mathcal{E}}^{A}I{P}_{Ad,j}+{\gamma }_j^{tr}{P}_{D^{\ast }A,j}=\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }d,j},$$ (5d)

where the probabilities on the left-hand side of these equations, $P_D={\int }_0^t{p}_{D}dt$, $P_A={\int }_0^t{p}_{A}dt$, $P_{Da}={\int }_0^t{p}_{Da}dt$, and $P_{Ad,j}={\int }_0^t{p}_{Ad,j}dt$, are now constant. These equations will be used later on in this work to express the emission intensities of donors and acceptors as a function of rate constants and other experimental parameters for CW excitation. This applies to, e.g., steady-state studies using confocal microscopes.

Pulsed excitation and long integration time of fluorescence

If the excitation consists of trains of light pulses that are much shorter than the excited lifetime of the fluorescent species, the intensity may be, to a good approximation, described by

$$I=\iota \delta \left(t-t_0\right),$$ (6)

where $\iota$ is a dimensional coefficient and δ(t) is Dirac’s δ function. Using this formula and the sifting property of the Dirac δ function (which states that ${\int }_{t_0}^{t}p\left(t\right)\delta \left(t\right)dt=p\left(0\right)$ for t₀ < 0 < t and ${\int }_{t_0}^{t}p\left(t\right)\delta \left(t\right)dt=0$ at other times) in the Π integrals defined above, (1a), (1b), (1c), (1d) become

$${\mathcal{E}}^D\iota p_D\left(t_0\right)=\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }},$$ (7a)

$${\mathcal{E}}^A\iota p_A\left(t_0\right)=\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }},$$ (7b)

$${\mathcal{E}}^D\iota p_{Da}\left(t_0\right)=\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}+\sum _{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j},$$ (7c)

$${\mathcal{E}}^A\iota p_{Ad,j}\left(t_0\right)+{\gamma }_j^{tr}{P}_{D^{\ast }A,j}=\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }d,j}.$$ (7d)

The interpretation of the assumption used in the derivation of (1a), (1b), (1c), (1d) is that the ultrashort pulse applied to a sample at the initial time t₀ brings a fraction of the donors or acceptors into their excited states within a time much shorter than the lifetime of the donor, i.e., well before any loss of excitation occurs. The excitation/de-excitation cycle repeats itself at the repetition rate of the laser light pulses for the entire duration of the data collection (or integration time). If each pulse arrives at the sample a long time after the previous one (relative to the fluorescence lifetime of the molecules), it finds all the molecules in their ground states. In this case, we may assume that p_D(t₀) = p_Da(t₀) = p_A(t₀) = p_Ad(t₀) = 1, and (1a), (1b), (1c), (1d) become

$${\mathcal{E}}^D\iota =\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }},$$ (8a)

$${\mathcal{E}}^A\iota =\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }},$$ (8b)

$${\mathcal{E}}^D\iota =\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}+\sum _{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j},$$ (8c)

$${\mathcal{E}}^A\iota +{\gamma }_j^{tr}{P}_{D^{\ast }A,j}=\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)P_{A^{\ast }d,j}.$$ (8d)

(1a), (1b), (1c), (1d) will be used later to express the integrated emission intensity of the differing fluorescent species in the case of pulsed excitation and acquisition times much longer than the repetition rate of the light pulses, i.e., in the absence of temporal resolution. Such situations occur when two-photon excitation-based instruments are used.

Particular forms for pulsed excitation and temporally resolved fluorescence

If an ultrashort pulse, which may be described by Eq. 6, is applied to the sample, and then the fluorescence emission is measured repeatedly for integration times much shorter than both the lifetime of the fluorescent molecules and the time elapsed between arrival of two successive pulses, fluorescence decay curves may be acquired for each fluorescent species, such as donors only or donors in the presence of acceptors. Typical values are 10–100 ps for integration times, a few nanoseconds for the excited-state lifetime, and 10 or more ns for the repetition rate of the laser pulses.

Case A: Directly exciting the donors but not the acceptors

If the ultrashort pulse has a center wavelength that only matches the excitation maximum of the donor and does not excite the acceptors to any significant extent, then p_{Ad, j} = 1. Under these conditions, using Eq. 2 and separation of variables, Eqs. 1a and 1c become

$${\mathcal{E}}^D\iota \frac{p_D\left(t\right)}{1-p_D\left(t\right)}\delta \left(t\right)dt-\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)dt=\frac{d{p}_{D^{\ast }}}{p_{D^{\ast }}}$$ (9a)

and

$${\mathcal{E}}^D\iota \frac{p_{Da}\left(t\right)}{1-p_{Da}\left(t\right)}\delta \left(t\right)dt-\left({\gamma }^{r,D}+{\gamma }^{nr,D}+\sum _{j=1}^n{\gamma }_j^{tr}\right)dt=\frac{d{p}_{D^{\ast }a}}{p_{D^{\ast }a}}.$$ (9b)

Upon integrating the left side of (9a), (9b) from 0 to t and the right side from $p_{D^{\ast }}\left(0\right)$ [or $p_{D^{\ast }a}\left(0\right)$] to $p_{D^{\ast }}\left(t\right)$, the sifting property of the Dirac δ function now gives that the first terms on the left-hand sides vanish (because the lower limit of integration is not less than zero), and we obtain

$$-\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)\underset{0}{\overset{t}{\int }}dt=\underset{p_{D^{\ast }}\left(0\right)}{\overset{p_{D^{\ast }}\left(t\right)}{\int }}\frac{d{p}_{D^{\ast }a}}{p_{D^{\ast }a}}$$ (10a)

and

$$-\left({\gamma }^{r,D}+{\gamma }^{nr,D}+\sum _{j=1}^n{\gamma }_j^{tr}\right)\underset{0}{\overset{t}{\int }}dt=\underset{p_{D^{\ast }a}\left(0\right)}{\overset{p_{D^{\ast }a}\left(t\right)}{\int }}\frac{d{p}_{D^{\ast }a}}{p_{D^{\ast }a}}.$$ (10b)

Because each ultrashort pulse brings a fraction of donors in their excited state well before any excited-state depopulation occurs, we have $p_{D^{\ast }}\left(t\right),p_{D^{\ast }a}\left(t\right)\to p_{D^{\ast }0}$ when t → 0 for all the donors regardless of whether there are any acceptors nearby. Ideally, for this approximation to be valid, the pulse duration should be less than both the fluorescence decay time (i.e., nanoseconds) and the timescale of the excited-state relaxation (picoseconds). Therefore, femtosecond pulses are preferable to nanosecond or even picosecond ones. In addition, the probabilities that donors are in excited states tend to zero, i.e., $p_{D^{\ast }}\left(t\right),p_{D^{\ast }a}\left(t\right)\to 0$, for very long times, t → ∞. This upper limit is only infinite by comparison to the donor lifetime and is in fact equal to the time elapsed between the arrival of successive light pulses. With these boundary conditions, (9a), (9b) admit the following solutions:

$$p_{D^{\ast }}\left(t\right)=p_{D^{\ast }0}\text{exp}\left(-t/{\tau }^D\right)$$ (11a)

and

$$p_{D^{\ast }a}\left(t\right)=p_{D^{\ast }0}\text{exp}\left(-t/{\tau }^{Da}\right),$$ (11b)

in which

$${\tau }^D={\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)}^{-1}$$ (12a)

and

$${\tau }^{Da}={\left({\gamma }^{r,D}+{\gamma }^{nr,D}+\sum _{j=1}^n{\gamma }_j^{tr}\right)}^{-1}$$ (12b)

are the donor lifetimes in the absence and presence of acceptors, respectively, whereas

$$p_{D^{\ast }0}=\left({\gamma }^{r,D}+{\gamma }^{nr,D}+\sum _{j=1}^n{\gamma }_j^{tr}\right)P_{D^{\ast }a}$$ (12c)

is the total number of excitations, which is equal to the sum of excitations lost through all pathways of excitation energy loss. Equation 12c may be derived by integrating Eq. 1c (assuming p_{Ad, j} = 1) from 0 to a very long time and the probability limits of $p_{D^{\ast }0}$ and 0.

Case B: Directly exciting both the donors and the acceptors

When a light pulse described by Eq. 6 excites not only the donors but also the acceptors, competition occurs between energy transfer and laser light for exciting the acceptors, and hence p_{Ad, j} < 1. Under this condition and following the procedure described in Case A, integration of Eq. 1c gives

$$-\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)\underset{0}{\overset{t}{\int }}dt-\sum _{j=1}^n{\gamma }_j^{tr}\underset{0}{\overset{t}{\int }}\left(1-p_{A^{\ast }d,j}\right)dt=\underset{p_{D^{\ast }a}\left(0\right)}{\overset{p_{D^{\ast }a}\left(t\right)}{\int }}\frac{d{p}_{D^{\ast }a}}{p_{D^{\ast }a}}.$$ (13)

This type of equation has the following analytical solution for $p_{A^{\ast }d,j}\left(t\right)$ functions that have the property $p_{A^{\ast }d,j}=p_{A^{\ast }0}{\phi }_{A^{\ast }d,j}\left(t\right)$:

$$p_{D^{\ast }a}\left(t\right)=p_{D^{\ast }0}\text{exp}\left[-t/{\tau }^{Da}+p_{A^{\ast }0}\sum _{j=1}^n{\gamma }_j^{tr}\underset{0}{\overset{t}{\int }}{\phi }_{A^{\ast }d,j}\left(t\right)dt\right],$$ (14)

where $p_{A^{\ast }0}$ is an initial amplitude and ${\phi }_{A^{\ast }d,j}$ is an arbitrary decay function (which would take the form of an exponential decay when there is only direct excitation of the acceptors). The integral in the exponent may be evaluated numerically from experimentally determined acceptor fluorescence decay, while

$$p_{D^{\ast }0}=\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}+\sum _{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j}$$ (15)

is the total number of donor excitations lost through all the different energy-loss pathways. Equation 15 may be derived by integrating Eq. 1c from t = 0 to very long time, which corresponds to the probability limits of $p_{D^{\ast }0}$ and 0. Obviously, Eq. 14 reduces itself to Eq. 11b in the absence of direct excitation of the acceptor, i.e., for $p_{A^{\ast }0}=0$.

Fluorescence emission in the presence and absence of FRET

The fundamental equations of FRET

The quantities of interest in FRET are the quantum yields of the donor in the absence (Q^D) or presence (Q^Da) of acceptors and the efficiency of energy transfer (or FRET efficiency, E) from donors to acceptors, namely, the fractions of the number of excitations lost through radiative processes in the absence and presence of acceptors and through energy transfer to the acceptor, respectively. In general, the quantum yield is defined as the number of photons emitted divided by the total number of excitations, whereas the FRET efficiency is defined as the number of excitations transferred from donors to acceptors divided by the total number of excitations of the donor. The total number of excitations equals the sum of excitations lost through different de-excitation pathways (regardless of whether the excitation light is CW or pulsed or detection is with or without temporal resolution), and it may be computed by integrating (9a), (9b) over different time intervals and under different excitation conditions. Thus, expressions may be written for the donor and acceptor quantum yields in the absence of FRET,

$$Q^D=\frac{{\int }_{t_0}^t{\gamma }^{r,D}{p}_{D^{\ast }}dt}{{\int }_{t_0}^t\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)p_{D^{\ast }}dt}$$ (16a)

and

$$Q^A=\frac{{\int }_{t_0}^t{\gamma }^{r,A}{p}_{A^{\ast }}dt}{{\int }_{t_0}^t\left({\gamma }^{r,A}+{\gamma }^{nr,A}\right)p_{A^{\ast }}dt};$$ (16b)

for the donor quantum yield in the presence of FRET,

$$Q^{Da}=\frac{{\int }_{t_0}^t{\gamma }^{r,D}{p}_{D^{\ast }a}dt}{{\int }_{t_0}^t\left[\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)p_{D^{\ast }a}+{\sum }_{j=1}^n{\gamma }_j^{tr}\left(1-p_{A^{\ast }d,j}\right)p_{D^{\ast }a}\right]dt};$$ (16c)

and for the FRET efficiency,

$$E=\frac{{\int }_{t_0}^t{\sum }_{j=1}^n{\gamma }_j^{tr}{p}_{D^{\ast }a}{p}_{Ad,j}dt}{{\int }_{t_0}^t\left[\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)p_{D^{\ast }a}+{\sum }_{j=1}^n{\gamma }_j^{tr}\left(1-p_{A^{\ast }d,j}\right)p_{D^{\ast }a}\right]dt}.$$ (16d)

Because the different excited-state depopulation rates are all constant, making use of the notations for the integrals of the probabilities from Methods, these equations may be rewritten as

$$Q^D=\frac{{\gamma }^{r,D}}{{\gamma }^{r,D}+{\gamma }^{nr,D}},$$ (17a)

$$Q^A=\frac{{\gamma }^{r,A}}{{\gamma }^{r,A}+{\gamma }^{nr,A}},$$ (17b)

$$Q^{Da}=\frac{{\gamma }^{r,D}{P}_{D^{\ast }a}}{\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}+{\sum }_{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j}},$$ (17c)

$$E=\frac{{\sum }_{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j}}{\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)P_{D^{\ast }a}+{\sum }_{j=1}^n{\gamma }_j^{tr}{P}_{D^{\ast }A,j}}.$$ (17d)

It is noteworthy that Eqs. 16c and 16d as well as Eqs. 17c and 17d depend on the probabilities $P_{D^{\ast }A,j}$ and $P_{D^{\ast }a}$, which means that, in the most general case, they also depend to some extent on the excitation intensity as well as the extinction coefficients of the donors and acceptors. This is a departure from the widely used expressions for Q^Da and E, in which these probabilities are assumed to be equal to one another and therefore cancel out, leaving the two quantities dependent on radiative, nonradiative, and energy transfer rates only. The net effect of such a dependence on experimental conditions is negligible, if the probability to find acceptors in their ground state, p_{Ad, j}, is close to unity when the donor is in an excited state. This occurs when the acceptor is not directly excited by laser light. In that case, definitions (Eqs. 17c and 17d) reduce themselves to the classical ones, according to which Q^Da and E depend only on the excited-state depopulation rates (15). If, by contrast, the acceptor is also excited directly by laser light, as is the case in many FRET approaches, the probability p_{Ad, j} is smaller than unity when the donor is in an excited state, which has some consequences, as detailed in Results.

In either case, by rewriting Eq. 16d as

$$E=1-\frac{{\int }_{t_0}^t\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)p_{D^{\ast }}dt}{{\int }_{t_0}^t{\gamma }^{r,D}{p}_{D^{\ast }}dt}·\frac{{\int }_{t_0}^t{\gamma }^{r,D}{p}_{D^{\ast }a}dt}{{\int }_{t_0}^t\left[\left({\gamma }^{r,D}+{\gamma }^{nr,D}\right)p_{D^{\ast }a}+{\sum }_{j=1}^n{\gamma }_j^{tr}\left(1-p_{A^{\ast }d,j}\right)p_{D^{\ast }a}\right]dt}$$ (18)

and using Eqs. 16a and 16c to replace the first and second terms, we obtain

$$E=1-\frac{Q^{Da}}{Q^D}.$$ (19)

This is a fundamental relation of FRET (15), from which all expressions for the FRET efficiency, in terms of both temporally resolved and steady-state fluorescence emission, may be derived, as it will be shown below.

Time-integrated fluorescence emission

Using Eqs. 4a and 4b, the notations for the integrated probabilities used in (4a), (4b), (4c), (4d), and the definitions of quantum yields (Eqs. 17a and 17b), we can now introduce the steady-state integrated emission of D or A per molecule in the absence of FRET:

$${\mathit{\Phi }}^D\equiv {\gamma }^{r,D}{P}_{D^{\ast }}={\mathcal{E}}^D{\mathit{\Pi }}_D{Q}^D,$$ (20a)

$${\mathit{\Phi }}^A\equiv {\gamma }^{r,A}{P}_{A^{\ast }}={\mathcal{E}}^A{\mathit{\Pi }}_A{Q}^A.$$ (20b)

Successive use of Eqs. 4c and 17c gives the integrated emission per donor in the presence of FRET,

$${\mathit{\Phi }}^{Da}\equiv {\gamma }^{r,D}{P}_{D^{\ast }a}={\mathcal{E}}^D{\mathit{\Pi }}_{Da}{Q}^{Da},$$ (20c)

which, using Eq. 19, becomes

$${\mathit{\Phi }}^{Da}={\mathcal{E}}^D{\mathit{\Pi }}_{Da}{Q}^D-{\mathcal{E}}^D{\mathit{\Pi }}_{Da}E{Q}^D.$$ (20d)

Finally, using successively Eqs. 4c, 4d, and 17d, we obtain for A in the presence of D

$${\mathit{\Phi }}^{Ad}\equiv {\gamma }^{r,A}\sum _{j=1}^n{P}_{A^{\ast }d,j}={\mathcal{E}}^A{Q}^A\sum _{j=1}^n{\mathit{\Pi }}_{Ad,j}+{\mathcal{E}}^D{\mathit{\Pi }}_{Da}E{Q}^A.$$ (20e)

These equations will be used later on in this work to derive various expressions for FRET efficiency as a function of measurable quantities in steady-state situations.

Time-resolved fluorescence emission

In the absence of acceptor direct excitation, from Eqs. 11–b, we obtain for the emission intensities of the donors in the presence or absence of acceptors

$${\varphi }^D\left(t\right)\equiv {\gamma }^{r,D}{p}_{D^{\ast }}\left(t\right)={\gamma }^{r,D}{p}_{D^{\ast }0}\text{exp}\left(-t/{\tau }^D\right)$$ (21a)

and

$${\varphi }^{Da}\left(t\right)\equiv {\gamma }^{r,D}{p}_{D^{\ast }a}\left(t\right)={\gamma }^{r,D}{p}_{D^{\ast }0}\text{exp}\left(-t/{\tau }^{Da}\right)$$ (21b)

for temporal resolution higher than the fluorescence lifetime (i.e., $\delta t\gg \tau$). When (21a), (21b) are integrated over a time (δt) much longer than the lifetime of the excited state of the donor but shorter than the repetition time of the laser pulses, we obtain

$${\mathit{\Phi }}^D=\underset{0}{\overset{\delta t}{\int }}{\varphi }^D\left(t\right)dt=p_{D^{\ast }0}{Q}^D,$$ (22a)

$${\mathit{\Phi }}^{Da}=\underset{0}{\overset{\delta t}{\int }}{\varphi }^{Da}\left(t\right)dt=p_{D^{\ast }0}{Q}^{Da}.$$ (22b)

The results embodied by (21a), (21b) are customarily used to interpret the fluorescence decay of donors in FRET studies based on FLIM. The results expressed by (22b), (22a) are formally similar to those of a steady-state situation ((20c), (20b), (20a), (20e), (20d)), in which a CW light source is used and fluorescence emission is integrated over periods of time much longer than the excited lifetime of the donors and acceptors. This similarity provides a welcome consistency check of the kinetic theory outlined in this work.

Similarly, mathematical expressions may be obtained for the emission intensities of donors in the absence or presence of acceptors for the case of acceptors being directly excited by light,

$${\varphi }^D\left(t\right)\equiv {\gamma }^{r,D}{p}_{D^{\ast }}\left(t\right)={\gamma }^{r,D}{p}_{D^{\ast }0}\text{exp}\left(-t/{\tau }^D\right)$$ (23a)

and

$${\varphi }^{Da}\left(t\right)\equiv {\gamma }^{r,D}{p}_{D^{\ast }a}\left(t\right)={\gamma }^{r,D}{p}_{D^{\ast }0}\text{exp}\left[-t/{\tau }^{Da}+p_{A^{\ast }0}\sum _{j=1}^n{\gamma }_j^{tr}\underset{0}{\overset{t}{\int }}{\phi }_{A^{\ast }d,j}\left(t\right)dt\right],$$ (23b)

where τ^Da is as defined above—the donor lifetime in the presence of acceptors but in the absence of direct acceptor excitation. The integrals of these expressions depend on the particular form of ${\phi }_{A^{\ast }d,j}$, as we have discussed in Methods.

Results

FRET efficiency expressions for ensembles of pure oligomers

Throughout this work, an “oligomeric complex” or “oligomer” is defined as a group of two or more molecules associated through either weak (e.g., van der Waals) interactions or covalent bonds (including covalently bound linkers). To obtain useful relationships between the efficiency of energy transfer and experimentally measured quantities for pure oligomers (i.e., in the absence of free monomers), we will rewrite herein Eq. 19 in a few different ways. By inserting the quantum yields of the donor in the presence and absence of FRET from Eqs. 20a and 20c into Eq. 19, we obtain

$$E\text{'}=1-\frac{{\mathit{\Phi }}^{Da}}{{\mathit{\Phi }}^D}\frac{{\mathit{\Pi }}_D}{{\mathit{\Pi }}_{Da}},$$ (24)

which for constant excitation intensity (see (5a), (5b), (5c), (5d)) becomes

$$E\text{'}=1-\frac{{\mathit{\Phi }}^{Da}}{{\mathit{\Phi }}^D}\frac{P_D}{P_{Da}}$$ (25)

and for ultrashort-pulse excitation (see (8a), (8b), (8c), (8d)) becomes

$$E=1-\frac{{\mathit{\Phi }}^{Da}}{{\mathit{\Phi }}^D}.$$ (26)

The last equation has been widely employed, together with various experimental schemes that allow the determination of Φ^D (e.g., acceptor photobleaching or use of two different excitation wavelengths (22, 24), to compute the FRET efficiency from steady-state fluorescence intensities. Nevertheless, now we see that Eq. 26 should be used with caution because it only applies to pulsed excitation and is expected to give somewhat erroneous results when used in conjunction with CW excitation, as is the case with confocal or wide-field microscopes. In addition, the use of photobleaching or two different excitation wavelengths to determine the donor emission in the absence of FRET leads to loss of pixel-level information in FRET imaging because of the fact that diffusion causes the molecular makeup of an image pixel to change during the long time it takes to acquire all the needed data.

To avoid the use of multiple measurements or acceptor photobleaching, one can combine Eq. 20d with the particular case of Eq. 20e for the absence of acceptor direct excitation to obtain

$$Q^D=\frac{1}{{\mathcal{E}}^D{\mathit{\Pi }}_{Da}}\left({\mathit{\Phi }}^{Da}+\frac{Q^D}{Q^A}{\mathit{\Phi }}^{Ad}\right).$$ (27)

which, inserted into Eq. 19 together with Q^Da from Eq. 20c, gives

$$E={\left(1+\frac{Q^A}{Q^D}\frac{{\mathit{\Phi }}^{Da}}{{\mathit{\Phi }}^{Ad}}\right)}^{-1}.$$ (28)

Equation 28 has been proposed previously and used successfully in many practical applications (10, 20, 29). Remarkably, it does not depend on probabilities, and hence, it is independent of the excitation level regardless of whether excitation is performed using CW or pulsed lasers. In addition, with this formula, E may be determined upon a single excitation of the sample and does not rely on either multiple excitation wavelengths or acceptor photobleaching, as do other methods. This eliminates the need for strong approximations often used in FRET studies employing steady-state fluorescence emission and allows one to accurately compute E.

Using again the assumption that the acceptor is not directly excited by laser light (which leads to p_{Ad, j} = 1) and using the definitions of the lifetimes introduced by (12a), (12c), (12b), from Eq. 19 we immediately obtain

$$E=1-\frac{{\tau }^{Da}}{{\tau }^D}.$$ (29)

This equation is very popular with FLIM-FRET researchers because it allows one to determine E from the fluorescence decay curves described theoretically by (12a), (12b) and that are obtained from FLIM experiments. Unfortunately, it is very difficult to extract with accuracy more than two different lifetimes from fluorescence decay curves, which makes this particular method applicable to probing interactions between only two molecules (i.e., dimers). This problem may be elegantly circumvented using the following approach.

When the acceptors are also directly excited by light, if the excitation light intensities are equal between the measurements of donors only and donors in the presence of acceptors, the denominators in Eqs. 16a and 16c cancel each other out once these expressions are inserted into Eq. 19. Thus, in our usual notations, we obtain

$$E=1-\frac{P_{D^{\ast }a}}{P_{D^{\ast }}}=1-\frac{1}{{\tau }^D}\frac{P_{D^{\ast }a}}{p_{D^{\ast }0}},$$ (30)

where $p_{D^{\ast }0}$ may be interpreted as the amplitude of the fluorescence decay curve (i.e., its height at t = 0). Further, by explicitly writing $P_{D^{\ast }a}$ as an integral, we obtain

$$E=1-\frac{1}{{\tau }^D}\frac{{\int }_0^{\infty }{p}_{D^{\ast }a}dt}{p_{D^{\ast }0}},$$ (31)

where $p_{D^{\ast }a}$ may be replaced by the fluorescence decay curve of the donor in the presence of acceptors, which may be then integrated numerically over the time interval between two excitation pulses to compute the FRET efficiency. By using the expression of $p_{D^{\ast }a}$ from Eq. 14, it may be easily seen that Eq. 31 reduces itself to Eq. 29 if there is no direct excitation of the acceptor (i.e., for $p_{A^{\ast }0}$= 0).

Thus, Eq. 31 not only removes an approximation inherent in Eq. 29 but also provides a means to compute the FRET efficiency for systems of oligomers of unknown size—and hence, unknown number of lifetimes—using time-resolved fluorescence measurements. This feature could be exploited in the context of FRET spectrometry to determine the quaternary structure of macromolecules from distributions of FRET efficiencies obtained from pixel-level fluorescence measurements (20).

FRET efficiency expressions for mixtures of oligomers and free monomers

Fluorescence of mixtures of interacting and noninteracting molecules

Up to this point in our derivations, fluorescence emission, whether expressed as photons emitted per unit of time (and denoted by ϕ) or integrated over a longer time (denoted by upper case Φ), has implicitly referred to single molecules. This is indicated by the fact that we used probabilities of having the molecules in certain states instead of concentrations of molecules in those states.

To describe emission intensities for ensembles of excited donors or acceptors, we multiply the previous results for Φ by the total concentrations of donors or acceptors in the sample volume, as appropriate. Additionally, we now consider the more general case that includes free donors and acceptors, as well as D-only and A-only oligomers, and we also replace the probabilities by concentrations. In light of these considerations and proceeding along the lines of reasoning surrounding Eqs. 19 from (15), Eqs. 20d and 20e are replaced by

$$F^{Da}={\mathcal{E}}^D{Q}^D\left\{\left[D\right]+{\left[D\right]}_d\right\}{\mathit{\Pi }}_D+{\mathcal{E}}^D{Q}^D{\left[D\right]}_a{\mathit{\Pi }}_{Da}-{\mathcal{E}}^D{E}_{oligo}{Q}^D{\mu }_{oligo}{\mathit{\Pi }}_{Da},$$ (32a)

$$F^{Ad}={\mathcal{E}}^A{Q}^A\left\{\left[A\right]+{\left[A\right]}_a\right\}{\mathit{\Pi }}_A+{\mathcal{E}}^A{Q}^A{\left[A\right]}_d{\mathit{\Pi }}_{Ad}+{\mathcal{E}}^D{E}_{oligo}{Q}^A{\mu }_{oligo}{\mathit{\Pi }}_{Da},$$ (32b)

where [D]_a and [A]_d are the concentration of donors in oligomers with acceptors and the concentration of acceptors within oligomers with donors, respectively; the term ε^DQ^D{[D] + [D]_d}Π_D accounts for the emission of free donors and donors in complexes with other donors (but no acceptors); and ε^AQ^A{[A] + [A]_a} is the emission of free acceptors and acceptors in complexes with other acceptors (but no donors).

To simplify these expressions, we introduce the notations

$$F^{D^{\text{'}}}\equiv {\mathcal{E}}^D{Q}^D\left\{\left[D\right]+{\left[D\right]}_d\right\}{\mathit{\Pi }}_D+{\mathcal{E}}^D{Q}^D{\left[D\right]}_a{\mathit{\Pi }}_{Da}$$ (33a)

and

$$F^{A^{\text{'}}}\equiv {\mathcal{E}}^A{Q}^A\left\{\left[A\right]+{\left[A\right]}_a\right\}{\mathit{\Pi }}_A+{\mathcal{E}}^A{Q}^A{\left[A\right]}_d{\mathit{\Pi }}_{Ad}$$ (33b)

for the fluorescence of donors and acceptors and

$$F_{FRET}^D\equiv {\mathcal{E}}^D{E}_{oligo}{Q}^D{\mu }_{oligo}{\mathit{\Pi }}_{Da}$$ (33c)

and

$$F_{FRET}^A\equiv {\mathcal{E}}^D{E}_{oligo}{Q}^A{\mu }_{oligo}{\mathit{\Pi }}_{Da}$$ (33d)

for the loss or gain due to FRET. We also introduce the concept of apparent FRET efficiency, E_app, of a mixture of free as well as associated donors, some of which may be involved in FRET with acceptors, which is expressed by (12, 15)

$$E_{app}\equiv \frac{{\mu }_{oligo}}{\left[D\right]+{\left[D\right]}_d+{\left[D\right]}_a}{E}_{oligo}\equiv \frac{{\mu }_{oligo}}{{\left[D\right]}_T}{E}_{oligo}.$$ (33e)

This is the quantity of interest in FRET experiments and provides the connection to the oligomeric size and configuration (i.e., quaternary structure) (20).

With these notations and definitions, (32a), (32b) become

$$F^{Da}=F^{D\text{'}}-F_{FRET}^D$$ (34a)

and

$$F^{Ad}=F^{A\text{'}}+\frac{Q^A}{Q^D}{F}_{FRET}^D,$$ (34b)

as has already been proposed before (10, 15). Note that we used “prime” to denote F^D′ and F^A′ because, according to Eqs. 33a and 33b, they are equal to the donor-only and acceptor-only fluorescence emissions only if the probabilities follow the relations Π_D = Π_Da and Π_A = Π_Ad. In that case, Eqs. 33a and 33b become

$$F^{D^{\text{'}}}={\mathcal{E}}^D{Q}^D{\left[D\right]}_T{\mathit{\Pi }}_D\equiv F^D$$ (35a)

and

$$F^{A\text{'}}={\mathcal{E}}^A{Q}^A{\left[A\right]}_T{\mathit{\Pi }}_A\equiv F^A.$$ (35b)

The generally accepted definition of FRET efficiency in terms of integrated emission intensities (over entire emission spectra), by analogy to Eq. 26, is given by the equation

$$E_{app}\equiv \frac{F_{FRET}^D}{F^D}=1-\frac{F^{Da}}{F^D}.$$ (36)

If the donor and acceptor are chosen such that the acceptor is not directly excited by light at a wavelength at which the donor is excited, then F^A′ = 0, and combination of (34a), (35b) gives

$$F^{D\text{'}}=F^{Da}+\frac{Q^D}{Q^A}{F}^{Ad},$$ (37)

which is equal to F^D for pulsed excitation light but not for CW excitation. Inserting Eq. 37 into Eq. 36, we obtain an equation,

$$E_{app}^{\text{'}}={\left(1+\frac{Q^A}{Q^D}\frac{F^{Da}}{F^{Ad}}\right)}^{-1},$$ (38)

that has a similar form to Eq. 28, which applies to pure systems of oligomers.

Because we used F^D′ and not F^D to derive Eq. 38, it is necessary to verify that it actually gives the correct result. By inserting (34b), (34a) (with F^A′ = 0) into the right-hand side of Eq. 38, this equation reduces itself to the correct expression, $E_{app}^{\text{'}}={\mu }_{oligo}/{\left[D\right]}_T{E}_{oligo}\equiv E_{app}$, but only for pulsed and not for CW excitation because in the former case Π_Da = Π_D = 1, as mentioned above and further discussed below.

When ${\gamma }^{ex,A}\ne 0$, we have $F^A\ne 0$, and (34b), (34a) may be solved only if a second excitation wavelength is used because the system of (34b), (34a) is otherwise underdetermined. This problem has been previously tackled and its results successfully applied to probing oligomerization of membrane receptors (11, 12, 14).

Determination of E_app and concentrations using two excitation wavelengths

If, in addition to the donor concentration and the FRET efficiency, the acceptor concentration also needs to be determined (11, 14), the theory of the method has to incorporate the direct excitation of the acceptor as well as additional equations by adding a second excitation wavelength.

In the case of two excitation wavelengths, one may write the following variants of (34b), (34a) for the donor and acceptor emission in the presence of FRET:

$$F_1^{Da}=F_1^{D^{\text{'}}}-F_{FRET,1}^D,$$ (39a)

$$F_1^{Ad}=F_1^{A^{\text{'}}}+\frac{Q^A}{Q^D}{F}_{FRET,1}^D,$$ (39b)

$$F_2^{Da}=F_2^{D^{\text{'}}}-F_{FRET,2}^D,$$ (39c)

$$F_2^{Ad}=F_2^{A^{\text{'}}}+\frac{Q^A}{Q^D}{F}_{FRET,2}^D,$$ (39d)

where the subscripts “1” and “2” stand for the first and second excitation wavelength, respectively. Starting from the notations given by (33d), (33e), (33a), (33b), (33c), we introduce the following new notations:

$${\rho }^{ex,D}\equiv F_1^{D^{\text{'}}}/F_2^{D^{\text{'}}},$$ (40a)

$${\rho }^{ex,A}\equiv F_1^{A^{\text{'}}}/F_2^{A^{\text{'}}}.$$ (40b)

For mixtures of molecules in different oligomeric states, ρ^{ex, D} and ρ^{ex, A} may be easily determined, though only for the case of pulsed excitation (for which Π_D = Π_Da = Π_A = Π_Ad = 1, and therefore ${\rho }^{ex,D}={\epsilon }_1^D/{\epsilon }_2^D$ and ${\rho }^{ex,A}={\epsilon }_1^A/{\epsilon }_2^A$), by measuring separately the relative fluorescence emission after excitation at the two wavelengths of samples containing only donors or only acceptors.

After solving this new system of equations (see Supporting Materials and Methods, Section 1), we obtain

$$F_2^{A^{\text{'}}}=\left(F_2^{Ad}-F_1^{Ad}\frac{1}{{\rho }^{ex,D}}+F_2^{Da}\frac{Q^A}{Q^D}-F_1^{Da}\frac{1}{{\rho }^{ex,D}}\frac{Q^A}{Q^D}\right){\left(1-{\rho }^{ex,A}/{\rho }^{ex,D}\right)}^{-1}$$ (41)

For pulsed excitation, Π_D = Π_Da = 1, and Eq. 43 reduces to

$$F_2^{A^{\text{'}}}=\left(F_2^{Ad}-F_1^{Ad}\frac{1}{{\rho }^{ex,D}}\right){\left(1-{\rho }^{ex,A}/{\rho }^{ex,D}\right)}^{-1}.$$ (41′)

In addition, we have

$$F_1^{D^{\text{'}}}=F_1^{Da}+F_1^{Ad}\frac{Q^D}{Q^A}-F_2^{A^{\text{'}}}{\rho }^{ex,A}\frac{Q^D}{Q^A},$$ (42)

$$E_{app}^{\text{'}}={\left(1+\frac{F_1^{Da}}{F_1^{Ad}-F_2^{A^{\text{'}}}{\rho }^{ex,A}}\frac{Q^A}{Q^D}\right)}^{-1},$$ (43)

where $F_2^{A^{\text{'}}}$ is connected to experiment via Eq. 43. For pulsed excitation, we may substitute $F_2^{A^{\text{'}}}$ from Eq. 43′ and obtain

$$E_{app}^{\text{'}}={\left[1+\frac{F_1^{Da}\left(1-{\rho }^{ex,A}/{\rho }^{ex,D}\right)}{F_1^{Ad}-F_2^{Ad}{\rho }^{ex,A}}\frac{Q^A}{Q^D}\right]}^{-1}.$$ (43′)

Equation 43′, as well as similar or approximate forms of it, has been used previously by us or other researchers (11, 12, 17, 24) to determine the FRET efficiency for pure or mixed forms of molecular complexes of different sizes (11, 24). By inserting the particular forms taken by (32b), (32a) and (32b), (32a) for Π_D = Π_Da = Π_A = Π_Ad = 1 into the right-hand side of Eq. 43′, we find that this equation reduces itself to the correct expression, $E_{app}^{\text{'}}={\mu }_{oligo}/{\left[D\right]}_T{E}_{oligo}\equiv E_{app}$. By contrast, the more general Eq. 43 combines integrated probabilities of donors and acceptors to be in excited states for two different wavelengths—all of which take unknown values. Therefore, for CW excitation, the FRET efficiency is subject to systematic errors. These errors could be corrected for (see Discussion), but that process requires time-resolved measurements in addition to CW-based measurements.

Discussion

In this section, we will discuss, based on specific expressions for FRET efficiency presented in the Results, how some of the theoretical assumptions may lead to systematic errors if not carefully considered in the context of the experimental protocols used. Published experimental as well as simulated data are invoked to illustrate is point.

Determination of E from time-resolved measurements

As discussed above, if the acceptor has been directly excited before the donor, quantum mechanics rules prevent the donor from transferring its excitation to the acceptor. The magnitude of this effect is estimated by evaluating the integral in the exponent of Eq. 14 using the approximations that the acceptor fluorescence follows the same exponential decay curve as it would in the absence of FRET, ${\phi }_{A^{\ast }d,j}\left(t\right)=\text{exp}\left(-t/{\tau }^A\right)$, and that all acceptors are equally excited, whether by laser light or via FRET. As shown in Fig. S1, the change in the donor excited lifetime is rather small, even for tetramers consisting of three acceptors and one donor. To estimate the contribution of the acceptor direct excitation to E, assuming again that the acceptor fluorescence follows an exponential decay, after performing the integration in the exponent of Eq. 14 and inserting the resulting probability into Eq. 31, we obtain

$$E=1-\frac{1}{{\tau }^D}\underset{0}{\overset{\infty }{\int }}\text{exp}\left[-t\left(1/{\tau }^D+\sum _{j=1}^n{\gamma }_j^{tr}\right)+p_{A^{\ast }0}{\tau }^A\left(1-e^{-t/{\tau }^A}\right)\sum _{j=1}^n{\gamma }_j^{tr}\right]dt.$$ (44)

By inserting into this expression the parameter values used for simulating the fluorescence decay curves in Fig. S1, we obtain E = 0.783 in the absence and E = 0.768 in the presence of 10% acceptor direct excitation, respectively. This overestimate of E when acceptor direct excitation is taken into account is rather modest (∼2%), although it may be significant in interpreting the results from high-precision FRET experiments.

Regardless of whether the competition between energy transfer and laser light for exciting the acceptors produces detectable errors, Eq. 31 suggests a simple alternative way of computing the FRET efficiency in mixtures of monomers and oligomers with different proportions of donors and acceptors that generate a superposition of several exponential decay curves with different lifetimes. This proposed method, which is different from FLIM and which we tentatively name “time-resolved intensity measurements,” should be useable in conjunction with FRET spectrometry, which allows determination of quaternary structures but has so far been implemented using average-intensity-based fluorescence measurements only (20, 29).

As we have mentioned above, FRET efficiency may not be determined from experiments on mixtures of multiple types of oligomers and free monomers using Eq. 29. Even if it were possible to extract several lifetimes from a fluorescence decay curve, one would need to know a priori the number and sizes of the different types of oligomers present (to know how many lifetimes to extract), which is the very piece of information that one actually needs to extract from FLIM experiments. This creates a vicious circle, which may be avoided by integrating the fluorescence decay curves—rather than resolving them into multiple exponentials—and then using Eq. 31 to compute the FRET efficiency.

Estimating and testing systematic errors introduced by CW excitation

Assuming that the probability of the donors to be in their ground state in the absence of FRET is equal to that corresponding to the presence of FRET—i.e., Π_D = Π_Da (or P_D = P_Da)—may lead to errors in computing the FRET efficiency using the standard expressions for FRET efficiency and CW excitation light sources. To estimate the errors in the FRET efficiency introduced by assumption implicit in Eq. 26 for systems of pure oligomeric complexes, we first rewrite Eq. 25 in terms of the true FRET efficiency, E, given by Eq. 26, as

$$E^{\text{'}}=1-\left(1-E\right)\frac{P_D}{P_{Da}}.$$ (45)

Replacing the integrated probabilities by their corresponding expressions derived in Supporting Materials and Methods, Section 3, Eq. 45 becomes

$$E^{\text{'}}=1-\left(1-E\right)\frac{1+I{\mathcal{E}}^D{\tau }^{Da}}{1+I{\mathcal{E}}^D{\tau }^D}.$$ (46)

Let us assume that a laser beam with an average power of 1 mW and a wavelength of 433 nm is focused to a diffraction-limited spot of radius 200 nm onto a sample containing dimers consisting of single Cerulean (35) fluorescent proteins (with extinction coefficient ε^D = 4300 M⁻¹ m⁻¹) fused to some other fluorescent protein to form FRET dimers. The excitation rate for a donor molecule given by Eq. 2 is ${\gamma }^{ex,D}=I{\mathcal{E}}^D$ = 2.85 × 10⁸ s⁻¹. The lifetime of Cerulean in the absence of FRET is ∼3.2 ns (36). Its lifetime in the presence of FRET with a true FRET efficiency value of, let us say, E = 0.28 is estimated from Eq. 29 to be 2.3 ns. By inserting these values into Eq. 46, we obtain a FRET efficiency E′ = 0.38, which is some 34% larger than the true FRET efficiency, E, of our assumed dimers. The excitation power of 1 mW used in our estimates above is not atypical in experiments involving fluorescent molecules (see, e.g., (37)), and so this kind of error in the FRET efficiency could not be considered as exceptional. In fact, even if the excitation power decreased by an order of magnitude (to 0.1 mW), the error in FRET efficiency predicted by Eq. 46 for CW excitation would still be 6%.

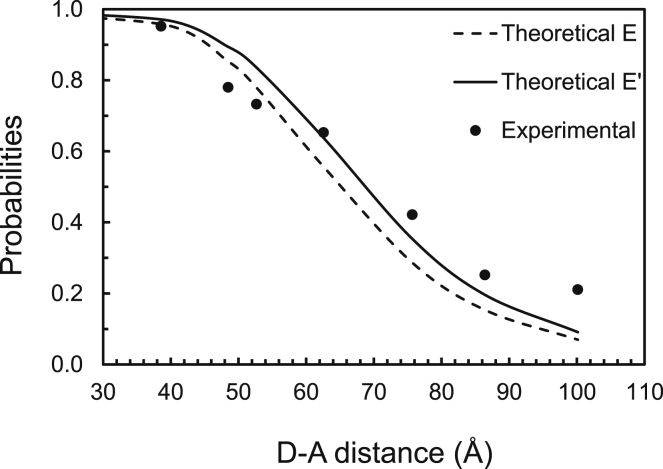
Systematic errors in FRET efficiency measurements based on CW excitation light have been noticed ever since Stryer’s introduction of the “spectroscopic ruler” (38). In a more recent study, Deniz and co-workers (39) used dinucleotides of the same lengths labeled fluorescently such that the tags were positioned at various distances from one another and performed single-particle FRET measurements using CW excitation. By plotting the FRET efficiency values versus distance, Deniz et al. noticed a shift toward larger distances in the experimental data plot compared to the plot predicted by Förster’s well-known formula (see Fig. 2).

Figure 2.

Comparison between measured and simulated dependence of the FRET efficiency of a FRET pair (consisting of tetramethylrhodamine as a donor, D, and cyanine 5 as an acceptor, A) using Förster’s formula (dashed blue line) and Eq. 46, with the experimental data points and the Förster distance value (R₀ = 65 Å) taken from Deniz et al. (39). Fitting residuals (i.e., the square root of the sum of the squares of fitting errors) were 2.54 for Förster’s formula and 2.16 for Eq. 46 using the same Förster radius (see text).

In light of our discussion above, it is reasonable to assume that least part of those discrepancies arose from approximations inherent in the integrated probabilities. To test that hypothesis, we substitute τ^Da from Eq. 29 into Eq. 46 to obtain a relationship,

$$E^{\text{'}}=1-\left(1-E\right)\left(1-\frac{I{\mathcal{E}}^D{\tau }^D}{1+I{\mathcal{E}}^D{\tau }^D}E\right),$$ (47)

that connects the measured efficiency E′ to that predicted by Förster’s formula for different values of the interfluorophore distance, R. We found that the E′ vs. R curve predicted by Eq. 47 is significantly shifted to the right and better fits the experimental data, as revealed by the fitting residuals (see Fig. 2), for the same Förster distance (R₀ = 65 Å) as in the work described above. This, of course, is not because Förster’s formula would be incorrect, but rather because an equation similar to our Eq. 26 (which is valid for pulsed but not CW excitation) has been used in calculating the FRET efficiency from experiment.

As for the systematic errors affecting the output of Eq. 38 when using CW excitation, we could only infer that they will be at least as large as those estimated in the paragraph above. For reference, we estimate the values of the four integrated probabilities using the expressions provided in the Supporting Materials and Methods, Section 3 for the experimental conditions described above and, in addition, assuming that the acceptors consist of Venus fluorescent molecules (40) with an extinction coefficient ε^A = 9200 M⁻¹ m⁻¹ and a lifetime of 3 ns. For 1 ms integration time and 1 mW of excitation power, these values are P_D = 5.2 × 10⁻⁴ s, P_Da = 6.0 × 10⁻⁴ s, P_A = 3.5 × 10⁻⁴ s, and P_Ad = 2.2 × 10⁻⁴ s, with the donor integrated probability being 13% smaller and the acceptor integrated probability 58% larger in the presence of FRET compared to their respective values in the absence of FRET. As seen, the acceptor’s integrated probability is lower in the presence of FRET compared to that in the absence of FRET because excitation through both FRET and laser light causes the acceptors to spend less time in their ground state. Because, in the expressions for F^Da and F^Ad in (32b), (32a), each such integrated probability multiplies the concentration of a different kind of donor or acceptor (i.e., free as well as bound to their own or a different kind of molecule), taking the ratio of F^Da/F^Ad to compute the FRET efficiency using Eq. 38 would lead to different values of E′_app depending on the relative proportion of the differing fluorescent species, with none of these values being actually equal to E′_app.

Finally, following the same line of reasoning as above, it may be concluded that Eq. 43 leads to systematic errors in the FRET efficiency when using CW excitation for mixtures of molecules in different states of association. Furthermore, the same kind of errors affect the determination of the concentrations of donors and acceptors using (32b), (32a) and (32b), (32a).

Avoiding systematic and random errors in E_app when using pulsed excitation

As mentioned above, for pulsed excitation light, Eqs. 38 and 43′ correctly lead to $E_{app}^{\text{'}}={\mu }_{oligo}/{\left[D\right]}_T{E}_{oligo}\equiv E_{app}$ and are expected to provide values of FRET efficiency with arbitrary accuracy because Π_Da = Π_D = 1, as long as the underlying assumption of no acceptor direct excitation is valid. Therefore, proper use of Eqs. 38 and 43′ allows one to determine the quaternary structure of proteins using FRET spectrometry, which relies on plotting histograms of frequencies of E_oligo values for systems of oligomers with different combinations of donors and acceptors (20). Additionally, it is possible to determine the donor concentration from Eq. 37 using the same measurement performed for determining E_app, as proposed previously (41).

Nevertheless, either one of those equations may be affected by systematic errors, depending on the particular experimental protocol used. For instance, Eq. 38 could overestimate the FRET efficiency if the acceptor is directly excited by light to a significant degree. At the same time, acceptor or donor photobleaching or photoswitching (42) could cause $F_2^{Ad}$, ρ^{ex, A}, and ρ^{ex, D} to change relative to the absence of photochemical effects. Specifically, if the excitation at the first wavelength leads to photobleaching of a fraction of donors or acceptors, the apparent concentration of the molecules detected upon excitation at the second wavelength scan decreases. To take these photochemical effects into account, for pulsed excitation (i.e., Π_D = Π_Da = Π_A = Π_Ad = 1), using Eq. 32b, we rewrite $F_2^{Ad}$ in Eq. 43′ as

$$F_{2,pc}^{Ad}={\epsilon }_2^A{Q}^A{\left[A\right]}_{T,2}+{\epsilon }_2^D{E}_{app}{Q}^A{\left[D\right]}_{T,2}={\epsilon }_2^A{Q}^A{\left[A\right]}_{T,1}{\alpha }^A+{\epsilon }_2^D{E}_{app}{Q}^A{\left[D\right]}_{T,1}{\alpha }^D,$$ (48)

where the subscript “pc” stands for “photochemical” effects (which may include photobleaching and photoswitching), α^A = [A]_{T, 2}/[A]_{T, 1}, and α^D = [D]_{T, 2}/[D]_{T, 1}.

Two situations are commonly encountered experimentally, as discussed next.

• 1)
  When the determination of the ρ^{ex, A} and ρ^{ex, D} values is done using the same sample (e.g., cells), these quantities too will be affected by photobleaching (or photoswitching), as illustrated by the following forms of (40b), (40a) for the case of pulsed excitation:

  $${\rho }_{pc}^{ex,D}\equiv \frac{{\epsilon }_1^D}{{\epsilon }_2^D}\frac{1}{{\alpha }^D},$$ (49a)

  $${\rho }_{pc}^{ex,A}\equiv \frac{{\epsilon }_1^A}{{\epsilon }_2^A}\frac{1}{{\alpha }^A},$$ (49b)

  which depend on α^A and α^D. By inserting (5a), (5b), (5c), (5d) and (49b), (49a) into Eq. 43′, it may be seen that α^A and α^D cancel out in Eq. 43′ and this equation still reduces itself to E′_app = E_app, as is desirable. When using this combination of FRET measurements and calibration, therefore, correct results are expected, even when using the more experimentally unstable equation (Eq. 43′).
• 2)If, by contrast, the FRET measurements are performed on cells, where the molecules are less free to diffuse and therefore more susceptible to photobleaching or photoswitching, whereas the determination of ρ^{ex, A} and ρ^{ex, D} is based aqueous solutions, in which molecules diffuse freely and therefore are less prone to photobleaching or photoswitching, the results obtained from Eq. 43′ will depend on α^A and α^D. In this case, the final computed FRET efficiency will be affected by photobleaching or photoswitching. This combination of FRET measurements and calibration methods may explain why the validity of the kinetic theory of FRET could not be confirmed in some of the previously published work (43).

It is also possible that the effect of photobleaching is seen even during the first excitation scan, which could in principle affect the output of both Eqs. 38 and 43′. Therefore, Eq. 43′ may be affected by additional systematic errors, depending on the particular type of calibration used.

The only systematic error affecting Eq. 38 that we could conceive of is the possibility for the acceptors to be directly excited by light to a small extent. This is probably why in a previous publication (30), any discrepancy between experiment and the kinetic theory of FRET was found to be small (∼4%, see appendix C in that reference) compared to the discrepancy of ∼15% registered in earlier work when an equation similar to Eq. 43′ and the above calibration method 2 was used.

Optimization of the protocols for determination of molecular concentrations

Our analysis above has already revealed optimal strategies for determination of the FRET efficiency using appropriate excitation wavelengths, equations, and calibration strategies that are both simple enough and free from systematic errors. At this point, it remains to identify robust methods for determining the total concentrations of molecules.

One method involves determining the donor concentration from a first scan of the sample using an excitation wavelength that does not produce any significant excitation of the acceptor and determining the acceptor concentration from a second scan at an excitation wavelength that excites the acceptor most efficiently. A theoretical expression for the donor concentration in the case of pulsed excitation light in the absence of acceptor direct excitation is obtained by combining Eqs. 35a and 37 as

$${\left[D\right]}_T=\frac{1}{{\mathcal{E}}_1^D{Q}^D\mathit{\xi }}\left(F_1^{Da}+\frac{Q^D}{Q^A}{F}_1^{Ad}\right),$$ (50)

in which the theoretical brightness (i.e., ${\mathcal{E}}^D{Q}^D$) has been multiplied by an instrumental factor, ξ, that accounts for detection laser excitation power, detection sensitivity, etc. An expression for the acceptor concentration is given by the equation

$${\left[A\right]}_T=\frac{1}{{\mathcal{E}}_2^A{Q}^A\mathit{\xi }}\left(F_2^{Ad}-F_1^{Ad}\frac{1}{{\rho }^{ex,D}}\right),$$ (51)

which was obtained by dividing Eq. 41′ by the effective acceptor brightness (including the instrumental factor ξ) and assuming that ρ^{ex, A} = 0. The total concentration in this case is obtained as the sum between the donor and acceptor concentrations.

The second method for determining the total concentration of donor and acceptor molecules has been suggested recently in a different context (28). In this method, the second excitation wavelength is chosen such that the excitation rates of the donor and acceptor are equal (i.e., ${\gamma }_2^{ex,D}={\gamma }_2^{ex,A}$, which is equivalent to ${\mathcal{E}}_2^D={\mathcal{E}}_2^A$). With this, we obtain the following expression by dividing Eq. 39c by ${\mathcal{E}}_2^D{Q}^D$ and Eq. 39d by ${\mathcal{E}}_2^A{Q}^A$ and adding the resulting expressions side by side:

$${\left[D\right]}_T+{\left[A\right]}_T=\frac{1}{{\mathcal{E}}_2^D{Q}^D\mathit{\xi }}\left(F_2^{DA}+F_2^{AD}\frac{Q^D}{Q^A}\right).$$ (52)

For all equations in this paragraph, the effective brightness (${\mathcal{E}}^D{Q}^D\mathit{\xi }$ or ${\mathcal{E}}^A{Q}^A\mathit{\xi }$) may be determined experimentally using either calibration against fluorescent molecule solutions with known concentrations (12) or, more elegantly and precisely, using fluorescence fluctuation analysis (44, 45, 46) of cells expressing monomeric constructs (47).

Conclusions

We have derived equations expressing the fluorescence emission of acceptors and donors in the presence of FRET (i.e., (33d), (33e), (33a), (33b), (33c)) rigorously from the kinetic model of FRET using certain assumptions regarding the transition rates and probabilities of fluorescent molecules to be in their ground or excited sates. We have found that those assumptions are not obeyed automatically and require deliberate decisions by the experimentalist in using one expression or the other, which is equivalent to choosing different sample excitation and detection conditions. Under those same assumptions, some known as well as some previously unknown expressions are rigorously derived that link the FRET efficiency to experimentally measurable parameters, such as fluorescence lifetimes or integrated fluorescence intensities. Also, interestingly, it was found that in situations in which excitation is produced by CW sources, significant systematic errors are introduced in the computation of FRET efficiency as well as concentrations of molecules. By contrast, pulsed light sources, whether or not used in conjunction with temporal resolution for detection of the fluorescence, provide the means of extracting the values of all of these quantities free from significant systematic errors. Nevertheless, systematic errors are still possible if calibrations are not performed carefully or inadequate equations are used for given experimental conditions.

Based on this analysis, we are able to suggest an optimal strategy for quantitative FRET spectrometric investigations. In the case of no temporal resolution, the following procedure is recommended.

• 1)Use pulsed excitation to avoid systematic errors caused by the dependence of all equations on integrated probabilities (and, hence, on concentrations).
• 2)Use spectral resolution and unmixing to separate donor and acceptor signals from each sample scan.
• 3)Perform a “FRET scan” of the sample at an excitation wavelength at which the acceptor is minimally excited by light while the donor is excited maximally and use Eq. 38 to compute the FRET efficiency as well as the donor concentration (Eq. 42 with ρ^{ex, A} = 0). If there is any direct excitation of acceptors by light and low errors are essential, scan the sample at a second wavelength and use Eq. 43′ together with careful calibrations, as described in Avoiding Systematic and Random Errors in Eapp When Using Pulsed Excitation.
• 4)(a) Perform a “concentration scan” of the sample at an excitation wavelength at which mostly the acceptor is excited and use Eq. 41′, assuming again ρ^{ex, A} = 0, to compute the concentration of acceptors. The total concentration is computed as the sum of [D]_T and [A]_T.

  (b) Alternatively, perform a concentration scan at a wavelength at which the donors and acceptors are excited equally well (i.e., ${\mathcal{E}}_2^D={\mathcal{E}}_2^A$) and use Eq. 52 to compute the total concentration.

Some of the precautions outlined above have already been used to determine quaternary structures of proteins as well as the relative proportion of the differing structures using large numbers of acquired cellular images. When combined with certain experimental tools, this approach will open the way for combining FRET spectrometry with FRET stoichiometry measurements for each image pixel in the future (20, 29).

As suggested in the previous sections, it should also be possible to devise a FRET spectrometry method based on time-resolved measurements, in which analysis should be done by integrating rather than separating the fluorescence decay curves into different lifetimes. In that case, Eq. 31 would have to be used for calculation of the FRET efficiency, whereas molecular concentrations could still rely on the same equations used in the case of no temporal resolution. This idea remains to be tested experimentally in the future.

It should be also stated that, although most of our discussion above is inherently biased toward the kind of research problems of interest to this investigator, the equations derived for FRET efficiencies and concentrations are quite general and should be applicable to any FRET study. That includes not only mixtures of oligomers with different D and A proportions and D to A distances (20) but also dimers (or oligomers) with fixed proportions of D and A molecules and varying distances between them (31).

Editor: Jochen Mueller.