Breast Cancer Cells Adapt Contractile Forces to Overcome Steric Hindrance

Abstract

Cell migration through the extracellular matrix is governed by the interplay between cell-generated propulsion forces, adhesion forces, and resisting forces arising from the steric hindrance of the matrix. Steric hindrance in turn depends on matrix porosity, matrix deformability, cell size, and cell deformability. In this study, we investigate how cells respond to changes in steric hindrance that arise from altered cell mechanical properties. Specifically, we measure traction forces, cell morphology, and invasiveness of MDA-MB 231 breast cancer cells in three-dimensional collagen gels. To modulate cell mechanical properties, we either decrease nuclear deformability by twofold overexpression of the nuclear protein lamin A or we introduce into the cells stiff polystyrene beads with a diameter larger than the average matrix pore size. Despite this increase of steric hindrance, we find that cell invasion is only marginally inhibited, as measured by the fraction of motile cells and the mean invasion depth. To compensate for increased steric hindrance, cells employ two alternative strategies. Cells with higher nuclear stiffness increase their force polarity, whereas cells with large beads increase their net contractility. Under both conditions, the collagen matrix surrounding the cells stiffens dramatically and carries increased strain energy, suggesting that increased force polarity and increased net contractility are functionally equivalent strategies for overcoming an increased steric hindrance.

Introduction

Most cells that are able to adhere, spread, and migrate on a two-dimensional extracellular matrix (ECM) can also adhere, change shape, and migrate when embedded in a biopolymer network of suitable adhesiveness, stiffness, and network porosity. However, when cells migrate through a three-dimensional (3-D) matrix, they must overcome not only the adhesion forces, as in a two-dimensional environment, but also the resisting forces imposed by the surrounding matrix (1, 2). Resisting forces mainly arise from steric effects. This steric hindrance, in turn, depends on the matrix properties (pore size and fiber stiffness (1, 3, 4, 5, 6)) as well as cell properties (cell size and cell stiffness (4, 7, 8, 9, 10, 11)). Studying cell-generated forces as the cells migrate through an ECM with varying degrees of steric hindrance is important for a mechanistic understanding of numerous physiological and pathophysiological cell functions in health and disease that involve cell adhesion, shape changes, and migration, such as tissue formation during embryogenesis, tumor metastasis formation, or the homing of immune cells.

To investigate cell migration under varying degrees of steric hindrance, previous studies have changed the protein concentration of a 3-D biopolymer network (1, 3), the pore size (4, 12), or the network fiber stiffness (3). These studies have consistently found a decreased cell migration or invasion with increasing steric hindrance of the matrix. What is unknown, however, is whether cells can partially compensate for this increase steric hindrance, either by an increased generation of traction forces or by changes in force polarity, which both have been previously shown to be essential for 3-D cell migration (13).

Although it is possible to measure cell-generated forces in a 3-D biopolymer network, it is problematic to compare measurements from gels with different protein concentrations and hence pore size and fiber stiffness because this can drastically change the nonlinear behavior of the matrix (14). Moreover, an altered matrix protein concentration inevitably leads to altered adhesive ligand density (1). An alternative way to modulate steric hindrance is to stiffen the biopolymer fibers with low doses of glutaraldehyde (3), but this, in turn, lowers the proteolytic degradability of the matrix and may lead to changes in cell migration that are unrelated to effects of steric hindrance.

In this study, we follow an alternative approach: instead of changing the ECM properties, we alter the cell mechanical properties. To do so, we either increase the nuclear stiffness of breast cancer cells by overexpression of the nuclear protein lamin A (15) or we introduce into the cells polystyrene beads with a diameter larger than the average pore size of the ECM. Although both interventions may also cause secondary cellular responses that are difficult to predict, we argue that the ability to measure cell-generated traction forces and migration behavior under identical matrix conditions compensates for the potential disadvantages.

We find that increasing the steric hindrance by stiffening the nuclear lamina causes a significant decrease in migration speed, which is partially compensated by an increase in directional persistence and force polarity. The traction force magnitude is equal to control cells.

Increasing the steric hindrance by loading the cells with polystyrene beads causes a small decrease in cell speed and directional persistence. To compensate, these cells increase their traction forces but not their force polarity. Taken together, our data demonstrate that breast cancer cells independently adapt their traction forces and force polarity to compensate for an increased steric hindrance imposed by the surrounding matrix.

Materials and Methods

Cell culture

MDA-MB 231 cells (obtained from ATCC, Manassas, VA) are cultured in 75 cm² cell culture flasks with low glucose (1 g/L) Dulbecco’s modified Eagle’s medium (DMEM; Biochrom, Cambridge, UK) supplemented with 10% fetal calf serum (Greiner, Kremsmünster, Austria) and 1% penicillin and streptomycin at 37°C, 5% CO₂, and 95% humidity. For lamin-A-transfected cells, 1 μg/mL puromycin is added to the medium. Cells are passaged every second day using 0.25% trypsin/EDTA.

MBA-MD 231 Lam-A lentiviral transduction and immunoblot analysis

For generating MDA-MB 231 cells expressing enhanced green fluorescent protein (eGFP)-lamin A, lentiviral transduction is used as described in (12). In brief, HEK293T cells are co-transfected with the vectors pMD2.G, psPAX2, and pLVX containing the coding sequence of lamin A N-terminally fused to eGFP using Lipofectamine LTX (Invitrogen, Carlsbad, CA). The cell culture supernatant is collected daily and replaced with fresh DMEM for the next 4 days. The collected medium containing assembled virus particles is pooled and filtered through 0.45-μm pores, supplemented with 8 mg/mL polyberene and added to MDA-MD 231 cells for 18 h. Starting from day 2 after lentiviral infection, cells are selected using 1 μg/mL puromycine. Previous studies demonstrated that after transduction, expression of eGFP-lamin A is detectable in 95% of cells (12). Total average lamin A levels increased by 200% above endogenous lamin A levels (8, 12, 15), and cell stiffness after transfection increased by 47% above the stiffness of control cells (from 560 to 820 Pa), as estimated from the increase of transit time when the cells are flushed through 5-μm microconstrictions (16).

Preparation of 3D collagen hydrogels

To prepare 1.2 mg/mL collagen type I hydrogel, we mix 1.2 mL of rat tail collagen (collagen R, 2 mg/mL; Matrix Bioscience, Mörlenbach, Germany), 1.2 mL bovine skin collagen (collagen G, 4 mg/mL; Matrix Bioscience), 270 μL NaHCO₃ (23 mg/mL), 270 μL 10× DMEM (Biochrom), and 43 μL NaOH (1 M) to adjust the pH to 10. The solution is then diluted with 3 mL of a mixture of one volume part NaHCO₃ (23 mg/mL), one part 10× DMEM, and eight parts distilled H₂O. All ingredients are kept on ice during the preparation process. 2 mL of the final collagen solution is pipetted in a 35-mm petri dish and polymerized in a tissue culture incubator at 37°C, 95% relative humidity, and 5% CO₂ for 1 h. After polymerization, 2 mL of complete cell culture medium is added to prevent dehydration of collagen gels (17).

Collagen gel mechanical properties

To quantify the traction-force-induced deformations of the biopolymer network during cell migration, we implement the finite element approach described in (14). Finite elements are randomly filled with one-dimensional collagen fibers that buckle under compressive strains according to a buckling strain scale d₀ and display a constant stiffness K₀ during extension up to a linear strain range L_S, beyond which the stiffness increases exponentially with a strain scale d_S. For a 1.2 mg/mL collagen gel, these four material parameters are K₀ = 1645 Pa, d₀ = 0.00032, L_S = 0.0075, and d_S = 0.033, as estimated from the stress versus strain relationship measured with a cone-plate rheometer and from the vertical gel contraction under uniaxial stretch (14) (Fig. S9).

3-D cell migration assays

To study the invasiveness of individual cells in 3-D collagen gels, 30,000 cells are mixed with 2.5 mL 1.2 mg/mL collagen solution and incubated for 4 h to ensure that cells have attained their typical elongated shape within the collagen gel. Subsequently, we image z-stacks with a z-distance of 10 μm, using a 10× objective with numerical aperture 0.30, a time interval of Δt = 5 min between subsequent stacks, and a total duration of 24 h. We automatically track the x/y-position of all cells in the image series based on their characteristic intensity profile in the minimal and maximal intensity projections of the z-stacks using a custom Python script. All three cell conditions (MDA-control, MDA-lamA, and MDA-beads) are imaged in parallel.

For the analysis of the resulting trajectories, we only consider cells that have been tracked for at least 4 h. A cell is classified as motile if it moves away from its initial position by at least 20 μm during the 24-h observation period. For statistical testing of the motile fraction, we use a χ-square test of independence of variables in a contingency table.

Cell speed s of a trajectory is computed as the mean absolute difference between two subsequent cell positions $\overrightarrow{r}\left(t\right)$ recorded at a time interval Δt of 5 min:

$$s=\langle \overrightarrow{v}{\left(t\right)}_t\rangle ={\langle \frac{\left|\overrightarrow{r}\left(t\right)-\overrightarrow{r}\left(t-\mathit{\Delta }t\right)\right|}{\mathit{\Delta }t}\rangle }_t$$

To quantify the directional persistence of migrating cells, we compute the mean cosine of the turning angles between two subsequent 30-min trajectory segments:

$$q={\langle \cos \left({\varphi }_t\right)\rangle }_t={\langle \text{atan}2\left(v_y\left(t\right)-v_y\left(t-\mathit{\Delta }t\right),v_x\left(t\right)-v_x\left(t-\mathit{\Delta }t\right)\right)\rangle }_{\text{t}}$$

Here, atan2 denotes the multivalued inverse tangent function. A value of q = 0 indicates diffusive (Brownian) motion, a positive value indicates persistent movement, and a negative value indicates antipersistent movement.

Finally, we determine the invasion distance of individual cells by the mean distance that each motile cell migrates within 1 h.

3-D force microscopy assay

15,000 cells are mixed with 1 mL unpolymerized collagen solution and incubated for 12 h before experiments. To compute the force-induced deformations of the biopolymer network, the collagen fibers are imaged with confocal reflection microscopy using a 20× dip-in water-immersion objective with numerical aperture 1.0. One image stack is recorded before cell forces are relaxed with 2 μM cytochalasin-D, and a second image stack is recorded 30 min after cytochalasin-D addition (Fig. 2, A–D). The first image stack represents the deformed state of the matrix, whereas the second image stack represents the undeformed force-free configuration of the matrix.

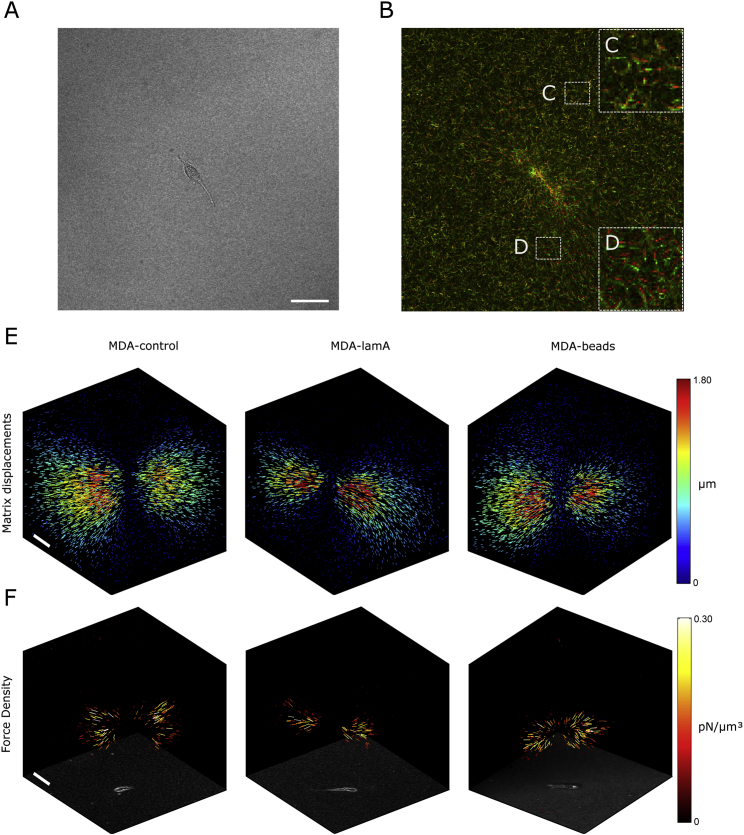
Figure 2.

3-D cell forces of MDA-MB 231 cells in collagen. (A) A bright-field image of an MDA-MD 231 breast carcinoma cell migrating within the collagen gel. (B) An overlay of confocal reflection images of collagen fibers before (red) and after (green) cell relaxation with cytochalasin-D. Enlarged section of two regions with small (C) and large (D) deformations. (E) 3-D matrix displacement field and (F) 3-D force density maps of a control cell (left), lam-A-overexpressing cell (middle), and a cell with a 5-μm polystyrene bead (right). Marker length and color indicate the magnitude of the displacement and force vectors. The bottom face shows a bright-field maximum intensity z-projection of the gel volume. Scale bars, 50 μm. To see this figure in color, go online.

To compute cell forces, we follow the approach described in (14). First, the displacement field of the collagen network between the deformed and the undeformed image stack is measured using a particle image velocimetry algorithm. Second, an unconstrained force reconstruction algorithm is used to calculate the cell forces. To this end, the matrix volume is tessellated and subdivided into a mesh of small (7.5 μm) finite elements of tetrahedral shape. For each tetrahedron, the constitutive equations that describe the relationship between the forces at the four nodes of the tetrahedron and the stresses and deformations are computed numerically. An iterative method is then used to modify the nodal forces of all finite elements until the measured and calculated matrix displacements match.

Cell shape-morphology analysis

Cell aspect ratio is computed from maximal intensity projections of bright-field image stacks. From the image projection, we calculate the aspect ratio as the distance between the two points of the cell outline with the largest separation (major axis length), divided by the largest cell dimension found anywhere perpendicular to the long axis (minor axis length).

Internalization of latex beads

For increasing the steric effects imposed by the matrix, MDA-MB 231 cells are loaded with 5-μm-diameter nondegradable carboxylated polystyrene beads that are larger than the average pore size of 3.8 μm for a 1.2 mg/mL collagen gel (3, 12). The network pore size was evaluated using the covering radius transformation of confocal image stacks of the collagen gel as described in (16, 18). The pore size distribution p(r) follows a Rayleigh distribution (16), indicating that 74% of the network pores of a collagen gel are smaller than the bead size of 5 μm and thus cause steric hindrance.

2 × 10⁵ beads (Thermo Fisher, Waltham, MA) are sonicated, added to MDA-MB 231 cells grown in a 35-mm cell culture dish, and incubated overnight (19, 20, 21). Cells are rinsed twice to remove unbound beads, harvested with 0.5% trypsin/EDTA, mixed with unpolymerized collagen, and cultured for another 12 h before force measurements or for 24 h single-cell invasion experiments. For cell force and invasion assay analysis, we selected only cells carrying exactly one bead.

Statistical analysis

Unless otherwise noted, all experimental results are taken from at least three independent experiments. Differences between measurements are considered statistically significant at p ≤ 0.05 using Student’s two-tailed t-test assuming unequal variances, including outliers.

Results

Response of cell invasiveness to altered steric hindrance

We hypothesize that cells with higher cell stiffness experience more steric hindrance when migrating through confining matrix pores. To explore how internal mechanical properties of cells influence cell invasiveness, we modulate the stiffness of MDA-MB 231 breast cancer cells with two different approaches. The first approach relies on overexpression of the nuclear protein lamin A using lentiviral transduction, which leads to an increase in overall cell stiffness by 47% (8, 12, 15, 16). In a second approach, we increase the apparent cell rigidity by binding or internalizing nondegradable 5-μm polystyrene beads. Polystyrene beads have been previously used to study remodeling processes of the cytoskeleton by tracking their spontaneous motion (19, 20, 21). MDA-MB 231 breast cancer cells readily internalize these beads. After 30 min of bead incubation, ∼70% of beads are internalized by the cells (21). To increase the fraction of internalized beads further, we incubate the cells with beads overnight. Fluorescent imaging of cells expressing tandem tomato-farnesyl for labeling the cell membrane confirms that the beads are internalized (Fig. S10).

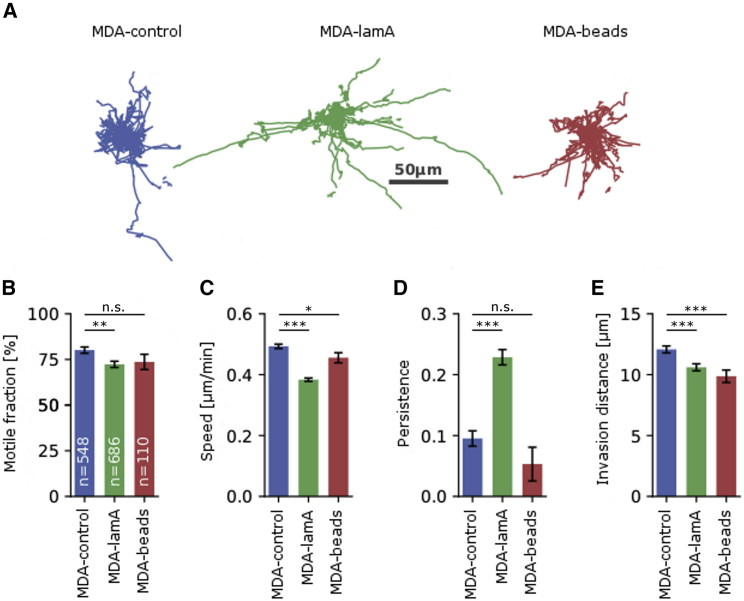
To quantify cell invasiveness, we track the movements of individual cells embedded in 1.2 mg/mL collagen gels over 24 h (Fig. 1 A). The resulting trajectories are classified into motile and nonmotile cells based on whether a cell moves away from its original position by more than 20 μm within the 24-h observation period. We find that 80% of MDA-control cells are motile. The motile fraction decreases to 72% for MDA-lamA cells and 74% for MDA-beads cells (Fig. 1 B).

Figure 1.

Cell invasion. (A) 50 randomly selected trajectories over a time course of 4 h of control cells (left), lam-A-overexpressing cells (middle), and cells with 5-μm polystyrene beads (right). (B) Motile fraction of cells. The number of analyzed cells is noted in white. (C) Cell speed, measured between subsequent images (Δt = 5 min). (D) Directional persistence, measured on a timescale of 1 h. (E) Mean Euclidean invasion distance over the course of 1 h. ^∗p ≤ 0.05, ^∗∗p ≤ 0.01, ^∗∗∗p ≤ 0.001, χ-square test of independence of variables in a contingency table for motile fraction and Student’s t-test assuming unequal variances including the outliers for all other variables; n.s., not significant (p > 0.05). To see this figure in color, go online.

The migration speed of the motile cell fraction is decreased by 22% in MDA-lamA cells and by 8% in MDA-beads cells (Fig. 1 C). MDA-lamA cells compensate by an increased directional persistence, in contrast to the cells with internalized beads. Consequently, the mean invasion distance within 1 h of MDA-lamA and MDA-beads cells is decreased by 12 and 18%, respectively, compared to control cells. We conclude that increasing the steric hindrance has a surprisingly small effect on cell invasion, suggesting that cells are able to partially compensate.

Adaptation of contractile forces to altered steric hindrance

We next test whether cells can actively counteract steric effects by generating higher contractile forces. Cells of the three groups studied (MDA-control, MDA-lamA, and MDA-beads) are mixed with 1.2 mg/mL unpolymerized collagen. After initiating collagen polymerization, cells are allowed to migrate in the collagen gels for 12 h. Subsequently, we image the cell morphology as well as the collagen network around cells with confocal reflection microscopy before and after cell relaxation with cytochalasin-D (Fig. 2, A–D). Cellular forces are then computed (Fig. 2 F) from the local displacements field of the collagen matrix (Fig. 2 E) using a nonlinear, semiaffine, finite-element 3-D force reconstruction algorithm (14).

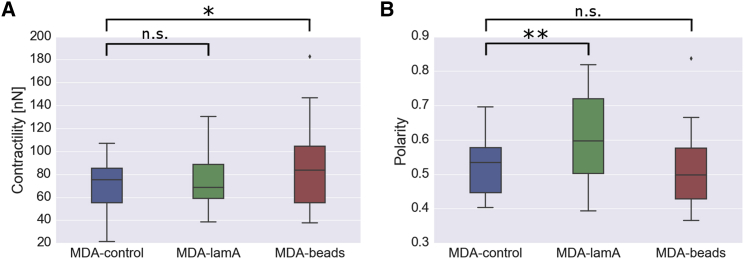
Force maps of cells from the three groups (Fig. 2) show inward-directed (contractile) forces that are highly polarized, but no obvious differences between the groups are visible (see Figs. S2–S7 for a complete set of the experiments). We therefore compute two robust scalar characteristics of the force field, namely cell contractility and force polarity (Fig. 3). Cell contractility measures the total magnitude of the projected force vectors in the direction of the force epicenter, which is the point at which the norm of the cross-products of the nodal forces and the vectors from their respective nodes to that point is minimal (14). Force polarity is the maximum (principal) dipole contractility divided by the total contractility. Thus, the force polarity quantifies the fraction of the contractile force that is oriented in a single direction. For a force dipole, the force polarity approaches unity, whereas for an isotropic spherical force field, the force polarity approaches 1/3.

Figure 3.

Influence of cell rigidity on magnitude and polarity of cell forces. (A) Total contractility and (B) force polarity of control cells (blue, n = 33), lam-A-overexpressing cells (green, n = 33), and cells with 5-μm polystyrene beads (red, n = 30) embedded in collagen gels. For all box plots, the central line indicates the median, the edges of the box denote the first and third quartiles, and the whiskers extend to the maximum and minimal value not considered as an outlier. Outliers are plotted as individual points. ^∗p ≤ 0.05, ^∗∗p ≤ 0.01, Student’s t-test assuming unequal variances including the outliers; n.s., not significant (p > 0.05). To see this figure in color, go online.

Total contractility is similar in MDA-control cells (70.2 ± 3.5 nN, mean ± standard error) and MDA-lamA cells (72.1 ± 4.3 nN) but is significantly (p < 0.05) increased in MDA-beads cells (85.4 ± 6.2 nN) (Fig. 3 A). By contrast, force polarity is similar in MDA-control cells (0.53 ± 0.01, mean ± standard error) and MDA-beads cells (0.51 ± 0.01) but is significantly (p < 0.05) increased in MDA-lamA cells (0.61 ± 0.02) (Fig. 3 B). This increased force polarity is in line with the higher directional persistence during migration.

Taken together, these findings suggest that cells can compensate for an increased steric hindrance of the matrix by independently adjusting the magnitude and polarity of contractile forces.

Strain energy and matrix stiffening

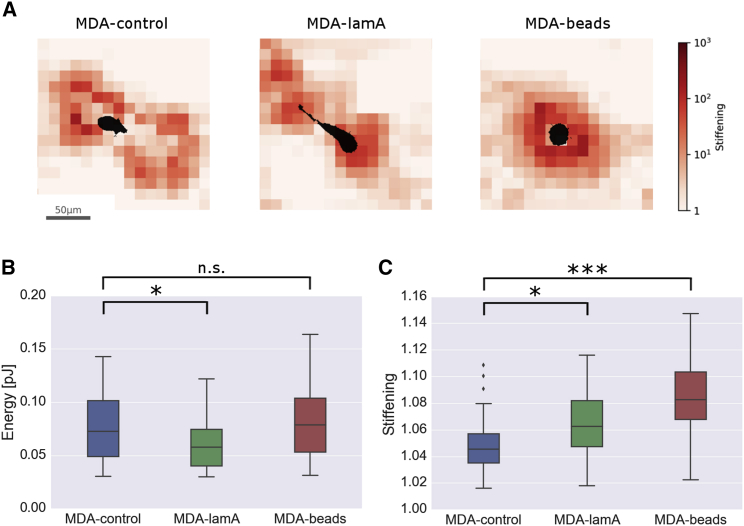
We next ask whether these compensatory strategies prompt the cells to invest different levels of energy for deforming the matrix. Deformation energy is calculated as the total elastic energy stored within in the imaged biopolymer network and released within 30 min after cells are treated with cytochalasin-D. Compared to MDA-control cells, MDA-lamA cells invest a significantly (p < 0.05) lower strain energy, whereas MDA-beads cells invest similar levels of strain energy despite their higher contractile forces (Fig. 4 B). Although we cannot measure the total energy expenditure of the cells, our finding of an equal or lower strain energy suggests that the generated forces are utilized more efficiently under conditions of higher steric hindrance.

Figure 4.

Influence of contractile forces on elastic strain energy and stiffness of the collagen matrix. (A) Strain-stiffening maps of the collagen network around an embedded control cell (left), lam-A-overexpressing cell (middle), and a cell with a 5-μm polystyrene bead (right). (B) Strain energy and (C) matrix strain stiffening of control cells (blue, n = 33), lam-A-overexpressing cells (green, n = 33), and cells with 5-μm polystyrene beads (red, n = 30) embedded in collagen gels. ^∗p ≤ 0.05, ^∗∗∗p ≤ 0.001, Student’s t-test assuming unequal variances including the outliers; n.s., not significant (p > 0.05). To see this figure in color, go online.

MDA-lamA cells achieve this higher efficiency with a more polarized force generation and hence by reducing “wasteful” forces perpendicular to the migration direction. In the case of MDA-beads cells, which have a similar force polarity but higher total forces compared to control cells, we hypothesize that the lower-than-expected strain energy may be a direct consequence of collagen fibers stiffening under higher forces. Fiber stiffening increases the alignment between collagen fiber orientation and cell-generated forces and generally allows for a more efficient conversion of tractions to movements.

To quantify the effective stiffening of the collagen matrix, we compute the second derivative of the total strain energy in response to an infinitesimal extra deformation of the cell, which gives the apparent matrix stiffness that the cell “feels.” This matrix stiffness is computed under two conditions: first, considering the full nonlinear collagen behavior, and second, considering only the linear and the buckling behavior of the collagen fibers but without any strain stiffening. The strain-stiffening value is the ratio of both stiffness values. It quantifies the additional overall matrix stiffness due to strain stiffening of the matrix.

We also compute the local map of strain stiffening of the collagen network around cells. From the strain vector of every node, we compute the matrix stiffness tensor and plot its magnitude averaged over a slice thickness of ±10 μm above and below the cell (Fig. 4 A). This value is then normalized by the median stiffness tensor magnitude within the imaged volume to quantify the local strain stiffening of the matrix. Note that the local matrix stiffening is much larger than the effective matrix stiffening that the cell “feels.” This is because stiffened matrix regions transmit cell deformations over large distances toward unstrained and thus softer matrix regions, which corresponds roughly to a serial arrangement of a stiff and a soft spring, with a total spring stiffness that is dominated by the soft spring.

No apparent structural changes can be observed in the collagen matrix for control cells, lamin-A-overexpressing cells, and cells with beads (Fig. S8). However, in support of our hypothesis, we find a significantly higher stiffening of the collagen matrix around MDA-beads cells compared to MDA-control cells (Fig. 4 C). Interestingly, the matrix around MDA-lamA cells, despite a lower strain energy value, also shows some additional stiffening, attributable to the larger principal component force aligned with the major cell axis (Fig. 4 A).

Effect of steric hindrance on cell morphology

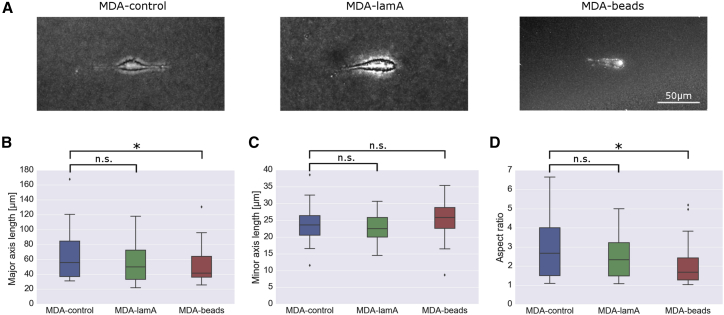
We next explore the role of cell shape during cell invasion within 3-D collagen gels. From bright-field images stacks of cells embedded in 1.2 mg/mL collagen gels after 12 h of culture, we quantify the maximum projected cell length (“major axis”), the largest cell dimension perpendicular to the major axis (“minor axis”), and the cell aspect ratio (the ratio of major axis/minor axis).

MDA-lamA cells show similar morphology compared to MDA-control cells (Fig. 5 A). This indicates that the higher force polarity seen in MDA-lamA cells does not originate from a more elongated cell shape but instead from an altered distribution of tractions across the cell surface. We also find a significantly shortened major axis and consequently lower aspect ratio in MDA-beads cells, but this does not translate into a lower force polarity, again pointing to an altered distribution of tractions across the cell surface (Fig. 5, B–D). In line with this interpretation, we find that the contractility and cell aspect ratio of individual cells under all three conditions show a weak negative correlation (Fig. S1; Supporting Materials and Methods, Note 1), indicating that the more elongated cells tend to generate slightly smaller contractile forces, but this correlation does not reach statistical significance in our data.

Figure 5.

Influence of steric hindrance on cell morphology. (A) Maximal intensity projection image of a control cell (left), lam-A-overexpressing cell (middle), and a cell with a 5-μm polystyrene bead (right) embedded on a 1.2 mg/ml collagen gel. (B) Major cell axis length, (C) minor cell axis length, and (D) aspect ratio of control cells (blue, n = 33), lam-A-overexpressing cells (green, n = 33), and cells with 5-μm polystyrene beads (red, n = 30) embedded in collagen gels. ^∗p ≤ 0.05, Student’s t-test assuming unequal variances including the outliers; n.s., not significant (p > 0.05). To see this figure in color, go online.

Discussion

In this study, we investigate how cells migrate through a collagen network and respond to changes in steric hindrance that arise from altered cell mechanical properties. We increase steric hindrance either by stiffening the nucleus by overexpression of the nuclear envelope protein lamin A or by introducing 5-μm polystyrene beads into the cells that are larger than the average network pore size of 3.8 μm. Although both interventions may also cause secondary cellular responses that are difficult to predict, we argue that the ability to measure cell-generated traction forces and the migration behavior under identical matrix conditions compensates for the potential disadvantages.

Under both interventions, the percentage of motile cells within the collagen gel remains high (>70%). Although the mean invasion distance of the stiffened cells is decreased by up to 18%, these findings suggest that a substantial increase in steric hindrance does not prevent cells from invading the surrounding matrix.

3-D force measurements reveal two distinct compensatory mechanisms. Under conditions of a moderately increased steric hindrance, as in the case of MDA-lamA cells, the cells increase the force polarity and thus employ their contractile forces more efficiently. Under conditions of greatly increased steric hindrance as in the case of MDA-beads cells, the cells increase their contractile forces. In addition, this force increase is accompanied by a reduction of the cell aspect ratio and force polarity back to control levels.

The elastic strain energy stored in the collagen matrix is not increased in cells carrying beads and is even reduced under conditions of increased nucleus stiffness. Instead, we find a more pronounced collagen matrix stiffening with increasing levels of steric hindrance in the vicinity of the cells, in line with previous results (22, 23). This matrix stiffening is the combined effect of an altered contractile force magnitude, force polarity, and force vector distribution.

Importantly, matrix stiffening does not arise from outward-directed squeezing forces as the cells attempt to migrate through the confining pores of the matrix. Pore widening leads to a dramatic stiffening of the circumferential collagen fibers that constitute the pore, but this stiffening is highly localized and not detectable at the resolution of our measurements (14). Rather, the observed matrix stiffening arises exclusively from the cell-generated inward-directed contractile forces. As the collagen fibers that carry the contractile stress are stretched, they cause an anisotropic and long-range stiffening of the collagen matrix that we are able to detect with our method (14). We argue that this force-induced matrix stiffening, because it is not causing any further steric hindrance, promotes cell migration and hence is an important mechanism that cells employ the counteract steric hindrance.

Conclusions

In summary, our data demonstrate that cells can compensate for an increased steric hindrance of a dense 3-D network and maintain their invasive behavior. The parameter repertoire of cells for this compensation includes alterations in cell shape, force magnitude, and force distribution. The specific strategy of individual cells for adjusting those parameters, however, appears to depend on individual cell mechanical properties and local mechanical properties as well as structural properties of the matrix.

Author Contributions

M.C. and B.F. designed the experiments. M.C. and N.C.G. performed the experiments. M.C., C.M., and A.B. analyzed the data. R.C.G. and C.M. helped with measurements. M.C., C.M., J.M.G., and B.F. wrote the manuscript.

Editor: Katharina Gaus.

Supporting Citations

References (24, 25) appear in the Supporting Material.