Flagellar ultrastructure suppresses buckling instabilities and enables mammalian sperm navigation in high-viscosity media

Abstract

Eukaryotic flagellar swimming is driven by a slender motile unit, the axoneme, which possesses an internal structure that is essentially conserved in a tremendous diversity of sperm. Mammalian sperm, however, which are internal fertilizers, also exhibit distinctive accessory structures that further dress the axoneme and alter its mechanical response. This raises the following two fundamental questions. What is the functional significance of these structures? How do they affect the flagellar waveform and ultimately cell swimming? Hence we build on previous work to develop a mathematical mechanical model of a virtual human sperm to examine the impact of mammalian sperm accessory structures on flagellar dynamics and motility. Our findings demonstrate that the accessory structures reinforce the flagellum, preventing waveform compression and symmetry-breaking buckling instabilities when the viscosity of the surrounding medium is increased. This is in agreement with previous observations of internal and external fertilizers, such as human and sea urchin spermatozoa. In turn, possession of accessory structures entails that the progressive motion during a flagellar beat cycle can be enhanced as viscosity is increased within physiological bounds. Hence the flagella of internal fertilizers, complete with accessory structures, are predicted to be advantageous in viscous physiological media compared with watery media for the fundamental role of delivering a genetic payload to the egg.

1. Introduction

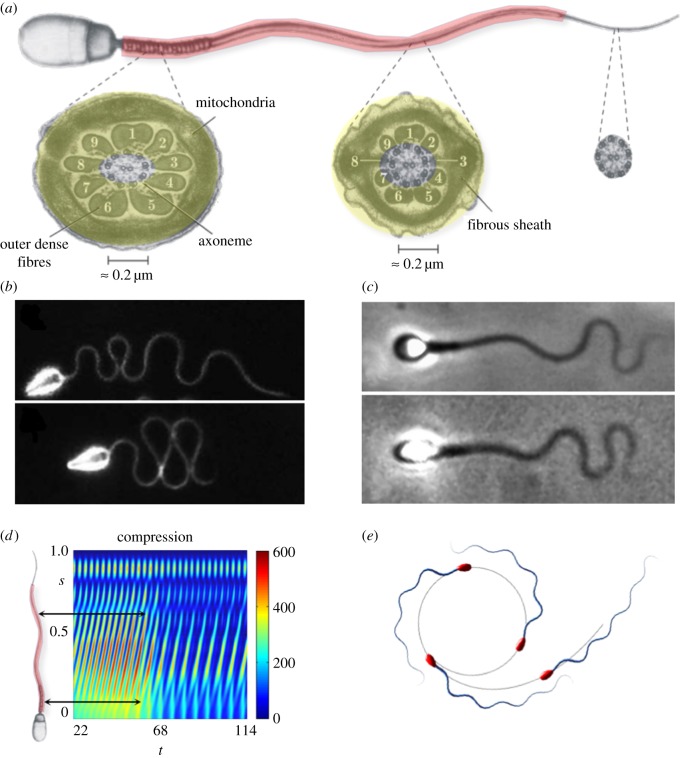
The mammalian sperm flagellum differs crucially from the simplest flagellar axonemes found in nature [1,2]. In addition to the intricate 9 + 2 axonemal scaffolding of the simple structure, each of the nine concentric axonemal microtubule doublets is attached to an outer dense fibre (ODF), forming a complex known as the 9 + 9 + 2 flagellum [3,4], as depicted in figure 1a. These ODFs consist of highly condensed, modified intermediate cytoskeletal filaments strengthened by disulfide linked keratin proteins, and taper along the flagellum length, terminating prior to the distal end. The 9 + 9 + 2 complex is further surrounded by a proteinaceous keratin-like material, which forms the fibrous sheath (FS) that provides two further longitudinal columns that are diametrically opposite and also taper along the flagellum, from the mid-piece to the principal piece, in effect structurally replacing two of the ODFs at the principal piece [2–4] (figure 1a). In addition, the mammalian flagellum is proximally sheathed by mitochondria in the mid-piece, and all of this flagellar structure is enveloped by a cell membrane.

Figure 1.

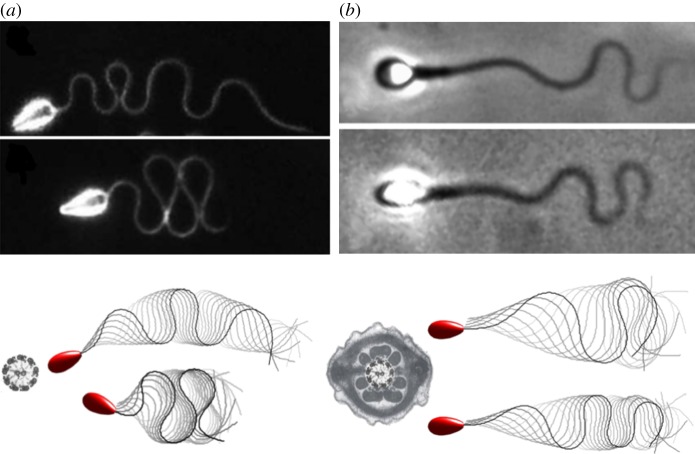
A comparison between mammalian sperm and the naive axonemal flagellum. Reprinted from [2,3] with permission from Elsevier. (a) A mammalian flagellum, depicting the additional reinforcing structures (red shading) and cross-sections of the mid-piece, characterized by the presence of nine outer dense fibres exterior to the axoneme and a fibrous sheath (yellow shading); all reinforcing fibres gradually taper along the flagellum, ending prior to the distal tip of the sperm. (b) Wave-compression and symmetry-breaking buckling instabilities in a high-viscosity methylcellulose solution for sea urchin sperm, which possess a flagellum without accessory structures of length approximately 42 μm; reproduced/adapted with permission from [11]. (c) Human spermatozoa, with reinforcing accessory structures on a flagellum of length approximately 50 μm, swimming in a similar highly viscous methylcellulose solution, which highlights a suppression of buckling instabilities; reproduced with permission (licence no. 4543770361396) from [10]. (d) Modelling predictions for the non-dimensional absolute compression, as a function of time t and arclength s for a naive flagellum undergoing buckling instability in high-viscosity medium [12]. The predicted transition can cause high curvatures and asymmetric waveforms, inducing circular swimming paths, depicted in (e), with a smaller circular radius for spermatozoa with larger heads. Note that (d) shows that high elastohydrodynamic internal compression is predicted at regions where the ultra-structural components are larger in mammalian flagella (black arrows in (d)). Plots (d,e), have been adapted from the simulations in [10]. (Online version in colour.)

Despite the mechanical significance of the ultrastructural flagellar components exhibited by mammalian sperm, little is known about their biological function nor the evolutionary pressures that led to these critical flagellar adaptations [4]. Since the first electron micrograph observations, it has been conjectured that the ultrastructural complex is necessary to provide the structural and mechanical support to stabilize the long flagella observed in most mammalian spermatozoa [2,3,5–9]. In particular, Lindemann [9] hypothesized that only a reinforced flagellum would be capable of harnessing the increased power from the larger number of molecular motors present in a long flagellum, which is especially relevant for motility within the highly viscous fluids of the mammalian female reproductive tract [10].

Such ideas are reinforced by experimental observations of sea urchin sperm, which possess flagella that consist of a simple axoneme with no additional ultrastructure [11]. In particular, when migrating in a high-viscosity methylcellulose solution with a similar viscosity to cervical mucus in the mammalian reproductive tract [10], such sperm reveal a rich flagellar dynamics (figure 1b and [11]), consistent with theoretical predictions of flagellar buckling instabilities [12]. Woolley & Vernon [11] further reported symmetric wave-compression behaviour, as also illustrated in figure 1b, and even more extreme levels of flagellar wave confinement if the head is attached to the coverslip, indicating sensitivity to dynamical constraints of the sperm head. Elastohydrodynamic systems are well known for their sensitivity to boundary conditions [13,14]. Indeed, nonlinear flagellar instabilities [10] are dramatically changed upon different end conditions, from fixed to free sperm head constraints. In particular, the magnitude of the symmetry-breaking events is highly dependent on the head size of free swimming spermatozoa, where tight circular swimming trajectories are associated with large head sizes, as depicted in figure 1e. By contrast, a very distinct behaviour is observed for human spermatozoa migrating in methylecellulose solutions of similarly high viscosity [10], as depicted in figure 1c, where the flagellar waveform is characterized instead by a smooth flagellar meandering envelope with a gradual increase of the wave amplitude along the flagellum. In particular, the human sperm flagellum responds very differently to viscosity increases compared with sea urchin. This may be observed by contrasting figure 1b with figure 1c. The latter highlights how the ultrastructural components of the mammalian flagellum are likely to have a major impact on the flagellar waveform, and thus the cell swimming behaviour in high-viscosity media.

Despite such observational evidence for the structural significance of accessory structures on flagellar bending propagation and modulation [4,10,11], their influence on the swimming behaviour of mammalian spermatozoa has been markedly overlooked in the literature. In the inaugural theoretical study, Lindemann and colleagues [8,9] modified the geometric clutch model [15] to incorporate the effect of accessory structures, by assuming a linear tapering of the elastic stiffness along the arclength for immobilized sperm cells. The model successfully predicted a reduction in the maximum flagellar curvature caused by the additional stiffness, together with a qualitative agreement for bull sperm experiments. In 2007, Riedel et al. [16] investigated the effects of perturbative, and thus small, structural inhomogeneity, via a linear decay of the bending rigidity. In particular, several existing models incorporating molecular motor coordination dynamics [15,17,18] were compared with the flagellar beating of bull spermatozoa. A satisfactory fitting was reported for the self-organization model with a load-dependent detachment rate of motors [18,19], if the variation of the elastic stiffness along the flagellum is negligible. The model curve fitting was not significantly improved by the flagellar tapering of the bending stiffness [16]. This suggested that the flagellar ultrastructural components may play a minor role in shaping the flagellar waveform at the perturbative level, and thus at the leading linear-order approximation considered. More recently, the role of temporal nonlinearities arising from the second harmonics of the flagellar beat was also shown to contrast very well with experiments, without recourse to the spatial structural inhomogeneity present along the human sperm flagellum [20]. These results are, however, in contrast with estimates from videomicroscopy experiments [4] for the distribution of hydrodynamic, elastic and internal sliding bending moments, which did not treat flagellar mechanical heterogeneity as a perturbation, nor was the flagellar beat truncated in the frequency domain [4]. In another empirical investigation, Lindemann and co-workers [21,22] estimated the internal sliding forces by considering an exponential decay of the flagellum stiffness. An approximately constant magnitude of the sliding force along the arclength was reported, agreeing with [4]. The flagellar elastic tapering was equally observed to influence the beating pattern of hyperactivated mammalian sperm [23], which was biochemically regulated within a model assuming a significant varying tensile stiffness. To date, theoretical investigations focusing on the effects of ultrastructural flagellar apparatus on sperm swimming in high-viscosity fluids are still lacking in the literature.

Here, our fundamental aim is to extend the elastohydrodynamic formulation presented in Gadêlha et al. [12] to study the mechanical role of accessory flagellar structures and their tapering in mammalian spermatozoa (figure 1a). Hence we investigate the impact of the flagellar bending stiffness decreasing monotonically and significantly with arclength for a virtual model of a free swimming human sperm. In particular, we will explore the observation highlighted in [12] that the ultrastructural components reinforce regions along the flagellum where high compression is expected, as illustrated in figure 1d. In the absence of flagellar reinforcement, this compression mechanics is predicted to subsequently induce asymmetric waveforms and circling trajectories, as shown in figure 1e. Hence we explore the consequences of flagellar reinforcement by accessory structures for waveform formation and cell motility in light of such mechanics, together with a consideration of how the underlying model dynamics is altered by the heterogeneity of the structural mechanics.

2. Flagellar ultrastructure elastohydrodynamic formulation

To proceed, we generalize the planar sliding filament mechanism [12,16,17,19,24–31] to incorporate the role of tapering in the accessory flagellar structures of mammalian sperm cells. The model axoneme filaments are represented by a pair of parallel, planar elastic Euler–Bernoulli rods, depicted in figure 2a, and associated with a reinforcing structure, represented by the light shading. The model filaments are assumed to be homogeneous, inextensible and separated by a constant gap space b, which corresponds to the axoneme diameter. Dynein motors induce active sliding stresses along the axoneme, thus inducing a relative sliding couple acting on the model axonemal filaments and the paired ultrastructural components. However, at the connecting piece of the sperm head junction, the axonemal filaments are highly constrained [11] and we assume no interfilament sliding is permitted at this point; thus the filaments bend due to the dynein couples, which is the basis of the sliding-filament mechanism.

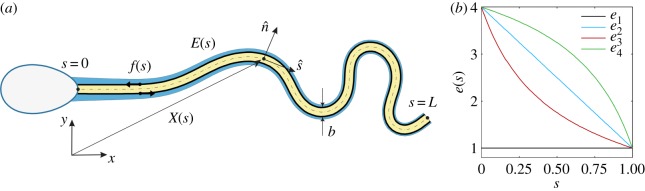
Figure 2.

A schematic of the sliding filament mechanism modified by the ultrastructural components of mammalian spermatozoa. Relative to a laboratory fixed frame $\{\hat{\mathbf{x}},\hat{\mathbf{y}}\}$, the vector X(s, t) describes the position of the flagellum neutral line (dashed curve) at time t. The internal shear force f(s, t) is acting tangentially and in opposite directions on each sliding filament (solid black arrows) within the axoneme (light yellow shading) with diameter b, with the flagellar reinforcing structure given by the light blue shading. Note that the relative spatial extents of the shaded regions are not to scale. The reinforcing structures are paired with each sliding filament, with a spatial heterogeneity that is captured by an effective elastic stiffness E(s), which monotonically decays with the arclength s. (b) Tapering functions, as discussed in §2.2: (i) e₁, represents the absence of additional structures, (ii) e₂, a linear taper [8,9], (iii) e₃, a cotangent taper, corresponding to the qualitative trend in flagellum stiffness measurements [21,22], and (iv) an inverse cotangent taper, relative to the function e₂. (a) Human sperm model; (b) tapering function. (Online version in colour.)

We describe the position of the flagellum, relative to the laboratory frame of reference, by its neutral line X(s, t) (figure 2a), noting that t is time and s denotes the distance along the flagellum with 0 ≤ s ≤ L, where L is the filament length. The local flagellum coordinate system is represented as an orthonormal pair with a positive orientation $\{\hat{\mathit{s}},\hat{\mathit{n}}\}$, where $\hat{\mathit{s}}={\mathbf{X}}_s\equiv \mathrm{\partial }\mathbf{X}/\mathrm{\partial }s$ is the tangent vector and $\hat{\mathit{n}}$ is the vector normal to the flagellum centreline (figure 2a). The flagellar dynamics is inertialess to an excellent approximation and is governed by balancing the viscous drags and couples per unit length with the internal forces and torques, both structural and dynein induced, per unit length.

We generalize the elastohydrodynamic formulation presented in [12] by incorporating the effect of the ultrastructural components, captured by the effective elastic stiffness E(s) that varies along the arclength s. Non-dimensionalizing with respect to the length scale L, time scale ω⁻¹ and force density E₀/L³, for a given beating frequency ω and a constant axonemal elastic stiffness E₀, the modified dimensionless elastohydrodynamic equation for a mammalian flagellum is given by

$$\begin{array}{rl}{\mathrm{Sp}}^4{\mathbf{X}}_t& =-{(e{\mathbf{X}}_{ss})}_{ss}-(\gamma -1)(e{\mathbf{X}}_s\cdot {\mathbf{X}}_{ssss}+2e_s{\mathbf{X}}_s\cdot {\mathbf{X}}_{sss}){\mathbf{X}}_s\\ & +(T{\mathbf{X}}_{ss}+\gamma T_s{\mathbf{X}}_s)+(f_s\hat{\mathit{n}}+\gamma f{\hat{\mathit{n}}}_s),\end{array}$$ 2.1

where the subscripts s and t, respectively, denote differentiation with respect to arclength and time. The sliding force density within the axoneme is given by f(s, t) and $\gamma ={\xi }_{\perp }/{\xi }_{\parallel }$ is the ratio between the perpendicular, ξ_⊥, and parallel, ${\xi }_{\parallel }$, fluid dynamic resistance coefficients. The function e(s) represents the flagellar bending stiffness relative to the axoneme stiffness, referred to here as the tapering function, as we discuss in §2.2 and in figure 2b. The dimensionless sperm-compliance parameter,

$$\mathrm{Sp}=L{\left(\frac{\omega {\xi }_{\perp }}{E_0}\right)}^{1/4},$$ 2.2

characterizes the relative importance of elastic forces to viscous drag [32]. The non-dimensional tensile force T(s, t) is the Lagrange multiplier for the inextensibility constraint, and it is implicitly determined by the identity ${\mathbf{X}}_s\cdot {\mathbf{X}}_s=1$,

$$\begin{array}{rl}\gamma T_{ss}-({\mathbf{X}}_{ss}\cdot {\mathbf{X}}_{ss})T& =-3e\gamma \hspace{0.17em}({\mathbf{X}}_{sss}\cdot {\mathbf{X}}_{sss})-e(3\gamma +1)({\mathbf{X}}_{ss}\cdot {\mathbf{X}}_{ssss})\\ & -e_s(7\gamma +2)({\mathbf{X}}_{ss}\cdot {\mathbf{X}}_{sss})-e_{ss}(2\gamma +1)({\mathbf{X}}_{ss}\cdot {\mathbf{X}}_{ss})\\ & -(\gamma +1)({\hat{\mathit{n}}}_s\cdot {\mathbf{X}}_s)f_s-\gamma \hspace{0.17em}({\hat{\mathit{n}}}_{ss}\cdot {\mathbf{X}}_s)f.\end{array}$$ 2.3

In the absence of structural components, the tapering function is a constant, e(s) = 1, and the governing equations are equivalent to earlier models [12,19,25,33]. A variety of derivations of active elastohydrodynamic systems have been presented in the literature, and thus these are not reproduced here. Instead, we direct the reader to excellent discussions and detailed derivations in [12,19,25,29,31,32,34–38] and their appendices.

Empirical estimates of the effective sliding moment density [4], resulting from the coupling between the dynein molecular motor activity and the passive cross-linking proteins within the flagellum [10,16,39–41], indicate that the observed flagellar waveform of human sperm migrating in high-viscosity fluid can be captured by a simple travelling wave of dynein contraction, with a single characteristic frequency and approximately constant magnitude along the flagellum length [10,42,43]. This in situ observation has motivated the use of a simple prescribed travelling wave to model the internal sliding density,

$$f(s,\hspace{0.17em}t)=a\cos (ks-t),0\le s<1,$$ 2.4

where a, k are, respectively, the dimensionless force amplitude and wavenumber. This allows the investigation of pure elastohydrodynamical effects arising from flagellar structural tapering, unbiased by further complications associated with dynein control. We further consider the distal end of the flagellum to be free from sliding forces owing to the lack of structural and motor elements at the very distal-most part of the flagellum [2,3,5,6,44].

2.1. Boundary conditions

The equations governing the flagellar dynamics are complemented by boundary conditions, in which either the movement of the flagellar endpoints is specified or a balance of forces and torques at each end is imposed [45]. In particular, at the distal boundary, s = 1, the flagellum is free to move and, therefore, the external contact forces and torques are zero, i.e.

$$\left.\begin{array}{rl}& 0={\mathbf{F}}_{\mathrm{ext}}=-e{\mathbf{X}}_{sss}-e_s{\mathbf{X}}_{ss}+f\hat{\mathit{n}}+T{\mathbf{X}}_s\\ \mathrm{and}& 0={\mathbf{M}}_{\mathrm{ext}}\times {\mathbf{X}}_s=e{\mathbf{X}}_{ss}.\end{array}\right\}$$ 2.5

At the proximal end, s = 0, the flagellum is driving the sperm head and thus experiences a non-dimensional viscous drag force, F_head, and moment, M_head, given by

$$\left(\begin{array}{c}{\mathbf{F}}_{\mathrm{head}}\\ {\mathbf{M}}_{\mathrm{head}}\end{array}\right)={\mathcal{L}}^4\mathcal{R}\left(\frac{r}{L},t\right)\left(\begin{array}{c}\mathbf{U}\\ \mathit{\Omega }\end{array}\right),$$ 2.6

where $\mathcal{L}=L{(\eta \omega /E_0)}^{1/4}$, and η denotes the fluid viscosity. $\mathcal{R}$ represents the dimensionless grand-resistance matrix for the sperm head, and depends on the head morphology, though we consider a ‘human-like’ sperm head geometry taken from [46]; in addition r denotes the distance between the head centre of mass and the sperm head–flagellum junction at s = 0. The torque and force balance at s = 0 yield the required boundary condition for the flagellum in terms of the motion of the sperm head from a specification of the head velocity field (U, Ω) via

$$\left.\begin{array}{cc}& {\mathbf{F}}_{\mathrm{head}}=e{\mathbf{X}}_{sss}+e_s{\mathbf{X}}_{ss}-f\hat{\mathit{n}}-T{\mathbf{X}}_s\\ \mathrm{and}& {\mathbf{M}}_{\mathrm{head}}\times {\mathbf{X}}_s=-e{\mathbf{X}}_{ss}-\hat{\mathit{n}}{\int }_0^{1}f(s^{\prime })\hspace{0.17em}\text{d}{s}^{\prime },\end{array}\right\}$$ 2.7

where the linear and angular velocity coupling with the basal flagellar movement via X_t|_s=0 = U and $[{\mathbf{X}}_s\cdot (\hat{\mathit{z}}\times {\mathbf{X}}_{ts})]{|}_{s=0}=\mathit{\Omega }$ closes the system.

2.2. Ultrastructure tapering function

The dimensionless tapering function e(s), depicted in figure 2b, captures the arclength variation of the bending stiffness associated with the tapering of the flagellar ultrastructure. These reinforcing components gradually decrease in size, terminating prior to the distal tip of the flagellum (figure 1). Here, the tapering function, e(s), measures the flagellar bending stiffness relative to the bending stiffness of the axoneme, E₀ = 0.9 × 10⁻²¹ Nm² [47–49], taken from demembranated sperm axonemal flagella of sea urchin Lytechinus pictus. Direct measurements of bending stiffness for human sperm flagella are not available; however, estimates can be inferred from rat sperm measurements, given the similarity of the ultrastructural components [4]. Mammalian flagellar structural properties are observed to allometrically scale with geometry, consistent with a fixed material [1], with the exception of the anomalous bull and guinea pig sperm. Since the cross-sectional area of the human mid-piece ODF is one-eighth that of the rat [1], the prediction for the bending stiffness of human flagellum yields 4 × 10⁻²¹ Nm² in this region, which is about four times the stiffness of the axoneme. Owing to the absence of quantitative studies on the elastic properties of accessory structures in other sections of the flagellum, we smoothly fitted the upper and lower bound of bending stiffness so that 1 ≤ e(s) ≤ 4. We considered four distinct cases for comparison purposes, illustrated in figure 2b: (i) a constant function e₁, representing the absence of additional structural components characteristic of simple flagellar axonemes [47–49], (ii) a linear decaying taper e₂, as used in [8,9,16], (iii) a cotangent decaying function e₃, motivated from spatially resolved data [21,22], and therefore the biologically relevant case, and finally (iv) an inverse cotangent decay e₄, representing the mirror image of e₃ relative to the linear function e₁.

2.3. Resistive force theory

One should note that the above framework captures the viscous interaction between the flagellum and the surrounding medium by resistive force theory (RFT), which approximates the local drag on a flagellar element by using the leading-order term of slender-body hydrodynamics [50]. Although RFT is theoretically only valid for sufficiently slender filaments that are of sufficiently low curvature and sufficiently far from intersection or self-intersection, its region of validity is still not entirely clear, given reasonable accuracy is regularly observed in comparison studies [14,32,34,51,52]. In particular, agreement with the high-precision microscopy imaging of bull sperm flagella is especially relevant in the context of this study [16,41].

Furthermore, RFT is popular in negotiating the complications of elastic and hydrodynamic interactions, including relaxational and forced dynamics of stiff polymers [13,14,29,51,53–58], as well as flagellar dynamics (e.g. [16–19,25,27–29,52,53,59–64]). While RFT is an approximation, its popularity in these previous elastohydrodynamical investigations arises from investigation objectives that are concerned with the overall mechanism rather than precise prediction. Under such circumstances, RFT is generally fit for purpose, and brings the additional convenience of mitigating the extreme numerical stiffness of elastohydrodynamic systems, especially in the presence of buckling instabilities, and we analogously inherit these motivations and considerations in implementing RFT for the current study.

2.4. Model parameter estimation

Numerical simulations were carried out for a free swimming cell with a ‘human-like’ sperm head geometry taken from [46], with dimensions 4.5 × 2.8 × 1.12 μm, and assuming a fluid dynamic resistance ratio γ = 2. For human sperm experiments [4,10,12], the sperm number may vary from Sp = 4, for a low-viscosity, watery, in vitro fertilization medium, up to Sp = 24, for a cervical mucus substitute, assuming Newtonian behaviour. We focus our attention on the consequences of a high-viscosity medium and thus the high sperm number regime Sp = 20 − 25, although we also display results for Sp as low as 5 for comparison.

Estimates for the sliding force density magnitude, a, may be inferred from measurements of the sliding bending moment density [4], extracted from spatial and temporal cinemicroscopy for a swimming cell, or from direct force measurements of molecular motors [65,66]. Indirect measurements of the sliding bending moment density extracted from human sperm indicate a maximum magnitude of 8 × 10⁻¹⁰ N, when the tapering of the structural components is taken into account. Taking the axonemal diameter b = 200 nm [21], with a maximum flagellar length of L = 60 μm, the upper limit of the dimensionless force density magnitude yields a = 3200. The inferred sliding bending moment density in [4] is also in agreement with direct measurements of the total force that a dynein motor can generate, which ranges between 2 and 8 pN per motor domain for, respectively, the inner arm axonemal dynein and cytoplasmic dynein [65,66]. In this context, we may also add the intrinsic contribution from the inter-doublet elastic resistance within the axoneme, observed to be 2 pN per structural repeat for a flagellar axoneme [67], which yields an average sliding force density magnitude of a = 2400. Here, we will allow the sperm-compliance parameter to vary in the range 5 ≤ Sp ≤ 25, with a sliding force density magnitude no larger than a = 2000, noting that the above values for a are estimates only, and the non-physiological behaviour of flagellar self-intersection can manifest once a is too large. For comparative purposes in the Results section, it is convenient to display a in terms of the sperm-compliance parameter; thus, hereafter, the force amplitude a is rescaled by E₀/ℓ³, where ℓ = L/Sp, also known as the penetration length [68].

Motivated by the observed flagellar waveform in different viscosities (figure 1 and [10,11]), we restrict our investigation to sliding force wavenumbers that are even multiples of π, k = 2π, 4π and 6π. Previous investigations have revealed that, in general, wavenumbers that are odd multiples of π do not generate realistic wave patterns [12]. The further property of a consistent wave amplitude without a significant decay as the waveform progresses depends on the interplay between k and Sp, and can be predicted from linear analysis [12,60]. Hence, we focus our investigation on the cases where a noticeable forward motion is achieved as a result of the flagellar beating. Typically, this corresponds to small (large) k for low (high) Sp, also in agreement with flagellar wavenumber viscous modulation in human spermatozoa [10]. Furthermore, the sliding force density magnitude a was gradually increased, within the range of validity above. This is necessary as higher force magnitudes are required for large amplitude motion when Sp is increased in elastohydrodynamic systems [12,31,68], though the relationship between the force and amplitude is nonlinear [12,32]. The described approach has allowed an investigation of the entire spectrum of beating patterns for each (Sp, k)-pair. For sufficiently large a, however, flagellar self-intersection occurs, even though the force magnitude is within its range of validity. In such cases, the numerical simulation is terminated and the upper limit of the force density is restricted so that flagellar self-intersection does not occur in the simulations.

3. Results

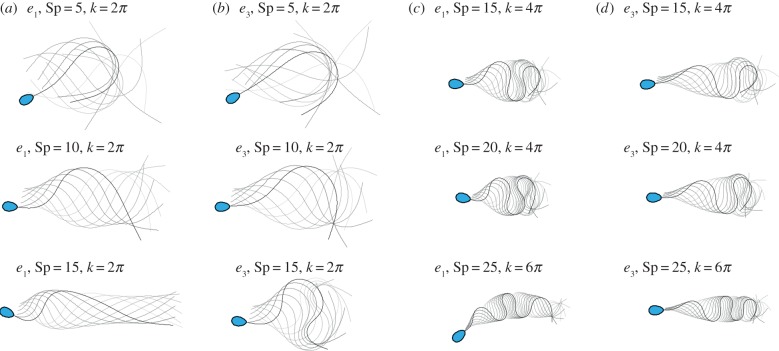
We begin by presenting a general overview of the distinct flagellar behaviours across a wide range of sperm-compliance factors, from as low as Sp = 5 to as high as Sp = 25. We firstly contrast large amplitude beating patterns for the flagellar axoneme and human sperm flagellum cases, given, respectively, by the tapering functions e₁ and e₃. Figure 3 illustrates the time evolution for six distinct pairs of sperm-compliance number and wavenumber (Sp, k), and force amplitude a, as detailed above. The flagellar waveform associated with low (Sp, k) is characterized by a large wave amplitude and a significant forward motion, as demonstrated for (Sp = 10, k = 2π). Meandering formation and wave-compression are distinctive characteristics of large (Sp, k) in figure 3.

Figure 3.

Snapshots of flagellar evolution for the tapering functions e₁ and e₃, and six distinct pairs of wavenumber and sperm-compliance number (Sp, k) across the parameter space, as indicated, plotted at equal time intervals over one period (darker curves denote later times and the sperm head is only shown at final time for clarity). In particular, there are four columns and three rows. In columns (a,b) one has the profiles e₁ and e₃, with the sperm number then increasing on descending the rows. In columns (c,d) the wavenumber is increased, as is the sperm number; again, one has the profiles e₁ and e₃ with sperm number increasing on descending the rows. The values of force amplitude a, for each row, from (a) to (d) are, respectively, a = 2.24, 2.54, 1.96, 2.37, a = 2.02, 2.93, 2.04, 2.55 and a = 2.54, 3.63, 1.30, 2.21, after non-dimensionalization with E₀/ℓ³, where ℓ = L/Sp. (Online version in colour.)

For large values of Sp, when the reinforcing flagellar components are absent, extensive wave confinement is observed (figure 4), in addition to the flagellar symmetry breaking, driving the cell in a circular trajectory; see plot (e₁, Sp = 25, k = 6π) in figure 3. This is in contrast with the case e₃ with a reinforced, tapering flagellum, akin to the human sperm, with the same values of Sp and k, where both flagellar wave confinement and symmetry-breaking buckling are not as pronounced in the results of figure 3. Instead, the meandering formation is characterized by a wave envelope that gradually changes with arclength. At low (Sp, k), however, the waveform is only weakly modified by the tapering function e₃, as shown in figure 3 for Sp = 5, 10, k = 2π. Hence, below we focus on the region of the parameter space where the flagellar ultrastructure is most relevant, i.e. for large (Sp, k).

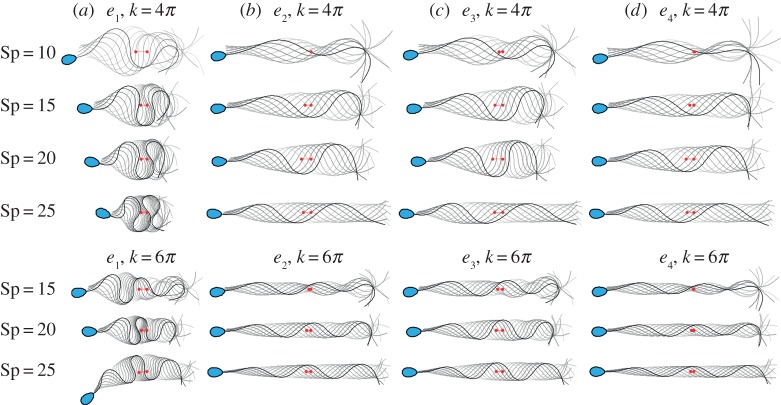
Figure 4.

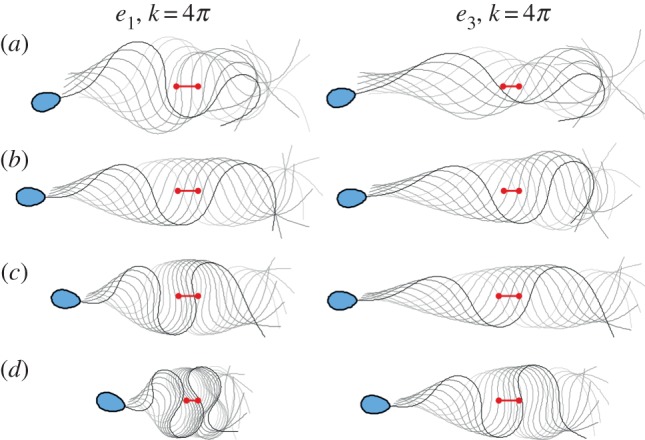
Snapshots of the flagellar evolution for the tapering functions (a–d) e₁ − e₄, and seven distinct pairs of wavenumber and sperm-compliance number (Sp, k), as indicated, plotted at equal time intervals over one period (darker curves denote later times and the sperm head is only shown at final time for clarity). The same force amplitude, a, given by the upper limit of the tapering case e₁ consistent with the absence of self-intersection (as discussed in the final paragraph of §2.4) is used for the other stiffness functions e₂, e₃ and e₄. The value of a for each row, from top to bottom, is thus a = 2.08, 1.96, 2.04, 2.09, 2.22, 1.81, 1.3, non-dimensionalized by E₀/ℓ³, where ℓ = L/Sp. Red markers depict the initial and final position of the flagellum centroid over a period. (Online version in colour.)

However, before continuing with our analysis, we take a brief interlude to discuss the mechanism behind the flagellar symmetry breaking described above (figures 3 and 4) [12]. The latter is a direct consequence of a dynamical buckling instability of the beating flagellum [12], though it is frequently found in filaments under large tangential forces [14,29,57,58,69,70]. In this case, the excess in elastohydrodynamic friction experienced by the flagellum causes the compressive forces to increase beyond a critical value (figure 1d), which the elastic structure cannot support and thus buckles (figure 1e) to release the excess in compression. Upon buckling, however, the flagellum is still driven by the same internal, periodic internal force, which continuously maintains the emerging asymmetric bending pattern, thus leading to circular trajectories for free swimming sperm cells (figure 1e), as described in [12].

The stabilizing effect of the ultrastructural components for high viscosities is further illustrated in figure 4, which plots the time evolution of the beating shape for each tapering function e₁, e₂, e₃, e₄ and seven pairs of (Sp, k). In this instance, the same force amplitude, a, given by the upper limit of the non-tapering, pure axonemal case e₁ is used for each e₂, e₃ and e₄ case, for each (Sp, k)-pair. The resulting waveform for the tapering functions e₂ − e₄ is characterized by the formation of a wave envelope with a gradual change of the wave amplitude and wave compression with increasing arclength, while still maintaining a meandering form. The wave envelope, however, carries critical signatures of the tapering function: narrow wave envelopes are observed for the tapering cases e₂ and e₄, while wider envelopes are associated with the tapering function e₃.

Furthermore, figure 4 also allows one to examine whether the waveform changes are dominated by the increase in overall stiffness with use of tapering functions e₂, e₃, e₄ compared with e₁, or whether the waveform changes are induced by the introduction of stiffness heterogeneity. Firstly, noting the quarter-power dependence of the sperm-compliance factor on inverse stiffness in equation (2.2), changing Sp from 20 to 15 represents a factor of 3 increase in the stiffness, while changing Sp from 25 to 15 represents approximately a factor of 8 increase. However, these factors of 3 and 8 changes in the homogeneous stiffness are insufficient to radically change the structure of the flagellar waveform, as seen from the persistence of wave confinement for e₁ on reducing Sp from 25 to 15 in figure 4a. By contrast, changing from homogeneous stiffness to any of the tapering cases e₂, e₃, e₄, with Sp = 25, for example, has an extensive impact on the waveform, modulating the wave envelope and suppressing waveform compression. Hence one can observe that it is the tapering, rather than the overall increase in stiffness, that dominates the observed waveform differences between homogeneous flagellar stiffness on the one hand and tapering flagellar stiffness on the other.

We proceed to consider the distance travelled per period, as depicted by the red markers in figure 4. For all tapering functions considered e₂ − e₄, an increase in the total swimming distance is observed as Sp increases (for clarity, see also figure 5 for the travelled distance over one period). In general, the swimming distance is larger for e₃ than for e₂, e₄ for each (Sp, k)-pair. However for lower values of the sperm-compliance number, and hence less viscous media together with typical wavenumbers, for example (Sp = 10, k = 4π), the beating shapes associated with the tapering functions e₂ − e₄ are marked by a sharp decay in the wave amplitude in the central part of the tail. As a consequence of such an erratic waveform, forward motion is relatively small for sperm with reinforced flagella, in distinct contrast with the untapered, e₁, case, where the associated sperm possesses a notable forward motion in figure 4. Hence in less viscous media the modelling indicates a trend that there is a modest mechanical advantage for swimming with the absence of accessory structures.

Figure 5.

Comparison between the stiffness functions e₁ and e₃: the flagellar waveform and centroid displacement (red markers) for the maximum travelled distance over one beat cycle, within the allowed range of the internal force magnitude, as discussed in §2.4. (a–d) are respectively for Sp = 10, 15, 20, 25 for k = 4π. Except for the final time, the sperm head has been omitted for clarity. (Online version in colour.)

The effect of ultrastructural components on the distance travelled per beat cycle is further shown in figure 5, where the flagellar wave and waveform centroid (red markers) across the allowed range of a instead are displayed for one period in (a–d) for Sp = 15, 20, 25 and k = 4π, respectively, for both stiffness functions e₁ and e₃, as indicated. For both cases, the irregular wave amplitude along the flagellum switches to a regular wave envelope, subsequently followed by a wave compression that is much more extensive for the naked axoneme, case e₁. Furthermore, one can again observe the trend of a modest increase for the predicted swimming distance per beat cycle for the reinforced flagellum, case e₃, as Sp increases from figure 5a to figure 5d by comparing the red tracers along each column with the converse trend for the undressed axoneme, case e₁, as quantified and further emphasized in table 1. In particular, it should be noted that while RFT may not be trustworthy at the highest waveform compression depicted in figure 5, owing to the near flagellar self-intersection, the trends in the movement per beat cycle emerge from far less extreme waveform patterns, away from flagellar self-intersection.

Table 1.

Sp is the sperm number and d_e3 denotes the distance moved by the centroid over a beat cycle for the reinforced flagellum, with stiffness function e₃, in figure 5, while d_e1 is defined analogously for the naked axoneme with stiffness function e₁. Hence by examining the ratio of these distances, one has that the reinforced flagellum travels significantly further per beat cycle at a high sperm number of 25 in figure 5, relative to the naked axoneme, with the converse observation at a lower sperm number of 10.

Sp	10	15	20	25
de3/de1	0.77	0.83	1.03	1.53

In figure 6, we present a qualitative comparison with the observations of sea urchin and human spermatozoa in methylcellulose solutions from figure 1b,c; a detailed description of the model and empirical parameters are provided in the figure caption. This firstly indicates the broad differences in waveforms across different tapering accessory structures. In particular, a comparison of the flagellar waveforms of the predicted beat patterns highlights the presence of extensive flagellar compression in figure 6a for both observation and simulation, where no accessory structures are present, as indicated by the bare axoneme in figure 6b. This contrasts the observations and simulations of sperm with a dressed axoneme in figure 6b. However, while one can readily find qualitative agreement between modelling and observation for both species, it is not feasible to attempt a quantitative test of the simulation framework by comparison with observation, for instance, since the viscosity measurements for the sea urchin experiments are lacking and the active forces should be assigned in the simulations. Nonetheless, the qualitative agreement further motivates the study of how accessory structures and their tapering impacts the flagellum waveform and, for example, the presence or the absence of waveform compression.

Figure 6.

A comparison of predictions of the virtual sperm flagellar waveform and observation in a highly viscous medium. (a) The sea urchin micrographs from figure 1b are reproduced, together with net plots of predicted flagellar waveforms (upper: Sp = 25, k = 6π, a = 1.3, as in figure 4a, bottom row; lower: Sp = 25, k = 4π, a = 2.09, as in figure 4a, 4th row). The naked axoneme cross-section in the plot emphasizes both that sea urchin sperm has no accessory structures and that the modelling predictions are for virtual sperm with the homogeneous non-tapering stiffness function, e₁. (b) Human sperm micrographs from figure 1b are reproduced, together with plots of simulated waveform netplots (upper: Sp = 20, k = 4π, a = 2.55, as in figure 3d, 2nd row; lower: Sp = 25, k = 6π, a = 2.21, as in figure 3d, 3rd row). The dressed human sperm flagellum cross section in the plot emphasizes both that the human sperm has accessory structures and that the modelling predictions are for virtual sperm with the tapering stiffness function, e₃. The sea urchin and human sperm micrographs are, respectively, reproduced with permission (licence no. 4543770361396) from [10] and with permission from [11]. For the observations in (a), the high viscosity was achieved by adding 2% methylcellulose to the medium with different molecular weights specified by a nominal viscosity of, respectively, 1.5 Pa.s (upper) and 4 Pa.s (lower). For (b), 1% methylcellulose was added for the upper frame and 2% methylcellulose added for the lower frame. However, the methylcellulose used had the same molecular weight, specified by a nominal viscosity of 4 Pa.s for a 2% methylcellulose aqueous solution at 20°C. The resulting methylcellulose solutions in (b) were explicitly measured using a cone-and-plate rheometer [10] with an effective viscosity given by 0.14 Pa.s (upper) and 1.6 Pa.s (lower), while the beating frequency was 11 Hz (upper) and 3 Hz (lower). Explicit measurements for the fluids in the observations of (a) are not available, though the averaged beat frequencies reported in [11] for nominal viscosities of 1.5 Pa.s (upper) and 4 Pa.s (lower) are, respectively, 3.8 Hz (a) and 2.8 Hz (b). The flagellum length reported for (a) was approximately 42 μm while for (b) it was is 50 μm. The sperm number for each case (a, upper; a, lower; b, upper; b, lower), respectively, is Sp = 23, 27, 20, 26. However, the Sp estimates for the experiments in (a) are likely to carry systematic errors as the viscosity of the medium was not explicitly measured. Micrographs in (a,b) reprinted from [3] with permission from Elsevier. (Online version in colour.)

The maximum curvature, κ_max, and maximum absolute tension, T_max, over one period are depicted in figure 7 for (Sp = 25, k = 4π), as a function of the scaled sliding force magnitude, a. The maximum curvature and tension for the tapering function e₁ is characterized by the presence of a sharp transition, depicted by the points ‘a’ and ‘b’ in figure 7. For the purpose of comparison, the same jump transitions ‘a’ and ‘b’ from figure 7a are depicted in figure 7b, in addition to the associated beating shape, shown on the right side of figure 7b. The beating patterns for ‘a’ and ‘b’ are separated by a transition from a diffuse waveform in ‘a’ to a large wave confinement in ‘b’. A distinct behaviour is found for the tapering functions e₂ − e₄, in which the maximum curvature and tension are always lower than the ones observed for the constant tapering function e₁. In this case, while the rapid transition in κ_max is gradually decreasing in magnitude for the stiffness functions e₃, e₂ and e₄, respectively, in figure 7a, no sharp increase in magnitude is detected for T_max. Instead, T_max is non-monotonic and decreases after the transition, as illustrated near the points ‘c’ and ‘d’ in figure 7b.

Figure 7.

The maximum curvature κ_max (a) and the maximum absolute tension T_max (b), over one period, as a function of the maximal sliding force density magnitude, a, non-dimensionalized by E₀/ℓ³, where ℓ = L/Sp. This magnitude is limited for the e₁ curves to ensure the absence of flagellar self-intersection, as detailed in the final paragraph of §2.4. The same points ‘a–f’ in (a) are depicted in (b), in addition to the associated beating shape, on the right side of (b), with the sperm head only shown at final time for clarity. Red markers depict the initial and final position of the flagellum centroid over a period. (Online version in colour.)

This transition is also associated with flagellar wave compression, as portrayed by the beating patterns in ‘c’ and ‘d’, for the tapering function e₃ in figure 7. After the waveform compression transition, T_max decreases with the sliding force density magnitude between points ‘d’ and ‘e’ before reverting to an increasing behaviour once more between ‘e’ and ‘f’. Despite the non-monotonic behaviour in T_max between ‘d’ and ‘f’, the variation in κ_max is monotonic in this region, as also portrayed by the beating patterns of ‘d’, ‘e’ and ‘f’. A similar behaviour to e₃ is observed for e₂ and e₄, with the appropriate scaling, as larger values of T_max are permitted in these cases. The tapering functions e₃, e₂, e₄ are able to withstand increasing values of T_max, respectively, before a transition associated with wave compression occurs, as seen from figure 7b. By contrast, the absence of wave compression and buckling for waveforms with Sp ∈ {5, 10} in figure 3 also highlights that the sharp transitions in maximal curvatures and tensions shown in figure 7a,b are absent at low sperm-compliance factors.

4. Discussion

Since the discovery of the flagellar ultrastructural components in mammalian spermatozoa, the biological function of this accessory complex has generated extensive debate [2,3,5–9]. Several studies, from electron microscopic to biochemical techniques, have revealed detailed information about the morphology, internal structure and molecular basis of these structures [2,3,5–8], ultimately unveiling their passive reinforcing nature. Despite this crucial advance, the functional significance of this adaptation of the sperm flagellum by passive, reinforcing structures is unclear. To provide further insight into such questions, we have considered the physical principles of the flagellar ultrastructural components for free swimming spermatozoa in a viscous fluid. The structural response of a virtual sperm flagellum is modified by the addition of reinforcing elastic components that gradually taper along the length of the flagellum. The fluid–structure interaction is simplified to the level of RFT, while keeping the geometrically exact nature of the flagellar elastic structure, as well as taking into account the presence of the sperm head. The internal forcing is represented via the sliding filament model of eukaryotic flagellar motility, which is ultimately responsible for generating complex flagellar waveforms that are examined in detail through numerical simulations.

While geometrically linear theory [16] and temporal nonlinearities of the beat [20] support the idea that gradual, spatial tapering of structural components play a minor role in shaping the flagellar waveform, we have demonstrated that these reinforcing flagellar appendages are fundamental for the emerging beating pattern, as well as the resulting swimming behaviour of the spermatozoa. A wide range of beating patterns emerged, from large amplitude waveforms and substantial sperm head yawing, for a low (Sp, k)-pair, to the meandering flagellar wave envelope formation, when (Sp, k) is large. In all cases, the flagellar accessory structures acted to significantly reduce the maximum flagellar curvature when compared with the naive flagellar axoneme, i.e. when the additional elastic components are absent. Such a reduction of flagellar curvature was also reported by the pioneering theoretical work by Lindemann [8].

Our numerical simulations further revealed the emergence of a wave-compression instability in the regime of high sperm compliance, illustrated in figure 4 (e₁, Sp = 25, k = 4π), similar to the symmetric waveform confinement reported for sea urchin sperm migrating in high viscosity [11] (figures 1b and 6). This wave-compression instability is characterized by an extreme wave confinement and formation of symmetric flagellar ‘loops’ in the limit of self-intersection, with a vanishing time-averaged curvature, resembling Euler elasticas [29,30]. The wave-compression instability we observe here is, however, triggered dynamically by internal sliding moments driving the flagellum, further augmented by large elastohydrodynamic friction for a high sperm-compliance number [12], or equivalently for high viscosity. As the sliding force magnitude increases, the internal flagellar compression rises until a critical value, which the flagellar structure cannot support; the flagellar waveform thus tends to collapse onto itself, releasing excessive internal stresses. As a result, the maximum absolute compression is characterized by a transition associated with a concomitant rise in the maximum curvature along the flagellum (figure 7) as the sliding force magnitude a is increased. This causes the beating patterns ‘a’ and ‘b’ in figure 7 to change from a spread waveform in ‘a’ to a large confinement in ‘b’. Naive flagellar axonemes are also predicted to be susceptible to a symmetry-breaking buckling instability, as previously reported in [12], in which asymmetric waveforms, instead, drive the sperm cell in circular swimming trajectories, as illustrated in figure 4 (e₁, Sp = 25, k = 6π). Asymmetric waveforms were also observed experimentally for sea urchin sperm swimming in a high-viscosity medium [11], in the absence of chemotactic cues, as depicted in figures 1b and 6.

These results provide evidence that asymmetric beating patterns and extreme wave confinement, as in figures 1b and 6, for sea urchin flagellar axoneme in a high-viscosity medium [11], may emerge dynamically, via compression-driven and buckling instabilities due to the large effective drag experienced by the flagellum, without recourse to variations in structure or signalling influencing the molecular motors within the flagellum. In this case, the sperm flagellum becomes unable to sustain the high internal compression, ultimately compromising the sperm migration in a high-viscosity medium. Sea urchin sperm however are not generally prone to flagellar compression and buckling as they fertilize in low-viscosity seawater. Internal fertilizers, on the other hand, are required to migrate in high-viscosity liquids, and therefore are susceptible to flagellar waveform compression and buckling without ultrastructural flagellar adaptation.

Hence the ultrastructural components found in mammalian spermatozoa are implicated as important for sperm migration in high-viscosity media, with further indirect support from the qualitative agreement between prediction and observation for the flagellar waveform in figure 6. By reinforcing the flagellum in regions where high compression may occur [12], between the mid- and principal pieces, the flagellar accessory complex is predicted to be able to prevent flagellar compression and buckling instabilities in a high-viscosity liquid [10,11], as shown in figure 4. Analysis of this figure has also revealed that the inhibition of wave compression and buckling is predominantly due to the tapering of flagellar stiffness rather than the overall stiffness of the flagellum, with the latter simply perturbing the sperm-compliance factor, Sp, owing to its quarter-power dependence on the inverse stiffness.

Furthermore, the tapering, heterogeneous stiffness of the ultrastructural complex is seen to stabilize the flagellar structure by reducing internal compression (figure 7), consequently decreasing the overall curvature along the flagellum. This regulates the absolute tension, thus suppressing large jumps in T_max, as illustrated in figure 7b. As a result, for an increasing sliding force amplitude, the beating patterns are characterized by a gradual increase in the wave amplitude along the flagellum, with the formation of a wave envelope and the decrease of waveform compression (figures 4 and 7). The shape of the wave envelope depends on the functional form of the ultrastructural tapering, associated with the functions e₂ − e₄. In particular, we have seen that the larger the gradient of stiffness in the distal regions of the flagellum, as depicted in figure 2b, the greater the stabilizing influence. Hence, for example, the tapering of e₄ inhibits wave compression and buckling more, albeit subtly in that this is only clear in figure 7, and is not evident in figures 3 and 4.

Nonetheless, compared with homogeneous stiffness, flagellar tapering is observed to prevent excessive flagellar wave compression (figure 7), and consequently reduce curvature and self-intersections, enabling a modestly increasing progressive movement per beat for a flagellum reinforced with tapering stiffness as the sperm-compliance number is increased (figures 4 and 5). It is also worth noting that such differences in progressive swimming will be cumulative, and thus not insignificant in absolute terms, for time scales longer than the 0.1 second scale of a single beat cycle period.

Modelling refinements to the presentation here are certainly possible. For instance, the fact that observations show that the wave compression is highly suppressed towards the mid-piece [10], as opposed to the end piece (figure 1c), indicate that a systematic parameter estimation study may increase current estimates for the average bending stiffness of the flagellum mid-piece, with subsequent refinement of the presented results. In addition, while elastic effects are relatively limited in methylcellulose solutions [10], which were used in both the observational human and sea urchin sperm studies considered here [10,11], elasticity is often extensive in physiological media [71,72] and may act to favour the concentration of large amplitude bending waves at the end-piece region [60] and warrants further study. Similarly, incorporating non-local hydrodynamic interactions [23,35,36,73,74] is likely to refine predicted waveforms, possibly further reducing the tendency to symmetry break [73], though this would require careful consideration of sperm head elastohydrodynamic boundary conditions.

However, such refinements are not anticipated to greatly alter the qualitative modelling observations: that the reinforcement of the flagellum in regions where high compression is expected [12] acts to prevent elastic instabilities that could compromise a core biological function, i.e. the transport of genetic material within high-viscosity environments. The presented results more generally demonstrate that the tapering of structural components plays an important role in shaping the flagellar waveform. They further suggest that the above aspects of the flagellar viscous modulation observed empirically [10] may be achieved without recourse to intricate molecular motor regulation [4] with only, for example, a constant sliding force amplitude along the flagellum [20]. It can also be hypothesized that the viscosity of the medium where the spermatozoa naturally swim may have acted decisively during the evolutionary process for internal fertilizers, such as human sperm, thus inducing specialized mutations favouring flagellar ultrastructural components to enable cell penetration in high-viscosity media. Finally, we note that the prospect that human sperm are adapted to swim in viscous media further emphasizes the importance of using high-viscosity fluid while assessing and screening spermatozoa in the clinical setting [4,10,43,75].

Appendix A. Numerical scheme

Numerical solutions of the elastohydrodynamic formulation for a free swimming cell, described by equations (2.1)–(2.7), were carried out by employing the numerical scheme devised in [12], which uses a combination of the second-order finite differences and second-order implicit time stepping. The latter has been validated against analytical and nonlinear numerical solutions, in addition to experiments for an oscillating elastic filament in a viscous fluid [12,29,51]. In particular, to avoid severe constraints on the time stepping, the higher-order terms in equation (2.1) are treated implicitly, by employing a second-order implicit–explicit method (IMEX) [76]. The spatial discretization is uniform in arclength. Second-order divided differences are used to approximate spatial derivatives [34], in which skew operators are applied at the boundaries. Finally, periodicity is expected from the imposed sliding force in equation (2.4), and therefore the time iteration continues until the maximum difference between consecutive solutions, D_max = max_s|X(s, t) − X(s, t + T)|, one period apart, is below 5 × 10⁻⁴.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

No funding has been received for this article.