Abstract
The heart epicardial layer, with elastin as the dominant component, has not been well investigated, specifically on how it contributes to ventricular biomechanics. In this study, we revealed and quantitatively assessed the overall status of prestraining and residual stresses exerted by the epicardial layer on the heart left ventricle (LV). During porcine heart wall dissection, we discovered that bi-layered LV surface strips, consisting of an epicardial layer and cardiac muscle, always curled towards the epicardial side due to epicardial residual stresses. We hence developed a curling angle characterization technique to intuitively and qualitatively reveal the location-dependency and direction-dependency of epicardial residual stresses. Moreover, by combining prestrain measurement and biaxial mechanical testing, we were able to quantify the epicardial prestrains and residual stresses on the unpressurized intact LV. To investigate the potential mechanical effect of epicardial prestraining, a finite-element (FE) model has been constructed, and we demonstrate that it is the prestraining of the epicardial layer, not the epicardial layer alone, providing an additional resistance mechanism during LV diastolic expansion and ventricular wall protection by reducing myocardial stress. In short, our study on healthy, native porcine hearts has revealed an important phenomenon—the epicardial layer, rich in elastin, acts like a prestrained ‘balloon’ that wraps around the heart and functions as an extra confinement and protection interface. The obtained knowledge fills a gap in ventricular biomechanics and will help design novel biomimicking materials or prosthetic devices to target the maintenance/recreation of this ventricle confinement interface.
Keywords: heart, epicardial layer, epicardial prestraining, epicardial residual stress, cardiac elastin, ventricle confinement interface
1. Introduction
Between 2011 and 2014, approximately 6.5 million adults experienced heart failure in the US, representing a major healthcare burden [1]. After coronary artery blockage, the downstream cardiomyocytes die and lead to myocardial infarction (MI), commonly known as heart attack [2–4]. This subsequently results in expansion of the infarcted region, formation of scar tissues, left ventricular wall thinning and dilatation, loss of cardiac function, and eventually fatal heart failure (HF) [5–12]. Current therapies for HF provide modest symptom relief but fail in preventing dilation and improving long-term survival outcomes [13–15]. The collagenous, parietal pericardium sac of the heart is not sufficient in preventing ventricular dilation during HF [16]. As a result, passive prosthetic devices that wrap the heart, such as woven textile (CorCap), Nitinol mesh (Paracor) and polyurethane half-ellipsoid balloon (Plyzen) [17–19], have been developed to limit ventricular dilation. During the past 20 years, passive prosthetic wrap devices have demonstrated an encouraging clinical safety profile and improved left ventricle (LV) function. However, they still face challenges with respect to limited reverse LV remodelling and long-term ventricular function or survival [17–19]. Improvements in elastic support device development and their modes of application can only be done once ventricular mechanics and its post-MI alteration are better understood [5–12,17–19].
The heart ventricular wall has three anatomically distinguishable layers: the epicardium, myocardium and endocardium. The epicardium (also known as the visceral pericardium) is the outermost thin layer which is largely made of elastin fibres along with a network of collagen [20–23]. The myocardium is the thick middle layer that fuses immediately with the epicardium and forms the main body of the heart wall. Myocardium contains mainly heart muscle fibres, which are delicately bound together by a network of type I and type III collagen, and the amount of elastin fibres in the myocardial extracellular matrix (ECM) is relatively sparse [21,23]. The innermost layer of the heart wall is the endocardium, which is also dominant with elastin fibres along with a network of collagen [21–23]. The endocardium lines the chambers and controls heart contraction through electrical signals conducted by the Purkinje fibres [22].
Previous research has mainly focused on the myocardium and the myocardial ECM (types I and III collagen as the dominant components). These studies have shown that heart muscle fibres interact with the myocardial ECM to perform the active contraction in systole and passive stretch in diastole in an effective and efficient manner. The myocardial ECM binds heart muscle fibres together, enables the overall architecture of multilayered helical orientation, provides tethering among muscle fibres and prevents the over-stretch of muscle fibres during LV diastolic expansion [23–29]. However, the mechanical properties and the impact of the epicardial layer to the LV during heart contraction and diastole have so far been largely ignored. From a material perspective, the previous cardiac ECM studies mainly focused on the collagen; the epicardial layer, with elastin as the dominant material component, has not been well investigated. Despite a few studies that hint that elastin may have an important role in cardiac mechanics and function [20,23], the biological and mechanical functionalities of elastin in the heart are poorly understood when compared to the knowledge of elastin in other dynamic soft tissues, such as blood vessels, lung and ligaments [23]. In those dynamic tissues, elastin provides long-range deformability, elastic passive recoil, and efficiency in storing and releasing energy during dynamic loading.
During our dissection of tissue samples from the heart surface, which consisted of an epicardial layer and cardiac muscle, we discovered an interesting phenomenon that the bi-layered LV surface strip always curls towards the epicardial side. This surface curling reveals that there is residual stress in the epicardial layer. Once dissected off the heart, the contraction of the epicardial layer bends the LV surface strip and a curling morphology occurs. Residual stress in an organ is the stress that remains in tissue after all external loads are removed [30]. A well-known example is the residual stress and strain in blood vessels. After the blood vessel is cut into ring segments, a single radial cut releases the residual stress in the blood vessel wall. The closed ring configuration cannot be maintained, and the ring opens up, forming an arc conformation [30]. Accordingly, the open angle is defined as the angle formed between two lines extending from the tips of the opened ring to the midpoint of the inner arc of the ring [30].
The concepts of residual stress have also been applied to the rat left ventricular wall. Omens and Fung showed that, if a radial cut was applied to an equatorial slice of a rat heart, the rat's LV exhibited an open angle-like morphology (approx. 30°), indicating the existence of residual stress in the whole ventricular wall [31]. Using the finite growth framework with fixed-point iteration, Genet et al. analysed and proposed that the residual stress in the ventricular wall was likely induced by the growth of the organ [32]. Jobsis et al. performed a study on the residual stress of the LV by examining the gross opening angle of the porcine LV wall [20]. They showed that peeling-off or disruption of the epicardium reduced the gross opening angle of the left ventricular wall, implying the likely contribution of the epicardium to the ventricular wall residual stress [20].
In this study, we revealed and quantitatively assessed the prestraining and residual stresses exerted by the epicardial layer on the heart LV. A finite-element (FE) model was also constructed and analysed to investigate the mechanical role of epicardial prestraining in ventricular diastolic expansion. Our study addresses a critical question in ventricular biomechanics, i.e. what is the biomechanical role of the epicardial layer and how does epicardial prestrained confinement contribute to cardiac function. The obtained knowledge will help design new therapies to target the maintenance/recreation of this ventricle confinement interface in diseases such as myocardial infarction and heart failure.
2. Material and methods
2.1. Sample preparation for the surface strip curling angle study
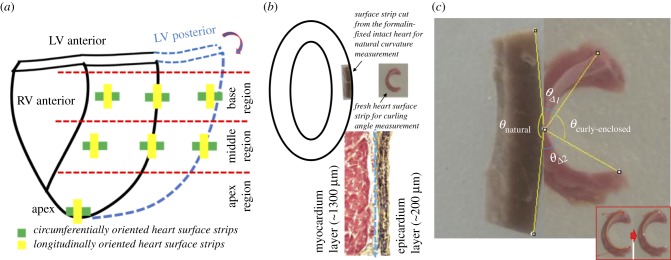
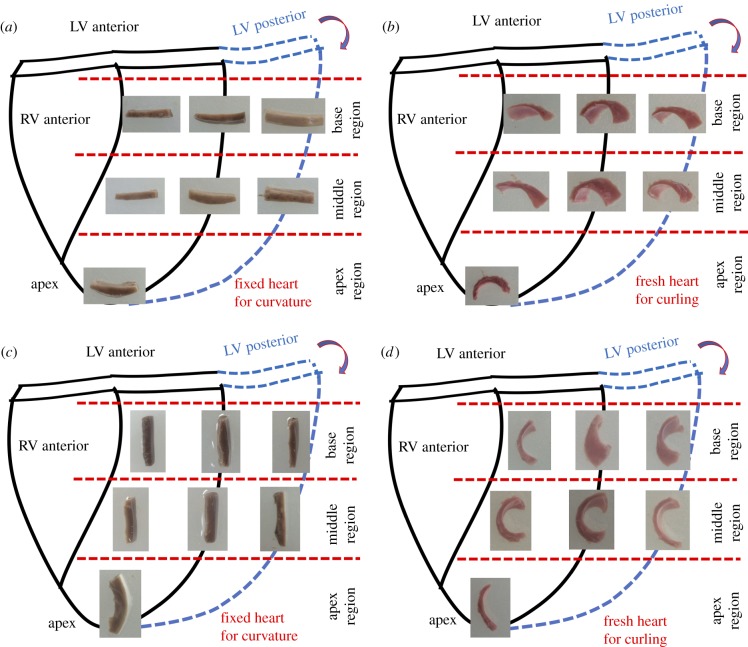
Fresh porcine hearts (approx. six-months old, Yorkshire) were obtained from a local abattoir and transported to the laboratory. Fresh porcine hearts were at unpressurized rest status after the routine stunning and exsanguination (draining of blood) slaughtering procedure. Both circumferential and longitudinal LV surface strip samples were collected. Native LV surface strips (approx. 15 mm × 5 mm × 1.5 mm) were dissected from seven locations of the LV (three from the basal region, three from the middle region and one from the apex point) (figure 1a). After examining the curling responses of strips with varying sizes, we chose approximately 15 mm × 5 mm × 1.5 mm dimensions to achieve optimal curling behaviour (justifications in §4.1). The 1.5 mm thickness consists of an approximately 200 µm elastin dominant epicardium and an approximately 1300 µm heart muscle layer (figure 1b, bottom). To use the natural curvature of heart as a reference, and to validate that the curling was from the contraction of epicardial layer, unpressurized intact native hearts were fixed in 10% buffered formalin solution for 72 h and rinsed in 1X phosphate-buffered saline (PBS) for 1 day. Formalin-fixed LV surface strips were then dissected for measuring the heart surface curvature (figure 1b). We found that 10% buffered formalin solution functioned to cross-link the collagen, elastin, and cells in tissue, fully fix the tissue [33], and preserve the natural curvature of heart surface even after dissection. For each group, sample size is N = 5.
Figure 1.
Protocol to characterize the curling phenomenon of the native heart surface strip. (a) Sample preparation plan. Circumferentially oriented heart surface strips and longitudinally oriented heart surface strips were dissected from basal anterior, basal lateral, basal posterior, middle anterior, middle lateral, middle posterior and apex locations. For each orientation, five hearts were used for curling angle quantification. (b) Schematic illustration showing the curling phenomenon of the heart surface strips dissected from the native intact heart. The bi-layered LV surface strip, dissected from the native heart, always curls towards the epicardial side (inserted picture on the right) revealing residual stress in the epicardial layer. Inserted picture on the left shows a LV strip dissected from the formalin-fixed heart which preserves the curvature of the heart surface as a comparison. Histology at the bottom shows the heart surface strip has a bi-layered structure consisting of the elastin-dominant epicardial layer (approx. 200 µm) and a myocardial layer (approx. 1300 µm). (c) Four types of angles were defined: θcurly-enclosed as the surface curly-enclosed angle from native LV strips after being dissected and reaching a stable curling status; θnatural is the angle defined by the natural curvature contour measured from the formalin-fixed heart tissue strip; θreflex represents the reflex angle of θcurly-enclosed; θΔ is the total curling angular change: Inserted picture in (c) demonstrates two important steps: (i) outlining the upper edge of the epicardial surface with two endpoints; (ii) finding the midpoint. (Online version in colour.)
2.2. Curling angle measurements
After dissection, each LV surface strip was immersed in 1X PBS in a Petri dish to create a free floating and stress-free status. The free floating LV surface strip could reduce the friction of the Petri dish's bottom to a minimum, thus the stress-free status could be obtained. Digital pictures (iSight, 8 megapixel with 1.5 µ pixel) of each strip (side view) were taken after the full occurrence of curling, which took place in a time frame of 1 min. We found that the 1-min waiting time was enough for a full release of residual stress, and the curvature of curled LV surface strip experienced no more change after that. LV surface strips dissected from the formalin-fixed hearts were imaged in the same way as the native LV surface strips.
ImageJ (NIH, Bethesda, MD) was used to analyse the curly-enclosed angle (θcurly-enclosed) via the following steps: (i) draw a curve outlining the upper edge of the epicardial surface and measure its length (figure 1c insert); (ii) use half length of the curve measured in step 1 to mark the midpoint (figure 1c insert); and (iii) draw straight lines connecting the two endpoints (upper edge) of the strip to the midpoint and measure the curly-enclosed angle (figure 1c). The upper edge of the standing strip is where the digital image focuses on and has a notable, clear, and smooth edge, which can be easily identified from the image. We thus used the upper edge of the epicardial surface as a representative of the curling curve (figure 1c insert).
To estimate the total curling angular change (θΔ) related to the natural curvature of heart, four types of angles were defined: θcurly-enclosed as the curly-enclosed angle of the native LV surface strip after being dissected out and reaching a stable curling status (figure 1c); θnatural as the angle defined by the natural curvature contour measured from the formalin-fixed heart surface strip, i.e. the angle enclosed by the two lines that link the two endpoints to the midpoint of the curvature contour (figure 1c); θreflex represents the reflex angle of θcurly-enclosed defined by equation (2.1) (figure 1c); and θΔ is the total curling angular change defined by equation (2.2) (figure 1c).
| 2.1 |
and
| 2.2 |
2.3. Quantitative estimation of the regional residual stresses of the left ventricle epicardial layer
A four-step estimation method was developed to quantify the regional residual stresses of the LV epicardial layer on the unpressurized intact heart. The four steps were as follows: (i) quantify the epicardial prestrains existing on the unpressurized intact heart; (ii) use a biaxial testing machine to capture the stress–strain curves along the circumferential and longitudinal directions of the dissected epicardial layer (with a 0.5 g tare load required by software load control protocol); (iii) adjust the biaxial stress–strain curves to the 0 g load reference status; (iv) for each location, estimate the residual stresses along the circumferential and longitudinal directions from the adjusted biaxial curves via the prestrains reported from step (i).
2.3.1. Estimation of prestrains of the epicardial layer on the unpressurized intact heart
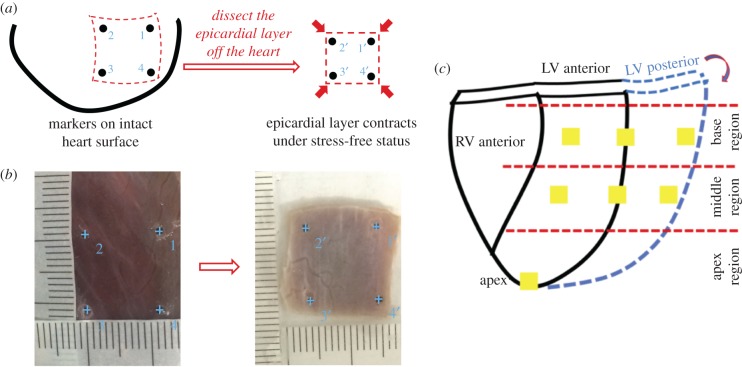
By putting four squarely arranged markers on the epicardial surface of the unpressurized intact heart, we could obtain the in situ marker dimensions while the prestrains existed. After dissecting the same region off the heart, the prestrains were found being released, and the isolated epicardial layer bore no stress. By immersing the isolated epicardial layer in 1X PBS in a Petri dish, we obtained the new marker dimensions of the epicardial layer under stress-free status. The prestrains of the epicardial layer along both the circumferential and longitudinal directions could thus be estimated (figure 2a). For each location, sample size N = 5.
Figure 2.
Schematic illustration shows the protocol to estimate the prestrains of the epicardial layer on the unpressurized intact heart. (a) By putting four squarely-arranged markers on the epicardial surface of the unpressurized intact heart, we could obtain the in situ marker dimensions while the prestrains existed. After dissecting the same region off the heart, the marker dimensions of the stress-free epicardial layer could be measured for the calculation of the prestrains. (b) Markers tagged from ImageJ for in situ unpressurized intact heart (left panel) and stress-free epicardial sample (right panel). The ruler with actual size was printed on a paper. The paper ruler could be placed onto the left ventricle surface, perfectly fitting the curvature of the left ventricle surface (left panel). In this way, the readings of the real marker dimensions on the unpressurized intact heart can be accurate, without being skewed by using a straight ruler for a curved surface. By immersing the isolated epicardial layer in the 1X PBS in a Petri dish, we obtained the new marker dimension of the epicardial layer under stress-free status (right panel). Ruler with actual size was printed on the transparent film and then placed beside the stress-free epicardial layer sample (right panel). (c) Sample dissection plan for estimating prestrains of the epicardial layer on the unpressurized intact heart. (Online version in colour.)
Fresh porcine hearts (approx. six-months old, Yorkshire) were transported from a local abattoir to the laboratory. Seven epicardial locations (approx. 10 mm × 10 mm) were chosen from the LV (three from the basal region, three from the middle region and one from the apex point) (figure 2c). By choosing approximately 10 mm × 10 mm sample dimension for prestrain measurement, we covered enough tissue in each anatomically distinguishable location. If, instead, a much smaller sample dimension (e.g. approx. 5 mm × 5 mm) is used, the image resolution of marker-enclosed area will be much lower, which will decrease the accuracy of prestrain measurement.
Before dissection, four markers were glued onto the surface of each location of the unpressurized intact LV using a minimal amount of cyanoacrylate glue. The ruler with actual size was printed onto paper and placed onto the LV surface, perfectly fitting the surface curvature. In this way, the readings of sample dimensions between markers on the unpressurized intact heart can be accurate and avoid being skewed by using a straight ruler for a curved surface (figure 2b-left panel). Digital pictures of each location were then taken to record the in situ marker dimensions. Note that the shape of the unpressurized intact heart experienced no changes during measurement. Thus, there was no geometrical or surface distortion of the LV during the in situ marker dimension measurement. After the in situ measurement, the epicardial layer of each location was dissected, the heart muscles were gently removed, and were immersed in 1X PBS in a Petri dish to ensure a stress-free status and flat configuration. A ruler with actual size was printed on a transparent film and then placed beside the stress-free epicardial layer sample. Digital pictures of each stress-free sample were taken to record the stress-free marker dimensions (figure 2b right panel). For each location, the sample size is N = 5.
The x and y coordinates of each marker were first acquired using ImageJ. For each sample, we converted the length in pixel to length in millimetres using each actual size ruler. For the markers on the heart surface, the coordinates were (x1, y1), (x2, y2), (x3, y3) and (x4, y4) (figure 2b). For the markers on the stress-free samples, the coordinates were (figure 2b). To calculate the prestrains (in the form of Green strain) of each location, we interpolated the displacements of all four markers from stress-free (the reference configuration), to in situ states inside the sample using the first-order shape function for quadrilateral element, as is commonly used for FE method (equation (2.3), where k denotes the indices of four markers). Then based on such interpolation we computed the deformation gradient tensor (equation (2.4), where I is the unity tensor), which, by definition, will give us the Green strain tensor, as in equation (2.5). We calculated the area average of the Green strain tensor E, as in equation (2.6) with Gaussian quadrature, and its components were used to estimate the prestrains along the circumferential direction (ɛX=xx) and longitudinal direction (ɛY=yy).
| 2.3 |
| 2.4 |
| 2.5 |
| 2.6 |
2.3.2. Biaxial mechanical testing
Biaxial mechanical testing was performed to obtain the tissue mechanical behaviour of the LV epicardial layer. Square samples (approx. 13 mm × 13 mm × 1 mm) were dissected from seven anatomical locations as described in §2.3.1 (basal anterior, basal lateral, basal posterior, middle anterior, middle lateral, middle posterior and apex locations, for each location, N = 5) (figure 2c). The thickness of epicardial layer sample was approximately 1 mm, which consists of the epicardium and the remaining cardiac ECM along with minimum muscle fragments that the scalpel could not fully remove. Accurate dimensions of each sample were measured using a digital caliper before biaxial testing. One axis of the square sample was aligned with the circumferential direction (CD) of the heart and the other with the longitudinal direction (LD). A custom made biaxial mechanical testing system was used to capture the tissue behaviour under physiologically relevant loading conditions. The principle, set-up and protocols of the biaxial mechanical testing system were covered by Grashow et al. [34]. Biaxial mechanical testing is well known for its sensitivity to detect stress–strain behaviour alterations due to subtle tissue microstructural changes [35–37].
Each side of the square sample was mounted onto four stainless steel hooks that are attached to two loops of 000 polyester sutures. Four fiducial graphite markers, affixed to the centre of the square sample with cyanoacrylate adhesive, were monitored via a CCD camera to capture the real time tissue deformation. Immersed in 1X PBS, the sample was preconditioned biaxially by imposing 10 cycles of 60 N m−1 maximum Lagrangian membrane tension [35]. After preconditioning, an equi-biaxial tension protocol of TCD : TLD = 60 : 60 N m−1 was performed to capture the biaxial behaviour. All the testings were performed with a 0.5 g tare load applied as a prerequisite for the software load control protocol, and the marker dimensions at 0.5 g tare load were used as the reference status of biaxial mechanical testing. The engineering stress–Green strain curves were then obtained.
2.3.3. Adjusting the biaxial curves to the 0 g load reference status
As we just mentioned above, a 0.5 g tare load was applied to allow the software load control protocol in biaxial mechanical testing. We hence needed to adjust the biaxial curves to the real 0 g load reference status for an accurate estimation. Samples were obtained in the same way as described in the biaxial mechanical testing protocol. Each sample mounted onto the biaxial machine was first applied the 0.5 g tare load, and the coordinates of four markers were saved as the 0.5 g tare load reference file. The tare load was then released by adjusting the motor movement to 0 g in both x (CD) and y (LD) directions. The tension-releasing motor movement was stopped once the load cell reading reported 0 g. The marker positions of 0 g loads in both the CD and LD were immediately saved by the software as the 0 g load reference files (electronic supplementary material, figure S1).
The compensatory strains were calculated by comparing the marker dimensions at the 0.5 g tare load status to the marker dimensions at the 0 g load status. Briefly, ImageJ was applied to obtain x and y coordinates for all markers. The compensatory strains (in the form of Green strain), ɛX(0.5) and ɛY(0.5), were estimated using a method similar to the prestrain computation as described in the §2.3.1.
For each anatomical location, the compensatory strains were averaged from three measurements. Schematic illustration (electronic supplementary material, figure S1A,B) describes how the compensatory strains were calculated. The compensatory strains of each anatomical location were then used to adjust the biaxial stress–strain curves by adding those amounts of strains (ɛX(0.5) and ɛY(0.5)) into the corresponding toe regions, and the biaxial curves were hence shifted toward the right (electronic supplementary material, figure S1C,D as a representative). After the adjustment, the new curves started from the real 0 g load reference status.
2.4. Finite-element model set-up
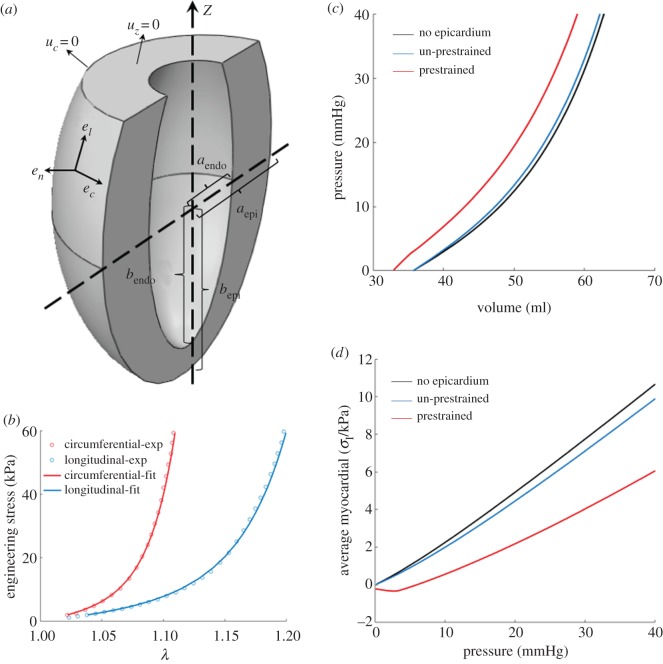
For simplicity, we used a truncated ellipsoid to represent the shape of the porcine LV (figure 6a). The lengths of the semi-axes of the endocardial surface are and , while those for the epicardial surface and . The distance between the apex and the base plane is . These geometrical parameters of LV were obtained by averaging the measurements from four porcine hearts (approx. six-months old, Yorkshire). The myocardium part consisted of 16 326 quadratic tetrahedral solid elements, and the epicardium was modelled as a shell covering the epicardial surface with 4430 quadratic shell elements with thickness of 1 mm, consistent with the overall thickness of the epicardial samples we dissected for biaxial mechanical testing (§2.3.2). The mesh density has been increased to check potential mesh dependency but no significant difference in result was observed.
Figure 6.
FE modelling of the effect of epicardial prestrain. (a) An illustration of the model geometry. The left ventricle is modelled as a truncated ellipsoid, characterized by five parameters: the semi-axes lengths of the endocardial () and the epicardial () surface, and the distance between apex and the basal plane (). To denote the material orientations, we employ the local coordinate system whose base vectors are , and , the circumferential, the longitudinal and the transmural normal vector. On the basal plane we prescribe , and on its outer edge (in circumferential direction). (b) The fitted biaxial stress–strain curve of the middle lateral sample. (c) The cavity volume and (d) the averaged myocardial first principle stress, plotted against the cavity pressure. The blue line shows the case without epicardial prestrain, and the red curve shows the case with epicardial prestrain, while the black line shows the case without epicardium. (Online version in colour.)
To model the passive mechanical properties of the myocardium, we adopted the Holzapfel–Ogden model [38,39]:
| 2.7 |
| 2.8 |
| 2.9 |
| 2.10 |
with
where and are fibre and sheet orientations in the original configuration. Note that if , the corresponding term in the above formula will be dropped since fibres buckle under compression. The parameters we used are [40] a = 0.496 kPa, b = 7.209, af = 15.193 kPa, bf = 20.417, as = 3.283 kPa, bs = 11.176, afs = 0.662 kPa, bfs = 9.466, and we chose to impose incompressibility.
To characterize the distribution of material orientations, we used the local coordinate system with , and (figure 6a) as the circumferential, longitudinal and transmural normal vectors, assuming with ramping linearly from on endocardial surface to on epicardial surface [41], and .
For epicardium, we used the Holzapfel–Ogden (equations (2.7)–(2.10)) model assuming and . We assumed that the values of and are the same as those of the porcine myocardium. By fitting the biaxial tension data of the middle lateral sample (figure 5e), we obtained a = 0.496 kPa, b = 6.82, af = 19.85 kPa, bf = 32.59, as = 11.26 kPa and bs = 8.20. The fitted stress–strain curve was compared against the experimental data in figure 6b which showed good agreement. The prestrains we applied come from the middle lateral sample (table 2) and were introduced through a pre-factor in deformation gradient . To compute stress, we will use , where represents the deformation happening afterwards.
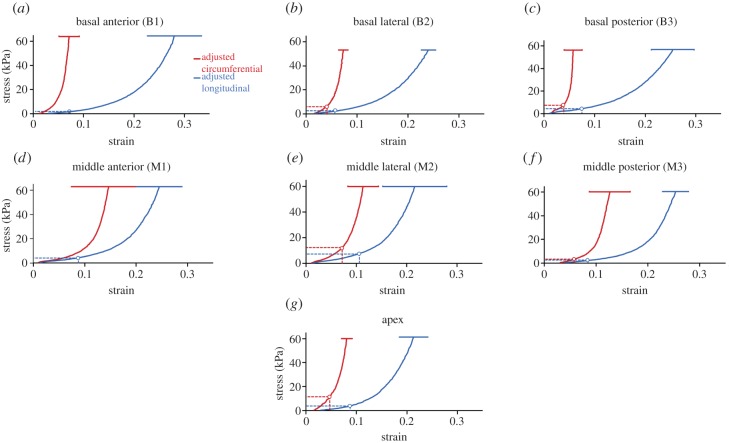
Figure 5.
Circumferential residual stresses σX(residual) (red dashed lines) and longitudinal residual stress σY(residual) (blue dashed lines) predicted by prestrains (ɛX and ɛY) for seven anatomical locations: (a) basal anterior, (b) basal lateral, (c) basal posterior, (d) middle anterior, (e) middle lateral, (f) middle posterior, and (g) apex locations. Adjusted biaxial stress–strain curves were used for the quantitative estimation of the regional residual stresses. Red solid curve: stress–strain curve along circumferential direction with error bar (red solid bar); blue solid curve: stress–strain curve along longitudinal direction with error bar (blue solid bar). (Online version in colour.)
Table 2.
Estimated prestrains and residual stresses of the epicardial layer on the unpressurized intact heart. Prestrains (ɛX, ɛY) for each anatomical location were estimated by comparing stress-free marker dimensions (dissected epicardial layer) and in situ marker dimensions (epicardial layer on the unpressurized intact heart). Note: Stress-free marker dimensions were used as reference to calculate the prestrains. The residual stresses (σX(residual), σY(residual)) for each anatomical location were predicted by prestrains (ɛX and ɛY) using the adjusted biaxial stress–strain curves (figure 5).
| N = 5 | ɛX | σX(residual) (kPa) | ɛY | σY(residual) (kPa) |
|---|---|---|---|---|
| basal anterior (B1) | −0.30 ± 4.25% | 0 | 8.59 ± 3.62% | 2.39 |
| basal lateral (B2) | 4.66 ± 0.44% | 8.95 | 6.75 ± 1.85% | 3.05 |
| basal posterior (B3) | 3.01 ± 4.58% | 4.68 | 7.72 ± 4.38% | 4.48 |
| middle anterior (M1) | −3.51 ± 3.07% | 0 | 8.72 ± 6.70% | 4.29 |
| middle lateral (M2) | 7.09 ± 3.43% | 12.09 | 10.70 ± 1.36% | 7.88 |
| middle posterior (M3) | 5.50 ± 3.10% | 2.89 | 8.31 ± 4.55% | 2.06 |
| apex | 4.89 ± 1.72% | 12.24 | 8.84 ± 3.37% | 3.89 |
For boundary conditions, we prescribed on the basal plane, and on its outer edge we prescribed in the circumferential direction (figure 6a). On the endocardial surface, we applied a pressure that increases from 0 to 40 mmHg. The calculations were performed using the open-source package FEBio [42].
2.5. Histological assessment
To reveal the structural contributors in surface strip curling, we performed a histological assessment to compare the epicardial microstructure on the unpressurized intact heart to the epicardial microstructure on the dissected, curled surface strip. For the intact heart surface strip, the intact heart was fixed in 10% buffered formalin solution for 72 h. The dissected heart surface strip, which preserved the natural curvature of heart surface, was then embedded in paraffin and sectioned into 5 µm slices for Movat's pentachrome staining. To obtain the curled surface strip for histology, we put the freshly dissected heart surface strip into PBS as mentioned in §2.2 and waited for full curling to occur. The PBS solution was then replaced with 10% buffered formalin solution for fixation. The fixation was able to preserve the curled surface strip configuration, and the curled sample was embedded in paraffin and sectioned into 5 µm slices for Movat's pentachrome staining, in which the elastin appears black, collagen appears yellow and muscle appears red under white field light microscopy (Eclipse Ti, Nikon).
3. Results
3.1. Left ventricle surface strip curling and total curling angular change
The curling of LV surface strips provides us with a sensitive characterization of the epicardial residual stress. Native heart surface strips along the circumferential direction (CD) (figure 3b) and longitudinal direction (LD) (figure 3d) were quantified for curling angle measurement. Heart surface strips from the formalin-fixed heart were also quantified for heart surface curvature measurement (figure 3a,c). We observed that the native heart surface strips showed various degrees of curling in different anatomical locations (figure 3b,d).
Figure 3.
Native heart surface strips show the curling phenomenon. All seven anatomical locations of the left ventricle, i.e. basal anterior, basal lateral, basal posterior, middle anterior, middle lateral, middle posterior and apex, are shown. (a) Circumferentially oriented heart surface strips dissected from the formalin-fixed intact heart; 10% buffered formalin solution fixation was able to preserve the natural curvature of the intact heart. Images are side views of the dissected formalin-fixed strips, showing the circumferential natural curvatures of the heart at seven anatomical locations. (b) Circumferentially oriented heart surface strips dissected from the unpressurized native intact heart. Images are side views of the dissected native strips, showing a various degree of curling towards the epicardial side at seven anatomical locations. (c) Longitudinally oriented heart surface strips dissected from the formalin-fixed intact heart; 10% buffered formalin solution fixation was able to preserve the natural curvature of the intact heart. Images are side views of the dissected formalin-fixed strips, showing the longitudinal natural curvatures of the heart at seven anatomical locations. (d) Longitudinally oriented heart surface strips dissected from the unpressurized native intact heart. Images are side views of the dissected native strips, showing a various degree of curling towards the epicardial side at seven anatomical locations. (Online version in colour.)
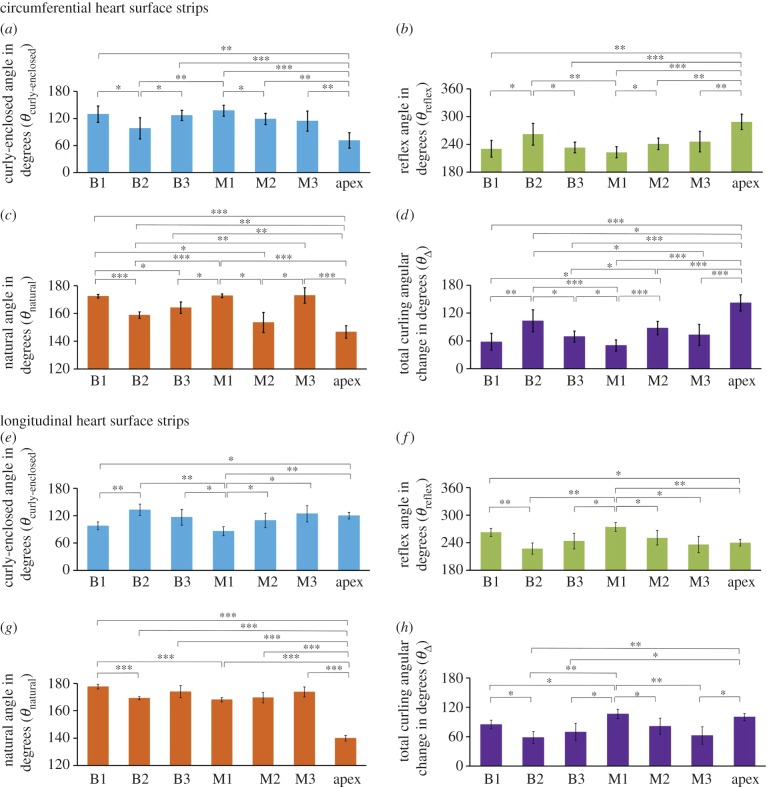
As shown in figure 3a,c, 10% buffered formalin solution was able to preserve the natural curvature of the unpressurized intact heart even after the surface strips were dissected out from the heart. Based on our definition, the smaller the natural angle (θnatural), the larger the curvature of the heart. We noticed that, for the CD, the basal lateral location (B2), middle lateral location (M2), and apex location had larger heart surface curvatures when compared to the basal anterior location (B1), basal posterior location (B3), middle anterior location (M1), and middle posterior location (M3) (figure 4c). As for the LD, the apex region had an obviously larger heart surface curvature and other anatomical locations had relatively small curvatures (figure 4g). Based on the definition of curly-enclosed angle (θcurly-enclosed), the smaller the curly-enclosed angle, the larger the reflective angle (θreflex), and the more likely the larger curling would happen. Using natural angle (θnatural) as the baseline, we were able to obtain the total curling angular change (θΔ) by using equation (2.1) and equation (2.2).
Figure 4.
Measurements of four types of angles to quantify the degree of curling in the circumferentially dissected and longitudinally dissected heart surface strips at seven anatomical locations. Circumferentially oriented heart surface strips: (a) curly-enclosed angle (θcurly-enclosed) in degrees; (b) reflex angle (θreflex) in degrees; (c) natural angle (θnatural) in degrees; and (d) total curling angular change (θΔ) in degrees. Longitudinally oriented heart surface strips: (e) curly-enclosed angle (θcurly-enclosed) in degrees; (f) reflex angle (θreflex) in degrees; (g) natural angle (θnatural) in degrees; and (h) total curling angular change (θΔ) in degrees. *, ** and *** denote the statistical significance between different anatomical locations of four types of angles (one-way ANOVA) when p < 0.05, p < 0.01 and p < 0.001, respectively. (Online version in colour.)
A summary of θcurly-enclosed and θnatural measurements, as well as the calculated total curling angular change (θΔ), was presented in figure 4 and table 1. For the CD, the total curling angular change revealed that (i) the larger curling occurred in the basal lateral location (B2) (θΔ = 103.2 ± 23.7°) when compared to the basal anterior location (B1) (θΔ = 60.0 ± 18.2°) and basal posterior location (B3) (θΔ = 69.1 ± 12.1°); (ii) the larger curling occurred in the middle lateral location (M2) (θΔ = 87.6 ± 14.4°) when compared to the middle anterior (M1) (θΔ = 50.0 ± 12.3°) and middle posterior (M3) (θΔ = 72.9 ± 22.8°); (iii) the apex location had the largest circumferential curling (θΔ = 142.0 ± 17.5°) (figure 4d).
Table 1.
Calculation of total curling angular change (θΔ). Data summary for measurements of θcurly-enclosed, θnatural and θΔ for each anatomical location. Note: θcurly-enclosed is the curly-enclosed angle, θnatural is the natural angle and θΔ is the total curling angular change. CD represents the circumferential direction, and LD represents the longitudinal direction.
|
N = 5 (unit: degree °) |
θcurly-enclosed | θnatural | θΔ | |
|---|---|---|---|---|
| basal anterior (B1) | CD | 129.6 ± 18.1 | 172.4 ± 1.4 | 60.0 ± 18.2 |
| LD | 97.4 ± 8.6 | 117.6 ± 1.7 | 85.0 ± 8.8 | |
| basal lateral (B2) | CD | 98.0 ± 23.5 | 158.8 ± 2.3 | 103.2 ± 23.7 |
| LD | 132.8 ± 12.3 | 169.2 ± 1.1 | 58.0 ± 12.3 | |
| basal posterior (B3) | CD | 126.7 ± 11.4 | 164.1 ± 4.1 | 69.1 ± 12.1 |
| LD | 116.4 ± 17.2 | 173.9 ± 4.4 | 69.6 ± 17.8 | |
| middle anterior (M1) | CD | 137.2 ± 12.2 | 172.7 ± 1.3 | 50.0 ± 12.3 |
| LD | 85.8 ± 9.7 | 168.0 ± 1.5 | 106.2 ± 9.8 | |
| middle lateral (M2) | CD | 110.0 ± 12.5 | 153.4 ± 7.2 | 87.6 ± 14.4 |
| LD | 109.3 ± 15.9 | 169.5 ± 3.9 | 81.2 ± 16.4 | |
| middle posterior (M3) | CD | 114.2 ± 22.1 | 173.0 ± 5.6 | 72.9 ± 22.8 |
| LD | 124.1 ± 17.7 | 173.7 ± 3.6 | 62.3 ± 18.1 | |
| apex | CD | 71.3 ± 16.9 | 146.7 ± 4.5 | 142.0 ± 17.5 |
| LD | 120.0 ± 7.1 | 139.9 ± 2.0 | 100.1 ± 7.4 | |
For the LD, (i) the curling was larger in the basal anterior location (B1) (θΔ = 85.0 ± 8.8°) when compared to the basal lateral location (B2) (θΔ = 58.0 ± 12.3°) and basal posterior location (B3) (θΔ = 69.6 ± 17.8°); (ii) the curling in the middle anterior location (M1) (θΔ = 106.2 ± 9.8°) was larger than the middle lateral location (M2) (θΔ = 81.2 ± 16.4°) and middle posterior location (M3) (θΔ = 62.3 ± 18.1°); (iii) again, the curling in the apex location was very large (θΔ = 100.1 ± 7.4°) (figure 4h).
It is also possible to compare the directional differences in the same anatomical location. For instance, we found that for the basal anterior location (B1), the circumferential curling angular change (θΔ = 60.0 ± 18.2°) was smaller than the longitudinal curling angular change (θΔ = 85.0 ± 8.8°), indicating that, in the basal anterior location (B1), the circumferential residual stress is smaller than the longitudinal residual stress. For the basal lateral location (B2), the circumferential curling angular change (θΔ = 103.2 ± 23.7°) was much larger than the longitudinal curling angular change (θΔ = 58.0 ± 12.3°), indicating that, in the basal lateral location (B2), the circumferential residual stress is much larger than the longitudinal residual stress.
3.2. Estimation of the prestrains of the epicardial layer
The average prestrains (ɛX and ɛY) for each anatomical location were calculated and listed in table 2. Several observations of table 2 are summarized as follows: (i) for nearly all the anatomical locations, the prestrains of both the circumferential and longitudinal directions (ɛX and ɛY) were positive, except for ɛX in the basal anterior location (B1) and middle anterior location (M1). The positive prestrains on the unpressurized intact heart mean that the epicardial layer was under tension and positive residual stresses existed. (ii) We found that ɛY was much larger than ɛX in the basal anterior location (B1: ɛX = −0.30 ± 4.25%; ɛY = 8.59 ± 3.62%) and middle anterior location (M1: ɛX = −3.51 ± 3.07%; ɛY = 8.72 ± 6.70%). (iii) ɛX was slightly smaller than ɛY in the basal lateral location (B2: ɛX = 4.66 ± 0.44%; ɛY = 6.75 ± 1.85%) and middle lateral location (M2: ɛX = 7.09 ± 3.43%; ɛY = 10.70 ± 1.36%), while both ɛX and ɛY were large. (iv) ɛX was smaller than ɛY in the basal posterior location (B3: ɛX = 3.01 ± 4.58%; ɛY = 7.72 ± 4.38%) and middle posterior location (M3: ɛX = 5.50 ± 3.10%; ɛY = 8.31 ± 4.55%). (v) For the apex location, both ɛX and ɛY were relatively large (apex: ɛX = 4.89 ± 1.72%; ɛY = 8.84 ± 3.37%).
3.3. Estimation of the residual stresses (σX(residual), σY(residual)) for each anatomical location
The final compensatory strains (ɛX(0.5), ɛY(0.5)) with respect to the 0 g load reference are listed in electronic supplementary material, table S1 and used to shift the biaxial stress–strain curves accordingly (figure 5). With the adjusted biaxial stress–strain data (figure 5) and the prestrain data (table 2), we could estimate the residual stresses for each anatomical location. In figure 5, red dashed lines label the circumferential residual stresses (σX(residual)) predicted by the circumferential prestrains (ɛX), and blue dashed lines label the longitudinal residual stresses (σY(residual)) predicted by the longitudinal prestrains (ɛY). The detailed numbers of ɛX → σX(residual) and ɛY → σY(residual) for each anatomical location are listed in table 2.
The mapping of residual stresses on the LV showed that residual stresses did exist and varied with different anatomical locations. Both the basal anterior location (B1) (σX(residual) = 0 kPa, σY(residual) = 2.39 kPa) and middle anterior location (M1) (σX(residual) = 0 kPa, σY(residual) = 4.29 kPa) showed a longitudinal residual stress of several kilopascals but predicted negligible circumferential residual stress. The basal posterior location (B3) (σX(residual) = 4.68 kPa, σY(residual) = 4.48 kPa) had both the circumferential residual stress and longitudinal residual stresses of several kilopascals; the middle posterior location (M3) (σX(residual) = 2.89 kPa, σY(residual) = 2.06 kPa) also had comparable circumferential and longitudinal residual stresses around 1 kPa. However, both the basal lateral location (B2) (σX(residual) = 8.95 kPa, σY(residual) = 3.05 kPa) and middle lateral location (M2) (σX(residual) = 12.09 kPa, σY(residual) = 7.88 kPa) showed a pattern of circumferential residual stress being larger (around 10 kPa) than the longitudinal residual stress. The apex region (σX(residual) = 12.24 kPa, σY(residual) = 3.89 kPa) showed a pattern similar to the laterals, i.e. a large circumferential residual stress around 10 kPa, but a longitudinal residual stress of several kilopascals.
3.4. Finite-element modelling of ventricular cavity volume against hydrostatic pressure
The computed cavity volume–pressure curve was plotted in figure 6c and the relation between the pressure and the average myocardial first principle stress was shown in figure 6d, where the blue curve showed the case without epicardial prestrain, the red curve with prestrain, and the black curve without epicardium at all. We could notice that, with the presence of epicardial layer alone, the cavity volume barely differed from the pristine ventricle model and the average myocardial first principle stress only decreased slightly. Yet when prestrain was applied, a non-trivial shift (up to approx. 4.8 ml, approx. 13% shift) towards smaller volume and lower average myocardial first principle stress emerged (figure 6c,d). This showed that, by contracting against the myocardial tension, the epicardial layer provided additional confining and protection to LV wall. The contrast between the prestrained and the un-prestrained cases also implied the majority of the confinement effect actually comes from the prestraining instead of the epicardial layer alone.
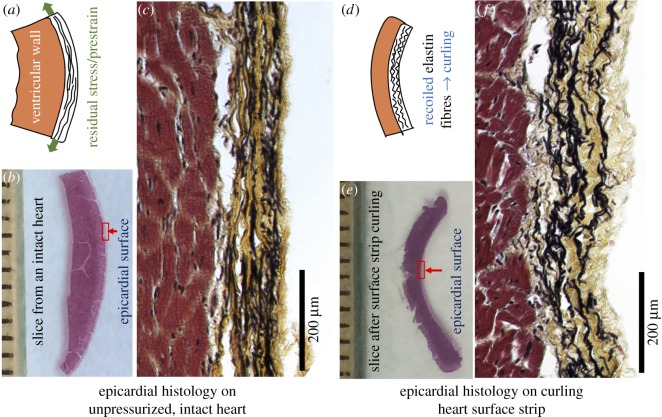
3.5. Epicardial microstructure on heart surface and curled surface strip
Figure 7b shows a histological slice of the sample dissected from the formalin-fixed intact heart. The slice shows that the natural curvature of the surface of the heart was preserved, indicating that the microstructure of the epicardium (red rectangular box) reflects the elastin and collagen network configurations on the unpressurized intact heart. Histological image of the epicardium showed that the elastin fibres (black colour) exhibited a low degree of waviness, and the network had a pre-tensioned morphology (figure 7c). Interestingly, the collagen fibres (yellow colour) that were associated with the elastin fibres demonstrate a moderate degree of waviness.
Figure 7.
A histological study to compare the epicardial microstructure on the unpressurized intact heart to the epicardial microstructure on the curled heart surface strip. Movat's pentachrome staining was performed, in which elastin was black, collagen yellow and muscle red. (a) Schematic illustration shows the existence of prestraining/residual stress. (b) Histological slice from an intact heart. (c) On the intact heart, elastin network in epicardium appears less wavy, with a pre-tensioned morphology. (d) Schematic illustration shows that the recoiled elastin fibres bend the bi-layered surface strip. (e) Histological slice obtained after full curling of the native heart surface strip. (f) On the curled surface strip, the elastin pre-tensioned morphology disappears and the elastin network appears recoiled and having more waviness, indicating the release of residual stress. (Online version in colour.)
Figure 7e shows a histological slice sectioned from the curled heart surface strip. It is worth reiterating that the surface strip was first dissected from a fresh pig heart and went through the curling; after the full curling occurred, the curled strip was fixed with formalin solution and the curled tissue morphology was preserved. The morphological observation indicates that, on the curled surface strip, the elastin pre-tensioned morphology disappears, and the elastin fibres (black colour) showed a recoiled, highly wavy morphology, indicating the release of tension (figure 7f). The collagen fibres (yellow colour) that were associated with the elastin fibres also showed a more wavy morphology than that on the intact heart (figure 7f).
4. Discussion
4.1. Curling of heart surface strips
The heart surface strip curling clearly reveals the existence of residual stress in the epicardial layer. In other words, the epicardial layer is under tension (prestrained) when it covers the unpressurized intact heart in its in situ 3D configuration (figure 7a). After a bi-layered surface strip (myocardial layer + epicardial layer) is dissected from the heart, the boundary condition that restricts the prestrained epicardial layer from contraction does not exist anymore. As a result, the contraction of the epicardial layer bends the tissue strip and a curling morphology occurs (figure 7d). By measuring the curly-enclosed angle (θcurly-enclosed) of the dissected native heart surface strip and the natural angle (θnatural) that reflects the heart surface curvature, we were able to obtain the total angular change due to curling (θΔ). This total curling angular change (θΔ) gives us a qualitative assessment of the degree of residual stress.
The reason we call the total curling angular change (θΔ) qualitative assessment is due to the fact that the θΔ will be affected by the surface strip dimensions. So, the comparison should be based on the same sample dimensions. As to the selection of approximately 15 mm × 5 mm × 1.5 mm for our study, we chose the dimensions by examining the curling responses of strips with varying sizes, as well as the following considerations. (i) Strip thickness is a crucial factor that determines optimal curling. We need a bi-layered structure with one side as the epicardial layer and the other side as the myocardium. The approximately 1.5 mm thickness includes the elastin-dominated epicardial layer (approx. 200 µm) and a myocardial layer (approx. 1300 µm), which were found to generate an optimal curling behaviour along with the chosen strip length and width (figure 1b). (ii) The chosen strip length and width also helped achieve the stress-free status easily in 1X PBS solution, experiencing minimum friction from the bottom of the Petri dish while not floating around and being unstable. A stress-free ‘curling’ configuration is of importance for obtaining the side view picture of the surface strip for curly-enclosed angle quantification. The robustness of the curling measurement was shown in electronic supplementary material, figure S3.
During the surface strip dissection, we attempted to make sample dimensions consistently at approximately 15 mm × 5 mm × 1.5 mm; however, experimentalists understand the challenge of soft tissue dissection, i.e. the dissected samples always have small variations in dimensions. Even though the uncertainties caused by factors such as dissection and heart-to-heart variation have been averaged out by repetitive testing (N = 5), we did notice that the standard deviations of curling measurements were relatively large. Furthermore, some images in figure 3b,d show that the curling is accompanied by a degree of diagonal twisting. We speculate that, if the overall orientation of the elastin fibres is not fully aligned with the long axis of the rectangular surface strip, the curling can be accompanied by certain diagonal twisting, a phenomenon worthy of further investigation.
4.2. Quantification of the location-dependent epicardial residual stress
In this study, the prestrains and residual stresses of the epicardial layer on the LV were revealed and quantitatively estimated. Our prestrain measurement method provided a straightforward and practical approach to capture the change of epicardial tissue dimension after dissection via the tracking of markers. Via the adjusted biaxial stress–strain curves, the residual stresses could be predicted from the prestrains. We found that there are residual stresses in all anatomical locations (table 2). Moreover, the residual stresses along the CD (σX(residual)) and LD (σY(residual)) were all location-dependent. For example, both the basal lateral location (B2) and middle lateral location (M2) had relatively large circumferential residual stresses (basal lateral: σX(residual) = 8.95 kPa, σY(residual) = 3.05 kPa, middle lateral: σX(residual) = 12.09 kPa, σY(residual) = 7.88 kPa). We also noticed a similar pattern in the apex region (σX(residual) = 12.24 kPa, σY(residual) = 3.89 kPa).
Considering the geometry of the intact heart, the circumferential direction of the lateral locations as well as the apex location experience large curvature. The relatively large circumferential residual stresses (σX(residual)) of the basal lateral location (B2), middle lateral location (M2), and apex might be correlated with the large curvature of the heart surface. We also noticed that the basal anterior location (B1) and middle anterior location (M1) had very low circumferential residual stresses (σX(residual)) and prestrains (table 2). We speculate that this might also be related to their anatomical configuration, possibly a relatively flat circumferential contour. It should still be noted that, by using equibiaxial tension protocol, not all information of the material anisotropy could be revealed, and thus future detailed testings are required for a full mechanical characterization.
4.3. Finite-element modelling of the epicardial prestraining
In most FE modelling of ventricles, the epicardium is usually absent and considered negligible. Yet in our model, we found that the ventricular volume would be non-trivially smaller under the same static pressure with prestrained epicardium, and lower average myocardial first principle stress was observed due to the epicardial prestraining. Usually, parietal pericardium sac is associated with an important function of limiting ventricular filling and preventing high diastolic pressure [16], and our results indicate that such capability can also come from epicardial prestraining. If prestrain is absent, the confining capability of the epicardium to reduce the cavity volume and the average myocardial first principle stress would be significantly impaired even if the epicardium itself is intact. Moreover, how the epicardial prestraining would participate in the cardiac cycle, affect ventricular filling and protect the myocardium, especially during the early ejection phase, remains an open but interesting question. These could be some important aspects in cardiac biomechanics/physiology to be addressed in the future studies and modelling.
We also noted that the end-diastolic pressure–volume curve was in good agreement with the experiment data [43] despite the simplified geometry in our model. However, in this paper for simplicity, we did not account for the inhomogeneous distribution of epicardial mechanical properties and prestrain, and it may imply important local features as the epicardial curvature varies spatially as well. As a preliminary attempt to investigate how the different epicardial parameters at different locations may influence the ventricle system, we employed the data from several other locations (figure 5, table 2) in our homogeneous model. The results (electronic supplementary material, figure S2) showed that, though the effects were varied, the parameters from different locations all had confining capability. Future FE modelling will include the inhomogeneous distribution of epicardial mechanical properties and prestrains. Future study will also examine the physical basis of prestraining, such as its detailed relation with heart surface curvature and whether the configuration of myocardial fibres adjacent to the epicardial layer plays any role in influencing the epicardial prestraining.
4.4. Elastin network and collagen network in epicardial prestraining
As we discussed in §4.1, the epicardial layer is under tension when it covers the unpressurized intact heart. One can envision that the elastin network, along with collagen fibres, is pre-tensioned and contributes to the residual stress. Once a surface strip is dissected from the heart, the boundary condition that restricts the elastin network from contraction vanishes. Consequently, the pre-tensioned elastin network contracts and bends the bi-layered surface strip. In the curled surface strip, the histological study demonstrated that the elastin pre-tensioned morphology disappears, and the elastin network demonstrates a recoiled, higher degree of waviness, indicating the release of tension (figure 7f). Note that the epicardial elastin network on the unpressurized intact heart still showed a lower degree of waviness, and collagen fibres that associated with the elastin fibres had a moderate degree of waviness (figure 7c). Those configurations remind us that the intact heart is still in an unpressurized status, and both fibre networks will be straightened and recruited more once the LV wall is pressurized and deformed.
Considering the epicardial elastin fibres on the unpressurized intact heart had a lower degree of waviness and collagen fibres had a moderate degree of waviness, we speculate that the elastin network might contributes more to epicardial residual stress than the collagen network. The recoiled, highly wavy elastin fibre morphology on the curled surface strip further support this speculation. Indeed, on an unpressurized heart, preservation of a moderate degree of waviness gives epicardial collagen network the much-needed extensibility for later large ventricular wall deformation. Although the contribution from collagen network to epicardial residual stress seems to be smaller than the elastin network based on our histological observation, future quantitative studies are needed to accurately determine the portions of contribution from elastin network and collage network.
The aortic valve leaflet is another good example showing elastin network's contribution to tissue residual stress [44]. Aortic valve leaflets consist of three layers: a collagen-dominated fibrosa layer, a glycosaminoglycan-dominated spongiosa layer (middle cushion layer) and an elastin fibre-dominated ventricularis layer. Vesely [44] showed that, in the intact aortic valve leaflet, the collagen-dominated fibrosa is under compression and the elastin fibre-dominated ventricularis layer is under tension (prestraining of elastin network); once those two layers are separated from each other to release internal stresses, the areal dimension of fibrosa enlarges and the areal dimension of ventricularis shrinks (due to elastin network contraction). As for the collagen network, the prestraining of collagen has been reported in aneurysm walls, i.e. the collagen fibres can be deposited by the fibroblasts in a pre-stretched condition during the aneurysm tissue turnover [45,46].
4.5. Porcine heart arrest status and rigour mortis
It is important to note that in our studies fresh porcine hearts were at an unpressurized status after the captive bolt stunning and exsanguination (draining of blood) slaughtering procedure. After captive bolt stunning, the significantly thicker left ventricular myocardium in healthy animals squeezes the blood out of the ventricles as the heart muscle goes into rigour, which accounts for the slight contracture of the heart after death when rigour mortis has occurred [47–49]. The existence of epicardial prestrains on those slightly contracted hearts indicates that the observed prestraining is not caused by artefact. Indeed, if the slight contracture of the arrested hearts (due to the slaughtering procedure) does not happen, the prestrains will be measured with slightly larger numbers. In our whole study, all of the hearts were obtained and subjected to experiments the same day as the slaughter of the pigs. Due to the fact that elastin (dominant) and collagen are the major components of the epicardial layer, the postmortem effect has minimal influence on the passive mechanical properties of the epicardial layer. The heart muscles, however, experienced rigour mortis (stiffening) compared to the in vivo condition. This rigidity seems not to affect the overall trend of surface strip curling since a less stiff muscle layer will likely be bent more when the epicardial layer contracts.
5. Conclusion
Built on our observation that the bi-layered heart surface strip always curls towards the epicardial side, we successfully developed a qualitative approach to reveal the residual stress in the epicardial layer. The curling angle characterizations of the circumferential strip and longitudinal strip provide not only an intuitive method to reveal the existence of residual stresses by measuring the total curling angular change (θΔ), but also a semi-quantitative method to display the location-dependency and direction-dependency of the epicardial residual stresses.
We further developed a method to quantitatively assess the epicardial residual stresses of the LV by combining prestrain measurement and biaxial mechanical testing. For the first time, we were able to quantitatively estimate (i) the epicardial prestrains along the circumferential direction (ɛX) and longitudinal direction (ɛY), and (ii) the circumferential residual stress (σX(residual)) and the longitudinal residual stress (σY(residual)) of the left ventricular epicardial layer. We also noticed correlation between our prestrain/residual stress results and curling angle measurements. For instance, we found that the basal lateral location (B2) had relatively large circumferential prestrain (ɛX) and residual stresses (σX(residual)) when compared to the basal anterior (B1) and basal posterior (B3) location, and the middle lateral location (M2) also had relatively large circumferential prestrain (ɛX) and residual stresses (σX(residual)) when compared to the middle anterior (M1) and middle posterior (M3) locations (table 2). Those observations were consistent with total curling angle measurements, which showed that θΔ of basal lateral (B2) was larger than θΔ of basal anterior (B1) and basal posterior (B3), and θΔ of middle lateral (M2) was larger than θΔ of middle anterior (M1) and middle posterior (M3) (table 1). We know that the circumferential direction of the lateral location experiences very large curvature. The relatively large σX(residual) of the basal lateral location (B2) and middle lateral location (M2) might be correlated with the large curvature of the heart surface at those locations.
The existence of residual stresses and prestraining has its physiological relevance for organ/tissue functionality. To investigate the potential mechanical effect of epicardial prestraining, a FE model was constructed, and we found that the prestrained epicardial layer can provide additional confining to the ventricle and reduce its cavity volume. We further showed that, such resistance mainly comes from the prestraining instead of the epicardium alone.
In short, the epicardial layer, with its rich elastin content, acts like a prestrained ‘balloon’ wrapping around the heart. From a biomechanical perspective, the epicardial prestrained confinement (residual stress) provides an additional resistance mechanism during LV diastolic expansion and ventricular wall protection by reducing myocardial stress, and might further assist with the contraction of the LV by epicardial recoiling. Our future studies will focus on the understanding of how the epicardial prestraining facilitates cardiac biomechanical functions, and how heart diseases, such as MI, could possibly alter the prestrained confinement (residual stress) of the epicardial layer and hence weaken the protections in ventricular diastolic expansion and efficiency of ventricular contraction. Future therapeutic efforts for MI/heart failure can possibly target the maintenance/recreation of this ventricle confinement interface via designing novel biomimicking materials or prosthetic devices. For example, passive prosthetic wrap devices and cardiac patch/meshing techniques might benefit from applying a similar prestrained confinement, as well as mimicking the material properties of the epicardial layer.
Supplementary Material
Acknowledgement
The authors gratefully thank Dr Bryn Brazile, Sarah Fitzgerald, Sammira Rais-Rohani, Dr Jim Cooley, and Amanda Lawrence for assistance and support.
Data accessibility
The primary data are available in the figures, tables and electronic supplementary material.
Authors' contributions
All listed authors contributed substantially to the work presented in this paper.
Competing interests
We declare we have no competing interests.
Funding
The authors would like to thank the support of 1R01EB022018-01 from NIH, 13GRNT17150041 from AHA, and UT STARS. K.M.C. is supported by NIH T32 HL134613. Y.L. and H.G. have been supported by NSF grant no. CMMI-1562904.
References
- 1.Benjamin EJ, et al. 2017. Heart disease and stroke statistics—2017 update: a report from the American Heart Association. Circulation 135, e146–e603. ( 10.1161/CIR.0000000000000485) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Raab W. 1963. The nonvascular metabolic myocardial vulnerability factor in ‘coronary heart disease’. Fundamentals of pathogenesis, treatment, and prevention. Am. Heart J. 66, 685–706. ( 10.1016/0002-8703(63)90327-2) [DOI] [PubMed] [Google Scholar]
- 3.Baroldi G. 1973. Coronary heart disease: significance of the morphologic lesions. Am. Heart J. 85, 1–5. ( 10.1016/0002-8703(73)90519-X) [DOI] [PubMed] [Google Scholar]
- 4.Baroldi G. 1965. Acute coronary occlusion as a cause of myocardial infarct and sudden coronary heart death. Am. J. Cardiol. 16, 859–880. ( 10.1016/0002-9149(65)90704-6) [DOI] [PubMed] [Google Scholar]
- 5.Erhardt LR, Unge G, Boman G. 1976. Formation of coronary arterial thrombi in relation to onset of necrosis in acute myocardial infarction in man. A clinical and autoradiographic study. Am. Heart J. 91, 592–598. ( 10.1016/S0002-8703(76)80144-5) [DOI] [PubMed] [Google Scholar]
- 6.Reichenbach DD, Moss NS. 1975. Myocardial cell necrosis and sudden death in humans. Circulation 52, 60–62. [PubMed] [Google Scholar]
- 7.Silver MD, Anderson TW, Vand Dreumel AA, Hutson RE. 1973. Letter: Nutritional muscular dystrophy and human myocardial infarction. Lancet 2, 912–913. ( 10.1016/S0140-6736(73)92046-1) [DOI] [PubMed] [Google Scholar]
- 8.Narula J, et al. 1996. Apoptosis in myocytes in end-stage heart failure. N. Engl. J. Med. 335, 1182–1189. ( 10.1056/NEJM199610173351603) [DOI] [PubMed] [Google Scholar]
- 9.Robin ED. 1977. Special report: dysoxia. Abnormal tissue oxygen utilization. Arch. Intern. Med. 137, 905–910. ( 10.1001/archinte.1977.03630190059015) [DOI] [PubMed] [Google Scholar]
- 10.Cleutjens JP, Blankesteijn WM, Daemen MJ, Smits JF. 1999. The infarcted myocardium: simply dead tissue, or a lively target for therapeutic interventions. Cardiovasc. Res. 44, 232–241. ( 10.1016/S0008-6363(99)00212-6) [DOI] [PubMed] [Google Scholar]
- 11.De Celle T, Cleutjens JP, Blankesteijn WM, Debets JJ, Smits JF, Janssen BJ.. 2004. Long-term structural and functional consequences of cardiac ischaemia–reperfusion injury in vivo in mice. Exp. Physiol. 89, 605–615. ( 10.1113/expphysiol.2004.027649) [DOI] [PubMed] [Google Scholar]
- 12.Gaby AR. 2010. Nutritional treatments for acute myocardial infarction. Altern. Med. Rev. 15, 113–123. [PubMed] [Google Scholar]
- 13.Janicki JS, Brower GL, Gardner JD, Chancey AL, Stewart JA Jr. 2004. The dynamic interaction between matrix metalloproteinase activity and adverse myocardial remodeling. Heart Fail. Rev. 9, 33–42. ( 10.1023/B:HREV.0000011392.03037.7e) [DOI] [PubMed] [Google Scholar]
- 14.Spinale FG, Janicki JS, Zile MR. 2013. Membrane-associated matrix proteolysis and heart failure. Circ. Res. 112, 195–208. ( 10.1161/circresaha.112.266882) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tsuruda T, Costello-Boerrigter LC, Burnett JC Jr. 2004. Matrix metalloproteinases: pathways of induction by bioactive molecules. Heart Fail. Rev. 9, 53–61. ( 10.1023/B:HREV.0000011394.34355.bb) [DOI] [PubMed] [Google Scholar]
- 16.Katz AM. 2006. Physiology of the heart, 4th edn Philadelphia, PA: Lippincott Williams & Wilkins. [Google Scholar]
- 17.Kwon MH, Cevasco M, Schmitto JD, Chen FY. 2012. Ventricular restraint therapy for heart failure: a review, summary of state of the art, and future directions. J. Thorac. Cardiovasc. Surg. 144, 771–777. ( 10.1016/j.jtcvs.2012.06.014) [DOI] [PubMed] [Google Scholar]
- 18.Lee LS, Ghanta RK, Mokashi SA, Coelho-Filho O, Kwong RY, Bolman RM 3rd, Chen FY. 2010. Ventricular restraint therapy for heart failure: the right ventricle is different from the left ventricle. J. Thorac. Cardiovasc. Surg. 139, 1012–1018. ( 10.1016/j.jtcvs.2009.09.064) [DOI] [PubMed] [Google Scholar]
- 19.Naveed M, et al. 2018. The promising future of ventricular restraint therapy for the management of end-stage heart failure. Biomed. Pharmacother. 99, 25–32. ( 10.1016/j.biopha.2018.01.003) [DOI] [PubMed] [Google Scholar]
- 20.Jöbsis PD, Ashikaga H, Wen H, Rothstein EC, Horvath KA, McVeigh ER, Balaban RS. 2007. The visceral pericardium: macromolecular structure and contribution to passive mechanical properties of the left ventricle. Am. J. Physiol. Heart Circ. Physiol. 293, H3379–H3387. ( 10.1152/ajpheart.00967.2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Williams C, Black LD III. 2015. The role of extracellular matrix in cardiac development. In Biomaterials for cardiac regeneration (eds EJ Suuronen, M Ruel), pp. 1–35. Cham, Switzerland: Springer. [Google Scholar]
- 22.Farquharson C, Robins SP. 1989. The distribution of elastin in developing and adult rat organs using immunocytochemical techniques. J. Anat. 165, 225. [PMC free article] [PubMed] [Google Scholar]
- 23.Fomovsky GM, Thomopoulos S, Holmes JW. 2010. Contribution of extracellular matrix to the mechanical properties of the heart. J. Mol. Cell. Cardiol. 48, 490–496. ( 10.1016/j.yjmcc.2009.08.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Borg T, Caulfield J. 1981. The collagen matrix of the heart. Fed. Proc. 40, 2037–2041. [PubMed] [Google Scholar]
- 25.Sussman MA, McCulloch A, Borg TK. 2002. Dance band on the titanic biomechanical signaling in cardiac hypertrophy. Circ. Res. 91, 888–898. ( 10.1161/01.RES.0000041680.43270.F8) [DOI] [PubMed] [Google Scholar]
- 26.Granzier HL, Irving TC. 1995. Passive tension in cardiac muscle: contribution of collagen, titin, microtubules, and intermediate filaments. Biophys. J. 68, 1027–1044. ( 10.1016/S0006-3495(95)80278-X) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kang T, Humphrey J, Yin F. 1996. Comparison of biaxial mechanical properties of excised endocardium and epicardium. Am. J. Physiol. Heart Circ. Physiol. 270, H2169–H2176. ( 10.1152/ajpheart.1996.270.6.H2169) [DOI] [PubMed] [Google Scholar]
- 28.Kluge T, Hovig T. 1967. The ultrastructure of human and rat pericardium. Acta Pathol. Microbiol. Scand. 71, 547–563. ( 10.1111/j.1699-0463.1967.tb05176.x) [DOI] [PubMed] [Google Scholar]
- 29.Chadwick R. 1982. Mechanics of the left ventricle. Biophys. J. 39, 279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fung Y. 1991. What are the residual stresses doing in our blood vessels? Ann. Biomed. Eng. 19, 237–249. ( 10.1007/BF02584301) [DOI] [PubMed] [Google Scholar]
- 31.Omens JH, Fung Y.-C. 1990. Residual strain in rat left ventricle. Circ. Res. 66, 37–45. ( 10.1161/01.RES.66.1.37) [DOI] [PubMed] [Google Scholar]
- 32.Genet M, Rausch M, Lee LC, Choy S, Zhao X, Kassab GS, Kozerke S, Guccione JM, Kuhl E. 2015. Heterogeneous growth-induced prestrain in the heart. J. Biomech. 48, 2080–2089. ( 10.1016/j.jbiomech.2015.03.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Weed BC, Borazjani A, Patnaik SS, Prabhu R, Horstemeyer MF, Ryan PL, Franz T, Williams LN, Liao J. 2012. Stress state and strain rate dependence of the human placenta. Ann. Biomed. Eng. 40, 2255–2265. ( 10.1007/s10439-012-0588-2) [DOI] [PubMed] [Google Scholar]
- 34.Grashow JS, Yoganathan AP, Sacks MS. 2006. Biaxial stress–stretch behavior of the mitral valve anterior leaflet at physiologic strain rates. Ann. Biomed. Eng. 34, 315–325. ( 10.1007/s10439-005-9027-y) [DOI] [PubMed] [Google Scholar]
- 35.Wang B, Wang G, To F, Butler JR, Claude A, McLaughlin RM, Williams LN, de Jongh Curry AL, Liao J.. 2013. Myocardial scaffold-based cardiac tissue engineering: application of coordinated mechanical and electrical stimulations. Langmuir 29, 11 109–11 117. ( 10.1021/la401702w) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang B, et al. 2012. Structural and biomechanical characterizations of porcine myocardial extracellular matrix. J. Mater. Sci. Mater. Med. 23, 1835–1847. ( 10.1007/s10856-012-4660-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang B, Borazjani A, Tahai M, Curry AL, Simionescu DT, Guan J, To F, Elder SH, Liao J. 2010. Fabrication of cardiac patch with decellularized porcine myocardial scaffold and bone marrow mononuclear cells. J. Biomed. Mater. Res. A 94, 1100–1110. ( 10.1002/jbm.a.32781) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Eriksson TSE, Prassl AJ, Plank G, Holzapfel GA. 2013. Influence of myocardial fiber/sheet orientations on left ventricular mechanical contraction. Math. Mech. Solids 18, 592–606. ( 10.1177/1081286513485779) [DOI] [Google Scholar]
- 39.Holzapfel GA, Ogden RW. 2009. Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Phil. Trans. R. Soc. A 367, 3445–3475. ( 10.1098/rsta.2009.0091) [DOI] [PubMed] [Google Scholar]
- 40.Goktepe S, Acharya SNS, Wong J, Kuhl E. 2011. Computational modeling of passive myocardium. Int. J. Numer. Method. Biomed. Eng. 27, 1–12. ( 10.1002/cnm.1402) [DOI] [Google Scholar]
- 41.Streeter DD, Bassett DL. 1966. An engineering analysis of myocardial fiber orientation in pigs left ventricle in systole. Anat. Rec. 155, 503 ( 10.1002/ar.1091550403) [DOI] [Google Scholar]
- 42.Maas SA, Ellis BJ, Ateshian GA, Weiss JA. 2012. FEBio: finite elements for biomechanics. J. Biomech. Eng. 134, 011005-011005-10 ( 10.1115/1.4005694) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Amirhamzeh MMR, Dean DA, Jia CX, Cabreriza SE, Starr JP, Sardo MJ, Chalik N, Dickstein ML, Spotnitz HM. 1996. Iatrogenic myocardial edema: increased diastolic compliance and time course of resolution in vivo. Ann. Thorac. Surg. 62, 737–743. ( 10.1016/S0003-4975(96)00391-8) [DOI] [PubMed] [Google Scholar]
- 44.Vesely I. 1996. Reconstruction of loads in the fibrosa and ventricularis of porcine aortic valves. ASAIO J. 42, M739–M746. ( 10.1097/00002480-199609000-00087) [DOI] [PubMed] [Google Scholar]
- 45.Kroon M, Holzapfel GA. 2007. A model for saccular cerebral aneurysm growth by collagen fibre remodelling. J. Theor. Biol. 247, 775–787. ( 10.1016/j.jtbi.2007.03.009) [DOI] [PubMed] [Google Scholar]
- 46.Martufi G, Gasser TC. 2012. Turnover of fibrillar collagen in soft biological tissue with application to the expansion of abdominal aortic aneurysms. J. R. Soc. Interface 9, 3366–3377. ( 10.1098/rsif.2012.0416) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Grandin T. 1994. Euthanasia and slaughter of livestock. J. Am. Vet. Med. Assoc. 204, 1354–1360. [PubMed] [Google Scholar]
- 48.Jerlström J. When and what determines the death of an animal? A study investigating the heart activity during slaughter of farm animals. PhD thesis, Swedish University of Agricultural Sciences.
- 49.Maxie G. 2015. Jubb, Kennedy & Palmer's pathology of domestic animals, 6th edn London, UK: Elsevier. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The primary data are available in the figures, tables and electronic supplementary material.