Abstract
Purpose
To identify artificial intelligence (AI) classifiers in images of blastocysts to predict the probability of achieving a live birth in patients classified by age. Results are compared to those obtained by conventional embryo (CE) evaluation.
Methods
A total of 5691 blastocysts were retrospectively enrolled. Images captured 115 hours after insemination (or 139 hours if not yet large enough) were classified according to maternal age as follows: <35, 35‐37, 38‐39, 40‐41, and ≥42 years. The classifiers for each category and a classifier for all ages were related to convolutional neural networks associated with deep learning. Then, the live birth functions predicted by the AI and the multivariate logistic model functions predicted by CE were tested. The feasibility of the AI was investigated.
Results
The accuracies of AI/CE for predicting live birth were 0.64/0.61, 0.71/0.70, 0.78/0.77, 0.81/0.83, 0.88/0.94, and 0.72/0.74 for the age categories <35, 35‐37, 38‐39, 40‐41, and ≥42 years and all ages, respectively. The sum value of the sensitivity and specificity revealed that AI performed better than CE (P = 0.01).
Conclusions
AI classifiers categorized by age can predict the probability of live birth from an image of the blastocyst and produced better results than were achieved using CE.
Keywords: artificial intelligence, blastocyst, deep learning, live birth, neural network
1. INTRODUCTION
Securing a live birth is the ultimate goal of assisted reproductive technology. Failed embryo development, or miscarriage, results in the loss of time and cost in addition to likely negative psychological outcomes for the patients and other involved individuals. Both embryonic chromosomal abnormalities and the age of the patient are major fertility‐related factors that affect live birth.
Morphological structures, such as meiotic spindles, zona pellucidae, vacuoles or refractile bodies, polar body shapes, oocyte shapes, dark cytoplasm or diffuse granulation, the perivitelline space, central cytoplasmic granulation, cumulus‐oocyte complexes, cytoplasmic viscosity, and membrane resistance characteristics, have been investigated, but none of these features have been conclusively found to have prognostic value for the further developmental competence of oocytes.1 Additionally, conventional morphological evaluation has had limited success in identifying aneuploid embryos.2, 3, 4, 5, 6 Some investigations have been able to predict aneuploidy. Time‐lapse parameters have been reported to be predictive of aneuploidy, although these have produced diverging conclusions. The available evidence may still be too weak to justify introducing time‐lapse microscopy in routine clinical settings.2 There are reports showing that embryos of good morphological quality can be aneuploid, while suboptimal embryos may be euploid.2, 7, 8 A morphological classification for aneuploidy and euploidy has not been established. Preimplantation genetic testing for aneuploidy (PGT‐A)9, 10 is another method for examining chromosomal profiles. PGT‐A is an invasive technique for the embryo associated with considerable ethical debate. The transfer of the embryo after biopsy is prohibited in some countries. The chromosomal profile of the biopsy specimen does not always represent the profile of the rest of the embryo because of genetic heterogeneity within the embryo. Mosaicism in the trophectoderm (TE) has been observed, and a single TE biopsy may not be representative of the complete TE.11 A global Internet‐based survey indicated that more randomized controlled trials are needed to support PGT‐A.12 Thus, no procedure to detect abnormalities that predict live birth has been established.
Age is one of the most important factors when considering fertility. Many published Original Articles have explored age as follows. Oocyte number and quality decrease with advancing age, and patients older than 35 years should receive prompt evaluation for causes of infertility.13 Aged oocytes display increased chromosomal abnormalities and dysfunction of cellular organelles, both of which factor into oocyte quality.14 Advanced age is a risk factor for female infertility, pregnancy loss, fetal anomalies, and stillbirth.15 Advanced age has a negative effect on fertility.16, 17 The fecundity of women decreases gradually but significantly beginning approximately at 32 years and subsequently decreases more rapidly after 37 years. Women older than 35 years should receive an expedited evaluation, and women older than 40 years should warrant more immediate evaluation and treatment.18 In a total of 7341 single vitrified‐armed blastocyst transfer cycles, the delivery rate stratified by women's age (<35, 35‐37, 38‐39, 40‐41, 42‐45 years) was significantly related to the developmental speed of the embryo (P < 0.0001).19 The Japan Society of Obstetrics and Gynecology reported that the live birth rates associated with assisted reproductive technology in patients categorized by age into <35, 35‐37, 38‐39, 40‐41, and ≥42 years were 0.20, 0.17, 0.12, 0.08, and 0.01, respectively, in 2015.20 Thus, age is well known to be one of the major fertility factors that affects live birth, and there is no established procedure to treat patients or blastocysts by age.
There is now a clear need for a means of noninvasively predicting live birth, and the means may have to be selected according to the age of a patient. We therefore created a system for applying deep learning in a convolutional neural network21, 22, 23, 24 with artificial intelligence (AI) and applied it to blastocyst images classified by maternal age to seek a solution to this challenge. A system consisting of a classifier for all ages was also created using the same method for comparison. Deep learning is becoming very popular among all machine learning methods, such as logistic regression,25 naive Bayes,26 nearest neighbors,27 random forest,28 neural network,29 and deep learning. We selected deep learning and made a classifier program that retrospectively predicts the probability of live birth. The confidence score is the estimated probability of belonging to the live birth category and can be viewed in terms of a ranking of blastocysts; thus, it will make it easier for doctors and embryologists to select superior blastocysts for transfer. Here, we show the results of our retrospective predictions of live birth achieved using the multivariate regression function by a conventional embryo evaluation method that involves observation, assessment, and manual grading of the morphological features of blastocysts evaluated in a laboratory. Then, we present the feasibility of using the classifier of the image of the blastocyst for predicting the probability of achieving live birth classified by age.
2. MATERIALS AND METHODS
2.1. Patients
In this study, we used fully deidentified data, and the study was approved by the Institutional Review Board (IRB) at Okayama Couples’ Clinic (IRB No. 18000128‐05). This study was carried out with explanations provided to the patients and a Web site with additional information, including an opt‐out option for the study. A total of 5691 blastocysts obtained from consecutive patients from January 2009 to April 2017 were enrolled in this study. Every blastocyst was tracked, as was whether a live birth or a nonlive birth was confirmed as the outcome. The total live birth ratio was 0.279. The live birth ratios for the age groups <35, 35‐37, 38‐39, 40‐41, and ≥42 years were 0.387 (876/2265), 0.306 (381/1244), 0.231 (164/709), 0.162 (130/804), and 0.054 (36/669) (live birth cases/all cases), respectively.
2.2. Conventional embryo evaluation
Every blastocyst with the following morphological features and clinical information, such as patient age, time of embryo transfer, time of in vitro fertilization, anti‐Müllerian hormone value, FSH value, blastomere number on day 3 after insemination, blastocyst grade on day 3, embryo cryopreservation day, grade of inner cell mass, grade of TE, averaged diameter of the blastocyst, antral follicle count, body mass index, existence of endometriosis, existence of immune infertility, existence of oviduct infertility, ovarian stimulation procedures, insemination procedures, smooth endoplasmic reticulum (sERC) grade, refractile body, existence of a vacuole, degree of blastocyst expansion, male age, and male body mass index, was pursued to evaluate the final outcome of live or nonlive birth. The information above is defined as the conventional embryo evaluation in this study.
The relationships between live birth outcomes and each factor included in the conventional embryo evaluation were investigated, and univariate regression functions were obtained. The significant factors that showed no multicollinearity, indicating a state of very high correlations among the independent variables, were selected for use in the multivariate analysis. Then, a multivariate regression function performed for the conventional embryo evaluation was used to predict whether a live birth was obtained.
2.3. Blastocyst images
An image of the incubated blastocyst was captured on approximately day 5 at 115 hours after insemination (or day 6 at 139 hours if the blastocyst was not yet large enough) and saved in JPEG format containing no data that could be used to identify the individual. The deidentified image data were transferred to the AI system offline. The images were classified by maternal age into five categories of patients who were less than 35, 35‐37, 38‐39, and 40‐41, or equal to or greater than 42 years old. The numbers of live births and nonlive births were 876 and 1389, respectively, in the <35‐year‐old group; 381 and 863, respectively, in the 35‐year‐old≤and <38‐year‐old group; 164 and 545, respectively, in the 38‐year‐old ≤ and <40‐year‐old group; 130 and 674, respectively, in the 40‐year‐old ≤ and <42‐year‐old group; and 36 and 633, respectively, in the ≥42‐year‐old group. The live birth probability was 0.387 for the <35‐year‐old group; 0.306 in the 35 ≤ and <38‐year‐old group; 0.231 in the 38 ≤ and <40‐year‐old group; 0.162 in the 40 ≤ and <42‐year‐old group; and 0.054 in the ≥42‐year‐old group. The images of blastocysts that led to live births and those of blastocysts that led to undeveloped embryos or miscarriages, etc, and resulted in nonlive births were used to create the AI classifiers.
2.4. Preparation for AI
All deidentified images stored offline were transferred to our AI‐based system. Each image was cropped to a square and then saved. Twenty percent of the images in the live birth and nonlive birth categories were randomly selected as the test dataset, and the rest were used as the training dataset. Then, twenty percent of the training dataset was used as the validation dataset, and the rest was used to train the AI classifier. Thus, the training, validation, and test datasets did not overlap. In this way, the AI classifier was trained by a training dataset and simultaneously validated and then tested for the test dataset. The number of training datasets was augmented, as is often done in computer science, in a process known as data augmentation. The training dataset was augmented in this study because the blastocyst image processing of the arbitrary degrees of rotation can lead to images being included in the same category of different vector data.
2.5. AI classifier
We developed classifier programs in each age category using supervised deep learning with a convolutional neural network30, 31 that tried to mimic the visual cortex of the mammal brain21, 23, 32, 33, 34, 35 and used L2 regularization36, 37 to categorize blastocyst images as either in the live birth or the nonlive birth category and to obtain the mathematical probability for predicting each category. We performed deep learning with a convolutional neural network with eleven layers consisting of a combination of convolution layers with varying output channels and kernel sizes,38, 39 pooling layers,41, 42 flattened layers,45 linear layers,46, 47 rectified linear unit layers,48, 49 and a softmax layer50, 51 that demonstrated the probability of a live birth from an image of the blastocyst. We applied cross‐validation,52, 53 a powerful method for model selection, to identify the optimal method of machine learning. The suitable number of images for the training data was investigated by evaluating accuracy and variances using the 5‐fold cross‐validation method as follows (Figure 1). First, the test data were the initial one‐fifth of the images collected in each category, and a classifier was trained by the training data. Then, the test data were changed to the next one‐fifth of the images. This procedure was repeated five times to encompass all images as potential test data. The number of augmented training images was analyzed until the accuracy and variance were likely to show the maximum and minimum value, respectively. This calculation procedure reveals the optimal number of training data and can be used to avoid overfitting,55, 56 which is a modeling error that occurs when a classifier is too closely fit to a limited set of data points. After the optimal number of training data was obtained, the best classifier that showed the best accuracy and the smallest variance was selected by varying the architecture of the convolutional neural network and by varying parameters such as L2 regularization values within a range of 0.0‐0.40 and an image size (40 × 40, 50 × 50, 75 × 75, and 100 × 100 pixels). If the accuracies did not clearly differ, the best classifier was determined based on the values of the sum of the sensitivity and the specificity. The AI classifiers (with the softmax function showing the confidence score) were obtained for each age category. An AI classifier for all ages was also obtained in the same procedures.
Figure 1.
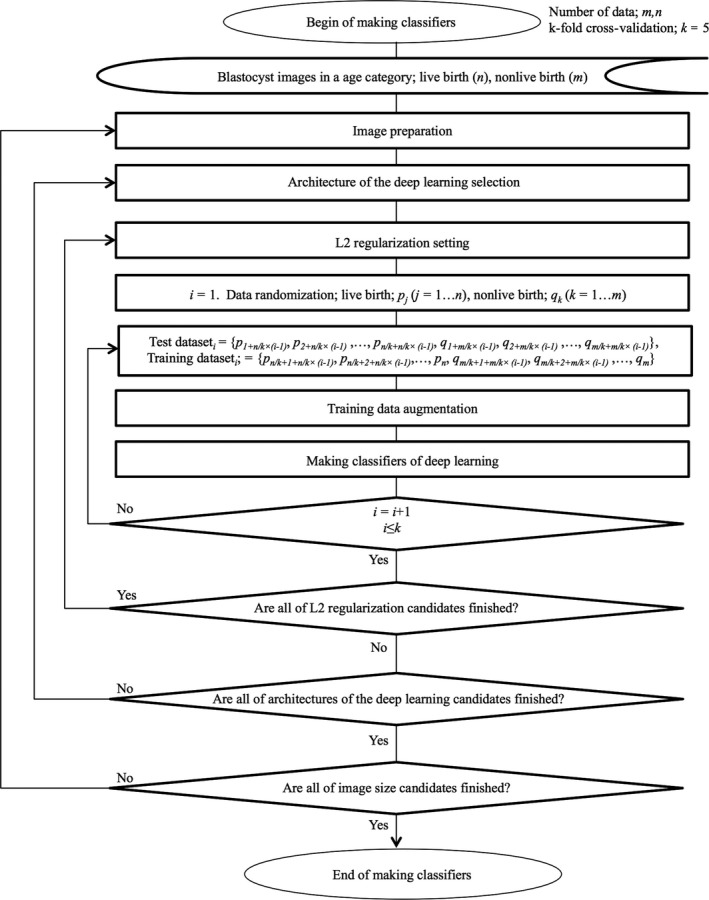
A flowchart to make classifiers
2.6. Live birth prediction function by the AI classifier
A histogram of the values of the confidence scores obtained from images of the blastocysts in both the live and nonlive births was obtained. This histogram was converted to show the ratio of live births to all births. A logistic regression model that fit the ratios was constructed as the function to predict the probability of live birth.
2.7. Development environment
The following development environment was used in the present study: a Mac running OS X 10.11.6 (Apple, Inc, Cupertino, CA, USA) and Mathematica 11.3.0.0 (Wolfram Research, Champaign, IL).
2.8. Statistics
The results of the laboratory data and the AI classifier were compared. Mathematica 11.3.0.0 (Wolfram Research) was used for all statistical analyses.
3. RESULTS
3.1. Live birth prediction by the conventional embryo evaluation
Univariate regression functions and the multivariate regression function of the conventional embryo evaluation used to predict the probability of live birth are shown in Table 1 and Table 2, respectively. After no multicollinearity was found among the variables, ten independent variables remained for the multivariate regression function, which showed the minimum value of the deviances. The variables shown in Table 2 were obtained using the formulae shown in Table 1. The results showed that the age at which the P‐value was the minimum among ten variables seemed to be the most important independent variable, as shown in Table 2. When these ten values, which were derived from the conventional embryo evaluation, were substituted to the multivariate logistic regression function, 1/(1 + Exp(β 0+β 1 x 1+ … +β 10 x 10), the calculated value showed the predicted probability of live birth by the conventional embryo evaluation.
Table 1.
Univariate regression functions of conventional embryo evaluation parameters used to predict the probability of live birth
| Independent variable | Formula | Coefficient |
|---|---|---|
| Age | k/(1 + Exp(β 0+β 1 x)) | β 0 = −10.80 ± 4.038 (P = 0.0075) |
| β 1 = 0.287 ± 0.107 (P = 0.0074) | ||
| k = 0.447 | ||
| Time of embryo transfer | 1/(1 + Exp(β 0+β 1 x)) | β 0 = 0.535 ± 1.187 (P = 0.652) |
| β 1 = 0.287 ± 0.107 (P = 0.181) | ||
| Anti‐Müllerian hormone (ng/mL) | 1/(1 + Exp(β 0+β 1 x)) | β 0 = 1.263 ± 2.637 (P = 0.632) |
| β 1 = 0.059 ± 0.139 (P = 0.671) | ||
| Blastomere number on day 3 | k/(2πσ 2)1/2 Exp(‐(x‐m)2/(2σ 2)) | σ = 4.758 ± 0.761 (P = 0.00003) |
| m = 11.518 ± 0.646 (P < 1.612 × 10−10) | ||
| k = 4.632 ± 0.587 (P < 2.59 × 10−6) | ||
| Grade on day 3 (Class A = 1, B = 2, C = 3, D = 4) | k/(1 + Exp(β 0+β 1 x)) | β 0 = −9.914 ± 10.619 (P = 0.351) |
| β 1 = 3.137 ± 3.686 (P = 0.352) | ||
| k = 0.306 | ||
| Embryo cryopreservation day (Day 5 = 1, Day 6 = 2) | β 0+β 1 x | β 0 = 0.444 |
| β 1 = −0.137 | ||
| Inner cell mass (A = 1, B = 2, C = 3) | β 0+β 1 x | β 0 = 0.490 ± 0.018 (P = 0.023) |
| β 1 = −0.1356 ± 0.008 (P = 0.039) | ||
| Averaged diameter (µm) | 1/(1 + Exp(β 0+β 1 x)) | β 0 = 2.788 ± 5.263 (P = 0.596) |
| β 1 = −0.012 ± 0.030 (P = 0.692) | ||
| Body mass index (kg/m2) | 1/(1 + Exp(β 0+β 1 x)) | β 0 = −0.662 ± 0.810 (P = 0.414) |
| β 1 = 0.079 ± 0.037 (P = 0.020) |
Independent variables, which were related to live birth and also used in the multivariate regression, are presented. Each formula was determined to fit the data distribution. Coefficients are shown as the mean ±SE.
Table 2.
The multivariate logistic regression function, 1/(1 + Exp(β 0+β 1 x 1+ … +β 10 x 10), of the conventional embryo evaluation for predicting live birth
| Independent variable | Coefficient | P‐Value | Odds ratio |
|---|---|---|---|
| Constant (β 0) | β 0 = 6.756 ± 0.461 | 1.06 × 10−48 | ‐ |
| Age value (β 1) | β 1 = −4.101 ± 0.330 | 1.05 × 10−35 | 60.42 |
| Average diameter value (β 2) | β 2 = −5.098 ± 0.619 | 1.792 × 10−16 | 163.76 |
| TE value (β 3) | β 3 = −1.970 ± 0.398 | 7.226 × 10−7 | 7.17 |
| Embryo cryopreservation day value (β 4) | β 4 = −3.299 ± 0.741 | 8.577 × 10−6 | 27.10 |
| ET times value (β 5) | β 5 = −2.592 ± 0.638 | 0.0000481 | 13.35 |
| ICM value (β 6) | β 6 = −1.243 ± 0.469 | 0.0081 | 3.47 |
| AMH value (β 7) | β 7 = −1.143 ± 0.726 | 0.1156 | 3.13 |
| Blastomere number value (β 8) | β 8 = −0.612 ± 0.567 | 0.280 | 1.84 |
| Body mass index value (β 9) | β 9 = −0.648 ± 0.738 | 0.379 | 1.91 |
| Grade on day 3 value (β 10) | β 10 = 0.079 ± 0.994 | 0.936 | 0.92 |
AMH, anti‐Müllerian hormone, ET, embryo transfer; ICM, inner cell mass; TE, trophectoderm.
The values of independent variables (except constant β 0) are values calculated by the univariate regression functions shown in Table 1. Multicollinearity was not observed between any two independent variables. Coefficients are shown as the mean ±SE.
3.2. Live birth prediction by AI
The profiles of the accuracies, with standard deviation (SD), are shown according to the number of the training dataset, as shown in Figure 2. The best numbers obtained in the training dataset were 17112, 7848, 8085, and 12 144 in the age groups 35‐37, 38‐39, 40‐41, and ≥42 years, respectively. Because the accuracies did not vary as a function of the number in the training dataset in the <35‐year‐old age group and the all age group, the sum of the sensitivity and the specificity was investigated. For the age category <35 years, the sum value for the numbers of the training dataset, 3333, 9999, 13 332, 16 665, 19 998, and 26 664, was 1.002 ± 0.007, 1.016 ± 0.034, 1.032 ± 0.339, 1.058 ± 0.153, 1.024 ± 0.080, and 1.017 ± 0.028 (mean ± SD), respectively. Hence, the best number for the training dataset in the age category <35 years was determined to be 16 665. The same procedure revealed that the best number of training data for all ages was 49 245. The best numbers in the L2‐regularization were 0.15, 0.37, 0.10, 0.30, 0.20, and 0.12 for the age groups <35, 35‐37, 38‐39, 40‐41, and ≥42 years and all ages, respectively. The best image size in our study was 50 × 50 pixels (data not shown). Using the best number of training data, we obtained the best classifiers for each age category with the convolutional neural network, for which the architectures are shown in Table 3. The rectified linear unit function was the best among the logistic sigmoid function, the hyperbolic tangent function, and the Heaviside theta function (data not shown). It took only 0.2 seconds per image to classify and show the confidence score.
Figure 2.
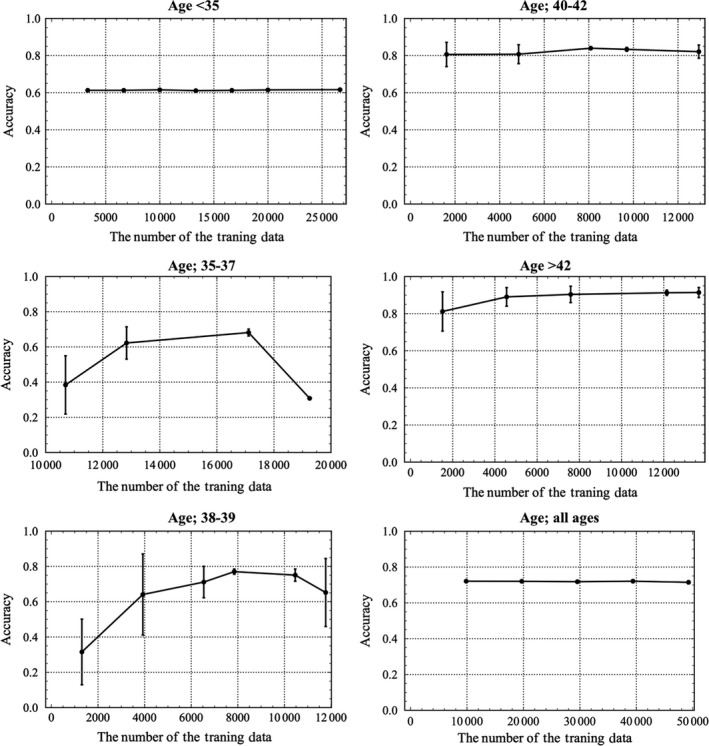
The profiles for accuracy with standard deviation (SD) according to the number of training data and classified by age into <35, 35‐37, and 38‐39 y are shown above in the left column, while those for 40‐41 and ≥42 y and all ages are shown above in the right column. The number of training data that achieved the best accuracy with the minimum SD was obtained for each age category. For patients aged <35 y and all ages, the accuracies do not differ; thus, the best number for the training data was determined according to the maximum number of the sum of the sensitivity and the specificity. The best numbers for the training data were 16 665, 17 112, 7848, 8085, 12 144, and 49 245 for patients aged <35, 35‐37, 38‐39, 40‐41, and ≥42‐y and all ages, respectively
Table 3.
Architectures of the best classifier that showed the best accuracy for each age category
| Age (y) | |||||||
|---|---|---|---|---|---|---|---|
| Layers | <35 | 35‐37 | 38‐39 | 40‐41 | ≥42 | All ages | |
| 1. Convolution layer | |||||||
| Output channels | 50 | 40 | 20 | 40 | 40 | 50 | |
| Kernel size | 5 × 5 | 5 × 5 | 5 × 5 | 5 × 5 | 5 × 5 | 5 × 5 | |
| 2. ReLU† | |||||||
| 3. Pooling layer | |||||||
| Kernel size | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | |
| 4. Convolution layer | |||||||
| Output channels | 64 | 64 | 64 | 64 | 64 | 64 | |
| Kernel size | 5 × 5 | 5 × 5 | 5 × 5 | 5 × 5 | 5 × 5 | 5 × 5 | |
| 5. ReLU | |||||||
| 6. Pooling layer | |||||||
| Kernel size | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | |
| 7. Flatten layer | |||||||
| 8. Linear layer size | 210 | 210 | 210 | 210 | 210 | 210 | |
| 9. ReLU | |||||||
| 10. Linear layer size | 2 | 2 | 2 | 2 | 2 | 2 | |
| 11. Softmax layer | |||||||
ReLU, rectified linear units.
The proper convolutional neural network structures, which consisted of eleven layers in convolutional deep learning, were obtained. The numbers of output channels in the first convolution layer were different.
As for a sample, the histogram for live birth and nonlive birth in patients aged 35‐37 years is demonstrated in the upper graph shown in Figure 3. These data were transformed to obtain the incidence of live birth and then fitted to a logistic regression model, as shown in the lower graph in Figure 3. The logistic regression models were used as the function to predict the probability of live birth in all age categories as shown in Table 4 and plotted in Figure 4. The functions for age <35 and 35‐37 years were similar. As age advances, the predicted probability of live birth becomes lower, and the coefficient of the independent variable increases. Some example images of the blastocyst in patients aged 38‐39 years are shown in Figure 5.
Figure 3.
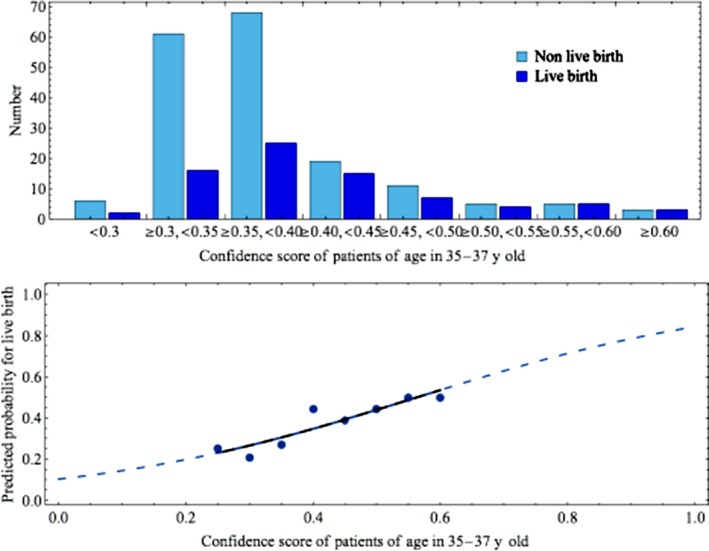
The process used to obtain the function of the logistic regression model from the confidence score, which was the estimated probability of belonging to the live birth category, was determined in order to predict the probability of live birth by applying the data distribution of the patients. A sample of patients aged 35‐37 y is shown. The histogram of the confidence scores for both live and nonlive births that were confirmed by tracking is shown in the upper panel. The incidence of live birth as a function of the probability is plotted as dots and shown in the lower panel. The logistic regression model with extrapolations that fit the dots was constructed as the function of the confidence scores to predict the probability of live birth
Table 4.
Coefficients of the logistic regression, y = 1/(1 + Exp(β 0+β 1 x)), showing the probability of live birth as a function of the confidence score, which is the AI‐generated predicted probability of live birth obtained from an image of the blastocyst
| Patient age (y) | β 0 (±SE) | β 1 (±SE) | Odds ratio |
|---|---|---|---|
| <35 | 3.81 (±2.79) | −7.91 (±5.65) | 2724.39 |
| 35‐37 | 3.23 (±3.18) | −6.87 (±7.08) | 962.95 |
| 38‐39 | 2.12 (±1.97) | −3.36 (±4.33) | 28.79 |
| 40‐41 | 3.04 (±2.99) | −3.70 (±5.61) | 40.45 |
| ≥42 | 2.93 (±5.12) | −0.71 (±11.19) | 2.03 |
| all ages | 1.70 (±1.23) | −3.30 (±2.47) | 27.11 |
β 0, β 1, coefficients; SE, standard error; x, confidence score of the blastocyst; y, probability of live birth.
Figure 4.
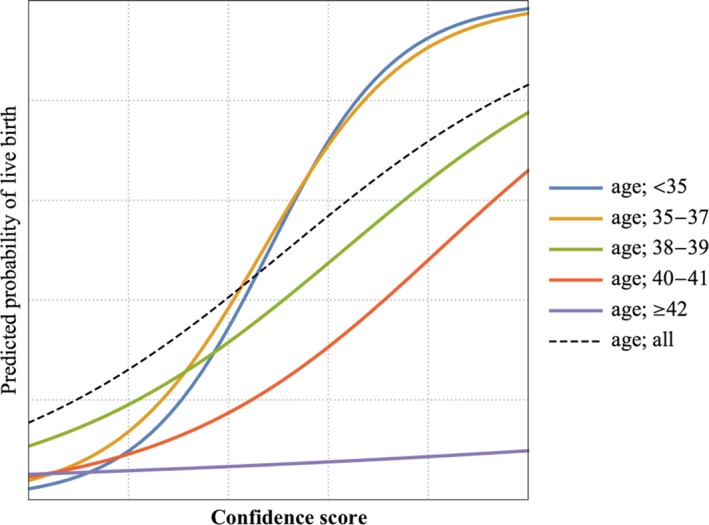
The functions used to predict the probability of live birth are plotted according to age categories into <35, 35‐37, 38‐39, 40‐41, and ≥42 y and all ages, respectively. The functions for ages <35 and for 35‐37 y seemed similar. When the age advanced above 35 y, and especially when it was equal to or greater than 42 y, the probability of live birth decreased. These functions, which were derived from artificial intelligence, seemed to be consistent with the significance of age
Figure 5.
Examples of original images of the blastocyst in patients aged 38‐39 y
3.3. Comparison of the AI and conventional embryo evaluation
The accuracies for predicting live birth achieved by the AI/conventional embryo evaluation methods for test datasets were 0.639/0.610, 0.708/0.700, 0.782/0.768, 0.807/0.834, 0.881/0.941, and 0.721/0.740 for ages <35, 35‐37, 38‐39, 40‐41, and ≥42 years and all ages, respectively (Table 5). The accuracies increased as age advanced in both the AI and the conventional embryo evaluation with P < 1.5 × 10−10 and P < 1.1 × 10−17, respectively, by the Cochran‐Armitage test. The overall average accuracies of the AI and laboratory data were 0.763 ± 0.093 and 0.771 ± 0.126 (mean ± SD), respectively, indicating no significant difference according to the Mann‐Whitney test (P = 0.83). The values for the area under the curve (AUC) of the AI and the laboratory data were 0.661 ± 0.049 and 0.713 ± 0.064 (mean ± SE), respectively, for the data classified by age, but there was no significant difference (P = 0.29).
Table 5.
Live birth prediction by the classifiers of the AI, deep learning of the convolutional neural network (upper panel) and the multivariate regression of the conventional embryo evaluation (lower panel)
| Patient age (y) | Actual live birth | Actual nonlive birth | Predicted live birth | Predicted nonlive birth | accuracy | sensitivity | specificity | PPV | NPV | AUC | 95% CI of AUC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| The AI with deep learning in the convolutional neural network | |||||||||||
| <35 | 176 | 278 | 80 | 374 | 0.639 | 0.261* | 0.878 | 0.575 | 0.652 | 0.592 | 0.538‐0.646 |
| 35‐37 | 77 | 173 | 20 | 230 | 0.708 | 0.156 | 0.954 | 0.600 | 0.717 | 0.634 | 0.558‐0.711 |
| 38‐39 | 33 | 109 | 12 | 130 | 0.782 | 0.212 | 0.954 | 0.583 | 0.800 | 0.671 | 0.560‐0.782 |
| 40‐41 | 26 | 135 | 25 | 136 | 0.807 | 0.385* | 0.889 | 0.400 | 0.882 | 0.713 | 0.594‐0.831 |
| ≥42 | 8 | 127 | 14 | 121 | 0.881 | 0.375 | 0.913 | 0.214 | 0.959 | 0.696 | 0.488‐0.904 |
| All ages | 318 | 821 | 93 | 1046 | 0.721 | 0.148 | 0.944 | 0.505 | 0.741 | 0.574 | 0.537‐0.612 |
| The conventional embryo evaluation | |||||||||||
| <35 | 176 | 278 | 167 | 287 | 0.610 | 0.471* | 0.697 | 0.497 | 0.676 | 0.632 | 0.579‐0.685 |
| 35‐37 | 77 | 173 | 12 | 238 | 0.700 | 0.090 | 0.971 | 0.583 | 0.706 | 0.634 | 0.557‐0.711 |
| 38‐39 | 33 | 109 | 0 | 142 | 0.768 | 0.000 | 1.000 | NA | 0.768 | 0.775 | 0.675‐0.875 |
| 40‐41 | 26 | 135 | 0 | 161 | 0.839 | 0.000* | 1.000 | NA | 0.839 | 0.736 | 0.620‐0.851 |
| ≥42 | 8 | 127 | 0 | 135 | 0.941 | 0.000 | 1.000 | NA | 0.941 | 0.764 | 0.567‐0.960 |
| All ages | 318 | 821 | 172 | 967 | 0.740 | 0.305 | 0.909 | 0.564 | 0.771 | 0.723 | 0.688 −0.757 |
The ability of a test is usually presented as its sensitivity, specificity, and AUC. The clinical outcome is presented as the accuracy. In the AI, the accuracy increases as a function of age (P < 1.5 × 10−10), while the sensitivity or the specificity does not (Cochran‐Armitage test). The ranges of the sensitivity and specificity were nearly 0.20‐0.40 and 0.88‐0.95, respectively. In conventional embryo evaluation, the accuracy, sensitivity, and specificity changed as a function of age (P < 1.1 × 10−17, P < 1.3 × 10−13, and P < 3.6 × 10−25, respectively (Cochran‐Armitage test)). When patient was older than 37 years, the sensitivities were 0, and the specificities were 1 because of the low probability of a live birth. This phenomenon occurs when all judgments are determined to be always nonlive births. The conventional embryo evaluation method seems to be ineffective in patients aged older than 37 years. The sum value of the sensitivity and the specificity of the AI and the conventional embryo evaluation was 1.196 ± 0.08 and 1.046 ± 0.07, respectively (P = 0.01 and P = 0.034 by unpaired t test and Mann‐Whitney test, respectively). AUC, area under the curve; CI, confidence interval; NPV, negative predictive value; PPV, positive predictive value.
P < 0.05 for the AI vs the conventional embryo evaluation.
The sensitivity and the specificity of the AI were almost 0.15‐0.40 and 0.88‐0.95, respectively, in any age category. In the conventional embryo evaluation, however, the sensitivity decreased and the specificity increased as a function of age (P < 1.3 × 10−13 and P < 3.6 × 10−25, respectively). In particular, when the mother was older than 37 years, the sensitivity was 0.000, and the specificity was 1.000. The sum values of the sensitivity and specificity of the AI and of conventional embryo evaluation were 1.196 ± 0.08 and 1.046 ± 0.07 (mean ± SD), respectively, indicating that the AI achieved significantly better results (P = 0.01 and P = 0.034 by unpaired t test and Mann‐Whitney test, respectively), as shown in Figure 6. As maternal age advanced, the sum of the sensitivity and the specificity increased in the AI and decreased in the conventional embryo evaluation, respectively. The more the age advanced, the more accurate the outcome of the AI classifier was.
Figure 6.
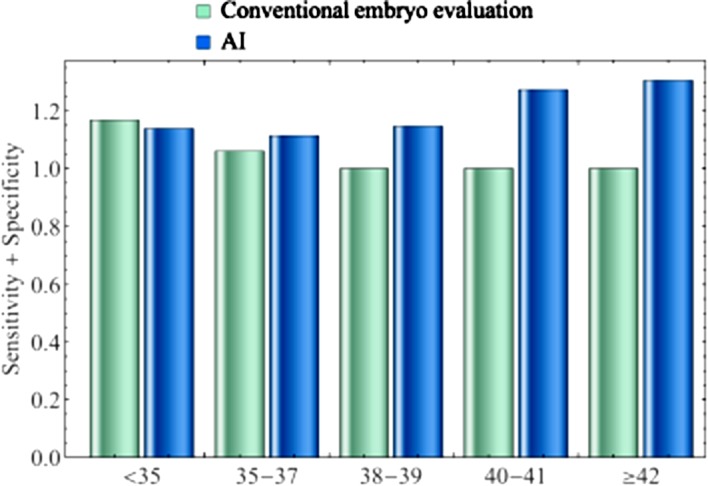
The sum of the sensitivity and the specificity by the classifier of the artificial intelligence (AI) and the laboratory data for the age categories <35, 35‐37, 38‐39, 40‐41, and ≥42 y. As age advances, the sum of the sensitivity and the specificity increased in the AI and decreased in the laboratory data. The sum values for the AI and the laboratory data were 1.196 ± 0.08 and 1.046 ± 0.07 (mean ± SD), respectively. The AI achieved significantly higher values (P = 0.01 and P = 0.034 by unpaired t test and Mann‐Whitney test, respectively). As age advanced, the AI classifier became more useful
4. DISCUSSION
We developed an AI classifier of deep learning with convolutional neural networks using images of blastocysts categorized by maternal age to predict the probability of achieving live birth. In our study, the overall average of the accuracies achieved by the AI classifiers was 0.763 ± 0.093 (mean ± SD). The accuracies achieved by the AI as well as the conventional embryo evaluation were both dependent on the age category. We suggest that the classifiers should be classified by age. In several reports, deep learning with convolutional neural networks as AI61 has been used in medicine.62 The accuracies of this method with deep learning have been published and were 0.997 for histopathological diagnosis of breast cancer,63 0.90‐0.83 for the early diagnosis of Alzheimer's disease,64 0.83 for urological dysfunctions,65 0.7266 and 0.5067 for colposcopy, 0.83 for the diagnostic imaging of orthopedic trauma,68 and 0.98 for the morphological quality of blastocysts and evaluation by embryologist.69 In one report, embryos with fair‐quality images that were classified as poor and good quality were scored as 0.509 and 0.614, respectively, for the likelihood of achieving a positive live birth.69 In our study, the accuracy for predicting a live birth using images of the blastocyst when using the AI was 0.639, 0.708, 0.782, 0.807, and 0.881 for the age categories <35, 35‐37, 38‐39, 40‐41, and ≥42 years, respectively, as shown in Table 5. Our results show that in spite of clinical impediment factors that are beyond images, factors such as uterine factors70 seem to be average methods used in deep learning approaches to classify objects in medicine. To the best of our knowledge, no reports have predicted the probability of live birth from images of the blastocyst. One study, however, reported that the live birth rate per transfer was 0.668 based on clinical factors, such as age and body mass index.71 Another study reported that the grading of the TE was the only statistically significant independent predictor of live birth outcomes and that the live birth probabilities of grade A, B, or C in the TE were 0.499, 0.339, and 0.080, respectively.72 In our study, the average of the accuracies achieved by the AI was 0.763, and there were no significant differences between the AI and the conventional embryo evaluation method regarding the accuracy and the AUC. However, the sum value of the sensitivity and the specificity of the AI was 1.196 ± 0.08 (mean ± SD), which was significantly higher than that of the conventional embryo evaluation method. If the AI classifier is applied in practical medicine, the blastocyst can be selected according to the order of the value of probability of achieving a live birth so that outcomes might be improved.
We made the classifiers according to age categories. The AI classifier used in this study revealed that the more age advances, the more useful the AI classifier will be (Figure 6). This is important because patients with advanced age have less time to be treated. The best number for the training datasets as shown in Figure 2, and the regression functions as shown in Figure 4 and Table 4 differed by age. When the patient is older than 37 years, the classifiers by age achieved better results than were achieved by the classifier that was not classified by age. Although the age categories <35 and 35‐37 years could be joined, this should be avoided so that all data are without age classification. The significance of age for sterility has been emphasized for a long time, and this has been experienced in practical medicine. The conventional method of evaluating embryos, however, does not yet clearly detect the morphological features associated with the significance of age. The results of this study suggest that the AI that included deep learning with convolutional neural networks seemed to recognize some types of information related to age from images of the blastocyst. This is one of the critical points supporting the use of the AI for predicting live birth based on the image of the blastocyst as well as the goal of causing no harm to the embryo. For the function to predict live birth by the regression, the conventional embryo evaluation is related to age, as shown in Table 5. When the patient is older than 37 years, the sensitivity is 0, and the specificity is 1. This phenomenon occurs when the results of all tests are always negative. Predicting a live birth based on conventional embryo evaluation is not actually feasible in patients with advanced age who are older than 37 years. Because of the low incidence of live birth in advanced age patients, the accuracies show apparent good results at a glance because of the high specificities. Therefore, age is a very important factor, and the AI classifier is actually superior to conventional embryo evaluation.
In this study, the sensitivities were relatively low, and the specificities were relatively high for the AI, as shown in Table 5. There are some clinical disincentives for an embryo to achieve live birth. These include uterine factors70 (eg, intrauterine adhesions,73, 74 uterine myomas,75 and endometrial polyps76), endometriosis,77 ovarian function,78 oviduct obstruction,79, 80 maternal diseases such as diabetes mellitus,81 immune disorders,82, 83 and the uterine microbiota.84, 85 Because these factors cannot be detected by the AI classifier from an image of the blastocyst, the accuracy, sensitivity, and specificity for live birth cannot reach 1. These clinical characteristics of the blastocyst prevent the accuracy of predicting live birth by any means from reaching close to 1. However, we found that the AI seemed to perform better than conventional embryo evaluation because it had superior positive numbers for sensitivity.
The AUC is also a good parameter for estimating a test. The AUC value of the AI was 0.661 ± 0.049 (mean ± SE) and showed a range of 0.592‐0.713. There are no comparable published data for predicting live birth. However, regarding the AUC of preimplantation genetic screening, a study reported in a prediction model that classified embryos into high‐, medium‐ or low‐risk categories achieved an AUC of 0.72.86 That model could be useful for ranking embryos and prioritizing them for PGT‐A. However, it does have limited predictive value for patients undergoing IVF in general,87 and it might have to be avoided because of possible harm to the embryo.
In spite of some of the clinical disincentives for an embryo to achieve live birth, it is possible that some improvements in the architecture of the neural network and the parameters used for training could make the classifiers better. The architecture of this study consisted of eleven layers. The LeNet study published in 199888 consisted of 5 layers. AlexNet, published in 2012,89 consisted of 14, and Google Net, published in 2014,90 was constructed of a combination of micronetworks. ResNet, published in 2015,91 consisted of modules with a shortcut process. Squeeze‐and‐Excitation Networks, published in 2017,92 induced Squeeze‐and‐Excitation Blocks, which are building blocks for convolutional neural networks that improve channel interdependencies. The AI used for image recognition is still being developed. Progress in AI will allow us to achieve better results. We used 50 × 50 pixels for the images of blastocysts. Only 15 × 15 pixels are used to detect cervical cancer.93 In a colposcopy study,67 it was reported that the accuracy for images of 150 × 150 pixels was better than that for 32 × 32 or 300 × 300 pixels, although images of uterine cervical lesion, including white epithelium and punctuation, seemed to be more complicated than images of blastocysts. Hence, one issue that remains open to question is that of image size, and we propose that a size of 50 × 50 pixels is acceptable. A high‐performance computer is needed to resolve this issue. Regularization values are also important parameters for constructing a good classifier that avoids overfitting. In this study, for the L2 regularization, the best numbers were 0.15, 0.37, 0.10, 0.30, and 0.20 for ages <35, 35‐37, 38‐39, 40‐41, and ≥42 years, respectively. If the regularization value is too low, overfitting occurs. If the value is too large, the classifier will not be trained well. Choosing the appropriate number for the training dataset is also very important. If the number of training datasets is too high, the accuracy will be lower, and more variances will occur. The validation dataset as well as L2 regularization also prevent overfitting. The appropriate balance between the regularization value and the number of training datasets must be achieved to obtain a good classifier. The other biological parameters, such as information related to time lapse, should be investigated in terms of their ability to predict live birth. Moreover, although we used images of blastocysts obtained at 115 or 139 hours after insemination, further investigation might be needed to prepare datasets, potentially by adding time‐lapse data or images obtained at different times.
When the AI system we made is applied to clinical use, the confidence scores could be used to select better blastocysts among all blastocysts according to the value. However, it is recommended that the regression function, which was applied to the data distribution of the patients, as shown in Figure 4 and Table 4, should be used to estimate the probability. For example, when the confidence scores of images obtained from blastocysts in patients who were 35 years old and 42 years old are both predicted to be 0.6, the predicted probability applied to the data distribution of the patients’ ages was 0.7 and 0.07, respectively (Figure 4). Because the function of the logistic regression model is a monotonically increasing function, the blastocyst can be selected based on the confidence score. However, the function of the logistic regression model may provide better results in clinical practice because of the implications of the distribution of patient data.
Ethically speaking, the AI classifier we constructed inflicts no harm on the blastocyst. It offers economic savings for patients and/or clinical institutes, provides a quick and efficient diagnosis of the classification, and permits examination over distances. We believe that this AI, which is a product of the development of computer science, will be much more useful in biology, including reproductive medicine, in the near future. Further study that integrates the conventional evaluations in addition to blastocyst images in deep leaning might be conducted.
We applied deep learning with a convolutional neural network in the realm of AI to develop classifiers for predicting the probability of a live birth from a blastocyst image categorized by maternal age. The range of accuracy was 0.639‐0.881, and the average was 0.763 ± 0.093 (mean ± SD). Less than a second is needed to complete the analysis of each image. This method does not harm the embryo, which can subsequently be transferred after the prediction is established. Although further study may be required to validate the classifiers, this system demonstrates the possibility that this AI could be feasible for clinical use and may provide benefits to both patients and medical personnel.
The contents in this manuscript were approved as a patent in Japan; patent 6468576.
DISCLOSURE
Conflict of interest: Yasunari Miyagi, Toshihiro Habara, Rei Hirata, and Nobuyoshi Hayashi declare that they have no conflicts of interest. Human rights statements and informed consent: Human rights statements and informed consent: All procedures followed were performed in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1964 and its later amendments. Informed consent was obtained from all patients for inclusion in the study. Additional informed consent was obtained from all patients for which identifying information is included in this article. A Web site with additional information, including an “opt‐out” option, was set up for the study. Animal studies: No animals were used in this study. Approval by ethics committee: The protocol for the research project including human participants was approved by the Institutional Review Board at Okayama Couples’ Clinic (IRB no. 18000128‐05).
Miyagi Y, Habara T, Hirata R, Hayashi N. Feasibility of deep learning for predicting live birth from a blastocyst image in patients classified by age. Reprod Med Biol. 2019;18:190–203. 10.1002/rmb2.12266
Clinical Trial Registry: This study is not a clinical trial.
REFERENCES
- 1. Rienzi L, Vajta G, Ubaldi F. Predictive value of oocyte morphology in human IVF: a systematic review of the literature. Hum Reprod. 2011;17:34‐45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Kirkegaard K, Ahlström A, Ingerslev HJ, Hardarson T. Choosing the best embryo by time lapse versus standard morphology. Fertil Steril. 2015;103:323‐332. [DOI] [PubMed] [Google Scholar]
- 3. Finn A, Scott L, O'Leary T, Davies D, Hill J. Sequential embryo scoring as a predictor of aneuploidy in poor‐prognosis patients. Reprod Biomed Online. 2010;21:381‐390. [DOI] [PubMed] [Google Scholar]
- 4. Eaton JL, Hacker MR, Barrett CB, Thornton KL, Penzias AS. Influence of patient age on the association between euploidy and day‐3 embryo morphology. Fertil Steril. 2010;94:365‐367. [DOI] [PubMed] [Google Scholar]
- 5. Eaton JL, Hacker MR, Harris D, Thornton KL, Penzias AS. Assessment of day‐3 morphology and euploidy for individual chromosomes in embryos that develop to the blastocyst stage. Fertil Steril. 2009;91:2432‐2436. [DOI] [PubMed] [Google Scholar]
- 6. Wells D. Embryo aneuploidy and the role of morphological and genetic screening. Reprod Biomed Online. 2010;21:274‐277. [DOI] [PubMed] [Google Scholar]
- 7. Alfarawati S, Fragouli E, Colls P, et al. The relationship between blastocyst morphology, chromosomal abnormality, and embryo gender. Fertil Steril. 2011;95:520‐524. [DOI] [PubMed] [Google Scholar]
- 8. Ziebe S, Lundin K, Loft A, et al. FISH analysis for chromosomes 13, 16, 18, 21, 22, X and Y in all blastomeres of IVF pre‐embryos from 144 randomly selected donated human oocytes and impact on pre‐embryo morphology. Hum Reprod. 2003;18:2575‐2581. [DOI] [PubMed] [Google Scholar]
- 9. Dahdouh EM, Balayla J, Audibert F, et al. Technical update: preimplantation genetic diagnosis and screening. J Obstet Gynaecol Can. 2015;37:451‐463. [DOI] [PubMed] [Google Scholar]
- 10. Brezina PR, Kutteh WH. Clinical applications of preimplantation genetic testing. BMJ. 2015;19:350. [DOI] [PubMed] [Google Scholar]
- 11. Gleicher N, Metzger J, Croft G, Kushnir VA, Albertini DF, Barad DH. A single trophectoderm biopsy at blastocyst stage is mathematically unable to determine embryo ploidy accurately enough for clinical use. Reprod Biol Endocrinol. 2017;15:33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Weissman A, Shoham G, Shoham Z, Fishel S, Leong M, Yaron Y. Preimplantation genetic screening: results of a worldwide web‐based survey. Reprod Biomed Online. 2017;;35(6):693‐700. [DOI] [PubMed] [Google Scholar]
- 13. Crawford NM, Steiner AZ. Age‐related infertility. Obstet Gynecol Clin. 2015;42:15‐25. [DOI] [PubMed] [Google Scholar]
- 14. Igarash H, Takahashi T, Nagase S. Oocyte aging underlies female reproductive aging: biological mechanisms and therapeutic strategies. Reprod Med Biol. 2015;14:159‐169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Sauer MV. Reproduction at an advanced maternal age and maternal health. Fertil Steril. 2015;103:1136‐1143. [DOI] [PubMed] [Google Scholar]
- 16. Weiss RV, Clapauch R. Female infertility of endocrine origin. Arq Bras Endocrinol Metabol. 2014;58:144‐152. [DOI] [PubMed] [Google Scholar]
- 17. Shirasuna K, Iwata H. Effect of aging on the female reproductive function. Contracept Reprod Med. 2017;2:23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. American College of Obstetricians and Gynecologists Committee on Gynecologic Practice and Practice Committee . Female age‐related fertility decline. Committee Opinion No. 589. Fertil Steril. 2014;101:633‐634. [DOI] [PubMed] [Google Scholar]
- 19. Kato K, Ueno S, Yabuuchi A, et al. Women's age and embryo developmental speed accurately predict clinical pregnancy after single vitrified‐warmed blastocyst transfer. Reprod Biomed Online. 2014;29:411‐416. [DOI] [PubMed] [Google Scholar]
- 20. Saito H, Jwa SC, Kuwahara A, et al. Assisted reproductive technology in Japan: a summary report for 2015 by the ethics committee of the Japan society of obstetrics and gynecology. Reprod Med Biol. 2018;17(1):20‐28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Fukushima K. Neocognitron: a self‐organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol Cybern. 1980;36:193‐202. [DOI] [PubMed] [Google Scholar]
- 22. Hubel D, Wiesel T. Receptive fields and functional architecture of monkey striate cortex. J Physiol. 1968;195:215‐243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Hubel DH, Wiesel TN. Receptive fields of single neurones in the cat’s striate cortex. J Physiol. 1959;148:574‐591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Schmidhuber J. Deep learning in neural networks: an overview. Neural Networks. 2015;61:85‐117. [DOI] [PubMed] [Google Scholar]
- 25. Dreiseitl S, Ohno‐Machado L. Logistic regression and artificial neural network classification models: a methodology review. J Biomed Inform. 2002;35:352‐359. [DOI] [PubMed] [Google Scholar]
- 26. Ben‐Bassat M, Klove KL, Weil MH. Sensitivity analysis in Bayesian classification models: multiplicative deviations. IEEE Trans Pattern Anal Mach Intell. 1980;3:261‐266. [DOI] [PubMed] [Google Scholar]
- 27. Friedman J, Baskett F, Shustek L. An algorithm for finding nearest neighbors. IEEE Trans Comput. 1975;100:1000‐1006. [Google Scholar]
- 28. Breiman L. Random forests. Mach Learn. 2001;45:5‐32. [Google Scholar]
- 29. Rumelhart D, Hinton G, Williams R. Learning representations by back‐propagating errors. Nature. 1986;323:533‐536. [Google Scholar]
- 30. Bengio Y, Courville A, Vincent P. Representation learning: a review and new perspectives. IEEE Trans Pattern Anal Mach Intell. 2013;35(1): 1798–1828. [DOI] [PubMed] [Google Scholar]
- 31. LeCun Y, Bottou L, Orr GB, Müller KR. Efficient BackProp In: Montavon G, Orr GB, Müller KR, eds. Neural networks: tricks of the trade. Berlin, Heidelberg: Springer; 1998. [Google Scholar]
- 32. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient‐based learning applied to document recognition. Proc IEEE. 1998;86:2278‐2324. [Google Scholar]
- 33. LeCun Y, Boser B, Denker JS, et al. Backpropagation applied to handwritten zip code recognition. Neural Comp. 1989;1:541‐551. [Google Scholar]
- 34. Serre T, Wolf L, Bileschi S, Riesenhuber M. Robust object recognition with cortex‐like mechanisms. IEEE Trans Pattern Anal Mach Intell. 2007;29:411‐426. [DOI] [PubMed] [Google Scholar]
- 35. Wiatowski T, Bölcskei H. A mathematical theory of deep convolutional neural networks for feature extraction. IEEE Trans Inf Theory. 2018;64:1845‐1866. [Google Scholar]
- 36. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J Mach Lean Res. 2014;15:1929‐1958. [Google Scholar]
- 37. Nowlan SJ, Hinton GE. Simplifying neural networks by soft weight‐sharing. Neural Comput. 1992;4:473‐493. [Google Scholar]
- 38. Bengio Y. Learning deep architectures for AI. Found Trends® Mach Learn. 2009;2:190‐127. [Google Scholar]
- 39. Mutch J, Lowe DG. Object class recognition and localization using sparse features with limited receptive fields. Int J Comput Vision. 2008;80:45‐57. [Google Scholar]
- 40. Neal RM. Connectionist learning of belief networks. Artif Intell. 1992;56:71‐113. [Google Scholar]
- 41. Ciresan D, Meier U, Masci J, Maria Gambardella L, Schmidhuber J. Flexible, high performance convolutional neural networks for image classification. IJCAI. 2011;22:1237‐1242. [Google Scholar]
- 42. Scherer D, Müller A, Behnke S. Evaluation of pooling operations in convolutional architectures for object recognition In: Diamantaras K, Duch W, Iliadis LS, eds. Artificial neural networks–ICANN 2010. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer; 2010:92–101. [Google Scholar]
- 43. Huang FJ, LeCun Y. Large‐scale learning with SVM and convolutional for generic object categorization. Computer vision and pattern recognition. 2006 IEEE computer society conference. 2006;1:284–91. [Google Scholar]
- 44. Jarrett K, Kavukcuoglu K, Ranzato M, LeCun Y. What is the best multi‐stage architecture for object recognition? Computer vision. 2009 IEEE international conference. 2009; 2146–2153.
- 45. Zheng Y, Liu Q, Chen E, Ge Y, Zhao JL. Time series classification using multi‐channels deep convolutional neural networks. International conference on web‐age information management. Springer: Cham;2014:298–310.
- 46. Mnih V, Kavukcuoglu K, Silver D, et al. Human‐level control through deep reinforcement learning. Nature. 2015;518:529–533. [DOI] [PubMed] [Google Scholar]
- 47. Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, et al. Going deeper with convolutions. Proceedings of the IEEE conference on computer vision and pattern recognition. 2015:190–9.
- 48. Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. Proceedings of the fourteenth international conference on artificial intelligence and statistics. 2011:315–323.
- 49. Nair V, Hinton G. Rectified linear units improve restricted Boltzmann machines. Proceedings of international conference on machine learning. 2010:807–814.
- 50. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst. 2012;1:1097–1105. [Google Scholar]
- 51. Bridle JS.Probabilistic interpretation of feedforward classification network outputs, with relationships to statistical pattern recognition In: Soulié FF, Hérault J, eds. Neurocomputing. Berlin, Heidelberg: Springer; 1990. [Google Scholar]
- 52. Kohavi R.A study of cross‐validation and bootstrap for accuracy estimation and model selection. Proceedings of the 14th international joint conference on artificial intelligence. 1995;2:1137–1143. [Google Scholar]
- 53. Schaffer C. Selecting a classification method by cross‐validation. Mach Learn. 1993;13:135–143. [Google Scholar]
- 54. Refaeilzadeh P, Tang L. Cross‐Validation In: Liu H, Özsu MT, editors. Encyclopedia of database systems. New York, NY: Springer; 2009. [Google Scholar]
- 55. Yu L, Chen H, Dou Q, Qin J, Heng PA. Automated melanoma recognition in dermoscopy images via very deep residual networks. IEEE Trans Med Imaging. 2017;36:994–1004. [DOI] [PubMed] [Google Scholar]
- 56. Caruana R, Lawrence S, Giles CL. Overfitting in neural nets: Backpropagation, conjugate gradient, and early stopping. Adv Neural Inf Process Syst. 2001;402–408. [Google Scholar]
- 57. Baum EB, Haussler D. What size net gives valid generalization? Neural Comput. 1989;1:151–160. [Google Scholar]
- 58. Geman S, Bienenstock E. Neural networks and the bias/variance dilemma. Neural Comput. 1992;1992(4):190–58. [Google Scholar]
- 59. Krogh A, Hertz JA. A simple weight decay can improve generalization. Adv Neural Inf Process Syst. 1992;4:950–957. [Google Scholar]
- 60. Moody JE. The effective number of parameters: An analysis of generalization and regularization in nonlinear learning systems. Adv Neural Inf Process Syst. 1992;4:847–854. [Google Scholar]
- 61. Miyagi Y, Fujiwara K, Oda T, Miyake T, Coleman RL. Development of new method for the prediction of clinical trial results using compressive sensing of artificial intelligence. J Biostat Biometric. 2018;3:202. [Google Scholar]
- 62. Abbod MF, Catto JW, Linkens DA, Hamdy FC. Application of artificial intelligence to the management of urological cancer. J Urol. 2007;178:1150–1156. [DOI] [PubMed] [Google Scholar]
- 63. Litjens G, Sánchez CI, Timofeeva N, et al. Deep learning as a tool for increased accuracy and efficiency of histopathological diagnosis. Sci Rep. 2016;6:26286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Ortiz A, Munilla J, Gorriz JM, Ramirez J. Ensembles of deep learning architectures for the early diagnosis of the Alzheimer’s disease. Int J Neural Syst. 2016;26:1650025. [DOI] [PubMed] [Google Scholar]
- 65. Gil D, Johnsson M, Chamizo J, Paya AS, Fernandez DR. Application of artificial neural networks in the diagnosis of urological disfunctions. Expert Syst Appl. 2009;36:5754–5760. [Google Scholar]
- 66. Simões PW, Izumi NB, Casagrande RS, et al. Classification of images acquired with colposcopy using artificial neural networks. Cancer Inform. 2014;13:119–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Sato M, Horie K, Hara A, et al. Application of deep learning to the classification of images from colposcopy. Oncol lett. 2018;15:3518–3523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Olczak J, Fahlberg N, Maki A, et al. Artificial intelligence for analyzing orthopedic trauma radiographs. Acta Orthop. 2017;2017(88):581–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Khosravi P, Kazemi E, Zhan Q, Toschi M, Makmsten J, Hickman C, et al. Robust Automated Assessment of Human Blastocyst Quality using Deep Learning; 2018. 10.1101/394882. [DOI]
- 70. Sanders B. Uterine factors and infertility. J Reprod Med. 2006;51:169–176. [PubMed] [Google Scholar]
- 71. Kresowik JD, Sparks AE, Van Voorhis BJ. Clinical factors associated with live birth after single embryo transfer. Fertil Steril. 2012;98:1152–1156. [DOI] [PubMed] [Google Scholar]
- 72. Ahlström A, Westin C, Reismer E, Wikland M, Hardarson T. Trophectoderm morphology: an important parameter for predicting live birth after single blastocyst transfer. Hum Reprod. 2011;26:3289–3296. [DOI] [PubMed] [Google Scholar]
- 73. Pabuccu R, Atay V, Orhon E, Urman B, Ergün A. Hysteroscopic treatment of intrauterine adhesions is safe and effective in the restoration of normal menstruation and fertility. Fertil Steril. 1997;68:1141–1143. [DOI] [PubMed] [Google Scholar]
- 74. Liu L, Huang X, Xia E, Zhang X, Li TC, Liu Y. A cohort study comparing 4 mg and 10 mg daily doses of postoperative oestradiol therapy to prevent adhesion reformation after hysteroscopic adhesiolysis. Hum Fertil. 2018;5:190–7. [DOI] [PubMed] [Google Scholar]
- 75. Ikhena DE, Bulun SE. Literature review on the role of uterine fibroids in endometrial function. Reprod Sci. 2018;25:635–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Taylor E, Gomel V. The uterus and fertility. Fertil Steril. 2008;89:190–16. [DOI] [PubMed] [Google Scholar]
- 77. Tomassett C, D’Hooghe T. Endometriosis and infertility: insights into the causal link and management strategies. Best Pract Res Clin Obstet Gynaecol. 2018;51:25–33. [DOI] [PubMed] [Google Scholar]
- 78. Christ JP, Gunning MN, Palla G, et al. Estrogen deprivation and cardiovascular disease risk in primary ovarian insufficiency. Fertil Steril. 2018;109:594–600. [DOI] [PubMed] [Google Scholar]
- 79. Arronet GH, Eduljee SY, O'Brien JR. A nine‐year surgery of fallopian tube dysfunction in human infertility: diagnosis and therapy. Fertil Steril. 1969;20:903–918. [DOI] [PubMed] [Google Scholar]
- 80. Segars JH, Hill GA, Herbert CM, Colston A, Moore DE, Winfield AC. Selective fallopian tube cannulation: initial experience in an infertile population. Fertil Steril. 1990;53:357–359. [DOI] [PubMed] [Google Scholar]
- 81. Ota K, Ohta H, Yamagishi S. Diabetes and female sterility/infertility: diabetes and aging‐related complications. Singapore: Springer; 2018. [Google Scholar]
- 82. Practice Committee of the American Society for Reproductive Medicine . The role of immunotherapy in in vitro fertilization: a guideline. Fertil Steril. 2018;110:387–400. [DOI] [PubMed] [Google Scholar]
- 83. Hong YH, Kim SJ, Moon KY, et al. Impact of presence of antiphospholipid antibodies on in vitro fertilization outcome. Obstet Gynecol Sci. 2018;61:359–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Moreno I, Simon C. Relevance of assessing the uterine microbiota in infertility. Fertil Steril. 2018;110:337–343. [DOI] [PubMed] [Google Scholar]
- 85. Kroon SJ, Ravel J, Huston WM. Cervicovaginal microbiota, women's health, and reproductive outcomes. Fertil Steril. 2018;110:327–336. [DOI] [PubMed] [Google Scholar]
- 86. Campbell A, Fishel S, Bowman N, Duffy S, Sedler M, Thornton S. Retrospective analysis of outcomes after IVF using an aneuploidy risk model derived from time‐lapse imaging without PGS. Reprod Biomed Online. 2013;27:140–146. [DOI] [PubMed] [Google Scholar]
- 87. Campbell A, Fishel S, Bowman N, Duffy S, Sedler M, Hickman CF. Modelling a risk classification of aneuploidy in human embryos using non‐invasive morphokinetics. Reprod Biomed Online. 2013;26:477–485. [DOI] [PubMed] [Google Scholar]
- 88. LeCun Y, Haffner P, Bottou L, Bengio Y. Object recognition with gradient‐based learning In: Forsyth DA, Mundy JL, Gesu Vd, Cipolla R, eds. Shape, contour and grouping in computer vision. Berlin, Heidelberg: Springer; 1999. [Google Scholar]
- 89. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In Proc. of neural information processing systems. 2012;1097–105.
- 90. Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, et al. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition. 2015:190–9.
- 91. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition. 2016:770–8.
- 92. Hu J, Shen L, Sun G.Squeeze‐and‐excitation networks. arXiv:1709.01507, 2017. [DOI] [PubMed]
- 93. Kudva V, Prasad K, Guruvare S. Automation of detection of cervical cancer using convolutional neural networks. Crit Rev Biomed Eng. 2018;46:135‐145. [DOI] [PubMed] [Google Scholar]


