Physics of growing biological tissues: the complex cross-talk between cell activity, growth and resistance

Abstract

For many organisms, shapes emerge from growth, which generates stresses, which in turn can feedback on growth. In this review, theoretical methods to analyse various aspects of morphogenesis are discussed with the aim to determine the most adapted method for tissue mechanics. We discuss the need to work at scales intermediate between cells and tissues and emphasize the use of finite elasticity for this. We detail the application of these ideas to four systems: active cells embedded in tissues, brain cortical convolutions, the cortex of Caenorhabditis elegans during elongation and finally the proliferation of epithelia on extracellular matrix. Numerical models well adapted to inhomogeneities are also presented.

This article is part of the theme issue ‘Rivlin's legacy in continuum mechanics and applied mathematics’.

1. Introduction

Shapes in nature, from cauliflower to brain, emerge from the growth of tissues. Growth intrinsically generates strains and stresses. Conversely, through mechanisms of mechano-transduction, stresses regulate growth [1,2]. Understanding ultimately the emergence of shapes, in particular in biological tissues, requires capturing the mechanical properties of tissues that are inherent to living matter, and related to growth. As detailed in this review, there is an important body of work that addresses tissue mechanics from the macroscopic view point, trying to analyse whole organ biomechanics. At the other end of the spectrum, cell-based computer modelling approaches the problem from the microscopic point of view. The questions addressed here are: what is an appropriate mechanical description of growing tissues at an intermediate scale between an individual cell and an organ? How can continuum mechanical theories model heterogeneous structures or the impact of isolated active cells on the mechanics of tissues?

The viewpoint adopted here is that starting with a theory of finite elasticity and refining it by introducing dissipative corrections and mechanical feedbacks could provide a unifying theoretical framework. Indeed, finite elasticity is the theory of large deformations and so concerns soft solids. Usually, this formalism is restricted to the simplest case where internal forces only depend on the deformation [3,4] but can include growth [5], and thus is able to predict shapes adopted by living systems during morphogenesis and embryogenesis. Finite elasticity requires constitutive laws which adjust to the soft body under study and the best choice has always been at the heart of the work of Rivlin.

In the context of this thematic issue, the theoretical tools elaborated by Rivlin in the last half century regarding anisotropy [6,7] and fibre networks [8] of rubber are highly relevant to understanding biological tissues. Indeed, he aimed at establishing the most precise constitutive laws for systems which were not completely solid nor completely fluid which is one of the key points of tissue embryogenesis. Thus, it is not surprising that his work serves as a valuable theoretical basis for living systems in their full complexity [9]. Our aim, here, is not a full review of all the contributions and formalisms developed ever since to describe morphogenetic events but to show better how finite elasticity with growth can apprehend modern models of biology. We illustrate our purpose with four examples which have received attention recently or will receive in the near future. These four examples are fully driven by cells, being either the elementary units of tissues as in epithelia or embedded into tissues. Our challenging perspective is to show that, even in these cases, finite elasticity can offer a valuable analysis.

The paper is organized as follows: §2 presents the basis of microscopic, cell-based models and contrasts it with the continuum approaches at larger scales, with an emphasis on finite elasticity theory. We then expose the challenges to overcome if we want to make finite elasticity a successful description of tissue mechanics and embryogenesis at large. In §§3–6, four selected systems of study are presented in detail: cells embedded in connective tissues, brain tissue, Caenorhabditis elegans embryo epithelial cortex in action and, finally, thin bilayers made of an epithelium and a soft extracellular matrix (ECM). All these systems have been or will be perfect examples of study in the finite elasticity framework. Finally, numerical models well adapted to treat inhomogeneities are presented in §7.

2. Modeling tissue mechanics at different scales

In the last two decades, numerous efforts have been devoted to the characterization of the material properties of individual cells [10]. However, in a living organism, cells are interacting both with neighbouring cells and with the surrounding ECM. Collections of interacting cells may exhibit emergent properties, which do not necessarily mirror the properties of their constitutive elements. This prompts mechanical modelling endeavours at the tissue level.

(a). From cells to tissue: the cell-based, microscopic view

Considerable advances were recently made in live imaging technology. Ever-improving confocal microscopes and genetically encoded fluorescent proteins allow us to image entire embryos at a subcellular resolution [11,12]. Imaging combined with laser ablation to infer tension at a subcellular scale [13–15] or opto-genetics to turn on/off cell contractility [16,17] have allowed developmental biologists to better understand how the behaviour of individual cells contributes to tissue scale mechanics. Investigation of developmental processes from this microscopic point of view has been done in systems such as Drosophila gastrulation and metamorphosis [18–21], zebrafish gastrulation [22] or chick neural-tube closure [23]—to name a few examples. This cell-centric approach of tissue mechanics has stressed the importance of actomyosin cortex contractility in tissue mechanics, as well as cell–cell adhesion. Studies were often conducted on simple monolayered epithelia and, most of the time, emphasized the role of cortex mechanics at apical junctions—although some recent studies now stress the role of basal mechanics and ECM in shaping three-dimensional tissues [24–26].

In line with this cell-centred approach, cell-based simulations were developed to explore tissue mechanics (reviewed in [27]). The goal is to make simple assumptions on cell behaviour (e.g. spatial anisotropies of cell interface tension) based on experimental observations (e.g. spatial distribution of molecular motors) and explore how these hypotheses translate to the tissue scale with computer simulations. Widely endorsed models are the vertex model [28], in which cells shapes are described by the vertices that join three neighbouring cells (in two dimensions), or the cellular Potts model, in which cells are represented by domains of nodes on a lattice with like identity (akin to magnetic domains in an Ising model) [29]. Finite element (FE) methods can also be used to represent cells, which are then divided into small polygons. In vertex, cellular Potts and FE methods, the configuration of the tissue is set by an energy minimization. In centre-based models (reviewed in [30]), cells can be represented by simple shapes (typically spheres) with slight deformability, for which trajectories are computed based on Newtonian dynamics. More realistic cell shapes can be achieved by discretizing cells in a number of viscoelastic elements.

In a seminal study on the link between mechanics and proliferation, Farhadifar and co-wokers used vertex models to simulate the cell assembly of developing Drosophila wings [31]. In this work, mechanical stresses can be relaxed through topological rearrangements: whenever energy minimization reduces a cell–cell interface below a certain cut-off length, the interface disappears through a T1 process when energitically favoured. Likewise, Ranft et al. used a centre-based model (dissipative particle dynamics) to model proliferating tissues [32]. Whenever cell distorsion reaches a certain threshold through the combined effect of mechanical stress and growth, a cell division is triggered. In their context, cell divisions fluidize the tissue leading to a stress free state. These two influential papers promoted the viewpoint that topological transitions such as T1 and cell divisions relax stresses in growing tissues, which emphasized the fluid behaviour of the tissues at long time scales.

(b). Organ biomechanics: the macroscopic view

Changes in the shape of tissues proceed at spatial scales much larger than the cell. In this context, continuum mechanics seems appropriate to describe processes with large-scale fields. This formalism gives a rigorous formulation of morphogenesis, providing explicit results as a function of macroscopic quantities, which can be evaluated experimentally. Comparison of the resulting analytical laws with experiments provides a strong predictive power and the sense that the problem under study is understood. Continuous models are also appropriate when mechanics interplays with processes that translate well into continuous equations, such as diffusion and transport in the context of chemotaxis [33,34].

There is a large body of work on the continuum mechanics of tissues from the bioengineering community [35,36]. Interestingly, contrary to cell-based approaches, the elastic nature of tissues is often emphasized. Studies on arteries [37], the mechanical properties of skin [38,39], gut lumen ridges [40,41] and gut looping [42], as well as cortical brain convolution [43,44], are examples of whole organ mechanics well described by elasticity theory. In line with elastic material properties, cutting experiments reveal residual stresses that perdure long after the growth process is finished. How can we reconcile the fluid perspective of the cell-based approach (see above) and the elastic perspective of the the bioengineering approach? As discussed below (see §1c(ii)), one possibility is that whole organ biomechanics encompasses the inhomogeneous structure of organs made of connected layers, which may confer elasticity to tissues. On theoretical grounds, a long-standing challenge in the continuum description of tissues has been to find the correct description for growing tissues. The mechanical description of growth is a quite recent addition to the theory of elasticity. Precursor works include those of Cowin & Hegedus [45], Skalak et al. [46] and Fung [36]. In their seminal work, which recapitulated and extended these initial efforts, Rodriguez et al. [47] developed the formalism of finite elasticity, which has now become the method of choice to account for the elasticity of growing bodies. Finite elasticity describes the final shape of a growing body as resulting from the elastic accommodation of a prescribed volumetric strain due to growth. Taking its roots from plasticity theory, this model turns out to describe a wide range of volume variation processes, for both inanimate matter (gels) and biological systems. A lot of works have been done with this formalism with the aim to extend its ability to treat biological features more efficiently as dissipation, pre-strained or pre-stressed tissues, and adequate constitutive laws, especially for fibre networks.

(c). Current challenges for continuum theory

(i). Bridging scales

It is certainly relevant to merge the best of the two worlds: the analytical capability of continuum theory to encapsulate tissue mechanics in a few equations, and the capability of cell-based models to take into account the wealth of information that modern biology provides. Some attention has already been given to mapping vertex to continuum models [48]. Methods to integrate experimental cell descriptors at the mesoscopic level were also recently published [49–51]. In parallel, as mentioned above, theoretical efforts should try to extend current formalisms to account for cell behaviour at a mesoscopic scale—trying to address for example questions of dissipation through the exchange of neighbours. Alan Turing, in his classic work on morphogenesis, has analysed this alternative between discrete and continuous modelling [52]. His work focused on reaction–diffusion of chemical species—not mechanics. However, the core of his pioneering paper concerns mostly a finite number of cells reacting with each other through morphogens. His effort to link the cellular scale with a process usually formalized in a continuum description (here diffusion) could be inspiring for tissue mechanics.

(ii). Which constitutive equation?

Different constitutive equations that range from elastic, visco-plastic to liquid-like behaviour have been used to model tissue mechanics [53,54], suggesting that the general behaviour of tissues is still controversial. Some cases are quite intuitive. For instance, plants are appropriately described as elastic solids, consistent with the solid wall of plant cells and limited remodelling [55,56]. This is also true for algae, although their cell walls are softer than the plant ones [57,58]. For tumour models, the situation is less clear, since tumour multicellular spheroids have been shown to be characterized by a surface tension reminiscent of a liquid at long times [59], while real tumours, whose microstructures are reinforced with stiff ECM [60,61] or pathological fibrosis are well described on elasticity basis [62]. Indeed, in vivo tumours (by opposition to in vitro cancer cell spheroids) recapitulate the organ complexity, with dynamic regulation and constituent cellular populations, during initiation, maintenance and progression [63]. Likewise, mechanical instabilities that seem to drive gut looping [42], vilification [40,41] and cortical folds [43,44,64–67] point to the elastic behaviour of these structures. An argument in favour of elastic behaviour is that cells usually tightly adhere to each other and most importantly to the underlying ECM. An argument in favour of fluid behaviour at long times is the presence of topological rearrangements associated with proliferation [32] leading to stress relaxation. Whether elastic energy is stored and leads to residual stress, or whether cell proliferation induces fluidization of the tissue, is still debated to the best of our knowledge. The fluidization of tissues finds its root in structural re-organization of the living samples, which is not always possible when layers are inter-connected, a fortiori when fibres are present. As a consequence, it mainly concerns epithelia without interactions. Inside an organ, cell layers are attached to connective tissues via collagenous membranes such as in the epidermis of our skin, which is separated from the dermis via the basement membrane. Connective tissues provide elasticity. These simple arguments may explain the difference between the fluid emphasis of the cell-based approaches, which focuses on model tissues and young embryos, and the elastic emphasis of bio-mechanicians, which focuses on whole organs.

(iii). Heterogeneities

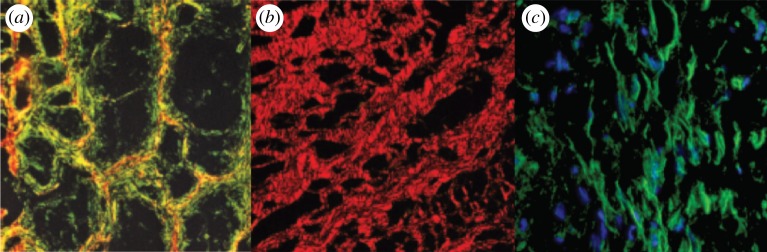
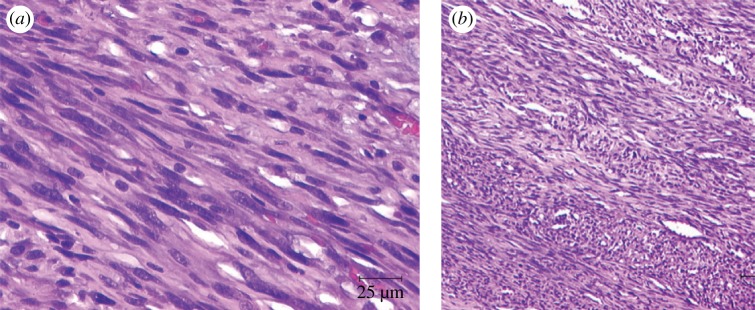
Connective tissues are constructed from an interconnecting network of collagen filaments, fibrils and fibres with a high tensile strength, fine and delicate reticular fibres and elastic fibres with a greater extensibility. They constitute the most predominant tissue in our body (20%). All these fibres are organized in a hierarchical multi-scale structure (see figure 1) inside a ground substance. How soft tissues adapt hierarchically to shear and compression is still little explored, which leaves unsolved the question of how, in soft connective tissues, cancer cells or fibroblasts change their mechano-phenotype to become more aggressive and invasive in pathological conditions. A unique modelling will never cover the whole diversity of growing living systems. Thus, different nonlinear modellings exist to represent the strain-stress laws under specific loadings. This is especially the case for fibre networks for which the link between the microscopic structure and the macroscopic constitutive laws have been investigated from different perspectives [69–71]. No attempt was made, however, to take into account the regulative function of fibroblasts. These isolated but very active cells are targeted to wound and change local stiffness there by making a fibrotic network. The consequent changes in compressive stresses affect in return fibroblast physiology. Another example of heterogeneous structures is sarcoma. Sarcomas are rare malignant tumours originating from mesenchymal tissue; they show an extremely high morphological and genotypic heterogeneity [72,73]. Their mesenchymal origin gives them an extremely high differentiation capacity, in various soft tissues. For example, and as shown in figure 2, leiomyosarcoma cells adopt a fibrillar structure. Their cytoplasm is finely fibrillar—a signature of a deep mechanical transformation of the embedded cells, both locally and globally. There is also a long-range ordering of cells (alignment) which is the result of a higher deformability of their cytoplasm, suggesting a higher unidirectional actomyosin tension. This ordering leads to the alignment of two cells which then fuse to give a very aggressive entity suspected to be at the origin of metastasis. Here again, this process is driven by mechanical cues since it seems to be induced by a local shear inside the tissue.

Figure 1.

From [68], (a) collagen network within a Baker II capsule (Baker grade indicates the degree of the pathology, Baker II being an intermediate level of pathology). The green birefringence shows the loose organization of collagen fibres wrapped around tighter organized collagen fibres in red. (b) Periodic spacing of collagen fibres making up the thick cables in Baker III capsules. (c) Cells aligned parallel to the collagen fibres in Baker II capsules. (Online version in colour.)

Figure 2.

(a) ‘Cigar shaped’ configurations of tumour cell nuclei of a leiomyosarcoma with nuclear atypia [74]. (b) Histological appearance of a leiomyosarcoma after resection of a tumour in the subclavicular region [75]. (Online version in colour.)

(iv). Singularities

Continuum models are particularly challenged when a very diluted and scattered population, such as the fibroblasts, plays an important role in the properties of the tissue. Besides fibroblasts and myofibroblasts [76,77], other examples of singular behaviour that may be hard to grasp in a continuum model are cancer stem cells [78–81], which are also isolated cells within a tumour that respond to environmental changes through proliferation. A single undifferentiated cancer cell can generate a complete tumour. They involve niches where stem cells are located and perhaps the cancer stem cells also. Cancer stem cells are then localized sources of proliferation. To conclude, the variability of living species (bacteria, plants, algae and fungi) and additionally the variability of our organ properties at different ages (fetus, childhood, adult or ageing) is too vast, quite infinite, to be relevant to a unique formalism. The formalism of finite elasticity alone cannot describe all the material properties of complex soft tissues at an intermediate scale above the cell size, with refinements including dissipative effects, feedback mechanism between growth and stress, localization and spatial disorders. There is also a price to pay to extend a formalism: first, the added complexity; second, the increase of unknown parameters.

A cross-fertilization of the two approaches we discussed—the macroscopic biomechanics and the cell-based biophysics—may allow us to revisit the material properties of growing tissues and putatively gain a more realistic insight into organ growth, shapes and pathologies. To explain this in a more concrete way, a selection of biological models is proposed hereafter where experimental data are available or will be available in a close future. It is important to underline that most debates in the last two decades originate from the lack of experimental data, suggesting that it is important to develop tools to access the mechanical properties of tissues in development. Both connective and epithelial tissues in growth will be considered with emphasis on the role of cells.

3. Active cells in connective tissues

Very active cells may be embedded in connective tissues generating mechanical stresses. To model this requires a good representation of the fibre network at the macro-scale modified by the presence of active, eventually aggressive cells which, in addition, may have the ability to change their phenotype. Classical models of fibres [82–87] in biomechanics are based on symmetries and represent the constitutive laws in term of the first invariants constructed with the deformation gradients. These macroscopic models have the advantages to treat simultaneously both the anisotropy of growth and also the structural anisotropy of tissues [88]. They also have the advantage of simplicity even if they were a matter of debate in the recent past, concerning mainly their adequacy to treat correctly all kinds of deformations. Indeed, they present some difficulty in mimicking compression which always exists in three-dimensional incompressible samples: in three dimensions, a tensional state in one direction implies quite automatically a compression in another direction. Recently, microscopic approaches have been proposed [69] to establish more realistic constitutive laws for the fibre network (without solving the compression problem), introducing the compliance of the cross-linkers and viscoelasticity. These approaches are based on affine kinematic assumptions [69], a hypothesis which has not yet been validated experimentally for fibrous organs [89], which have a more complex structure than the actin network proposed in [69].

More importantly, these biomechanical models of fibrous tissues do not include the existence of active cells, which generate local proliferation and global growth (fibroblasts, cancerous cells) but also active strain or stress (myofibroblasts), apart for the work of De Vita and colleagues [90,91] on smooth muscles. Clearly, this biological situation, where small-scale individuals may perturb a complex environment, open new challenges in finite elasticity. One may naturally think of the theory of defects [92] as a starting point. In addition to the complexity of tissue modelling, the interpretation of the experimental measurements is difficult as cells tend to react to any imposed perturbation, and thus to the imposed measurements. This is what happens to cells when the cytoskeleton is probed by atomic force microscopy (AFM). Two time scales have been detected [93]: the typical time scale of a passive elastic response, then a typical time scale of reactivity of the molecular motors. Even if these two time scales are different, this indicates a competition, at the cellular level of the cell of both passive and active processes.

Many classical biophysical experiments (such as micro-pipette aspiration) have been interpreted in the past by surface tension. It requires, now, to be revisited in the context of nonlinear elasticity as done by Holzapfel et al. [69] for micro-pipette aspiration and by [93,94] for AFM indentation. This is necessary for a proper interpretation of the data and this is the only way to provide some portability to the models when applied to in vivo situations. It is especially true for frequency-dependent stress–strain experiments done on three-dimensional fibrous samples. A recent study on fibrous materials submitted to cyclic extension has shown a complex response of these tissues under time-dependent loading, which is not trivial to interpret in the context of established formalisms [95,96].

The modelling of tumour growth under mechanical stress must decipher local and global (multi-scale) aspects. Cancer cells inside a tumour are not identical but form different clones which can be defined as subgroups of cancer cells sharing a common genotype. The epigenetic tumour cell heterogeneity cannot be fully explained without considering that tumour cells are not isolated but surrounded by their microenvironment (extracellular matrix) which is also very heterogeneous in composition. Malignant transformation, although primarily driven by genetic mutations in cells, is also accompanied by specific changes in cellular and extracellular mechanical properties such as adhesion, contractility, mechano-sensing, rigidity, viscoelasticity and plasticity. As the transformed cells grow into tumours, they interact with their microenvironment via physical contacts and application of forces which in turn alter the mechanical regulation of cells. It is therefore important to understand the effect of these peculiar changes in cellular and extracellular mechanical properties on the transformation of benign cells into cancer cells to establish the basis of a model for tumour growth and metastasis. For that purpose, computing tools are fundamental for estimating to which extent and at which scale the cross-talk of cancer cells with their microenvironment is going to impact their proliferation. Most of the previous studies of the biomechanics of cancer cells [97] have focused on the mechanical properties of the cancerous cells themselves and more rarely on their surrounding niche. They have led to disparate results since cancer cells can become stiffer or softer depending on their embedding tissue or their progression in the disease. The study of these fibrous tissues is especially important in the context of tumour growth.

4. Assembly of cells seen as tissues: cortex anomalies and ageing

The circumvolutions of the brain, called gyri, appear approximately at four months post fertilization for human fetuses. A number called the gyrification index is defined to characterize this shape instability. It is a number measuring the ratio between the outer surface of the cortex versus the averaged middle surface of the cortex layer. It is closed to 1 for smooth brain (rodents), around 2.6 for babies and 5 for dolphins. Recently, the bilayer model has encountered some success for the prediction of the gyrification index of the brain [43,44,98]. This model is based on simple ingredients. It assumes that the grey and white matter can be considered as two hyper-elastic layers in growth and that the origin of cortex gyrification comes from the differential growth between these two layers. A growth anisotropy in the grey matter originates from the fact that stem cell differentiation and differentiated cell proliferation occur simultaneously, in fetal life. The main assumption is only a differential and anisotropic volumetric growth of two gel layers (grey and white matter) with the added hypothesis that white matter is slightly stiffer than grey matter. These assumptions lead to a super-critical bifurcation in growth modelling. Except for the case of brain pathologies, this two-layer model recapitulates the gyrification index in fetal life quantitatively [44] by comparison with data compiled by [99,100] and new magnetic resonance imaging (MRI) studies for fetuses and pre-term newborns [101]. The model explains standard global pathologies as polymicrogyry (excess of cortical folds) and lissencephaly (lack of cortical folds).

Another challenge to raise is how to explain the existence of local creases in the cortex and their possible link to pathologies. If local creases have been observed in experiments involving layers of swelling gels [102–104], they are not completely understood from a theoretical point of view. Indeed the theory of bifurcations, which is well adapted for buckling, fails for local and singular instabilities like creases. Recent investigations in compression involving local defects are promising [105] although possibly not applicable to the brain. The question is mathematical: why does a growing elastic system select a periodic array of cusps instead of a nonlinear buckling? What kind of growth will lead to these cusps instead of smooth surface instabilities? Do we need specific growth repartition to observe such pattern? It is a challenging problem in the context of nonlinear elasticity. Material properties of the two layers (white and grey matter) change in the course of ageing. Not only the relative size of both layers change but their relative stiffness changes as well. This has been shown recently by studies on cadavers [106] indicating that the stiffness ratio between layers varies with age and that the cortex becomes stiffer than the white matter, in contrast to what happens for babies. How changes in material properties affect gyrification and the morphology of the cortical layers can be studied through a combination of modelling and MRI. In this context, important points to address are local variations or inhomogeneities, which seem to affect cognition such as language functions, and the width of sulci, which increases with age and seem to correlate with cognitive decline in the elderly. Neuro-degenerative diseases have also been linked with gyrification through the appearance of neuro-fibrillar tangles in the cortex, which increases the stiffness in comparison with the white matter, again modifying the gyri and sulci.

5. Active cells at work: the case of C. elegans embryonic elongation

C. elegans embryonic elongation asks specific questions of great interest for embryogenesis. It involves two time periods (figure 3) in which the lima-bean shape of the embryo is transformed into a quasi-cylinder with a fourfold increase in length. These two periods last approximately 2 h each. During the elongation period, no cell proliferation, cell migration, cell division or notable changes in embryonic volume are observed. The first period is controlled by the cytoskeleton of the epidermal cells, mostly the actomyosin couple, and provides an elongation by a factor of 1.8 [14,107,108]. To experimentally check this hypothesis, Vuong-Brender et al. [14] have measured the outer dimensions of each part of the epithelium during elongation which is composed of three different cell types. These cells located in four domains differ by the polarized orientation of the cytoskeleton. The cytoskeleton in the dorsal and ventral cells is strongly polarized in the ortho-radial direction, while it is less polarized in the seam cells. By measuring the opening induced by laser ablation in different parts of the embryo, these authors assess the stresses which drive the elongation. Indeed, this technique allows them to evaluate quantitatively the local stresses in the living embryo and to assess the rheology and structure of its compartments [15]. To be quantitative the laser ablation technique requires to revisit the theory of fracture as the crack shape in orthotropic material under bi-axial stresses (doable in linear elasticity) or the full theory of fracture in finite elasticity. Contrary to a naïve intuition, in linear elasticity, not all the problems of fracture have been investigated. In [14], for example, the linear analysis of fracture achieved initially by [109,110] has been extended to orthotropic materials to interpret correctly the laser indentation on C. elegans embryos. However, for an elongation of 80%, probably, linear elasticity is not enough and a better model should involve nonlinear elasticity. Indeed only finite elasticity can involve pre-stress/pre-stretch, passive and active stresses in the same formalism.

Figure 3.

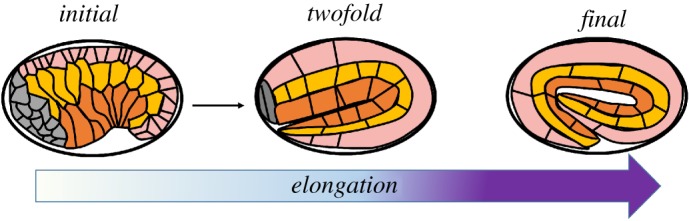
Embryonic elongation in C. elegans is driven in part by epidermal actomyosin contractility and in part by muscle contraction. Inspired by [14]. In pink, the dorsal epithelial cells, in yellow the seam epithelial cells, in orange the ventral cells. (Online version in colour.)

The second period of elongation [111–113] which lasts 2 h is controlled by nascent muscles, located below the epidermis, in the gelatinous intestinal inner cylinder. To understand how contractile cells can finally lead to an elongation process is challenging. Here again, it is known that four lines of muscle cells located below the epidermis elongate the embryo by a factor 2. It will require coming back to microscopic models of muscle formation and to an evaluation of the strains, which can be obtained after successive periods of compression on one side and stretch on the other side of the body. Indeed, when two muscular chains are in compression on one side of the embryo, the opposite side turns out to be in extension. Understanding how this succession of compression/extension can lead to such elongation and what we will learn on muscles in embryogenesis is an ambitious goal that will bring new insight into the role of muscles in embryogenesis. Indeed a factor 2 is huge and one can wonder if only mechanics is involved in this process or if new muscle cells appear in the stretching period, according to the naïve idea that a tensional state induces proliferation. Another question concerns the relaxation of stresses which have been accumulated during the total elongation period. Indeed, such elongation will put mostly all embryonic tissues into tension, which can be followed by cell proliferation hereafter.

6. Proliferative epithelial cells on an elastic substrate

As already underlined, there are a number of model experimental systems in which the growth of epithelia has been investigated. Surprisingly, however, the paradigm of finite elasticity with growth has not been applied to this context. In most of the theoretical biophysics contributions, an elastic coupling with the substrate is discarded and the notion of fluidity is promoted. It may be relevant to revisit the question of the best rheological model between viscoelasticity, elasticity and fluidity by comparison of experimental data with a finite elasticity model involving the bilayer composed of the epithelium and the extracellular matrix. Potential experimental models to confront the theory are the Drosophila wing (in vivo) or in vitro epithelial cysts. For the first model system, quantifying cell deformations and stresses, it was found that the growing wing imaginal disc displays a highly patterned field of mechanical stress [114,115]. In particular, the cell at the periphery of the tissue sustains a strong mechanical stretch. These results are in disagreement with the viewpoint of a growing tissue in a fluid state through the combined effect of cell divisions and cell rearrangements [32]. The observed pattern of mechanical stress impacts on tissue morphogenesis by polarizing the cytoskeleton of cells as well as the orientation of their divisions. To investigate more thoroughly the role of mechanics, localized perturbation (e.g. growth, or structure of the ECM) can be achieved, and the resulting tissues analysed under the microscope. This provides challenging objects of study for the modelling. Such experimental investigations allow us to assess the link between patterned growth and patterned stress. They should allow us to derive in the future the constitutive equations of the tissue, answering the question of their fluid or elastic nature. Figure 4 provides an example of a perturbation where the elastic ECM underlying the Drosophila imaginal wing epithelium has been degraded in a region at the centre of the tissue. The consequent distortions are typically reminiscent of an elastic buckling. Likewise, the tissue undergoes shape changes also analogous to the buckling of an elastic sheet in conditions of local hyper contractility of the apical surface of cells by expression of a constitutively activated form of Myosin (L. LeGoff 2018, unpublished).

Figure 4.

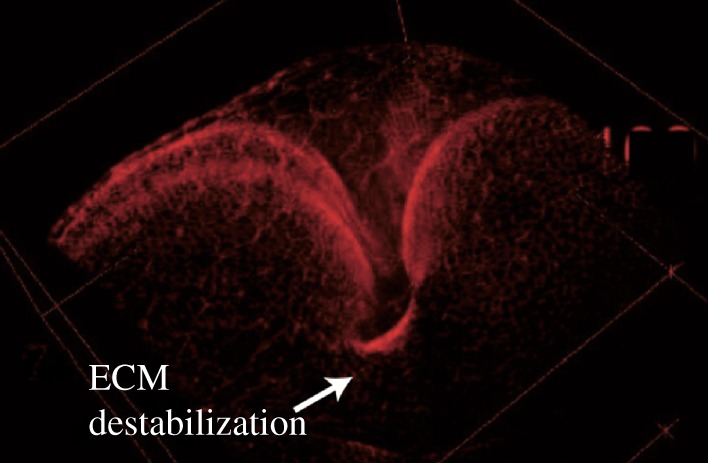
Generation of buckling-like three-dimensional shapes through localized destabilization of ECM after expression of the protease Mmp2 in a central band of the tissue, leading to a deep fold in the tissue (exact genotype: ubi-cad:GFP Gal80ts; UAS-Mmp2/DppGal4).

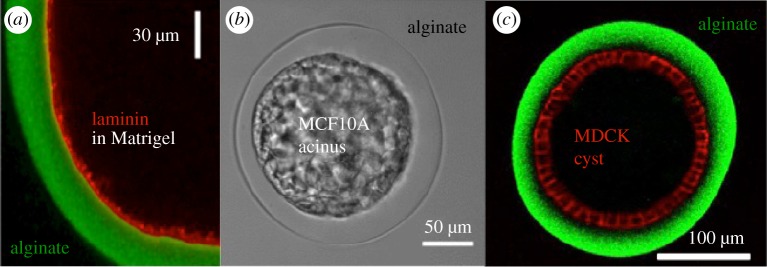
In vitro cysts were recently developed with morphometric, physico-chemical and mechanical properties which can be tuned easily (see figure 5) [116,117]. Here, epithelial cells are encapsulated in hydrogel hollow micro-spheres whose diameter can be varied from few tens of micrometres to millimetres. In the presence of ECM proteins anchored to the inner walls of the capsule, cells proliferate, readily spread onto it and self-assemble into a closed spherical epithelium. This set up gives a new opportunity to investigate epithelial growth with a prescribed curvature and with variable parameters. The fact that one can vary the parameters, such as the stiffness of the artificial ECM by tuning the composition of the hydrogel, is a unique opportunity for testing specific aspects of the theory. Indeed, morphogenesis is a complex highly regulated sequences of processes with a few degrees of freedom including the use of mutants. Using in vitro cysts allows one to dissect the different potential morphogenetic events and to investigate the impact of geometrical and morphological control parameters. Both systems are geometrically complex to handle analytically, but being made of thin layers a lubrication analysis of the equations of elasticity or viscoelasticity may be suitable [57,58].

Figure 5.

(a) Confocal section of an alginate capsule (green) coated with a layer of ECM (red); (b) Phase contrast videomicrograph of an encapsulated cyst of MCF10A (epithelial cell from the mammary gland); (c) Confocal equatorial section of an MDCK cyst (red) in an alginate capsule (green).

Undoubtedly, these two model systems will be helpful to test many aspects debated in the field of morphogenesis of tissues, such as dissipation, localization and stochasticity [118,119]. Even within the simplifying assumption that they behave elastically, one can decipher the role and the impact of growth, epithelium and ECM stiffness, and adhesion/friction with the substrate (ECM). In addition, determining the elastic strain and stress tensors as well as the current shape of the tissue (be it the wing disc or the encapsulated cyst) gives the possibility of evaluating the growth tensor which dominates the geometric strain and the shape of the tissue during growth. To the best of our knowledge, such a study has never been achieved. Finite elasticity with growth has been established for organs where usually the growth tensor is not known a priori. This lack of information has forced theorists to make reasonable assumptions mainly based on symmetry arguments, then allowing to carry off semi-quantitative results. These model systems offer a situation to test in detail the development with the nonlinear elasticity of soft tissues. Comparing experimental data with theoretical predictions will clarify the question of viscoelasticity in growth processes, thus eliminating endless debates in the community.

7. Methodology

(a). Analytical treatments

Giving the best description of living tissues in morphogenesis is an ambitious objective. Considering mostly the scale of organs or embryos, the continuum description is preferred, at least in the biomechanics community. However, living tissues present a diversity of behaviours that inert physical systems do not exhibit. In physical systems, volumetric growth is not so common. Swelling or drying gels, although very useful tools for mimicking growth with adaptable geometries do not fully correspond to volumetric growth or resorption. In physical situations with inert matter, growth is very often the result of an out-of-equilibrium phase transition process such as dendritic growth. This process is governed by diffusion equations and elasticity plays a minor role. It is why the theory of elasticity with growth [5] has been so much debated. In addition, the fact that all geometric deformations have the scale of the samples indicate that the theorist cannot use linear elasticity. After two decades of discussions about the foundations of the modelling, the time has come to test the model in the full complexity of living systems, addressing their dynamics and disorders. Four up-to-date biological systems have been presented here where cells play a key role. Cells are the sole sources in the systems through their proliferation and their ability to generate new connective tissues. They also power other deformations, such as stretching via their actomyosin network. Finite elasticity allows analytical treatments when the shape result from bifurcations. However, when the study concerns extremely active cells embedded into a fibrous tissue, microscopic methods or semi-microscopic methods may be preferred.

(b). Microscopic methods

A possible microscopic method is the kinetic theory of active particles (KTAP), which takes into account both the cellular and tissue scales. The principle of the method can be found in [120,121] for the case of fibrosis. It is based on a generalization of the Boltzmann equation for gas. The system is decomposed into different functional subsystems involving a large number of interacting entities, called active particles: their microscopic state, in addition to geometrical and mechanical variables, also includes an additional variable, called activity, which represents the ability to express a specific strategy such as mutation or proliferation. The overall state of each subsystem is described by a distribution function over the microscopic states of the cells. Interactions, which modify the state of the interacting cells, produce transitions of the activity variable, proliferation and mutations. An external field (imposed by shear for example, as observed in sarcomas) is represented by an action into the system, thus moving the system out of equilibrium. By balancing the inlet and outlet flows into the elementary volume of the possible microscopic states, the evolution equation of each functional entity can be derived. The description at the cellular scale brings important information on the dynamics at tissue scale. The macroscopic behaviour of tissues can be derived from the dynamics at the cellular level by letting intercellular distances tend to those of the tissue level. The link between the cellular and the tissue scales is thus obtained through usual hydrodynamic limit procedures [122,123]. Typically sarcoma tumour growth would be a good candidate for such treatment.

(c). Semi-microscopic modelling

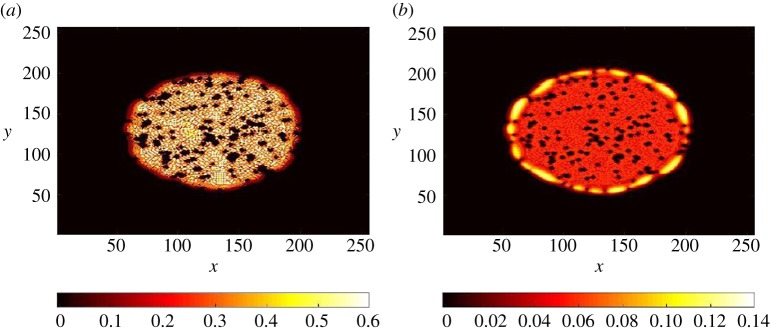
Semi-microscopic models will consist in treating the tissue as a mixture of different entities [124–126]. The formalism can be extended to finite elasticity for fibres and for cells positioned in average position. Indeed, for fibrotic tissues, the fibroblast cells are located at specific positions (see figure 1). It is likewise the case for cancer stem cells which, as healthy stem cells, occupy preferential niches. The advantage in these models is that growth can be easily introduced. The introduction of drugs or nutrients can also be easily modelled. Another semi-analytical method will consist in using discrete–continuous models, then treating cells as singularities in a continuum medium. This approach is well adapted to the low density of extremely active cells, which have a notable impact on the tissues through proliferation or exertion of forces. When it is necessary to decipher local and global aspects of tumour growth in fibrotic tissues, continuum models (at scales larger than the cell size) must be combined to microscopic units to describe their fascicular orientation, with local anisotropic subcellular mechanical moduli to include the intracellular organization of the cell cytoskeleton and its change with mechanical modulation. These units may involve distinct cell populations, differentiated cancer cells, cancer stem cells, fused cells. Mixture models [124–126] are the most flexible tools, since various elasticities for the different cell phases and cell–cell interactions can be introduced according to their phases and their rate of proliferation. As an example, see fig. 6 from [127], where the patterns of cell repartition are shown in the presence of solid obstacles, always present in tumours. Also of importance will be the mechanical constraints imposed by the stroma which opposes a resistance on the tumour. The response of substrate elasticity that has been largely neglected so far may be at the heart of future studies.

Figure 6.

Distribution of cells computed with the two-dimensional mixture model including cancer stem cells, differentiated cells and inert cells (dead, of different type such as blood cells). The computation was seeded from a small number of cells. (a) Differentiated cell distribution. (b) Cancer stem cell distribution. The black dots represent obstacles (vessels, fibres). This numerical computation includes a chemical signal exchange in between cells (such as growth factors) and growth feedback control loops (unpublished preliminary data [127]). (Online version in colour.)

8. Conclusion

Across four different examples chosen in embryogenesis, morphogenesis and tumour genesis, a panorama of living tissues properties and modelling is presented. The examples are at an intermediate scale between cells and organs with a moderate complexity. Among the biological diversity, we focus on the case where cells are not only present but very active [128], making ordinary modelling uneasy, sometimes not appropriate. We have emphasized the need to describe tissues at a scale intermediate between the large scale of whole organs and the cellular scale. A controversy originates from tissue growth: what is the most appropriate modelling? It was proposed that in growth, tissues behave as a fluid at a long time to reorganize the cells and dissipate the stresses. However, it was also suggested that because growth is a very slow process, all transient states disappear very quickly and tissues are mostly elastic when they grow. To clarify this debate, Mongera el al. propose a transition described by a fluid-to-solid jamming transition in vertebrate body elongation [129], also in favour of a solid view point at long times. However, the answer is probably not universal and only predictions of models adapted to specific biological experiments or situations where data are available will have a real scientific impact in the future.

Data accessibility

This article has no additional data.

Author's contributions

All authors contributed equally, read and approved the manuscript.

Competing interests

We declare that we have no competing interests.

Funding

The authors acknowledge the support of ANR (Agency Nationale de la Recherche) under the contract MecaTiss (ANR-17-CE30-0007). M.B.A. acknowledges also the support of ANR under the contract (ANR-18-CE13-008) EPIMORPH and L.L.G. the support of ANR under the contract (ANR-18-CE13-028) GuideFusion.