Abstract
Attosecond pump–probe spectroscopy is a unique tool for the direct observation of the light-activated electronic motion in molecules and it offers the possibility to capture the first instants of a chemical reaction. Recently, advances in attosecond technology allowed the charge migration processes to be revealed in biochemically relevant molecules. Although this purely electronic process might be key for a future chemistry at the electron time scale, the influence of this ultrafast charge flow on the reactivity of a molecule is still debated. In this work, we exploit extreme ultraviolet attosecond pulses to activate charge migration in two aromatic amino acids, namely phenylalanine and tryptophan. Advanced numerical calculations are performed to interpret the experimental data and to discuss the effects of the nuclear dynamics on the activated quantum coherences. By comparing the experimental results obtained in the two molecules, we show that the presence of different functional groups strongly affects the fragmentation pathways, as well as the charge rearrangement. The observed charge dynamics indeed present peculiar aspects, including characteristic periodicities and decoherence times. Numerical results indicate that, even for a very large molecule such as tryptophan, the quantum coherences can survive the nuclear dynamics for several femtoseconds. These results open new and important perspectives for a deeper understanding of the photo-induced charge dynamics, as a promising tool to control the reactivity of bio-relevant molecules via photo-excitation.
This article is part of the theme issue ‘Measurement of ultrafast electronic and structural dynamics with X-rays’.
Keywords: amino acid, time-resolved photo-fragmentation, attosecond spectroscopy
1. Introduction
Capturing a chemical reaction in real time has long been the ‘Holy Grail’ of time-resolved chemistry. In 1981, Zewail and co-workers [1] were able for the first time to trigger a coherent quantum beat in the anthracene molecule via picosecond photo-excitation. Only a few years later, the advent of femtosecond laser technology allowed a bond breakage in the ICN molecule to be observed [2], paving the way for the new field of femtochemistry. While femtochemistry was establishing a new experimental protocol in time-resolved spectroscopy, ultra-intense lasers were used to generate bursts of light in the extreme ultraviolet (XUV) spectral range via the extremely nonlinear optical process dubbed high-order harmonic generation (HHG) [3,4]. Several years later, advances in the HHG-based technology allowed the first isolated subfemtosecond laser pulse to be generated [5], giving birth to the field of attosecond science. This new branch of photo-physics offered a unique tool to capture the electronic motion in matter on its natural time scale. In its infancy, attosecond science was mostly exploited to investigate ultrafast electron dynamics in atoms and small molecules [6–8], while several theoretical works were already envisioning the possibility of probing charge motion in more complex biochemically relevant systems [9–12]. In particular, a prompt ionization of a large molecule by a relatively high-energy photon was predicted to induce an ultrafast charge flow along the molecular backbone on a time scale ranging from a few femtoseconds down to a few hundred attoseconds [10–12]. This purely electron dynamics was dubbed charge migration [11].
In this work, we investigate charge migration in two aromatic amino acids, i.e. phenylalanine (Phe) and tryptophan (Trp), and we present a close comparison of the results obtained in the two molecules. We show that the presence of different functional groups strongly affects the photo-induced charge rearrangement and the fragmentation pathways. We demonstrate that, although the charge oscillations observed in the two systems have a similar periodicity, they exhibit a different time evolution. First, they show an out-of-phase behaviour; and second, the main frequency detected in the case of Trp presents a faster decoherence time with respect to the one detected in Phe.
Advanced numerical calculations are performed on the cation dynamics induced by the attosecond pulse. These simulations employ a realistic description of the electronic wave packet launched by the attosecond pulse and, furthermore, they account for non-adiabatic and nuclear motion effects at the time-dependent density functional theory (TDDFT) level. Here, we present the results obtained for the largest molecule, namely Trp. By comparing these new results with the ones obtained for Phe and reported in [13], we demonstrate that the charge density fluctuations evidenced in the experimental data involve different functional groups for the two molecules. This allows us to draw preliminary conclusions on the hole dynamics activated in the two amino acids and, in general, to reach a deeper understanding of the interplay between electron and nuclear motion in XUV-induced charge migration in bio-relevant molecules.
2. Charge migration in bio-relevant molecules
The interaction of light with large molecules is likely to initiate a charge transfer mechanism, which plays a crucial role in a number of biochemical processes. The term charge transfer traditionally indicates a charge flow along the molecular backbone mediated by the nuclear motion, which occurs in several tens of femtoseconds. As mentioned in the introduction, charge migration—on the contrary—is a purely electronic process occurring from a subfemtosecond to few-femtosecond time scale. The process has been at first only theoretically investigated and attributed to the ionization of correlated states [11]. Experimentally, charge migration has been initiated by creating a superposition of a number of cationic states [13]. In the experiment, the amino acid Phe was suddenly photo-ionized by an isolated attosecond pump pulse and the induced charge dynamics in the molecular cation was probed by a few-femtosecond near-infrared pulse. The main observable of the experiment was the yield of the produced photo-fragments as a function of the pump--probe delay. The yield of the immonium dication (resulting from the loss of the carboxylic group) has been found to oscillate with a sub-4.5 fs periodicity, which is faster than any nuclear rearrangement. This oscillation was assigned to charge density fluctuations occurring at the amine site of the molecule [13]. State-of-the-art simulations based on a combination of time-dependent first-order perturbation theory and static-exchange density functional theory (DFT), in the framework of the fixed-nuclei approximation (FNA), were used to interpret the experimental findings. This work demonstrated for the first time the capability of exploiting attosecond technology for the investigation of ultrafast electron dynamics in bio-relevant molecular systems. This has triggered further experiments aiming at clarifying the role of the electron dynamics in the photochemistry of complex molecules [14,15]. Among them, Kraus et al. [15] exploited high-order harmonic spectroscopy to investigate charge migration in oriented iodoacetylene, with particular interest in the interplay between the molecular orientation and the influence of the external laser field. They demonstrated that the effect of the laser field on charge migration is negligible for molecules aligned perpendicular to the laser polarization. For parallel molecules, instead, the laser field induces substantial population transfer between different electronic states, which depends on the head-to-tail orientation of the molecule.
A lot of effort has also been made to model the charge migration process initiated by broadband attosecond pulses, with particular emphasis in clarifying how long the electronic coherences could survive in the presence of nuclear dynamics [16–18]. Lara-Astiaso and co-workers [16] have recently presented a theoretical study on the XUV-induced charge migration dynamics in glycine. They used the static-exchange DFT method combined with the time-dependent perturbation theory to evaluate the ionization amplitudes, while the evolution of the ionic system (when nuclear motion is included) was described by using the time-dependent Kohn–Sham (TDKS) method combined with Ehrenfest molecular dynamics (TDDFT-MD). They demonstrated that the ionized electron does not affect the hole dynamics beyond the first half femtosecond, and the nuclear displacements accounted for at the TDDFT-MD level have only a significant effect after approximately 8 fs, and—in some cases—it does not destroy completely the coherent motion of the electronic wave packet during at least a few additional tens of femtoseconds. Furthermore, the role of non-adiabatic correlations has been recently discussed by Perfetto et al. [18]: a theoretical model based on non-equilibrium Green's functions demonstrated that dynamical non-adiabatic correlations are necessary to quantitatively model charge migration in molecules. This approach has been applied to model the charge migration process observed by Calegari et al. [13], showing an excellent agreement with the existing experimental data. More recently, charge migration has been experimentally investigated in the relatively large amino acid Trp [19]. Upon XUV photo-ionization, this molecule has been found to exhibit similar charge density fluctuations as for the phenylalanine case [13]. Advanced modelling of the experiment, using the above-mentioned approach combining the static-exchange DFT and TDDFT-MD methods [16], has shown that, although nuclear motion and non-adiabatic effects can introduce some decoherences, they do not significantly modify the frequency and the amplitude of the experimentally observed electronic beatings.
All these recent achievements opened new and important perspectives in the understanding of the influence of pure electron dynamics on the transient reactivity of a molecule, paving the way for the new field of ‘attochemistry’ [20].
3. Attosecond technology for tracking charge migration
The experimental works carried out to investigate charge migration are based on high-harmonic generation (HHG) spectroscopy or attosecond time-resolved photo-fragmentation spectroscopy. In the first case, the attosecond pulse generation is used itself as an in situ observable of the experiment [15,21,22]. In particular, a strong laser field is used to tunnel-ionize the molecule under study. The photo-electron is accelerated in the continuum by the external laser field and then it recombines with the molecular cation, leading to the emission of a high-energy photon. This XUV radiation carries the signature of the charge dynamics occurring in the time range between the ionization and the electron recombination, thus offering the unique possibility of following charge migration in real time with a subcycle temporal resolution. On the other hand, this technique requires a deep a priori knowledge of many variables contributing to the HHG in the molecule under study—such as the angle-dependent photo-ionization rates and the photo-recombination dipole matrix elements—in order to disclose the signature of charge migration in the experimental observable. This aspect becomes a strong limitation when large complex molecules are investigated.
The second approach could be considered as ex situ (from the HHG process) time-resolved scheme: an attosecond pulse photo-ionizes the molecule under study and the induced charge dynamics is probed by a second femtosecond pulse. Then, the produced ions are collected as a function of the pump–probe delay. The delay dependence of the fragment yields is expected to carry a signature of the transient charge motion occurring in the molecule before fragmentation and it represents the main observable of this experimental technique. This ex situ approach has been used to obtain the experimental results presented in this work.
In the experimental set-up, a clean plume of isolated and neutral molecules is produced in the interaction region by evaporation from a thin metallic foil heated by a continuous-wave laser. An isolated 200 as pulse, with an XUV spectrum in the range of 17–40 eV, is used to photo-ionize the molecular ensemble. A second near-infrared (NIR) pulse, with a sub-4 fs duration, is properly delayed with respect to the attosecond pump pulse and used to probe the dynamics initiated in the molecule by ionization. As the main observable of the experiment, the photo-fragmentation pattern is collected in a time-of-flight mass spectrometer as a function of the delay between the XUV attosecond pulse and the NIR probe pulse.
While the temporal resolution of this pump–probe scheme is limited by the duration of the probe pulse (still providing few-femtosecond resolution), this approach relies on an observable, i.e. the delay-dependent mass spectrum of the target, that can be easily measured even for extremely large molecules. This aspect, together with the possibility of independently tuning the properties of the pump and the probe pulses, represents a unique tool to study—and eventually control—ultrafast electron dynamics in complex molecular systems.
4. Experimental results
In the following, we will focus on the comparison of the experimental results obtained for phenylalanine and tryptophan. Phe and Trp are both aromatic amino acids; the aromaticity of this class of amino acids is generally related to a ring-shaped group that is present on the side chain of the molecule. In the case of Phe and Trp, these are the benzene ring and the indole group, respectively. In particular, the indole group in Trp has unique photochemical properties. Indeed, it strongly absorbs light in the ultraviolet (UV) and in the vacuum ultraviolet (VUV) spectral range and this characteristic absorption is extremely sensitive to the local environment.
For this reason, Trp is currently used to probe protein folding and to investigate electron and proton dynamics in these large molecular systems. Therefore, time-resolving electron dynamics in this molecule may be useful to extend the applicability of Trp-based photochemical techniques to the attosecond time domain.
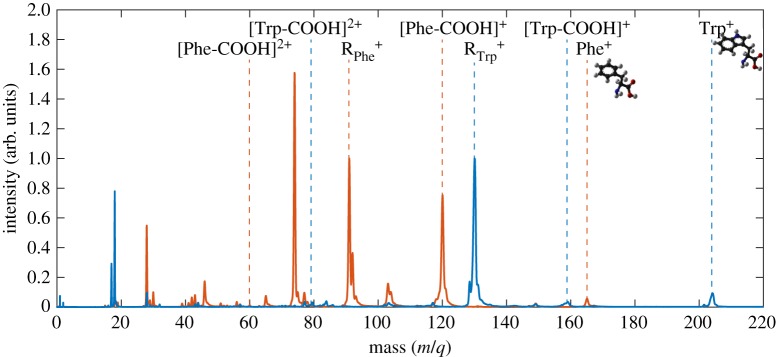
Figure 1 shows a comparison between the mass spectrum of Trp (blue line) and the mass spectrum of Phe (red line) resulting from photo-ionization by the attosecond pulse only. The yield at mass/charge (m/q) 204 corresponds to the parent ion of Trp and represents 3.5% of the total yield, indicating a low photo-stability in this energy range.
Figure 1.
Mass spectra of Trp (blue line) and Phe (red line) produced by XUV photo-ionization. The two spectra are normalized to the yield of the side chains RTrp+ and RPhe+ for Trp and Phe, respectively.
A large fraction of the spectrum consists of lower-mass fragments, with the largest contribution from the side chain (RTrp+) at 130 m/q. The relative counterpart fragment ([Trp-R]+), instead, is barely visible in the spectrum. The mass spectrum reported in figure 1 also shows an extremely low yield of the immonium ion ([Trp-COOH]+). Although the presence of a very small peak at 165 m/q (Phe+) indicates a reduced photo-stability as in the case of Trp, the fragmentation pattern shows remarkable differences. In particular, for Phe, three dominant peaks can be observed in the mass spectrum, including fragment 91 m/q (RPhe+), its counterpart at 74 m/q [Phe-R]+ and the immonium ion at 120 m/q [Phe-COOH]+, in evident contrast with what is observed in Trp. This behaviour suggests that the hole created by XUV ionization in the Trp cation is preferentially localized on the indole group before fragmentation, while in the case of Phe, where the benzene ring replaces the indole group, this process is less likely to occur and it competes with other fragmentation channels. Additionally, it is worth noting that the yield of the immonium dication originated by XUV-only ionization, at 60 m/q for Phe and at 79.5 m/q for Trp, is almost negligible for Phe, while it is more pronounced for Trp. This indicates that XUV ionization (in the absence of the NIR probe pulse) leads to a relatively stable immonium dication only in the case of Trp.
Sending a few-femtosecond NIR probe pulse at variable delays allows the charge dynamics induced by the attosecond pump pulse to be measured with extremely high temporal resolution. In particular, it has been found that the delay dependence of the immonium dication exhibits a peculiar dynamics for both molecules. In figure 2, we show the integrated immonium dication yield as a function of the pump–probe delay for both Trp (blue dots) and Phe (red dots).
Figure 2.
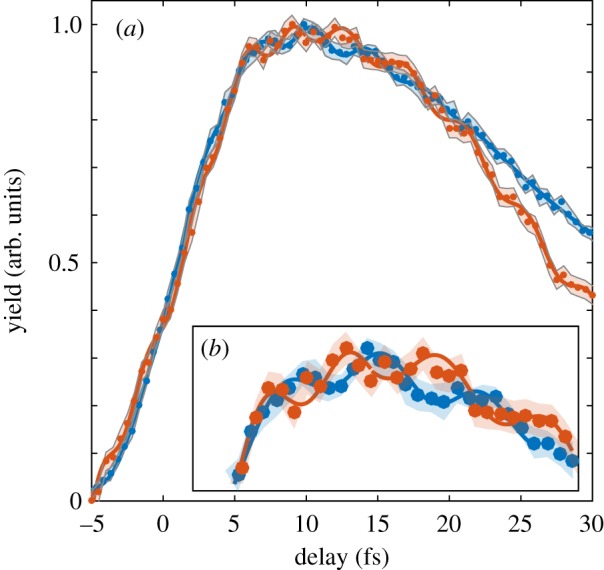
(a) Ion yield of the immonium dication for Trp (blue dots, shaded error band) and Phe (red dots, shaded error band) as a function of the delay between the XUV attosecond pump pulse and the NIR few-femtosecond probe pulse. The two signals are fitted with a sum of sinusoidal functions (blue and red lines). (b) Inset of the slow envelope of the decaying dynamics in the delay range between 5 and 20 fs.
As already shown in [13,19], the rising edge of the dynamics consists of a sharp increase at the zero time delay followed by a rapid decay with a time constant of 30 fs in the case of Trp and 25 fs for Phe. On top of the slow femtosecond dynamics, clear periodic oscillations can be observed for both the molecules (figure 2b). The periodic modulation is fitted with a sinusoidal function (following the method described in [13]). In the case of Trp, a single-frequency component at 0.252 ± 0.011 PHz is identified, corresponding to a period T smaller than 4 fs. The behaviour in the case of Phe is more complicated, as more than one frequency is found [13]. Nevertheless, also for Phe, a main frequency at 0.234 ± 0.012 PHz (T = 4.3 fs) can be identified for delays larger than 10 fs. The most interesting observation here is the relative phase between the oscillations measured for the two molecules. The zero time delay of the two scans has been set with subfemtosecond time resolution by measuring an autocorrelation signal between the NIR pump pulse generating the XUV light and the NIR probe pulse.
The two scans have been then overlapped according to the measured zero time delay. As can be clearly observed in figure 2b, the oscillatory signals are out of phase in the delay range between 10 and 20 fs, although being triggered exactly at the same instant by the attosecond photo-ionization.
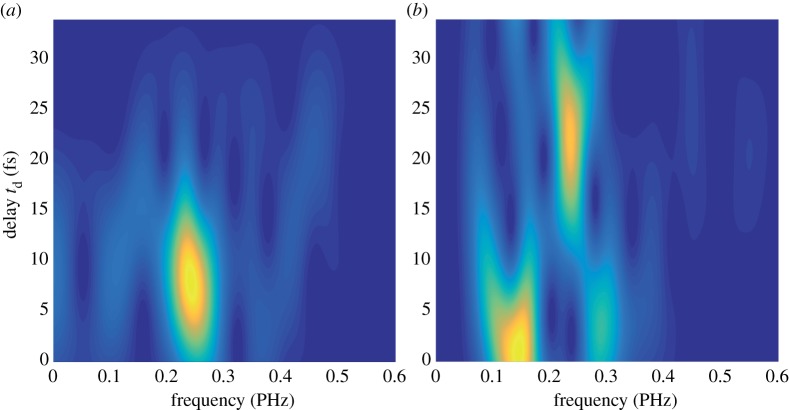
We further investigated the differences between the oscillatory dynamics initiated in the two molecules by performing a time-dependent Fourier analysis of the traces reported in figure 2 and the results are shown in figure 3. In order to calculate the sliding-window Fourier transforms, a Gaussian window function was used, with t0 = 10 fs and the peak at td (gate delay time). In figure 3a, we reported the delay-dependent Fourier spectrum of Trp. The frequency already calculated appears at early delay and it is dumped for td < 20 fs. The spectrum for Phe (figure 3b) is obviously richer. Two different frequencies, at around 0.15 PHz and 0.3 PHz, dominate the spectrogram for td < 10 fs. For larger delays, the spectrum converges to a single peak around 0.23 PHz with a lifetime of 20 fs, i.e. disappearing at td around 30 fs, much later than what is observed in Trp. The different behaviour observed for the two molecules is already a clear indication that different functional groups are involved in the charge migration process.
Figure 3.
Delay-dependent Fourier spectra of the oscillations shown in figure 2b, for Trp (a) and Phe (b). These sliding-window Fourier transforms were obtained by applying a Gaussian window function exp[−(t − td)2/t02], with t0 = 10 fs. (Online version in colour.)
5. Numerical results and discussion
The observed charge dynamics is modelled by state-of-the-art numerical simulations for both the molecules. In particular, we investigate the interplay between electron and nuclear motion in the molecule with the larger molecular weight, i.e. Trp, for which non-adiabatic effects may be significant [16,19]. The charge dynamics in Phe is modelled as in [13]. For both the molecules, the probe pulse was not included in the simulations, because it is beyond the capability of any model currently available.
We examine the coupled electron–nuclear dynamics triggered in the Trp cation by employing a TDDFT methodology implemented in the CPMD package [23]. In this approach, we first compute the electronic wave packet created by the interaction of an attosecond pulse using the static-exchange DFT method [13,24,25]. The ensuing electron–nuclear dynamics is however tracked using an extension of the time-dependent DFT formalism combined with Ehrenfest molecular dynamics (TDDFT-ED) [16,19], assuming the neutral molecule initially at its equilibrium geometry at 0 K. While the initial electron density is represented as a coherent superposition of one-hole states, its subsequent time evolution effectively accounts for electron correlation at the TDDFT level. Moreover, non-adiabatic effects and nuclear motion are included within the Ehrenfest formalism. In short, our TDDFT-based Ehrenfest approach consists of the following steps. Consistent with the spirit of DFT and TDDFT, all properties of the system are expressed as a functional of the (time-dependent) density, which—in the Kohn–Sham (KS) representation—is described uniquely by a set on N non-interacting one-particle orbitals. Following the Runge–Gross theorem [26], the orbitals are propagated in time using the corresponding time-dependent KS equations, giving access to the electronic density at a later time t + dt. The density is then used to compute the Hellmann–Feynman forces acting on the nuclei, which determine the corresponding nuclear equations of motion. These two propagation steps (electron and nuclear) are computed consistently using a third-order Runge–Kutta algorithm [27,28]. Owing to the nature of the process, the ultrafast time scales and the computational costs of the simulation, a single Ehrenfest trajectory was computed for each initial condition (nuclear coordinates, velocities and pulse shape). In fact, during the time window of the experiments (and corresponding simulations), we observe large electronic rearrangements while the nuclear motion, even though important because it can couple to the electronic dynamics, is mostly ballistic and therefore well approximated by a single trajectory. It is important to note that despite the use of a plane-wave basis set, the implementation of the Ehrenfest MD approach does not differ from the ‘traditional’ one based on a localized basis set. For more technical details, see [28–30]. Further, note that due to the complexity of the system under investigation, we had to restrict our simulations to classical nuclear trajectories. As a consequence, nuclear wavepacket decoherence effects induced by initial nuclear quantum state zero-point position spread [31] are not considered in this study. The dephasing induced by the nuclear quantum amplitude fluctuations will indeed cause an additional modulation of the measured absorption and emission spectra; however, due to the difference between electronic and nuclear masses, we expect this effect to occur at lower frequencies than the electronic ones.
In brief, the laser–molecule interaction is described within the dipole approximation, using a first-order time-dependent perturbative approach [13,16]. We consider a Fourier transform limited pulse; thus the ionization amplitudes are given by the experimental spectrum of the attosecond pulse and the dipole transition moment for the transition from the ground state of the neutral to the electronic continuum of the ionized target. The relevant dipole matrix elements for the transition from the ground state of the neutral molecule to the ionization continuum are computed using the static-exchange DFT method, where proper boundary conditions are imposed for the photo-electron. The reliability of the one-photon ionization amplitudes is checked by comparison with available experimental photo-electron spectra [19]. We thus employ a reduced density matrix formalism to define the amplitudes that describe the coherent superposition of (one-hole) cationic states in the pumped target. The resulting ionized electron density is first projected in the basis of the corresponding KS orbitals using the following representation:
| 5.1 |
where γij is the reduced density matrix that defines the electronic density of the residual ions according to
| 5.2 |
and are the KS orbitals describing the density of the molecule before the ionization takes place.
This configuration is then propagated in time using the TDDFT approach via real-time real-space propagation of the time-dependent KS orbitals and the nuclear coordinates. The resulting Ehrenfest dynamics is obtained by the combined solution of the following equations of motion:
| 5.3 |
and
| 5.4 |
Here is the (TDDFT) energy of the system, ψi(r; R(t), t) are the time-dependent KS orbitals that depend implicitly on the nuclear positions Rα (α = 1, … , Na), VKS({ψi(ri, t)}; R) is the KS potential at the time-dependent density and Na is the number of nuclei [27,30]. The Ehrenfest dynamics correctly accounts for the non-adiabatic electron–nuclear interaction, while describing the nuclear motion at a classical level [29].
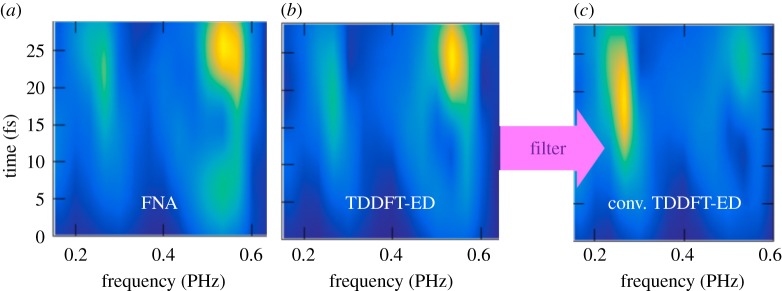
We integrate the resulting spin densities in the TDDFT-ED simulations around the amine group (it was previously demonstrated that the observed charge oscillations involve this site of the molecule [19]) and we carry out a time-dependent Fourier analysis of the signal. The result is reported in figure 4. In figure 4a,b, we show a direct comparison between the FNA and the TDDFT-ED approach accounting for nuclear motion, respectively. In figure 4c, the results obtained with TDDFT-ED are convoluted with a Gaussian filter function with a full width at half-maximum (FWHM) of 0.7 PHz that accounts for the time resolution of the experiment. From figure 4, it is evident that the main frequencies at which the delocalized charge in the cation fluctuates remain mostly unaffected within the first tens of femtoseconds when accounting for the nuclear motion. The nuclear displacements thus do not destroy the initially created electronic coherences in the early stages of the cation evolution. Indeed, even if the coupled electron–nuclear dynamics actually leads to appreciable changes in the orbitals' character in time, the resulting electron density is not necessarily modified significantly [16,18,19].
Figure 4.
Time-window Fourier transform of the electronic density generated by the attosecond pulse around the amine group in Trp within the FNA (a) and with TDDFT-ED (b). (c) Convolution of the results given in (b) with a Gaussian filter function with an FWHM of 0.7 PHz that accounts for the time resolution of the experiment. Adapted with permission from [19]. (Online version in colour.)
We also performed the time–frequency analysis of the hole density evolution for different molecular orientations with respect to the light polarization. This analysis shows that rather similar frequencies result regardless of the molecular orientation, but, more interestingly, that the largest charge fluctuations occur in a given molecular orientation, in agreement with the findings in [15].
One can further identify the pairs of one-hole states involved in the electronic beatings responsible for the main observed frequencies. Figure 5 shows the KS orbitals obtained in the DFT simulation for the neutral Trp. These orbitals are initially computed using the LB94 function implemented in the ADF package [32], although these are then projected into the KS orbitals resulting from the exchange–correlation potential, given by the generalized gradient approximation Perdew–Burke–Ernzerhof (PBE) functional, which has been demonstrated to provide a more accurate description of the electronically excited states of Trp [19].
Figure 5.
Calculated KS valence orbitals of neutral Trp. The orbitals are initially computed using the LB94 function and then projected into the KS orbitals resulting from the exchange–correlation potential. (Online version in colour.)
The frequency analysis of the hole density allows us to energetically identify the pairs of orbitals responsible for the largest signal. These are components of the wave packet creating a hole from neutral orbitals numbered as 30–36, 35–41 and 50–51. Because the frequency analysis is performed from the hole fluctuations around the amine group, it is expected that these pairs of orbitals present a non-negligible overlap around the nitrogen atom. These pairs also present a similar electron density around the indole group, which lead to appreciable charge fluctuations between the amino and indole groups. A significant probability for the hole to be located at the indole group is also in agreement with the observed fragmentation pattern (figure 1). The charge oscillations observed in Phe, instead, have been mainly assigned to periodic charge migration from the amine functional group to the carboxylic group [13,24]. The involvement of different functional groups for the two molecules may be the reason for the different features observed in the oscillatory patterns (figure 2). In particular, it is worth noting that, in the case of Phe, the observed charge migration occurs along a small portion of the molecular backbone, while in the case of Trp, the hole dynamics is more distributed. This may result in a larger impact of the nuclear dynamics on the charge migration in Trp—as observed in the experiment—and therefore in a faster decoherence time.
Finally, we would like to mention that the numerical simulations reported in figure 4—although reproducing the main frequency for Trp—do not precisely capture the time window in which the oscillations are experimentally observed. This discrepancy may suggest the need for a more sophisticated modelling of the attosecond experiments reported here. In particular, a complete treatment of the nuclear dynamics, together with non-adiabatic effects and dynamical correlations, as well as a realistic modelling of the probe pulse, are required to reach a deeper understanding of the process [16–20].
6. Conclusion
Attosecond pump–probe spectroscopy provides a compelling tool to investigate charge dynamics in large molecular systems. The interplay between electron and nuclear motion upon photo-ionization is still a matter of debate, as well as the role of ultrafast electron dynamics in the molecular reactivity. In this work, we investigated charge migration in the two amino acids Trp and Phe. We showed that the fragmentation pathways are strongly mediated by the building blocks of the side chains. We find that the charge density fluctuations occurring around the amino group of the two molecules display a clear oscillatory dynamics with an out-of-phase behaviour. Moreover, the observed dynamics in Trp lasts for a shorter time window compared to Phe, which might be a signature of the different functional groups involved in the quantum beatings. Our theoretical model also indicates that electronic coherences can survive the nuclear dynamics for several femtoseconds even in a large molecule such as Trp. At the same time, we believe that a more sophisticated model, including non-adiabatic effects and dynamical correlations, is required to reach a comprehensive understanding of the process.
Our work contributes to the ongoing discussion for a future attochemistry and it provides new insights on the photo-induced electron dynamics occurring in biochemically relevant molecules.
Data accessibility
This article has no additional data.
Authors' contributions
A.T., M.G., A.P., F.M. and F.C. drafted the manuscript. M.L.-A., J.G., I.T., P.D. and M.N. helped draft the manuscript. All authors gave final approval for publication.
Competing interests
The authors declare that they have no competing interests.
Funding
Work supported by the MINECO project FIS2016-77889-R, the European Research Council under the ERC starting grant no. 637756 STARLIGHT and LASERLAB-EUROPE (grant agreement no. 284464, European Commission's Seventh Framework Programme). We acknowledge computer time from CCC-UAM and Marenostrum Supercomputer Center. F.M. acknowledges support from the ‘Severo Ochoa’ Programme for Centres of Excellence in R&D (MINECO, Grant SEV-2016-0686) and the ‘María de Maeztu’ Programme for Units of Excellence in R&D (MDM-2014-0377).
References
- 1.Lambert WR, Felker PM, Zewail AH. 1981. Quantum beats and dephasing in isolated large molecules cooled by supersonic jet expansion and excited by picosecond pulses: anthracene. J. Chem. Phys. 75, 5958–5960. ( 10.1063/1.442052) [DOI] [Google Scholar]
- 2.Dantus M, Rosker MJ, Zewail AH. 1987. Real-time femtosecond probing of ‘transition states’ in chemical reactions. J. Chem. Phys. 87, 2395–2397. ( 10.1063/1.453122) [DOI] [Google Scholar]
- 3.McPherson A, Gibson G, Jara H, Johann U, Luk TS, McIntyre IA, Boyer K, Rhodes CK. 1987. Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Opt. Soc. Am. B 4, 595–601. ( 10.1364/JOSAB.4.000595) [DOI] [Google Scholar]
- 4.Corkum PB. 1993. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997. ( 10.1103/PhysRevLett.71.1994) [DOI] [PubMed] [Google Scholar]
- 5.Hentschel M, et al. 2001. Attosecond metrology. Nature 414, 509–513. ( 10.1038/35107000) [DOI] [PubMed] [Google Scholar]
- 6.Drescher M, et al. 2002. Time-resolved atomic inner-shell spectroscopy. Nature 419, 803–807. ( 10.1038/nature01143) [DOI] [PubMed] [Google Scholar]
- 7.Goulielmakis E, et al. 2010. Real time observation of valence electron motion. Nature 466, 739–743. ( 10.1038/nature09212) [DOI] [PubMed] [Google Scholar]
- 8.Sansone G, et al. 2010. Electron localization following attosecond molecular photoionization. Nature 465, 763–766. ( 10.1038/nature09084). [DOI] [PubMed] [Google Scholar]
- 9.Lépine F, Ivanov MY, Vrakking MJJ. 2014. Attosecond molecular dynamics: fact or fiction? Nat. Photon. 8, 195 ( 10.1038/nphoton.2014.25) [DOI] [Google Scholar]
- 10.Remacle F, Levine RD. 2006. An electronic time scale in chemistry. Proc. Natl Acad. Sci. USA 103, 6793–6798. ( 10.1073/pnas.0601855103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cederbaum LS, Zobeley J. 1999. Ultrafast charge migration by electron correlation. Chem. Phys. Lett. 307, 205–210. ( 10.1016/S0009-2614(99)00508-4) [DOI] [Google Scholar]
- 12.Kuleff AI, Breidbach J, Cederbaum LS. 2005. Multielectron wave-packet propagation: general theory and application. J. Chem. Phys. 123, 044111 ( 10.1063/1.1961341) [DOI] [PubMed] [Google Scholar]
- 13.Calegari F, et al. 2014. Ultrafast electron dynamics in phenylalanine initiated by attosecond pulses. Science 346, 336–339. ( 10.1126/science.1254061) [DOI] [PubMed] [Google Scholar]
- 14.Marciniak A, et al. 2015. XUV excitation followed by ultrafast non-adiabatic relaxation in PAH molecules as a femto-astrochemistry experiment. Nat. Commun. 6, 7909 ( 10.1038/ncomms8909). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kraus PM, et al. 2015. Measurement and laser control of attosecond charge migration in ionized iodoacetylene. Science 350, 790–795. ( 10.1126/science.aab2160) [DOI] [PubMed] [Google Scholar]
- 16.Lara-Astiaso M, Ayuso D, Tavernelli I, Decleva P, Palacios A, Martín F. 2016. Decoherence, control and attosecond probing of XUV-induced charge migration in biomolecules. A theoretical outlook. Faraday Discuss. 194, 41–59. ( 10.1039/C6FD00074F) [DOI] [PubMed] [Google Scholar]
- 17.Arnold C, Vendrell O, Santra R. 2017. Electronic decoherence following photoionization: full quantum-dynamical treatment of the influence of nuclear motion. Phys. Rev. A 95, 033425 ( 10.1103/PhysRevA.95.033425) [DOI] [Google Scholar]
- 18.Perfetto E, Sangalli D, Marini A, Stefanucci G. 2018. Ultrafast charge migration in XUV photo-excited phenylalanine: a first-principles study based on real-time nonequilibrium Green's functions. J. Phys. Chem. Lett., 9, 1353–1358 ( 10.1021/acs.jpclett.8b00025) [DOI] [PubMed] [Google Scholar]
- 19.Lara-Astiaso M, et al. 2018. Attosecond pump–probe spectroscopy of charge dynamics in tryptophan. J. Phys. Chem. Lett. 9, 4570–4577. ( 10.1021/acs.jpclett.8b01786) [DOI] [PubMed] [Google Scholar]
- 20.Arnold C, Vendrell O, Welsch R, Santra R. 2018. Control of nuclear dynamics through conical intersections and electronic coherences. Phys. Rev. Lett. 120, 123001 ( 10.1103/PhysRevLett.120.123001) [DOI] [PubMed] [Google Scholar]
- 21.Baker S, Robinson JS, Haworth CA, Teng H, Smith RA, Chirilă CC, Lein M, Tisch JWG, Marangos JP. 2006. Probing proton dynamics in molecules on an attosecond time scale. Science 312, 424–427. ( 10.1126/science.1123904) [DOI] [PubMed] [Google Scholar]
- 22.Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, Ivanov MY. 2009. High harmonic interferometry of multi-electron dynamics in molecules. Nature 460, 972–977. ( 10.1038/nature08253) [DOI] [PubMed] [Google Scholar]
- 23.CPMD Consortium. 2014. Welcome to CPMD.org. The CPMD Consortium page. IBM Corp. and Max Planck Institute für Festkörperforschung, Stuttgart. See http://www.cpmd.org/.
- 24.Calegari F, et al. 2015. Ultrafast charge dynamics in an amino acid induced by attosecond pulses. IEEE J. Sel. Top. Quant. Electron. 21, 1–12. ( 10.1109/JSTQE.2015.2419218) [DOI] [Google Scholar]
- 25.Nisoli M, Decleva P, Calegari F, Palacios A, Martín F. 2017. Attosecond electron dynamics in molecules. Chem. Rev. 117, 10 760–10 825. ( 10.1021/acs.chemrev.6b00453) [DOI] [PubMed] [Google Scholar]
- 26.Runge E, Gross EKU. 1984. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 52, 997 ( 10.1103/PhysRevLett.52.997) [DOI] [Google Scholar]
- 27.Tavernelli I. 2006. Electronic density response of liquid water using time-dependent density functional theory. Phys. Rev. B 73, 094204 ( 10.1103/PhysRevB.73.094204) [DOI] [Google Scholar]
- 28.Curchod BFE, Rothlisberger U, Tavernelli I. 2013. Trajectory-based nonadiabatic dynamics with time-dependent density functional theory. ChemPhysChem 14, 1314–1340. ( 10.1002/cphc.201200941) [DOI] [PubMed] [Google Scholar]
- 29.Tavernelli I. 2015. Nonadiabatic molecular dynamics simulations: synergies between theory and experiments. Acc. Chem. Res. 48, 792–800. ( 10.1021/ar500357y) [DOI] [PubMed] [Google Scholar]
- 30.Tavernelli I, Röhrig U, Rothlisberger U. 2005. Molecular dynamics in electronically excited states using time-dependent density functional theory. Mol. Phys. 103, 963–981. ( 10.1080/00268970512331339378) [DOI] [Google Scholar]
- 31.Vacher M, Bearpark MJ, Robb MA, Malhado JP. 2017. Electron dynamics upon ionization of polyatomic molecules: coupling to quantum nuclear motion and decoherence. Phys. Rev. Lett. 118, 083001 ( 10.1103/PhysRevLett.118.083001) [DOI] [PubMed] [Google Scholar]
- 32.Baerends EJ. et al. 2013. ADF. Powerful DFT software for modeling chemistry. SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. See https://www.scm.com/product/adf/. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.