Measuring non-equilibrium dynamics in complex solids with ultrashort X-ray pulses

Abstract

Strong interactions between electrons give rise to the complexity of quantum materials, which exhibit exotic functional properties and extreme susceptibility to external perturbations. A growing research trend involves the study of these materials away from equilibrium, especially in cases in which the stimulation with optical pulses can coherently enhance cooperative orders. Time-resolved X-ray probes are integral to this type of research, as they can be used to track atomic and electronic structures as they evolve on ultrafast timescales. Here, we review a series of recent experiments where femtosecond X-ray diffraction was used to measure dynamics of complex solids.

This article is part of the theme issue ‘Measurement of ultrafast electronic and structural dynamics with X-rays’.

1. Introduction

Ultrashort laser pulses have made possible the control of materials functionality at femtosecond timescales. Highlights include the manipulation of ferroic orders like magnetism [1,2] and ferroelectricity [3], the control of phase transitions [4,5] and the coherent excitation of different modes of the solid [6–8]. In the case of strongly correlated-electron systems, these phenomena have revealed highly unconventional behaviours, including photo-induced insulator-to-metal phase transitions [9–11] and ultrafast changes in magnetic order [12]. However, most of these experiments have been based on excitations at near-infrared wavelengths, a type of stimulation that drives the material into highly non-equilibrium states and results in strongly incoherent dynamics. A different approach, based on the application of optical sources at terahertz and mid-infrared frequencies [13–15], has been shown to achieve a higher degree of control and reduced heating. For example, the targeted excitation of vibrational modes has been used to deform the lattice dynamically and to drive the system into hidden structural and electronic phases [16], controlling complex orders [17,18] and inducing new types of electronic coherence like in the case of light-induced superconductivity [19–21]. These experiments have also been combined with ultrafast X-ray probes to interrogate the time-dependent microscopic properties of these systems.

The development of ultrafast X-ray diffraction techniques dates back to the 1990s, using X-ray pulses generated in plasmas from terawatt optical pulses [22,23]. These early femtosecond X-ray sources, which were weak and difficult to tune, were nevertheless useful in identifying new trends in this field and allowed for a number of rudimentary first experiments. These have included the study of laser-induced disordering of organic films [24], ultrafast melting of semiconductors [4,5,25], detection of coherent phonons [26–28] and photo-induced phase transitions [29]. In this exploratory phase, femtosecond-laser modulation of electron-bunches in storage rings [30–33] was also developed, yielding similarly weak but tuneable X-ray pulses, opening up femtosecond X-ray spectroscopies [10,34,35].

However, it was only with the advent of X-ray free electron lasers [36], with gains in intensity of many orders of magnitude, that photo-induced effects in complex materials have become comprehensively accessible. In the following, we review some contributions by our group, in which femtosecond X-rays from free electron lasers were used to study lattice, electronic and magnetic degrees of freedom in complex oxides. Specifically, we will cover photo-induced dynamics in bulk manganites, in rare-earth nickelate heterostructures and in cuprate superconductors.

2. Electronic and magnetic order dynamics in complex oxides

Many ultrafast studies of complex materials have focused on the study of manganites, a prototype of correlated-electron materials that exhibits colossal negative magneto-resistance, which is itself underpinned by exotic microscopic properties like charge, orbital and magnetic order. Their electronic and magnetic properties can be tuned widely with moderate structural perturbations. This can be understood qualitatively by considering the Goodenough–Kanamori rules for semi-covalent bonds [37], which connect the sign of the exchange interaction to the overlap of the d orbitals in the manganese cations with the p orbitals of the oxygen anion (O²⁻). One finds large hopping probability and ferromagnetic coupling as long as the Mn³⁺–O²⁻–Mn⁴⁺ bonds are ‘straight’, while ‘bent’ bonds, with angles ≪ 180°, give rise to insulating, antiferromagnetic behaviour. Hence, by changing the structure of the material one can control both magnetism and conductivity. Control of the electronic properties directly through the lattice is especially evident in the octahedral manganite Pr_0.7Ca_0.3MnO₃, which is an insulator with a strongly distorted perovskite structure. The application of static pressure, where the lattice distortion qualitatively ‘straightens’ the bonds, turns this material into a ferromagnetic metal [38].

Optical control experiments in a Pr_0.7Ca_0.3MnO₃ single crystal made use of mid-infrared optical pulses to distort the lattice through the resonant excitation of the infrared-active Mn–O stretching vibration [16]. These studies revealed a large increase in electrical conductivity, consistent with an insulator-to-metal transition. Although initial interpretations suggested that a displacement of a bending vibration may be responsible for these physics, the underlying mechanisms could only be clarified with time-resolved resonant X-ray diffraction experiments. Specifically, it was posited that excitation of this vibration should remove the charge order that underpins the insulating state, a phenomenon that can only be measured with a femtosecond X-ray probe.

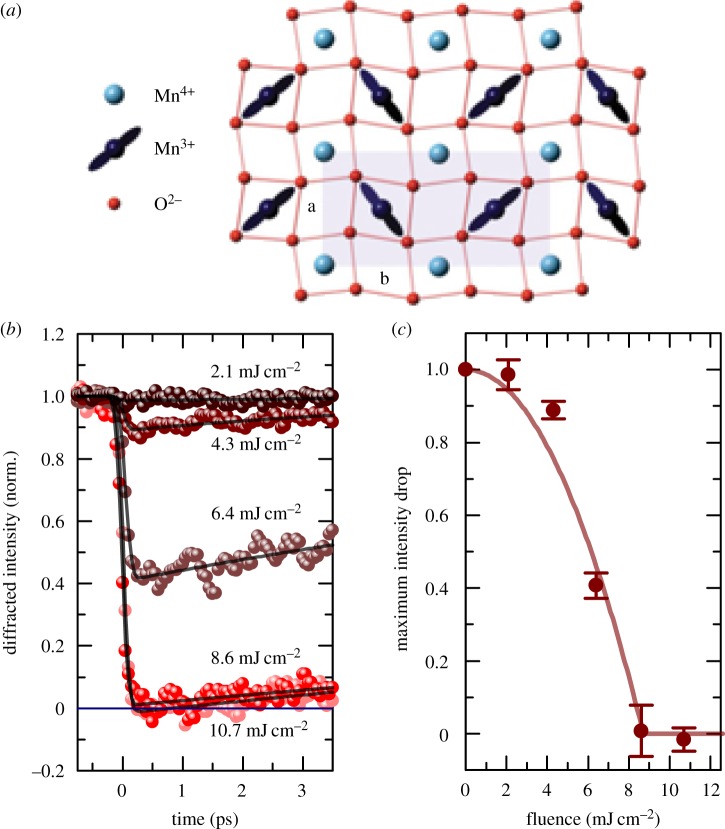
The response of the charge order, sketched for Pr_0.5Ca_0.5MnO₃ in figure 1a, upon mid-infrared photo-excitation, was directly measured by monitoring the time evolution of the (0–3 0) charge-order reflection [39] using resonant X-ray diffraction at the 6.5-keV Mn K-edge [40]. The results of these studies, reported in figure 1b, show a prompt disappearance of this reflection indicating the melting of the charge order. The fluence dependence of this phenomenon is shown in figure 1c, highlighting the threshold-like behaviour of the photo-induced charge order melting. These results were initially explained in light of new theories of ‘nonlinear phononics’ [41–43], which predict that oscillatory excitation of one specific bond can couple to an average change in the angle of the Mn–O–Mn bond. However, further analysis of the X-ray results also introduced an additional notion that involves the direct coupling between the optically driven lattice and the electronic structure, a so-called nonlinear electron phonon coupling.

Figure 1.

(a) Schematic drawing of the low-temperature CE-type charge and orbital order within the ab-planes of Pr_0.5Ca_0.5MnO₃. (b) Dynamics of the charge order in a Pr_0.5Ca_0.5MnO₃ film, measured as the intensity change of the (0 −3 0) reflection at the Mn K-edge, induced by the resonant large-amplitude excitation of the infrared-active apical Mn–O stretching vibration at 17.7 THz frequency (73 meV photon energy). (c) Transient integrated diffraction intensity of the (0 −3 0) peak measured at approximately 0.25ps pump-probe delay as a function of the excitation fluence. Adapted from [39]. (Online version in colour.)

Similar investigations were performed on the single-layer manganite La_0.5Sr_1.5MnO₄, in which charges, orbitals and spins form the so-called CE-type pattern [44]. The response of charge/orbital and antiferromagnetic order, induced by resonant excitation of the infrared-active in-plane Mn–O stretching mode, was measured as transient intensity changes of certain superlattice reflections for photon energies made resonant with the 640-eV Mn L-edge [12]. Also in this case, the initial results were interpreted in terms of the same ‘nonlinear phononics’ mechanism, in which a displacive force on the spin and orbital order was thought to quench the equilibrium order parameters to different values. However, in view of the results in Pr_0.5Ca_0.5MnO₃ discussed above, it is not unlikely that the direct coupling of the driven phonon mode with the electrons through nonlinear spin-lattice and orbital-lattice coupling may be playing an important role.

3. Ultrafast strain engineering in complex oxide heterostructures

Similarly to the manganites, the functional properties of the rare-earth nickelates RNiO₃ (R = rare earth) are very sensitive to octahedral tilts and rotations [45,46]. Controlling these distortions through static strain engineering in heterostructure devices has been successfully exploited in recent years to create novel functionalities [47–49].

Inspired by such ‘strain engineering’ experiments, femtosecond mid-infrared light pulses were tuned not to specific vibrations of the RNiO₃ crystals, as discussed for manganites, but to phonon modes of the heterostructure substrate. In this way, dynamical but indirect control through lattice deformations was demonstrated, as a means to drive the electronic properties of a functional oxide grown on top. In the case of a LaAlO₃/NdNiO₃ heterostructure, the experiments targeted the stretching vibration of the LaAlO₃ substrate, leading to a long-lived metallic phase in the NdNiO₃ film [50].

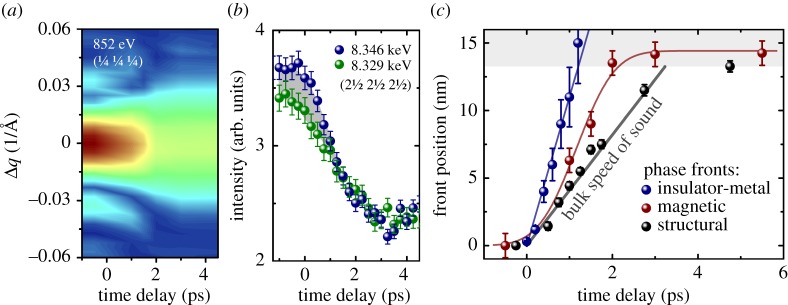
These early demonstrations motivated a comprehensive set of investigations with X-ray free electron lasers, to measure the dynamics of antiferromagnetic order, charge order and lattice dynamics [51,52]. Figure 2a shows the time evolution of the (¼ ¼ ¼) diffraction peak at the 852 eV Ni L₃-edge, which is sensitive to antiferromagnetic order in the material. Significant peak broadening and suppression of the Laue oscillations, which indicate sharp boundaries of the magnetic order at equilibrium, were observed after optical excitation of the substrate. This result indicates that the optical excitation melts the magnetic order only over a fraction of the film, and yields an estimate of the speed at which this melting occurs. Recently, this interpretation was substantiated by phasing the diffraction patterns to show that these dynamics indeed arise from a propagating demagnetization front launched at the interface [53].

Figure 2.

Dynamics of the magnetic, electronic and structural degrees of freedom of a NdNiO₃ thin film, observed when resonantly driving a specific vibrational mode in an LaAlO₃ substrate below. (a) Transient momentum-resolved intensity of the (¼ ¼ ¼) diffraction peak measured at the 852-eV Ni L₃-edge, sensitive to antiferromagnetic ordering. (b) Transient peak intensity of the NdNiO₃ (2½ 2½ 2½) reflection, measured at X-ray energies resonant (8.346 keV, blue data) and off-resonant (8.329 keV, green data) with the Ni K-edge. (c) Spatio-temporal evolution of the NdNiO₃ lattice, magnetic and insulator-metal dynamics along the thin film out-of-plane direction. Individual phase fronts of insulator-to-metal, antiferromagnetic-to-paramagnetic and structural transitions propagate at different speeds from the hetero-interface into the nickelate film. Panel (a) is adapted from [51], panels (b,c) are adapted from [52].

Figure 2b shows additional measurements of the time dependent (2½ 2½ 2½) reflection, measured at X-ray energies resonant (8.346 keV, blue data) and off-resonant (8.329 keV, green data) with the Ni K-edge. The measured resonant diffraction intensity comprises a charge-order contribution to the Bragg scattering (illustrated by the grey shaded region), which disappears promptly and in fact before the lattice has completely rearranged. Figure 2c illustrates how the lattice, magnetic and insulator-metal dynamics evolve as different types of order–disorder fronts that propagate from the interface into the functional film at different speeds. Presumably, charge order melting is the driving force of these dynamics, as its phase front advances ahead of demagnetization and structural relaxation.

4. Light-induced superconductivity in single-layer cuprates

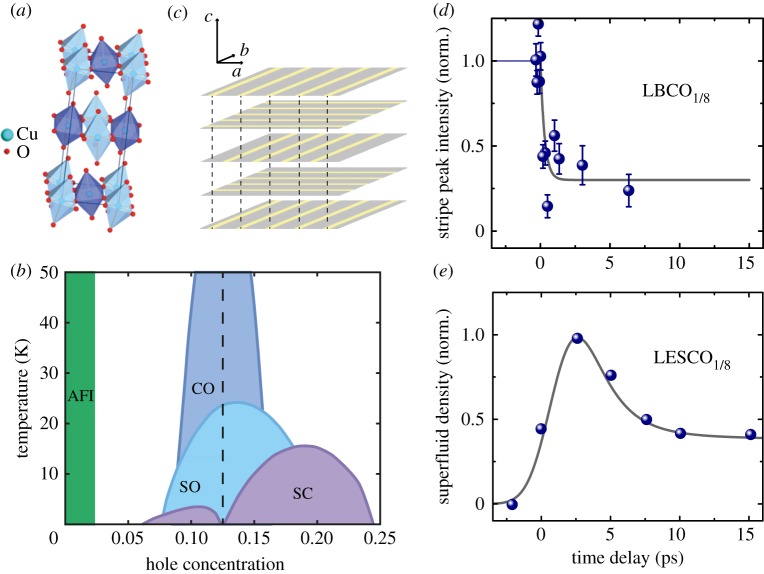
High-T_c superconductivity is found in many layered cuprates, of which La_2−xBa_xCuO₄ is a prototypical example [54]. This material crystallizes in a perovskite structure composed by a stacking of CuO₂ layers separated by two La/Ba-O planes along the crystal c-axis (figure 3a). Superconductivity is obtained from the antiferromagnetic parent compound (La₂CuO₄) by doping holes into the CuO₂ planes, through substitution of La³⁺ with Ba²⁺ atoms. The charge doping weakens the antiferromagnetic order and superconductivity sets in for doping concentrations x > 0.05, reaching its maximum T_c near the optimal doping of x ∼ 0.16 [58].

Figure 3.

Schematic crystal structure (a) and phase diagram (b) for La_1.8−xEu_0.2Sr_xCuO₄. For x < 0.025 the compound is an antiferromagnetic insulator (AFI). For x < 1/8 (vertical dashed line) a structural LTT distortion sets in and superconductivity (SC) is strongly suppressed. At x = 1/8 a one-dimensional modulation (stripe order) of charge (CO) and spin (SO) order appears in the planes. (c) Illustration of the in-plane stripe order in single-layered cuprates. The stripes are periodically stacked along the c-axis with a 90° rotation between adjacent layers. (d) Time evolution of the integrated intensity of the (0.24 0 0.5) stripe order peak in La_1.875Ba_0.125CuO₄. Upon vibrational photo-excitation the stripe order is promptly melted. (e) Transient normalized superfluid density in La_1.675Eu_0.2Sr_0.125CuO₄ where vibrational excitation induces a transient superconducting state. Panel (b) is adapted from [55]. Panels (c,d) are reproduced from [56]. Panel (e) is adapted from [57]. (Online version in colour.)

The doped cuprates host a number of other phenomena that participate or even compete with superconductivity. For example in La_2−xBa_xCuO₄ close to x ∼ 1/8 doping, T_c is strongly suppressed due to the presence of one-dimensional modulation of charge and spin density, known as stripes [58]. At x = 1/8, the stripes become statically ordered, concomitantly with a structural phase transition to a low-temperature tetragonal phase (LTT) that comprises periodically buckled CuO₂ planes [59,60]. Stripe order, LTT distorted structure and suppressed T_c are found also in several other single-layer cuprates, as for example in La_1.8−xEu_0.2Sr_xCuO₄ [61]. The phase diagram of this compound (figure 3b) is peculiar with superconductivity being strongly suppressed for x < 1/8, and completely suppressed at x = 1/8.

Although the interplay between stripes, LTT distortion and superconductivity has a key role in determining the phase diagram of single-layer cuprates, the mechanisms of this interplay are still to be understood. For example, stripes emerge even in the absence of the LTT distortion [62,63], which seems to indicate that charge order alone might be responsible for the suppression of the superconducting state. More recent experiments [64,65] suggest that the stripe phases may be characterized by a spatially oscillating superconducting order parameter (pair density wave) and their specific alignment in the structure suppresses the interlayer c-axis superconducting transport (figure 3c).

Ultrashort optical pulses tuned to resonance with an in-plane Cu–O stretching mode were used in our experiments to dynamically excite the lattice of the non-superconducting La_1.675Eu_0.2Sr_0.125CuO₄ [57]. Transient optical measurements in the driven phase of this material revealed the presence of a reflectivity edge around 2 THz, where the Josephson plasma resonance is observed in the equilibrium phase of La_1.84Sr_0.16CuO₄ [57]. This observation suggested the onset of a non-equilibrium superconducting transport between the planes. The time evolution of the quantity $\underset{\omega \to 0}{lim}\omega {\sigma }_2$, proportional to the superfluid density, is shown in figure 3e. The superfluid density grows after optical excitation and then relaxes to a plateau within a few picoseconds, indicating the formation of a metastable superconducting state. This effect is observed all the way to the charge-order temperature T_CO [66].

This phenomenon is presumably related to a weakening of stripe order, although no direct proof was found in the initial experiments. The evolution of stripe order after excitation was investigated by femtosecond resonant soft X-ray diffraction in La_1.875Ba_0.125CuO₄ [56]. In this material, which is closely related to La_1.675Eu_0.2Sr_0.125CuO₄, both stripe order and LTT distortion can be tracked by X-ray diffraction, tuning the X-ray photon energy near resonance to the oxygen K-edge. In the following, we label Bragg peaks using the conventional notation of the high-temperature tetragonal unit cell. A charge-order diffraction peak at the wavevector q = (0.24 0 0.5) appears as the static charge stripes strengthen [61,67]. On the other hand, the LTT distortion can be quantified by the appearance of the (0 0 1) structural diffraction peak that is forbidden in the high-temperature undistorted phases [68].

Figure 3d shows the integrated intensity of the (0.24 0 0.5) charge-order diffraction peak as a function of time-delay with respect to the mid-infrared excitation. Within less than 1 ps, a timescale similar to that observed for the onset of superconductivity in La_1.675Eu_0.2Sr_0.125CuO₄ [57], the intensity shows a sudden approximately 70% decrease. The time evolution of the (0 0 1) diffraction peak, instead, reveals that the LTT phase is significantly less affected by the lattice excitation. In this case, the integrated intensity only drops by approximately 12% and with a longer time constant of approximately 15 ps.

The combination of the results from optical and X-ray experiments reveal that photo-excitation in stripe-ordered cuprates induces the formation of an out-of-equilibrium superconducting state where stripe order has disappeared but the LTT distortion still exists. In this picture, the melting of the charge order eliminates the periodic potential that suppresses interlayer Josephson coupling at equilibrium [64,69], and restores the coherent transport between the two-dimensional superconducting condensates in the CuO₂ planes.

Overall, the X-ray experiments revealed that LTT distortion plays a minor role in the light-induced superconducting state, as also demonstrated by the observation of light-induced superconductivity in striped compounds upon non-resonant excitation at near-infrared and optical wavelengths [70–72].

5. Light-induced superconductivity in bilayer cuprates

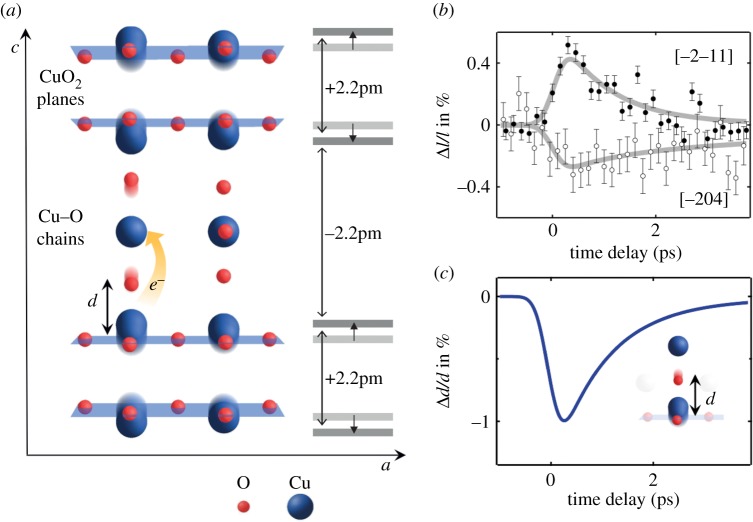
YBa₂Cu₃O_6+x crystallizes in an orthorhombic perovskite structure where CuO₂ bilayers are stacked along the crystal c-axis, separated by insulating yttrium layers (figure 4a). Analogously to single-layer cuprates, the doping of the CuO₂ planes crucially determines the superconducting character of the sample and is controlled by the Cu–O chains in between the CuO₂ bilayers [74]. At equilibrium, the system becomes superconducting owing to the coherent tunnelling of Cooper pairs between neighbouring CuO₂ bilayers. Changing the distance, d, between apical O and planar Cu atoms, can control the superconducting properties at equilibrium. For example, superconductivity can be enhanced by reducing d with the application of external pressure in the range of a few kilo-bars [75–77].

Figure 4.

(a) Crystal structure of bilayer YBa₂Cu₃O_6.5. CuO₂ bilayers (shaded) are stacked along the crystal c-axis and alternate with thicker layers containing Ba, Cu and O. Y and Ba atoms are not shown for clarity (left). d is the distance between an apical O atom and a Cu atom in the plane. Schematic of the changes in the intra-bilayer (+2.2 pm) and inter-bilayer (–2.2 pm) distances due to the nonlinear coupling of the driven B_1u mode to the A_g modes (right). Light and dark grey represent the CuO₂ planes in the equilibrium and driven positions, respectively. (b) Transient integrated intensity (I) of two exemplary Bragg peaks. The solid dark grey curve is a fit with ab initio calculated structure factor changes. (c) Transient change in the O–Cu distance d obtained from the calculated structure. Adapted from [73]. (Online version in colour.)

YBa₂Cu₃O_6+x was excited in our experiments with intense mid-infrared pulses tuned to resonance with a phonon mode of B_1u symmetry that causes oscillations in the distance d, while the material low-frequency electrodynamics was investigated using time-resolved transient terahertz spectroscopy. At all temperatures above T_c and all the way to room temperature, upon photo-excitation, the transient optical response showed the presence of a clear reflectivity edge indicative of a coherent interlayer transport with a prompt build-up of a finite superfluid density [19,20].

The presence of a charge-density-wave (CDW) phase competing with superconductivity in the under-doped part of the phase diagram of bilayer cuprates [78,79] initially suggested that also in the case of YBa₂Cu₃O_6+x the vibrational excitation might destroy the CDW phase that was preventing superconductivity to set in at higher temperatures. The evolution of the charge density wave after mid-infrared photo-excitation was followed in YBa₂Cu₃O_6.6 with time-resolved soft X-ray diffraction in which the X-ray probe was tuned to the Cu L₃-edge [80]. The time evolution of the integrated intensity of the charge-order peak revealed that concomitantly to the enhancement of the coherent inter-bilayer transport, the CDW order is melted by approximately 50%. This result reveals a clear competition between the CDW phase and superconductivity in YBa₂Cu₃O_6.6 at least up to the CDW ordering temperature. However, the observation, in YBa₂Cu₃O_6.45, of a light-induced enhancement in the c-axis transport at 300 K and above [20], where there is no CDW order [78], suggests that additional physics is responsible for this transient phenomenon.

As discussed above, the superconducting properties of YBa₂Cu₃O_6+x are very sensitive to modulations in the distance d between apical O and planar Cu atoms. To follow the dynamic of the lattice upon photo-excitation in YBa₂Cu₃O_6.5, a time-resolved hard X-ray diffraction experiment [73] was performed in the same vibrational excitation conditions of [19,20]. The time evolution of the intensity of selected Bragg reflections sensitive to changes in the distance d was measured to identify atomic motions that are concomitant with the rise and decay of the light-induced superconducting state (figure 4b). The results of this experiment were interpreted in the framework of ‘nonlinear phononics’ [42]. Density functional theory calculations were performed to compute the coupling strength between specific A_g Raman modes that are nonlinearly coupled to the driven B_1u mode, yielding a model of the driven crystal structure. Structure factor calculations allowed fitting simultaneously the observed changes in the measured Bragg reflection intensity using as the only free parameter the driving amplitude of the B_1u mode.

The atomic rearrangements in the equilibrium crystal structure reconstructed in this experiment are shown in figure 4a. Most importantly, photo-excitation induces a transient reduction of the apical O to planar Cu distance (figure 4c). Analogously to the effect of static pressure [75–77], density functional theory calculations reveal that this structural change may facilitate the onset of coherent Cooper pair transport along the crystal c-axis, above the equilibrium transition temperature. Furthermore, a transfer of electrons from the CuO₂ planes to the Cu–O chains, similar to hole doping in equilibrium, was predicted and later confirmed by femtosecond resonant soft X-ray absorption experiments [81].

6. Conclusion and perspectives

Short X-ray pulses from free electron lasers have been key to clarifying many important aspects of the non-equilibrium properties of materials, with important advances in the area of correlated-electron transition-metal oxides. We expect these experiments to have an impact in material discovery. Intense terahertz pulses were used to selectively drive phonon modes to large amplitudes, shaping materials in non-trivial ways to unleash unconventional behaviours that are not seen at equilibrium. Ultrafast X-ray pulses then allowed reconstructing the transient crystallographic and electronic structure of the photo-excited material, which may identify pathways towards the discovery of new materials with novel functional properties.

Further progress in this field can be expected from inelastic X-ray techniques, which have recently been extended to the time domain. The study of the time evolution of elementary excitations, such as, for example, phonons or magnons, can provide deeper insight into the fundamental interactions at play [82]. In addition, time- and momentum-resolved X-ray diffuse scattering techniques have been developed, which, for example, allow measurement of phonon dispersion curves [83] or anharmonic couplings between excitations [84]. We expect this technique to impact the research in condensed matter systems where low-lying excitations are linked to such complex long-range orders as, for example, magnetism and superconductivity.

The future success of these experiments will strongly benefit from the constant effort spent in the development of more advanced free electron lasers. A key aspect in the design of new sources is the use of various seeding schemes [85–87] that promise near Fourier transform limited pulses and a dramatically increased shot-to-shot stability in their parameters. We expect that both elastic and inelastic X-ray scattering experiments will take advantage of seeded free electron lasers to reach even higher energy and time resolution.

Furthermore, it will be possible to achieve better control of the X-ray pulse parameters in order to achieve pulses with sub-fs duration and arbitrary shape. Synchronizing X-ray pulses to the absolute phase of the pump pulses has already become possible [88,89] in the terahertz and mid-infrared regime. On the basis of this new generation of X-ray free electron lasers, we expect these advances to enable new experiments in which the role of the driven lattices, and the coherent control of the materials, is understood and optimized.

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed equally to the preparation of this article.

Competing interests

The authors declare no competing interests.

Funding

The authors acknowledge funding from the European Research Council (ERC) under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC grant no. 319286 (Q-MAC) and acknowledge support from the Deutsche Forschungsgemeinschaft through the ‘Hamburg Centre for Ultrafast Imaging—Structure, Dynamics and Control of Matter at the Atomic Scale’ excellence cluster and the priority programme SFB925.