Ultrafast dynamics of spin and orbital correlations in quantum materials: an energy- and momentum-resolved perspective

Abstract

Many remarkable properties of quantum materials emerge from states with intricate coupling between the charge, spin and orbital degrees of freedom. Ultrafast photo-excitation of these materials holds great promise for understanding and controlling the properties of these states. Here, we introduce time-resolved resonant inelastic X-ray scattering (tr-RIXS) as a means of measuring the charge, spin and orbital excitations out of equilibrium. These excitations encode the correlations and interactions that determine the detailed properties of the states generated. After outlining the basic principles and instrumentations of tr-RIXS, we review our first observations of transient antiferromagnetic correlations in quasi two dimensions in a photo-excited Mott insulator and present possible future routes of this fast-developing technique. The increasing number of X-ray free electron laser facilities not only enables tackling long-standing fundamental scientific problems, but also promises to unleash novel inelastic X-ray scattering spectroscopies.

This article is part of the theme issue ‘Measurement of ultrafast electronic and structural dynamics with X-rays’.

1. Introduction

Quantum materials are a class of solids in which quantum mechanical effects are especially apparent, generating states such as high-temperature superconductivity, colossal magneto-resistance, exotic magnetism and metal-to-insulator transitions, and are also among the least understood. One key observation is that many of these exotic phases emerge when antiferromagnetic parent compounds are chemically doped, revealing the rich physics of Mott insulators [1]. In these phases, the charge, spin, orbital and lattice degrees of freedom are intrinsically intertwined. This opens the fascinating prospect of photo-exciting one degree of freedom in order to modify another with the aims of generating new phases, improving the properties of known phases or disentangling the interdependencies among these degrees of freedom in order to better understand the ground state [2–4]. Probing the properties of these photo-excited states can, however, be challenging. In this article, we argue that the time-resolved (tr)-resonant inelastic X-ray scattering (RIXS) technique has great potential for improving our understanding of ultrafast transient states.

Figure 1 illustrates a typical tr-RIXS experiment. An optical pump pulse photo-excites the material into a transient state, which is then interrogated by an X-ray probe pulse. RIXS tracks the changes in energy and momentum of the scattered X-rays. Through energy and momentum conservation, the dispersion and lifetime of the spin, charge or orbital quasi-particles can be mapped throughout the Brillouin zone. This enables establishing minimal models and extracting the interaction parameters describing these quasi-particles. For example, the magnon energy at the Brillouin zone boundary in an antiferromagnet quantifies the strength of the magnetic exchange interaction.

Figure 1.

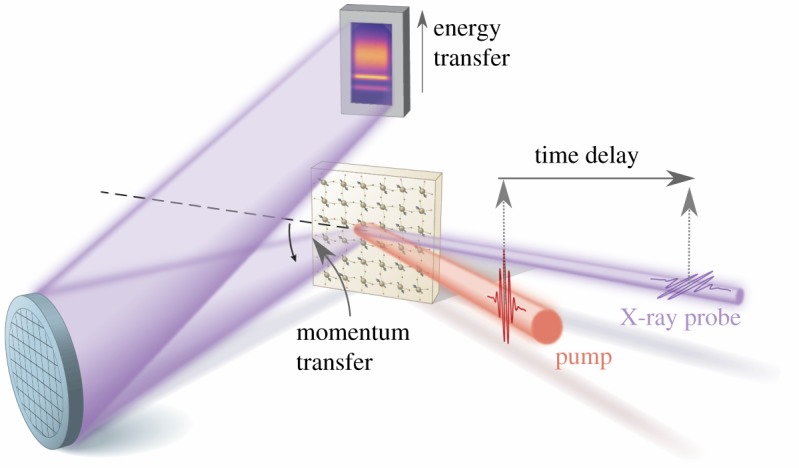
Schematics of a tr-RIXS experiment. Generally in an RIXS measurement, the momentum transfer is determined by the angle between the incident and scattered X-rays from the sample, along with the wavelength of the X-ray. The energy of the scattered photons is resolved by a grating or crystal analyser onto a CCD detector. In tr-RIXS, a second pump laser pulse is used which arrives at a controllable time ahead of the incident X-rays. The tr-RIXS spectrum is then obtained by scanning the time delay.

Time-resolved RIXS offers new opportunities to investigate the dynamics of bosonic quasi-particles in the time domain. While facilities that can provide sufficiently short and bright X-ray pulses to carry out such experiments remain limited, the landscape is changing quickly with the increasing number of new X-ray sources over the next few years. The article is organized as follows: in §2 and §3, we review the principles and instrumentations of tr-RIXS. We revisit our first measurements in a photo-excited Mott insulator Sr₂IrO₄ in §4, and discuss future technical developments that enable the search for novel physics in §5.

2. RIXS as a probe of quantum materials

RIXS exploits energy and momentum transfer to infer the excitation spectrum of a material. By tuning the incident X-ray energy to a core-hole resonance, it is possible to go beyond the typical selection rules of X-ray scattering and couple to magnetic, orbital and charge modes. Since X-rays have a wavelength comparable to the inter-atomic spacing in materials, the dispersion of these excitations can be measured across a sizable fraction of the Brillouin zone—something that is not possible with infra-red or Raman spectroscopy. Such rich information, however, comes at a price as RIXS involves multiple interactions and can be challenging to interpret. Researchers often distinguish two types of processes: direct ‘operator’ RIXS and indirect or ‘shakeup’ RIXS [5]. Direct RIXS involves excitations that are created by the photon absorption operators $\mathcal{D}$ and ${\mathcal{D}}^{\prime †}$ described below. Indirect RIXS, on the other hand, arises due to the interaction of the core hole with electrons in the valence bands of the material. In cases where direct RIXS is not forbidden, such as the L- and M-edges of d electron-based transition metals, it tends to be the dominant process and this review will focus on direct RIXS.

RIXS is formally described by the Kramers–Heisenberg formula, which involves transitions from the ground state |g〉, through an intermediate state |n〉, to the final state | f〉 as [5]

$$I(\mathit{Q},\omega ,\mathit{ϵ},{\mathit{ϵ}}^{\mathrm{\prime }})\propto {\left|\sum _n\frac{⟨\hspace{0.17em}f|{{\mathcal{D}}^{\prime }}^{†}|n⟩⟨n|\mathcal{D}|g⟩}{E_g+{\omega }_{\mathit{k}}-E_n+i{\mathrm{\Gamma }}_n}\right|}^2\delta (E_g-E_f+\omega ).$$ 2.1

In this process, incident photons with wavevector k, polarization ϵ and energy ω_k are scattered to states k^′, ϵ^′ and ω_k^′ creating excitations with wavevector Q = k^′ − k and energy ω = ω_k^′ − ω_k. E_g, E_n and E_i are the energies of |g〉, |n〉 and | f〉 and Γ_n is the inverse core hole lifetime. Several important facts follow from a detailed consideration of equation (2.1). Since the X-ray wavelength (1∼10 Å) is significantly larger than the extent of an atomic orbital (∼0.1 Å), $\mathcal{D}$ and ${\mathcal{D}}^{\prime †}$ can often be considered under the dipole approximation. As the dipole transitions depend on ϵ and ϵ^′, the X-ray polarization can be exploited to help select the desired excitation [6]. The fact that two dipole operators are present means that, unlike in infra-red or Raman spectroscopies, electronic transitions within the same orbital manifold, often called dd-transitions, are allowed. At an L-edge, |n〉 contains a strongly spin–orbit coupled 2p core hole, which means that the orbital angular momentum of the photon can be exchanged with the spin angular momentum in the valence band in order to create spin-flip excitations, such as magnons [7,8]. This is illustrated schematically in figure 2 and will be discussed in more detail in §4. One should note that RIXS is a coherent quantum mechanical process, and since |n〉 is not observed, the process involves a superposition of all possible intermediate states distributed throughout the lattice, which is why the collective, Q-dependent excitations of the material are accessible. This is distinct from X-ray absorption spectroscopy (XAS) where there is a core hole in the final state.¹ Being a second-order process, RIXS has a relatively low cross-section compared to the first-order processes, although this is offset somewhat by the enhancement of the scattering intensity on resonance [5].

Figure 2.

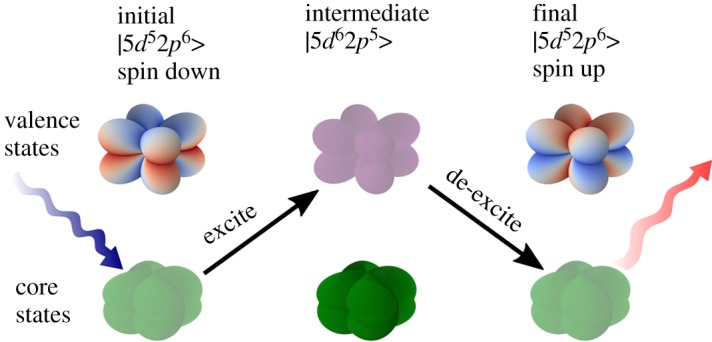
An illustration of the L₃-edge RIXS process for a 5d⁵ iridate. Orbital states with (without) an active hole are in full colour (translucent). Incident (scattered) X-ray are shown as blue (red) wavy arrows. The initial iso-spin down state is flipped to an up state via the spin–orbit coupling in the intermediate state.

RIXS is particularly well suited to probe magnetism in transient states. It is element and orbital resolved, bulk sensitive and compatible with small samples down to a few micrometres in size, which is important for pump-probe matching considerations. It is the only technique that has the proven ability to measure the dispersion of magnetic excitations in transient states. The best-established technique for studying these magnetic excitations, inelastic neutron scattering, is incompatible with ultra-fast experiments due to the slow velocity and large penetration depth of neutrons. Spin-polarized electron energy loss spectroscopy can also access magnetic dispersions [9], but it has not yet been successfully implemented in an ultrafast experiment as space charge effects present significant challenges.

Regardless of how it is measured, the full magnetic excitation spectrum can be formalized in the magnetic dynamic structure factor S^αβ(Q, ω), which characterizes the magnetic correlations in a magnetic material. This quantity is the space and time Fourier transform of the spin–spin correlation function 〈s^αs^β(r, t)〉 between a reference spin component s^α and another spin s^β(r, t) at distance r and time t > 0. This fact makes it clear that similar information can, in principle at least, be obtained by either frequency domain or the time domain. An excellent discussion of such correlation functions is provided in books such as [10]. It is further known that these correlations encode the interactions present in the magnetic Hamiltonian [11]. In general, fast processes correspond to high frequencies and are often probed best in the frequency domain, whereas the converse is true for slow processes.

Connecting I(Q, ω, ϵ, ϵ^′) to S^αβ(Q, ω) is a topic of considerable active research [7,8,12–14]. But the connection between these quantities is particularly well-established for Mott insulators based on 5d⁵ electrons, including iridates such as Sr₂IrO₄ [15]. The interpretation of such spectral information will be covered in §4.

3. Instrumentation

The primary consideration of tr-RIXS instrumentations is to achieve sufficient time and energy resolution while ensuring reasonable photon throughput. RIXS is one of the most photon-hungry X-ray measurement techniques due to its small inelastic scattering cross-section. Recent advances in energy-analysing spectrometer designs have made possible much-improved energy resolution and faster data collection at synchrotron light sources [16–19]. In this section, we will focus on aspects specific to the time-resolved experiments.

(i). Spatial overlap

Similar to most other pump-probe experiments, the probe X-ray footprint needs to be contained within that of the pump laser. Equally important, the penetration depth of the X-ray normal to the sample surface should not exceed that of the pump laser. At normal incidence, the X-ray penetration depth is usually much larger than that of the optical laser. To ensure a good match between the laser pumping volume and the X-ray probing volume, we could resort to one, or both of the following approaches: (1) using samples thinner than the penetration depth of the pump laser and (2) aligning the X-ray to come in more grazing relative to the sample surface. Approach (1) could be achieved by thinning down bulk samples, or using films. For thicker samples, approach (2) needs to be used. The X-rays are usually at less than 2° incidence angle relative to the sample surface and the laser is typically at e.g. 10°. This non-collinear geometry in approach (2) can contribute to reduced time resolution. Also, the large X-ray footprint due to gracing incidence gives rise to a large laser spot and hence reduced pump fluence.

The X-ray penetration depth in the soft X-ray regime (ℏω < 2000 eV) is usually a fraction of a micrometre on resonance. This makes it easier to implement approach (1) with a collinear pump-probe geometry. For harder X-rays (ℏω > 4000 eV), the penetration depth of a few micrometres requires approach (2) in many cases.

(ii). Energy resolution

RIXS spectrometers work under the principle that energy dispersive optics distribute X-ray photons with different energies into distinct directions. After propagating a sufficient distance, X-ray photons with different energies are spatially separated, and can be distinguished by detectors with good spatial resolution. The following are some of the most important factors affecting the spectrometer energy resolution: (1) the length of the spectrometer arm; (2) the photon footprint along the energy dispersing direction and (3) the size of the X-ray detector pixels. In the soft X-ray regime, ruled gratings are used to disperse X-rays, while high-quality diced single crystals are used for hard X-rays. A detailed description of the principles of spectrometer designs, as well as estimates of the energy resolution, are presented in the electronic supplementary materials. State-of-the-art spectrometers often deliver sub-50 meV energy resolution Full-Width at Half Maximum (FWHM) relatively comfortably. Some of the more modern spectrometers and novel designs have an energy resolution approaching 10 meV [17,19], though often only in a particular X-ray energy range.

With these advances in X-ray spectrometers, the incident X-rays need to be well monochromated to achieve a high combined total energy resolution. The generic X-ray bandwidths from existing X-ray free electron lasers (XFELs) are much larger than the resolution of the spectrometers. For example, in the Self-Amplified Spontaneous Emission (SASE) mode, the typical FWHM of the incident X-ray at 9 keV is approximately 20 eV before entering the monochromator. Ideally, the energy resolution of the X-ray shining on the sample should match that of the spectrometer. In this scheme, only a tiny fraction of the SASE beam (within much less than 100 meV) is expected to pass the monochromator for an optimized set-up. To achieve a higher X-ray intensity at the sample without compromising the total energy resolution, we argue that tr-RIXS will benefit greatly from the seeded operation mode of X-ray free electron lasers (XFEL)s [20,21]. While the total X-ray flux exiting the undulator is reduced compared with that in the SASE mode, the incident photon flux within the desired energy bandpass will actually increase. For the current XFELs, self-seeding tends to be more reliable in the hard X-ray regime.

As mentioned in §2, the different X-ray polarization dependences of different excitations can be used to help isolate the desired signal. Since magnetic X-ray scattering rotates the X-ray polarization, it is often useful to place the spectrometer as close as possible to 90°, using a horizontal scattering plane and horizontal incident X-ray polarization. In this way, the undesirable Thompson structural scattering is suppressed, and the visibility of the magnetic signal is enhanced. This works especially well for hard X-ray experiments, in which the whole Brillouin zone can be covered by moving the spectrometer only a few degrees. With a horizontal scattering plane, the X-ray footprint will tend to elongate the beam horizontally, so setting the spectrometer to disperse the X-rays vertically is useful to maintain a constant vertical X-ray source size, independent of the scattering angle.

(iii). Momentum resolution

An important advantage of RIXS, as compared with Raman spectroscopy, is the much larger momentum transfer between the incident and scattered photons. The main contribution to the momentum resolution is the acceptance angle of the RIXS spectrometer. Typical momentum resolution is of the order of approximately 0.01 Å⁻¹ for soft X-rays around 1 keV and approximately 0.1 Å⁻¹ for hard X-rays around 10 keV. The worse momentum resolution in the hard X-ray regime is simply due to the larger photon momentum. In most cases, the momentum resolution can be improved with a smaller acceptance angle provided there are enough scattered X-ray photons to make the experiment feasible. Notably, hard X-rays have significantly larger momentum transfer than soft X-rays, which allows access to multiple Brillouin zones even within the constraint of grazing incidence geometry needed for the penetration depth correction noted above.

(iv). Time resolution

In tr-RIXS, the temporal and energy resolution are fundamentally limited by the time-bandwidth product, ΔEΔτ∼ℏ setting an ultimate limit on the best resolution. For a phase coherent Gaussian pulse with 100 meV energy resolution, the temporal resolution limit is approximately 40 fs. On top of the energy-time indeterminacy, the total time resolution has contributions from both the durations of the X-ray pulse and of the pump optical laser, similar to other pump-probe experiments at X-ray free electron laser (XFEL)s.

Another potential contribution to the time resolution can come from what is called the ‘wave-front-tilt’ effect [22]. In this process, the incident X-ray pulse entering the monochromator is stretched in time upon exit due to different X-ray photon path lengths through the optics. This effect tends to be more severe for longer-wavelength X-rays and for higher-resolution monochomators, and could reach a few picoseconds in the very soft X-ray regime with a single grating.

The total time resolution can be further limited by the so-called ‘jitter’, which is the uncertainty in the relative arrival time between the pump and probe pulses. The ‘jitter’ tends to be between 20 and 100 fs depending on the XFEL in question and can be corrected for using a ‘timing tool’ [23,24]. There is also a potential geometrical contribution to the total time resolution arising from the relative optical path length difference between the X-ray and the pump laser over the photon footprint. The collinear geometry where the laser is parallel to the X-ray minimizes the geometrical contribution. This geometry is widely adopted in the soft X-ray elastic scattering experiments, and is expected to be used in tr-RIXS in the soft X-ray regime. For hard X-rays and in the presence of bulk samples, matching the pump-probe volume may require a substantial angle between the X-ray and the pump laser at the price of time resolution. One can, in principle, compensate for this effect by imparting a spatially dependent delay in the laser pulse.

4. First results

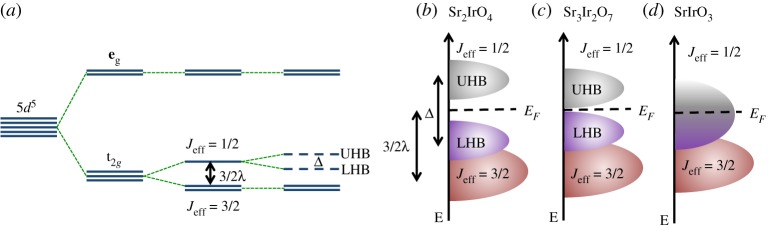
The first reported magnetic tr-RIXS experiments were conducted on Sr₂IrO₄ [25], a model quasi-two-dimensional square-lattice quantum antiferromagnet [26–28]. Long-range magnetic order occurs below T_N ≈ 240 K and arises from the interplay of several degrees of freedom [29,30]. Each Ir atom has a 5d⁵ electronic configuration and sits at the centre of an oxygen octahedron. All five d-electrons reside in the t_2g level due to the large crystal field splitting. Strong spin–orbit coupling of approximately 400 meV further splits the t_2g level into the J_eff = 3/2 state occupied by four 5d electrons, and a single-occupied J_eff = 1/2 state. The Ir atoms form a square net resembling that of the copper ions in the layered high-T_C cuprates, and a modest Coulomb repulsion induces an insulating band gap of 600 meV (figure 3a,b). Sr₂IrO₄ belongs to the Ruddlesden–Popper series of layered iridates Sr_n+1Ir_nO_3n+1. The band-gap of the spin–orbit Mott insulating state successively reduces with increasing neighbouring Ir–O layers, n. In the n → ∞ end member SrIrO₃ the gap is closed making the system metallic (cf. figure 3c,d) [31].

Figure 3.

(a) Crystal-field splitting, spin–orbit coupling, λ and Coulomb-induced Mott-gap, Δ, in Sr_n+1Ir_nO_3n+1. (b)–(d) Schematic electronic structure of Sr_n+1Ir_nO_3n+1.

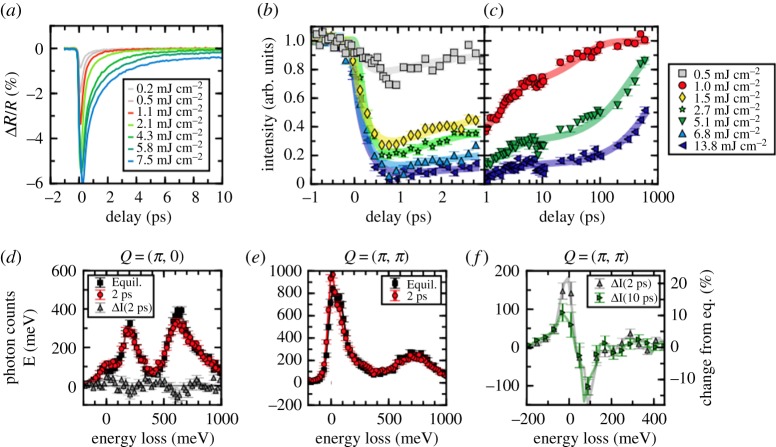
The charge degree of freedom in these materials was studied by time-resolved optical reflectivity measurements [25]. Here electrons are excited from the lower (LHB) into the upper Hubbard band (UHB) by 2 μm laser pulses with an energy that matches the electronic band gap. Figure 4a shows the relevant timescales in Sr₂IrO₄ that are needed to recombine the charge carriers under different laser fluences. The plot reveals a decay time that is attributed to the excitation of charge carriers, and a fast and slow recovery process in the sub-picosecond and few-picosecond regime, respectively.

Figure 4.

Time dependence of (a) the relative optical reflectivity (ΔR/R) and (b) and (c) the magnetic Bragg peak in Sr₂IrO₄ after 620 meV photo-excitation at different laser fluences. Excitation spectrum at (d) Q = (π, 0) and (e) Q = (π, π) in the non-perturbed state and 2 ps after the laser pulse, under the pump fluence of 6 mJ cm⁻². The difference in the RIXS spectrum before and after the optical excitation at Q = (π, π) is shown in (f ). Adapted from Ref. [25].

Since the magnitude of the electron bandwidth, the Coulomb repulsion and the spin–orbit coupling share similar energy scales in the iridates, the same 2 μm (620 meV) laser pulse also affects the magnetic properties [25]. A combined resonant elastic X-ray scattering (REXS) and RIXS study at the hard X-ray Ir L₃ edge probed the energy, momentum and time-dependent response of the transient magnetic state at T = 110 K (cf. figure 2). Figure 4b,c displays the time and fluence dependence of a magnetic Bragg peak in Sr₂IrO₄. After the initial suppression of peak intensity following the optical excitation, the three-dimensional long-range antiferromagnetic order fully recovers within several hundred picoseconds. Intriguingly, a partial restoration of magnetism is observed already within a few picoseconds. This is further clarified by tr-RIXS, as discussed below.

The RIXS spectra displayed in figure 4d–f show the first ever view of magnetic short-range correlations within a photo-excited ultrafast transient state. Magnetic excitations were measured before, and 2 ps after, the arrival of pump laser pulses, and with a pump fluence large enough to fully suppress the three-dimensional magnetic order [25]. The low-energy excitation spectrum of Sr₂IrO₄ features a dispersing spin-wave below 200 meV (figure 4d) and an orbital excitation of the J_eff = 1/2 state around 600 meV. The main result of the study demonstrates that despite the destruction of the long-range magnetic order, magnons are already observed 2 ps after the impact of the laser pulse. Furthermore, the recovery timescale of these predominantly two-dimensional in-plane magnetic fluctuations matches the partial recovery of long-range magnetic order as found by time-resolved REXS (shown in figure 5 and discussed below).

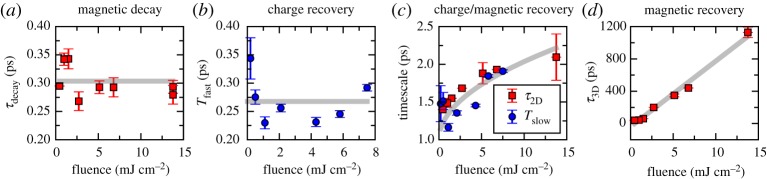
Figure 5.

(a) Fluence dependence of the decay time that is required to destroy the ground state. (b) Fast recovery of the charge degree of freedom measured via optical reflectivity. (c) Slow recovery of the charge degree of freedom that matches the recovery timescale of the two-dimensional magnetic correlations. (d) Slow recovery of the three-dimensional magnetic long-range order. Adapted from [25]. (Online version in colour.)

The various timescales and their fluence dependences are shown in figure 5. Both charge and magnetic degrees of freedom exhibit fast and slow recovery dynamics [25]. Most strikingly, the recovery timescale of the two-dimensional magnetic fluctuations matches that of slower charge recovery, providing direct evidence for a coupling between them. The authors further suggest that the slower restoration of three-dimensional magnetic order may be attributed to incoherently oriented IrO₂ planes along the tetragonal axis.

This pioneering experiment paves the way for further time-resolved REXS/RIXS experiments that may lead to a full microscopic understanding of the correlated ground state in the Sr_n+1Ir_nO_3n+1 series. While electrons were pumped across the Mott-gap, the bandwidth, Coulomb repulsion and spin–orbit coupling were not tuned directly in this work. A selective pump of the Ir–O bonds in Sr₂IrO₄ with mid-infrared ultrafast laser pulses, for instance, could tune the crystal-field environment and modulate the magnetic interaction strength of the system.² Observing the time-dependent evolution of the transient state after shaking the Ir–O bonds will not only disentangle the lattice and electronic degrees of freedom, but may also demonstrate how to drive the material into specific magnetic states by pumping another degree of freedom (in this case, the lattice). The role of Coulomb repulsion may be clarified by investigating other members in the series. For example, Sr₃Ir₂O₇ features two closely coupled Ir–O layers in the crystal structure and shows major modifications in the materials properties [33,34]. This material lies on the verge of a metal-to-insulator transition with a heavily reduced Mott-gap (figure 3c) [33]. Magnetic long-range order emerges below T_N ≈ 285 K with a magnetic moment orientation perpendicular to the tetragonal basal plane [35]. The excitation spectrum strongly deviates from the isotropic Heisenberg model that describes Sr₂IrO₄ with a much-increased magnetic gap. Thus, the restoring forces for the magnetic ground state in Sr₃Ir₂O₇ are expected to be different from those in Sr₂IrO₄, and a study of their dynamics following a pump may further clarify the underlying processes.

In contrast to other members of the series, SrIrO₃ is a correlated paramagnetic metal close to the metal-to-insulator transition (figure 3d) [33]. It can be grown as thin films on substrates where the relative lattice mismatch between the film and the substrate provides an additional tuning parameter. The epitaxial strain induces changes in the Ir–O bond angle and could drive the system over the metal-to-insulator transition. Thus, the variation of film thickness and substrate material enables a selective realization of the material properties. This further adds to the possibilities of altering the magnetic ground state by optical means, and may finally allow one to fully disentangle the coupled degrees of freedom in the series.

The strong experimental push towards the understanding of electronic short-range correlations in transient states parallels several recent theoretical studies of the Hubbard model that is believed to describe the main properties of many strongly correlated materials [36–45]. Particularly relevant in view of the tr-RIXS study on Sr₂IrO₄ are the results in Ref. [36] that report the interaction of short-range spin fluctuations with the charge degree of freedom in photo-excited Mott insulators. Using non-equilibrium dynamical mean-field theory, the study provides evidence for short-range magnons in a two-dimensional paramagnetic system with relaxation times in the femtosecond time domain. The extension of the theoretical model to an antiferromagnetically ordered state may lead to a microscopic understanding of the time difference between two-dimensional fluctuations and three-dimensional order in Sr₂IrO₄ [25].

5. Vision for the future

As demonstrated in previous sections, tr-RIXS has unique advantages for investigating quantum magnetism in transient states. Here, we discuss future developments of tr-RIXS instrumentations and the scientific problems that will be addressed because of these advances.

(a). New XFELs and RIXS spectrometers

Hitherto, progress in tr-RIXS has been slowed by the limited availability of suitable X-ray sources and spectrometers. In the past 10 or so years since the first XFELs came online, their primary focus has been on numerous exciting opportunities in more tractable techniques such as XAS and X-ray diffraction. Efforts to realize more complex experiments are, however, already well under way. A major increase in the availability and quality of XFEL sources is likely to drive further progress in realizing highly challenging experiments such as tr-RIXS. In particular, the more established sources such as the Hamburg Free-electron LASer (FLASH), the Trieste Free Electron laser Radiation for Multidisciplinary Investigations (FERMI), the Stanford Linac Coherent Light source (LCLS) and the SPring-8 Angstrom Compact free electron LAser (SACLA) will be joined by the European XFEL, Pohang Accelerator Laboratory X-ray Free Electron Laser (PAL-XFEL), the Stanford LCLS-II and Switzerland's X-ray free-electron laser (SwissFEL) [46–52]. Dramatic improvements in brightness, stability, pulse length and pulse repetition rate are expected. The small RIXS cross-section may particularly benefit from improved time-averaged spectral brightness that can potentially exceed that of synchrotrons significantly, making feasible new experiments, e.g. probing magnetism in single-layer films. These improvements are particularly beneficial when ultra-high energy resolution is pursued.

The spectrometer required to analyse the X-ray energy also represents a significant challenge, but several teams have successfully performed experiments at XFELs [25,53–55]. To date, XFEL-based RIXS tends to lag behind synchrotron experiments in terms of energy and momentum resolution. Many of the technical developments implemented at synchrotrons [17,56] can potentially be employed at XFELs provided further practical complications, such as limited experimental floor space, compatibility with other experiments, finite beam stability, can be avoided or overcome. In many cases, shorter spectrometers (અ2 m compared to ∼15 m at synchrotrons) are more practical at XFELs. A recent compact soft X-ray spectrometer design has delivered down to 300 meV resolution at 1 keV incident energy [55,57]. Hard X-ray experiments with a 1 m spectrometer achieved 70 meV at 11.2 keV [25]. Looking to the future, multiplexing techniques that can efficiently measure the RIXS incident energy dependence [58], streaking approaches to measuring the time-delay or analysing the scattered X-ray polarization [59] will be interesting routes to consider.

(b). Evolution of tr-RIXS

Driven by these technical developments, we anticipate considerable advances in tr-RIXS in the coming years. A primary focus will be far more detailed and precise characterizations of spin, charge and orbital behaviours in transient states, which opens routes disentangling the complex interplay between these different degrees of freedom. For example, time-resolved diffraction measurements have recently quantified how terahertz-frequency optical pulses modify the crystal structure of cuprates [60]. RIXS could potentially be used to quantify how magnetic exchange is modified in such a transient state. One can also consider using RIXS to evaluate change in spin stripe-magnon interactions in similar transient states [61]. These types of coupling are generic to many different types of correlated system including 3d, 4d and 5d-electron oxides such as cuprates, nickelates and osmates—systems in which steady-state RIXS is becoming more insightful [13,62,63]. By carefully choosing the optical pump, it would be desirable to selectively drive the different forms of order in the material. With the help of RIXS, it is then possible to address the chicken and egg interdependencies of these order parameters. More ambitiously, the application of higher laser pump fluences, and oscillatory Fluoquet-type pluses, can potentially access transient states not adiabatically connected to the states at thermal equilibrium. The extent to which these states have novel properties remains to be seen [64]. It is also notable that Fourier Transform (FT)-Inelastic X-ray Scattering (IXS) has recently observed the decay of optical phonons into pairs of acoustic phonons [65], direct measurement of similar processes between spin waves would be very insightful in conceptualizing the evolution of magnetic states out of equilibrium.

(c). New types of RIXS at XFELs

The high brilliance of new sources should allow ‘diffract-then-destroy’ types of RIXS experiment for detecting the collective excitations in quantum materials under extreme conditions at equilibrium. These involve problems in which the state of interest only exists fleetingly, but the experiment can be performed within the short X-ray pulse duration before the state is destroyed. The most prominent example of this approach is in protein crystallography where diffraction data are collected before the sample is destroyed by radiation damage. With expected higher XFEL peak brightness, similar ideas will also likely become important for ultrafast quantum materials research. Single-shot XFEL experiments in pulsed magnetic fields have been demonstrated using X-ray diffraction, paving the way for investigations of magnetic excitation under large magnetic fields in quantum materials [66]. One can also envisage accessing ultra-high pressures transiently, following themes in XFEL-based geology research and other areas. An as yet unexploited idea would be to try to measure RIXS at extremely low temperatures, where the sample temperature would be elevated by beam heating under normal circumstances.

In standard IXS experiments, one determines the dynamical properties of the sample in the frequency domain through the energy dependence of S^αβ(Q, ω). XFELs open the opportunity to determine S^αβ(Q, ω) in the time domain. This approach has been illustrated in recent experiments by Trigo and collaborators [67]. In this study, the structural X-ray diffuse scattering of crystalline germanium was measured as a function of time delay after photo-excitation. Fourier transforming the oscillatory component of the diffuse scattering yielded the low-energy phonon dispersion. In the limit of negligible pump intensity, the phonon energy dispersion obtained should be the same as that accessible by standard IXS, leading to this technique being dubbed FT-IXS. Notably, the energy resolution of FT-IXS is determined not by the spectrometer as in conventional IXS, but by the longest delay possible, so FT-IXS has good sensitivity to slow, low-energy excitations. Clever choices of photo-excitations may also open the way to picking out modes of particular interest, which have small structure factors in standard IXS measurements. Combining FT-IXS with atomic core-hole resonance may allow access to electronic excitations from the charge, spin and orbital degrees of freedom (see §2) similar to RIXS. This would represent what might be thought of as Fourier-transform or time-domain RIXS, but as far as we are aware such experiments have not yet been successfully performed. Some of these low-energy charge and orbital excitations, e.g. amplitudons, phasons, orbitons, etc., are not accessible by neutrons, and could require energy resolution well below that of any spectrometer-based RIXS at XFELs and synchrotrons either today or anticipated over the next decade. Experimentally identifying these charge/orbital excitations and understanding their evolution in the temperature-doping phase diagram would be particularly interesting for cuprates and Fe-based superconductors, especially since these excitations are theoretically proposed as critical to the formation of superconductivity [68,69].

Not only the time structure, but also the large peak intensity of XFEL pulses will allow access to novel types of RIXS processes. To date, in the vast majority of RIXS experiments, the X-ray has been assumed to be a linear perturbation to the material [5]. Under this assumption, the RIXS spectrum is interpreted as originating from the interaction of a single photon with the sample, where the incident photon density is low enough for there to be a negligible probability of one photon encountering the effects of other photons. XFELs now deliver peak photon intensity sufficient to access nonlinear processes. In general, two cases are distinguished, in which the stimulating X-rays arise either from a separate X-ray beam, or they arrive from scattered photons in the sample. The former case is often referred to as stimulated Raman scattering and has only been realized using photons in the ultra violet regime so far [70]. The latter case takes advantage of the finite energy distribution in the XFEL beam, leading to an amplified spontaneous emission that emerges from noise around the centre of the X-ray pulse [71]. The last few years have seen 2p core hole stimulated emission in crystalline silicon proving the feasibility of solid-state nonlinear experiments [72]. As emphasized by Beye et al. [72] stimulated processes can enhance the efficiency of RIXS by several orders of magnitude and confine emission into a well-defined cone allowing the scattered photons to be more efficiently collected. Nonlinear RIXS therefore has potential to circumvent radiation damage problems. Perhaps even more interestingly, one can use the enhanced specificity of such a process to access, for example, hidden order parameters and excitations, such as those only accessible via quadrapole resonances [73].

6. Summary

Recent years have seen the advent of tr-RIXS as a flexible and rich probe of non-equilibrium phenomena. We argue that this technique has great potential for measuring spin, charge, orbital and lattice excitations after photo-excitation as a means of unpicking how these degrees of freedom intertwine to form emergent states and for characterizing the new laser-driven transient states. The increasing number of operating XFEL facilities and tr-RIXS instruments will not only serve as a basis to solve long-standing scientific questions, but also to investigate physics beyond the limit of linear response theory and to enable the development of novel techniques such as stimulated or Fourier-transform RIXS. Ultra-bright X-ray pulses may also be used to perform future experiments on samples susceptible to radiation damage or at extremely low temperatures and high magnetic fields, accessing phase-space regions that could not be reached via X-ray scattering before. Thus, the prospected capabilities of tr-RIXS in its various forms are pointing towards a bright future.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This work is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Early Career Award Program under Award No. 1047478. Work at Brookhaven National Laboratory was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-SC0012704. The work at Argonne National Laboratory was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-AC0206CH11357. The work at ShanghaiTech U. was partially supported by MOST of China under the grand No. 2016YFA0401000. The work at ICFO received financial support from Spanish MINECO (Severo Ochoa grant SEV-2015-0522), Ramón y Cajal programme RYC-2013-14838, FIS2015-67898-P (MINECO/FEDER), Fundació Privada Cellex, and CERCA Programme/Generalitat de Catalunya. D.G.M. acknowledges funding from the Swiss National Science Foundation, Fellowship No. P2EZP2_175092.