Imaging of transition charge densities involving carbon core excitations by all X-ray sum-frequency generation

Abstract

X-ray diffraction signals from the time-evolving molecular charge density induced by selective core excitation of chemically inequivalent carbon atoms are calculated. A narrowband X-ray pulse selectively excites the carbon K-edge of the –CH₃ or –CH₂F groups in fluoroethane (CH₃–CH₂F). Each excitation creates a distinct core coherence which depends on the character of the electronic transition. Direct propagation of the reduced single-electron density matrix, using real-time time-dependent density functional theory, provides the time-evolving charge density following interactions with external fields. The interplay between partially filled valence molecular orbitals upon core excitation induces characteristic femtosecond charge migration which depends on the core–valence coherence, and is monitored by the sum-frequency generation diffraction signal.

This article is part of the theme issue ‘Measurement of ultrafast electronic and structural dynamics with X-rays’.

1. Introduction

X-ray absorption near-edge structure (XANES) spectroscopy has long been used to probe the core electronic structure in the frequency domain. Its spectral resolution is limited by the core lifetime. The signals show satellite peaks which result from core electron transitions to higher unoccupied valence orbitals. Their intensity can be stronger than the fundamental (lowest-energy excitation, i.e. core to the lowest unoccupied molecular orbital (LUMO)) depending on the overlap between the molecular orbitals (MOs) involved in the electronic transitions.

A diffraction signal following an impulsive core excitation may provide a better window into the electron dynamics by visualizing a real-space electron–hole density map that reveals the position and the character of the excited core electrons. Time-resolved diffraction imaging generates a movie of the time-evolving charge density subjected to interaction with several pulses by using the diffraction probe for the detection. In this way, we can obtain richer information on the electron dynamics and than XANES.

In this work, we investigate X-ray sum-frequency generation (XSFG) diffraction, the simplest nonlinear variant of time-resolved diffraction. In the conventional sum-frequency generation (SFG) experiment, a pump pulse first creates a coherent superposition of the ground and the excited states at time t = 0, and a probe pulse then detects the electronic coherence by monitoring the light emission at time t = T, where T is the time delay between the pump and the probe pulses. SFG diffraction imaging uses a diffraction probe for the direct imaging of the electronic coherence (see figure 1 for pulse configuration for XSFG diffraction). In XSFG, an X-ray pump pulse creates a superposition of the ground state and core hole states. This time-dependent scheme of SFG detection is routinely used in lower-energy regimes and is usually described using a dipolar coupling between light and matter, where the interaction Hamiltonian has the form H^dipolar_int = − μ · E, where μ and E are the electric dipole moment of the matter and the external electric field. The signal is then expressed by a second-order nonlinear response, i.e. a three-point correlation function of transition electric dipoles 〈μμμ〉. XSFG, which uses high-energy off-resonant X-ray coupling, can be described using the minimal coupling Hamiltonian, $H_{\mathrm{int}}^{\min }=-\int \mathrm{d}\mathbf{r}\hspace{0.17em}(\mathbf{j}(\mathbf{r})-\frac{1}{2}\sigma (\mathbf{r})\cdot \mathbf{A}(\mathbf{r}))\cdot \mathbf{A}(\mathbf{r})$, in atomic units, where j(r), σ(r) and A(r) are the current density, charge density and the electromagnetic vector potential, respectively. Since the charge density interacts at second order in the fields with the molecule, the three-point correlation function of conventional SFG is replaced in off-resonant X-ray SFG by a two-point correlation function with one current and one charge contribution, that is 〈jσ〉 instead of 〈μμμ〉. See §2a and the appendix for the details of the XSFG diffraction signals.

Figure 1.

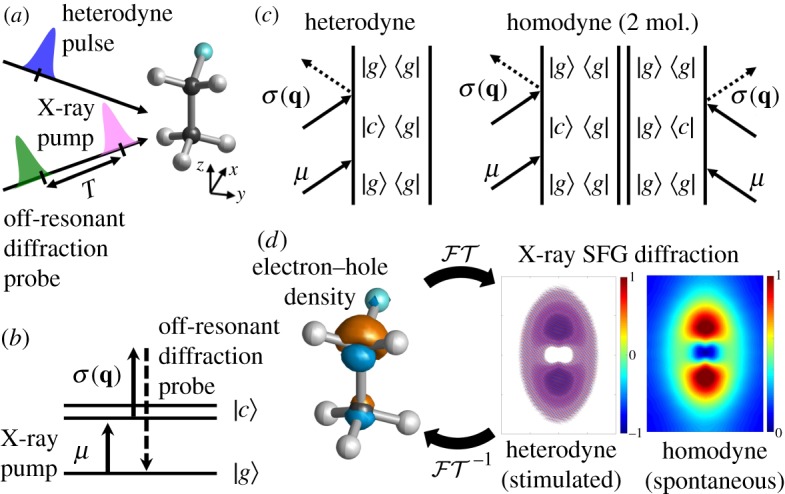
(a) Pulse configuration for XSFG imaging and equilibrium geometry of fluoroethane (CH₃–CH₂F) molecule. All pulses are Z-polarized. (b) Level scheme for the X-ray sum-frequency generation (XSFG) diffraction technique (|g〉 and |c〉 represent ground and core excited states) and (c) corresponding ladder diagrams for heterodyne and homodyne signals. The homodyne signal requires a long-range order in the sample. (d) Fourier and inverse Fourier transform ($\mathcal{F}\mathcal{T}$ and ${\mathcal{F}\mathcal{T}}^{-1}$, respectively) link the diffraction signals and the real-space electron–hole density. (Online version in colour.)

Since XSFG creates a coherent superposition of the ground and core hole states, its description requires a computational method that provides the balanced description of both core hole and partially filled unoccupied valence orbitals. We use real-time time-dependent density functional theory (RT-TDDFT) [1–4] to simulate the time-evolving charge density following a resonant carbon K-edge core excitation of fluoroethane. This provides a practical algorithm for propagating a many-electron system driven by external laser fields. The field is included non-perturbatively in the propagation and the molecular reduced single-electron density operator and various spectroscopic and diffraction signals can be computed directly, avoiding the expensive explicit calculation of many-body states. This technique has been broadly applied to compute absorption spectra of large molecules [5], core ionization dynamics [6], charge transfer [7,8], light absorption of photocatalyst [9], molecular conductance [10] and ultrafast charge migration following a peptide ionization [11]. RT-TDDFT accounts for the molecular response to an arbitrary sequence of external fields under the dipole approximation for the light–matter interaction. This technique could be useful for exploring the role of the core hole and the interplay between valence electrons following the core excitation. Lopata et al. have used this level of theory to calculate the core excitation and ultrafast molecular response in H₂O, CO, fluorobenzene and Ru complex [12]. They calculated XANES spectra from the Fourier transform of the time-dependent dipole moment as well as snapshots of the time-evolving charge density along the dynamics.

We employ XSFG diffraction to study the spatially resolved dynamical features of a fluoroethane molecule (CH₃–CH₂F) which has two chemically inequivalent carbon atoms (2.4 eV core level shift), and reveal the dynamics following selective excitation of either of the carbon core states. We simulate both homodyne and heterodyne detected diffraction imaging of the electron–hole density following core excitation and study the role of valence orbitals in the time-evolving charge density. We find that core excitations also leave a different set of partially filled valence orbitals to launch a characteristic femtosecond charge migration by the interactions among the valence orbitals.

2. Real-time time-dependent density functional theory simulation of excited-state dynamics following carbon core excitations

(a). The time-evolving charge density and diffraction signals

Computational methods employed for calculating core excited states include time-dependent Hartree–Fock [13], TDDFT [1], coupled cluster [14] and multi-configurational self-consistent field calculations [15]. RT-TDDFT simulates the electronic dynamics by propagating the reduced single-electron density matrix ρ(t) driven by multiple pulses [16], avoiding the explicit calculation of many-electron eigenstates. Intense external fields can be accounted for since the incoming fields are treated non-perturbatively. The dynamics is obtained by solving the TDDFT equations of motion [1,16]

$$\mathrm{i}\frac{\mathrm{\partial }\rho (t)}{\mathrm{\partial }t}=[\mathbf{F}(t),\rho (t)]$$ 2.1

(in atomic units), where the time-dependent Fock matrix F(t) is given by [17]

$$\begin{array}{rl}\mathbf{F}[\rho (t)]& ={\mathbf{H}}^{\mathrm{core}}+{\mathbf{G}}^{\mathrm{J}}[\rho (t)]+\alpha {\mathbf{G}}^{\mathrm{K}}[\rho (t)]+\beta {\mathbf{G}}^{\mathrm{X}-\mathrm{DFT}}[\rho (t)]\\ & +\gamma {\mathbf{G}}^{\mathrm{C}-\mathrm{DFT}}[\rho (t)]-\mathit{\mu }\cdot \mathbf{E}(t).\end{array}$$ 2.2

Here the core Hamiltonian H^core is the sum of the nuclear repulsion energy and the one-electron energy, G^J[ρ(t)] is the Coulomb electron repulsion, and α, β and γ are the coefficients for the Hartree–Fock exact exchange G^K[ρ(t)], the density functional theory (DFT) exchange G^X-DFT[ρ(t)] and the DFT correlation G^C-DFT[ρ(t)], respectively, for a hybrid DFT functional. The last term represents the dipole interaction with the external field E(t), where μ is the dipole operator. We assume a Gaussian electric field envelope

$${\mathbf{E}}_i(t)=A\sin ({\omega }_i(t-t_i)+{\varphi }_i)\exp [-\frac{{(t-t_i)}^2}{(2{\sigma }_i^2)}],$$ 2.3

with an electric field strength A = 0.01 au = 3.51 × 10¹² W cm⁻² for all incoming fields, ω_i is the central frequency, t_i central time, ϕ_i phase and σ_i pulse duration of the pulse. All fields are z-polarized (see figure 1 for geometry).

The single-electron density matrix ρ_ij(t) obtained by integrating equation (2.1) allows one to calculate the expectation value of any single-body operator such as the time-dependent dipole moment

$$⟨\mathit{\mu }(t)⟩=\sum _{i,j}{\rho }_{ij}(t)⟨{\psi }_i|\mathit{\mu }|{\psi }_j⟩$$ 2.4

and the time-dependent charge density

$$⟨\sigma (\mathbf{r},t)⟩=\sum _{i,j}{\rho }_{ij}(t){\psi }_i^{\ast }(\mathbf{r}){\psi }_j(\mathbf{r}),$$ 2.5

where ρ_ij(t) is the single-electron density matrix in a MO basis and ψ_i are the ground-state MOs.

The charge density in momentum space 〈σ(q, t)〉 is calculated by a spatial Fourier transform of the real-space charge density

$$⟨\sigma (\mathbf{q},t)⟩=\int \mathrm{d}\mathbf{r}\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}\mathbf{q}\cdot \mathbf{r}}⟨\sigma (\mathbf{r},t)⟩,$$ 2.6

where q = k_s − k_x is the scattering wavevector, and k_s and k_x are the scattered and incoming X-ray wavevectors, respectively.

The XANES spectrum is given by the Fourier transform of the time-evolving dipole

$$S_{\mathrm{XANES}}(\omega )\propto \mathrm{\Im }\int \mathrm{d}t\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}\omega t}⟨\mathit{\mu }(t)⟩$$ 2.7

and the charge density provides the diffraction signal (see equations (2.10) and (2.11)).

Since the simulation includes all orders of interactions with the external field, a phase cycling protocol is required to sort out the desired signal from the density matrix [18]. To extract the time-evolving charge density created by the SFG (first-order interaction as shown in figure 1c) 〈σ(r, t)〉^SFG, we employed a two-step phase cycling protocol to eliminate the ground-state (zeroth-order interaction) contribution, which is independent of the phase of the external field, as follows:

$${⟨\sigma (\mathbf{r},t)⟩}^{\mathrm{SFG}}=⟨\sigma (\mathbf{r},t,\varphi =0)⟩-⟨\sigma (\mathbf{r},t,\varphi =\pi )⟩.$$ 2.8

We kept the pump pulse weak enough so that contributions from higher-order interactions to the external field are negligible compared to the SFG contribution. Similarly, the SFG contribution to the time-dependent dipole moment can be extracted as follows (see §3 in the electronic supplementary material for the phase cycling protocol)

$${⟨\mathit{\mu }(t)⟩}^{\mathrm{SFG}}=⟨\mathit{\mu }(t,\varphi =0)⟩-⟨\mathit{\mu }(t,\varphi =\pi )⟩.$$ 2.9

The XSFG diffraction imaging technique can monitor core coherence and its dynamics [19,20]. Figure 1 shows the pulse and level schemes together with ladder diagrams for XSFG diffraction imaging. An X-ray pump pulse μ first launches the electronic dynamics at t = 0, $|g⟩⟨g|\to |c⟩⟨g|$. Since the first X-ray pump pulse interacts only once with the molecules (see figure 1), the density matrix is prepared in a coherence |c〉〈g|, i.e. a coherent superposition of the ground |g〉 and core |c〉 states, oscillating at the transition frequency between the ground and the core excited state. An off-resonant X-ray diffraction probe σ(q) then detects the charge density through inelastic transition after time delay T, $|c⟩⟨g|\to |g⟩⟨g|$ (see figure 1b,c). Since the probe pulse is off-resonant to any molecular transition, the detection process does not trigger any electronic transitions.

There are two detection modes for nonlinear signals: spontaneous (homodyne) and stimulated (heterodyne) (figure 1c). Homodyne detection employs a single probe pulse and requires two-molecule interactions with the ${\mathcal{A}}_{\mathrm{X}}$ pulse yielding the magnitude of the charge density (equation (2.10)). We cannot extract the real and imaginary parts of the signals from this technique. On the other hand, heterodyne detection uses an additional heterodyne pulse to stimulate the light emission, and the signal is given by the imaginary part of the convolution of the charge density 〈σ(q, t)〉 and the pulse envelopes ${\mathcal{A}}_{\mathrm{het}}(t)$ and ${\mathcal{A}}_{\mathrm{X}}(t)$ (equation (2.11)). The use of the heterodyne pulse ${\mathcal{A}}_{\mathrm{het}}$ allows one to extract the phase information of the charge density.

Diffraction signals of oriented samples have so far been measured in the spontaneous (homodyne) detection mode [21]

$$S_{\mathrm{hom}}(\mathbf{q},t)\propto 2{|\int \mathrm{d}t\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}{\omega }_{s}t}{\mathcal{A}}_{\mathrm{X}}^{\ast }(t)⟨\sigma (\mathbf{q},t)⟩|}^2,$$ 2.10

where ${\mathcal{A}}_{\mathrm{X}}$ is the vector potential envelope of the diffracted X-ray pulse.

By contrast, the stimulated coherent (heterodyne) diffraction signals [21] employ two pulses with envelopes ${\mathcal{A}}_{\mathrm{X}}$ and ${\mathcal{A}}_{\mathrm{het}}$ (heterodyne pulse) for the diffraction and the signal is given by

$$S_{\mathrm{het}}(\mathbf{q},t)\propto 2\hspace{0.17em}\mathrm{\Im }\int \mathrm{d}t{\mathcal{A}}_{\mathrm{het}}(t){\mathcal{A}}_{\mathrm{X}}(t)⟨\sigma (\mathbf{q},t)⟩.$$ 2.11

The pulse envelope ${\mathcal{A}}_{\mathrm{X}}$ and ${\mathcal{A}}_{\mathrm{het}}$ are taken as delta functions in time, i.e. A_het(t) = A_X(t) = δ(t). Therefore, only the first external field μ was taken into account in the actual RT-TDDFT simulations. For completeness, sum-over-states expressions for the homodyne and heterodyne detected SFG diffraction signals are given in the time domain and the frequency domain in appendices A(a) and A(b), respectively. The appearances of Dirac delta functions in equations (A 9) and (A 10) indicate that this is an SFG signal, i.e. the signal appears at ω_s(3) = ω₁ + ω₂.

We have employed RT-TDDFT as implemented in NWChem [17,22] to simulate the time-evolving charge density and the corresponding X-ray diffraction signals. The geometry optimization of the ground state was carried out at the B3LYP [23] exchange-correlation functional and 6-311++G** basis set level. Closed-shell calculations were performed at the B3LYP/6-31+G* level (denoted RT-TDDFT/B3LYP/6-31+G*). The total simulation times for the real-time propagation is 2500 au = 60.5 fs with a Δt = 0.02 au (0.48 as) time step to capture the ultrafast core coherences, yielding XANES spectral resolution of 0.068 eV. We focus on the early dynamics up to 15 fs following the core excitation where the core hole recombination processes can be neglected. Once the Auger decay, after approximately 10 fs occurs, the core coherence is lost and the subsequent dynamics changes. The description of core relaxation processes is an interesting topic for future work.

To facilitate the analysis of the RT-TDDFT results, we also performed linear-response (LR) restricted excitation window TDDFT (REW-TDDFT) [12] frequency-domain calculations of the energy levels and the transition charge densities σ_gci from ground to the carbon K-edge states at the B3LYP/6-31+G* (denoted LR-REW-TDDFT/B3LYP/6-31+G*).

All calculations are done for oriented molecules. This allows us to measure directly the Fourier transform of the charge density. The signal can also be detected in randomly oriented ensembles where some of the spatial information is averaged out [20]. Such averaging can be computationally costly since the response is a tensor field rather than a single tensor. The averaging has been carried out numerically either by summing over an ensemble of orientations or by projecting on a subset of rotational invariant tensor field. This is in contrast to the response tensors expressed in the multipolar approximation that are conventional tensors and can be averaged by contraction with an averaging tensor [24]. Note that, unlike its conventional IR/VIS counterpart used to study vibrational dynamics at interfaces, which uses the multipolar approximation, diffraction detected SFG does not vanish in isotropic media. The reason is that a scalar field can be expanded into its symmetric and antisymmetric parts σ = σ_as + σ_s, unlike point multipoles (like electric or magnetic dipoles) that clearly belong to one irreducible representation of the inversion group. Thus, the charge density has antisymmetric and symmetric contributions, and the signal is sensitive to one or the other in a rotationally oriented sample at a given nonlinear order.

(b). Carbon K-edge XANES spectra of chemically inequivalent carbon atoms

Figure 2a shows the XANES spectrum of the C K-edge states in fluoroethane calculated at the LR-REW-TDDFT (sticks) and RT-TDDFT (black line) (both at the B3LYP/6-31+G* level). The calculated X-ray absorption energies are shifted by Δ = + 11.0 eV to match experiments [12]. The two calculation methods yield similar results. The transition charge densities shown in figure 2b clearly show the localized core excitation of each peak. The transition charge densities indicate |c₁〉 is –CH₃ core excitation, and |c₂〉 and |c₃〉 are –CH₂F core excitations. The fluorine-substituted –CH₂F carbon core, |c₃〉 state, is blue shifted by 2.4 eV compared to –CH₃ carbon core, |c₁〉 state, making the selective excitation by a narrowband X-ray pulse possible.

Figure 2.

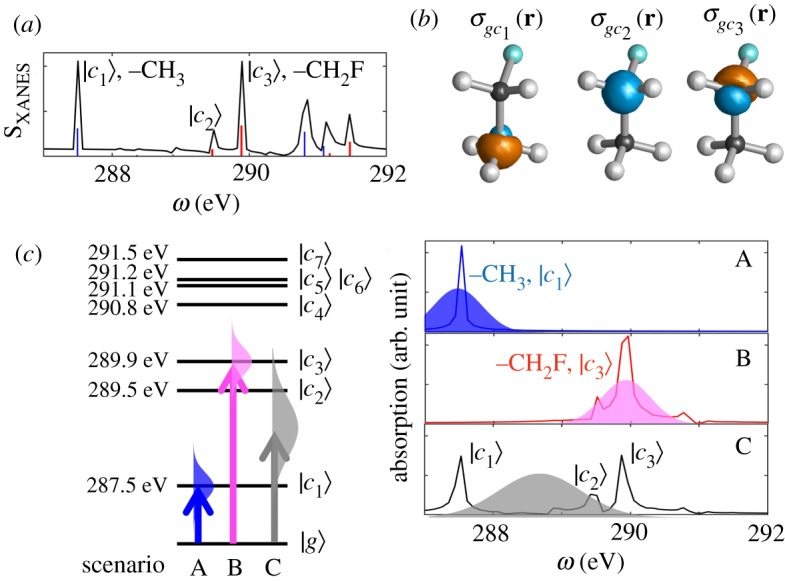
(a) XANES spectra for carbon K-edge states. Black line: RT-TDDFT/B3LYP/6-31+G* (equation (2.7)); sticks: LR-REW-TDDFT/B3LYP/6-31+G*. (b) Transition charge densities σ_gci for |c₁〉–|c₃〉 states. (c) Left: Relevant carbon K-edge level scheme of fluoroethane (states with μ²_ig,z > 0.00006). Right: XANES spectra for excitation scenarios (A) |c₁〉, (B) |c₃〉 and (C) both states calculated at RT-TDDFT/B3LYP/6-31+G*. Electric field envelopes are also drawn. (The calculated X-ray absorption energies and XANES spectra are shifted by Δ = + 11.0 eV to match experiment.) (Online version in colour.)

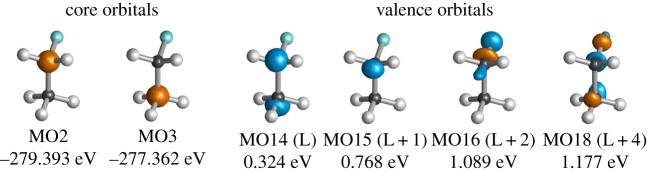
The left panel of figure 2c shows the relevant carbon K-edge levels of fluoroethane and the pulse scheme for the three excitation scenarios A–C. Table 1 gives the contributions of MO transitions to the core excitations |c₁〉–|c₃〉 in order to analyse the character of the excited states (MO shapes are given in figure 3). The |c₁〉 excitation is constructed by a single dominant MO3 to MO14 transition. By contrast, |c₂〉 and |c₃〉 contain multiple MO transitions, MO2 to MO14 (LUMO), MO15, MO16 or MO18. Then, |c₁〉 is localized on the –CH₃ carbon and |c₂〉 and |c₃〉 on the –CH₂F carbon, since MO3 and MO2 are the core orbitals of those carbons, respectively.

Table 1.

Contributions of MO transition to the core excited states in fluoroethane calculated at the LR-REW-TDDFT/B3LYP/6-31+G*.

|c1〉		|c2〉		|c3〉
MO trans.	contrib. (%)	MO trans.	contrib. (%)	MO trans.	contrib. (%)
3 → 14	98.3%	2 → 14	82.6	2 → 14	14.8
3 → 15	1.3%	2 → 15	8.3	2 → 15	13.6
		2 → 16	5.9	2 → 16	59.8
				2 → 18	6.3

Figure 3.

Core and valence MO shapes, energies and energy differences. L = LUMO; L+n = LUMO+n. (Online version in colour.)

To illustrate the capability of diffraction signals to differentiate between excitations of chemically inequivalent carbon cores, we have simulated the following three scenarios: resonant excitation by an X-ray pulse of either the (A) –CH₃ (resonant to |c₁〉; ω_i = 287.5 eV; σ_i = 1.45 fs; FWHM of 1.07 eV), or (B) –CH₂F (resonant to |c₃〉; ω_ii = 289.9 eV; σ_ii = 1.45 fs; FWHM of 1.07 eV) carbon and (C) both carbons in fluoroethane (resonant at the middle of |c₁〉 and |c₃〉; ω_iii = 288.7 eV; σ_iii = 0.77 fs; FWHM of 2.00 eV).

The right panel of figure 2c shows XANES spectra for the three excitation scenarios A–C calculated at RT-TDDFT/B3LYP/6-31+G* by the Fourier transform of the time-evolving dipole moment 〈μ(t)〉 which will be shown in figure 4. We see a clear separation of the core states in scenarios A and B, indicating the selective excitation of the |c₁〉 and |c₃〉, respectively. A superposition of the core states |c₁〉–|c₃〉 is observed in scenario C. Therefore, we expect a single core coherence |c₁〉〈g| in scenario A, |c₃〉〈g| in scenario B, and the superposition of those in scenario C.

Figure 4.

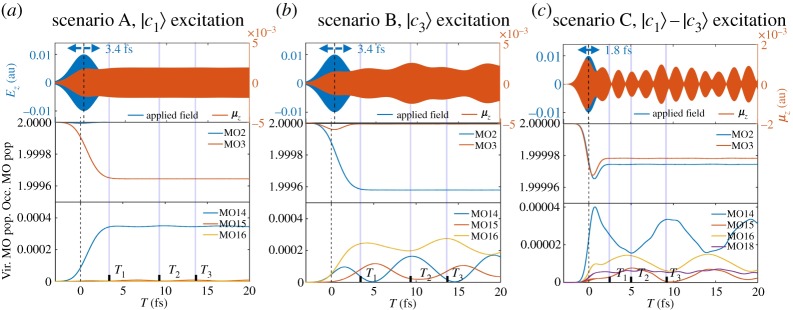
RT-TDDFT simulation of charge migration following the selective excitation of (a) |c₁〉, (b) |c₃〉 and (c) broadband excitation of both. External fields E_z, time-dependent dipole moment μ_z, and populations of dominant core (MO2 and MO3) and valence (MO14, MO15, MO16, MO18) MOs. (Online version in colour.)

(c). X-ray diffraction signals of the chemically inequivalent carbon atoms

Figure 4 depicts the applied pulse E_z(t), the total dipole moment along z (μ_z), and populations of selected core and valence orbitals for the three excitation scenarios. Several points should be noted. First, selective excitation of a core state, either the |c₁〉 or the |c₃〉, is evidenced by the decrease of a single core orbital population as seen in the middle panels of figure 4a,b (MO2 and MO3 represent the core orbital of –CH₂F and –CH₃ carbons, respectively.). Similarly, the superposition of core states, |c₁〉–|c₃〉, in scenario C is apparent by the decrease of both MO2 and MO3 populations as seen in the middle panel of figure 4c. Since the core hole recombination processes, such as Auger decay, are not considered in our calculations, the core coherence survives after the excitation process. We focus on the early dynamics and neglect core extinction processes. Second, core coherences created by the X-ray pumps, central frequency in the range 287.5–289.9 eV, oscillate at approximately 14 as period as shown in the electronic supplementary material, figures S4–S12. The oscillation periods slightly vary for the different excitation scenarios (excitation energy of 287.5 eV corresponds to 14.38 as and 289.9 eV to 14.27 as). We see a strong coherence between the core orbital and partially filled unoccupied orbitals by ultrafast in-phase oscillation of the MO populations, shown in the electronic supplementary material, figures S4–S12, which induces an attosecond charge migration.

Third, the interplay between partially filled unoccupied MOs populated by core excitations creates a valence coherence and a 9 fs charge migration as shown in the bottom panels of figure 4. In scenario A, only MO14 is populated and no significant valence charge oscillation is observed (yet core coherence persists). By contrast, in scenarios B and C, multiple unoccupied orbitals (MO14, MO15, MO16 and MO18) are partially populated upon core excitation so that we can see a strong valence coherence and femtosecond charge migration. In scenario C, there is interesting dynamics in the core and valence regimes due to the interaction among multiple excited states |c₁〉–|c₃〉. The interaction between the core states can be modulated by adjusting the centre frequency of the excitation field and/or pulse shaping to investigate the interactions between the two excited states. The approximate femtosecond oscillation periods (T₃ − T₁) in scenarios B and C, 9.41 and 8.95 fs, respectively, indicate the interaction among valence orbitals: MO14 and MO15 (ΔE = 0.444 eV $\to 9.31$ fs), MO15 and MO16 (ΔE = 0.321 eV $\to 12.9$ fs), and MO14 and MO16 (ΔE = 0.765 eV$\hspace{0.17em}\to 5.41$ fs). Finally, the time evolution of the total dipole moment is a convolution of the core and valence coherences, which induce attosecond and femtosecond charge oscillation, respectively. In this sense, a direct propagation of the density matrix can adequately describe the core and valence dynamics in a seamless and non-perturbative manner.

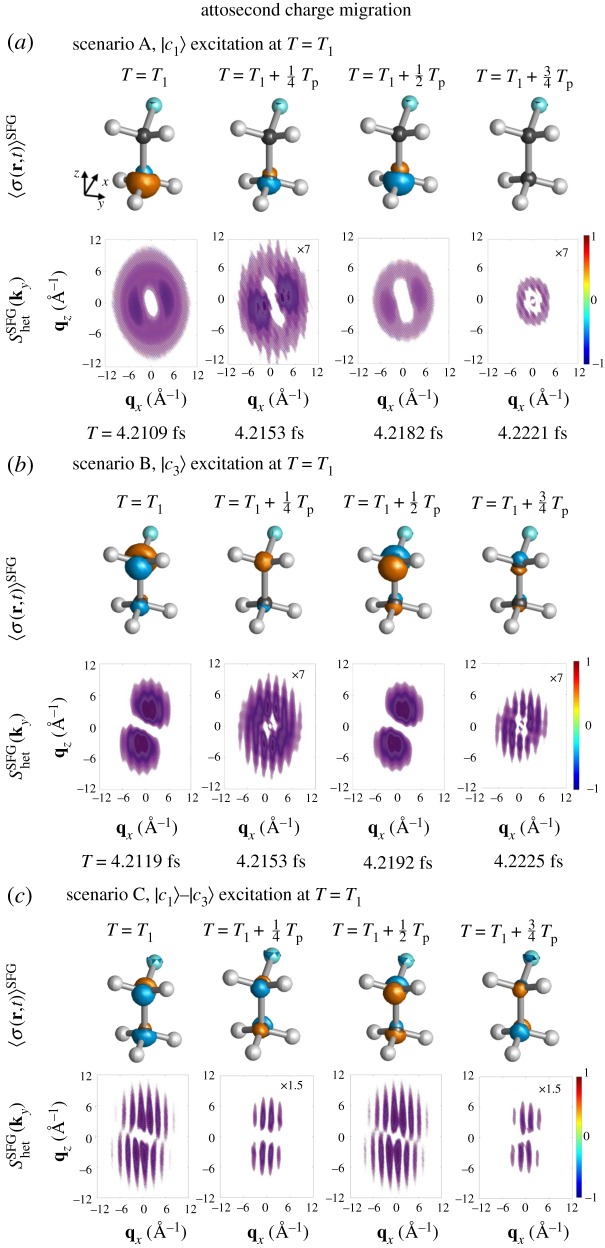
Figure 5 shows attosecond charge migration around T = T₁ induced by core coherence and the corresponding heterodyne X-ray diffraction signals (see the similar figures for T = T₂ and T₃ and the homodyne signals in the electronic supplementary material, figures S4–S12. The 〈σ(q, t)〉^SFG at T₁ in scenarios A and B resembles the transition charge densities σ_gc1 and σ_gc3 and so the corresponding S_het(k_y) signals. This indicates that the SFG density in the early dynamics is created from transition charge densities, and evolves in time on a longer time scale. The heterodyne diffraction signal shows attosecond oscillations which reflect the electron–hole density evolution. Since the electron and hole interchange their position upon oscillation, the electron–hole density changes sign. The three excitation scenarios show distinct signals and the oscillation provides the time scale of the core coherence.

Figure 5.

Attosecond charge migration around T = T₁ due to core coherences created by (a) |c₁〉, (b) |c₃〉 and (c) |c₁〉–|c₃〉 excitations. 〈σ(r, t)〉^SFG (blue, electron; orange, hole density; isovalue of 0.00006) and corresponding heterodyne diffraction signals S_het(k_y) are shown. (Online version in colour.)

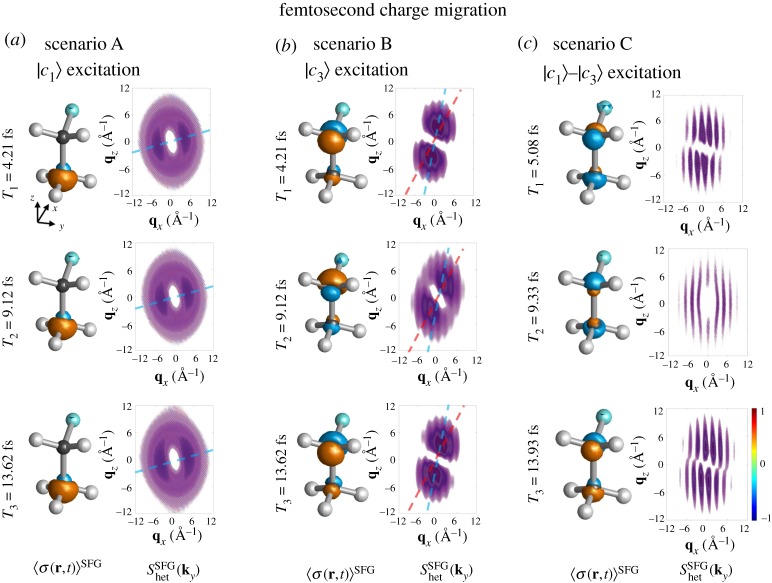
Figure 6 shows the femtosecond valence charge migration snapshots at T = T₁, T₂ and T₃ for the three excitation scenarios (see electronic supplementary material, figure S13 for the homodyne signals). Owing to the absence of valence coherence among partially filled unoccupied orbitals, in scenario A, no significant valence charge migration was found and thus no significant change in the diffraction signal. By contrast, strong valence coherences are created in scenarios B and C depending on the excitation characters of the excited states and the interaction among them as discussed in table 1 and figure 4b,c. As an example, the diffraction pattern following the |c₃〉 excitation in scenario B rotates forwards (red line) and backwards (blue line) upon the valence charge migration; the two limits are marked with blue and red lines. This comes from the population change among the partially filled unoccupied valence orbitals possessing different shapes (see electronic supplementary material, figure S1). In scenario C, the total dynamics is given by the interplay between the excited states |c₁〉–|c₃〉 in a certain ratio and the interaction among them generates an interesting pattern. Since the participating MOs have different characters and orientations, 〈σ(r, t)〉^SFG at each carbon atom changes and thus the rotation in the diffraction signals S_het(k_y).

Figure 6.

Charge migration following (a) scenario A, |c₁〉 excitation, (b) scenario B, |c₃〉 excitation and (c) scenario C, |c₁〉–|c₃〉 excitations and the corresponding heterodyne diffraction signals. Diffraction pattern following the |c₃〉 excitation in the scenario B rotates forwards (red line) and backwards (blue line). Guides for the alignment of the signals are drawn in blue and red lines. (Online version in colour.)

This implies that the present diffraction imaging captures the detailed spatial profile of an electron–hole density and time scales of the dynamics. At T = T₃, S_het(k_y) is symmetric with respect to the q_x axis due to the symmetry of the electron–hole density at –CH₃ and –CH₂F carbons with respect to the xy plane, while different at T = T₂. The diffraction pattern following the |c₁〉 excitation is almost mirror symmetric with respect to q_y and q_x axes, while that following the |c₃〉 excitation is highly asymmetric with respect to q_x due to the –CH₂F carbon having stronger interaction with fluorine than –CH₃.

3. Conclusion

We have employed RT-TDDFT to simulate diffraction signals following selective excitation of core electrons from the two chemically inequivalent carbon atoms in fluoroethane (CH₃–CH₂F) by an X-ray pulse with 1 eV bandwidth. Real-time propagation of the reduced single-electron density matrix driven by the incoming fields yields the time-evolving transition charge density and the corresponding diffraction signals in a non-perturbative manner. Both homodyne and heterodyne diffraction signals were obtained by Fourier transform of the time-evolving charge density. A 1 eV bandwidth pulse can selectively excite either the –CH₃ or –CH₂F carbon atoms separated by 2.4 eV. The two core excitations induce core coherence and launch attosecond charge migration occurring at similar time scale, but also leave electron–hole density at different carbon atoms which can be detected by the diffraction signal. The core excitations also leave a different set of partially filled valence orbitals to start characteristic femtosecond charge migration by the interactions among the valence orbitals. Monitoring the femtosecond dynamics following a core excitation reveals how the core excitation induces coherent populations in the valence orbitals, triggers interesting valence charge migration, and how they interact. The SFG diffraction signals with an X-ray pump, which combines the element sensitivity of X-ray absorption and the spatial resolution of diffraction detection, can distinguish excitations that are difficult to identify by the frequency-domain analysis. The diffraction signals further allow us to pinpoint the aspect of charge migration dynamics driven by the interactions among complicated core and valence orbitals following core excitation.

Appendix A

(a) Sum-over-states expressions of homodyne- and heterodyne-detected sum-frequency generation diffraction signals

The homodyne-detected SFG diffraction is obtained by a first-order expansion in the X-ray pump pulse [19]:

$$\begin{array}{c}{S}_{\mathrm{hom}}(\mathbf{q},T)=2\hspace{0.17em}\mathrm{\Re }{F}_2(\mathbf{q}){|\frac{e}{2mc}\int \mathrm{d}t\hspace{0.17em}\mathrm{d}{t}_1\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\omega }_{s}t}{\mathcal{A}}_{\mathrm{X}}(t){\mathcal{A}}_{\mathrm{pump}}(t-t_1+T)⟨{\sigma }_L(\mathbf{q},t){\mathit{\mu }}_L^{†}(t-t_1)⟩|}^2.\hfill \end{array}$$ A 1

The F₂ function is the usual structure factor for the diffraction of an ensemble of scatterers

$$F_2(\mathbf{q})=\sum _{\alpha \beta ,\alpha \ne \beta }{\mathrm{e}}^{\mathrm{i}\mathbf{q}\cdot ({\mathbf{r}}_{\alpha }-{\mathbf{r}}_{\beta })}.$$ A 2

The sum-over-states (SOS) expression of the signal is given by

$$S_{\mathrm{hom}}^{\mathrm{SFG}/\mathrm{SOS}}(\mathbf{q},T)=2\hspace{0.17em}\mathrm{\Re }{F}_2(\mathbf{q}){|\frac{e}{2mc}\sum _c{g}_{cg}(T){\sigma }_{gc}(\mathbf{q}){\mathit{\mu }}_{cg}|}^2,$$ A 3

where g is the envelope function given by

$$\begin{array}{c}{g}_{cg}(T)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\hspace{0.17em}\mathrm{d}{\tau }_2{\int }_{-\mathrm{\infty }}^{{\tau }_2}\hspace{0.17em}\mathrm{d}{\tau }_1\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\omega }_s{\tau }_2}\hspace{0.17em}{A}_X({\tau }_2)\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}{\omega }_{\mathrm{X}}{\tau }_2}{A}_{\mathrm{pump}}({\tau }_1+T)\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}{\omega }_{\mathrm{pump}}({\tau }_1)}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\omega }_{cg}{\tau }_1-{\mathrm{\Gamma }}_{cg}{\tau }_1}.\hfill \end{array}$$ A 4

The heterodyne-detected SFG diffraction signals are given by

$$\begin{array}{rl}{S}_{\mathrm{het}}^{\mathrm{SFG}}(\mathbf{q},T)& =-\frac{1}{\hslash }\frac{e}{2mc}\mathrm{\Im }{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\hspace{0.17em}\mathrm{d}t{\int }_0^{+\mathrm{\infty }}\hspace{0.17em}\mathrm{d}{t}_1\hspace{0.17em}{\mathcal{A}}_{\mathrm{het}}^{\ast }(t)\\ & \times {\mathcal{A}}_{\mathrm{X}}(t){\mathcal{A}}_{\mathrm{pump}}(t-t_1+T)⟨{\sigma }_L(\mathbf{q},t){\mathit{\mu }}_L^{†}(t-t_1)⟩\end{array}$$ A 5

and the corresponding SOS expression is

$$\begin{array}{rl}{S}_{\mathrm{het}}^{\mathrm{SFG}/\mathrm{SOS}}(\mathbf{q},T)& =-\frac{1}{\hslash }\frac{e}{2mc}\mathrm{\Im }[{\mathit{ϵ}}_{\mathrm{het}}^{\ast }\cdot {\mathit{ϵ}}_{\mathrm{X}}\sum _c{f}_{cg}(T){\sigma }_{gc}(\mathbf{q}){\mathit{ϵ}}_{\mathrm{pump}}\cdot {\mathit{\mu }}_{cg}],\end{array}$$ A 6

with

$$\begin{array}{rl}{f}_{cg}(T)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\hspace{0.17em}\mathrm{d}{\tau }_2{\int }_{-\mathrm{\infty }}^{{\tau }_2}\hspace{0.17em}\mathrm{d}{\tau }_1{A}_{\mathrm{het}}({\tau }_2)A_{\mathrm{X}}({\tau }_2)A_{\mathrm{pump}}({\tau }_1+T)\hspace{0.17em}{\mathrm{e}}^{-\mathrm{i}{\omega }_{\mathrm{pump}}{\tau }_1}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\omega }_{cg}{\tau }_1-{\mathrm{\Gamma }}_{cg}{\tau }_1},\end{array}$$ A 7

where A_het, A_X and A_pump are the field envelopes. The diffraction probe and heterodyne pulse are taken as delta functions in time, i.e. A_het(t) = A_X(t) = A_pump(t) = δ(t). The f and g lineshape functions simplify to

$$f_{cg}(T)=g_{cg}(T)={\mathrm{e}}^{-\mathrm{i}{\omega }_{\mathrm{pump}}T}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\omega }_{cg}T-{\mathrm{\Gamma }}_{cg}T}.$$ A 8

(b) Frequency-domain representation of sum-frequency generation diffraction signals

The sum-frequency generation nature of the SFG diffraction signal is highlighted by expressing the homodyne and the heterodyne signals in the frequency domain:

$$\begin{array}{rl}{S}_{\mathrm{hom}}^{\mathrm{SFG}/\mathrm{SOS}}(\mathit{q},T)& =2\hspace{0.17em}\mathrm{\Re }{F}_2(\mathbf{q})|\frac{e}{2mc}\frac{1}{{(2\pi )}^2}\sum _c{\sigma }_{gc}(\mathbf{q}){\mathit{\mu }}_{cg}\\ & {\times \int \mathrm{d}{\omega }_2\hspace{0.17em}\mathrm{d}{\omega }_1\hspace{0.17em}{A}_{\mathrm{X}}({\omega }_2)A_{\mathrm{pump}}({\omega }_1)\frac{\mathrm{i}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\omega }_{1}T}\delta ({\omega }_s-{\omega }_2-{\omega }_1)}{{\omega }_1-{\omega }_{cg}+\mathrm{i}{\mathrm{\Gamma }}_{cg}}|}^2,\end{array}$$ A 9

$$\begin{array}{rl}{S}_{\mathrm{het}}^{\mathrm{SFG}/\mathrm{SOS}}(\mathit{q},T)& =\frac{1}{{(2\pi )}^3}\frac{2}{\hslash }\sum _c\mathrm{\Re }{\mathit{ϵ}}_{\mathrm{het}}^{\ast }\cdot {\mathit{ϵ}}_{\mathrm{X}}\hspace{0.17em}{\sigma }_{gc}(\mathit{q}){\mathit{\mu }}_{cg}\cdot {\mathit{ϵ}}_{\mathrm{pump}}\int \mathrm{d}{\omega }_1\hspace{0.17em}\mathrm{d}{\omega }_2\hspace{0.17em}\mathrm{d}{\omega }_3\\ & \times A_{\mathrm{het}}({\omega }_3)A_{\mathrm{X}}({\omega }_2)A_{\mathrm{pump}}({\omega }_1)\frac{\mathrm{i}\hspace{0.17em}{\mathrm{e}}^{\mathrm{i}{\omega }_{1}T}\delta ({\omega }_3-{\omega }_2-{\omega }_1)}{{\omega }_1-{\omega }_{cg}+\mathrm{i}{\mathrm{\Gamma }}_{cg}}.\end{array}$$ A 10

The Dirac δ function occurs naturally after integration over the time variable and ensures that the process under consideration is indeed a sum-frequency one.

Data accessibility

Electronic supplementary material is available: (i) MO shapes and transition charge densities, (ii) Attosecond charge migration due to core coherences and femtosecond charge migration due to valence coherences and (iii) Effect of the phase cycling protocol.

Authors' contributions

S.M. and J.R.R. designed the signal. D.C. carried out the simulation. D.C., M.K., J.R.R. and J.Y.L. performed the data analysis and drafted the manuscript. All authors read and approved the manuscript.

Competing interests

The authors declare that they have no competing interests.

Funding

The support of the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy through Awards No. DE-FG02-04ER15571 and DE-SC0019484; and of the National Science Foundation (grant no. CHE-1663822) is gratefully acknowledged. D.C. was supported by the DOE grants.