Attosecond soft X-ray high harmonic generation

Abstract

High harmonic generation (HHG) of an intense laser pulse is a highly nonlinear optical phenomenon that provides the only proven source of tabletop attosecond pulses, and it is the key technology in attosecond science. Recent developments in high-intensity infrared lasers have extended HHG beyond its traditional domain of the XUV spectral range (10–150 eV) into the soft X-ray regime (150 eV to 3 keV), allowing the compactness, stability and sub-femtosecond duration of HHG to be combined with the atomic site specificity and electronic/structural sensitivity of X-ray spectroscopy. HHG in the soft X-ray spectral region has significant differences from HHG in the XUV, which necessitate new approaches to generating and characterizing attosecond pulses. Here, we examine the challenges and opportunities of soft X-ray HHG, and we use simulations to examine the optimal generating conditions for the development of high-flux, attosecond-duration pulses in the soft X-ray spectral range.

This article is part of the theme issue ‘Measurement of ultrafast electronic and structural dynamics with X-rays’.

1. Introduction

The discovery of high harmonic generation (HHG) in the late 1980s heralded a new era in nonlinear optics, and it paved the way for attosecond science. Theoretical understanding of the microscopic [1,2] and macroscopic [3,4] aspects of the process was developed through the 1990s, and the first measurement of attosecond pulses followed in 2001 [5,6]. Some of the distinguishing features of HHG compared with low-order harmonic generation are a weak variation of flux with harmonic order, a time-energy structure that enables the generation of attosecond pulses, a dependence of the harmonic phase upon the driving laser intensity, and a maximum emitted photon energy of 3.17U_P + 1.3I_P∝Iλ². Here, U_P = e²Iλ²/(8π²ϵ₀ c³ m) is the ponderomotive energy of the laser field, I and λ are the driving laser intensity and wavelength, respectively, ϵ₀ is the vacuum permittivity, c is the speed of light, m is the electron mass and I_P is the ionization potential of the target gas. Compared to the only other demonstrated route of generating attosecond pulses, X-ray-free electron lasers [7], HHG benefits from its relative compactness (few square metre footprint), relatively low cost, high stability and intrinsic synchronization to the driving laser, while suffering from a flux many orders of magnitude lower [8]. Attosecond pulses from HHG have since been applied to study a wide variety of physical phenomena, but until recently they have been limited to the XUV spectral range (10–150 eV). Extending HHG and attosecond pulse generation to the soft X-ray (150 eV to 3 keV) has long been a topic of interest, because it would both grant access to the powerful techniques of X-ray spectroscopy and scattering, and allow high-harmonic radiation to be used to study materials with prohibitively strong absorption in the XUV. Of particular interest is the so-called water window region between the carbon K-edge at 284 eV and the oxygen K-edge at 540 eV in which water is relatively transparent making in vivo spectroscopy and imaging possible, but further increases in photon energy to access the L-edge spectra of transition metals are also of great interest.

While the first demonstration of HHG in the water window was in 1997 using 800 nm wavelength lasers [9], there has recently been renewed interest in using HHG to generate radiation in the soft X-ray regime spurred by the development of high energy ( ≈ 0.5 mJ), few-cycle duration sources at longer wavelengths, from 1.5 μm to 3 μm, based upon either optical parametric amplifiers (OPAs) and subsequent pulse compression using hollow-core fibres (HCFs), or upon optical parametric chirped-pulse amplifiers (OPCPAs) [10]. Using this new generation of driving lasers, soft X-ray HHG has progressed rapidly, and the last three years have seen a number of breakthroughs. These include the first measurements of attosecond pulses in the water window [11,12], the first X-ray spectroscopy measurements at the carbon K-edge or above with HHG-based sources [13–15], the first time-resolved X-ray measurements with HHG-based sources [16,17], the first carrier-envelope phase (CEP)-dependent harmonics in the water window [18–20], and an increase in flux of more than seven orders of magnitude compared to the first water window harmonic generation [15,21].

These developments have been aided by theoretical examination of the wavelength scaling of HHG at the single atom level. While it was originally believed that the efficiency of HHG would scale as λ⁻³ [2], more recent examinations using both the time-dependent Schrödinger equation and the strong-field approximation have concluded that the efficiency of a single-atom scales as between λ⁻⁵ and λ⁻⁹ [22–24]. This suggests that in moving from 800 nm to 1800 nm driving lasers, the single-atom emission should decrease by a factor of between 50 and 1500. Despite this, recent experiments have managed to generate fluxes of over 10⁹ photons per second in the water window [15,21], comparable to XUV HHG driven by 800 nm lasers [8]. These high fluxes have been made possible by the favourable macroscopic response, the collective action of the many emitting atoms in the laser volume, which changes when moving to SXR HHG driven by longer wavelengths. The propagation of the driving laser and the build-up of the harmonic radiation are affected by, among other things, plasma refraction and the intensity-dependent harmonic phase, which scale strongly with the driving wavelength. Despite the renewed importance of the macroscopic aspects of HHG for SXR radiation, most work has been focused on a range of parameters where the problem can be treated as quasi-one-dimensional [25,26]. As the primary barrier to the widespread application of soft X-ray attosecond pulses is their prohibitively low flux, understanding and optimizing the macroscopic response is the key challenge for SXR HHG sources.

Here, we discuss SXR HHG and the generation of attosecond pulses in the water window. We begin by reviewing the so-called three-step model, which describes HHG from a single atom, with an emphasis on the wavelength scaling. We then discuss the macroscopic aspects of HHG and attosecond pulse generation and how conventional pictures of the harmonic build-up are modified when considering longer wavelength driving fields, where the impacts of intensity gradients and plasma generation are amplified. Numerical simulations examine scaling laws discussed in Johnson et al. [21] and Lu et al. [27], which show for SXR attosecond pulse generation high fluxes can be obtained through overdriving the generation medium, creating a strong plasma response and re-shaping the driving laser. Finally, we discuss the next generation of SXR attosecond sources and spectroscopy.

2. Wavelength scaling of high harmonic generation

HHG cannot be described using the conventional perturbative approach employed for lower-order nonlinear optical effects, and it is instead described by the so-called three-step model [1]. An excellent tutorial thereupon can be found in S. Haessler et al. [28]. In the three-step model, when an atom is exposed to a strong, low-frequency laser field, the laser field is treated not as a perturbation to the system, but rather as a slowly varying time-dependent potential, which competes with the binding Coulomb potential. The strong field ‘tips’ the potential and allows a valence electron to tunnel through the now finite potential barrier into the continuum. After ionization, the electron propagates under the influence of the strong laser field. When the laser field switches direction, the electron is accelerated back, and provided it was born at the correct time into the continuum, may recollide with the cation. The electron can then recombine with the ion and release its kinetic energy as a high-energy photon. The classical trajectories obey the following equation (in atomic units):

$$x(t)=\frac{E_0}{{\omega }_0^2}[\cos ({\omega }_{0}t)-\cos ({\omega }_0{t}_b)]+\frac{E_0}{{\omega }_0}\sin ({\omega }_0{t}_b)(t-t_b),$$ 2.1

where x(t) is the displacement of the electron from the ionic core, E₀ and ω₀ are the amplitude and angular frequency of the driving laser field, respectively, and t_b is the time the electron enters the continuum. Only electrons born at certain t_b will return to the x = 0 position and recombine at a corresponding time t_r; for those that do, their kinetic energy at recollision is a well-defined function of the birth time. Perhaps the most important aspect of the model is that it correctly predicts the highest photon energy released in HHG, E = 3.17U_P + 1.3I_P, as it can be shown that the maximum kinetic energy of a recolliding electron is given by 3.17U_P. That this energy depends on the intensity and wavelength squared (through U_P) follows directly from the recollision picture; as the intensity increases, the electron accelerates faster in the field and accumulates higher energy, while increasing the wavelength (i.e. period of the field) gives the electron a longer time to accelerate in the continuum before returning.

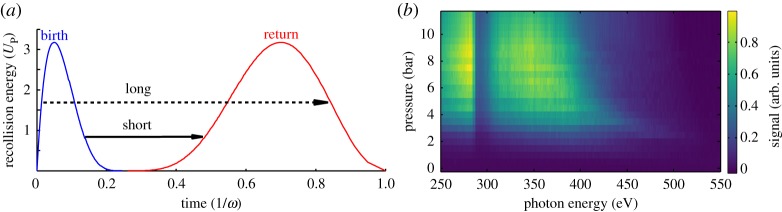
Figure 1a shows the relation between birth times, recollision times and recollision energies. The emission of the highest energy harmonics is localized in time, leading to the emission of attosecond pulses. In a multi-cycle pulse, the recollision process repeats every half cycle, leading to a train of pulses separated by one half of the laser period, whose interference leads to the emission of discrete high-order harmonics in the frequency domain. If the driving pulse is sufficiently short, the highest energy harmonics are produced by a single laser half cycle at the peak of the driving pulse, and spectral filtering of these harmonics results in isolated attosecond pulses in a scheme known as amplitude gating [6]. Additionally the harmonic emission is chirped; that is to say, the frequency of the emitted radiation varies within a single cycle of the driving laser. For each emitted photon energy, there are two contributing electron trajectories, one short trajectory and one long trajectory, with chirps of opposing sign. These trajectories lag the driving field by different times and thus have different phases of emission, which will have significant impacts upon phasematching, as discussed later.

Figure 1.

Micro- and macroscopic aspects of HHG. (a) Energy-time structure of classical trajectories in HHG. Birth times and corresponding recollision are in blue, recollision times and energies are in red. Arrows link the corresponding birth and return times for the short and long trajectories. (b) Experimental SXR HHG spectrum as a function of He backing pressure, showing spectral shaping as macroscopic parameters are changed. (Online version in colour.)

Two quantum models of HHG, the strong field approximation (SFA) [2] and its extension the quantum orbit model [29] successfully recreate the intuition of the three-step model while leading to quantitative predictions. In the quantum orbit model, the harmonic emission comes from the coherent superposition of contributions from electron trajectories; the most important trajectories largely follow those from the classical three-step model. Here, we are interested in two predictions: first, that the amplitude of the harmonic emission is proportional to g(t_r), the amplitude of the atomic ground state at the time of recollision. Figure 1a shows that increasing the intensity acts as a linear amplitude scaling on the trajectories—for a fixed wavelength, the maximum harmonic energy increases linearly and the harmonic chirp decreases linearly. However, the dependence upon g(t_r) means that increasing the intensity leads to a phenomenon known as ground state depletion, in which high intensity causes the rapid ionization of the ground state, decreasing g(t_r) and turning off the harmonic emission. Increasing the intensity thus cannot be used to arbitrarily scale the harmonic energy. The second prediction of the quantum models is that the phase of the harmonic emission is given by the classical action of the electron trajectory

$$\varphi (\omega )=\omega t_r-[{\int }_{t_b}^{t_r}\mathrm{d}t\frac{{[p_{st}+A(t)]}^2}{2}+I_p],$$ 2.2

where A(t) is the vector potential and $p_{st}=1/(t_r-t_b){\int }_{t_b}^{t_r}A(t)\mathrm{d}t$ is the stationary momentum corresponding to the trajectory that returns to the ion [2]. This non-trivial phase dependence upon the driving field results in complex phasematching behaviour; figure 1b shows the experimentally measured harmonic emission from a two-cycle, 550 μJ, 1.8 μm wavelength driving field focused into an 800 μm needle filled with helium as a function of backing pressure. The harmonic emission, which spans the water window, is strongly modified by the backing pressure, illustrating the importance of phasematching, and thus the harmonic phase, in SXR HHG.

As ground state depletion leads to a hard limit for the maximum usable intensity, we instead increase the driving wavelength to increase the harmonic energy; this comes at the expense of longer electron excursion times in the continuum. Long excursion times have two significant drawbacks—the first is a direct decrease in the harmonic yield at the single-atom level, with estimates of the exact scaling between λ⁻⁵ and λ⁻⁹ [22,24]. This is because (i) the electron wavepacket has more time to spread in the transverse direction, decreasing the probability of colliding with the atom, (ii) the increased longitudinal spreading of the electron wavepacket means the electron amplitude is spread over a wider range of energies, (iii) the fact that the dipole matrix elements responsible for the harmonic emission generally decrease with emitted photon energy and (iv) the intrinsic 1/ω² scaling of dipole emission [24]. For a fixed harmonic energy, increasing the wavelength causes the corresponding long trajectories to be born closer to the peak of the field, and the short trajectories to be born further away from it; the exponential scaling of the tunnel ionization probability then leads to a suppression of the short trajectories. The second effect of the long excursion times is an increase in the harmonic phase ϕ(ω), and in the intensity dependence of this phase. In particular, it can be shown that, for a given trajectory,

$$\frac{\mathrm{\partial }\varphi (\omega )}{\mathrm{\partial }I}={\int }_{t_b}^{t_r}\frac{{[p_{st}-A(t)]}^2}{2I}=\rho (\frac{\omega -I_p}{U_p})\frac{{\mathrm{\lambda }}^3}{4{(2\pi c)}^3},$$ 2.3

where I is the intensity and ρ is a normalized coefficient that depends only upon the energy relative to the cut-off [30]. The middle term of the equality shows that all explicit dependence upon the intensity cancels and the phase depends on the field parameters through the birth and return times only, given by ρ. The value of ρ is approximately linear with intensity, but larger for the long trajectories than the short trajectories. Phasematching will be significantly more sensitive to intensity variation with long wavelength driving fields because of the λ³ scaling.

A comprehensive treatment of the macroscopic build-up of high harmonics requires solving coupled wave equations for the driving and harmonic fields, but this is a very demanding computational problem, which can additionally be difficult to interpret. Instead, a simplified picture introduced by Balcou et al. [3] is often used, which treats the harmonic phasematching as the sum of two terms,

$$\mathrm{\Delta }\mathit{k}=\mathrm{\Delta }{\mathit{k}}_P+{\mathit{K}}_D,$$ 2.4

where Δk is the k-vector mistmatch between the generated and propagating harmonic wave, Δk_P is the propagation mismatch of the fundamental wave and the harmonic wave, and K_D is the effective k-vector of the intensity-dependent dipole phase. The Δk_P term is the familiar term from perturbative nonlinear optics, accounting for the different phase velocities in the medium of the fundamental and harmonic waves. If the fundamental propagates with k-vector k(ω₀) and the harmonic with k-vector k(ω) then, as a delay in the fundamental of ϕ is a delay of (ω/ω₀)ϕ = qϕ for the harmonic, Δk_P = k(ω₀) − qk(ω). This contribution can be expressed as a sum of the contributions from the neutral gas, plasma and geometric terms, Δk_P = Δk_n + Δk_p + Δk_g [4]. The neutral gas term is given by Δk_n ≈ (1 − η)Pω/(c[n(ω) − n(ω₀)]), where η is the ionization fraction of the medium, P is the pressure and n is its refractive index. The plasma term is given by Δk_p ≈ 2πcr_ePN_aηω/ω₀, where r_e is the classical electron radius and N_a is the number density at unit pressure. Finally, the geometric phase term comes from a change in driving laser phase throughout the focus, and is given by Δk_g = (ω/ω₀)∇arg[E(ω₀)], where the planewave component is neglected. For a Gaussian beam, this is the gradient of the Gouy phase through the focus. The last term in equation (2.4) is the intensity-dependent dipole phase, unique to HHG. Because the intensity of the laser varies throughout the beam, so does the harmonic phase as described in equation (2.3). This phase variation can be described by an effective k-vector K_D = ∇ϕ(ω, I(r)). The complex interplay between the neutral gas dispersion, plasma, geometric phase and dipole phase terms can lead to regions of low Δk and efficient build-up of harmonic radiation.

HHG is often considered in the low ionization limit, where the laser is weakly disturbed by the nonlinear propagation in the medium. This has enabled various guiding principles to be developed for XUV HHG, such as the optimizing of the harmonic flux by positioning the gas target downstream from the laser focus [3]. For waveguides, the geometric phase term is given by the waveguide dispersion and, because in this limit the beam propagates without changing, the intensity-dependent phase can be ignored. The problem is then static, and an optimal phasematching pressure and ionization fraction, which vary with the driving wavelength, can be determined [4]. Using a specific model for the ionization rate, the maximum photon energy that can be phasematched effectively can then be estimated [26].

We can attempt to use the low ionization limit to treat the wavelength scaling of HHG phasematching. We start from equation (2.4) and consider a Gaussian beam. On-axis at the focus of a Gaussian beam, the intensity is at a maximum and so the intensity-dependent phase term vanishes i.e. K_D∝∇I = 0. The geometric phase is given by Δk_g = − (ω/ω₀)z⁻¹_R, where z_R = πw²₀/λ is the Rayleigh range and w₀ is the beam waist. Setting the phase mismatch Δk = 0 in equation (2.4) and expanding gives

$$\mathrm{\Delta }{\mathit{k}}_n+\mathrm{\Delta }{\mathit{k}}_p+\mathrm{\Delta }{\mathit{k}}_g+{\mathit{K}}_D=2\pi c{r}_{e}P{N}_a\eta \frac{\omega }{{\omega }_0}+(1-\eta )P\frac{\omega }{c}[n(\omega )-n({\omega }_0)]-\left(\frac{\omega }{z_R{\omega }_0}\right)=0.$$

We can isolate the pressure that phasematches as

$$P_{\mathrm{PM}}=\frac{{\mathrm{\lambda }}^2}{\pi w_0^2[2\pi (1-\eta )(n(\omega )-n({\omega }_0))-2\pi r_e{N}_a\eta {\mathrm{\lambda }}^2]}.$$ 2.5

The phasematching pressure will thus scale as higher than λ². At some critical ionization fraction η_c, the denominator is zero and the phasematching pressure diverges. The maximum harmonic flux will occur at this point, where the number of contributing emitters is maximized while maintaining the Δk = 0 condition, with higher pressures compensating the increased effect of the plasma refractive index for longer wavelengths. The critical ionization fraction scales approximately as η_c∝λ⁻², as can be seen by examining the denominator. Because tunnel ionization rates are only weakly wavelength dependent, the critical ionization fraction thus forces the use of lower intensities when using longer driving wavelengths. This line of reasoning assumes low density and minimal distortion of the driving laser field. However, the nonlinear distortion of the driving laser depends only on the plasma refractive index which increases with both increasing pressure and wavelength, scaling as $|\mathrm{\Delta }n|\propto \mathrm{\lambda }\sqrt{P\eta }$. Even considering operation at the critical plasma density η = η_c , which already decreases with longer driving wavelength to achieve longitudinal phasematching, the plasma term still scales as |Δn|∝λ. This means that with increasing driving wavelength, the increasing effect of the plasma upon the driving field is not compensated by the decreasing ionization fraction, and the driving field will be increasingly distorted [21]. Simultaneously, the intensity-dependent dipole phase (scaling as λ³), which is not considered in this simple model, means that even small fluctuations in intensity will result in large changes in the phase and break the phasematching condition at long wavelengths. Thus working in the low ionization limit, and the associated slow build-up of the harmonics over an extended distance, becomes less appropriate as the driving wavelength is longer.

We have recently introduced an alternative approach in which much higher intensities and pressures are used to generate soft X-ray harmonics [21]. In this new regime, which we dub overdriven, the driving laser generates a high-density plasma (up to 10% ionization fraction) which strongly defocuses and distorts the driving laser field. This strong defocusing leads to rapid variation in the geometric, plasma and intensity-dependent dipole phase terms [27]. These strong gradients lead to regions of transient spatio-temporal phasematching and rapid build-up of the harmonic radiation over distances of only a hundred microns. While SXR HHG with comparable flux is likely possible in the conventional limit, almost all previous demonstrations of SXR harmonic generation have been done with high pressures and intensities, meaning operation in the overdriven limit is ubiquitous and practical, even if the responsible physics has only recently been realized [11,16,20]. Understanding this new regime is then key to further improvements in the practical generation of SXR attosecond pulses with HHG, and we examine phasematching in this regime in more detail now.

3. Phasematching of soft X-ray high harmonic generation

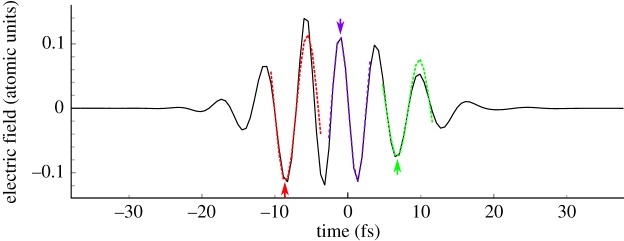
To examine the phasematching of SXR HHG, we have adopted the approach from Chipperfield et al. [31] and calculated the k-vector mismatch throughout the focus. We simulated the propagation of the fundamental using the forward Maxwell equation in three dimensions with cylindrical symmetry, and including the full χ⁽³⁾ nonlinearity with self steepening. Ionization was included through the Ammosov, Delone and Krainov ionization rate.¹ We then resampled the simulation finely around the focus and fit each half cycle with a cosine field using the instantaneous peak field and frequency at the peak of the half cycle; an example of such fits to three half-cycles is shown in figure 2 for a laser field at the centre of the target which has been strongly reshaped by ionization. Such a decomposition allows us to consider phasematching for each half-cycle of the driving laser field separately, examining the sub-cycle temporal gating of the phasematching, by calculating the dipole phase at each point using equation (2.2) with birth and recombination times found from the classical electron trajectories for a cosine field. We neglect sub-cycle or inter-cycle deformation effects for the harmonic trajectories² but our approach does capture slower cycle-to-cycle variation. The wavevector mismatch is extracted directly from the gradient of the propagated field without division into the constituent neutral gas, plasma and geometric terms. We consider pulses at 1.8 μm central wavelength, 550 μJ energy and 12 fs FWHM pulse duration to facilitate comparison with recent experiments [20,21].

Figure 2.

Laser field intensity on axis at the centre of the harmonic target for a pulse of 550 μJ and CEP = 0 focused 1.4 mm after the target, which is filled with 2 bar of helium. Fits to three different half-cycles are also shown (coloured dashed lines), where the half-cycle used for the fit is indicated by the coloured arrow. The three half-cycles correspond to timings of −9 fs, 0 fs and 9 fs at the entrance of the medium. Plasma-induced blue-shifts cause deviation between the fits and the underlying driving field at times after the fitted peak; for looser focusing or driving pulse energies, the quality of the fit over larger time spans improves. (Online version in colour.)

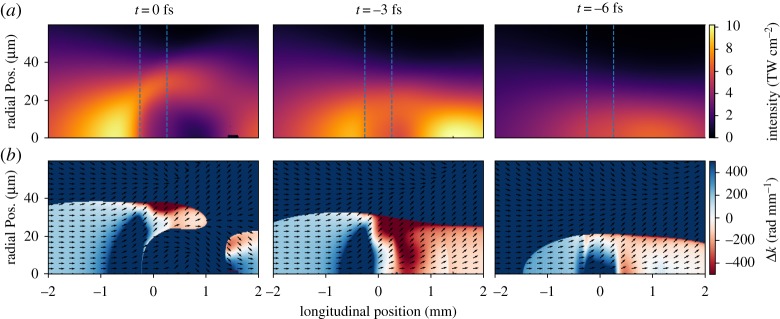
Figure 3 shows the instantaneous-intensity distribution (∝|E|²) through the focus for the three most important half-cycles (top row) and the corresponding phasematching maps for the short-trajectory (bottom row). The time of each half-cycle relative to the field envelope prior to propagation is indicated above; negative times indicate half-cycles before the peak of the field. Inset arrows show the direction in which phasematching is locally satisfied; this angle has been exaggerated such that 45° corresponds to 10 mrad divergence, approximately the maximum angle detectable by our soft X-ray flat-field spectrometer [32]. The phasematching maps are furthermore clipped to the region where the intensity is high enough that harmonics at 350 eV are emitted. There are pronounced differences in the evolution and phasematching maps between the three adjacent half-cycles caused by the build-up of free electrons from one half-cycle to the next, with the effects of plasma lensing readily apparent in the later half-cycles. Regions of phasematching (Δk = 0) can be observed for each case, but they move to increasingly off-axis as the plasma density increases. More importantly, the direction of phasematching changes greatly between the three half-cycles; while the half-cycle at −3 fs has the phasematching condition satisfied on-axis and with a low divergence, the half-cycle at −6 fs has the phasematching condition satisfied in a strongly off-axis direction, meaning the harmonic flux contribution at the detector will be minimal despite the fact that, locally, the ‘quality’ of the phasematching is clearly comparable between the three cases. While phasematching being satisfied in regions away from the central axis is not generally a problem, as the virtual source position is before the harmonic target and thus these contributions can be re-focused to a common point [21], phasematching in the off-axis direction is more problematic as it means the harmonic radiation cannot be recaptured and will usually have a spread of virtual source positions.

Figure 3.

(a) Peak intensity and (b) short-trajectory phasematching maps for the three most important half-cycles (columns) for 350 eV photon emission from 4 bar of helium when a pulse of 550 μJ and CEP = 0.3π is focused 1.4 mm after the target. The corresponding times of the half-cycles relative to the driving field envelope before the target are indicated above, and the dashed blue lines indicate the extent of the gas target. (Online version in colour.)

That the best on-axis phasematching occurs for the −3 fs half-cycle is in agreement with previous full-dimensional HHG calculations [21], as is the relatively short distance (a few hundred micrometres) over which the phasematching condition is satisfied, though quantitative agreement is neither seen nor expected at this level of theory. We can see the transient nature of the phasematching condition very clearly in both the spatially limited extent of the build-up and in the strong half-cycle to half-cycle variation. These maps also strongly suggest that harmonics generated off-axis in the focus are very important for the final harmonic yield, as in the last half-cycle shown it is clear there will be no harmonics generated on-axis. This emphasizes the importance of considering the full spatio-temporal evolution of driving pulses for soft X-ray harmonic generation, and that one-dimensional models will lead to erroneous results.

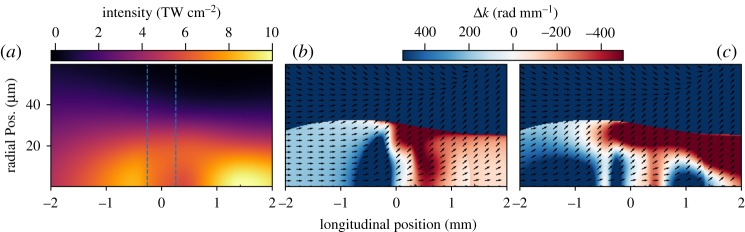
A somewhat surprising result occurs when examining the relative contributions of the long and short trajectories in the overdriven limit. Figure 4 shows the half-cycle at −3 fs from figure 4 along with the phasematching maps for the harmonic emission from the short and long trajectories, which vary through the intensity dependence of the atomic dipole phase. In contrast to expectation from scaling laws, we can see there are good regions of phasematching for both the short and long trajectories, and that the harmonic emission from the long trajectory is similarly emitted at low divergence. Owing to computational limitations, the long-trajectory contribution was neglected in earlier full-HHG simulations [21], but these results suggest that long trajectories may have a significant role for HHG in the soft X-ray region. It is worth noting that this is not a result of the emission coming from regions where the intensity is low enough that 350 eV is near the cut-off frequency and the short and long trajectories coalesce; the long trajectories phasematch both in this region and further away from the cut-off. This can be clearly seen in that there are actually distinct phasematching regions in the long trajectory map where there is no corresponding phasematching for the short trajectories. The long trajectory phasematching can be understood as a consequence of the numerous strong gradients present in the overdriven limit; while in the conventional HHG limit, the smoothly decaying radial profile leads to long trajectories being phasematched with higher wavefront curvature and emitting more off-axis than the short trajectories, this does not hold for the more complex spatio-temporal distribution here. Strong plasma effects can lead to greater variation in the driving laser field, which can actually be phasematched by having a larger intensity-dependent gradient. As a result, regions can be found that satisfy the conditions for long-trajectory phasematching, even on-axis, though we note the phasematching is still over a short longitudinal distance. Note that the relative weighting of the short and long trajectories may be heavily modified by sub-cycle deformations of the driving field (figure 2), which is not captured here. Near the cut-off, where attosecond pulses are generally produced, these contributions coalesce, and so the production of isolated attosecond pulses should not be impeded by this effect.

Figure 4.

Peak intensity (a) and phasematching maps for the short (b) and long (c) trajectories for harmonic emission at 350 eV from the half-cycle cut-off at −3 fs, under identical conditions as in figure 3. (Online version in colour.)

This ties in strongly to the idea of non-adiabatic phasematching, first proposed by Tempea et al. [33]. The sub-cycle deformation of a driving laser field caused by the plasma-induced blueshift can lead to bright harmonic emission at photon energies much higher than predicted from adiabatic models. Figure 2 shows a clear half-cycle to half-cycle blueshift for the leading half-cycles, exactly those that are found to result in the best phasematching both here (figure 3) and for full propagation simulations [21]. Because non-adiabatic phasematching results primarily from the changing return-times throughout the medium because of the increasing blueshift, it should impact the short and long trajectories significantly differently. Thus if non-adiabatic effects are important (as they appear to be), they will apply another filter effect, enhancing either the short or long trajectories. Non-adiabatic effects have been shown to dramatically decrease the effectiveness of quasi-phasematching schemes [34]. As in the overdriven limit, the harmonic flux is strongly phasematching limited; this suggests alternative routes, like the shaping of gas-density profiles and spatio-temporal shaping of the driving pulses, should be explored to further increase the coherence length and the harmonic flux. Though these techniques are challenging, they could afford increases in conversion efficiency of several orders of magnitude.

4. Outlook: towards attosecond soft X-ray spectroscopy

Recent advances in SXR HHG have seen the first water window attosecond pulses [11,18], first time-resolved water window spectroscopy [16,17] and the complete spanning of the water-window [20,21], all in the last 4 years. This is far from the end of the story, and we can expect to see a variety of advances in the near future, in both source development and spectroscopy. The attosecond temporal nature of these sources has yet to be exploited; while the broad bandwidths have been exploited for extended X-ray absorption fine structure spectroscopy [15], only femtosecond time-resolution measurements have been performed. With a number of theoretical proposals suggesting that atto-XANES measurements could be ideal probes for ultrafast dynamics [35], including charge migration, this is a clear future frontier. Additionally, time-resolved measurements with SXR HHG sources have so far been limited to the gas phase; the application to both the solid and liquid phase is soon to follow, with a number of groups having already demonstrated static XANES in solid samples [13–15], while others are developing vacuum compatible thin liquid-jet targets for the application of SXR spectroscopy to liquids [36]. In principle, the current generation of harmonic sources are now ready to start examining problems like the metal-insulator transition in vanadium oxides, charge transfer in small organic molecules, and strong-field-driven dynamics inside materials; though challenging, fluxes are also high enough to perform surface-science experiments, even after monochromation if narrowband excitation is preferable. Recent guides to the development of few-cycle sources for SXR HHG [10], and of apparatus for the generation and detection of SXR HHG [32], will help the proliferation of SXR sources and time-resolved XANES spectroscopy.

But, there is certainly still significant room for improvement in regard to the flux of SXR HHG sources. Some applications, which are probably beyond the reach of the current generation of harmonic sources, include X-ray holography and two-photon absorption spectroscopy. The outlook is encouraging on this front as well though, as the impressive results obtained so far have, with few exceptions, been driven by relatively modest laser systems, with repetition rates of 1 kHz or below and pulse energies around 0.5 mJ. There would appear to be no barrier to further improvement to repetition rates tens to hundreds of times higher, and pulse energies an order of magnitude higher, suggesting harmonic fluxes of one to three orders of magnitude higher (around 10⁹ photons s⁻¹/1%BW) without any further improvements in harmonic conversion efficiency. Such high fluxes have proved sufficient for diffraction-limited holographic imaging in the XUV [37]. Though the flux required to reach the diffraction limit increases as the wavelength decreases, the elemental, bond and magnetic sensitivity of SXR absorption make even non-diffraction limited SXR holography very valuable, for instance in imaging phase co-existence [38]. Holography and other coherent diffraction imaging schemes will be a key application for the next-generation SXR HHG sources. Looking further ahead, we have some reason to be optimistic even for the possibility of nonlinear optics with SXR HHG sources. Current sources reach pulse durations of down to ≈50 as [11], with pulse energies of tens of picojoules and excellent spatio-spectral properties [21]. Assuming focusing to a 1 μm spot size and increase in pulse energy of 100 times (accounting for increased driving pulse energies and conversion efficiencies), an attosecond pulse of intensity ≈ 1 × 10¹⁸ W cm⁻² could be delivered to experiments—this is comparable to the first-generation XFEL sources, and sufficient to drive nonlinear optics in the SXR [39].

We have presented here a discussion of attosecond pulse generation from SXR HHG. We have discussed single-atom scaling laws, the key physics for phasematching, and illustrated why the development of few-cycle driving lasers at longer wavelengths (greater than 1.5 μm) has been the key to the rapid improvements in SXR attosecond sources in the last 4 years. We have examined the overdriven limit for SXR HHG in detail, showing that the strong plasma-defocusing induced when a long wavelength, high-intensity laser is focused into a high-density gas target leads to transient phasematching conditions in space and time. We see that the phasematching condition is satisfied in very different regions for different half-cycles within the driving pulse, generally being restricted to only a small number of half-cycles, giving naturally temporally confined harmonic pulses. There are significant phasematched contributions from regions away from the central axis, emphasizing the importance of full spatio-temporal considerations in SXR HHG. The unexpected phasematching of long-trajectory contributions along with plasma-induced blueshifts suggests that non-adiabatic effects may be important in the overdriven regime, and that gas-density engineering and spatio-temporal shaping of the driving pulse are promising routes to further improvements in conversion efficiency. Finally, we discuss some applications for SXR attosecond sources in the near future, along with next-generation sources and their potential extension to X-ray holography and nonlinear optics. SXR attosecond HHG sources may be in their infancy, but there is a clear and promising future ahead.

Data accessibility

The datasets supporting this article have been uploaded as electronic supplementary material.

Authors' contributions

A.S.J. and T.A. carried out and analysed the simulations; D.R.A. wrote the simulation code; all authors contributed to the interpretation of the results and to the writing of the article.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by EPSRC grant nos. EP/I032517/1 and EP/R019509/1, ERC ASTEX project no. 290467, and EPSRC/DSTL MURI EP/N018680/1. D.R.A. acknowledges support from the Imperial College JRF scheme. A.S.J. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness through the ‘Severo Ochoa’ program for Centres of Excellence in R&D (SEV-2015-0522), from Fundaci Privada Cellex, and from the Generalitat de Catalunya through the CERCA program.