Optoelectronic Properties of Ternary I–III–VI₂ Semiconductor Nanocrystals: Bright Prospects with Elusive Origins

Abstract

Colloidal nanocrystals of ternary I–III–VI₂ semiconductors are emerging as promising alternatives to Cd- and Pb-chalcogenide nanocrystals because of their inherently lower toxicity, while still offering widely tunable photoluminescence. These properties make them promising materials for a variety of applications. However, the realization of their full potential has been hindered by both their underdeveloped synthesis and the poor understanding of their optoelectronic properties, whose origins are still under intense debate. In this Perspective, we provide novel insights on the latter aspect by critically discussing the accumulated body of knowledge on I–III–VI₂ nanocrystals. From our analysis, we conclude that the luminescence in these nanomaterials most likely originates from the radiative recombination of a delocalized conduction band electron with a hole localized at the group-I cation, which results in broad bandwidths, large Stokes shifts, and long exciton lifetimes. Finally, we highlight the remaining open questions and propose experiments to address them.

Colloidal semiconductor nanocrystals (NCs) exhibit size- and shape-dependent optoelectronic properties, combined with easy solution processability and surface functionalization.¹ This makes them promising materials for many applications, such as solution-processed solar cells,^2,3 luminescent solar concentrators,² low-threshold lasers,² light-emitting and optoelectronic devices,^2,4,5 photodetectors,^4,6 and biomedical imaging.⁷ Many of these applications have already been realized using Cd- and Pb-chalcogenide based NCs (e.g., CdSe quantum dots in displays⁸ or PbS colloidal quantum dot solar cells with certified power conversion efficiency of 12.01%³), because control over these NCs has reached a very mature level, owing to several decades of extensive research. However, the widespread deployment of these NCs is severely limited by the intrinsic toxicity of Cd and Pb. This has motivated a worldwide research effort on alternative materials based on non- (or less) toxic elements.

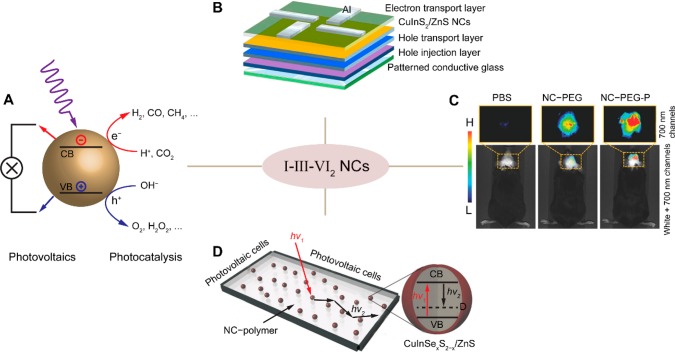
Ternary I–III–VI₂ (I = Cu⁺, Ag⁺; III = Al³⁺, Ga³⁺, In³⁺; VI = S^2–, Se^2–, Te^2–) NCs are emerging as promising alternatives to Cd- and Pb-chalcogenide-based NCs because of their inherently lower toxicity. They offer wide photoluminescence tunability, spanning a spectral window that extends from the visible to the second near-infrared (NIR) biological window (470–1200 nm), depending on the composition and size of the nanocrystals.⁹⁻¹² Moreover, they also offer characteristics that are unmatched by Cd- and Pb-chalcogenide NCs, such as large global Stokes shifts and plasmonic properties.⁹⁻¹¹ We use the term “global Stokes shift” here, because the more conventional term “Stokes shift” describes the energy difference between absorption and emission energy of the same electronic transition. As we will discuss below, the electronic states dominating the absorption and emission spectra are (most likely) not the same for I–III–VI₂ NCs. The promising emission properties of I–III–VI₂ NCs may allow them to challenge the performance of the established class of Cd- and Pb-chalcogenide-based NCs in a wide range of applications, such as quantum dot-sensitized solar cells, light-emitting devices, and biomedical applications (Figure 1A–C).^10,13−16 They also show promise as photocatalysts, for example for H₂ evolution¹⁷ or CO₂ conversion¹⁸ (Figure 1A). Moreover, their large global Stokes shifts and tunable absorption and emission spectra make them ideally suited as luminophores for luminescent solar concentrators, as recently demonstrated by several groups (Figure 1D).¹⁹⁻²⁵

Figure 1.

(A) Schematic illustration of solar light-driven photovoltaics and photocatalysis using semiconductor nanocrystals (the valence and conduction bands are indicated as VB and CB, respectively). Adapted from ref (14). Copyright 2017 American Chemical Society. (B) Device schematic of a multilayered CuInS₂/ZnS NC light-emitting diode. The emitting layer of CuInS₂/ZnS NCs is sandwiched between an organic hole transport layer and an inorganic electron transport layer of ZnO NCs. Reproduced from ref (26). Copyright 2016 American Chemical Society. (C) Intravital whole-body fluorescence imaging (dorsal view) of brain tumor-bearing mice injected with a buffer solution (PBS), water-soluble PEGylated CuInSe₂/ZnS NCs (NC-PEG), or a NC-PEG-P conjugated to a tumor-specific vascular homing peptide. Adapted from ref (27). (D) Schematic diagram of a neutral-density luminescent solar concentrator composed of a polymer matrix incorporating CuInSe₂/ZnS NCs. The cartoon on the right shows a simplified picture of the band-edge electronic states in CuIn(S,Se)₂/ZnS NCs that are responsible for light emission and absorption. The band-edge absorption transition is shown by the red arrow, while the black arrow indicates the strongly Stokes-shifted emission transition. Adapted from ref (19).

However, the realization of the full potential of colloidal I–III–VI₂ NCs has been hindered both by their underdeveloped synthesis, which has yet to reach the same level of mastery achieved for the prototypical Cd- and Pb-chalcogenide NCs, and by the poor understanding of their optoelectronic properties, whose origins are still under intense debate. In this Perspective, we provide novel insights on the latter aspect by reviewing and critically discussing the accumulated body of knowledge on the optoelectronic properties of I–III–VI₂ NCs, with particular emphasis on recent experimental and theoretical developments. We focus on CuInS₂ NCs as a representative example, because CuInS₂ is the most thoroughly investigated I–III–VI₂ semiconductor, both at the bulk level and on the nanoscale. For the sake of conciseness, the synthesis of these nanomaterials is not addressed, but instead we refer the reader to recent reviews on the subject⁹⁻¹² and, when necessary, to recent works clarifying aspects that are relevant to the understanding of the optoelectronic properties of colloidal CuInS₂ NCs.

Colloidal NCs of I–III–VI₂ semiconductors differ in many fundamental ways from those of II–VI and IV–VI semiconductors. Some of these differences are already present at the bulk level, while others become evident only at the nanoscale. The analysis of these differences provides insights that are instrumental in understanding the origins of the optical properties of I–III–VI₂ NCs. Therefore, we start this Perspective by comparing bulk I–III–VI₂ semiconductors with their II–VI counterparts and subsequently address the impact of the nanoscale on both CuInS₂, as the most investigated member of the I–III–VI₂ family, and CdSe, as a prototypical representative of the II–VI family and the best-understood colloidal semiconductor NC to date. We then present and critically examine the different models proposed to explain the optical properties of CuInS₂ NCs. From our analysis, we conclude that the luminescence in these nanomaterials most likely originates from the radiative recombination of a delocalized conduction band electron with a hole localized at a Cu⁺ ion, and thus, we dedicate the final part of this Perspective to discuss recent experiments attempting to shed light on the nature of this process. Finally, we highlight the remaining open questions and propose experiments to answer them.

Bulk Structure, Composition, and Defect Chemistry. Most bulk I–III–VI₂ materials crystallize in the chalcopyrite crystal structure.⁹⁻¹¹ Ternary chalcopyrite I–III–VI₂ semiconductors can be seen as isoelectronic analogues of the binary zinc-blende II–VI semiconductors, because the former structure is derived from the latter by doubling the unit cell and replacing every two group-II cations by one group-I and one group-III cations, so that each group-VI anion is tetrahedrally coordinated by two group-II and two group-III cations, and each cation is tetrahedrally coordinated by four anions (Figure 2).^28,29 The ordered distribution of the group-I and group-III cations is favored over random distributions because this ensures that every anion has 4 tetrahedral bonds with 2 electrons per bond, thereby satisfying the valence-octet rule.³⁰ However, the chemical disparity between the group-I and the group-III cations induces that, compared to the zinc-blende structure, the unit cell is tetragonally distorted and hence the space symmetry is lowered from T_d² (cubic) to D_2d¹² (tetragonal), and the anions are displaced from the ideal tetrahedral site.^28,29 It should be noted that both families of semiconductors can also adopt the wurtzite structure, in which the anionic sublattice follows a hexagonal close packing, instead of the cubic close packing (face-centered cubic) characteristic of the zinc-blende structure. The wurtzite structure is a metastable, high-temperature phase for most II–VI and I–III–VI₂ compounds (including CuInS₂), with the important exception of CdSe, which adopts the wurtzite structure under normal conditions. The anions and cations are tetrahedrally coordinated in both structures, and therefore, the changes induced by the chemical disparity between the group-I and group-III cations also hold for wurtzite I–III–VI₂. Interestingly, wurtzite I–III–VI₂ crystals have been recently shown to accommodate multiple domains with distinct ordering patterns within one uninterrupted, coherent anion sublattice, with strain-free, defect-free interdomain boundaries.³⁰

Figure 2.

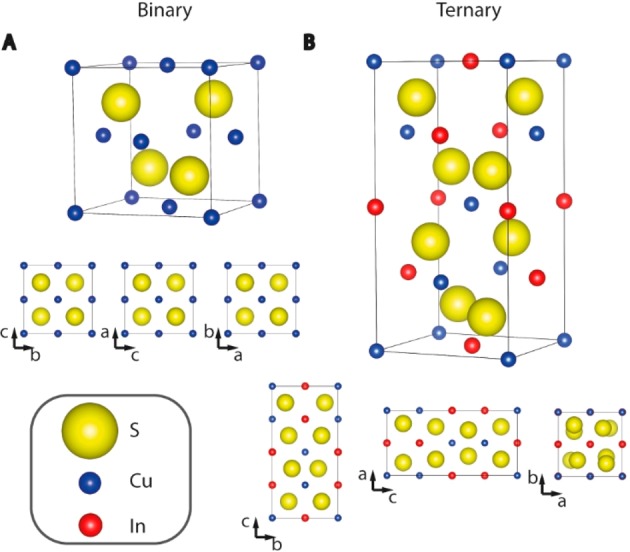
Schematic representation of the binary zinc blende unit cell (A) and its ternary analogue chalcopyrite (B). Representations of the crystal structures are made with the program Vesta.³¹

The structural and chemical dissimilarities between I–III–VI₂ semiconductors and their binary II–VI analogues lead to several important differences. The most evident of these differences is that the latter do not accommodate significant off-stoichiometry (at most 5 × 10^–4 atom % for both CdSe and CdTe),³² while the former can readily deviate from the ideal I–III–VI₂ stoichiometry by several percentage points, both in the ratio between the group-I and group-III cations and in the anion/cation ratio.³³⁻³⁶ Consequently, bulk I–III–VI₂ materials have a rich defect chemistry, which allows their growth as both n-type and p-type semiconductors without resorting to any extrinsic dopant, by simply making use of native point defects (e.g., vacancies such as V_Cu^–, V_In^3–, V_S²⁺, and antisites such as In_Cu²⁺ or Cu_In^2– in CuInS₂).³³⁻³⁶ In contrast, only very limited carrier excesses can be achieved in bulk II–VI materials by using native defects (typically dominated by neutral Frenkel pairs, i.e., a cation vacancy associated with a cation interstitial, II_i²⁺–V_II^2–, and charged defects such as VI_II antisites, cation vacancies, and interstitials).³⁷ The difference in the defect chemistry of these two semiconductor families is due to the fact that the formation energies of native defects are much lower in ternary I–III–VI₂ compounds than in the binary II–VI analogues (e.g., <2 eV for CuInSe₂ and ≥6 eV for ZnSe),^33,35,37 being particularly low for electrically neutral defect pairs such as (2 V_Cu^1– + In_Cu²⁺) and (2 Cu_In^2– + In_Cu²⁺) (viz., −1.46 eV, under optimal chemical potential).³³ In addition, interactions between different defect pairs further lowers their formation energy, thus making periodic defect structures energetically favorable.³³ The lower formation energy of defects in I–III–VI₂ compounds also impacts on the solid-state diffusion rates in these materials, which are much higher than in II–VI semiconductors. For example, the Cu⁺ self-diffusion rate in bulk CuInS₂ single crystals at 100 °C is 3 × 10^–13 cm² s^–1 (as determined from the line width of the ⁶³Cu NMR line),³⁸ while that of Cd²⁺ in CdSe at the same temperature is only ∼2 × 10^–19 cm² s^–1 (extrapolated from the diffusion coefficients determined in the 550–880 °C range).³⁹

Bulk Electronic Structure. Another critical difference between ternary I–III–VI₂ and binary II–VI compounds is the nature of their electronic structure. In II–VI semiconductors, the valence band is formed mainly by the p orbitals of the group VI element, while the conduction band is formed by the s orbitals of the group-II element.²⁸ Therefore, the valence band to conduction band transition is essentially an interatomic transition, which can be seen as akin to a “ligand to metal charge-transfer” transition. In contrast, the upper valence band of chalcopyrite I–III–VI₂ compounds is formed by p–d hybridization of the d orbitals of the group-I element and the p orbitals of the group-VI element, whereas the lower conduction band is formed by the s orbitals of the group-III element, with a small contribution of the s orbitals of the group-I element and a significant contribution of p orbitals of the group-VI element (the antibonding combinations from the p–d hybridization).^28,29,35,40 In the specific case of CuInS₂, the Cu(3d) orbitals contribute 45–60% to the valence band maximum.²⁸ Furthermore, the Cu–S bond is covalent but highly polar (i.e., excess electron density on the S site), while the In–S interaction appears nonbonding.²⁸ Interestingly, the transition from the valence band maximum to the conduction band minimum couples states that have a considerable amplitude on the same anion sublattice site (and to a lesser extent also on the same Cu site).^28,40 The transition has thus a partial intra-atomic character and is akin to a highest occupied molecular orbital–lowest unoccupied molecular orbital (HOMO–LUMO) transition in which the HOMO is a Cu(3d)–S(3p) bonding orbital and the LUMO is an In(5s)–S(3p) nonbonding orbital (i.e., to a certain extent a “metal to metal charge-transfer” transition between the group-I and group-III metals), with some Cu d–s character. The d–s contribution increases for higher-energy transitions because the Cu(3d) character reaches 90% at about −2 eV below the valence band maximum,^28,35 while the contribution of Cu(4s) to the conduction band increases with increasing energy.³⁵ The strong one-center character of the valence band maximum to conduction band minimum transition explains the anomalously low temperature dependence of the band gap of ternary I–III–VI₂ chalcopyrites, despite their normal thermal expansion coefficient.⁴⁰

Bulk Optical Spectra. Despite the fundamental differences between bulk I–III–VI₂ and II–VI semiconductors discussed above, their emission spectra are similar in nature, in the sense that they are both dominated by defect-assisted recombination, which is characterized by weak and sharp near band-edge lines accompanied by stronger and broader features at lower energies (Figure 3). This is typical for bulk intrinsic semiconductors and results from a combination of small exciton binding energies (at most a few tens of millielectronvolts), due to the effective dielectric screening of the electron–hole Coulomb interaction, and high carrier mobilities, which leads to exciton dissociation followed by trapping of the photogenerated carriers at native defects or adventitious impurities.⁴¹

Figure 3.

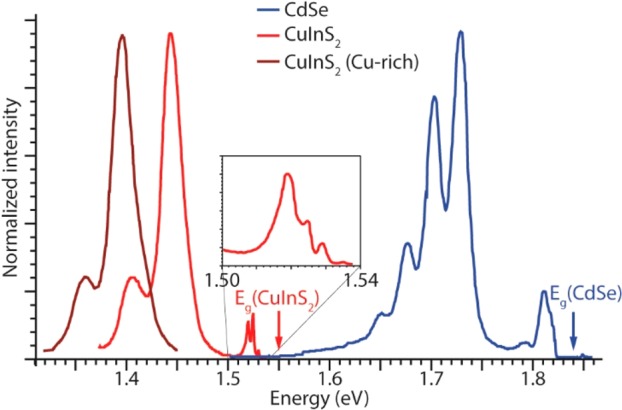
Emission spectra of bulk CdSe (blue),⁴² CuInS₂ (red),^34,43 and Cu-rich CuInS₂ (brown)^34,43 single crystals at 4.2 K. The inset shows a zoom-in of the near-edge emission peaks of CuInS₂. For clarity, the near-edge emission region and all features above 1.45 eV are omitted in the spectrum of Cu-rich CuInS₂ (see text for details). The spectra were adapted from refs (34, 42, and 43).

The highest-energy emission line in the spectrum of bulk wurtzite CdSe is observed at 1.823 eV (Figure 3). This line is shifted from the bulk band gap energy (1.838 eV at 4.2 K) by the exciton binding energy (15 meV)⁴⁴ and has been assigned to radiative recombination of the free exciton (or Wannier exciton, i.e., an electron–hole pair bound by the Coulomb interaction).⁴² The free-exciton emission line is followed by a number of poorly resolved and weak lines around 1.81 eV (ascribed to excitons bound to defects or impurities)⁴² and a series of five equally spaced lines, the first of which at 1.73 eV with full width at half-maximum (fwhm) of 20 meV (Figure 3). The energy separation between these lines corresponds well to the LO-phonon frequency of CdSe (viz., 25 meV), and therefore, they were ascribed to a LO-phonon replica progression (zero-phonon line at 1.73 eV) originating from a donor–acceptor pair recombination.⁴² The donor and acceptor involved in this transition were not identified in the original work,⁴² but most likely they are related to Cd vacancies (acceptors) and Cd interstitials (donors), because Frenkel pairs (V_Cd–Cd_i) are the most common native defects in II–VI materials, as discussed above.^37,39

The emission of bulk CuInS₂ single crystals was studied in detail in the 1980s by several groups, most notably by Bloem and co-workers (Figure 3)^34,43 and has also been recently revisited by Mudryi et al. using higher-quality single crystals, which allowed investigation up to room temperature, while corroborating the essential findings reported in the earlier works.⁴⁵ The free-exciton emission line is observed at 1.535 eV at 4.2 K, with a fwhm of 1.6 meV.^34,43,45 The exciton binding energy depends slightly on the composition: 18.5 meV for In-rich and 19.7 meV for stoichiometric CuInS₂.⁴⁵ The line width of the free-exciton emission is strongly temperature-dependent, being essentially constant up to 40 K (2 meV), and then increasing to 7 meV at 78 K, 26 meV at 160 K, and 60 meV at room temperature.^34,43,45 Moreover, the emission intensity is strongly reduced upon increasing the temperature (3 orders of magnitude from 4.2 to 120 K), but its spectral position hardly changes with temperature,^34,43,45 because of the very weak temperature dependence of the band gap of CuInS₂, as discussed above.⁴⁰ Besides the free-exciton emission line, the near band-edge emission region (1.50–1.54 eV, inset in Figure 3) also shows another 4 sharp lines at slightly lower energies, which were ascribed to bound-exciton emission.⁴³ The broader line at 1.520 eV (fwhm 2–12 meV, depending on the composition of the crystal) was ascribed to donor-to-valence band transition.⁴³ The stronger and broader (fwhm ∼23 meV) bands at lower energy (1.45 eV for CuInS₂ and 1.40 eV for Cu-rich CuInS₂) were ascribed to donor–acceptor pair recombination, with the strongest band being assigned to recombination from the same donor level to different acceptor levels, and the weaker band originates from deeper donor levels to the same acceptor level.³⁴

Impact of the Nanoscale on the Optoelectronic Properties of CdSe and CuInS₂. As discussed above, there are a number of structural differences between bulk I–III–VI₂ and II–VI semiconductors. Nevertheless, these differences are not clearly manifested in their emission spectra, which are dominated by defect-assisted recombination in both cases. In the following, we will show that this is no longer the case on the nanoscale, which has a strong impact on both classes of materials and reveals the full extent of the fundamental disparities between them (Figure 4).

Figure 4.

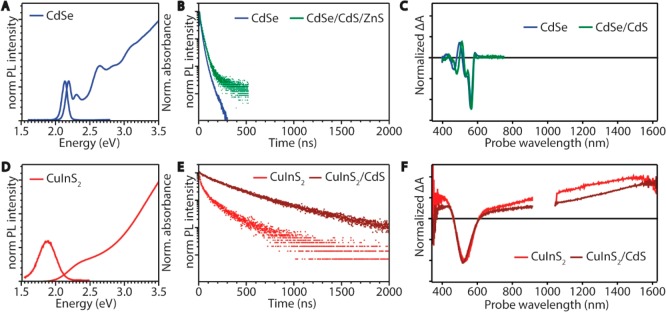
Optical properties of colloidal CdSe and CuInS₂ nanocrystals. (A) Absorption and emission spectra of 4.4 nm diameter CdSe NCs. Data from ref (46). (B) Photoluminescence decay curves of 4.3 nm CdSe (blue) and CdSe/CdS/ZnS core/shell/shell NCs (green). (C) Transient absorption spectra of 4.4 nm CdSe (blue) and 5.2 nm CdSe/CdS core/shell NCs (green). Data from ref (47). (D) Absorption and emission spectra of 2.5 nm CuInS₂ NCs. Data from ref (48). (E) Photoluminescence decay curves of 2.5 nm CuInS₂ NCs (red) and CuInS₂/CdS core/shell (1 monolayer) NCs (brown). Data from ref (48). (F) Transient absorption spectra of 2.5 nm CuInS₂ NCs (red) and CuInS₂/CdS core/shell (1 monolayer) NCs showing negative bleach features and positive photoinduced absorption. Data from ref (48).

The impact of spatial confinement to the nanoscale on the optoelectronic properties of semiconductor nanocrystals is determined by the exciton Bohr radius (a₀) of the material. For NC sizes of approximately a₀ and smaller, the exciton wave function is affected by spatial confinement, which induces size-dependent changes in the density of electronic states and in the energy separation between them.⁴⁹ These changes are manifested in an increase of the band gap and the appearance of discrete energy levels near the band edges with decreasing NC dimensions, making the optoelectronic properties of semiconductor NCs size- and shape-dependent.⁴⁹ The effect is evident in the optical spectra of CdSe NCs with diameters below ∼10 nm (a₀ = 4.9 nm) (Figure 4A–C).⁵⁰ The discrete energy levels give rise to well-defined absorption features (especially near the band-edge) and narrow ensemble emission bands (fwhm 80–150 meV at room temperature for ensembles of CdSe NCs in the 6–2.6 nm diameter range with ≤5–10% size dispersion),⁵¹ which shift to higher energies with decreasing NC size following a 1/d² dependence.⁵⁰ The emission transition (1S_(e) → 1S_3/2(h)) is characterized by small global Stokes shifts (21 ± 4 meV in the 2.6–8 nm diameter range for ensembles with ≤10% size dispersion)⁵¹ and room-temperature radiative decay times of 18–40 ns, depending on the NC size (8 to 2.6 nm).⁵⁰ Transient absorption spectra of CdSe and CdSe/CdS NCs show a clear negative signal due to the bleach of the lowest-energy exciton transition (1S_3/2(h) →1S_(e)) and a small positive signal at somewhat lower energies reflecting biexciton or negative-trion absorption (Figure 4C).⁴⁷

The optical properties of CuInS₂ (and other I–III–VI₂ semiconductors) are also strongly affected by size reduction to the nanoscale but are strikingly different from those of CdSe NCs, as clearly demonstrated by Figure 4. The absorption spectra of CuInS₂ NCs are essentially featureless and do not show a distinct first excitonic peak (Figure 4D).^9,10,52 Furthermore, a low-energy tail extending up to several hundreds of millielectronvolts is often observed.^9,10,52 The lack of clear features in the absorption spectra can be ascribed to broad bandwidths, as indeed recently demonstrated for the lowest-energy exciton transition of both 2.5 nm chalcopyrite CuInS₂ NCs (fwhm = ∼400 meV),⁴⁸ and wurtzite CuInS₂ NCs (fwhm = 320–180 meV in the 2.7–7.2 nm diameter range).⁵³ Broad bandwidths are also observed for the emission of CuInS₂ NCs (fwhm = ∼200–400 meV),^10,48 which is further characterized by large global Stokes shifts (∼300–500 meV) and multiexponential decays with long radiative lifetimes (∼200–400 ns)^{10,48,54−57} (Figure 4D,E). Interestingly, the emission bandwidths and the global Stokes shifts have been reported to be independent of the size, shape, and crystal structure of the CuInS₂ NCs.^53,58 In contrast, the band-edge absorption and the emission peak shift to higher energies with decreasing NC size, following a 1/d-dependence for both chalcopyrite (a₀ = 4.1 nm) and wurtzite CuInS₂ NCs.⁵³ The size-dependence is weaker for wurtzite CuInS₂ because of the larger electron and hole effective masses of this material (viz., m_e = 0.173m₀ and m_h = 2.181m₀ in bulk while those for chalcopyrite CuInS₂ are m_e = 0.16m₀ and m_h = 1.3m₀ in bulk).^53,59 Another important characteristic of CuInS₂ NCs is the observation of two features in their transient absorption spectra: a negative band-edge bleach attributed to the lowest-energy exciton transition (1S_h →1S_e) and a positive photoinduced absorption (Figure 4F).⁴⁸ These features and their significance will be discussed in more detail later in this Perspective.

Impact of Shelling on the Optical Properties of CdSe and CuInS₂ NCs. An effective strategy to enhance the photoluminescence quantum yields (PLQYs) and photostability of colloidal semiconductor NCs is to overcoat them with a shell of a wide band gap semiconductor, thereby confining both the electron and hole in the core material.¹ In this way, surface trap states are passivated, which eliminates nonradiative recombination centers, resulting in longer exciton lifetimes and high PLQYs. The heteroepitaxial overgrowth of a shell of a different semiconductor can also be used to tune the carrier localization regime in the hetero-NC from Type-I (electron and hole in the same material) to Type-II (spatially separated charge carriers) through an intermediate regime (Type-I^1/2, one carrier is delocalized over the whole hetero-NC volume while the other is localized in one of the segments), thereby allowing the exciton radiative lifetimes, exciton–phonon coupling strength, and spectral characteristics (i.e., peak position, bandwidth, and Stokes shift) of colloidal hetero-NCs to be tailored.¹ This has been extensively investigated for hetero-NCs based on Cd-chalcogenides and other II–VI semiconductors and for Pb-chalcogenides,¹ but it is still underdeveloped for I–III–VI₂ NCs.^10,11 Shelling of colloidal NCs is an intricate multivariable chemical process, whose outcome results from a competition between a number of reactions (Figure 5).

Figure 5.

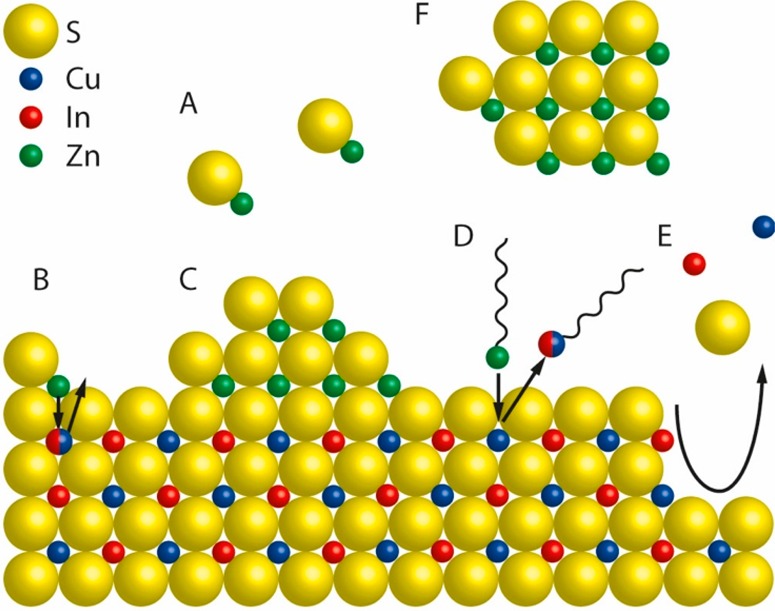
Schematic representation of a nanocrystal surface depicting the chemical processes that can take place during a shelling reaction, taking CuInS₂/ZnS as an example. (A) [ZnS] monomers form homogeneously in solution from Zn- and S-precursors. (B) Alloying. Zn²⁺ from adsorbed [ZnS] monomer units diffuses inward while Cu⁺ and/or In³⁺ ions diffuse outward. (C) Heteroepitaxial shell overgrowth. A stable ZnS phase grows on the CuInS₂ surface. (D) Cation exchange. Upon adsorption of Zn-R species (R= organic ligand) at the CuInS₂ surface, a place-exchange reaction can occur, through which Zn²⁺ is incorporated in the NC, while Cu⁺ or In³⁺ cations are extracted as M-R species. (E) Etching. Chemical species in the reaction medium can promote the partial dissolution of the CuInS₂ NC by extracting cations and/or S^2– from the lattice. (F) Homogeneous nucleation. [ZnS] monomers can form ZnS NCs through homogeneous nucleation. Reproduced from ref (60). Copyright 2018 American Chemical Society.

In the case of CdSe-based core/shell hetero-NCs, additive heteroepitaxial shell overgrowth with limited interfacial diffusion dominates,^61,62 while PbX/CdX (X = S, Se, Te) core/shell hetero-NCs result from superseded shell ingrowth by topotactic Pb²⁺ for Cd²⁺ cation exchange, without any intermixing and alloying because of the different coordination numbers of the cations involved (6 for Pb²⁺ in the rock-salt structure and 4 for Cd²⁺ in the zinc-blende structure).⁶³ The shelling chemistry of CuInS₂ (and likely also other I–III–VI₂) NCs is however far more complex, resulting from an interplay between several dynamic processes taking place in solution, at the surface of and within the seed NC (Figure 5).⁶⁰ As a result, ZnS shelling of CuInS₂ NCs typically leads to spectral blue-shifts (ranging from 60 to 340 meV) in both the absorption and the PL spectra^{9,10,48,52,64} due to a combination of etching, cation exchange and Zn interdiffusion, which contribute to different extents depending on the reaction conditions and surface chemistry of the CuInS₂ seed NCs.⁶⁰ It has only recently been that CuInS₂/ZnS core/shell hetero-NCs displaying absorption spectra with small redshifts (as expected for a type-I band alignment)¹ have been obtained by using CuInS₂ seed NCs with residual acetate at the surface, which was observed to facilitate heteroepitaxial ZnS shell overgrowth.⁶⁰ CdS shelling of CuInS₂ NCs is less affected by interdiffusion,⁴⁸ likely because of a combination of larger lattice mismatch (viz., 5.2%) and larger ionic radius (Cd²⁺ = 78 pm, Cu⁺ = 60 pm, In³⁺ = 62 pm, in tetrahedral coordination),⁶⁵ in comparison to ZnS (lattice mismatch: 2%, ionic radius Zn²⁺ = 60 pm). Shelling by either ZnS or CdS increases the PLQYs of CuInS₂ NCs from a few percent up to 50–85%.^9,10,48,52 CdS is more effective than ZnS, leading to PLQYs as high as 86% with a single monolayer, which is about 3 times higher than that obtained for 1 monolayer ZnS.⁴⁸ Nevertheless, the nontoxic nature of ZnS makes it the preferred shell material in the majority of studies. The impact of ZnS or CdS shelling on the PLQYs of CdSe NCs is similar to that on CuInS₂ NCs, although the more mature stage of the CdSe NC chemistry has lead in recent years to near-unity PLQYs,⁶¹ which are not yet within reach for CuInS₂/ZnS core/shell hetero-NCs. Interestingly, shelling of CdSe (and other II–VI’s such as CdTe and CdS) NCs not only increases their PLQYs and exciton radiative lifetimes but also eliminates broad PL bands that are often observed at sub-band gap energies in bare NCs, which are ascribed to radiative recombination of carriers localized at defects (the so-called “trap PL”).¹ In contrast, shelling of CuInS₂ NCs impacts only on the PLQYs and exciton radiative lifetimes, without any significant effect on the PL bandwidths and global Stokes shifts, and only a minor spectral shift that follows the one observed in the absorption spectra. This implies that surface defects in CuInS₂ (and other I–III–VI₂) NCs are involved only in nonradiative decay pathways and do not have any relevant role in the radiative recombination.

Impact of the Nanoscale on the Chemistry of CuInS₂ and Other I–III–VI₂ Materials. The complexity of the shelling chemistry of CuInS₂ NCs demonstrates that their surface chemistry is drastically different from that of the II–VI and IV–VI analogues. This is not only due to a very dynamic inorganic surface but also the result of strong and disparate interactions with ligands, because the NC facets expose Cu⁺ (a soft Lewis acid with absolute hardness η = 6.28 eV),⁶⁹ In³⁺ (a hard Lewis acid with η = 13 eV),⁶⁹ and S^2– (a Lewis base),⁶⁹ in different ratios depending on their crystallographic nature. Consequently, different ligands will bind with different strengths to different facets or surface sites. This leads to a variety of outcomes in the synthesis of colloidal CuInS₂ NCs or in postsynthetic reactions using them as seed NCs (viz., shelling, ligand exchange, and cation exchange), depending on the exact reaction conditions and composition of the reaction.^60,70,71 Moreover, the tolerance to off-stoichiometry of nanoscale CuInS₂ and other I–III–VI’s is even greater than that of their bulk counterparts, and as a result, CuInX₂ (X = S, Se) NCs can be synthesized with Cu/In ratios ranging from 0.3 to 2.9.^9,10,71 Size reduction to the nanoscale gradually increases the surface/volume ratio of the NCs, which has a number of important consequences: larger contribution of surface–ligand interactions, size- and site-dependent positional reconstruction, lower activation energy for the formation of native point defects, and faster and site-dependent solid-state diffusion rates.^1,63,72−74 The complex and highly dynamic character of the chemistry of CuInS₂ NCs can thus be rationalized by considering that nanoscale effects will synergistically amplify the atypical properties exhibited by bulk I–III–VI₂ materials (viz., tolerance to off-stoichiometry, low activation energy for the formation of native defects, and high solid-state diffusion rates).

Origin of the Singular Optical Properties of CuInS₂ NCs. It may be anticipated that the exceptionally broad emission bands and essentially featureless absorption spectra of colloidal CuInS₂ NCs are a consequence of a poor control over their size and shape, in combination with composition inhomogeneities. However, whereas synthetic developments have substantially decreased ensemble size, shape, and composition distributions,^9,10 a sharp first absorption transition has not yet been observed and emission bands have remained broad. In particular, a recent work on nearly spherical wurtzite CuInS₂ NCs with ensemble size polydispersity ≤10% in the 2.7–6.1 nm diameter range and small composition variations (In/Cu = 0.91 ± 0.11 throughout the investigated size range) has shown that both the emission peak and the lowest-energy absorption transition are broad (fwhm_(abs) = 320–180 meV, fwhm_(PL) = 310 ± 20 meV in the 2.7–6.1 nm size range) and that the global Stokes shift is large and size-independent (Δ_ST = 455 ± 27 meV).⁵³

Furthermore, recent single-NC measurements have shown that the PL fwhm of single CuInS₂ NCs is only slightly narrower than that of the ensemble (viz., 190–270 meV vs 300–400 meV, respectively).⁷⁵ This observation unambiguously demonstrates that the broad spectral bandwidths (and likely also the large Stokes shifts) of CuInS₂ NCs cannot be ascribed to ensemble inhomogeneities of any kind (i.e., size, shape, or composition) and must thus have their origin in the intrinsic characteristics of individual NCs. The full significance of single-NC spectroscopic data will be discussed in more detail later in this Perspective, after the possible radiative recombination mechanisms have been examined. To date, several models have been proposed to explain the intriguing characteristics of the radiative recombination in CuInS₂ NCs. These models are schematically summarized in Figure 6 and will be critically discussed in more detail below, taking into account the most recent experimental and theoretical developments. We will first address the two extreme models: donor–acceptor pair recombination (Figure 6A), in which both carriers are localized on defects, and the exciton fine-structure model (Figure 6D), which is based on the intrinsic electronic structure of CuInS₂ NCs and precludes the involvement of localized carriers. Subsequently, we will consider the two models based on a “free-to-bound” recombination, in which only one of the carriers is localized: either the electron (Figure 6B) or the hole (Figure 6C). It should be noted that, although we will focus primarily on CuInS₂ NCs, the following discussion is also valid for other I–III–VI₂ NCs, because very similar properties have been reported for CuInSe₂ and AgInS₂ NCs.^{9,10,12,76,77}

Figure 6.

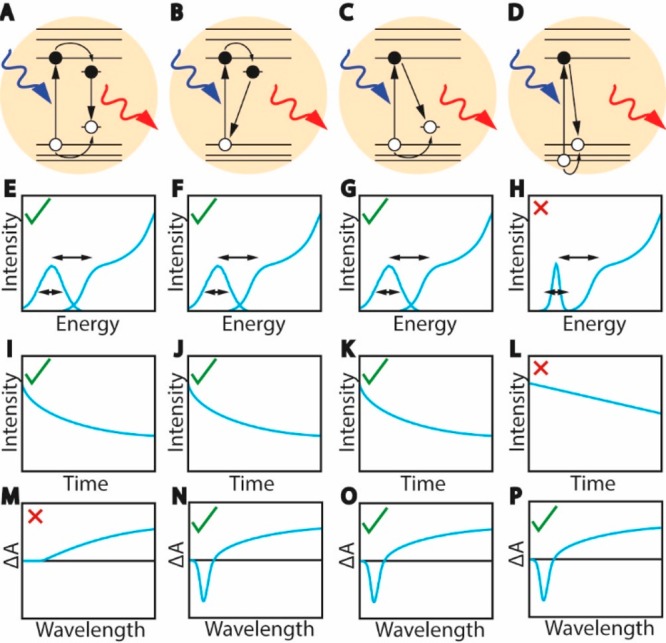
Schematic representation of the different mechanisms proposed for the exciton radiative recombination in CuInS₂ NCs and the expected optical spectra and PL decay for each scenario (see text for details). (A) Donor–acceptor pair recombination. (B) Localized electron recombines with delocalized valence band hole. (C) Delocalized conduction band electron recombines with localized hole. (D) Exciton fine-structure: absorption transition occurs to a higher-energy hole state while emission takes place from a lower-energy hole state. (E–H) Absorption and PL spectra expected for the scenarios represented in panels A–D. All models would result in broad bands and large Stokes shift, except the fine-structure model that predicts narrow PL bands. (I–L) PL decay curves showing long radiative decay times due to limited electron–hole wave function overlap (scenario’s A–C) or the forbidden nature of the transition (scenario D). In scenarios A–C, also multiexponential radiative decay is expected because of a distribution of localized states. However, single-exponential radiative decay is expected in scenario D. (M–P) Transient absorption spectra expected for the different models. In the donor–acceptor pair recombination model both charge carriers localize on subnanosecond time scales, resulting in a very weak or absent negative bleach signal that decays fast. The other three models could result in both a negative bleach signal and a positive photo-induced absorption signal. The dynamics (here not schematically drawn) would however be different (see text for a detailed discussion). The bleach magnitude in panels N, O, and P is not necessarily the same but depends on the degeneracy of the electron and hole band edge levels.

Donor–Acceptor Pair Recombination Model. The emission of I–III–VI₂ NCs has long been interpreted by analogy with the bulk counterparts and thus ascribed to radiative recombination involving donor and acceptor intragap states (Figure 6A).^56,57 This model can explain some of the characteristics of the PL of I–III–VI₂ NCs: the stronger electron–phonon coupling of the localized carriers and the distribution of donor–acceptor pair energies would lead to broad bandwidths, while the energy relaxation following carrier localization in the donor and acceptor states would account for the large Stokes shifts (Figure 6E).^77,78 The reduced overlap between the electron and hole wave functions in combination with a distribution of donor–acceptor pair distances would result in long and multiexponential PL decays (Figure 6I).⁷⁷ Nevertheless, the donor–acceptor pair mechanism cannot adequately explain the size dependence of the PL energies, which follow the same trend as the lowest-energy absorption transition,^9,77,83 because the smaller spread in donor–acceptor pair energy separations is expected to shift the PL bands by no more than several tens of millielectronvolts.⁸⁴ More importantly, the transient absorption results reported in refs (48, 66, and 80) imply that the lowest absorption transition is blocked after excitation, which clearly invalidates the donor–acceptor pair recombination model, because in this mechanism both charge carriers localize on a subnanosecond time scale, and therefore, the band-edge transition should become fully available again, resulting in very weak or absent bleach signals (Figure 6M), in striking contradiction to the experimental observations.

Exciton Fine-Structure Model. A radically different mechanism for the origin of the PL in CuInS₂ NCs has been recently proposed by Efros and co-workers (Figure 6D).⁸⁸ They calculated the fine-structure of delocalized levels at the conduction and valence band edges using a multiband effective mass model. It was found that the lowest-energy hole level in spherical CuInS₂ NCs with the tetragonal chalcopyrite crystal structure has p-type symmetry, so that the transition to the lowest-energy electron level, which has s-type symmetry, is forbidden. The first hole level with s-symmetry, with an optically allowed transition to the lowest electron level, is 100–300 meV higher in energy.

There is an analogy with the fine-structure splitting of the lowest-energy 1S_h1S_e exciton of binary II–VI, IV–VI, and III–V NCs, which is due to crystal field asymmetry, anisotropy of the NC shape, and electron–hole exchange interaction.⁸⁹⁻⁹¹ The lowest-energy exciton state is akin to a triplet excited state in organic molecules. It is a dark state; that is, radiative decay to the NC ground state is forbidden. However, the energy separation between exciton fine-structure states is typically small (<20 meV), and therefore, exciton fine-structure effects in conventional II–VI, IV–VI, and III–V NCs become noticeable only at low temperatures (below 100 K), where they affect the temperature- and magnetic-field dependences of the exciton lifetimes. Nevertheless, the exciton fine-structure is of great fundamental interest and has thus been extensively investigated for a large number of NC compositions, both theoretically and experimentally, e.g., CdSe,⁸⁹⁻⁹⁴ CdTe,^94,95 InAs,⁹⁴ PbSe,⁹⁴ ZnSe,⁹⁶ InP,^97,98 CdSe/CdS,⁹⁹ and CdTe/CdSe.¹⁰⁰

The situation is slightly different in the model of Efros and co-workers for spherical chalcopyrite CuInS₂ NCs.⁸⁸ Here, the lowest-energy exciton is dark because of the p-type wave function symmetry of the lowest-energy hole level. More importantly, the energy gap to higher-energy bright exciton states is as large as 100–300 meV, depending on NC size. Efros and co-workers propose that the bright exciton states dominate the absorption spectrum of the NCs, while Stokes-shifted PL originates from the lower-lying dark exciton state. This model makes a number of predictions: (i) size-dependent absorption and PL transitions, (ii) a low-energy tail in the absorption spectra, (iii) broad and size-dependent 1S_h →1S_e absorption line widths (energy separation between the highest- and the lowest-energy bright states varies from 100 to 30 meV in the 2–3.6 nm diameter range) (Figure 6H), (iv) long single-exponential radiative lifetimes increasing with decreasing NC size (Figure 6L), (v) a narrow PL peak, and (vi) a strongly size-dependent Stokes shift (viz., 300–100 meV in the 2–3.6 nm diameter range) (Figure 6H).⁸⁸ Prediction i is in good agreement with the experimentally observed size-dependence of the band gap,⁵³ while prediction ii is consistent with a large number of experimental observations.^9,10 Prediction iii is in qualitative agreement with the recent observation of size-dependent 1S_h →1S_e absorption line widths in wurtzite CuInS₂ NCs (320–180 meV in the 2.7 to 6.1 nm size range) but significantly underestimates the line widths.⁵³ Further experimental support for predictions i–iii has been recently given by the observation of two-photon absorption transitions below the one-photon absorption band edge of spherical chalcopyrite CuInS₂/ZnS core/shell NCs (core diameter ranging from 2.1 to 3.1 nm) and by the ability of the model to account for both the two-photon and one-photon transitions.⁵⁸ Prediction iv is consistent with the long lifetimes experimentally observed for CuInS₂ NCs, but not with the multiexponential character of the PL decay curves. Moreover, there is no experimental evidence supporting the notion of longer radiative lifetimes for smaller NCs. On the contrary, time-resolved PL spectroscopy seems to suggest that larger NCs have longer radiative lifetimes, because the PL is observed to shift to lower energies with increasing delays after photoexcitation.^70,79 Furthermore, predictions v and vi are inconsistent with the experimental observations, because the PL bands of CuInS₂ NCs are invariably very broad, even at the single NC level (see above for details), and the global Stokes shift has been recently shown by two different groups to be size- and shape-independent for both chalcopyrite CuInS₂/ZnS core/shell NCs (Δ_ST = 320 ± 30 meV core diameter: 2.1–3.1 nm)⁵⁸ and wurtzite CuInS₂ NCs (Δ_ST = 455 ± 27 meV in the 2.7 to 7.2 nm size range).⁵³ While the work of Efros and co-workers may thus give us important insights into the energy level structure of the delocalized band-edge levels in CuInS₂ NCs, it does not seem to provide a good model for the PL mechanism, which may involve localized states that the model does not consider explicitly.

Localized Electron–Valence Band Hole Recombination. The inadequacy of both models discussed above to account for the characteristics of the PL of CuInS₂ (and other I–III–VI₂) NCs clearly demonstrates that the radiative recombination must involve one delocalized carrier and one localized carrier. We will first discuss the scenario in which the electron is the localized carrier and radiatively recombines with a valence band hole (Figure 6B). Such transitions have already been proposed to explain additional emission lines in the spectrum of bulk CuInS₂ crystals that could not be assigned to donor–acceptor pair recombination or bound excitons.⁴³ In the case of CuInS₂ NCs, most authors propose that the electron is localized at either Cu_In⁰ antisite defects or sulfur vacancies.^52,84,85 In particular, the localized electron–valence band hole recombination mechanism has been advocated as a way to explain the spectral differences observed between chalcopyrite and wurtzite CuInS₂ NCs (viz., lower-energy PL, weaker size-dependence, broader bandwidths, and larger Stokes shifts in wurtzite NCs).^52,101 However, recent work has unambiguously shown that there is no significant difference between the PL bandwidths and Stokes shifts of wurtzite and chalcopyrite CuInS₂ NCs^53,68 and that the weaker size dependence of the band gap and PL at lower energies can be explained by the larger electron and hole effective masses (viz., m_e = 0.173m₀, m_h = 2.181m₀)⁵⁹ and narrower band gap (1.3 eV)⁵⁹ of bulk wurtzite CuInS₂ in comparison to chalcopyrite CuInS₂ (viz., m_e = 0.153m₀, m_h = 0.958m₀,⁵⁹E_g = 1.535 eV²⁹).⁵³ Moreover, as we will discuss below, a localized electron is incompatible with transient absorption spectroscopic data reported by several groups.

Conduction Band Electron–Localized Hole Recombination. We will now discuss the scenario in which the hole is the localized carrier and radiatively recombines with a conduction band electron (Figure 6C).^48,54,66,86 In this mechanism, the quantized nature of the conduction band electron and its lower effective mass (m_e is 0.153m₀, while m_h is 0.958m₀)⁵⁹ explains the size-dependence of the PL energies in terms of the quantum confinement, while the large Stokes shift originates from the energy difference between the top of the valence band and the localized hole state (Figure 6G). The other characteristics, i.e., broad PL bands, long exciton radiative lifetimes, and multiexponential PL decays (Figure 6G,K), are rationalized by a stronger carrier–phonon coupling for the localized hole, reduced electron–hole wave function overlap due to the hole localization, and distribution in the hole-localization sites, respectively. Evidence for a recombination mechanism involving a delocalized carrier and a localized carrier has been provided by transient absorption measurements.^48,66,85,86 Following the excitation event by a pump laser, charge carriers relax to their respective band edges. We argued above that in the case of a donor–acceptor pair recombination, the charge carriers should rapidly localize, and therefore the bleach of the lowest-energy exciton transition would decay rapidly (subnanosecond scale), in contrast with the experimental observations.⁴⁸ In addition, the decay dynamics of the two signals observed (i.e., negative bleach and positive photoinduced absorption, Figure 4F) are different on a picosecond time scale, indicating that they originate from different charge carriers that initially follow different decay pathways.⁴⁸ In fact, the dependence of the bleaching signal on the pump power pointed out that the bleaching of the lowest-energy exciton transition was primarily due to a 2-fold degenerate state, which corresponds to the degeneracy of the bottom of the conduction band (i.e., the 1S_e state) and rules out that the valence band plays a role in the bleaching, because it has a much higher degeneracy (see above for details).^40,66,86 This observation indicates that the electron is the delocalized carrier, while the hole becomes localized shortly after excitation (on a subpicosecond time scale), giving rise to the photoinduced absorption signal (Figures 4F and 6O).⁴⁸

From the discussion above it is clear that the radiative recombination of a delocalized conduction band electron with a localized hole is the only mechanism that explains all the observed PL characteristics (viz., broad PL bands with size-dependent spectral positions but size-independent bandwidths, large and size-independent Stokes shift, long radiative lifetimes and multiexponential PL decays, long lifetime of bleach signal in transient absorption, decoupled bleach and photoinduced absorption kinetics, and bleach saturation). The question that then emerges is how and where the photogenerated valence band hole localizes. There are many possible answers to this question, as schematically depicted in Figure 7. In the remainder of this Perspective, we will analyze the currently available data in order to establish the (most probable) nature of the hole-localization center.

Figure 7.

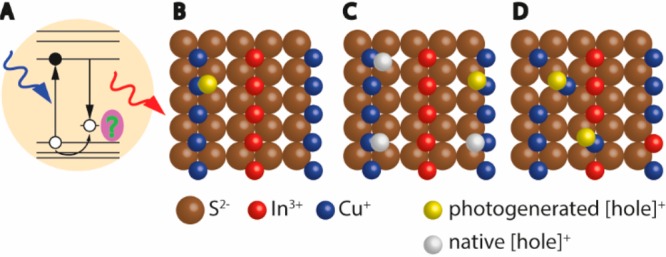
(A) Recombination of a delocalized conduction band electron with a localized hole. The green question mark highlights the remaining question on the nature of the hole-localization center. (B–D) Proposed hole-localization centers: (B) Photogenerated hole localizes on a regular Cu⁺ ion. (C) Photogenerated hole localizes on a Cu⁺ ion, and there are also native holes present (i.e., Cu²⁺ ions). (D) Photogenerated hole localizes on Cu⁺-related native defects.

Nature of the Hole Localization. Interesting insight into the nature of the hole-localizing state in CuInS₂ NCs has come from two recent comparative studies. The first one, by the Klimov and Crooker groups, compared CuInS₂ NCs to copper-doped Cu²⁺:ZnSe NCs.¹⁰² In the second one, Gamelin and co-workers compared CuInS₂ NCs to copper-doped NCs with compositions Cu⁺:CdSe and Cu⁺:InP.⁵⁴ These different types of NCs show strikingly similar PL properties, including emission energy, bandwidth, Stokes shift, and their temperature- and magnetic-field dependence (Figure 8). The PL mechanism in the copper-doped NCs involves radiative decay of an electron from a conduction band level to a copper-localized level. Based on the similarity in PL properties, in both papers it was proposed that the PL mechanism of CuInS₂ NCs must be similar.^54,102 Effectively, the emission transition in CuInS₂ NCs would be akin to a metal-to-ligand charge-transfer (MLCT) transition,⁵⁴ where an electron is transferred from the conduction band (CB, analogous to the LUMO of a “ligand” following photoexcitation) to the Cu-center (metal):

1

where ℏω denotes an emitted photon. Gamelin and co-workers discussed the proposed electron–hole recombination pathway in more detail, suggesting that a photoexcited hole rapidly localizes on a Cu⁺ site, thereby changing its formal charge to 2+, followed by radiative recombination with the conduction band electron.⁵⁴ Indeed, cyclic voltammetry reveals a redox feature within 1 eV (depending on size and composition) of the top of the valence band of CuInS₂ NCs, which can be ascribed to the Cu¹⁺/Cu²⁺ couple.¹⁰³ This is consistent with density functional theory (DFT) calculations showing that the HOMO in Cu⁺:CdSe and Cu⁺:InP NCs,¹⁰⁴ as well as in CuInS₂ NCs, is localized on a Cu-center (or, for particular atomic arrangements, delocalized over at most three nearby Cu-centers¹⁰⁵). We note that this is also consistent with the bulk electronic structure, because the top of the valence band in bulk CuInS₂ has been shown to have a large contribution of Cu(3d) orbitals (45–60%, see above for details).^28,29,35,40 The initial driving force for hole localization on a Cu site may thus simply come from the energy level structure of CuInS₂ NCs. Additional stabilization of the localized hole may come from strong electron–phonon coupling, which would induce a Jahn–Teller nuclear reorganization of the immediate surroundings of the photogenerated Cu²⁺-center (a common type of distortion for transition metal ions with a d⁹ configuration).^104,105 The large reorganization energy would explain why radiative recombination of the localized hole with the conduction band electron (the “MLCT” transition) yields Stokes-shifted and strongly broadened PL bands.

Figure 8.

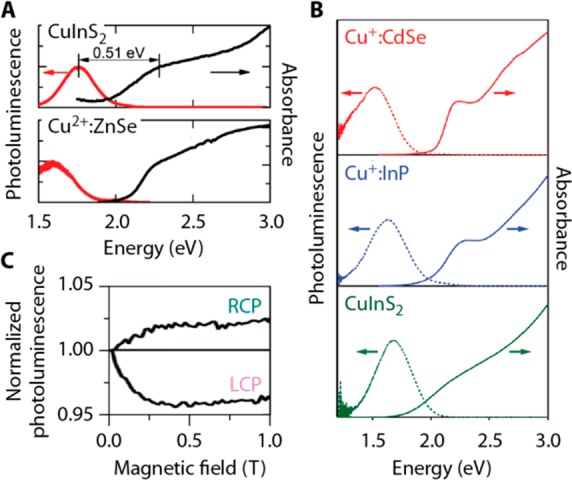
(A) Absorption (black) and emission (red) spectra of CuInS₂ NCs (top) and Cu²⁺-doped ZnSe NCs at 3 K. (B) Absorption (solid lines) and emission (dashed lines) spectra of Cu⁺-doped CdSe NCs (top; red), Cu⁺-doped InP NCs (middle; blue), and CuInS₂ NCs (bottom; green) at room temperature. (C) The magnetic-field dependence of the right circularly polarized (RCP) and left circularly polarized (LCP) emission from CuInS₂ NCs was interpreted as indicating the presence of paramagnetic Cu²⁺ in the excited state of the nanocrystals. Panels A and C are adapted from ref (102). Copyright 2014 American Chemical Society. Panel B is adapted from ref (54). Copyright 2015 American Chemical Society.

Cu⁺ or Cu²⁺? Interestingly, the experimental data and interpretations of Rice et al.¹⁰² and Knowles et al.⁵⁴ disagree on one important aspect. Both groups find evidence for a paramagnetic Cu²⁺-center in the excited state of the NCs from the temperature- and magnetic-field dependence of the circularly polarized PL (Figure 8C),^54,102 consistent with the proposed recombination mechanism (eq 1). However, on the basis of the observation of a temperature-dependent magnetic circular dichroism (MCD) signal, Rice et al. proposed that paramagnetic Cu²⁺ ions are already present in ground-state CuInS₂ NCs (Figure 7C).¹⁰² In contrast, MCD experiments by Knowles et al. provided no evidence for divalent copper sites in ground-state CuInS₂ NCs.⁵⁴ Whether or not Cu²⁺ is present in the ground state of CuInS₂ NCs would potentially impact the emission mechanism. In the model proposed by Knowles et al.⁵⁴ the essential first step after photoexcitation is localization of the photoexcited hole on a Cu⁺ ion, formally oxidizing it to Cu²⁺

2

after which recombination with the conduction-band electron takes place (eq 1). If, on the other hand, Cu²⁺ is present in the ground state of CuInS₂ NCs,¹⁰² it has been suggested that rapid hole localization (eq 2) is not necessarily the first step of the emission mechanism. Instead, the photoexcited conduction-band electron may decay radiatively to a localized level on a Cu²⁺-center (eq 1) that already existed prior to photoexcitation.^103,106

Spectroelectrochemical experiments by the groups of Brovelli and Klimov have provided support for the scenario where pre-existing Cu²⁺ sites were involved in the photoluminescence mechanism in CuInS₂ NCs (Figure 9A,B).^103,106 It was found that a reductive electrochemical potential, filling electron traps but generating hole states, has a beneficial effect on the photoluminescence quantum yield¹⁰⁶ (at least for Cu-deficient CuInS₂ NCs¹⁰³). Brovelli and co-workers established that the efficiency-limiting factor is electron trapping,¹⁰⁶ in agreement with the proposition previously made by Berends et al.⁴⁸ Further, it was concluded by both groups that radiative recombination requires Cu²⁺-centers, either pre-existing or accumulated as a result of photoconversion of Cu⁺ by localization of the photogenerated valence band hole.^103,106,107 This latter conclusion has been recently challenged by van der Stam et al.¹⁰⁸ based on spectroelectrochemical experiments. According to this work, radiative recombination will occur only on Cu²⁺-centers that have been generated by localization of the photogenerated valence band hole in Cu⁺-based defects, so that electrochemical reduction of Cu²⁺ to Cu⁺ results in photobrightening, while oxidation of Cu⁺ to Cu²⁺ leads to quenching.¹⁰⁸ The authors proposed that pre-existing Cu²⁺-centers are involved in a nonradiative Auger-type quenching mechanism, rendering some NCs in the ensemble dark.¹⁰⁸ However, we note that the presence of pre-existing Cu²⁺-centers in ground-state CuInS₂ NCs is inconsistent with X-ray photoelectron spectroscopy (XPS) studies that found no evidence for Cu²⁺ in CuInS₂ or (Cu,In,Zn)S₂ NCs of various stoichiometries.^60,64 Interestingly, a recent study of chalcopyrite CuInS₂ NCs (2–3 nm diameter) employing steady-state X-ray absorption spectroscopy, X-ray absorption near-edge structure (XANES), and extended X-ray absorption fine structure have excluded the presence of Cu²⁺ in the ground state, while providing evidence for its formation after photoexcitation by carrying out XANES under laser excitation.¹⁰⁹ This study also showed the presence of a significant fraction of undercoordinated Cu⁺ (i.e., coordination number <4), which were attributed to surface Cu⁺ sites, because their concentration increased with decreasing NC size.¹⁰⁹

Figure 9.

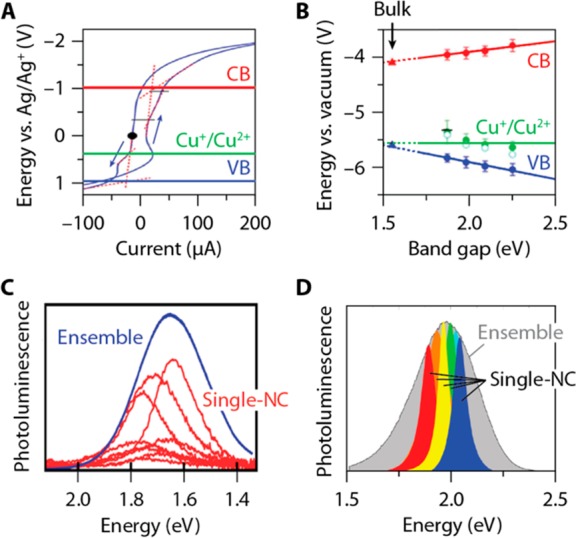
(A) Cyclic voltammetry measurements on CuInS₂ NCs in electrolyte solution in chloroform revealing a redox feature ascribed to the Cu⁺/Cu²⁺ couple at approximately 0.5 V (vs. Ag/Ag⁺). The conduction band (CB) and valence band (VB) edges are also indicated. (B) Potentials extracted for Cu⁺/Cu²⁺ (green data points), the CB (red), and the VB (blue) for stoichiometric NCs with different band size. Linear trends are extrapolated to the bulk band gap, where the Cu⁺/Cu²⁺ potential and the VB edge are approximately resonant. (C) Whitham et al.⁷⁵ measure single-nanocrystal emission bands with fwhm between 190 and 270 meV on a batch of CuInS₂/CdS NCs with a slightly broader ensemble fwhm of 300 meV. (D) Zang et al.⁶⁷ measure emission spectra from single CuInS₂/ZnS NCs with fwhm between 60 and 220 meV, much narrower than the ensemble fwhm of 352 meV. Colored spectra are Lorentzian fits to the single-NC emission spectra, not the actual measurements. Panels A and B are adapted from ref (103). Copyright 2017 American Chemical Society. Panel C is adapted from ref (75). Copyright 2016 American Chemical Society. Panel D is adapted from ref (67). Copyright 2017 American Chemical Society.

Transient absorption studies by Berends et al. (Figure 4F, see above for details) also found no evidence for Cu²⁺ in ground-state CuInS₂, CuInS₂/ZnS, and CuInS₂/CdS NCs.⁴⁸ Broadband photoinduced absorption in the near-infrared is absent in ground-state NCs but appears within 1 ps after photoexcitation. This signal was ascribed to excitation of a Cu²⁺-localized hole to valence band levels, Cu²⁺ + ℏω → Cu⁺ + h⁺(VB).⁴⁸ We note that this assignment is consistent with the conclusions derived from the XANES measurements under laser excitation carried out by Ludwig et al. on similarly sized CuInS₂ NCs.¹⁰⁹ A weak photoinduced absorption feature was later observed in copper-doped Cu⁺:CdSe NCs and interpreted similarly.⁴⁷ These observations support the mechanism proposed by Knowles et al.⁵⁴ in which Cu²⁺ is created only after localization of a photogenerated valence band hole (eq 2). In CuInS₂ NCs the time scale of hole localization on Cu⁺ is subpicosecond, faster than the instrument response of Berends et al.⁴⁸ This could explain why hole-localizing states introduced at reductive electrochemical potentials have been reported to be ineffective at reducing the quantum yield of (most types of) CuInS₂ NCs.^103,106 Hole localization in Cu⁺:CdSe NCs is slower than in CuInS₂ NCs, as evidenced by a rise of the metal-to-ligand charge-transfer luminescence (eq 1) on a time scale of 25 ps upon pulsed excitation.⁴⁷ Whether or not Cu²⁺ is present in the ground state of CuInS₂ NCs might depend on their stoichiometry and/or surface chemistry.¹⁰³ Indeed, the oxidation state of Cu responds to an external potential or prolonged illumination.^103,108 While the prevailing idea in the studies of Pinchetti et al.¹⁰⁶ and Fuhr et al.¹⁰³ has been that Cu²⁺-centers can be beneficial for efficient emission from CuInS₂ NCs, the recent work by van der Stam et al.¹⁰⁸ casts doubt on the generality of this notion. It remains an open question whether these conflicting results can be reconciled by taking into account stoichiometry and/or surface chemistry deviations.

Native Defects or Regular Cu⁺ Sites? Not only is the formal charge of copper ions in the NC ground state still under debate, but also the nature of the Cu-centers at which radiative recombination takes place. The Cu-center involved may be a “regular” Cu⁺ ion with the intrinsic CuInS₂ crystalline surrounding (Figure 7B),⁵⁴ or a Cu-related defect (for example, a Cu²⁺ ion neighboring a Cu vacancy or a Cu⁺ ion in an antisite defect, Figure 7D).^{58,103,106,108} A few papers have recently provided more insight into the nature of the hole-localizing Cu-site by studying individual NCs of Cu⁺:CdSe¹¹⁰ and CuInS₂.⁷⁵ They find single-NC line widths ranging from 190 to 270 meV fwhm (Figure 9C,D), only slightly narrower than the ensemble fwhm of ∼300–400 meV, but significantly broader than the typical line widths of single II–VI or III–V NCs (20–150 meV).¹¹¹ Strongly broadened single-NC emission spectra are easily rationalized if we consider that the emitting transition is akin to a metal-to-ligand charge-transfer transition.⁷⁵ The formal charge state of a Cu ion changes from 2+ to 1+ in the transition (eq 1). This charge redistribution must introduce a strong reorganization of the crystal lattice surrounding the Cu ion.^104,105 This strong electron–phonon coupling explains broad spectra at the single-emitter level¹¹² and is also consistent with the observation that the ensemble PL line widths of CuInS₂ NCs are only weakly temperature-dependent (fwhm decreases from 270 meV at 300 K to 235 meV at 2 K), indicating that it is dominated by homogeneous broadening.^54,56 Alternatively, considering the similarities with single Cu⁺:CdSe NCs (which are doped by multiple Cu⁺ ions occupying Cd²⁺ sites), the broad emission spectra of single CuInS₂ NCs may also reflect a distribution of Cu²⁺ radiative recombination centers with slightly different surroundings.

Strikingly, the broad single-NC spectra reported by Whitham et al.⁷⁵ for CuInS₂/CdS core/shell NCs are inconsistent with relatively narrow spectra measured recently by Zang et al.⁶⁷ on individual CuInS₂/ZnS core/shell NCs, which show an ensemble emission fwhm of 352 meV but single-NC spectra as narrow as 128 meV on average. The narrowest spectra are no wider than 60 meV,⁶⁷ comparable to values typically found for individual II–VI or III–V NCs, and 18 out of 20 NCs show (significantly) narrower emission spectra than even the narrowest spectrum measured by Whitham et al.⁷⁵ Zang et al. conclude that the ensemble emission spectrum is strongly inhomogeneously broadened.⁶⁷ Indeed, they measure narrow single-NC spectra with a distribution of peak energies covering the ensemble emission band. However, because the size dispersion of their sample is as small as 10%, they discuss that size dispersion alone cannot explain the wide distribution of peak energies. They propose that additional inhomogeneous broadening originates from variations in the radial position of emitting Cu-related defects in the NCs. In their model the attractive electron–hole Coulomb energy depends on the location of the Cu-related defect at which the hole is localized, differing by approximately 300 meV between the NC center and the surface.⁶⁷ This explanation for the energy distribution of the conduction band electron to localized hole transition (eq 1) is analogous to the one previously considered for the energy distribution of donor–acceptor pair recombination, in which the distance between the donor and acceptor determines the Coulomb interaction.⁷⁷ The explanation for these discrepant results is currently unclear. It may be related to the fact that the structure of the CuInS₂/ZnS core/shell NCs investigated by Zang et al.⁶⁷ is more affected by interdiffusion than that of the CuInS₂/CdS core/shell NCs analyzed by Whitham et al.⁷⁵ (see above for details). Indeed, Zang et al. observed a pronounced spectral blue-shift (viz., 230 meV) upon ZnS shelling of the CuInS₂ core NCs.⁶⁷ This is indicative of a significant degree of alloying, which could impact on the nature of the Cu radiative recombination centers. It is thus likely that the behavior observed for individual CuInS₂/CdS core/shell NCs⁷⁵ is more representative of the intrinsic characteristics of single CuInS₂ NCs. Alternatively, phonon coupling in the CuInS₂/CdS NCs of Whitham et al. might be enhanced by the (quasi-)type-II charge-carrier localization,¹¹³ compared to the type-I CuInS₂/ZnS structure of Zang et al.

An important aspect of the model of Zang et al. is the assumption that the emitting centers are “Cu-related defects”.⁶⁷ Similar terms are used in several other papers to discuss the conduction band electron-to-localized hole recombination in CuInS₂ NCs.^{58,103,106,108,114} A “Cu-related defect” may for example be an extrinsic defect, such as a Cu²⁺ on a Cu⁺ site (Cu_Cu⁺) or an interstitial Cu²⁺ (Cu²⁺_i) neighboring a Cu vacancy (V_Cu^–), or a native defect such as a Cu⁺-based Frenkel pair (V_Cu^––Cu⁺_i) or a Cu⁺ antisite (Cu_In^2–), as they are known from bulk CuInS₂. The notion that a Cu-related defect must be involved probably comes from the many defect-related emission lines known from bulk CuInS₂. For example, donor–acceptor pair recombination leads to relatively broad (fwhm: 23 meV at 4 K) emission bands at energies 100–150 meV below the band gap, while donor to valence band recombination yields narrower lines (fwhm: 2 to 12 meV) at 30 meV below the band gap, and bound exciton recombination yields lines as narrow as 0.5–1.5 meV with binding energies in the 20–30 meV range (see Figure 3).^34,43,45 However, these values are significantly smaller than the PL line widths and Stokes shifts observed for CuInS₂ NCs, even at 4 K or at the single-NC level. This suggests that additional relaxation and broadening mechanisms would be needed to account for the experimentally observed values. Furthermore, it is noteworthy that band-edge PL has never been reported for CuInS₂ NCs, not even at 4.2 K,⁵⁴ in striking contrast not only to II–VI and IV–VI NCs, but also to bulk CuInS₂, where radiative recombination of the free-exciton has been observed up to room temperature,⁴⁵ despite the dominance of donor–acceptor recombination (see above for details). This implies that the driving force for hole localization is larger in CuInS₂ NCs than in the bulk, suggesting that the nature of the exciton radiative recombination in CuInS₂ NCs differs not only from II–VI, IV–VI, and III–V NCs, but also from bulk CuInS₂. From this viewpoint, CuInS₂ (and other I–III–VI₂) NCs are unique materials.

Moreover, no experimental evidence is available that photogenerated valence band holes in CuInS₂ NCs preferably localize on a “Cu-related defect” rather than on any other Cu-site. In fact, a large number of studies on CuInS₂ NCs and CuInS₂-based core/shell NCs have consistently found broad Stokes-shifted emission with lifetimes of >100 ns (see above for details) (refs (9−11, 48, 52−54, 56,57, 60,64, 66, 67, 75, 78−82, 84−87, 102, 103, and 106)). Until now, NCs with a qualitatively different recombination pathway have not been detected, not even as a subset of NCs in a synthesis batch. Additionally, as discussed above, shelling of CuInS₂ NCs, in particular with CdS, results in PLQYs as high as 85%, without significant changes in spectral positions, line widths, and magnitude of the Stokes shift. This implies that the Cu-related radiative recombination center is not only oblivious to the passivation of surface defects but also virtually ubiquitous. As discussed above, defect concentrations in bulk CuInS₂ are high, and NCs may be even more defect-tolerant than the bulk material. However, the idea that a particular type of defect is required for the characteristic emission mechanism of CuInS₂ NCs (i.e., hole localization, eq 2, and subsequent radiative recombination with the conduction band electron, eq 1) is difficult to defend. It would imply that all CuInS₂ NCs studied so far contain this same type of defect. Given the variety of stoichiometries and surface chemistries studied and the small sizes of many CuInS₂ NCs (a 3 nm diameter corresponds to just 42 unit cells!), this seems unlikely.

Interestingly, recent DFT calculations show that localization of photoexcited holes on a Cu-center in CuInS₂ NCs may occur independently of whether crystal defects are present, because the HOMO in any CuInS₂ NC is always Cu-localized.¹⁰⁵ Nevertheless, the energy and localization of the HOMO is shown to depend sensitively on the precise atomic arrangement in the NC and on the NC surface.¹⁰⁵ For example, an antisite defect introduces a higher-energy HOMO in a NC.¹⁰⁵ In other words, native crystal defects may be preferable sites for hole localization, but they are not required for localization. The photoluminescence mechanism in CuInS₂ NCs would thus be fundamentally different from that of bulk CuInS₂ (see above), in the sense that carrier localization at native defects would no longer be required to lead to broad, Stokes-shifted PL.⁵⁴

The origin of this fundamental difference remains an open question. Gamelin and co-workers first postulated that Jahn–Teller distortions may be more pronounced in NCs than in bulk, thereby promoting exciton self-trapping.⁵⁴ However, their recent theoretical work on CuInS₂ NCs seems to be inconsistent with this explanation, as it showed that holes in CuInS₂ NCs localize on Cu even in the ground-state geometry of the NC (i.e., even in the absence of Jahn–Teller distortions).¹⁰⁵ Alternatively, it has been suggested that in NCs the energy gain from hole delocalization is smaller than the energy gain from localization because of quantum confinement, while in bulk CuInS₂ the driving force for delocalization is larger.⁵⁴ Indeed, cyclic voltammetry places the Cu²⁺/Cu⁺ redox potential approximately at the same energy as the bulk valence band edge.¹⁰³ Additional work, for example on larger CuInS₂ NCs (>10 nm) outside the strong-confinement regime, may shed more light on the differences between bulk and nanocrystalline CuInS₂.

Moreover, as shown by the DFT calculations carried out by Nelson and co-workers,¹⁰⁵ native crystal defects are not required for hole localization in CuInS₂ NCs, but they remain preferable sites, if present. Given that the formation of native defects in CuInS₂ NCs is a very favorable process, especially considering that nanoscale effects should lower their formation energy even further with respect to bulk, one can expect that native defects will be present in a large fraction of CuInS₂ NCs within an ensemble, if not omnipresent. We argue that it is thus plausible that hole self-localization on regular Cu⁺ sites and localization on native defects (e.g., Cu_In^2–) coexist and lead to similar relaxation energies and comparable final configurations due to the very dynamic nature of CuInS₂ NCs and the small activation energies involved. This may be the reason behind the broad (and highly variable) single-NC emission observed for both CuInS₂/ZnS NCs⁶⁷ and CuInS₂/CdS NCs.⁷⁵

Further research is needed to unambiguously establish the roles of both regular Cu⁺-sites and native Cu⁺-defects in the hole-localization process and the subsequent radiative recombination with the conduction band electron and to disentangle their contributions if needed. This will require the use of an array of sophisticated techniques, such as electron spin echo detected electron paramagnetic resonance (ESE-EPR), electron–nuclear double resonance (ENDOR), and optically detected magnetic resonance (ODMR) spectroscopies. ESE-EPR and ENDOR spectroscopies have been successfully used to reveal the presence of Jahn–Teller distorted Ag²⁺ sites (also d⁹) in AgCl after photoexcitation¹¹⁵ and to identify the nature of donors and acceptors in Li-doped ZnO quantum dots.¹¹⁶ Further experimental and theoretical work is also needed to allow the full understanding of the exciton transitions (absorption and emission) in both chalcopyrite and wurtzite CuInS₂ NCs. The strong exciton–phonon coupling in these materials is of particular interest as it seems to surpass that observed for bulk CuInS₂. As a final remark, it should be noted that, although we focused this Perspective mostly on CuInS₂ NCs because of the wealth of data available on this material, the discussion above also applies to the less investigated members of the I–III–VI₂ NCs, because very similar properties have been reported for CuInSe₂ and AgInS₂ NCs.^{9,10,12,76,77,117} It is therefore very likely that the radiative recombination mechanism is the same in all members of the I–III–VI₂ family.

Biographies

Anne C. Berends received her M.Sc. in Chemistry from Utrecht University in 2014. In September 2018 she obtained her Ph.D. degree from the same university. She is currently working as materials scientist at Seaborough Research B.V., focusing on new materials for LEDs.

Mark J. J. Mangnus pursues a M.Sc. degree in Nanomaterials Science at Utrecht University. After graduating, he will start working as a Ph.D. candidate in the group of Freddy Rabouw, using optical microscopy and spectroscopy of fluorescent nanoparticles to study diffusion dynamics.

Chenghui Xia participated from September 2013 to September 2014 in a Combined Master and Doctor Program in Marine Chemical Engineering and Technology in Ocean University of China. He received his Ph.D. degree from Utrecht University in February 2019. His Ph.D. research focused on the synthesis and optical properties of colloidal CuInS₂-based heteronanocrystals.

Freddy T. Rabouw received his Ph.D. from Utrecht University in 2015. After a 2-year postdoctoral position (Rubicon fellow) at ETH Zurich, Switzerland, he has now returned to Utrecht University as an assistant professor. His research currently focuses on the optical spectroscopy of individual nanocrystals to study their emission and catalysis dynamics.

Celso de Mello Donega is an Associate Professor in the Chemistry Department of the Faculty of Sciences at Utrecht University. He earned his Ph.D. degree in Chemistry from Utrecht University in 1994. His research is focused on the chemistry and optoelectronic properties of nanomaterials, with particular emphasis on colloidal nanocrystals and heteronanocrystals of semiconductors.

Author Present Address

^† A.C.B.: Seaborough Research B.V. Science Park 106, 1098 XG Amsterdam, The Netherlands

The authors declare no competing financial interest.