Lightweight, flaw-tolerant, and ultrastrong nanoarchitected carbon

Significance

A long-standing challenge in modern materials manufacturing and design has been to create porous materials that are simultaneously lightweight, strong, stiff, and flaw-tolerant. Here, we fabricated pyrolytic carbon nanolattices with designable topologies by a two-step procedure: direct laser writing and pyrolysis at high temperature. The smallest characteristic size of the nanolattices approached the resolution limits of the available 3D lithography technologies. Due to the designable unit-cell geometries, reduced feature sizes, and high quality of pyrolytic carbon, the created nanoarchitected carbon structures are lightweight, can be made virtually insensitive to fabrication-induced defects, attain nearly theoretical strength of the constituent material, and achieve specific strength up to one to three orders of magnitude above that of all existing micro/nanoarchitected materials.

Abstract

It has been a long-standing challenge in modern material design to create low-density, lightweight materials that are simultaneously robust against defects and can withstand extreme thermomechanical environments, as these properties are often mutually exclusive: The lower the density, the weaker and more fragile the material. Here, we develop a process to create nanoarchitected carbon that can attain specific strength (strength-to-density ratio) up to one to three orders of magnitude above that of existing micro- and nanoarchitected materials. We use two-photon lithography followed by pyrolysis in a vacuum at 900 °C to fabricate pyrolytic carbon in two topologies, octet- and iso-truss, with unit-cell dimensions of ∼2 μm, beam diameters between 261 nm and 679 nm, and densities of 0.24 to 1.0 g/cm³. Experiments and simulations demonstrate that for densities higher than 0.95 g/cm³ the nanolattices become insensitive to fabrication-induced defects, allowing them to attain nearly theoretical strength of the constituent material. The combination of high specific strength, low density, and extensive deformability before failure lends such nanoarchitected carbon to being a particularly promising candidate for applications under harsh thermomechanical environments.

Lightweight porous materials, such as wood, bone, Euplectella sponges, diatoms, and bamboo, are ubiquitous in nature. These natural structural materials have been extensively investigated (1–5) and have been shown to be resilient against externally applied loads and powerful in absorbing and dissipating impact energy. Such properties have been enabled by two design principles: (i) a multiscale hierarchy of constituent materials and length scales, which generally consist of complex multilevel architectures with characteristic dimensions from nano- to macroscale (5) and (ii) their tolerance of flaws when the characteristic material length scale falls below a critical value (4). Both principles have been applied to engineering advanced materials to various degrees of success (5, 6).

A general guideline for a material to be considered “lightweight” is for its density to be less than that of water (i.e., ρ ≤ 1.0 g/cm³) (1, 7). Recent breakthroughs in material processing techniques, especially in 3D microfabrication and additive manufacturing, provide a particularly promising pathway to fabricate lightweight materials, which often possess a suite of other beneficial properties such as high specific stiffness, high specific strength, and good resilience/recoverability (7–27). A penalty for the ultralight weight of such nano- and microarchitected materials is a severe reduction in their stiffness and strength through power law scaling: σ_y ∼ (ρ/ρ_s)^m, E ∼ (ρ/ρ_s)ⁿ, where σ_y is the yield strength, E the Young’s modulus, ρ the density, and ρ_s the density of the fully dense constituent solid (1). The exponents m and n are generally greater than 1, which renders developing methodologies to create materials that are simultaneously lightweight and strong/stiff while maintaining their other properties (i.e., thermal stability, electrical conductivity, magnetism, recoverability, etc.) a grand unsolved challenge because of restricted material choices and limited architectures.

Most work on micro/nanoarchitected materials to date has been focused on hollow-beam-based architectures, which offer exceptionally light weight with a concomitant high compliance [e.g., nickel-based hollow-tube microlattices with a Young’s modulus of 529 kPa and a compressive strength of ∼10 kPa at a density of ∼0.010 g/cm³ (7) and ceramic hollow-tube nanolattices with Young’s moduli of 0.003 to 1.4 GPa and compressive strengths of 0.07 to 30 MPa at densities of 0.006 to 0.25 g/cm³ (10–14)]. These micro/nanoarchitected materials have a common feature of length scale hierarchy, that is, relevant dimensions of their structural elements span three to five orders of magnitude, from tens of nanometers to hundreds of micrometers and even greater. Structural features of nickel-alloy hollow-tube nanolattices fabricated using large-area projection microstereolithography span seven orders of magnitude in spatial dimensions, from tens of nanometers to tens of centimeters. These nanolattices attain tensile strains of >20% with a low modulus of 125 kPa and a low tensile strength of ∼80 kPa at a density of ∼0.20 g/cm³, which corresponds to the relative density of 0.15% (17). The deformability of these nanolattices is attributed to a combination of bending- and stretching-dominated hierarchical architectures distributed over successive hierarchies and shell buckling, an elastic instability characteristic of thin-walled hollow cylinders (17). Among the thin-walled architectures, 3D periodic graphene aerogel microlattices have been synthesized via direct ink writing; these materials are exceptionally lightweight (with a density of 0.031 to 0.123 g/cm³), compliant (with a modulus of 1 to 10 MPa), and weak (with a low strength of 0.10 to 1.6 MPa) and exhibit nearly complete recovery after compression to 90% strain (23).

Some efforts have also been dedicated to the synthesis and development of mechanical properties of micro- and nanoarchitected materials that are composed of nonhollow beams of various materials, achieving greater stiffness and higher densities compared with their hollow-beam counterparts. Most of these studies have been on architectures composed of core-shell types of beams, usually with an acrylic polymer core and a thin (from tens of nanometers to several hundred nanometers), rigid outer coating. For example, triangular-truss microlattices with polymer-core-alumina-shell beams have been synthesized by combining two-photon lithography (TPL) direct laser writing (DLW) and atomic layer deposition and sustained a modulus of ∼30 MPa at a low fracture strain of ∼4 to 6% and a density of 0.42 g/cm³ (16). Octet-truss nanolattices made up of 262- to 774-nm-diameter polymer beams with sputtered 14- to 126-nm-thick high-entropy alloy (HEA) coatings were reported to have a Young’s modulus of 16 to 95 MPa and a compressive strength of 1 to 10 MPa at densities between 0.087 and 0.865 g/cm³ (20). Samples with HEA thicknesses less than 50 nm completely recovered after being compressed for >50% (20). Beyond core-shell-beamed nano- and microarchitected materials, several reports exist on the fabrication and deformation of 3D structural metamaterials with monolithic beams. For example, nanocrystalline nickel octet-truss nanolattices with 300- to 400-nm-diameter monolithic beams and 2-μm unit cells, created via TPL on custom-synthesized resins followed by pyrolysis, exhibited a modulus of ∼90 MPa, a compressive strength of 18 MPa, and a high fracture strain of >20% at a density of 2.5 g/cm³ (20). Reports on vitreous carbon octet-truss microlattices with beam diameters of ∼100 μm, fabricated by pyrolyzing a UV-mask patterned polymer template, reported a modulus of 1.1 GPa, a compressive strength of 10.2 MPa, and a fracture strain of only ∼3% at a density of 0.19 g/cm³ (24). Glassy carbon microlattices with rhombic dodecahedron unit-cell and beam diameters of 50 to 150 μm, fabricated using stereolithography and pyrolysis, had densities of 0.03 to 0.05 g/cm³, moduli of 5 to 25 MPa, compressive strengths of 0.08 to 0.35 MPa, and fractured at a strain of ∼5% (25). Glassy carbon nanolattices with tetrahedral unit cells created via TPL and pyrolysis had smaller dimensions (0.97- to 2.02-μm unit cells and beam diameters of ∼200 nm), a modulus of 3.2 GPa, and a compressive strength of ∼280 MPa at a density of ∼0.35 g/cm³ (18). These advances highlight a strong coupling between the density and compliance of architected materials: The lower the density, the softer and the weaker the material.

We developed an approach to fabricate nanoarchitected pyrolytic carbon and to demonstrate two prototype unit-cell geometries, octet- and iso-truss, shown in Fig. 1, using TPL and pyrolysis. The octet-truss architecture has cubic anisotropy and superior overall properties compared with other conventional lattices, such as triangular, tetrahedral, or cubic trusses and foams (28), whereas the iso-truss structure is isotropic and has been theorized to possess optimal stiffness compared with traditional lattice topologies (29). Uniaxial compression experiments revealed their Young’s moduli to be 0.34 to 18.6 GPa, their strengths to be 0.05 to 1.9 GPa, and prefailure deformability of 14 to 17% at density varying from 0.24 to 1.0 g/cm³. The highest specific strength is up to 1.90 GPa⋅g⁻¹⋅cm³, which outperforms all other reported mechanically robust lightweight meso/micro/nanolattices (7–27). We attribute this distinction to the optimized unit-cell geometries, reduced feature sizes, and high-quality pyrolytic carbon.

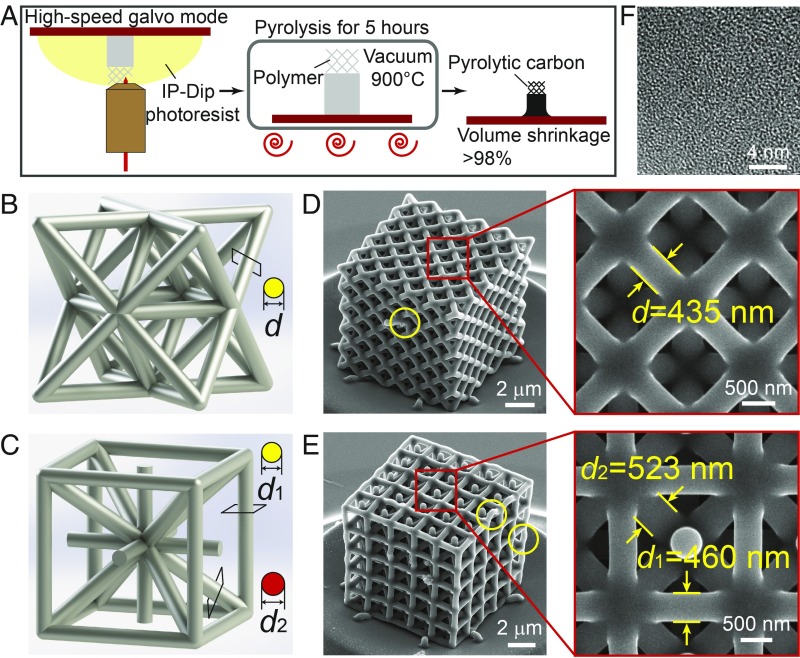
Fig. 1.

Fabrication and microstructural characterization of pyrolytic carbon nanolattices. (A) Schematic illustration of the fabrication process of pyrolytic carbon nanolattices. (B and C) CAD rendition of an octet- and iso-truss unit cell. (D and E) SEM images of an octet nanolattice with a strut diameter of d = 435 nm and an iso-truss nanolattice fabricated with a vertical strut diameter of d₁ = 460 nm and a slanted strut diameter of d₂ = 523 nm. (F) An HRTEM image of pyrolytic carbon extracted from the nanolattice, which indicates an amorphous nature of the pyrolytic carbon. Initial detectable structural imperfections caused by fabrication process are circled in D and E.

Results

Fig. 1A illustrates our fabrication process, which begins with printing 5 × 5 × 5 unit-cell microlattices out of IP-Dip photoresist using TPL. We used the high-speed galvo mode to print 7- to 10-μm-long struts with 0.8- to 3.0-μm-diameter circular cross-sections. The high-speed galvo mode operates in a layer-by-layer fashion, which creates beams with circular cross-sections, in contrast to many existing reports on nanolattices with elliptical beams (11, 12, 14, 16, 18, 21) that were produced via the piezo mode scanning in a vectorial manner. The polymer samples were heated in a vacuum furnace at a ramp rate of 7.5 °C⋅min⁻¹ up to 900 °C and then pyrolyzed for 5 h and cooled to room temperature at a natural rate (see Materials and Methods for more details). Fig. 1 B and C show computer-aided design (CAD) designs of 10-μm-sized octet- and iso-truss unit cells. Strut diameters d in the octet-truss were designed to be in the range 0.8 to 2.4 μm. In the iso-trusses, the vertical strut diameters d₁ were 1.4 to 3.0 μm, and the prescribed slanted strut diameters d₂ were maintained at $d_2=\sqrt{3\sqrt{3}}{d}_1/2$ with a d₂/d₁ ratio of ∼1.14 based on the topological optimization (29). After pyrolysis, the polymer transformed into a form of carbon and underwent significant volumetric shrinkage and mass loss (30). Each strut shrunk to ∼20 to 25% of its initial dimensions (Fig. 1 D and E) with a concomitant shrinkage in unit-cell size from ∼10 μm to ∼2 μm. The resulting strut diameters of ∼261 to 679 nm after pyrolysis, and the smallest diameter is significantly below the limits of resolution of most available 3D lithographic technologies (18, 20, 30). We estimated the relative density $\overline{\rho }$ of pyrolytic carbon nanolattices to be between 17% and 72% by calculating the volume fraction of solid materials in the nanolattices based on 3D CAD models and dimensions measured by SEM. The magnified image in Fig. 1E reveals that the d₂/d₁ is maintained at ∼1.14 after pyrolysis, which suggests uniform volume shrinkage. Fig. 1F shows a high-resolution transmission electron microscopy (HRTEM) image of a typical sample extracted from the nanolattice via focused-ion-beam milling and its glassy/amorphous microstructure. The density of pyrolytic carbon produced under these conditions is ∼1.40 g/cm³ (18), which is consistent with that of type-I glassy carbon fabricated under the pyrolysis temperature of below 2,000 °C (31). We calculated the density of nanolattices by multiplying this absolute density by the relative density of nanolattices to vary from 0.24 g/cm³ to 1.0 g/cm³, which is well within the lightweight range.

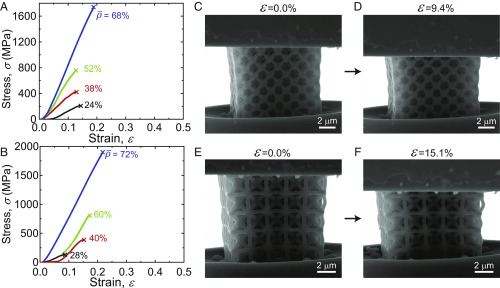
We performed uniaxial compressions on all polymer microlattices and pyrolytic carbon nanolattices (see details in Materials and Methods). Engineering stress versus strain curves was obtained by normalizing the load-displacement data from compression experiments by the cross-sectional footprint area of the overall samples and the initial height. Fig. 2 A and B convey the compressive stress–strain response of some representative octet- and iso-truss pyrolytic carbon nanolattices, which appear to be similar across all samples. As the relative density of the octet-truss nanolattices ranged from 24 to 68%, its Young’s modulus increased from 2.57 GPa to 10.73 GPa, and its compressive strength increased from 0.21 GPa to 1.73 GPa (Fig. 2A). The relative density of the iso-truss nanolattices was slightly higher (from 28 to 72%), its Young’s modulus increased from 2.28 GPa to 9.67 GPa, and its compressive strength rose from 0.14 GPa to 1.90 GPa (Fig. 2B). The initial nonlinearity in the stress–strain data arises from imperfect initial contact and slight initial misalignment between the rough lattice surfaces and the flat punch (16). Linear elastic loading persists up to a strain of ∼10 to 20%, after which all pyrolytic samples catastrophically failed via brittle fracture (SI Appendix, Fig. S1 A–D). The average fracture strains were 14.0% for octet- and 16.7% for the iso-truss nanolattices, which exceed the value of ∼10% reported for glassy carbon nanolattices (18) and the value of ∼3 to 5% for glassy carbon microlattices (24, 25). This enhanced deformability is enabled by better mechanical stability of circular struts, allowing more uniform transfer of load compared with elliptical struts (32), and a longer pyrolysis time to ensure sufficient carbonation. Fig. 2 C–F show the SEM images of typical octet- and iso-truss nanolattices during in situ compression. More detailed deformation processes are shown in Movies S1 and S2. SI Appendix, Fig. S2 shows the compressive stress–strain data of typical polymer microlattices with octet- (SI Appendix, Fig. S2A) and iso-truss (SI Appendix, Fig. S2E) unit cells for comparison and completeness. These data also have an initial nonlinear region over ∼2.5% strain caused by the slightly imperfect initial contact and misalignment between the rough lattice surfaces and the flat punch (16). Linear elastic loading commences over the strain range of ∼2.5 to 7.5% and is subsequently followed by a stress plateau that extends over 5 to 7.5%. The stress plateau corresponds to buckling of the struts, as supported by SEM images (SI Appendix, Fig. S2 C and G). SI Appendix, Table S1 summarizes the Young’s moduli and strengths of the tested polymeric microlattices with different relative densities and reveals that, for comparable relative densities, the Young’s modulus of iso-truss microlattices is a factor of ∼2, and the strength is 1.3× higher than those of the octet-truss microlattices, which is consistent with predictions (29).

Fig. 2.

In situ uniaxial compression experiments on pyrolytic carbon nanolattices. (A and B) Typical mechanical response of pyrolytic carbon octet- and iso-truss nanolattices with different relative densities obtained from in situ compressions. (C and D) SEM images of an octet-truss nanolattice with relative density of 37.5% at different strains during compression. (E and F) SEM images of the iso-truss nanolattice with relative density of 39.4% at different strains during compression.

Discussion

SI Appendix, Fig. S3 A and B show the variations of Young’s modulus and compressive strength with relative density, respectively. As the relative density ranges from 17 to 72%, our pyrolytic carbon nanolattices have the scaling relations of Young’s modulus as E ∼ $\overline{\rho }$^2.25 for the octet-truss and E ∼ $\overline{\rho }$^1.90 for the iso-truss, and relations of compressive strength as σ_y ∼ $\overline{\rho }$^2.41 for the octet-truss and σ_y ∼ $\overline{\rho }$^2.50 for the iso-truss. These scaling relations deviate from theoretical predictions for ideal, stretching-dominated structures (1), that is, E ∼ $\overline{\rho }$ and σ_y ∼ $\overline{\rho }$, which is mainly attributed to fabrication-induced structural imperfections and to the use of nonslender beams. The SEM images in Fig. 1 D and E (also SI Appendix, Fig. S1 A and C) show some representative detectable fabrication-induced defects that we found to be present in virtually all samples, including beam junction offsets and bulges, slight curvature of the struts, and micropits and voids. During compression, these imperfections induce localized deformation and microcracking around the nodes, as well as buckling/bending of struts, which leads to premature structural failure (11). When such local deformation and failure occur in stretching-dominated lattices, the scaling exponents for the modulus and strength of lattices exceed theoretical predictions and are generally in the range of 1.4 to 2.5, as exemplified by previous studies (8, 11, 12, 18). The slenderness ratio, defined as R/L, where R is the beam radius and L is the beam length, as well as the nodal geometry, have been shown to have significant effects on the stiffness and strength of lattices (9, 12, 33). The nodes generally form solid joints that impede beam rotation and, to some extent, shorten the effective length of the adjoining beams and lead to stiffening of overall lattices (12). Recent computational and experimental studies have found that for solid-beam octet-truss lattices, with a beam slenderness ratio greater than 0.06 and corresponding relative density beyond 10%, the scaling relations for the modulus and strength diverge from existing analytic theories, with the exponents of 2.20 and 1.88 instead of 1.0 (12). The beam slenderness ratios, R/L, of the octet-truss nanolattices in this work are 0.07 to 0.24, similar to 0.07 to 0.12 associated with monolithic polymer octet-truss nanolattices (12), as well as to 0.06 to 0.20 associated with glassy carbon nanolattices with tetrahedral unit cells (18). The scaling exponents of 2.25 (octet-truss) and 1.90 (iso-truss) for Young’s modulus and of 2.41 (octet-truss) and 2.50 (iso-truss) for strength found for the nanoarchitected carbon with a relative density between 15% and 80% in this work agree with these existing reports (12).

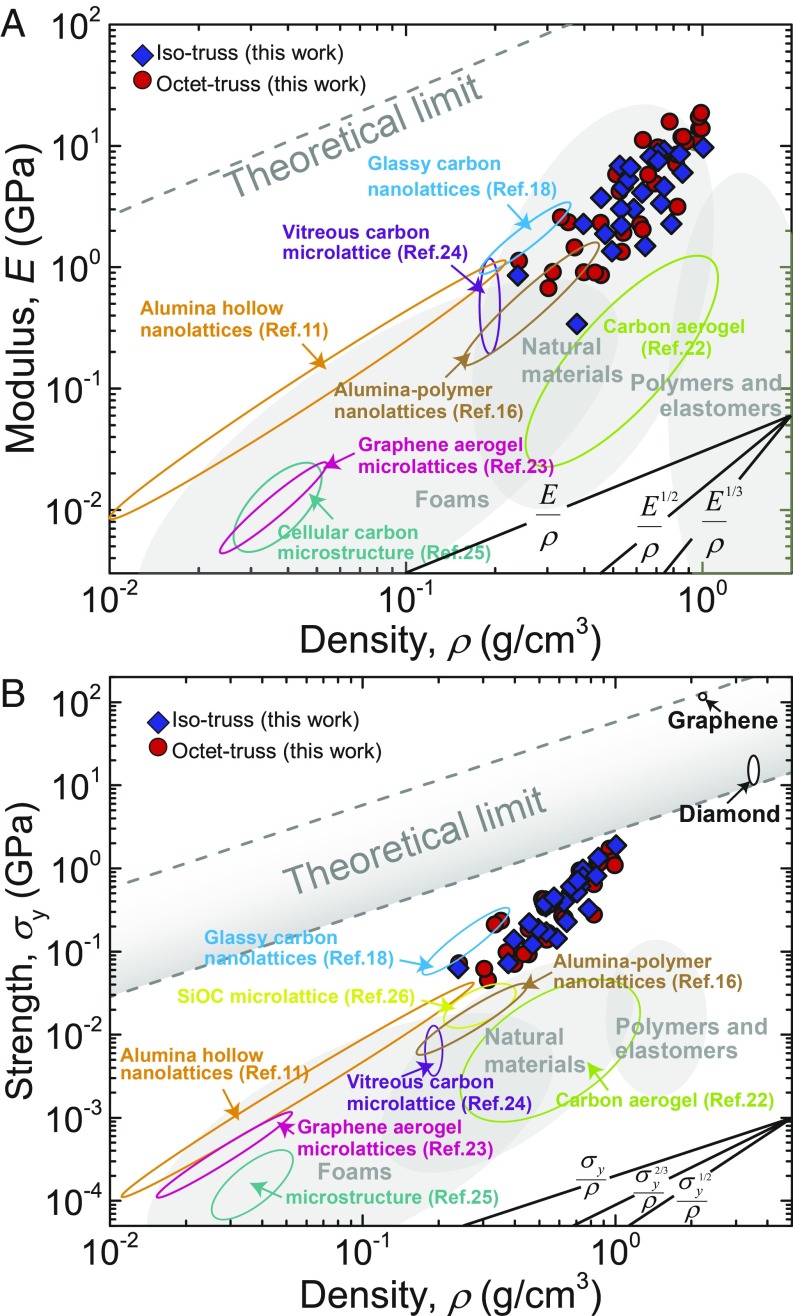
Fig. 3 shows the material property space for Young’s modulus (Fig. 3A) and compressive strength (Fig. 3B) versus density of the pyrolytic carbon nanolattices in this work in the context of all reported micro/nanoarchitected materials made up of carbon, ceramics, or ceramic–polymer composites (11, 16, 18, 22–26). These plots reveal that their moduli and strengths are approximately one to two orders of magnitude greater compared with monolithic carbon aerogels with nonordered open-cell structures (22), vitreous carbon microlattices (24), and alumina–polymer nanolattices (16) with comparable densities. The mechanical attributes of pyrolytic carbon nanolattices in this work span a large density range, from 0.24 to 1.0 g/cm³. The scaling exponents between mechanical attributes and density of pyrolytic carbon nanolattices are 2.25 (octet-truss) and 1.90 (iso-truss) for Young’s modulus and 2.41 (octet-truss) and 2.50 (iso-truss) for strength, all of which are larger than the exponents of 1.61 for modulus and 1.76 for strength of alumina hollow nanolattices (11), as well as the exponents of 1.67 for modulus and 2.00 for strength of glassy carbon nanolattices (18). If we extrapolate the existing data of alumina hollow nanolattices (11) and glassy carbon nanolattices (18) to a density of 1.0 g/cm³ by following their corresponding scaling relationships, pyrolytic carbon nanolattices have relatively higher modulus and strength than both alumina hollow nanolattices and glassy carbon nanolattices at a comparable density (>0.4 g/cm³) because of larger scaling exponents. It is noted that glassy carbon nanolattices (18) possessed the highest stiffness and strength over all previous micro/nanoarchitected materials (11, 16, 18, 22–26) with density below 1.0 g/cm³. Therefore, Fig. 3 conveys that the relatively high scaling exponents for the mechanical attributes of pyrolytic carbon nanolattices lead to the highest stiffness and strength values reported to date for lightweight micro/nanoarchitected materials. The strength of pyrolytic carbon nanolattices with iso-truss geometries at a density of 1.0 g/cm³ is 1.90 GPa, and that for the octet-truss at a density of 0.95 g/cm³ is 1.73 GPa, which are comparable to the theoretical strength of glassy carbon of ∼E_s/10, that is, 2 to 3 GPa, where E_s is the modulus of glassy carbon (34–36). Fig. 3A demarcates the theoretical limit of Young’s modulus as a function of density, expressed as E = 250ρ (11), and Fig. 3B includes the theoretical limit of strength versus density, whose lower bound is defined by diamond, and the upper bound corresponds to graphene (18). More details regarding the determination of these theoretical limits are supplied in Materials and Methods.

Fig. 3.

Mechanical properties versus density maps of pyrolytic carbon nanolattices. (A and B) Young’s modulus and compressive strength of pyrolytic carbon nanolattices plotted versus density on a log-log scale. For comparison, these charts include several micro- and nanoarchitected materials reported so far, such as alumina hollow nanolattices (11), alumina–polymer nanolattices (16), glassy carbon nanolattices (18), monolithic carbon aerogels (22), graphene aerogel microlattices (23), vitreous carbon nanolattices (24), cellular carbon microstructures (25), and SiOC microlattices (26).

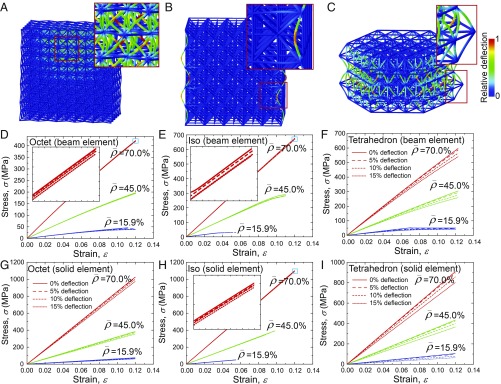
To further investigate the influence of the initial imperfections on the mechanical properties of pyrolytic carbon nanolattices, we performed a series of finite-element (FE) simulations of compressing samples with relative densities varying from 15.9 to 70%. Details for the FE simulations are provided in Materials and Methods. The simulated nanolattices had three types of unit-cell geometries: octet-truss and iso-truss for comparison with experiments and tetrahedron-truss for comparison with previous literature (18) that found that the initial deflection of struts can reduce the compressive strength of nanolattices at lower relative densities. Fig. 4 A–C show the simulated nanolattices with different unit cells, where preexisting defects were created by imposing the corresponding buckling eigenmodes with a maximum deflection of the struts prescribed as 5%, 10%, and 15% of the edge length, similar to ref. 18. After introducing these initial deflections, some struts remained prebent before compression, which resembles structural imperfections in the experimental samples (Fig. 2 C and E). We also simulated the compression of a perfect nanolattice as a reference. Fig. 4 D–I show compressive stress–strain responses up to 12% strain from FE simulations based on beam and solid elements, respectively. These curves reveal that the strengths of nanolattices with initial deflection are always lower than those of their perfect counterparts. SI Appendix, Fig. S4 shows the dependence of modulus and strength on relative density from experiments and FE simulations. These plots reveal that FE results based on solid elements appear to capture experiments better than those based on beam elements, which exhibit a similar trend with larger deviations from experiments at higher relative densities, for reasons including that the beam model is accurate only when the beam has a large aspect ratio and that the beam model ignores the effect of nodes in the overall deformation of nanolattices. SI Appendix, Fig. S5 quantifies the variation in strength reduction as a function of initial deflection relative to that of a perfect nanolattice from FE modeling with beam and solid elements. It is noted in SI Appendix, Fig. S5 that the results from FE modeling with beam and solid elements show very similar variations in relative reduction in strength. These quantitative results indicate that (i) for a given relative density and architecture, the relative reduction in strength increases with greater initial deflection; (ii) for a given architecture, the nanolattices with higher densities experience smaller relative weakening associated with defects; and (iii) nanolattices with tetrahedron-truss unit cells are most susceptible to flaws, followed by octet-truss and iso-truss unit cells for all densities. For example, for the relative density of 15.9%, the relative reduction in strength is 2.5% (beam-element modeling) and 3.4% (solid-element modeling) for the iso-truss architectures and 15% (beam-element modeling) and 17% (solid-element modeling) for the octet-truss architectures at a maximum deflection of 15%. The same relative weakening for a relative density of 70% is only ∼1% (beam-element modeling) and <4.9% (solid-element modeling).

Fig. 4.

FE simulations of uniaxial compression of pyrolytic carbon nanolattices with different unit cells. (A–C) Simulated configurations of octet-, iso-, and tetrahedron-truss nanolattices with preexisting defects introduced by imposing an initial deflection of struts. The insets are zoomed-in views of local structures with initial deflection of struts. The color represents the extent of initial deflection. (D–F) Compressive stress–strain curves from simulations (with beam elements) of octet-truss, iso-truss, and tetrahedron-truss nanolattices with different relative densities and initial specific deflection. (G–I) Compressive stress–strain curves from simulations (with solid elements) of octet-truss, iso-truss, and tetrahedron-truss nanolattices with different relative densities and initial specific deflection.

To reveal the underlying deformation mechanisms, we compared deformation snapshots of octet- and iso-truss nanolattices obtained from in situ SEM experiments with FE modeling with solid elements (SI Appendix, Figs. S6 and S7). We observe that for both the octet- and iso-truss nanolattices the deformed configurations are similar. In particular, both simulations and experiments captured the same deformation mechanisms in the iso-truss nanolattices: buckling of the outermost vertically oriented struts in the course of compression. For the octet-truss nanolattices, the modeling revealed the high stresses to occur at the nodes, which suggests localized deformation and eventual failure near the nodes.

The results from our current experimental and computational studies indicate that carbon nanolattices with iso-truss and octet-truss architectures, which are intrinsically brittle, exhibit a reduced susceptibility to flaws at higher densities. This can be explained by the local failure in individual struts redistributing stored elastic energy among other load-bearing truss members instead of triggering catastrophic structural failure. This is consistent with the attainment of nearly theoretical strengths of carbon nanolattices with densities higher than 0.95 g/cm³. When the struts’ diameters are reduced by hundreds of nanometers to dimensions comparable to the critical size for flaw insensitivity of pyrolytic carbon (see details about determination of critical size in Materials and Methods), the struts exhibit high strength and good flaw tolerance (4), which to some extent contributes to the high strength of carbon nanolattices, which is dictated by local stresses and the volume fractions of the struts. Nanolattices with lower densities have thinner and more slender struts, which leads to higher local stresses during compression due to their smaller cross-sectional areas, and the nodal contributions are negligible (12, 33). In this case, the higher local stresses lead to earlier buckling of some struts or higher stress concentration around the nodes. Together with the lower volume fraction of thinner struts, the nanolattices with lower densities (i.e., thinner struts) might fail at lower global stresses. In contrast, nanolattices with higher densities (i.e., thicker struts) have lower local stresses because of the greater cross-sectional area in each strut, with significant contribution of the nodes to the load-bearing ability, which results in a relatively uniform distribution of applied load throughout the nanolattice (12, 33). Under these conditions, the nanolattices fail when the local stresses in the struts approach the theoretical strength of constitute carbon. Such local stress and higher volume fraction of struts eventually result in the high strength of nanolattices at higher densities. The optimized unit-cell geometries, such as octet- and iso-truss, with better flaw tolerance also facilitate the achievement of high strength.

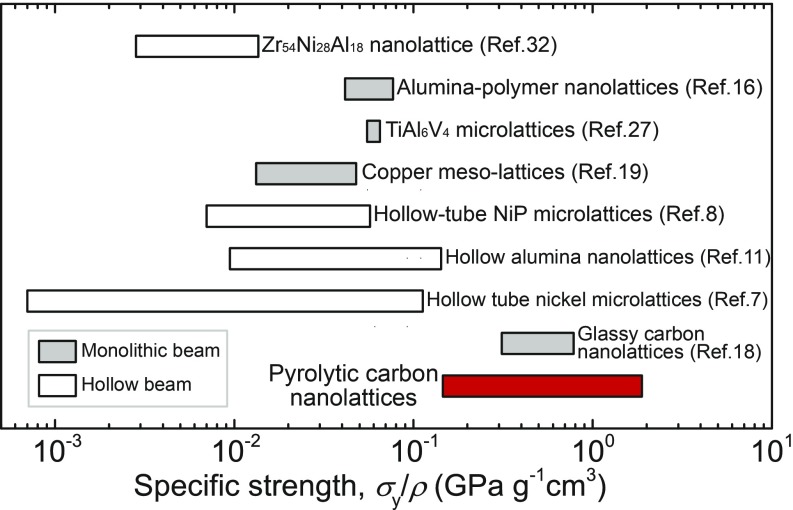
Fig. 5 shows that the specific strengths of pyrolytic carbon nanolattices range from 0.146 to 1.90 GPa⋅g⁻¹⋅cm³, which represents one to three orders of magnitude improvement over all nano- and microarchitected periodic lattices reported to date, including hollow-tube nickel (7) and NiP (8), copper (19), and TiAl₆V₄ (27) microlattices, as well as of hollow-beam alumina (11), alumina–polymer (16), and metallic glass Zr₅₄Ni₂₈Al₁₈ nanolattices (32). The maximum specific strength of the carbon nanolattices in this work, at a density of 1.0 g/cm³, is 2.4 times higher than that of 0.80 GPa⋅g⁻¹⋅cm³ reported for glassy carbon nanolattices (18) and represents 35% of fully dense diamond, at 5.60 GPa⋅g⁻¹⋅cm³, which has the highest specific strength of all bulk materials (18). Such ultrahigh specific strength of our pyrolytic carbon nanolattices arises from both the nanosized beam diameters and the optimized lattice topology.

Fig. 5.

Comparison of the specific strength between our pyrolytic carbon nanolattices and other micro- and nanolattices that have been reported to date.

Conclusions

We advanced an additive fabrication methodology to create micro- and nanoarchitected pyrolytic carbon with densities below 1.0 g/cm³, GPa-level strengths, and >10% deformability before failure. As a point of departure from all existing work on micro/nanolattices (11, 16, 18, 22–26), the strength of nanoarchitected carbon in this work approaches the theoretical limits. A rational design of lattice topologies with appropriate microstructure and nano- and microscale characteristic material dimensions enabled us to create prototype architectures of octet- and iso-truss pyrolytic carbon nanolattices with Young’s moduli of 0.34 to 18.6 GPa and strengths of 0.05 to 1.90 GPa at densities of 0.24 to 1.0 g/cm³, which translates into a specific strength of 0.146 to 1.90 GPa⋅g⁻¹⋅cm³, a level that has not been attained by any carbon-based or architected material. This nanoarchitected carbon also exhibited average fracture strains of 14.0 to 16.7%, exceeding those of all other reported brittle architected materials. Experiments and simulations demonstrate that for densities higher than 0.95 g/cm³ these samples become virtually insensitive to fabrication-induced defects, giving rise to nearly theoretical strength of 1.90 GPa. This work provides insights into the fundamental scientific principles that govern the design and properties of nanoarchitected materials and provides a feasible pathway for their use in scalable fabrication of robust porous materials with defect tolerance, ultralight weight, and superior strength.

Materials and Methods

Fabrication of Pyrolytic Carbon Nanolattice.

We first fabricated polymeric microlattices out of IP-Dip photoresist, using TPL DLW (Nanoscribe, GmbH) with a speed of 10,000 μm⋅s⁻¹ and laser power of 17.5 mW. During the DLW process, we printed struts with 0.8- to 3.0-μm-diameter circular cross-sections via the high-speed galvo mode in a layer-by-layer fashion. All of the printed polymeric microlattices have two typical unit-cell geometries: one is the octet-truss (Fig. 1B) and the other is the iso-truss (Fig. 1C). The iso-truss structure is isotropic and has optimal stiffness compared with most traditional lattice topologies (29), while the octet-truss structure is anisotropic. Recent computational studies (37) have investigated the anisotropic elastic modulus and yield strength of the octet-truss, with results showing that the elastic modulus is maximum in [111] direction and about 5/9 of the maximum value in [001] direction (37). The compressive yield strengths in both [111] and [001] directions are maximum over all directions (37). In subsequent in situ testing and FE modeling, uniaxial compression in [001] direction is applied on the octet-truss to achieve maximum yield strength. The unit-cell size of polymeric microlattices is ∼10 μm. Then, the polymeric microlattices were pyrolyzed at 900 °C for 5 h in a vacuum with a ramp rate of 7.5 °C⋅min⁻¹ up to the target temperature and were then cooled to room temperature at a natural rate. After pyrolysis, the polymeric microlattices were transformed into pyrolytic carbon nanolattices due to the mass-loss-induced carbonation of the polymers at the elevated temperature (30). The diameters of all struts in pyrolytic carbon nanolattices isotropically shrunk to ∼261 to 679 nm, which is ∼20 to 25% of their initial dimensions (Fig. 1 C and E). The unit-cell size of all pyrolytic carbon nanolattices is ∼2 μm.

Mechanical Testing.

We conducted uniaxial compression experiments on all fabricated polymer microlattices and pyrolytic carbon nanolattices. Some of these experiments were performed in an in situ instrument (InSEM; Nanomechanics) with a 170-μm-diameter flat diamond punch at a constant strain rate of 10⁻³ s⁻¹ to reveal the deformation morphology simultaneously with mechanical data acquisition. Other experiments were performed at a constant loading rate of 0.2 mN⋅s⁻¹ in a nanoindenter (G200; Agilent/Keysight Technologies) using a 120-μm-diameter diamond flat punch.

Finite Element Modeling.

We performed a series of FE modeling for the compression of pyrolytic carbon nanolattices via Abaqus. The isotropic linear elastic material was used for modeling. All nanolattices were modeled by using 2-node beam elements (B31 in Abaqus) and 10-node tetrahedral solid elements (C3D10 in Abaqus). The Young’s modulus of the material was 20 GPa (34) and the Poisson’s ratio was 0.15 (18). The simulated nanolattices have three types of unit-cell geometries, including octet-truss, iso-truss, and tetrahedron-truss. For each type of nanolattice, the unit-cell size was set to be 2 μm, and the relative density varies from 15.9 to 70% by alternating the diameter of struts. Before compression, we introduced initial deflection to the struts of simulated nanolattices by imposing the corresponding buckling eigenmodes of nanolattices shown in Fig. 4 A–C. These eigenmodes of nanolattices are obtained from the FE modal analysis with the beam elements. The maximum deflection of the struts was set as 5%, 10%, and 15% of the edge length. After introducing the initial deflection, some struts remained prebent before compression, which is very similar to some structural imperfections in the experimental samples (Fig. 1 D and E and SI Appendix, Fig. S1 A and C). During compression, the bottom of the nanolattice was fixed, and the top was imposed by displacement loading. We simulated the compression of the nanolattice with perfectly straight struts as a reference to address the influence of imperfections/flaws on mechanical properties and response of the nanolattice.

Determination of Theoretical Limits for Young’s Modulus and Strength Versus Density.

The modulus-density theoretical limit was taken from the literature (11) and was determined by the bound of many data of real materials based on Granta Design, which is a standard software for materials selection and graphical analysis of materials properties. More information regarding Granta Design can be found on its webpage (https://www.grantadesign.com/) and in relevant software documentation. The strength-density limit is defined in the literature (18) and is only a specific range based on measurements for all materials that have been made to date. The lower bound of this range is defined by diamond, which has the highest specific strength of all bulk materials, whereas the upper bound is determined by graphene, which holds the highest strength in all materials so far.

Determination of Critical Size for Flaw Insensitivity of Pyrolytic Carbon.

Existing theoretical, computational, and experimental studies (4, 38, 39) demonstrated that brittle materials become insensitive to flaws when their dimensions are reduced below a critical size, which drives their strength toward theoretical limit. Such critical size h* can be determined by the following equation (38):

$$h^{\ast }=1.87\frac{\mathrm{\Gamma }E}{{\sigma }_{th}^2},$$ [1]

where Γ is the fracture energy, E is the Young’s modulus and σ_th is the theoretical tensile strength. Substituting previous experimental measurements on various parameters, that is, E = 22.5 GPa (18), Γ = 29.9 to 61.9 J/m² (36), and σ_th = 2.3 to 2.8 GPa (18), into Eq. 1, we obtained the critical size for flaw insensitivity of pyrolytic carbon as 160.5 to 492.3 nm. This range is consistent with the characteristic diameters (261.2 to 678.7 nm) of struts in nanolattices we fabricated. This indicates that during deformation, individual struts can exhibit flaw insensitivity and undergo high stresses approaching the theoretical limit and associated large deformation, leading to high strength and good deformability of the overall nanolattice. Therefore, controlling strut size to nanoscale seems to be an essential factor for the design and fabrication of nanolattices with high strength and good deformability.