ABSTRACT
Since the demand for health services is the key driver for virtually all of a health care organisation’s financial and operational activities, it is imperative that health care managers invest the time and effort to develop appropriate and accessible forecasting models for their facility’s services. In this article, we analyse and forecast the demand for radiology services at a large, tertiary hospital in Florida. We demonstrate that a comprehensive and accurate forecasting model can be constructed using well-known statistical techniques. We then use our model to illustrate how to provide decision support for radiology managers with respect to department staffing. The methodology we present is not limited to radiology services and we advocate for more routine and widespread use of demand forecasting throughout the health care delivery system.
KEYWORDS: Radiology services, demand forecasting, multiple regression analysis, personnel staffing, forecast error
1. Introduction
Almost every individual involved with administration of a radiology business unit (either in academic or private practice) has puzzled over tables or graphs showing procedure volumes over time. For any number of reasons, viewers of such information want to know what governs the variability in these numbers and how to predict future trends. One example is that of a radiology group practice deciding to recruit new associates for the next several years. Likewise, residency programme directors want to know future clinical volume so as to plan for and justify class sizes. When generating capital budgets, projections of the volume of procedures must be made; this information, along with cost data, informs those responsible about whether to buy new radiology equipment or to revamp or dispose of existing equipment. These are examples where decision-makers mostly want to know about general long-term (i.e., months or years) trends in volume.
Other situations necessitate short-term analyses and predictions. For example, department administrators need to plan ahead for scheduling technologists, transcriptionists, and front desk personnel. This is often done on a per shift basis for several weeks into the future. Similarly, with picture archiving and communications systems (PACS), moving and storing electronic images become issues for medical informatics workers (Samei et al., 2004). Procedures not only need to be scheduled, performed, and read but large amounts of data must be transmitted, stored, and retrieved. Capacity planning for acquisition processors, network infrastructure, and storage archives is critical to successful PACS implementation and deployment. Procedure mix and volume translates into data traffic whose time-dependent behaviour over periods as short as seconds may be of intense interest to those responsible for building and maintaining these systems.
Efficient and effective delivery of radiological services is especially critical when considering the role radiology plays within the overall delivery of health care. Medical imaging is used to examine virtually all anatomical areas of the body, from the brain to the toes, providing needed information to most medical specialties. Patients might receive radiological imaging at any point in their lives from paediatrics to gerontology. Radiological information is needed for both acute care (e.g., emergency departments) and non-urgent care (e.g., routine screenings such as mammograms or bone scans) as well as for inpatient and outpatient services. Although mostly used in clinical settings, radiological imaging also plays an important role in clinical trials and research (Miller, Krasnow, & Schwartz, 2014). Medical providers in developing countries, too, have a critical need for high-quality, timely radiological services (Mohd-Nor, 2011). From this perspective, maladroit oversight of a radiology department has the potential to permeate much of the health system.
Radiology departments often undergo special scrutiny because of their high capital equipment costs. Computed tomography (CT) and positron emission topography (PET) scanners, for example, can cost in excess of two million dollars and require expensive long-term equipment service contracts. Especially when space is at a premium, projections of future growth (and the need for additional equipment to service it) have important implications for all units within a radiology department, since the large size of medical imaging devices means competition for alternative uses of floor space including registration and nursing desks, offices, examination rooms, medical records areas, and so forth. Hence, the need for careful consideration of future revenues and costs comes down to one integral component: volume forecasts.
Thus, decision-makers tasked with managing radiology departments benefit from understanding future demand. Among the many service-providing units in the health system, radiology presents some special challenges to forecasters. Historical records that demonstrate stable patterns produce better forecasts than those with more noise. Yet radiology is an unusual hybrid in that some service requests are mostly controllable (e.g., routine mammogram screening) while others (e.g., urgent care) are not. In this sense, the success of a radiology forecasting project hinges, in part, on the ratio of planned to unplanned service requests if the unplanned service requests are both highly variable and represent a large proportion of total radiology volume.
From a broader perspective, the last two decades have seen a dramatic resurgence of operations research tools being developed and applied to all facets of the health care industry. An important and ongoing debate centres on the utility of these applications for the “real world” health care managers. In particular, questions like: Do they understand the model? Will they use the model? If they use the model, will it improve the delivery of their health care services? are frequently posed (Reid, Compton, Grossman, & Fanjiang, 2005; Woolsey & Swanson, 1975). Pragmatic models are better for “real-world” decision-makers such as those in the health care industry where training in very sophisticated quantitative modelling is not consistent (or even available) across providers (Woolsey & Swanson, 1975). This has also been confirmed more recently in the National Academy of Engineers and Institute of Medicine report, Building a Better Delivery System: A New Engineering/Health Care Partnership (Reid et al., 2005). Despite the increased attention, there remains a distinct gap between the models that operations researchers can construct and their acceptance and use by the health care decision-makers. Consistent with Woolsey and Swanson (1975) and Reid et al.’s (2005) guiding principles, forecasting models ought to be both pragmatic and easily relatable to health care decision-makers.
In this article, we explore the question of whether reliable forecasts of radiological services might be obtained. We do so within the context of a radiology department at a teaching hospital in Florida. Of particular interest is whether volume forecasts can help guide the assignment of staff to three 8 h daily shifts. We begin with a literature review followed by a description of the study setting and data. We then describe the analytical approach taken to develop the forecasting model and produce the forecasts. A discussion of the results is followed by concluding remarks that places our work in a broader health care operations context.
2. Literature review
Forecasting applications have found their ways to most corners of the health care industry. Examples include projecting the growing prevalence of diseases over time (Heidenreich et al., 2011) and tracking shortages of health care workers (O'Brien-Pallas et al., 2001; Scheffler, Liu, Kinfuc, & Dal Pozd, 2008). Both micro- and macro-level decision-makers have benefited from health care-related forecasts. Batal, Tench, McMillan, Adams, and Mehler (2001), for example, predict admissions to an urgent care centre at a Denver hospital whereas Lapierre, Goldsman, Cochran, and DuBow (1999) consider optimal allocation of beds across hospital units. Still others have relied on health care trends to inform public policy; see, for example, the Lightwood et al. (2009) study of the medical, economic, and policy implications of adolescent obesity.
Some projects require short-term forecasts, some medium-range, while others concern the long term. Data needs and measurement of the outcome variable are dictated accordingly (Getzen, 2000). Jones et al. (2009), for example, studied the short-term (i.e., hourly) operational and resource needs of an emergency department whereas another emergency department study (Jones & Joy, 2002) found that daily data were better suited for forecasting number of occupied beds. Similarly, but instead of volume, Cerrito and Pecoraro (2005) sought to forecast amount of time needed to treat individual emergency department patients as a function of their triage level and associated diagnosis and the congestion that may exist in the emergency department at the time of patient arrivals. Because 18-month projections were needed for budgetary purposes, Gardner (1979) used monthly data to forecast the demand for blood tests in a hospital laboratory. Myers and Green (2004), on the other hand, describe a situation needing 10-year annual forecasts of demand for capacity planning of a large health system in the northeastern US.
Trend and seasonality tend to capture the analytical focus of health care forecasting projects. For purposes of long-term capacity planning, trend is of primary importance (e.g., Chrysanthopoulou et al., 2007) whereas seasonality dominates an analysis of day-to-day operations (e.g., Jones & Joy, 2002). In some settings, both trend and seasonality need to be considered (Côté & Tucker, 2001).
Many different forecasting methodologies may be found in the health literature including extrapolation (e.g., Choo, 2000; Heidenreich et al., 2011), advanced time-series methods (e.g., Jones & Joy, 2002; Jones et al., 2009), econometric models (e.g., Lakdawalla et al., 2003), regression (e.g., Côté, Smith, Eitel, & Akçali, 2010), and simulation (e.g., Hoot et al., 2008; Lapierre et al., 1999). Some advocate for using a mix of qualitative and quantitative procedures (e.g., Connor, Alldus, Ciapparelli, & Kirby, 2003). Thus, forecasting applications to health care settings run the full gamut of analytical sophistication. Increasingly, though, health care managers seek straightforward forecasting methodologies whose results can be easily understood by decision-makers. Given the ready availability of patient data in electronic form, practitioners also value forecasting methodologies that can be repeatedly updated in real time without relying on statistical expertise or advanced forecasting software: “Virtually all of the forecasting that a healthcare organisation normally requires can be performed on a spreadsheet without use of special software” (Dommert & Getzen, 2005, p. 107). Goldstein and Gigerenzer (2009) argue that simple forecasting methodologies can make better predictions than complicated ones in some settings, so the pursuit of workable, even if not optimal, solutions holds some promise. To that end, several tutorial-type articles seek to enlighten managers about data, methods, and practices pertinent to health care forecasting projects (Côté, Smith, Eitel, & Akçali, 2013; Côté & Tucker, 2001; Dommert & Getzen, 2005; Finarelli & Johnson, 2004).
Regarding the delivery of radiology services such as the focus of this article, much of the published work in this area is retrospective. Bhargavan and Sunshine (2005), for example, use Medicare claims data to describe historical patterns in radiology services by US census region and across imaging modalities. Likewise, Lang, Huang, Lee, Federico, and Menzin (2013) study MRI and CT utilisation rates using Medical Expenditure Panel Survey (MEPS) data from 2000 to 2009. A few works focus on trends in imaging practices related to specific medical maladies such intestinal obstruction (Otero et al., 2008) and hepatocellular carcinoma (Hyder et al., 2013). Many investigations focus on historical trends at the national (e.g., Wu et al., 2013) or global (e.g., Thomas, 2011) level. We found only one article that, like ours, uses facility-level data to produce specific numerical forecasts of radiological volume: Chrysanthopoulou et al. (2007). In that article, 60 monthly forecasts of radiology volume are used to compare differences in utilisation rates across different imaging modalities at a teaching hospital in Greece with the intent to better understand how future demand for the modalities might increase (or decrease) over the next five years. They used a combination of linear and log-linear autoregressive techniques to extrapolate the underlying trend associated with a range of radiology modalities. Our work appears to be the first to employ a formal forecasting methodology to: (1) forecast radiology volume at a stated shift level, and (2) use that forecast inform decision-makers about how staffing needs might vary in accordance with the forecast.
3. The study setting
Our focus is the radiology department of an 800-bed tertiary care teaching hospital in Florida. This department provides radiological studies for inpatient services, the emergency department, and ambulatory patients from outpatient clinics associated with the teaching hospital. It also conducts radiological studies requested by referral from the surrounding community. The full range of imaging modalities are available including radiography (i.e., X-rays), CT and PET scans, magnetic resonance imaging (MRI), ultrasound, nuclear imaging, and mammography. The workflow that produces these images typically unfolds in this fashion. Arrivals at the radiology department are broadly classified as either emergent or nonemergent patients where emergent patients originate in the hospital’s emergency department and nonemergent patients are either existing inpatients or scheduled outpatients. For outpatients, they check in at a registration desk and are then seen by a financial representative who collects patient information, insurance information, and any applicable copays or self-pays. This step is bypassed for emergent and inpatient arrivals. Regardless, a radiologic technologist leads the patient to an examination room, performs the imaging procedure, and ensures the quality of the image produced. The technologist then releases the patient, if outpatient, or coordinates with other hospital staff for transport of inpatients. The scan enters a work queue to be read and reported on by radiologists.
Given its high capital costs, the radiology department undergoes monthly and yearly budget reviews. A requisite component of the annual review is a five-year outlook of expected capital expenditures. Operating costs such as supplies (e.g., contrasts, catheters), labour, and non-service-contract items (e.g., CT tubes) are important inputs to both budgetary reviews. Recent budget cycles have looked closely at labour costs, in part because labour costs are the largest piece of the operating budget. Local and industry-wide shortages of radiologists and radiologic technologists have generated an interest in alternative staffing schedules that might involve a mix of full-time, part-time, or overtime hours. To prepare these schedules, accurate predictions of shift-level and daily procedure volumes are needed and managers must learn how best to translate procedure volume forecasts into staffing needs.
This radiological department is open 24 h a day, 7 days a week. Staff are scheduled into three 8 h shifts (i.e., Midnight to 8 am, 8 am to 4 pm, and 4 pm, to Midnight). The method used to produce the shift-level data are described next.
4. Data
The basic work unit of the radiology department is a single episode of care where a patient is examined with one of the medical imaging modalities. An inspection of a particular body region or organ system produces a set of images for interpretation by a radiologist. Each examination is uniquely identified with an accession number at the time the study is formally ordered in the radiology management system (RMS). It is this time that is recorded for each of the examinations in our data-set. For outpatients, order time is when the patient arrives in the department on the day of the examination. For inpatients, order time is the time at which the hospital information system (HIS) transmits orders for radiology studies to the RMS once a nursing unit clerk enters a physician’s order in the patient’s chart. Aggregated across all medical imaging modalities, the relative volume of inpatients and outpatients is approximately 60% and 40%, respectively. Unfortunately, the time series data do not distinguish whether procedures were planned or unplanned.
The radiology volume data were extracted from an enterprise database containing the number of orders per hour for all imaging procedures done in the study facility over a two-year period from 2003–2004. The hourly data were then aggregated by shift per day to create 2,193 shift-level observations (i.e., 731 days × 3 shifts per day). The variables in the data-set are Volume (i.e., number of procedures), Shift (i.e., 1 for midnight to 8 am, 2 for 8 am to 4 pm, and 3 for 4 pm to midnight) and Day (i.e., day of the week: Monday, Tuesday, etc.). Recognising potential concern associated with the age of the time series, we consulted with a range of health care decision-makers who confirmed that, despite its age, our time series was indeed representative of radiology volume both in terms of its currency and applicability to facilities beyond ours.
5. Exploratory data analysis
Forecasting projects benefit from initial exploration of the data to guide the construction and evaluation of the eventual forecasting model. Figure 1 displays the frequency distribution of Volume by shift. Upon inspection, shift 1 (Panel A) and shift 3 (Panel C) have similar distributions while shift 2 (Panel B) is distinctly bimodal. All shift 1 and 3 volumes are below 250 and volumes exceeding 250 are exclusively from shift 2. Thus, differences in shifts are important sources of variation in Volume and should be captured in the forecasting model. Figure 1 also displays a small cluster of shift 2 volumes (Panel B). Further investigation reveals that most of those observations occur on holidays. Accordingly, the variable Holiday was added to the data-set for observations representing statutory United States federal holidays like New Year’s Day, Labour Day, Thanksgiving, and Christmas; approximately 2.6% of the observations in the data-set are holidays.
Figure 1.
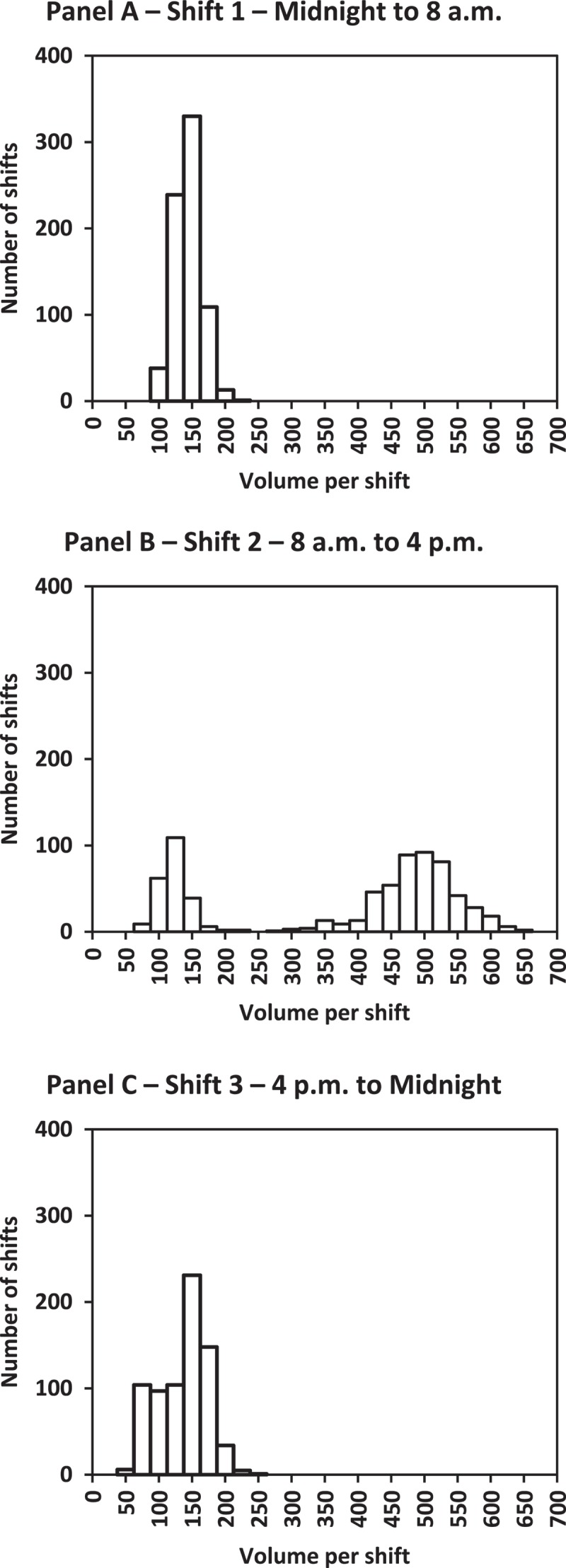
Frequency distribution of radiology volume by shift.
Figure 2 shows boxplots of Volume by Day and Shift. Holidays are indicated by the asterisk symbol, “*”. Several important insights arise from Figure 2. Seasonality exists by day and by shift. In a given week, weekdays (i.e., Monday through Friday) and shift 2 typically have highest radiology volume. Despite radiology services being available continually, radiology services are primarily delivered on weekdays during normal business hours. On weekends (i.e., Saturday and Sunday), shift 2 distributions closely resemble shifts 1 and 3. This finding indicates a need to account for interactions between Day and Shift in the forecasting methodology.
Figure 2.
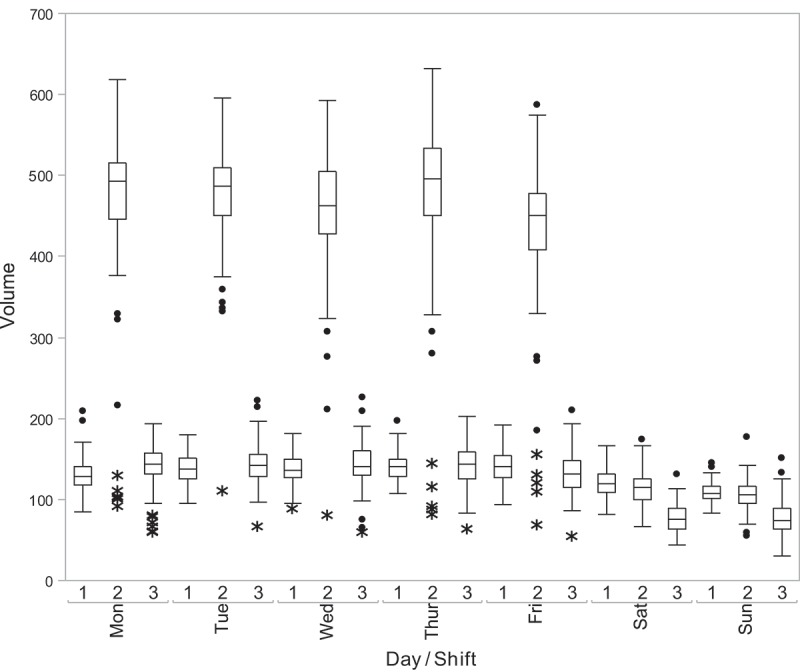
Distributions of radiology volume by day and shift.
Holidays reduce the volume of radiological services at this department, as seen by the positions of the asterisk symbols in Figure 2. Yet the reduction in volume on holidays is dependent on shift. Visually, the holiday asterisk symbols tend to fall between 50 and 150 across all weekdays and shifts, suggesting a median holiday volume of about 100 procedures. The non-holiday volumes are roughly approximated by the mid-box horizontal lines; they show non-holiday volume is more markedly different from holiday volume for shift 2 than for shifts 1 and 3. Specifically, median holiday volume is 102, while the non-holiday shift 2 median volume is 450, and 130 for shifts 1 and 3 non-holidays, respectively. Hence, an interaction between Holiday and Shift is warranted.
Figure 2 also suggests some commonalities. For example, the shift 1 distributions are remarkably similar across the weekdays of Monday through Friday. The same is true of shift 2 and shift 3. Similarly, each shift’s Saturday distribution coincides closely with that for Sunday. This suggests that a parsimonious representation might be achieved by grouping. To that end, a new variable is added to the data-set (named Weekday/Weekend) in which Monday through Friday are coded as “weekday” and Saturday and Sunday are coded as “weekend”.
The overall summary measures for the three shifts are provided in Table 1. At first glance, one might ask whether shift 1 and shift 3 be combined. Shift 1 and shift 3 (those occurring outside of the normal working hours) exhibit comparable patterns during weekdays (see Figure 2) and summary measures (see Table 1), but, on weekends, the median volume for shift 3 is only about 75% of the median volume of shift 1. Additional variation might be captured by keeping the three shifts as distinct categories.
Table 1.
Summary statistics for radiology volume by shift.
| Statistic | Shift 1 | Shift 2 | Shift 3 |
|---|---|---|---|
| Minimum | 81 | 55 | 30 |
| 25th percentile | 116 | 126 | 93 |
| Mean | 130.47 | 361.19 | 123.02 |
| Median | 131 | 447 | 129 |
| 75th percentile | 144 | 498 | 150 |
| Maximum | 209 | 632 | 226 |
Figure 3 is used to assess the existence of long-term trend. For all three shifts, trend lines are mostly flat over the study time period as seen in Figure 3. The average daily volume per shift is 196.1 procedures in 2003 and 213.7 in 2004. Trend is negligible here because of the relatively short time period of two years. Rather, Figure 3 illustrates that radiology volume, regardless of shift, tends to be “predictably variable” within each shift implying that “good” forecasting models ought to be relatively uncomplicated. Last, long-term growth in radiology volume comes about via increased patient population, expansion of infrastructure and staff or replacement of capital equipment with more efficient imaging technologies, or the departure of competitors, none of which was seen over this time period.
Figure 3.
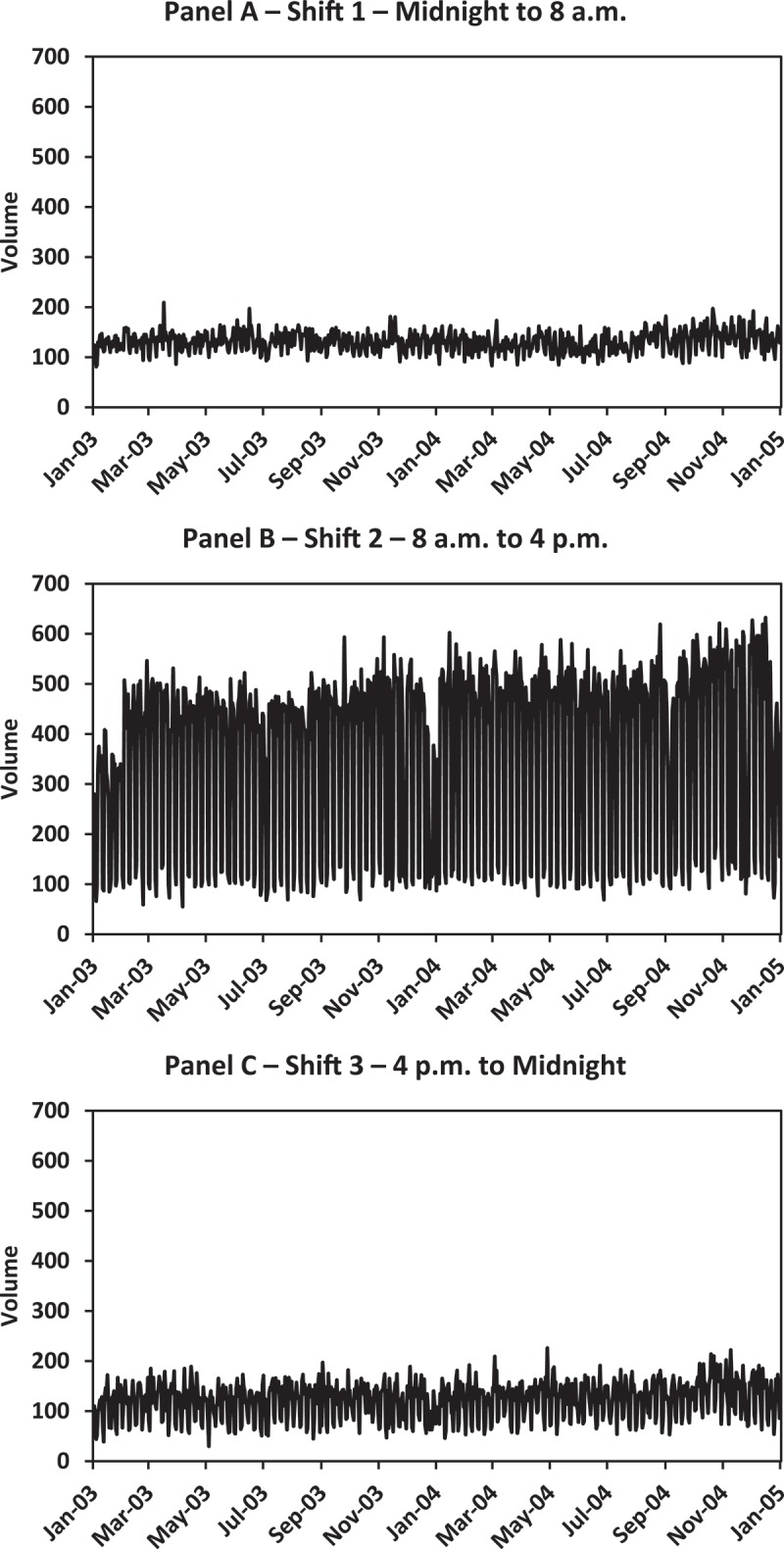
Daily time series plot of radiology volume by shift.
6. The forecasting model
Exploratory data analysis provides the starting point for the radiology volume forecasting model. Given that both day of the week and shift present considerable guidance regarding anticipated radiology volume, it is natural that these factors be used as predictors of radiology volume. Consequently, a multiple regression model was estimated with days of the week, grouped into weekdays and weekends, all three shifts during a given day, the existence of a holiday, and all possible two-way interactions between Weekday/Weekend, Shift, and Holiday as independent variables. (There are no holiday weekends, since holidays that fall on Saturday or Sunday are observed on Friday or Monday. Consequently, a model containing the Holiday × Weekday/Weekend interaction cannot be estimated.)
The exploratory data analysis greatly guided the selection of independent variables in the regression model presented in Table 2. When building regression models, more explanatory variables reduce the unexplained variation and should (ideally) result in an improved fit to the data. But there is also a trade-off between the number of parameters and a “good” model. More independent variables does not necessarily imply a better model, especially if the percentage of unexplained variation changes only slightly. The model overall is statistically significant (F-ratio = 4846.28 with p-value < .001), as are each of the individual terms in the regression equation. With R 2 = 0.947, nearly 95% of the variation in daily shift volume is associated with the terms in this regression model. The root mean square error (RMSE) is 35.32 procedures (as a percentage of average radiology volume, the RMSE is 17.3%), and represents the spread of the distribution of radiology volume values around the estimated multiple regression model.
Table 2.
Estimated regression coefficients.
| Term | Parameter estimate | Standard error | t-statistic | p-value |
|---|---|---|---|---|
| Intercept | 77.93 | 2.449 | 31.82 | <.0001 |
| Shift 1 | 35.90 | 3.463 | 10.37 | <.0001 |
| Shift 2 | 32.26 | 3.463 | 9.32 | <.0001 |
| Holiday | −64.84 | 8.254 | −7.86 | <.0001 |
| Weekday | 65.38 | 2.911 | 22.46 | <.0001 |
| Shift 1 × holiday | 41.48 | 11.673 | 3.55 | 0.0004 |
| Shift 2 × holiday | −303.45 | 11.673 | −26.00 | <.0001 |
| Shift 1 × weekday | −41.28 | 4.116 | −10.03 | <.0001 |
| Shift 2 × weekday | 298.82 | 4.116 | 72.59 | <.0001 |
6.1. Evaluating the forecasting model
Although the model shown in Table 1 has very good cohesion between the actual and forecasted values, its measures of fit can be deceptive since the least squares procedure produces estimates that optimise fit to the data used to estimate the regression model. When a regression model is intended for forecasting, it is common to undertake cross-validation to gauge how the model performs in a simulated forecasting environment. The model in Table 1 is used to forecast January 1 2005 through April 25 2005 (the last observation available). Then the root mean square prediction error (RMSPE) is calculated for the within-sample group (2003–2004) and the holdout group (January 1–April 25 2005). The within-sample RMSPE is 35 procedures; as expected, the holdout RMSPE is larger at 54 procedures. Because the difference of 19 procedures has a negligible impact on the use of the model for staffing the radiology department (as we shall see shortly), cross-validation provides further evidence of the worthiness of the model as a forecasting tool.
The regression model in Table 1 served as a benchmark against which to compare other regression models. As one example among several, a regression model was estimated in which the seven days of the week (Monday through Sunday) replaced the two weekday/weekend groupings. The usual measures of fit, both within-sample and out-of-sample, are, for all practical purposes, identical. For example, the difference in adjusted R 2 statistics between the two models is 0.003 and the holdout-sample RMSPEs differ by 1.2 procedures. The regression model in Table 1 demonstrates excellent statistical properties and also has the advantage of simplicity of use for the end-user. It is chosen to produce the radiology volume forecasts as will be discussed in the next section.
6.2. Forecasting radiology volumes
The primary purpose of the multiple regression prediction model is to forecast average radiology volumes. The forecasts start with the estimated intercept in Table 1; its value of approximately 78 represents the average radiology volume for a weekend (non-holiday) shift 3. All other parameter estimates are additive to this value. For example, the average radiology volume would be 35.9 higher for a weekend shift 1, approximately 114 procedures. Likewise, for a shift 2 holiday weekday, average radiology volume would be 77.9 + 32.3–64.8 + 65.4–303.5 + 298.8, or about 106 procedures. Forecasts for average radiology volume for all other combinations are obtained similarly and may be found in Table 2 under the column labelled “Predicted Volume”.
Translating volume predictions from Table 2 into staffing needs requires knowledge of number of procedures read per shift. We illustrate with the example of staffing physician radiologists. For this hospital, radiologists process between 80 and 120 images per shift, with 80 images per shift a more realistic figure when reading more complex images. If we assume 100 images per shift then the number of radiologists required per eight-hour shift can be determined from Table 2 by simply moving decimal points two places to the left. For example, the predicted average volume for a non-holiday shift 2 weekday is 474.4 procedures, so the estimated average number of radiologists is about 4.75 FTEs: perhaps four full-time and one part-time radiologist if that configuration is possible or 5 full-time radiologists if not.
A secondary purpose of the multiple regression model is to generate ranges for a given forecast. Ranges indicate the extent of likely errors that are associated with a forecast (Krajewski, Malhotra, & Ritzman, 2016), and managers generally view forecast ranges as useful for operational decision-making (Önkal & Bolger, 2004). Table 3 provides prediction intervals (PIs) for the forecasts at varying confidence levels (i.e., 75, 90, 95, and 99%). Knowing when to use which value is a critical decision that managers must make when deciding how best to implement the forecasting model. As an important aside, if the PIs generated negative lower bounds, we truncated those estimates to 0 as negative radiology volume is practically impossible. This transformation happened for the 99% PIs for shift 3 for holiday weekdays and weekends.
Table 3.
Predicted radiology volumes and prediction intervals.
| Shift | Lower limits |
Predicted |
Upper limits |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 99% | 95% | 90% | 75% | Volume | 75% | 90% | 95% | 99% | ||
| Non-holiday weekdays | 1 | 46.8 | 68.6 | 79.8 | 97.3 | 137.9 | 178.6 | 196.1 | 207.3 | 229.1 |
| 2 | 383.2 | 405.1 | 416.2 | 433.7 | 474.4 | 515.1 | 532.6 | 543.7 | 565.5 | |
| 3 | 52.2 | 74.0 | 85.1 | 102.6 | 143.3 | 184.0 | 201.5 | 212.6 | 234.5 | |
| Holiday weekdays | 1 | 21.2 | 43.5 | 54.9 | 72.9 | 114.6 | 156.3 | 174.2 | 185.6 | 208.0 |
| 2 | 12.7 | 35.0 | 46.5 | 64.4 | 106.1 | 147.8 | 165.7 | 177.2 | 199.5 | |
| 3 | 0.0 | 7.4 | 18.8 | 36.8 | 78.5 | 120.2 | 138.1 | 149.5 | 171.9 | |
| Weekends | 1 | 22.6 | 44.4 | 55.6 | 73.1 | 113.8 | 154.6 | 172.1 | 183.3 | 205.1 |
| 2 | 18.9 | 40.8 | 51.9 | 69.5 | 110.2 | 150.9 | 168.5 | 179.6 | 201.5 | |
| 3 | 0.0 | 8.5 | 19.7 | 37.2 | 77.9 | 118.7 | 136.2 | 147.4 | 169.2 | |
Consider again the estimates for the shift 2 non-holiday weekdays in Table 2, which range from 383.2 procedures (the 99% lower limit) to 565.5 procedures (the 99% upper limit) or roughly 3.8 FTEs to 5.7 FTEs. Two things happen when moving from 3.8 FTEs to 5.7 FTEs: turnaround improves while personnel costs increase. Staffing decisions must be made in that context by weighing the trade-off of service timeliness and costs. Of course, the choice of staffing levels (beyond what may be suggested by our models) remains the prerogative of the health care decision-makers and their tolerance for idleness of the employees (and their associated cost) to set their staff levels at the upper prediction levels. The implicit trade-off here is the possible consequence associated with demand exceeding capacity and how overtime (or other related costs) might be incurred to meet demand if staffing is below demand. We illustrate this through three hypothetical representative examples.
In the first scenario, consideration is given to staffing shift 3 on weekends. This shift sees mostly emergency procedures so fast turnaround is desired; it is typically staffed with part-time radiologists who are less expensive per hour than those working full-time. This suggests using one of the upper limit estimates: perhaps 147.4 procedures from the 95th PI. Images during this shift tend to be routine so that 120 images per shift is a better estimate of productivity than 100. In this setting, 147.4/120 = 1.2 FTEs might be used as a staffing guideline.
The second scenario addresses normal working hours (i.e., shift 2, non-holiday weekdays). Most non-emergency readings (e.g., mammograms) are scheduled during this shift, so turnaround needs are typically lower; more complex images are often presented during this shift. This shift is staffed with relatively high-cost, full-time, academic radiologists. An estimate that captures these characteristics might be the 75th PI using 80 images per shift or 515.1/80 = 6.4 FTEs.
The third scenario addresses an ongoing year-end anomaly at this facility. As patients are closing their insurance plans at year’s end and have met their deductibles, the facility sees a higher mix of requests for elective and non-urgent (but postponed) diagnostic tests. These typically have lower turnaround needs. That might prompt decision-makers to rely on the 75th PI for purposes of December staffing.
In these scenarios, upper prediction limits were used as the forecasts; the numbers in the “Predicted Volume” column were not chosen. Keep in mind that these forecasts will be used in a services setting that relies on reasonable turnaround (Boland, Guimaraes, & Mueller, 2008). Because the values in the “Predicted Volume” column are averages (or expected values), using them would imply that the radiology department would be understaffed about half the time, suggesting that a better choice is one of the upper limit percentiles. However, which upper limit to use will become clearer with time as management monitors the difference between values predicted from the model and actual volume, and makes periodic adjustments in the face of ongoing over- or under-utilisation of labour.
While these scenarios focused on staffing radiologists, similar calculations can be used for other employees including radiologic technologists, front desk employees, and financial representatives. In all cases, the integral component is anticipated volume, which is produced by the forecasting model. Knowing that, and estimated productivity per shift, such as procedures read, for each job type, implies that translating radiology procedure counts into FTEs could be easily accomplished with spreadsheet software.
7. Conclusions and recommendations for further research
The process of forecasting the demand for health services can support the entire spectrum of decision-making from strategic planning though real-time adjustment of work schedules. For our setting, our work is best-suited for intermediate (e.g., workforce scheduling) and long-term (e.g., determining workforce size and composition) horizons. Thus, consistent with the Vital Directions for Health and Health Care discussion paper series provided by the National Academy of Medicine, the collection, assimilation, and modelling of health care demand data (such as our demand for radiologic images) represents a key activity as health systems aspire to become learning systems (Krumholz et al., 2016). Likewise, our work lends itself readily to support health system leaders in the pursuit of high-value care (Institute of Medicine, 2015).
Our work, however, is not without limitations and data availability and timeliness represent our two primary constraints. This is a common roadblock to using federally protected medical information for publication in the public domain. Even so, we believe two important goals have been achieved. We hoped to use these data in an exploratory setting to learn whether the demand for radiology services can be predicted with reasonable accuracy. Using data from an academic hospital setting, we developed a forecasting model that accounts for nearly 95% of the variation in procedure volume and produces respectable forecast fit. This bodes well for a wider use of prediction models for managing radiology business units.
Equally important, we hope to use this work as a platform to encourage health care managers to consider widespread adoption of the practices and methods used here. To that end, the successful development of forecasting models hinges upon three components: (1) a detailed time series, (2) intermediate knowledge of statistical and operations management tools, and (3) vested interest and commitment from the parties involved. This last point highlights the need for an interdisciplinary team to guide model development and support the use of the model results in the decision-making processes associated with planning, staffing, and scheduling for radiology services. Simply constructing a forecasting tool without regard to the affected individuals (primarily radiologists) provides little credibility for the use of quantitative modelling. It is easy to see that any health care service will be able to provide a detailed time series of its demand. The ease of doing so hinges greatly upon the level of technology available that can capture sufficient detail on each time series element. Obviously, the more detail the time series contains, the better for model development and implementation and this detail must be established prior to any forecasting effort. For the statistical and operations management analysis and application, health care managers ought to be able to replicate our approach with varying degrees of effort. As noted in Reid et al. (2005), the ability to use quantitative tools is not uniform across the entire health care industry and developing this skill set remains a challenge. Last, as we described at the outset, given the ongoing universal emphasis on the cost and quality of health care, we suspect that very few health care managers have the luxury to ignore forecasting the demand for their services since demand is the key driver for all of the health care activities that follow.
Specific to our models, we recommend that health care managers should avoid using predictions about averages for their service settings. Instead, the forecast error, and the forecast intervals that can be produced from the forecast error, should be factored into the decision-making. Illustrative examples from our radiology application demonstrate why upper values in the forecast range can be better choices for staffing decisions in settings in which expeditious turnaround is important.
Regression analysis has several desirable features that should make it especially appealing to health care managers. Although we illustrate in an application of staffing personnel into 8 h shifts that demonstrate clear seasonal patterns, regression is more widely applicable to many other situations. For instance, although we had no trend in our data, trend can be modelled by adding an integer counter variable to the regression model. Regression readily handles long-term, medium-term, short-term, and even very short-term forecasting needs. Regression accommodates a need for variable interactions as we found here. Furthermore, multiple regression analysis has found favour with practitioners because it requires only a moderate level of understanding of statistical methods. Multiple regression methods and applications are finding their way into the required coursework of health care management curricula. Those not already proficient in regression methods might seek out any number of massive open online courses that cover the topic. Another alternative is to sponsor an internship of an undergraduate business analytics or statistics student for model construction and implementation. Thus, regression has the potential to generate usable forecasts without the need for advanced statistical expertise. Equally important, multiple regression is standard in spreadsheet software so regression analysis, with its versatility, accessibility, and ease of use, should become an important tool for all health care managers.
Disclosure statement
No potential conflict of interest was reported by the authors.
References
- Batal H., Tench J., McMillan S., Adams J., & Mehler P. S. (2001). Predicting patient visits to an urgent care clinic using calendar variables. Academic Emergency Medicine, 8(1), 48–53. 10.1111/acem.2001.8.issue-1 [DOI] [PubMed] [Google Scholar]
- Bhargavan M., & Sunshine J. (2005). Utilization of radiology services in the United States: Levels and trends in modalities, regions, and populations. Radiology, 234(3), 824–832. 10.1148/radiol.2343031536 [DOI] [PubMed] [Google Scholar]
- Boland G. W. L., Guimaraes A. S., & Mueller P. R. (2008). Radiology report turnaround: Expectations and solutions. European Radiology, 18(7), 1326–1328. 10.1007/s00330-008-0905-1 [DOI] [PubMed] [Google Scholar]
- Cerrito P. B., & Pecoraro D. (2005). Visits to the emergency department as transactional data. Journal of Healthcare Management, 50(6), 389–397. [PubMed] [Google Scholar]
- Choo L. (2000). Forecasting practices in the pharmaceutical industry in Singapore. Journal of Business Forecasting Methods and Systems, 19(2), 10–15. [Google Scholar]
- Chrysanthopoulou A., Kalogeropoulos A., Terzis G., Georgiopoulou V., Kyriopoulos J., Siablis D., & Dimopoulos J. (2007). Trends and future needs in clinical radiology: Insights from an academic medical center. Health Policy, 80(1), 194–201. 10.1016/j.healthpol.2006.03.007 [DOI] [PubMed] [Google Scholar]
- Connor P., Alldus C., Ciapparelli C., & Kirby L. (2003). Long term pharmaceutical forecasting: IMS Health’s experience. Journal of Business Forecasting Methods and Systems, 22(1), 10–15. [Google Scholar]
- Côté M. J., Smith M. A., Eitel D., & Akçali E. (2010). Forecasting the demand for emergency department services In Shiver J. & Eitel D. (Eds.), Optimizing emergency department throughput (pp. 151–167). Boca Raton, FL: CRC Press. [Google Scholar]
- Côté M. J., Smith M. A., Eitel D., & Akçali E. (2013). Forecasting emergency department arrivals: A tutorial for emergency department directors. Hospital Topics, 91(1), 9–19. [DOI] [PubMed] [Google Scholar]
- Côté M. J., & Tucker S. L. (2001). Four methodologies to improve healthcare demand forecasting. Healthcare Financial Management, 55(5), 54–58. [PubMed] [Google Scholar]
- Dommert H. J., & Getzen T. E. (2005). On the money: Making forecasts what they should be. Healthcare Financial Management, 59(11), 106–110. [PubMed] [Google Scholar]
- Finarelli H. J., & Johnson T. (2004). Effective demand forecasting in 9 steps. Healthcare Financial Management, 58(11), 52–58. [PubMed] [Google Scholar]
- Gardner E. S. (1979). Box-Jenkins vs multiple regression: Some adventures in forecasting the demand for blood tests. Interfaces, 9(4), 49–54. 10.1287/inte.9.4.49 [DOI] [Google Scholar]
- Getzen T. E. (2000). Forecasting health expenditures: Short, medium, and long (long) term. Journal of Health Care Finance, 26(3), 56–72. [PubMed] [Google Scholar]
- Goldstein D. G., & Gigerenzer G. (2009). Fast and frugal forecasting. International Journal of Forecasting, 25(4), 760–772. 10.1016/j.ijforecast.2009.05.010 [DOI] [Google Scholar]
- Heidenreich P. A., Trogdon J. G., Khavjou O. A., Butler J., Dracup K., Ezekowitz M. D., … Orenstein D. (2011). Forecasting the future of cardiovascular disease in the United States: A policy statement from the American Heart Association. Circulation, 123(8), 933–944. 10.1161/CIR.0b013e31820a55f5 [DOI] [PubMed] [Google Scholar]
- Hoot N. R., LeBlanc L. J., Jones I., Levin S. R., Zhou C., Gadd C. S., & Aronsky D. (2008). Forecasting emergency department crowding: A discrete event simulation. Annals of Emergency Medicine, 52(2), 116–125. 10.1016/j.annemergmed.2007.12.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyder O., Dodson R. M., Weiss M., Cosgrove DP., Herman J. M., Geschwind J. F. H., … Pawlik T. M. (2013). Trends and patterns of utilization in post-treatment surveillance imaging among patients treated for hepatocellular carcinoma. Journal of Gastrointestinal Surgery, 17(10), 1774–1783. 10.1007/s11605-013-2302-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Institute of Medicine (2015). Integrating research and practice: Health system leaders working toward high-value care: Workshop summary. Washington, DC: The National Academies Press. [PubMed] [Google Scholar]
- Jones S. A., & Joy M. P. (2002). Forecasting demand of emergency care. Health Care Management Science, 5(4), 297–305. 10.1023/A:1020390425029 [DOI] [PubMed] [Google Scholar]
- Jones S. S., Evans R. S., Allen T. L., Thomas A., Haug P. J., Welch SJ., & Snow G. L. (2009). A multivariate time series approach to modeling and forecasting demand in the emergency department. Journal of Biomedical Informatics, 42(1), 123–139. 10.1016/j.jbi.2008.05.003 [DOI] [PubMed] [Google Scholar]
- Krajewski L. J., Malhotra M. K., & Ritzman P. (2016). Operations management: Processes and supply chains (11th ed.). Upper Saddle River, NJ: Pearson Prentice Hall. [Google Scholar]
- Krumholz H. M., Bourne P. E., Kuntz R. E., Mcclellan M., Paz H. L., Terry S. F., & Waldstreicher J. (2016). Data acquisition, curation, and use for a continuously learning health system. Vital directions for health and health care series (Discussion Paper). Washington, DC: National Academy of Medicine; Retrieved from http://nam.edu/wp-content/uploads/2016/09/dataacquisition-curation-and-use-for-a-continuouslylearning-health-system.pdf [Google Scholar]
- Lakdawalla D., Goldman D. P., Bhattacharya J., Hurd M. D., Joyce G. F., & Panis C. W. A. (2003). Forecasting the nursing home population. Medical Care, 41(1), 8–20. 10.1097/00005650-200301000-00003 [DOI] [PubMed] [Google Scholar]
- Lang K., Huang H., Lee D. W., Federico V., & Menzin J. (2013). National trends in advanced outpatient diagnostic imaging utilization: An analysis of the medical expenditure panel survey, 2000–2009. BMC Medical Imaging, 13(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapierre S. D., Goldsman D., Cochran, & DuBow J. (1999). Bed allocation techniques based on census data. Socio-Economic Planning Sciences, 33(1), 25–38. 10.1016/S0038-0121(98)00008-1 [DOI] [Google Scholar]
- Lightwood J., Bibbins-Domingo K., Coxson P., Wang C., Williams L., & Goldman L. (2009). Forecasting the future economic burden of current adolescent overweight: An estimate of the coronary heart disease policy model. American Journal of Public Health, 99(12), 2230–2237. 10.2105/AJPH.2008.152595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller C. G., Krasnow J., & Schwartz L. H. (2014). Medical imaging in clinical trials. London: Springer-Verlag; 10.1007/978-1-84882-710-3 [DOI] [Google Scholar]
- Mohd-Nor R. (2011). Medical imaging trends and implementation: Issues and challenges for developing countries. Journal of Health Informatics in Developing Countries, 5(1), 89–98. [Google Scholar]
- Myers C., & Green T. (2004). Forecasting demand and capacity requirements. Healthcare Financial Management, 58(8), 34–37. [PubMed] [Google Scholar]
- O'Brien-Pallas L., Baumann A., Donner G., Murphy G., Lochhaas-Gerlach J., & Luba M. (2001). Forecasting models for human resources in health care. Journal of Advanced Nursing, 33(1), 120–129. 10.1046/j.1365-2648.2001.01645.x [DOI] [PubMed] [Google Scholar]
- Önkal D., & Bolger F. (2004). Provider-user differences in perceived usefulness of forecasting formats. OMEGA: The International Journal of Management Science, 32(1), 31–39. [Google Scholar]
- Otero H. J., Erturk S. M., Ochoa R. E., Ondategui-Parra S., Rybicki FJ., and Ros PR. (2008). Intestinal obstruction: Trends in imaging utilization and their influence in its rising hospital bill. Emergency Radiology, 15(5), 317–323. 10.1007/s10140-008-0726-1 [DOI] [PubMed] [Google Scholar]
- Reid P. P., Compton W. D., Grossman J. H., & Fanjiang G. (Eds.). (2005). Building a better delivery system: A new engineering/health care partnership. Washington, DC: National Academies Press. [PubMed] [Google Scholar]
- Samei E., Seibert J. A., Andriole K., Badano A., Crawford J., Reiner B., … Chang P. (2004). AAPM/RSNA tutorial on equipment selection: PACS equipment overview: General guidelines for purchasing and acceptance testing of PACS equipment. RadioGraphics, 24(1), 313–334. 10.1148/rg.241035137 [DOI] [PubMed] [Google Scholar]
- Scheffler R. M., Liu J. X., Kinfuc Y., & Dal Pozd M. R. (2008). Forecasting the global shortage of physicians: An economic- and needs-based approach. Bulletin of the World Health Organization, 86(7), 516–523. 10.2471/BLT.00.000000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas K. E. (2011). CT utilization–Trends and developments beyond the United States’ borders. Pediatric Radiology, 41(S2), 562–566. 10.1007/s00247-011-2101-8 [DOI] [PubMed] [Google Scholar]
- Woolsey R. E. D., & Swanson H. S. (1975). Operations research for immediate application: A quick and dirty manual. New York, NY: HarperCollins. [Google Scholar]
- Wu C. Y., Hu H. Y., Chen L., Huang N., Chou Y. J., & Li C. P. (2013). Investigating the utilization of radiological services by physician patients: A population-based cohort study in Taiwan. BMC Health Services Research, 13(1), 284. [DOI] [PMC free article] [PubMed] [Google Scholar]


