Skip to main content
PMC home page
Health Systems logoLink to Health Systems
. 2018 Jan 15;7(2):111–119. doi: 10.1080/20476965.2017.1390185

Modelling and forecasting daily surgical case volume using time series analysis

Nazanin Zinouri a,*, Kevin M Taaffe a, David M Neyens a
PMCID: PMC6452838  PMID: 31214342

ABSTRACT

Hospitals and outpatient surgery centres are often plagued by a recurring staff management question: “How can we plan our nursing schedule weeks in advance, not knowing how many and when patients will require surgery?” Demand for surgery is driven by patient needs, physician constraints, and weekly or seasonal fluctuations. With all of these factors embedded into historical surgical volume, we use time series analysis methods to forecast daily surgical case volumes, which can be extremely valuable for estimating workload and labour expenses. Seasonal Autoregressive Integrated Moving Average (SARIMA) modelling is used to develop a statistical prediction model that provides short-term forecasts of daily surgical demand. We used data from a Level 1 Trauma Centre to build and evaluate the model. Our results suggest that the proposed SARIMA model can be useful for estimating surgical case volumes 2–4 weeks prior to the day of surgery, which can support robust and reliable staff schedules.

KEYWORDS: Time series analysis, ARIMA modelling, seasonality, forecasting, surgical case volume, perioperative Systems

1. Introduction

Over 60% of total hospital costs are related to labour (Kreitz & Kleiner, 1995), making the nursing staff one of the most critical hospital resources. Moreover, poorly planned weekly or monthly nurse schedules can lead to costly day-of-surgery adjustments and can ultimately lead to increased stress levels among staff and patients. This can also adversely affect patient safety, as well as increase health care costs (Jalalpour, Gel, & Levin, 2015). In order to utilise this scarce and costly nursing resource more efficiently, reliable forecasts for daily surgical volume are needed.

Patient volume information can be used in resource allocation, staff scheduling, and planning future developments. The ability to forecast accurately is essential for hospitals to be able to plan efficiently (Abdel-Aal & Mangoud, 1998; Jones & Joy, 2002). In the United States, health care systems are challenged to deliver high-quality care with limited resources while also attempting to operate at the lowest possible cost. Variability in demand for health care services, especially in the short run, makes hospital resource planning and staff management even more difficult (Litvak & Long, 2000).

Health care organisations are experiencing an increase in the demand for surgeries, partially due to expanding and ageing populations (Lim & Mobasher, 2012). This surgical demand (or case volume) is a critical factor that impacts staffing decisions. It is recognised that seasonal variability in patient volumes exists, and there are certain times of the year that are even more volatile such as holidays (Boyle et al., 2011). However, at any time of the year, many factors influence the actual surgical demand experienced on the day of surgery. The possibility of cancellations, add-on cases (i.e., cases that are added after the master schedule has been completed), and last-minute changes all add to the variability on or within 1–2 days of the day of surgery.

While add-ons can be managed to some degree (by prioritisation based on patient type, acuity, type, length of surgery, and resource availability), it is still difficult to adjust staffing to meet the demand a few days prior to the day of surgery (Tiwari, Furman, & Sandberg, 2014). Some hospitals may choose not to apply any specific demand forecasting model because they feel the high fluctuations in surgical case volume is too difficult to forecast. However, there is evidence that suggests historical data can be used to predict future demands as well as estimate variability (Tiwari, Furman, & Sandberg, 2014). Our motivation for studying this problem is the impact that the surgical schedule has on daily staffing. Hospitals would like to avoid hiring temporary (on-call) staff or flexing staff out since both are costly in different ways. Creating a staff schedule (for both full-time and part-time staff) that more accurately reflects patient demand can help the hospital address this issue.

A majority of previous work on patient volume forecasting has focused on emergency department (ED) admission rates and bed occupancy, with several of these studies using time series approaches (including Autoregressive Integrated Moving Average, or ARIMA, modelling) to develop forecasting models (e.g., Ekström et al. 2015; Farmer & Emami, 1990; Jalalpour, Gel, and Levin 2015; Jones & Joy, 2002; Milner, 1988, 1997; Peck et al. 2012; Schweigler, Desmond, & McCarthy, 2009; Upshur, Knight, & Goel, 1999). A number of authors have used predictive variables to improve forecast accuracy (Eijkemans et al., 2009; Ekström et al., 2015). However, choosing these variables is important as more complex models run the risk of over fitting the data (Hoot et al., 2007). ARIMA models have successfully been used to describe current and future behaviour of time series variables in terms of their past values. These models have been described as the most commonly used forecasting models in health care analytics (Jones et al., 2008). For these reasons, such models can provide insight into forecasting daily surgical case volume. However, there is no evidence in the literature where ARIMA (or seasonal ARIMA, SARIMA) models have been successfully used to predict daily surgical case volumes. In this study, we show that a time series forecasting approach for predicting daily surgical case volume can be implemented using SARIMA models with predictive variables. Tiwari, Furman, and Sandberg (2014) reported that time series models such as ARIMA are not sufficient for short-term prediction of surgical case volume. However, their study was based on only eight months of historical data, and holidays were excluded. In our approach, we included 45 months of historical data, accounting for the additional unique data patterns by including indicator variables in addition to moving average and autoregressive terms that capture some of the variability inherent in the process.

2. Materials and methods

We obtained surgical demand data from a major hospital in the US to assess the ability to forecast daily surgical volumes, with a particular focus on how far in advance of the day of surgery we could create useful predictions. We employed a data-set of 976 consecutive surgical days (January 2011–September 2014) for the analysis. At the time data were retrieved, demand for the only the first three quarters of 2014 were available. Having nearly four years of potential seasonality cycles in the data-set allowed us to account for both holidays and seasonal effects. The typical perioperative schedule spans Monday–Friday. The weekends contain a separate, unique demand pattern, and are not considered in the analysis of weekday demand. For the weekday data, we did not exclude any non-standard days (e.g., holidays or extremely low/high volume days), but instead we allowed the model to determine the relevance of each data point.

The average daily surgical volume at this hospital was estimated to be 67 (SD = 14) cases per weekday. Figure 1 represents the time series of daily surgical case volume, which includes elective and non-elective surgeries.

Figure 1.

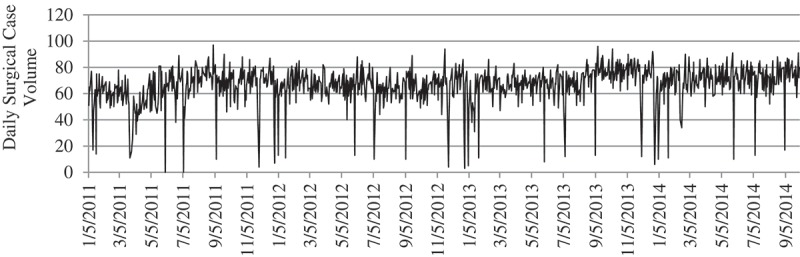
Figure 1.

Open in a new tab

Time series of daily surgical case volume.

At this hospital, the method employed for predicting demand is to annualise historical demand with team or expert opinion concerning trends for the next year, including surgeon feedback for anticipated caseload. Daily case volume is obtained from the yearly volume predicted by the business analyst. The annual budget for each department is also driven based on this prediction, and the total number of full time equivalents (FTEs) is determined based on the allocated budget. As a result, the predicted volume and the number of staff assigned (in theory) is constant for every day regardless of seasonality and trends. In practice, however, the managers make adjustments within the month and such adjustments come at a cost to the hospital.

We investigated the data-set for trends, cyclical variations, seasonal variations, and irregular variation. In particular, we observed that seasonal changes impact surgical case volumes by examining box plots and the location of median and the variation differs between subgroups (months and weekdays). Figure 2 presents box plots of the daily surgical volume grouped both monthly and weekly.

Figure 2.

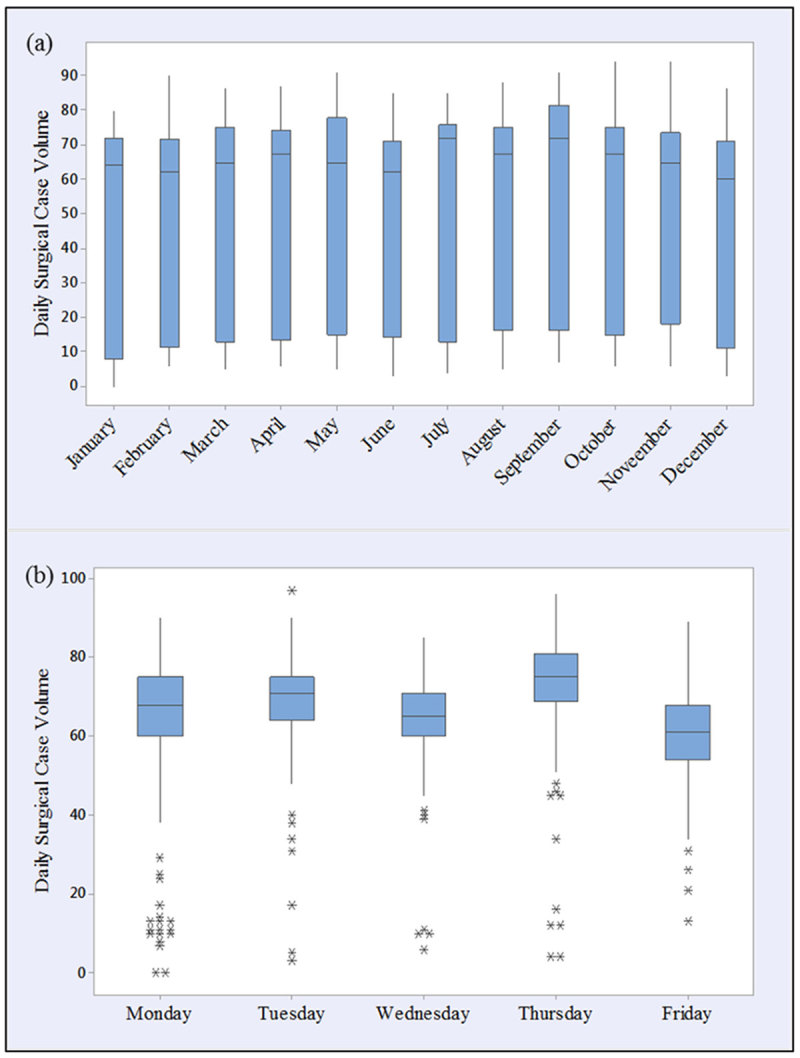
Figure 2.

Open in a new tab

Box plots of daily surgical case volume by (a) month of the year and (b) day of the week (January 2011–September 2014).

No data appear as outliers at the monthly level (see Figure 2(a)), perhaps since there were fewer measurements taken within each bucket (roughly 60–80 data points). However, for the weekly chart, Figure 2(b), each column represents between 150 and 200 data points, since each year has 52 repetitions of that day. We observe several “apparent” outliers with volumes less than 40–45 surgeries on a given day. The expected values are much tighter (and different) by day of week, indicating that this could be a strong indicator of surgical volume (which will be further explained when introducing the model in Section 4). Beyond the outliers shown in Figure 2(b), a two-sample t-test identified that Thursdays have the highest volume and Fridays have the lowest volume (F = 23.26, p = 0.0001). There seems to be less variation in daily surgical case volume by month. The data suggest that different months of the year have different demand levels (see Table 1). A monthly weighting was determined by dividing the workload of each month by the total annual workload.

Table 1.

Average monthly trend for daily surgical volume.

Month Weighted average (%)
January 91
February 92
March 95
April 94
May 100
June 101
July 100
August 111
September 103
October 111
November 104
December 102
Open in a new tab

By conducting a one-way ANOVA, we found that there is a significant difference between the average case volume for different weekdays (F = 23.26, p = 0.0001). Tukey’s multiple comparison tests provide pairwise comparison of the men of the demand of each weekday; see Figure 3. We verified that the data were independent within each day of the week and among the days, were normally distributed, and the variances were equal within each group. The data fit all the assumptions for Tukey’s test. Mondays and Fridays tend to be the lowest census days. Surgeons at the case study hospital (and, in general) try to avoid weekend stays for patients, so there is a natural tendency to schedule more cases in the middle of the week (see, e.g., Gupta & Denton, 2008; Hostetter & Klein, 2013). In particular, Thursdays are often the highest census day since surgeons are trying to schedule patients and have them leave the hospital by Friday afternoon (prior to the weekend). At the case study hospital, Wednesdays are the education day at the hospital, so there is one less hour in the schedule, and it is reflected in the daily case volume being smaller than Tuesdays and Thursdays.

Figure 3.

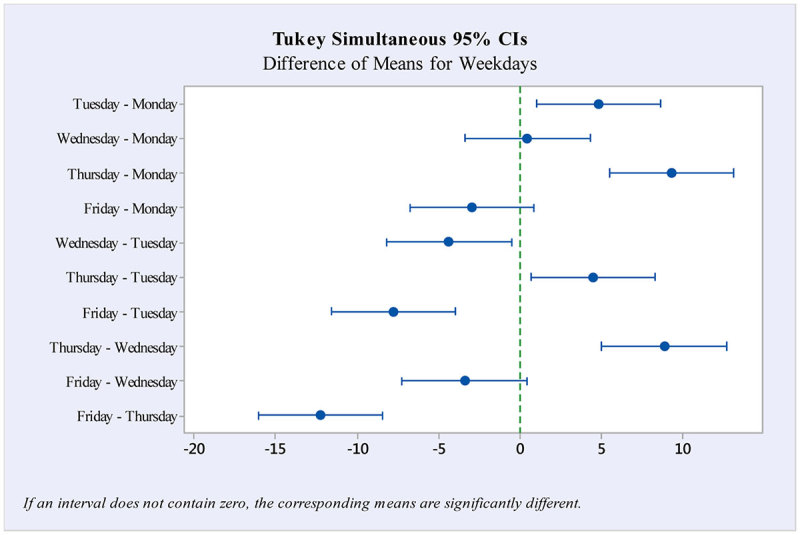
Figure 3.

Open in a new tab

Tukey simultaneous comparison of weekdays with 95% confidence intervals.

Figure 4 presents a scatter plot of surgical case volume according to date of surgery. The data are highly variable, with some points – mostly holidays – exhibiting “outlier behaviour,” which makes the prediction very difficult. Due to the complex, seemingly irregular nature of the data, and the presence of strong random components such as add-on cases, straight-forward methods like extrapolation or simple averages may not represent the data effectively. It can also be observed that weekdays (standard volume) and holidays (low volume) have different patterns. The data for these sets are partitioned by two distinctive bands on the scatter plot. We can arrive at meaningful estimates for both types of days, whether it falls into the prediction ellipses for the standard volume day or the estimates for those non-standard days with less volume.

Figure 4.

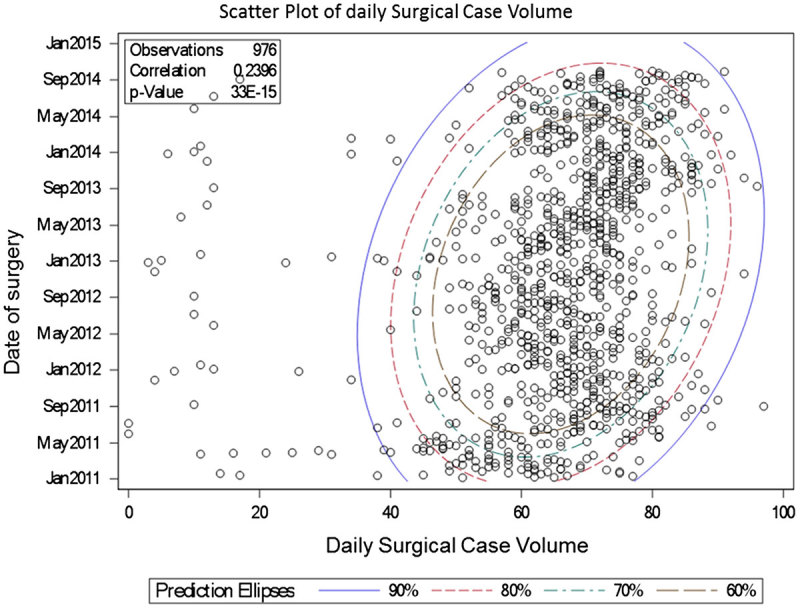
Figure 4.

Open in a new tab

Scatter plot of daily surgical case volume, January 2011–October 2014.

3. Model development

Our goal was to identify if a SARIMA model could adequately represents the historical surgery demand data. The general ARIMA model is a combination of autoregressive (AR) coefficients multiplied by previous values of our time series plus moving average (MA) coefficients multiplied by past random shocks (Box, Jenkins, & Reinselm, 1994; Pankratz, 1983). The ARIMA models are usually fitted using the Box-Jenkins ARIMA computational method (Box et al., 1994). The order of the AR and MA terms should be chosen such that the theoretical autocorrelation (ACF) and partial autocorrelation (PACF) functions approximately match the ACF and PACF of our modelled time series (Abdel-Aal & Mangoud, 1998). Time series often contain a seasonal component that repeats every s period. ARIMA processes have been generalised to SARIMA models to deal with seasonality (Abraham, Byrnes, & Bain, 2009). During model generation, 39 months of data were used for parameter estimation (or training data), while the last six months in the data-set were reserved for validation (or validation data).

We followed the three-stage SARIMA model building procedure proposed by (Box et al., 1994), which are identification, estimation, and diagnosis. We used the statistical package SAS 9.4 Web Application to develop, analyse, and compare our models. The ARIMA procedure in most statistical software packages, including SAS, uses the computational methods outlined by Box and Jenkins (Box et al., 1994). We selected the maximum likelihood method to compute our model parameters. In addition, two information criteria are computed for SARIMA models, Akaike’s Bayesian criterion (AIC) (Akaike 1974) and (Harvey, 1981) and Schwarz’s Bayesian criterion (SBC) (Schwarz 1978). The AIC and SBC are used to compare the fit of competing models to the same time series. The model with the smallest information criterion is said to fit the data better. We note that the Schwarz’s Bayesian criterion is sometimes called Bayesian information criterion (BIC).

4. Results

The AIC and BIC are being used as the main information criterion by which models are compared. Model accuracy is the main criteria in selecting a forecasting method, and there are many error measures from which to choose (Yokum & Armstrong, 1995). In maintaining consistency with prior demand forecasting in health care, we calculate and present the MAPE as our error performance measure (e.g., Jones et al., 2008; Marcilio, Hajat, & Gouveia, 2013). Most ED forecasting papers also suggest a MAPE below 10% demonstrations satisfactory performance. In all our models, α = 0.05 was used as the criterion. As a reminder, our training data-set consisted of over three years of data, and we reserved six months of data in the validation set for observing model performance.

4.1. Identification

First, we considered the time series plot of daily surgical case volume (see Figure 1). The data did not show any significant trend requiring differencing. So we can assume that we have a stationary stochastic process, a process with no significant shifts and drifts. There is a week-based (five weekday) seasonality effect discussed in Section 2 and is referred to as seasonality in the model. The extremely low volume days were identified to be holidays (i.e., New Year’s Day, Memorial Day, Labour Day, and Martin Luther King Jr. Day). As seasonal differencing might miss some of the holiday variability, we accounted for holiday patterns by introducing a predictive variable representing holidays.

Next, in order to obtain further insight into the statistical properties of our time series, we developed ACF and PACF functions using SAS. The ACF and PACF of our time series are represented in Figure 5. While both the ACF and PACF have larger spikes initially, the patterns gradually dissipate over time which suggests that there are both AR and MA processes. Significant autocorrelations at the seasonal level (i.e., lag 5 for a five-day week), suggest that the time series seasonality should be accounted for using SARIMA modelling.

Figure 5.

Figure 5.

Open in a new tab

The ACF and PACF of surgical case volume time series.

4.2. Estimation

Parameters for the SARIMA model were estimated using the SARIMA procedure of SAS® 9.4. In addition to the intercept, AR, MA, SAR, and SMA terms, binary indicator variables were used to represent holidays, days of the week, and months of the year. These variables were used as predictive variables to account for patterns and to improve the forecast accuracy of the model. We eliminated the insignificant dummy weekday and month variables following a backward elimination procedure. After analysing all the coefficients, only variables with coefficients significantly greater than zero (|t| > 2.00) were chosen to be in the best fit model. The final variables, along with their coefficient estimates and standard errors, are presented in Table 2.

Table 2.

Coefficient estimate and standard error for the best ARIMA model.

Variable Coefficient estimate Standard error t-value Pr > |t|
Intercept μ 63.21 0.94 66.87 <0.0001
Holidays H −56.21 1.65 −33.96 <0.0001
Monday M 7.35 0.93 7.89 <0.0001
Wednesday W −2.85 0.92 8.5 <0.0001
Thursday Th 12.82 0.92 13.88 <0.0001
January J −5.03 1.22 −4.13 <0.0001
April A −4.84 1.22 −3.95 <0.0001
MA2 θ 2.91 0.02 54.09 <0.0001
AR3 φ 2.98 0.01 138.05 <0.0001
SMA1 Θ −1.90 0.03 −2.92 <0.0001
SAR2 Φ 1.14 0.01 2.74 <0.0001
Open in a new tab

4.3. Diagnosis

We tested the residuals for the selected model to determine whether the SARIMA model adequately represents the statistical properties of the original time series. The residuals plot shown in Figure 6 exhibits independence, a required property of the proposed model. The residual plot displays a random process where error values are distributed above and below zero with no significantly large spikes.

Figure 6.

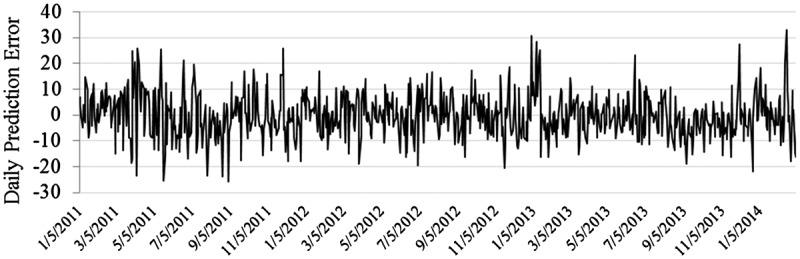
Figure 6.

Open in a new tab

Residual Plot of “SARIMA(3, 0, 2)(2, 0, 1)5 + H + M + W + Th + J + A” model.

The residual ACF plot of the time series using SARIMA(3, 0, 2)(2, 0, 1)5 + H + M + W + Th + J + A shows only one significant autocorrelation at lag 14 (see Figure 7). This is not deemed problematic, as some significant residuals and autocorrelations may exist due to the random errors (Abdel-Aal & Mangoud, 1998).

Figure 7.

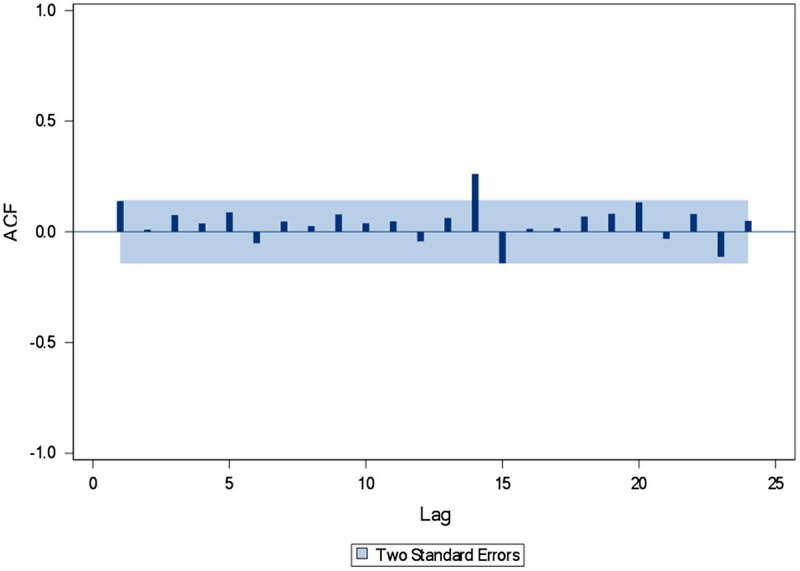
Figure 7.

Open in a new tab

Residual ACF function for the SARIMA(3, 0, 2)(2, 0, 1)5 + H + M + W + Th + J + A model.

4.4. Forecasting

The final stage to test the adequacy of our estimated model is to examine its ability to forecast. Using the six months of reserved data in the validation set, Table 3 presents the resulting MAPE when using the SARIMA(3, 0, 2)(2, 0, 1)5 + H + M + W + Th + J + A model to predict one week to six months in advance of observed demand. We also include a comparison against the current prediction generated by the hospital (based on monthly averages obtained from annualising historical demand with team or expert opinion). Overall, the model performs well, with MAPE < 10% when forecasting up to three months in advance. When compared against the hospital prediction, there is a 46% reduction in error for up to four weeks prior to day of surgery, and a 36% error reduction when evaluated for three-month forecasts.

Table 3.

Forecasting error of daily surgical case volume made 1–4 weeks in advance.

Forecasting method MAPE (%) at forecast horizon
1 Week 2 Weeks 3 Weeks 4 Weeks 2 months 3 months 4 months 5 months 6 months
ARIMA(3,0,2)(2,0,1)5+H+M+W+Th+J+A 7.0 7.4 7.6 7.8 8.3 9.1 11.7 13.3 15.8
Hospital prediction 14.2
Open in a new tab

In addition, it has been suggested that time series modelling may not be able to effectively predict caseload far enough in advance to be relevant for staff planning and scheduling decisions (Tiwari, Furman, & Sandberg, 2014). We have illustrated that not to be the case here. The SARIMA(3 ,0, 2)(2, 0, 1)5 model – with holidays, weekdays, and month indicator variables – provides a MAPE < 10% for forecasting up to three months prior to the day of surgery. The MAPE resulting from the hospital’s prediction is much higher, and the time series forecasting method indicates a significant improvement. This indicates the ability to predict daily demands and, thus, daily staffing assignments up to one month prior to surgery – a point in time when significant cost savings may be achieved.

Finally, as can be observed in Figure 8, the prediction intervals have a consistent range for up to three months, i.e., the confidence interval increases slightly for the first three months and more dramatically beyond that point. This suggests that the model is also applicable for strategic decisions, not just the tactical decisions made up to one month prior to the day of surgery.

Figure 8.

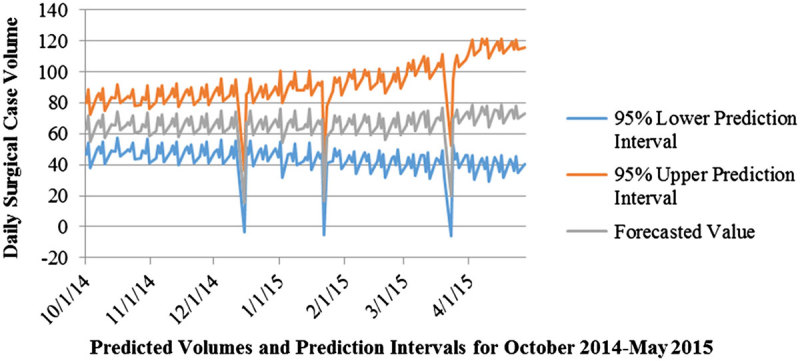
Figure 8.

Open in a new tab

Change in prediction interval (October 2014–May 2015).

5. Conclusions

This study demonstrates the value of using an SARIMA model to estimate surgical demand and forecast future demand. Using several years worth of data, and accounting for days that may represent outliers (e.g., holidays) we are able to predict future demand relatively accurately. In fact, the SARIMA(3, 0 ,2)(2, 0, 1)5 model predicted final surgical case volume within 7.8 cases as far in advance as four weeks prior to the day of surgery. Our analysis reveals the benefits to using time series models to estimate and forecast surgical caseloads. Through explicit use of all weekly historical data over several years, and accounting for special patterns, (e.g., holidays) by adding indicative variables, surgical volume can be predicted up to months in advance. Our results indicate that the SARIMA(3, 0, 2)(2, 0, 1)5 model along with indicator variables can be a useful tool in forecasting daily surgical case volume. Using daily surgical case volumes of preceding years and indicator variables as input, the proposed model generated short-term forecasts with MAPE < 10% for predictions less than three months out. The MAPE of our forecasts four weeks prior to day of surgery was over 46% smaller than the prediction error obtained from average-based method. This indicates the ability to predict daily demands and, thus, daily staffing assignments up to one month prior to surgery – a point in time when significant cost savings may be achieved. SARIMA modelling was useful for modelling our time series as there are significant random component and holidays which both result in difficult to predict demand profiles. This is especially true for time series values than with simpler methods that only consider deterministic components of seasonality and trend. Due to the variability in the data, it is difficult to identify and remove outliers (low volume days) by simple adjustment of the data such as differencing or transforming operations. Adding predictive indicator variables for these factors serves as a useful approach to improve the performance of the model.

Previous research has used ARIMA models to predict bed utilisation (Kadri et al., 2014; Kumar & Mo, 2010). Tiwari, Furman, and Sandberg (2014) suggested that time series techniques may not be robust enough to account for the large variability and stochastic aspects of surgical demand. However, with the use of more time-based data, accounting for seasonality, day effects, month effects, and holidays, we were able to construct a robust model that had predictive value in forecasting future demand. Hoot et al. (2007) found value in using ARIMA models to predict ED activity and provide warning more than an hour before the crowding. They have used the Emergency Department Work Index (EDWIN), the Demand Value of the Real-time Emergency Analysis of Demand Indicators (READI), the work score, and the National Emergency Department Overcrowding Scale (NEDOCS) to improve their predictions. Ekström et al. (2015) developed ARIMA models to predict ED visits and identify behavioural trends to more accurately allocate resources and prevent ED crowding. They found that using the Internet data (i.e., Website visits) as a predictor of the ED attendance for the coming day, improved the performance of their models.

There were a few assumptions that were made that influence the direct applicability of this work. Only weekdays were included in the model, as weekend scheduling is a different process and thus this model does not capture all of the variability within surgical demands. A future model of similar format could be used to predict weekend demand and thus support weekend scheduling as well. Additionally, assumptions for holidays were driven by the actual demand data and not necessarily all of the holidays noted on calendars. Thus, there may be holidays that impact other hospitals differently than the impacts in the demand data used for this analysis. The seasonality effects identified in this model may be more pronounced for hospitals that are in locations with much colder and snowy winters or more pronounced hurricane seasons. Future work should apply this type of model development for hospitals in areas that may have more pronounced seasonal effects as the models may have very different characteristics and predictors than this case study hospital.

Our primary focus in this paper is on creating workload forecasts that can be used to create decision support tools for staffing in different perioperative services departments – preoperative (Preop), operating room (OR), post anaesthesia care unit (PACU), and Sterile Processing Department. As an example, bed occupancy in Preop can be calculated based on daily surgical case volume and then translated into workload using nurse per patient ratios. Surgical workload can also be used for capacity adjustment, supply requirements, and process management in areas such as bed management and case cart preparation. Future research should evaluate the use of similar models for managing and estimating the demand of other services that have data profiles that include autoregressive and moving average characteristics. It may also be of value to separate elective and non-elective surgeries from the models to evaluate if the models can assist in scheduling elective surgeries to balance workload. Additionally, future research should also evaluate how much value these predictive models (when used) may have on cost containment when implemented and used.

Disclosure statement

No potential conflict of interest was reported by the authors.

References

  1. Abdel-Aal R. E., & Mangoud A. M. (1998). Modeling and forecasting monthly patient volume at a primary health care clinic using univariate time-aeries analysis. Computer Methods and Programs in Biomedicine, 56, 235–247. 10.1016/S0169-2607(98)00032-7 [DOI] [PubMed] [Google Scholar]
  2. Abraham G., Byrnes G. B., & Bain C. A. (2009). Short-termforecasting of inpatient flow. IEEE Transactions on Information Technology in Biomedicine, 13(3), 1–8. [DOI] [PubMed] [Google Scholar]
  3. Akaike H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716–723. 10.1109/TAC.1974.1100705 [DOI] [Google Scholar]
  4. Box G. E. P., Jenkins G. M., & Reinsel G. C. (1994) Time series analysis: Forecasting and control. (Third ed., pp. 197–199). Englewood Cliffs, NJ: Prentice Hall. [Google Scholar]
  5. Boyle J., Jessup M., Crilly J., Green D., Lind J., Wallis M., … Fitzgerald G. (2011). Predicting emergency department admissions. Emergency Medicine Journal, 1–8. [DOI] [PubMed] [Google Scholar]
  6. Eijkemans M. J. C., Van Houdenhoven M., Nguyen T., Boersma E., Steyerberg E. W., & Kazemier G. (2009). Predicting the unpredictable: A new prediction model for operating room times using individual characteristics and the surgeon’s estimate. Anesthesiology, 112(1), 41–49. [DOI] [PubMed] [Google Scholar]
  7. Ekström A., Kurland L., Farrokhnia N., Castrén M., & Nordberg M. (2015). Forecasting emergency department visits using internet data. Annals of Emergency Medicine, 65(4), 436–442.e1. 10.1016/j.annemergmed.2014.10.008 [DOI] [PubMed] [Google Scholar]
  8. Farmer R. D., & Emami J. (1990). Models for forecasting hospital bed requirements in the acute sector. Journal of Epidemiology & Community Health, 44(4), 307–312. 10.1136/jech.44.4.307 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gupta D., & Denton B. (2008). Appointment scheduling in healthcare: Challenges and pportunities. IIE Transactions, 40(9), 800–819. 10.1080/07408170802165880 [DOI] [Google Scholar]
  10. Harvey A. C. (1981). Time series models. Journal of forecasting, 3(1), 93–94. [Google Scholar]
  11. Hoot N. R., Zhou C., Jones I., & Aronsky D. (2007). Measuring and forecasting emergency department crowding in real time. Annals of Emergency Medicine, 49, 747–755. 10.1016/j.annemergmed.2007.01.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hostetter M., & Klein S. (2013, October/November). In focus: Improving patient flow—In and out of hospitals and beyond. Quality Matters. Retrieved from http://www.commonwealthfund.org/publications/newsletters/quality-matters/2013/october-november/in-focus-improving-patient-flow [Google Scholar]
  13. Jalalpour M., Gel Y., & Levin S. (2015). Forecasting demand for health services: Development of a publicly available toolbox. Operations Research for Healthcare, 5, 1–9. [Google Scholar]
  14. Jones S. S., & Joy M. P. (2002). Forecasting demand of emergency care. Health Care Management Science, 5, 297–305. 10.1023/A:1020390425029 [DOI] [PubMed] [Google Scholar]
  15. Jones S., Thomas A., Evans R. S., Welch S. J., Haug P. J., & Snow G. L. (2008). Forecasting daily patient volumes in the emergency department. Academic Emergency Medicine, 15, 159–170. 10.1111/acem.2008.15.issue-2 [DOI] [PubMed] [Google Scholar]
  16. Kadri F., Harrou F., Chaabane S., & Tahon C. (2014). Time series modelling and forecasting of emergency department overcrowding. Journal of Medical Systems, 38(9), 1024. 10.1007/s10916-014-0107-0 [DOI] [PubMed] [Google Scholar]
  17. Kreitz C., & Kleiner B. H. (1995). The monitoring and improvement of productivity in healthcare. Health Manpower Management, 21(5), 36–39. 10.1108/09552069510097156 [DOI] [PubMed] [Google Scholar]
  18. Kumar A., & Mo J. (2010). Models for bed occupancy management of a hospital in Singapore In Proceedings of the 2010 International Conference on Industrial Engineering and Operations Management (pp. 1–6).
  19. Lim G., & Mobasher A. (2012) Operating suite nurse scheduling problem: A column generation approach In Proceedings of the 2012 Industrial and Systems Engineering Research Conference, Orlando, FL. [Google Scholar]
  20. Litvak E., & Long M. C. (2000). Cost and quality under managed care: Irreconcilable differences. American Journal of Managed Care, 6(3), 305–312. [PubMed] [Google Scholar]
  21. Marcilio I., Hajat S., & Gouveia N. (2013). Forecasting daily emergency department visits using calendar variables and ambient temperature readings. Academic Emergency Medicine, 20(8), 769–777. 10.1111/acem.2013.20.issue-8 [DOI] [PubMed] [Google Scholar]
  22. Milner P. C. (1988). Forecasting the demand on accident and emergency department in health districts in the Trent region. Statistics in Medicine, 10, 1061–1072. 10.1002/(ISSN)1097-0258 [DOI] [PubMed] [Google Scholar]
  23. Milner P. C. (1997). Ten year follow-up of arima forecasts of attendance at accident and emergency departments in the Trent region. Statistics in Medicine, 16, 2117–2125. 10.1002/(ISSN)1097-0258 [DOI] [PubMed] [Google Scholar]
  24. Pankratz A. (1983). Forecasting with univariate Box-Jenkins models: Concepts and cases (pp. 80–93). New York, NY: Wiley; 10.1002/SERIES1345 [DOI] [Google Scholar]
  25. Peck J. S., Benneyan J. C., Nightingale D. J., & Gaehde S. A. (2012). Predicting emergency department inpatient admissions to improve same-day patient flow. Academic Emergency Medicine, 19(9), E1045–E1054. 10.1111/j.1553-2712.2012.01435.x [DOI] [PubMed] [Google Scholar]
  26. Schwarz G. E. (1978). Estimating the dimension of a model. The Annals of Statistics, 6(2), 461–464. 10.1214/aos/1176344136 [DOI] [Google Scholar]
  27. Schweigler L. M., Desmond J. S., & McCarthy M. L. (2009). Forecasting models of emergency department crowding. Academic Emergency Medicine, 16, 301–308. [DOI] [PubMed] [Google Scholar]
  28. Tiwari V., Furman W. R., & Sandberg W. S. (2014). Predicting case volume from the accumulating elective operating room schedule facilitates staffing improvements. Anesthesiology, 121, 171–183. 10.1097/ALN.0000000000000287 [DOI] [PubMed] [Google Scholar]
  29. Upshur R. E. G., Knight K., & Goel V. (1999). Time-series analysis of the relationship between influenza virus and hospital admissions of the elderly in Ontario, Canada, for pneumonia, chronic lung disease, and congestive heart failure. American Journal of Epidemiology, 149(1), 85–92. 10.1093/oxfordjournals.aje.a009731 [DOI] [PubMed] [Google Scholar]
  30. Yokum J. T., & Armstrong J. S. (1995). Beyond accuracy: Comparison of criteria used to select forecasting methods. Retrieved from http://repository.upenn.edu/marketing_papers/62 [Google Scholar]

Articles from Health Systems are provided here courtesy of Taylor & Francis

RESOURCES