A systematic literature review of operational research methods for modelling patient flow and outcomes within community healthcare and other settings

Abstract

An ambition of healthcare policy has been to move more acute services into community settings. This systematic literature review presents analysis of published operational research methods for modelling patient flow within community healthcare, and for modelling the combination of patient flow and outcomes in all settings. Assessed for inclusion at three levels – with the references from included papers also assessed – 25 “Patient flow within community care”, 23 “Patient flow and outcomes” papers and 5 papers within the intersection are included for review. Comparisons are made between each paper’s setting, definition of states, factors considered to influence flow, output measures and implementation of results. Common complexities and characteristics of community service models are discussed with directions for future work suggested. We found that in developing patient flow models for community services that use outcomes, transplant waiting list may have transferable benefits.

1. Introduction

In recent decades, an ambition of healthcare policy has been to deliver more care in the community by moving acute services closer to patient homes (ENGLand NHS, 2014; Munton et al., 2011). This is often motivated by assumed benefits such as reduced healthcare costs, improved access to services, improved quality of care, a greater ability to cope with an increasing number of patients, and improved operational performance in relation to patient health and time (Munton et al., 2011).

A scoping review analysed the evidence regarding the impact that shifting services may have on the quality and efficiency of care (Sibbald, McDonald, & Roland, 2007). It found that under certain conditions moving services into the community may help to increase patient access and reduce waiting times. Across multiple types of care, however (minor surgery, care of chronic disease, outpatient services and GP access to diagnostic tests), the quality of care and health outcomes may be compromised if a patient requires competencies – such as minor surgery – that are considered beyond those of the average primary care clinician. On the evidence for the effect on the monetary cost of services, Sibbald et al. (2007) stated that it was generally expected that community care would be cheaper when offset against acute savings; however, increases in the overall volume of care (Hensher, 1997) and reductions in economies of scale (Powell, 2002; Whitten et al., 2002) may lead to an increase in overall cost in certain instances.

Considering the questions that remain over the impact of shifting services from acute to community sector, it is important to understand how community services may be best delivered. This is where applying operational research (OR) methods to community care services can contribute. For instance, services may be modelled to evaluate how goals, such as better patient access and improved outcomes, may be achieved considering constraints and objectives, such as fixed capacity or reducing operational costs. An example of one such method is patient flow modelling, the focus of this review.

2. Modelling patient flow

In a model of flow, the relevant system is viewed as comprising a set of distinct compartments or states, through which continuous matter or discrete entities move. Within healthcare applications, the entities of interest are commonly patients (although some applications may consider blood samples or forms of information). Côté (2000) identified two viewpoints from which patient flow has been understood, an operational perspective and, less commonly, a clinical perspective. From an operational perspective, the states that patients enter, leave and move between are defined by clinical and administrative activities and interactions with the care system, such as consulting a physician or being on the waiting list for surgery. Such states may be each associated with a specific care setting or some other form of resource but this need not be the case. In the clinical perspective of patient flow, the states that patients enter, leave and move between are defined by some aspect of the patient’s health, for instance by whether the patient has symptomatic heart disease, or the clinical stage of a patient’s tumour. A more generic view is that the states within a flow model can represent any amalgam of activity, location, patient health and changeable demographics, say, patient age (Utley, Gallivan, Pagel, & Richards, 2009). A key characteristic is that the set of states and the set of transitions between states comprise a complete description of the system as modelled.

Within the modelling process, characteristics of the patient population and of the states of the system are incorporated to evaluate how such factors influence flow. Examples of the former include patient demographics or healthcare requirements, whilst for the latter, capacity constraints relating to staffing, resources, time and budgets may be considered. The characteristics used depend upon the modelled system, modelling technique and questions being addressed. Considering these, the performance of a system may be evaluated through the use of output measures such as resource utilisation (Cochran & Roche, 2009), average physician overtime (Cayirli, Veral, & Rosen, 2006) and patient waiting times (Zhang, Berman, & Verter, 2009).The output measures calculated within an application depends upon the modelled problem, modelling technique and the factors that are consider to influence flow.

Within acute care settings patient flow modelling has been applied to various scenarios – see Bhattacharjee and Ray (2014). There are also several publications for community care settings; however, no published literature review exists. This systematic literature review was undertaken to gather and analyse two types of patient flow modelling literature relevant for community services. The first were publications that present models of operational patient flow within a community healthcare context, denoted as “Patient flow within community care”. The second were publications that present combinations of patient outcomes and patient flow modelling in any setting, denoted as “Patient flow and outcomes”. Incorporating patient outcomes within the patient flow modelling process is increasingly pertinent within community healthcare. Patient outcomes are used not only to track, monitor and evaluate patient health throughout a care pathway, but also assess the quality of care and inform improvement. The justification for increasing the provision of community care includes improved patient outcomes and satisfaction, thus in combining outcomes and patient flow modelling new and helpful metrics may be developed to evaluate this assertion. Furthermore, such methods help to inform the organisation of healthcare services according to operational capability and the clinical impact on the patient population, unifying two main concerns of providers and patients with a single modelling framework. No specific setting was sought in the “Patient flow and outcomes” to find potentially transferable knowledge and methods for community settings.

To the best of our knowledge, this is the first literature review focussing on OR methods for modelling patient flow applied to community healthcare services and the first to review methods for modelling patient flow and outcomes in combination. This review has been undertaken as part of a project in which OR methods will be developed that combine patient flow modelling and patient outcomes for community care services. The aim of this review was thus twofold. Firstly, to explore different applications of OR methods to community services. Secondly, to understand how patient outcomes have been previously incorporated within flow models. In the discussion section of this paper, we suggest directions for the future of patient flow modelling applied to community care.

3. Method of review

We conducted a configurative systematic literature review (Gough, Thomas, & Oliver, 2012), an approach intended to gather and analyse a heterogeneous literature with the aim of identifying patterns and developing new concepts. Two searches were performed to find peer-reviewed operational research (OR) publications, relating to “Patient flow within community care” and “Patient flow and outcomes” as previously detailed. We considered all papers published in English before November 2016 with no lower bound publication date, and searched the electronic databases Scopus, PubMed and Web of Science. Using a combination of the search terms listed in Table 1, to find papers related to “Patient flow within community care” we sought records with at least one operational research method term in the article title, journal title or keywords AND at least one patient flow term in the article title, journal title, keywords or abstract AND at least one community health setting term in the article title, journal title, keywords or abstract. Likewise, to fi papers related to “Patient flow and outcomes” we sought records with at least operational research method term in the article title, journal title or keywords AND at least one patient fl term in the article title, journal title, keywords or abstract AND at least one outcome term in the article title, journal title, keywords or abstract.

Table 1. Final terms for literature searches.

OR method terms	Patient flow terms	Setting terms	Outcome terms
Computer simulation	Access time	Community based	Outcome
Discrete event simulation	Bed occupancy	Community clinic	Patient class
Heuristics	Capacity allocation	Community facility	Patient type
Markov chain	Capacity management	Community level	Quality of life
Markov decision	Capacity planning	Diagnostic facilities	Readmission
Markov model	Care management	Health care center	Referral
Mathematical model	Patient flow	Health care centre	Disease progression
Mathematical programming	Patient pathway	Health care clinic	Health status
Metaheuristics	Patient process	Health care practice
Operational management	Patient route	Health care service
Operational research	Patient throughput	Health center
Operations management	Process flow	Health centre
Operations research	Wait time	Health clinic
Optimisation	Waiting list	Health facility
Optimization	Waiting time	Healthcare center
Queueing	Care access	Healthcare centre
Queuing	Demand management	Healthcare clinic
Simulation model	Flow of patients	Healthcare facility
System dynamics	Patients' flow	Healthcare practice
Integer programming	Flow of care	Healthcare service
Linear programming		Home care
Modelling patient		Home health care
Network analysis		Long term care
Stochastic analysis		Mental health
Stochastic modelling		Primary care
Stochastic processes		Care facility
Visual simulation		Community care
		Community health
		Community healthcare
		Homecare
		Medical center
		Medical centre
		Multi facility
		Multiservice
		Residential care
		Walk in

Initial sets of search terms relating to community healthcare settings and OR methods were informed by Hulshof, Kortbeek, Boucherie, Hans, and Bakker (2012). Synonyms were added to these lists prior to the preliminary searches for papers. For patient flow terms and outcome terms, we formed initial lists that we considered relevant. The first batch of papers found using these lists was examined for further applicable search terms. The initial search terms are highlighted in bold in Table 1.

Papers obtained from the final searches were assessed for inclusion for full review at three levels. If a paper was not a literature review it was required to meet all the inclusion and none of the exclusion criteria outlined in Table 2. For each included paper, references were assessed using the same inclusion and exclusion process to find any papers that may have been missed in the searches.

Table 2. Inclusion and exclusion criteria for assessing papers presenting models of patient flow.

Assessment level	Criteria	Patient flow within community care	Patient flow and outcomes
Title and journal	Inclusion	At least one operational research method term in the article title, journal title or keywords	At least one operational research method term in the article title, journal title or keywords
		AND	AND
		At least one patient flow term in the article title, journal title, keywords or abstract	At least one term patient flow term in the article title, journal title, keywords or abstract
		AND	AND
		At least one community health setting term in the article title, journal title, keywords or abstract	At least one outcome term in the article title, journal title, keywords or abstract
		English language; published before November 2016 in peer-reviewed journals
	Exclusion	Title or journal of publication had no relevance to OR, healthcare or patient flow
Abstract	Inclusion	Abstract suggested that the paper focussed on operational processes of healthcare and that OR methods were used to model patient flow
	Exclusion	Papers based within management settings other than operational management
		The delivery of healthcare was not evaluated
		Only different scheduling policies were evaluated
		Abstract indicated that the paper was not based in community care	Abstract indicated that the paper did not use patient outcomes
Full text	Inclusion	Abstract level inclusion criteria met in the full text
		A model was presented using mathematical concepts and language
		The model was well specified and reproducible
		Quantitative analysis of a healthcare system was conducted within the paper
	Exclusion	Criteria for exclusion at abstract level met in the full text
		A model was viewed only in terms of its inputs and outputs without knowledge of its internal workings
		A model was formulated as a composition of concepts that could not be used for analysis
		A model was not rooted in analysis

Literature reviews were included at each level if they were concerned with OR methods for evaluating patient flow; focussed on operational processes of healthcare and no equivalent systematic review was included. Within the “Patient flow within community care” literature, review pieces were included if they focussed on community settings; whilst within the “Patient flow and outcome” literature, review pieces were included if they focussed on uses of patient outcomes in modelling processes.

Data tables were constructed to present key characteristics of the literature and shape our analysis. Informed by the initial readings, papers were grouped into five categories based on analytical method with five key characteristics of each model extracted and tabulated for comparison, given in Tables 4, 5 and 6.

Table 4. Papers included from “Patient flow within community care” search only.

Title	Authors	Setting	States	Factors considered to influence flow	Method output	Implementation of results
Markovian models
Modeling patient flows using a queuing network with blocking	Koizumi et al. (2005)	Community care -mental health	Multiple residential services	Service capacity	Queue lengths and wait times - with and without blocking	Not explicitly stated
				Traffic intensity per service
		-Physical queues		Congestive blocking
A block queueing network model for control patients flow congestion in urban healthcare system	Song et al. (2012)	Community and hospital pathways	Community services	Service capacity	Queue lengths and wait times - with and without blocking	Not explicitly stated
			Hospital registration	Traffic intensity per service
		-Physical queues		Congestive blocking
			General hospitals
				Batch arrival process
Non-Markovian steady state analysis
A model for planning resource requirements in health care organizations	Bretthauer and Côté (1998)	General approach, examples: blood bank, health maintenance organisation	Different services	Resource constraints e.g. Number of clinicians	Optimised total capacity costs	Not explicitly stated
			Stages of care
		-Physical queues
				Performanceconstraints e.g. Wait time
				Multiple time period extension
System dynamics analysis
A patient flow perspective of U.K. health services: exploring the case for new "immediate care" initiatives	Wolstenholme (1999)	UK health service	Primary care	Volume of patients arriving	Queue lengths	Some insights shared with NHS staff
		-Physical and non-physical queues	Secondary care		Waiting times
			Community care	Service capacity	Bed occupation
			NHS continuing care
					Scenario analysis
					Long run use of services
Simulation analysis of the consequences of shifting the balance of health care: A system dynamics approach	Taylor et al. (2005)	Community and acute care	Cardiac services in community	Wait time	Average wait times	Collaboration noted
		Non-physical queues		Size of waiting list	Cumulative patient referrals and activity
				Feedback mechanism
				Clinical guidelines
				Service capacity	Overall cost of care
					Scenario analysis
Analytical methods featuring time dependence
A continuous time Markov model for the length of stay of elderly people in institutional long-term care	Xie et al (2005)	Long-term care	Residential home care	Maximum likelihood estimation (MLE) of model parameters	Sojourn time	Not explicitly stated
		-Physical queues	Nursing home care		Estimation of LOS
			-Long stay		Patterns of care usage
			-Short stay
A model-based approach to the analysis of patterns of length of stay in institutional long-term care	Xie et al (2006)	Long-term care	Residential home care	MLE of model parameters	Sojourn time	Not explicitly stated
		-Physical queues	Nursing home care	Left truncated data	Estimation of LOS
				Right censored data
			-Long stay		Patterns of care usage
			-Short stay	Patient characteristics:
				-Previous care
				-Gender
Analytical methods for calculating the distribution of the occupancy of each state within a multi-state flow system	Utley et al. (2009)	Community mental health care	General states	Time spent in state	Time dependent distribution for occupancy of states	Suggestions made to stake holders
			Illustrated with states as different stages of care
		-Uncapacitated demand
A deterministic model of home and	Hare et al. (2009)	Long-term care	Different aspects of LTC:	Time varying population characteristics:	Future demand for each aspect of LTC	Model used for planning future care
communitycare client counts in British Columbia		-Uncapacitateddemand
			-Home care
			-Accommodation	-Patient age
				-Wealth
			Care environment	-Health status
				Initial conditions
			-Publicly funded/ non-publicly funded
A mathematical modelling approach for systems where the servers are almost always busy	Pagel et al. (2012)	Community mental health care	Different services	Capacity constraints e.g. Appointment slots	Optimal appointment allocation subject to wait time and capacity constraints	Formulation of a tool
		-Non-physical queues		Servers must always be busy (no steady state)
Appointment capacity planning in specialty clinics: a queueing approach	Izady (2015)	Specialty clinics	Waiting	Abandonment	Patient wait time	Not explicitly stated
		-Physical queues	In service	-Fixed	Queue length
				-Backlog dependent	Size of appointment queues
				Patients able to re-join queue
					No-show probability
				Capacity
					Referral variance
				Appointment type
					Panel size
Simulation Analysis
Improving outpatient clinic efficiency using computer simulation	Clague et al. (1997)	Outpatient-genito urinary medical clinic	Stages of care	Patient groups:	Patient wait time	Application of method in response to a feedback survey
				-Clinical staff required	Doctor wait time
		-Physical queues			Clinic overtime
				-New or returning	Scenario analysis
				Mixed arrivals
				No shows
				Staffing constraints
Evaluating the design of a family practice healthcare clinic using discrete-event simulation	Swisher & Jacobson (2002)	Family Practice	Stages of care	Patient groups:	Patient wait time	Not explicitly stated
		Healthcare Clinic	Locations in the clinic	-Health	Staffing costs
		-Physical queues		Mixed arrivals	Revenue
				No shows	Clinician overtime
				Staffing constraints	Scenario analysis
					Staff utilisation
					Facility utilisation
Improving patient flow at an outpatient clinic: Study of sources of variability and improvement factors	Chand et al. (2009)	Outpatient clinic	Stages of care	Variability in task times	Patient wait time	Some suggested changes have been implemented
		-Physical queues	Stages of patient information flow		Physician overtime:
				Patient characteristics:	-AM and PM
					Scenario analysis
				-New or returning
				-Administrative characteristics
Reducing patient wait times and improving resource utilization at British Columbia Cancer Agency's ambulatory care unit through simulation	Santibanez et al. (2009)	Community care-ambulatory care unit	Stages of care process	Shared resources	Scenario analysis	Suggestions made to senior management
				Appointment type	Patient wait time
		-Physical queues		Capacity constraints	Appointment duration
					Resource utilisation
				Scheduling policy	Time in system
					Clinician utilisation
Facilitating stroke care planning through simulation modelling	Bayer et al. (2010)	Stroke services	Stages of a stokepathway	Patient groups:	Scenario analysis	Not explicitly stated
		-Physical and non-physical queues		-Health related	Predicted bed days
			-Acute	Probabilistic:	-Acute
			-Community	-Death rate	-Care home
				-Length of stay	Cost of providing resource
				Capacity constraints
Using discrete event simulation to compare the performance of family health unit and primary health care centre organizational models in Portugal	Fialho et al. (2011)	Primary healthcare	Stages of clinic care	Administrative characteristics	Days to arrange a GP consultation	Not explicitly stated
		-Non-physical queues
				Consultation type	Annual number of different consultations
				Opening hours
				Duration of appointment	Waiting time
					Financial costs
				Routes of care
Modeling the demand for long-term care services under uncertain information	Cardoso et al. (2012)	Long-term care	Different aspects of LTC:	Patient groups:	Scenario analysis	Not explicitly stated
		-Uncapacitated demand		-Demographics	Future demand
			-Home based	-Chronic disease	Resources required to meet demand for each aspect of LTC
				-Level of dependency
			-Ambulatory	Mortality rates
			-Institutional
				Capacity
					Cost
A simulation Optimization Approach to Long-Term Care Capacity Planning	Zhang et al. (2012)	Long-term care	Waiting	Patient characteristics:	Scenario analysis	Collaboration, training and feedback highlighted
		-Uncapacitated demand	In service		Optimised capacity relating to waiting time targets
				-Age and gender
				-Arrival rate
				-LOS
				Initial conditions
					Future demand/capacity
Applying discrete event simulation (DES) in healthcare: the case for outpatient facility capacity planning	Ponis et al. (2013)	Outpatient clinics	Different services	Patient	Resource utilisation	Not explicitly stated
		-Non-physical queues		characteristics:	Cost of care
				-Administrative	Optimised service provision
				-Medical
				Budget constraints
				Capacity constraints
				Appointment types
				Abandonment
				Distance from clinic
Developing an adaptive policy for long-term care capacity planning	Zhang and Puterman (2013)	Long-term care	Waiting	Patient characteristics:	Scenario analysis	Not explicitly stated
		-Uncapacitated demand	In service	-Age and gender	Adaptive policy for capacity planning
				-Arrival rate
				-LOS
				Initial conditions
				Achievement of wait time targets in previous year	Optimised capacity relating to waiting time targets
					Future demand/capacity
Simulation analysis on patient visit efficiency of a typical VA primary care clinic with complex characteristics	Shi et al (2014)	Primary healthcare clinic -Physical queues	Stages of care	Patient groups:	Service utilisation	Suggestions made to management
				-Arrival type
				-Care requirements	Wait time
				No shows	Factor study
				Number of double booked appointments
Patient flow improvement for an ophthalmic specialist outpatient clinic with aid of discrete event simulation and design of experiment	Pan et al. (2015)	Specialist outpatient clinic	Stages of care and information flow	Patient characteristics:	Scenario analysis	Implementation of results
		-Physical queues	Waiting	-Services required	Turnaround time
				-Punctuality/no show	Waiting time
				Layout of clinic	Allocation of appointment slots
				Resource capacity:
				-Staffing levels
				-Shared resource
				Inter-relation of patient flow and information flow
				Batch arrivals in information flow
A simulation model for capacity planning in community care	Patrick et al. (2015)	Acute care	Different services	Patient groups:	Scenario analysis	Not explicitly stated
		Long-term care		-Care requirements	Necessary capacity to meet target:
				-Priority
		-Physical queues		-Preference	-Wait time/list size
				Capacity
				Reneging	-Percentage of patients who reach their preferred facility
A simulation optimisation on the hierarchical health care delivery system patient flow based on multi-fidelity models	Qiu et al. (2016)	Community care	Community services	Patient groups:	Queueing network:	Not explicitly stated
		General hospitals	General hospitals	-Care requirements	Optimised resources to achieve maximum profit
				Profit
		-Physical queues	Stages of care	Priority
				Inter-hospital flow
					Simulation:
					Evaluation of feasible solutions regarding:
					-Profit
					-Use of services
					-Cured patients

Table 5. Papers included from “Patient flow within community care” search and “Patient flow and outcomes” search.

Title	Authors	Setting	States	Factors considered to influence flow	Method output	Implementation of results
Markovian models
An analytical framework for designing community-based care for chronic diseases	Kucukyazici et al. (2011)	Community carepost acute services	Different services	Demographics of inter service flow	Scenario analysis Likely post care outcomes for common pathways	Not explicitly stated
		–Non-physical queues	Post care outcomes
The long-term effect of community-based health management on the elderly with type 2 diabetes by the Markov modeling	Chao et al. (2014)	Community services for diabetes	Health states	Treatment pathway Based on the results of a randomized controlled trial	Probability of a patients belonging to a given outcome state as time progresses	Not explicitly stated
				Variable health
				–Severity of disease
Analytical methods featuring time dependence
Intelligent patient management and resource planning for complex, heterogeneous, and stochastic healthcare systems	Garg et al. (2012)	Integrated care system including hospital, social, and community services	Post hospital services	Patient groups:	Forecast number of patients in post care outcome	Not explicitly stated
		–Non-physical queues		–Demographics
				–Care requirements
				–Length of stay	Forecast daily/total cost of care
Improving health outcomes through better capacity allocation in a community–based chronic care model	Deo et al. (2013)	Community carefor asthmatic patients	In serviceappointment	Variable health	Optimised appointment allocation subject to health benefit and capacity	Not explicitly stated
		–Non-physical queues	Waiting state	Time between appointment
			Health states	Service capacity
				Health benefit of treatment
Simulation analysis
Evaluating multiple performance measures across several dimensions at a multi– facility outpatient center	Matta & Patterson (2007)	Outpatient services	Different services	Day of week Patient groups:	Single parameter for analysing multiple, stratified performance measures	Some suggested changes have been implemented
		–Physical queues		–Care requirements	Scenario analysis
				Patient pathway
				Patient throughput
				Frequency of clinician overtime

Table 6. Papers included from "patient flow and outcomes" search only.

Title	Authors	Setting	States	Factors considered to influence flow	Method output	Implementationof results
Markovian models
Modeling the transplant waiting list: A queueing model with reneging	Zenios (1999)	Waiting list-transplant	Waiting list	Patient groups:	Wait time in system and until transplant-per group	Not explicitly stated
		-Non-physical queues	Obtained transplant	-Demographic	Fraction of patients who receive transplant per group
				-Transplant type
				Organ groups
				Reneging-death
Optimizing admissions to an intensive care unit	Shmueli et al. (2003)	Intensive Care Unit	ICU beds	Variable health:	Expected number of statistical lives saved by implementing an outcome based admission policy	Not explicitly stated
		-Physical queues	Waiting for service	-Survival probability
			In service	Capacity-beds
				Loss model
Modeling and analysis of high risk patient queues	Wang (2004)	Waiting list-transplant	Waiting list Obtained transplant	Patient priority:	Queue lengths and wait time-per group	Not explicitlystated
		-Non-physical queues		-Health related	Expected number of deaths
				Risk of death
				List size
Differentiated waiting time management according to patient class in an emergency carecenter using an open Jackson network integratedwith pooling and prioritizing	Kim and Kim (2015)	Emergency care centre	Waiting for service	Patient groups:	Waiting time	None explicitly stated
		-Physical queues	In service	-Acuity level	-FCFS
				Admission policy	-Hybrid (FCFS and priority)
				Patient group pooling
				Infinite waiting space	-Hybrid with pooled groups
A model for deceased-donor transplant queue waiting times	Drekic et al. (2015)	Waiting list-transplant	Waiting list	Variable health	Queue length and wait time Reneging probabilities-pergroup	Not explicitly stated
		-Non-physical queues	Obtained transplant	Prioritisation
			Patient priority-	Reneging
			Health related	List size
				Blocking probability
Non-Markovian steady state analysis
Efficiency and welfare implications of managed public sector hospital waiting lists	Goddard &Tavakoli (2008)	Waiting list-	Number of people on the waiting list	Service capacity	Wait time	Not explicitly stated
		hospital care-		Rationing system	-All patients
		Non-physical queues		Proportion of sick patients admitted	-For least ill patients
A multi-class queuing network analysis methodology for improving hospital emergencydepartment performance	Cochran and Roche (2009)	Emergency department	Stages of care	Patient group:	Queue lengths and wait time	Software made available to EDs
		-Physical queues		-Care requirements	Service utilisation
				Seasonality	Requirements for a desired level of utilisation	Feedback to clinicians and ED managers
				Number of beds
A queueing model to address wait time inconsistency in solid-organ transplantation	Stanford et al. (2014)	Waiting list-	Waiting list	Patient groups:	Wait time per patient type	Not explicitly stated
		transplant	Obtained transplant	-Care requirements
		-Non-physical queues		Organ groups
				Compatibility
System dynamics analysis
Modeling chronic disease patient flows diverted from emergency departments to patient-centered medical homes	Diaz et al. (2015)	Care for chronic disease	Stages of care	Patient groups:	Scenario analysis	Not explicitly stated
			-Emergency departments	-Insured and uninsured	Impact on demand for services and required capacity
			-Ambulatory services	-Care requirements	Resource utilisation
				Resource capacity	Cost
				Death	Health impact
				Congestion
Analytical methods featuring time dependence
Dynamic allocation of kidneys to candidates on the transplant waiting list	Zenios and Wein (2000)	Waiting list-transplant	Transplant queue	Variable health	Wait time in system and until transplant-per group	Not explicitly stated
		-Non-physical queues	Obtained transplant	Patient demographic	Fraction of patients who receive transplant per group
				Organ groups
				Availability of organ
				Transplant failure/re-join
				Quality of life measure
The optimal timing of living-donor liver transplantation	Alagoz et al. (2004)	Waiting list-transplant	Waiting list	Variable health	Optimal timing of transplant	Not explicitly stated
		-Non-physical queues	Obtained transplant	Organ quality
				Post-transplant survival rate
			Health states
			-Transplant in time period
			-Waiting in time period
A model for managing patient booking in a radiotherapy department with differentiated waitingtimes	Thomsen & Norrevang (2009)	Radiotherapy	Radiotherapy slots	Patient groups:	Lower and upper limits for slot allocation per group	Suggested use within department
		-Non-physical		-Care requirements
		queues		-Waiting time guarantee Capacity
Investigating hospital heterogeneity with a multi-state frailty model: application to nosocomialpneumonia disease in intensive care units	Liquet et al. (2012)	Intensive care	Admission Infection	Patient groups:	Number of patients with infection	None explicitly stated
			Death	-Frailty	-Death
			Discharge	-Type of admission	-Discharge
				-Infection
Optimizing intensive care unit discharge decisions with patient readmissions	Chan et al. (2012)	Intensive care	ICU beds	Variable health	Optimisation of cost incurred by demand dependent discharge	Not explicitly stated
		-Non-physical queues	Number of people in the system	Demand driven discharge	Readmission load andmortality rates
				-Cost such as loss in QUALY	-Low congestion
				Congestion	-High congestion
Planning for HIV screening, testing, and care at the veterans health administration	Deo et al. (2015)	Community care-for HIV patients	Stages of care Health states	Variable health	Optimal screening policy with regards to health benefit, budget and capacity	Several suggestions influenced decision making
		-Non-physical queues		Allocation of screening	Staffing levels
				Budgetary constraints
				Service constraints
Radiation Queue: meeting patient waiting time targets	Li et al. (2015)	Radiotherapy	Types of treatment slot for radiotherapy machines	Patient groups:	Required capacity to meet set waiting time targets	Not explicitly stated
		-Non-physical queues		-Care requirements	Optimal allocation of capacity for different patient groups
				-Service times	Utilisation
				Capacity
				Patient pooling
Simulation analysis
Simulating hospital emergency departments queuing systems:	Panayiotopoulos and Vassilacopoulos (1984)	Emergency department-	Waiting list	Variable clinician capacity	Average number of patients-in	Some
			In service	Waiting capacity	system and queue	suggested
(GJ/G/;„(t)) : (IHFF/N/oo)		Physical queues		Variable patient priority: -Health related	Average time-in system and queue	changes have been implemented
Development of a Central Matching System for the Allocation of Cadaveric Kidneys: A simulationof Clinical Effectiveness versus Equity	Yuan et al. (1994)	Transplant waiting list	Waiting list	Patient groups	Assessment of different allocation algorithms	Not explicitly stated
		-Non-physical queues	Received transplant	Organ groups	-Time until transplant
				Compatibility	-Time waiting if no transplant by year end
				Availability of organs	Number of unused organs
				Time spent waiting
Patient flows and optimal health-care resource allocation at the macro-level: a dynamic linear programming approach	van Zon and Kommer (1999)	General method for resource allocation	Stages of care	Variable health	Scenario analysis	Not explicitly stated
			Health states	Duration of medical activity	Optimisation of resources:
				Patient pathway	-Health of patients
				Health benefit	-Wait time
A simulation model to investigate the impact of cardiovascular riskin renal transplantation	McLean and Jardine (2005)	Waiting list-	Waiting list	Transplant failure	Post-transplant survival rate	Not explicitly stated
		transplant	Obtained transplant	Patient mortality rate	Scenario analysis
		-Non-physical queues		Patient characteristics:
				-Demographics
				-Health risk
A clinically based discrete-event simulation of end-stage liver disease and the organ allocation	Shechter et al. (2005)	Waiting list-transplant	Waiting list	Patient characteristics:	Post-transplant survival rate	Not explicitly stated
		-Non-physica queues	Obtained transplant	-Demographics	-1 year
				-Care requirements	-3 year
				Organ type
				Variable health
				Graft failure
Capacity planning for cardiac catheterization: acase study	Gupta et al. (2007)	Cardiac catheterization clinic	Stages of care	Patient group:	Wait times	Some suggested changes have been implemented
		-Physical queues		-Care requirements	Optimised capacity allocationsubject to desired wait times
				Clinician case load	Scenario analysis
A discrete event simulation tool to support and predict hospital and clinic staffing	DeRienzo et al (2016)	Neonata intensive carel	Intensive care beds	Patient groups:	Estimated staffing allocation	Not explicitly stated
		-Physical queues		-Admission type	Forecast future demand
				-Acuity	Cost of provision
				-Health
				Resource capacity

4. Results of literature searches

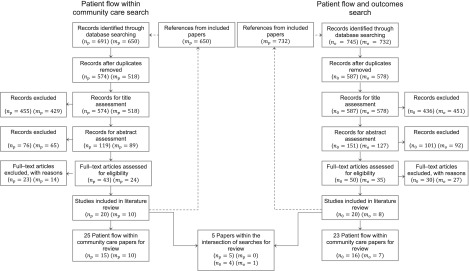
The results of the final searches for and selection of papers are shown in an adapted PRISMA flow chart (Moher, Liberati, Tetzlaff, & Altman, 2009), Figure 1. Reasons for the exclusion of texts at full text assessment are shown in Table 3.

Figure 1.

Flow chart of literature search results – 53 papers were eligible for review.

Table 3. Reasons for exclusion at full text assessment.

	Reason for exclusion
Number of papers excluded at full text assessment	No OR/patient flow modelling	Non-community settings	Model not reproducible/specified//quantitative	Analysis of different scheduling policies	No patient outcomes
23 “Patient flow within community care” literature	5	8	7	3	N/A
14 “Patient flow within community care” references	2	8	3	1	N/A
30 “Patient flow and outcomes” literature	8	N/A	2	7	13
27 “Patient flow and outcomes” references	4	N/A	–	1	22

Overall 25 “Patient flow within community” papers, 23 “Patient flow and outcomes” papers and 5 papers in the intersection entered the full review. An analysis of this literature is now presented with in the intersection of the two searches included in the “Patient flow within community care” section.

5. Analysis

5.1. Papers found within the “Patient flow within community care” search

5.1.1. Markovian models

A Markovian model views flow within a system as a random process within which the future movement of an entity is dependent only upon its present state and is independent of time spent in that state or the pathway it previously travelled. Whilst systems of healthcare are not truly Markovian, in using these methods, a steady-state analysis of a system may be formulated from which meaningful long-run averages of system metrics can be calculated.

The settings of these publications, presented in Tables 4 and 5, include residential mental healthcare (Koizumi, Kuno, & Smith, 2005), post-hospital care pathways (Kucukyazici, Verter, & Mayo, 2011), community services and hospital care (Song, Chen, & Wang, 2012) and community-based services for elderly patients with diabetes (Chao et al., 2014).

Within these models, states were defined as different services or stages of care. Kucukyazici et al. (2011) and Chao et al. (2014) also defined states of post-care outcomes. In the former these included patient mortality, admission to long-term care and re-hospitalisation, whilst the latter defined states of subsequent health progression.

Two main factors were considered to influence flow within these models: the effect of congestive blocking caused by limited waiting space (Koizumi et al., 2005; Song et al., 2012) and the diversity of patients: demographics (Kucukyazici et al., 2011) and severity of disease (Chao et al., 2014). In considering blocking, flow was influenced by the available capacity and average occupancy of each service.

The output measures were queue lengths and wait times for each state – with and without congestive blocking (Koizumi et al., 2005; Song et al., 2012) and the probability that patients would be in a given post-care outcome state (Chao et al., 2014; Kucukyazici et al., 2011).

An analysis of different scenarios was undertaken in both latter papers to identify how alternative treatments may help improve post-care outcomes.

None of the papers explicitly reported implementation of their results. We consider implementation to include any action to share or use the results of the work within the modelled setting.

5.1.2. Non-Markovian steady-state models

An optimisation approach for resource allocation by Bretthauer and Côté (1998) defined states as services within specified pathways. The aim was to minimise overall costs whilst maintaining a certain level of care as measured by metrics such as desired waiting. Within the model, flow was influenced by capacity constraints, such as number of beds.

5.1.3. System dynamics analysis

System dynamics is a modelling method whereby computer simulations of complex systems can be built and used to design more effective policies and organisations (Sterman, 2000). Two applications were found, modelling systems of markedly different sizes. Taylor, Dangerfield, and Le Grand (2005) evaluated the uses of community care services to bolster acute cardiac services whilst Wolstenholme (1999) evaluated the UK’s NHS.

States were defined as community or acute services (Taylor et al., 2005) and different sectors of care, namely primary, acute, NHS continuing care and community care (Wolstenholme, 1999).

Capacity and rate variables, such as waiting list size and clinical referral guidelines were considered to influence flow within both models. A feedback mechanism was used by Taylor et al. (2005) to evaluate how changes in these variables may stimulate and effect demand.

The main metrics of these models related to demand and access, namely waiting times and patient activity – for example, long-run use of services and length of queues (Wolstenholme, 1999). In both papers, a scenario analysis was performed to evaluate how changes within the model affected its output.

Wolstenholme (1999) reported that some findings were shared with NHS staff.

5.1.4. Analytical methods including time dependence

Applications of analytical methods with time dependence included specialist clinics (Deo, Iravani, Jiang, Smilowitz, & Samuelson, 2013; Izady, 2015), care after discharge from an acute stroke unit (Garg, McClean, Barton, Meenan, & Fullerton, 2012), long-term institutional care (Xie, Chaussalet, & Millard, 2005, 2006), community mental health services (Pagel, Richards, & Utley, 2012; Utley et al., 2009) and home/community care in British Columbia (Hare, Alimadad, Dodd, Ferguson, & Rutherford, 2009).

The state definitions within these models related to stages of care/different services (Garg et al., 2012; Hare et al., 2009; Pagel et al., 2012; Utley et al., 2009; Xie et al., 2005, 2006); “waiting” or “in service” (Deo et al., 2013; Izady, 2015) and health states – in particular stages of health progression (Deo et al., 2013) or post-care outcomes (Garg et al., 2012).

The factors considered to influence flow included capacity of services (Izady, 2015; Pagel et al., 2012); patient demographics and care requirements (Garg et al., 2012; Hare et al., 2009; Xie et al., 2005, 2006); patient health between recurrent appointments (Deo et al., 2013) and the length of time in which a person occupied a state (Utley et al., 2009).

Commonly, the system metrics used in these papers related to the time a patient spent interacting with parts of the system – such as expected length of stay, waiting times and time spent in states. Garg et al. (2012) calculated the daily cost of care and likely post-care outcome states for patients of different demographic groups. Pagel et al. (2012) and Deo et al. (2013) identified optimal capacity allocations subject to desired levels of queue lengths and wait times, and impact on patient health, respectively. Hare et al. (2009) evaluated the possible future demand for services under different scenarios and situations.

Of these applications, Pagel et al. (2012) and Utley et al. (2009) reported steps towards implementation. In the former, a software tool was created, whilst in the latter the fi dings of the model were shared with key stakeholders. Hare et al. (2009) also noted the use of their model for care planning within their given setting.

5.1.5. Simulation methods

The settings of these papers included long-term care (Cardoso, Oliveira, & Barbosa-PóVoa, 2012; Zhang & Puterman, 2013; Zhang, Puterman, Nelson, & Atkins, 2012), outpatient services (Chand, Moskowitz, Norris, Shade, & Willis, 2009; Clague et al., 1997; Matta & Patterson, 2007; Pan, Zhang, Kon, Wai, & Ang, 2015; Ponis, Delis, Gayialis, Kasimatis, & Tan, 2013; Swisher & Jacobson, 2002), primary care and ambulatory clinics (Fialho, Oliveira, & Sa, 2011; Santibáñez, Chow, French, Puterman, & Tyldesley, 2009; Shi, Peng, & Erdem, 2014) and provisions of integrated acute and community services (Bayer, Petsoulas, Cox, Honeyman, & Barlow, 2010; Patrick, Nelson, & Lane, 2015; Qiu, Song, & Liu, 2016).

States were defined as different services, clinics or sectors of care; or healthcare tasks within single clinics (Chand et al., 2009; Clague et al., 1997; Fialho et al., 2011; Santibáñez et al., 2009; Shi et al., 2014; Swisher & Jacobson, 2002). Chand et al. (2009) and Pan et al. (2015) modelled the flow of patient information alongside patient flow and thus defined states of information flow.

Factors considered to influence flow commonly included the healthcare requirements/demographics of patients (Chand et al., 2009; Clague et al., 1997; Fialho et al., 2011; Shi et al., 2014; Swisher & Jacobson, 2002), constrained capacity and rates of no show/reneging (Clague et al., 1997; Shi et al., 2014; Swisher & Jacobson, 2002). Bayer et al. (2010), Cardoso et al. (2012), Ponis et al. (2013), and Qiu et al. (2016) considered monetary influences such as budgetary constraints, cost of care and profitability. Chand et al. (2009) used the variability of time in completing care tasks.

Common metrics related to the time that a patient spent waiting in a state or in the system as whole. Optimised capacity levels relating to key performance measures were also widely considered (Ponis et al., 2013; Zhang & Puterman, 2013; Zhang et al., 2012). Matta and Patterson (2007) calculated a single system metric – an aggregate of multiple performance measures stratified by day, facility routing and patient group. This single metric was formed of measures such as average throughput, average system time and average queue time.

The implementation of suggested changes was recorded in several applications (Chand et al., 2009; Clague et al., 1997; Matta & Patterson, 2007; Pan et al., 2015; Santibáñez et al., 2009; Shi et al., 2014; Zhang et al., 2012).

5.2. Papers found within the “Patient flow and outcomes” search

5.2.1. Markovian models

As outlined in Tables 5 and 6, seven publications used Markovian methods and outcomes, two of which were also included within the “Patient flow within community care” section. The five new papers modelled transplant waiting lists (Drekic, Stanford, Woolford, & McAlister, 2015; Wang, 2004; Zenios, 1999), intensive care units (Shmueli, Sprung, & Kaplan, 2003) and emergency care (Kim & Kim, 2015).

In these models, states related to whether patients were “waiting” or had obtained a service/transplant. Drekic et al. (2015) defined patient priority states to reflect health deterioration.

The factors that influenced flow related to patient health with groups or states used to assign priorities (Drekic et al., 2015; Wang, 2004) or, represent patient demographics and care requirements. The reneging characteristics of different groups of patients were also considered in each transplant paper with patients modelled as leaving the waiting list due to death or for other reasons. (Drekic et al., 2015; Zenios, 1999).

The output measures of these papers commonly related to the wait time faced by patients. Other metrics included the probability of reneging per patient group (Drekic et al., 2015) and the expected number of deaths for waiting patients (Wang, 2004) or lives saved by an admission policy (Shmueli et al., 2003). Zenios (1999) calculated the average time spent in the system and in the queue for each demographic group, and the fraction of patients from each group who received a transplant.

None of the papers reported an implementation of their results within their care setting.

5.2.2. Non-Markovian steady-state models

The modelled settings and applications included an emergency department (Cochran & Roche, 2009) and two waiting lists, one for hospital care (Goddard & Tavakoli, 2008), the other for transplant patients (Stanford, Lee, Chandok, & McAlister, 2014). States were defined as stages of hospital care and as “waiting” or “in service”.

The factors considered to influence flow were patient group and seasonality (Cochran & Roche, 2009) and resource availability and patient health (Goddard & Tavakoli, 2008; Stanford et al., 2014). Each model used metrics relating to the amount of time a patient spent within parts of the system.

Cochran and Roche (2009) reported an implementation of their results with software developed and made available for clinicians and care managers. Feedback and educational sessions were also organised to help key stakeholders to understand the work.

5.2.3. System dynamics analysis

Diaz, Behr, Kumar, and Britton (2015) evaluated patient flow between states of acute care and home care for patients with chronic disease. The factors considered to influence flow related to patient groups based on their care requirements and whether they possessed insurance. Congestion and capacity of resources were also considered. A scenario analysis was performed to evaluate the impact of different patient routes and resource allocations on the level of demand for services and the cost of providing care.

5.2.4. Analytical methods including time dependence

Nine papers were found, two of which were included in the “Patient flow within community care” section. Of the seven remaining, the settings were care for chronic diseases (Deo, Rajaram, Rath, Karmarkar, & Goetz, 2015), two intensive care models (Chan, Farias, Bambos, & Escobar, 2012; Liquet, Timsit, & Rondeau, 2012), two radiotherapy models (Li, Geng, & Xie, 2015; Thomsen & Nørrevang, 2009) and two transplant waiting lists (Alagoz, Maillart, Schaefer, & Roberts, 2004; Zenios & Wein, 2000).

States were defined as “in service” or “waiting”, different services or different appointment slots (Li et al., 2015; Thomsen & Nørrevang, 2009). Alagoz et al. (2004), Liquet et al. (2012), and Deo et al. (2015) also defined multiple health states.

The factors considered to influence flow were commonly related to differences within the patient population pertaining to health (Alagoz et al., 2004; Deo et al., 2015); care requirements or demographic/health-related groups (Zenios & Wein, 2000) and the availability of resources such as organs (Alagoz et al., 2004; Zenios & Wein, 2000) or appointment slots (Deo et al., 2015; Li et al., 2015; Thomsen & Nørrevang, 2009).

Common metrics used by these methods focussed on the amount of time a patient spent waiting for a service – for example, the optimal timing of appointments (Deo et al., 2015) or transplants (Alagoz et al., 2004) subject to changes in patient health. Zenios and Wein (2000) calculated output measures for different groups of patients to evaluate equity within the process of organ allocation. Forecasts of capacity requirements and optimal allocation of resources based on patient groups were also common.

Thomsen and Nørrevang (2009) and Deo et al. (2015) reported that some of their suggestions had influenced decision-making.

5.2.5. Simulation methods

Eight applications were found with one included in the “Patient flow within community care” (Matta & Patterson, 2007). Of the seven remaining, applications included a cardiac catheterisation clinic (Gupta et al., 2007), three transplant waiting lists (McLean & Jardine, 2005; Shechter et al., 2005; Yuan, Gafni, Russell, & Ludwin, 1994), an evaluation of an emergency department (Panayiotopoulos & Vassilacopoulos, 1984), neonatal intensive care (Derienzo et al., 2016) and a healthcare resource allocation model (van Zon & Kommer, 1999).

Within these papers, states were defined as healthcare tasks (Gupta et al., 2007; van Zon & Kommer, 1999), number of beds and “waiting” or “in service”.

The factors considered to influence flow within these models included demographics/care requirements (Gupta et al., 2007; McLean & Jardine, 2005; Shechter et al., 2005; van Zon & Kommer, 1999); the health, mortality and survival rates of patients (McLean & Jardine, 2005; Shechter et al., 2005; van Zon & Kommer, 1999) and resource capacity.

Several metrics were calculated within these methods, with the time patients spent interacting with or waiting within parts of the system a common measure. Other outputs of interest included capacity allocation (Derienzo et al., 2016; Gupta et al., 2007; Yuan et al., 1994); the cost of care, health benefits of service (van Zon & Kommer, 1999) and the expected survival rate of patients (McLean & Jardine, 2005; Shechter et al., 2005).

Panayiotopoulos and Vassilacopoulos (1984) and Gupta et al. (2007) both noted that some of their suggested changes had been implemented.

5.3. Summary of findings and discussion across literatures

Findings from across the literature will now be summarised and discussed, drawing together common themes and key characteristics as presented in Tables 4, 5 and 6. In combination, we reviewed 53 papers presenting models of patient flow. 30 applied to community care services which included mental health services, physical health services, outpatient care and patient flow within acute and community settings. Furthermore, 32 applications used, in some form, either queue lengths or the amount of time that a patient spent within states as output measures. The next most common metrics were monetary costs in relation to patient use and the allocation of capacity-related resources.

Within the “Patient flow and community care” literature a range of flow characteristics were considered. For instance, patients access and arrivals to community services were modelled as unscheduled (e.g. Taylor et al., 2005), by appointment (e.g. Deo et al., 2013, 2015), by external referral (e.g. Koizumi et al., 2005), or a mixture of the above (e.g. Chand et al., 2009; Song et al., 2012). Furthermore, multiple care interactions were modelled as either sequential visits to different services (e.g. Koizumi et al., 2005; Song et al., 2012) or as single visits where multiple tasks were carried out (e.g. Chand et al., 2009). In either instance patients were sometimes modelled as being able to recurrently visit the same service over time with some patients using the service more frequently (e.g. Deo et al., 2013; Shi et al., 2014).

Within the “Patient flow and outcome” literature, there were 10 models of transplant/waiting lists, 8 of community, ambulatory and outpatient services, 3 of emergency departments, 4 for intensive care, 2 for radiotherapy and 1 general model of resource allocation. Outcome measures were incorporated within the outputs of these models in three broad ways: (1) system metrics were stratified by outcome related groups; (2) variable patient or population level health was used as an objective or constraint within a model to influence resource allocation or (3) health outcomes – such as patient mortality or future use of care – were used as system metrics. Notably, 15 papers used patient groups to represent differing health/outcomes, whilst 13 papers incorporated variable health/outcome which could change during a course of care. By including variable health/outcome, a model’s output was informed by the effect of a care interaction, or absence of a care interaction, on patient outcomes and on the operation of the system.

Patient groups relating to health/outcome were used in models of each method and were commonly used in resource and service capacity allocations. Notably, their application within steady-state methods is limited since it is difficult to model differing group-dependent variables, such as service times, since the order of patients within these queues is unknown.

Variable health/outcome which could change during a course of care was commonly used within time-dependent methods. They were used to model the effect of care on a population where the modelled time period was large, such as stays with residential care or where multiple interactions were considered.

Across both literatures, queues could be categorised as either physical – constrained demand – or non-physical – unconstrained demand, as per Tables 4, 5 and 6. Physical queues form when patients wait for service within a fixed physical space. Examples include, arrivals forming a queue within a clinic or emergency care (e.g. Chand et al., 2009; Santiba′n˜ ez et al., 2009; Shi et al., 2014) or when patients move between care interactions and immediately wait within another single physical location (e.g. Cochran & Roche, 2009; Xie et al., 2005, 2006). When physical queues occur, the time a patient spends waiting for service is typically of the order of their expected service time. These queues are constrained and patient demand is modelled from the point when they physically arrive to the service.

Given these dynamics, the most common analysis of physical queues related to the daily operation of single services. Such models were used to gain insight into the delivery of care (e.g. flow between multiple treatments/consultations in a single visit). Studies of physical queues were carried out using each type of method. The choice of method depended on the desired insight, factors considered to influence flow and size of the system. Steady-state methods were sufficient if queue lengths and wait times were of primary concern. However, if variability in input parameters or periodic influences were important, time variable methods were more appropriate. These models typically focus on shorter time frames of care, therefore health/outcome groups were used within these models.

Alternatively, non-physical queues occur when patients may wait in any location away from the service such as their place of residence-e.g. when care is scheduled (Deo et al., 2013) or a patients wait is potentially long and unknown (Zenios & Wein, 2000). Non-physical queues represent unconstrained demand which begins from the point when a patient is referred to a service. A patient’s wait is therefore typically of an order larger than their expected service time. Such models are commonly used to model the demand and access at a system level.

The most common analysis of non-physical queues related to waiting lists and multiple uses of a single or multiple services. Studies of these scenarios were carried out using steady-state analysis or time-dependent methods. Due to the long-run nature of steady-state models these models were appropriate for such situations, especially when variability and differences within the patient population were negligible. In scenarios of scarce appointment or resource allocation, time variable methods were increasingly used. Within these models, variable health/outcome was widely considered due to the longer time frames of care, possible multiple interactions and the benefits stated previously.

It should be noted that this work is limited due to the difficulty of systematically reviewing this literature. In particular, we found two main difficulties. Firstly, these papers are published within a wide range of journals, some within healthcare journals, others in operational research (OR) journals, whilst a proportion was found within journals that were neither health-specific nor OR specific. Secondly, we found that patient flow is described and referred to in myriad ways within literature. No clear standards were found; thus, locating these papers was particularly difficult.

Due to the complexity of finding literature, we cannot claim our findings to be exhaustive. However, by following an iterative process of literature searching our findings are representative of this literature, allowing us to draw meaningful conclusions in the next section.

As a final observation, the reporting of implementation and collaboration varied greatly within each group of analytical method.

6. Conclusions and directions for future work

Community healthcare consists of a diverse range of geographically disparate services, each providing treatment to patients with specific health needs. As a result, the factors that are considered to influence patient flow are often markedly different to acute services and vary from one service to another. Considering the characteristics discussed in this review, it is common for a mixture of complex dynamics to be modelled within community care applications. Modelling these services can thus become complicated, requiring innovative methods to include all or some of these dynamics. This is highlighted by the range of different methods presented in this review.

Future directions for patient flow modelling within community care are now explored motivated by known challenges for community care, gaps found within the literature and any transferable knowledge between the two sets of literature.

Few models considered patient flow within systems of differing community services with most studies focussing on single services. Likewise, few also considered the mix of patients within these services. Consider, however, a diabetes pathway where patients may require treatment for comorbidities from multiple services based in the community. Each of these services will also provide care to a range of patients, not just those with diabetes. This example highlights a significant challenge in the management of community services. Namely, how to co-ordinate and deliver care within physically distributed, co-dependent services considering increasing episodic use by patients with differing needs. With a shift of focus towards care for the increasing number of patients with multiple long-term illnesses (ENGLand NHS, 2014), the patient mix within each service further exacerbates this challenge. Therefore, it would be beneficial to develop methods for modelling patient fl through multiple services to investigate these scenarios.

Considering the above, another useful direction would be to develop time-dependent analytical methods and simulation models for these scenarios. Whilst often analytically difficult, there are important benefits in using these methods as shown by the wide range of applications within this review. Given the characteristics of community services previously discussed, a helpful addition to the research landscape would be models of systems for which steady-state assumptions do not hold or where capacity, demand and timing of patient use vary. This would be helpful in community care where – due to the decentralisation – it can be hard to measure and interpret the impact that changes to one part of the system have on the whole system over short-term and long-term time periods. In considering flow in a system of inter-related services, or situations where patients may re-use the same service over a time period, the development of system level, timedependent methods would be beneficial in analysing the time variable impact of changes in the immediate, short term and long term for the whole system.

Finally, 13 papers used variable health/outcomes, of which 5 applied to multiple care interactions. Again considering the purpose and nature of community care, we suggest that methods which use multiple health states to model the improvement and decline of patient health throughout a course of care would be a useful direction for future study. A good example of these methods is presented by Deo et al. (2013, 2015). Having otherwise not been widely explored, methods that quantify and evaluate the quality of care and include an interaction between patient outcomes, care pathways and flow within the system would be valuable and appropriate for community care modelling.

In considering OR methods for community services which combine patient flow modelling and patient outcomes, there may be some transferable knowledge from transplant models. For situations where non-physical are modelled, transplant list models may provide a useful basis as they share some distinct similarities to community care services – such as reneging, time-varying demand, limited resources and in some cases re-entrant patients. Transplant models may be informative for both scheduled care and unscheduled care.

Acknowledgements

This research was supported by the National Institute for Health Research (NIHR) Collaboration for Leadership in Applied Health Research and Care North Thames at Barts Health NHS Trust. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health. The first author was supported by the Health Foundation as part of the Improvement Science PhD programme. The Health Foundation is an independent charity committed to bringing about better health and healthcare for people in the UK.