The Structure of VOPc on Cu(111): Does V=O Point Up, or Down, or Both?

Abstract

The local structure of the nonplanar phthalocyanine, vanadyl phthalocyanine (VOPc), adsorbed on Cu(111) at a coverage of approximately one-half of a saturated molecular layer, has been investigated by a combination of normal-incidence X-ray standing waves (NIXSW), scanned-energy mode photoelectron diffraction (PhD), and density-functional theory (DFT), complemented by scanning tunnelling microscopy (STM). Qualitative assessment of the NIXSW data clearly shows that both “up” and “down” orientations of the molecule (with V=O pointing out of, and into, the surface) must coexist on the surface. O 1s PhD proves to be inconclusive regarding the molecular orientation. DFT calculations, using two different dispersion correction schemes, show good quantitative agreement with the NIXSW structural results for equal co-occupation of the two different molecular orientations and clearly favor the many body dispersion (MBD) method to deal with long-range dispersion forces. The calculated relative adsorption energies of the differently oriented molecules at the lowest coverage show a strong preference for the “up” orientation, but at higher local coverages, this energetic difference decreases, and mixed orientation phases are almost energetically equivalent to pure “up”-oriented phases. DFT-based Tersoff–Hamann simulations of STM topographs for the two orientations cast some light on the extent to which such images provide a reliable guide to molecular orientation.

1. Introduction

The fact that phthalocyanines (Pc) are promising materials for solar photovoltaic cells and other electronic devices^1,2 has been one factor motivating many studies in the past few years of these molecules adsorbed on surfaces, particularly on close-packed coinage metal surfaces and mostly using scanning tunnelling microscopy (STM).³ Much of this work has focused on copper phthalocyanine (CuPc) and other essentially planar phthalocyanines containing a single central atom that can be accommodated within the molecular plane. Only a few studies have been undertaken of nonplanar phthalocyanines centered by a diatomic moiety (GaCl, TiO, ClAl, VO) that is oriented perpendicular to the phthalocyanine ligand plane. While adsorption of these species on surfaces with which the interaction is mostly dispersion dominated (largely van der Waals in character) is expected to favor a molecular orientation in which this central diatomic moiety points out from the surface (“up”), on more strongly interacting substrates the expected preferred orientation is less clear. Here we report the results of an investigation of the structure of vanadyl phthalocyanine (VOPc, Figure 1) on Cu(111).

Figure 1.

Ball-and-stick model representation of the VOPc molecule. Coloring used is O = red, N = blue, C = black, H = white, and V = purple.

Very few quantitative structural investigations have been reported of phthalocyanine adsorption in general, but for nonplanar phthalocyanines, in particular, there have been only three such studies. The quantitative structural technique of normal-incidence X-ray standing wave (NIXSW)⁴ has been applied to study TiOPc on Ag(111).⁵ It was concluded that TiO points out of the surface (hereafter referred to as an “up” orientation) over the full range of submonolayer ordered phases, but at higher coverages, additional molecules with the TiO pointing “down” occur in a bilayer. These “head-to-head” bilayer structures are believed to be stabilized by the opposing dipole moments of the “up” and “down” species, and indeed, this is the same structural arrangement found in bulk crystals and thin films of these nonplanar phthalocyanines (e.g., refs (6−9)). NIXSW has also been used to investigate GaClPc on Cu(111)¹⁰ with the initial conclusion that the GaCl points down to the surface to form a Cl-substrate covalent bond at submonolayer coverages, although both orientations were believed to occur at bilayer coverage. Subsequently, however, the same group undertook density-functional theory (DFT) calculations on this system and concluded that the lowest energy low-coverage structure actually involves scission of the Ga–Cl bond, with the atomic Cl being coadsorbed with the remaining GaPc species. The NIXSW data were reinterpreted as consistent with this dissociation model.¹¹ Finally, a scanned-energy mode photoelectron diffraction (PhD) investigation of VOPc on Au(111) led to the conclusion that in this system, the V–O bond points out of the surface.¹²

In the absence of such quantitative structural investigations, the most commonly used technique upon which orientation assignments have been made in the literature is STM. As shown in Figure 1, VOPc, in common with other phthalocyanine molecules, is 4-fold symmetric with four conjugated isoindole subgroups and a central species, which in this case is the vanadyl ion VO²⁺. If the molecule is adsorbed with its molecular plane parallel to the surface, this 4-fold symmetric shape can be recognized in STM images, while in images recorded in the constant tunnelling current mode, the center of the molecule is sometimes imaged as a dip (dark) and sometimes as a protrusion (bright). These two alternative images have been assumed to correspond to the two possible orientations of the molecule, with the V=O bond either pointing “up” (out of the surface) or “down” (into the surface). Which image corresponds to which orientation has largely been a matter of conjecture, although complementary independent electronic structure information derived from X-ray absorption spectra (XAS) or X-ray photoelectron spectroscopy (XPS) has been used to support some assignments. Most commonly, it has been asserted, or assumed, that the image with the bright protruding center corresponds to the “up” orientation (e.g., refs (13,14)). Of course, it is clearly true that in this orientation, the O atom center lies higher above the surface than the surrounding C, N, and H atoms, so there certainly is a physical protrusion. However, STM maps the corrugation of the surface electronic structure, which does not necessarily follow the geometrical structure. STM images of VOPc adsorbed on Au(111) show no bright centers, but reasonable arguments have been presented as to why this may be compatible with an “up” orientation,¹⁵ and this conclusion is consistent with the findings of the PhD study¹²

TiOPc is reported to adopt an “up” orientation on Ag(111) both in a low-coverage commensurate phase, which appears in STM to contain an ordered arrangement of molecules showing both bright and dim centers, and in a higher-coverage phase, in which the imaged molecules all show a dip in their centers.¹⁶ This orientation assignment for the higher-coverage phase is consistent with the results of the NIXSW study.⁵ By contrast, a very recent STM and STS (scanning tunnelling spectroscopy) study of TiOPc on Cu(111), Ag(111), and Au(111)¹⁷ finds evidence in STM images of both orientations coexisting on all these surfaces at submonolayer coverages, with a tendency to form up/down dimers. On Ag(111), in particular, local work function measurements achieved by measuring the dependence of the tunnelling current on the tip height were used to determine the orientation of the molecular dipoles. The molecular images with the central protrusion showed a local increase in work function attributed to the “up” orientation, and those with no central protrusion showed a local work function decrease assigned to a “down” orientation. STM images of TiOPc on Cu(110) show both central dips and central protrusions that have been assigned, respectively, to “up”- and “down”-oriented species; these assignments seem to be based on the reduced (lower than 4-fold) symmetry of the images of the molecules attributed to those in the “down” orientation.¹⁸ It was argued that this reduced symmetry could result from a molecular tilt that would not be expected to occur in the “up” orientation with the molecular plane parallel to the metal surface. An STM study of ClAlPc on Cu(111) also shows two different types of molecular image. One with a bright center was assigned to an “up” orientation, while the other image shows no bright center but a feature with reduced (2-fold) symmetry that was assigned to a “down” species.¹⁹ ClB-subPc, which contains three conjugated isoindole groups, has also been investigated by STM on Cu(111).²⁰ Also in this system, two different local molecular images are seen. One with a bright center that was assigned to an “up” orientation, but the other image with a dim center was assigned to a dissociated (BPc) species; in this case, these assignments were based on the results of complementary DFT calculations. There is clearly a parallel here between ClB-subPc and GaClPc, in that DFT calculations indicate release of Cl from both molecules on interaction with the Cu(111) surface.

VOPc has also been studied on both Ag(111) and Si(111) using the XAS and synchrotron X-ray photoelectron spectroscopy (SXPS) techniques;²¹ the authors interpret their data as indicating that the molecule adopts an “up” orientation on Ag(111) but a “down” orientation on Si(111).

In the case of VOPc adsorbed on Cu(111), investigated here, STM images of submonolayer coverages show what appears to be a random mixture of the two different types of molecular images, most obviously interpreted as a mixture of “up” and “down” orientations.¹³ In order to try to understand the true situation better, we report here the results of the application of two quantitative structural techniques, NIXSW and PhD, to this system, complemented by DFT calculations of both the minimum energy structure and the expected STM images. The surface phases formed were further characterized by STM, low-energy electron diffraction (LEED), and SXPS.

2. Experimental and Computational Methods

Initial characterization of the Cu(111)/VOPc adsorption system was conducted using an ultrahigh-vacuum (UHV) room temperature Omicron STM instrument also equipped with low-current LEED optics (Omicron SPECTALEED) and the usual facilities for in situ sample preparation, at the University of Warwick. Additional STM imaging was performed using a second, commercial (Createc) low-temperature STM instrument at Warwick, to produce images at a sample temperature of ∼80 K. SXPS, NIXSW, and PhD measurements were undertaken at the I09 UHV end-station of the Diamond Light Source equipped with a VG Scienta EW4000 HAXPES hemispherical electron analyzer (angular acceptance range ±30°), which was mounted in the horizontal plane at 90° to the direction of the incident linearly polarized undulator radiation. This chamber was also fitted with low-current LEED optics (OCI BDL800IR-MCP LEED). The I09 beamline consists of two undulators that provide a separate “hard” and “soft” X-ray source. A Si(111) double crystal monochromator delivers the “hard” X-rays needed to perform the NIXSW experiments at I09, while a grazing incidence plane grating monochromator delivers the soft X-rays required for the measurement of high-resolution SXP spectra and PhD data. The sample surface preparation was the same at all instruments. Specifically, the Cu(111) single crystal was prepared in situ using cycles of 1 keV Ar⁺ ion bombardment for 30 min followed by annealing to ∼500 °C for another 30 min. All STM images were plane-corrected and flattened using the open source image-processing software Gwyddion.²² VOPc powder (85% pure (dye content), Sigma-Aldrich, UK) was triply purified by thermal gradient sublimation and degassed 20 °C below the temperature at which significant evaporation occurs for several days prior to use. VOPc was deposited onto the Cu(111) surface from two different standard commercial evaporation cells on the different analysis chambers, delivering similar VOPc fluxes when operated at nominal temperatures of ∼270 and ∼380 °C. respectively, as measured by K-type thermocouples.

All DFT calculations were performed with the all-electron local orbital code FHI-aims²³ and standard “tight” numerical settings using the PBE exchange-correlation functional.²⁴ The structures were relaxed with a force convergence criterion of 25 meV/Å. Long-range dispersion interactions were accounted for with the vdW^surf dispersion correction scheme²⁵ and the short-range screened many body dispersion (MBD) method,^26,27 with environment-dependent dispersion parameters as defined by Ruiz et al.²⁵ This approach has been previously described.²⁸ The optimized lattice constant of bulk Cu was 3.62 Å. We performed calculations for surface overlayers of VOPc on Cu(111) in a range of different surface meshes in order to represent low-coverage (LC) and high-coverage (HC) situations. Specifically for the LC case, a single molecule was placed in a (7 × 4√3)rect. unit mesh, while higher coverages were represented by a single molecule in a (6 × 6) unit mesh (HC1), two molecules in a (11 × 6) unit mesh (HC2), and two molecules in a (10 × 3√3)rect. unit mesh (HC3). A 4 × 4 × 1 Monkhorst–Pack Brillouin zone sampling was used for the LC, HC1, and HC2 unit mesh structures. A 2 × 2 × 1 sampling was used for the HC3 unit mesh structure. The substrate slab was modeled with four layers, of which the lowest layer was frozen in its bulk truncated structure during geometry relaxations. The vacuum above the slab was chosen to exceed 30 Å. The adsorption energies were calculated as the differences between the energies of the relaxed slab with the adsorbed molecules and the isolated molecule and the clean relaxed surface. All calculation inputs and outputs have been deposited as a data set in the NOMAD repository (https://repository.nomad-coe.eu/) and are freely available.²⁹

3. Results and Discussion

3.1. Surface Characterization

For deposition of VOPc onto the Cu(111) surface at room temperature, no ordered surface phase was seen in LEED until an estimated coverage of approximately 90% of a saturated single layer of the molecule was achieved. The LEED pattern of the resulting ordered adsorption phase is described by the surface mesh matrix , as shown in Figure S1. However, STM images recorded from this preparation showed that this procedure led to a surface in which partial coverage of a second layer of VOPc occurred (Figure S2). It appears that, at room temperature, it is not possible to prepare a surface comprising only a single complete layer of the molecule; instead, partial second layer growth occurs before the ordered LEED pattern appears.

As the objective of this investigation was to determine the orientation of VOPc molecules adsorbed only within a single layer on the Cu(111) surface, we have therefore concentrated on measurements of surfaces with VOPc coverages significantly less than those that give rise to the ordered 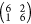overlayer. In order to provide a direct comparison of our results with earlier STM studies, we recorded some images of submonolayer coverages of VOPc on Cu(111) at a sample temperature of ∼80 K, suppressing the rapid surface diffusion that precludes such imaging at room temperature. Figure 2 shows such an image, which displays very similar features to those previously reported by Niu et al.¹³ recorded at a similar temperature. In particular, it shows two different features apparently attributable to VOPc molecules, namely, very dim crosses with a brighter center (circled in yellow) and slightly brighter crosses with no obvious darker or brighter center (circled in red). These are the two molecular images that have been attributed to the two different molecular orientations. Also, as seen in images reported by Niu et al., the molecules imaged as bright crosses seem prone to form ordered chains. A similar effect has also been reported in STM images from SnPc on Ag(111).³⁰ Indeed, in areas of the surface in which essentially all of the molecules are isolated, there appears to be a dominance of molecular images with the bright centers (see Figure S3). The two different types of molecular image are also evident in the higher-coverage 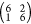phase as shown in Figure 3, also imaged at ∼80 K, on a surface prepared at room temperature.

Figure 2.

STM image recorded at ∼80 K at a lower coverage of VOPc (V = −1.5 V, I = 54 pA). Superimposed colored circles identify two different molecular image types described in the text, while the white arrows point along the <110> azimuthal directions of the surface.

Figure 3.

STM image recorded at ∼80 K of the phase of VOPc on Cu(111) (V = 1.3 V, I = 54 pA). Superimposed colored circles identify three different molecular image types described in the text, while the white arrows point along <110> azimuthal directions of the surface.

In this image a third type of feature, having the appearance of a very bright disc (circled in green), is also visible. Continuous imaging at ∼80 K revealed that these very bright features are actually mobile on the surface and must therefore correspond to adspecies above the single-layer VOPc film; indeed, some of these features appear as streaks rather than spots. Whether these are additional VOPc molecules or contaminant species is unknown. They appear to move between sites atop those VOPc molecules that are imaged as crosses of intermediate brightness with no brighter center.

3.2. SXPS and NIXSW Measurements

The NIXSW technique⁴ exploits the fact that at the conditions of an X-ray Bragg diffraction from a crystal, the incident and diffracted beams interfere to produce an X-ray standing wave with the same periodicity as that of the Bragg scattering planes. Under these conditions of total “reflection” (from a nonabsorbing crystal), extinction leads to a finite penetration of the X-rays, so the total reflectivity exists over a small but finite range of incidence energy or angle. Within this range, the nodal planes of the standing wave shift in a systematic fashion relative to the atomic scattering planes. Measuring the absorption of this X-ray standing wave as a function of photon energy at specific atoms immersed in this standing wavefield (both in and on the surface) therefore provides a means of determining the location of the absorber, relative to these scattering planes. In the present experiments, the (111) Bragg scattering condition was used with photon incidence near-normal to the Cu(111) surface to determine the heights of the VOPc constituent atoms above the substrate. Absorption at the different atoms was monitored in an element- and chemical-state specific fashion by measuring the C 1s, N 1s, O 1s, and V 2p core level photoemission spectra as a function of photon energy. Structural parameter values were then extracted after correction for the effects of nondipolar backward–forward angular distribution in the photoemission.⁴

NIXSW absorption profiles can be uniquely fitted by two parameters, the coherent fraction, f_co, and the coherent position, p. In the simple ideal situation, in which an absorbing atom occupies a single well-defined height above the scattering planes with no static or dynamic disorder, f_co = 1, and the actual height of the atom above the scattering planes is given by D = (n + p)d₁₁₁, where d₁₁₁ is the layer spacing of the (111) scattering planes (2.08 Å for Cu), and n is an integer. The ambiguity introduced by n is because NIXSW measures positions relative to the nearest extended bulk scattering plane. Excluding significant surface relaxations (i.e., more than ∼0.01–0.02 Å) or surface reconstruction of the outermost layer spacings of the underlying substrate, neither of which is expected to be the case for Cu(111), there is almost certain to be only one value of n that leads to a realistic adsorbate–substrate distance. More generally, f_co is commonly regarded as an order parameter, and indeed, small random static or dynamic displacements of the absorber atoms and of the underlying crystalline substrate are typically found to reduce the coherent fraction by up to about 20%, a value consistent with a calculated Debye–Waller factor based on reasonable assumptions regarding the size of these displacements. Values of f_co less than ∼0.8 are generally due to the co-occupation of two or more sites having different heights. Specifically, if several sites with heights z_j are equally occupied, each having a coherent fraction f_j, then the resulting coherent position and fraction are given by

Notice that this can be conveniently represented in an Argand diagram by vectors of length f_j and f_co and direction determined by angles (2πz_j/d₁₁₁) and 2πp.³¹ One particular consequence of this is that if one has two equally occupied sites with a height difference of d₁₁₁/2 the resulting value of f_co is zero.

In order to ensure that the measured NIXSW data corresponded to samples that only contained a single molecular layer, measurements were undertaken at the lowest coverages compatible with collecting data of an acceptable quality. Coverage estimates for these experiments were based on measurements of the relative intensities of the N 1s, C 1s, and Cu 3p emission peaks; the intensities of these spectra recorded from a higher-coverage surface that yielded the 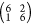LEED pattern provided an additional internal reference. On the basis of these measurements, the surface coverage used for the NIXSW measurements reported here was ∼50% of a saturated molecular layer or ∼0.015 ML (using the standard surface science definition that 1 ML corresponds to one adsorbate per surface atom). As this also corresponds to the atomic coverage of V and O, it is unsurprising that although even lower-coverage preparations allowed meaningful NIXSW measurements of C 1s and N 1s, it was not possible to obtain matching NIXSW data using the barely detectable O 1s or V 2p emission.

SXPS was also used to check on the possible influence of damage to the adsorbed VOPc, be it dissociation due to interaction with the substrate (as identified for GaClPc on Cu(111)^10,11) or radiation damage resulting from the incident synchrotron radiation. XP spectra were measured both at the photon energies of ∼3 keV used for the NIXSW measurements but also at lower photon energies (∼400–700 eV) using the soft X-ray capability of the beamline to achieve higher spectral resolution. In fact, evidence for radiation damage was more noticeable using the lower photon energies, so these soft SXP spectra were recorded after, rather than before, NIXSW measurements. Examples of spectra recorded at the higher energies are shown in Figure 4. Both O 1s and V 2p spectra showed evidence of a second chemically shifted component. Specifically, O 1s spectra showed a second peak with a binding energy ∼1.7 eV larger than the molecular peak, while similarly shifted components (by ∼2.0 eV to lower binding energy) were seen on the V 2p_1/2 and 2p_3/2 peaks. One possible interpretation of the two chemically shifted components is that they correspond to emission from “up” and “down” orientated VOPc molecules; indeed, the published assignment of VOPc adopting only a “down” orientation on Si(111) was supported by the observation of a chemical shift in the O 1s binding energy as a result of strong Si–O bonding.²¹ However, in the present system, the relative intensities of the main and shifted components varied very significantly between different preparations at similar coverages. Moreover, if these two components corresponded to the two differently oriented species, we would expect them both to show high coherent fractions in the NIXSW experiments; by contrast, as reported below, the main O 1s peak from which reliable NIXSW parameters could be obtained always showed very low coherent fractions.

Figure 4.

SXP spectra in the N 1s, C 1s, O 1s, and V 2p regions recorded at a photon energy in the NIXSW range, together with fits showing the different spectral components. The main peaks for each atomic species are shown in red, while the background, satellite structure, and chemically shifted components are shown in blue, green, and purple, respectively.

Our interpretation of the chemically shifted V 2p peaks in terms of dissociation is consistent with the fact that the shift appears to be the same as that seen in comparative spectra of VOPc and VPc on Ag(111).³² Indeed, both of these shifted components are to be seen in XP spectra recorded from thin films of VOPc on Ni(111), assigned to “interface states”¹⁴ that could also be a result of partial dissociation of VOPc at the reactive Ni(111) surface. The presence of these components does indicate that some partial fragmentation of the adsorbed VOPc occurs, and at least part of this seemed to be due to radiation damage. There was limited evidence that increased exposure of the sample to the X-ray beam caused these peaks to grow in the case of the low-coverage preparations, although this effect was seen to be more significant at higher (greater than one molecular layer) coverages. Notice, however, that the chemical-state specificity provided by photoemission-monitored NIXSW and PhD means that all NIXSW and PhD data presented here relate only to the O and V atoms in the undamaged VOPc molecules. The fit to the V 2p spectra also includes broad satellites previously attributed to multiplet effects in V (e.g., ref (14)).

In the case of the C 1s emission, the associated photoemission spectrum clearly contains multiple peaks as seen in Figure 4. As is clear from Figure 1, VOPc contains four chemically distinct C atom environments, of which three can be resolved in the SXPS, as shown in the fit of Figure 4. The components at 284.6 and 285.1 eV are attributed to C atoms in the peripheral benzene rings, whereas the component at 285.9 eV is attributed to the pyrrole C atoms located in the inner ring of the phthalocyanine macrocycle, consistent with similar assignments by Zhang et al.³³ A weak feature, also observed in the spectra at soft X-ray energies, is tentatively attributed to shake-up satellites. However, the reliability and uniqueness of this three-peak fit to individual spectra recorded during the NIXSW photon energy scans is questionable, so for the C NIXSW, the total area integrated over all components was used as a more reliable measurement of the C absorption profile and thus of the average height of all the constituent C atoms.

The key results obtained from the NIXSW measurements, the values of the coherent fraction and coherent position for each of the elementally distinct atomic absorbers, are summarized in Table 1. The measured NIXSW profiles are illustrated in Figure S4. A striking feature of these results is that, with the exception of the value for V, all the coherent fraction values are rather low, with that for O particularly low. The implication is that the C, N, and O atoms must occupy at least two different heights above the surface but that the V atoms are either all at the same height above the surface or at two or more heights that differ by integral multiples of d₁₁₁. The particularly low value of f_co for O implies that if there are just two different adsorption sites for the VOPc molecule, the height of oxygen atoms must differ by a value quite close to d₁₁₁/2. The fact that the coherent positions and fractions for C and N are very similar to each other would suggest that, even in the context of multiple adsorption geometries in which the molecular planes containing the C and N atoms are located at two or more different adsorption heights, all of these contributing geometries must have the molecular planes approximately parallel to the surface. Evidently, in qualitative terms, these observations would be consistent with the VOPc layer comprising a mixture of “up” and “down” orientated molecules. More quantitative modeling depends on the molecule–substrate bonding geometries, including any quantitative changes in the internal conformation of the molecules. This will be discussed further following presentation of the results of our DFT calculations that offer further insight into these parameters.

Table 1. NIXSW Structural Parameter Values Obtained from Low-Coverage VOPc on Cu(111)^a.

C		N		V		O
fco	p	fco	p	fco	p	fco	p
0.51(5)	0.22(3)	0.41(5)	0.23(3)	1.00(15)	0.46(3)	0.21(8)	0.27(10)

^aError estimates in the last digit are shown in brackets.

3.3. Scanned-Energy Photoelectron Diffraction (PhD) Results

The PhD technique³⁴ exploits the coherent interference of the directly emitted component of a photoelectron wavefield from a core level of an adsorbate atom with other components elastically scattered by nearby atoms. By scanning the photon energy, and thus the photoelectron energy and its associated wavelength, these scattering paths switch in and out of phase, leading to modulations in the angle-resolved photoemission signal detected outside the surface in specific directions. Calculations of this scattering (including the role of multiple scattering) lead to simulated PhD modulation spectra for different model structures, the best agreement with experiment corresponding to the best structural model. In investigations of atomic adsorbates, in particular, the dominant scattering events mostly involve backscattering from the outermost layers of the substrate. In the photoelectron energy range of interest (typically ∼50–300 eV), scattering events involving near-180° scattering often dominate as a result of a peak in the scattering cross section of many atoms at this angle. For this reason, a study of the O 1s and V 2p PhD seen in normal emission from VOPc adsorbed on a surface has the potential to distinguish the “up” and “down” geometries in a particularly simple fashion, exploiting the backscattering within the vanadyl V=O ligand that is expected to be oriented perpendicular to the surface. The previous application of PhD to determine the orientation of adsorbed VOPc was on the Au(111) surface.¹² This system was particularly well-suited to this simple interpretation, because the adsorption in this case is in an incommensurate ordered phase. This ensures that the molecules could not have a well-defined local registry to the Au(111) surface layer, while Au is a particularly weak backscattering atom in the energy range of the measurement. The O 1s PhD along normal emission was clearly dominated by backscattering from the underlying V atom with VOPc adsorbed in an “up” orientation, although inclusion of other purely intramolecular scattering was found to be important to give a good fit to the data.

For VOPc on Cu(111), on the other hand, the fact that the coverage investigated is below that at which any ordered phase occurs means it is certainly possible that a well-defined local geometry is occupied (albeit with rapid diffusion between such sites); moreover, Cu is a strong backscattering atom in the energy range investigated. It is therefore clearly essential to include the role of Cu backscattering in the multiple scattering simulations for this system and particularly for any VOPc in a “down” orientation, for which the O 1s PhD must be dominated by the substrate backscattering. Calculations were performed for model adsorption geometries varying the V–O bond length and the size of the displacement of the V atom out of the CN plane as well as the height of the molecule above the surface. Notice that bending of the phthalocyanine ligand plane (as subsequently found in the DFT calculations) was not explored, as the single normal emission PhD spectrum is not sensitive to this effect. For the “down” orientation, the O atoms were assumed to be located in a hollow site, as favored by the DFT calculations (see below). Specific models tested were “up” and “down” geometries individually, together with a model in which both “up” and “down” are equally occupied. Within this mixed model, the geometry of each orientation was optimized independently. In fact, the optimized geometries of the “up” and “down” models individually were found to be closely similar to the optimized model when both species were present. Figure 5 shows a comparison of the experimental normal emission O 1s PhD modulation with the three different best-fit models; also shown in this figure is the actual geometry of the two components of the mixed model (H atoms are too weakly scattering to play a significant role in PhD and thus are not included). Using our standard PhD methodology,^33,35 the best-fit structures were identified as those that give the lowest value of an objective R-factor (reliability factor). The values of this parameter for the three models were: “up”, 0.09; “down”, 0.13; mixed, 0.11. While the pure “up” geometry therefore gives the best fit, the small data range means that all models with R-values in the range defined by the minimum value and the calculated variance,³⁴ namely, 0.09 ± 0.04, are acceptable, so these measurements prove unable to distinguish the different models. However, the best-fit structures do provide some information on the preferred associated structural parameter values. In particular, the V atoms in the “up” and “down” geometries are at almost exactly the same height above the surface, while the height difference of the O atoms in the two geometries is 3.30 Å, corresponding to a difference in the anticipated coherent positions of 0.58. These conclusions are qualitatively consistent with the measured NIXSW coherent fractions for these two atoms: very high for V and very low for O. The mixed model implied by the NIXSW data is, therefore, consistent with the PhD results.

Figure 5.

Comparison of the experimental normal emission O 1s PhD modulation spectrum with the results of multiple scattering simulations for the best-fit “up”, “down”, and mixed “up” and “down” VOPc geometries. On the left are shown the two components of the mixed model (with H atoms omitted and assuming a rigid phthalocyanine ligand plane).

3.4. Density-Functional Theory Structure Calculations

As described in section 2, DFT calculations were performed using two different methods of correcting for the role of dispersion forces, namely the vdW^surf dispersion correction scheme²⁵ and the many body dispersion (MBD) method.²⁶ Both of these methods have been shown to accurately represent the adsorption geometry of complex organic molecules on metal surfaces including porphines adsorbed on Cu(111).^28,36,37 The known overestimation of adsorption energy in the pairwise description of vdW^surf is partly remedied by the MBD method.³⁸ The periodic boundary conditions implicit in surface slab calculations require a commensurate ordered phase, while the experimental data were taken at a coverage too low, at room temperature, for any ordered phase to develop in islands sufficiently large to be detectable by LEED.

In order to explore the possible influence of intermolecular interactions on the surface, several different periodic structures were thus calculated corresponding to different local coverages. For the lowest coverage, we used a near-square (7 × 4√3)rect. surface unit mesh containing a single VOPc molecule (“LC”, Figure 6). In this mesh, the molecule–molecule separation is 17.7 Å, considered a good approximation for isolated adsorbed molecules. The corresponding coverage is 0.018 ML, approximately the same as the average coverage used in the NIXSW experiments. However, these experiments were performed at room temperature, at which no ordered phase forms, and many of the molecules can be expected to occupy small dynamically forming islands that have a higher local coverage.

Figure 6.

Four different unit mesh structures used for the DFT calculations. LC, HC1, and HC2 structures shown here have only molecules in the “up” orientation, but other orientations were tested in the same unit meshes. The HC3 mesh contains one molecule of each orientation.

Higher coverages were simulated by several alternative structures. The simplest of these has a primitive (6 × 6) surface unit mesh containing a single molecule. This corresponds to a molecule–molecule spacing of 15.4 Å and a coverage of 0.028 ML (“HC1”, Figure 6). Further calculations were performed using larger unit meshes containing two molecules (either both with the same orientation or with two opposite orientations), allowing intermolecular interactions to render these two molecules locally inequivalent even with the same orientation. Specifically, the “HC2” model (Figure 6) has a primitive (11 × 6) surface unit mesh with dimensions of 15.4 × 28.2 Å, corresponding to a coverage of 0.030 ML. The HC2 mesh calculations were performed for both molecules “up”, both molecules “down”, and one molecule “up” with the other molecule “down”. Finally, calculations were performed using a (10 × 3√3)rect. unit mesh (dimensions of 13.3 × 25.6 Å) containing one “up” and one “down” molecule with a total coverage of 0.033 ML (“HC3”, Figure 6). Notice that the molecular packing densities of all of these higher-coverage models are closely similar to that of the experimentally observed 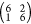high-coverage phase (0.029 ML), but their larger unit meshes allow the impact of the interaction between adjacent “up”- and “down”-oriented molecules to be investigated. As remarked above, in the surfaces explored experimentally by NIXSW and PhD, the high mobility of the VOPc molecules on the surface is expected to lead to many molecules transiently occupying islands of higher local coverage, for which the HC models can be expected to be relevant.

It is already clear from our qualitative discussion of the NIXSW results that structural models based on only “up” or “down” orientated molecules cannot be consistent with these results. In particular, as there is only one O atom in each molecule, such a model can only have one height of O atoms above the surface, so the associated coherent fraction must be high (unity in the absence of static or dynamic disorder), whereas experimentally, this parameter is very low. This is confirmed by the complete set of structural parameter values found for the LC, HC1, and HC2 unit mesh structures, containing VOPc molecules that are all either in the “up” or “down” orientations, calculated using the two different dispersion corrections that are listed in Table S1. Specifically, the values shown are the average heights of each atomic species above the mean location of the outermost Cu layer (which does suffer some adsorbate-induced buckling). In order to facilitate comparison with the NIXSW results, the calculated coherent fractions, which result from this range of heights, are also given. Because there is only a single molecule per unit mesh, the corresponding predicted f_co values for V and O are unity. Clearly, none of these single-orientation structures led to structural parameter values compatible with the experimental NIXSW results that show low coherent fractions for the C, N, and O atoms. To reproduce this effect, one must consider models involving co-occupation of both orientations. Before doing so, however, it is instructive to look into some of the details of the single-orientation models.

Calculations for the LC mesh with VOPc in the “up” orientation reveal the molecular geometry to be similar to that obtained from calculations of an isolated molecule in the gas phase. The molecule is positioned with the aromatic rings aligned with the high-symmetry directions of the surface, with a preference for adsorption centered above a bridge site (Figure 7). When describing the system with pairwise-additive van der Waals forces (PBE+vdW^surf), the vanadium atom is situated 0.70 Å above the average carbon position of the phthalocyanine core. In the “down” orientation, the molecule preferentially adsorbs with the V–O above a hollow site, and the small oxygen–copper distance generates a significant amount of steric strain. As a result, the adsorption height of the phthalocyanine carbon core is 0.21 Å higher, and the vanadium atom is situated only 0.13 Å further above the surface than the carbon atoms. When accounting for higher-order long-range dispersion interactions with the PBE+MBD method, which has been shown to yield excellent agreement with experiment for both molecular adsorption geometries and energetics,³⁹ we find that the adsorption heights of the molecule in both orientations are lower. Higher-order dispersion corrections screen the interactions and reduce the effective van der Waals radii that predominantly define the molecule–surface distance. The overall dispersion interactions are significantly reduced, as reflected in a reduction in adsorption energy by more than 1 eV.

Figure 7.

Side views of the structures obtained in the PBE+MBD calculations for the “up” and “down” molecules in the LC unit mesh and for two “up” molecules in the HC2 unit mesh.

PBE+vdW^surf results for the higher-coverage HC1 unit cell show a systematic upward shift of the molecular backbone by about 0.2 Å when compared to the LC results. However, the adsorption height differences between the “up” and “down” orientations are not significantly affected. In the case of PBE+MBD, the molecular geometries of the “up” and “down” molecules are asymmetrically distorted due to interactions with neighboring molecules. If one compares the atomic heights in the two different orientations, O, C, and N heights all differ significantly, whereas the vanadium atoms are found at almost exactly the same height. This would mean that a mixture of the two orientations would show a much higher coherent fraction for vanadium than for the other atoms, as also indicated by the PhD results and qualitatively consistent with the NIXSW results.

The HC2 unit cell corresponds to a coverage at which VOPc molecules can no longer be accommodated onto the surface in a planar geometry (Figure 7). For both “up” and “down” orientations, parts of the conjugated phthalocyanine system become tilted relative to the surface in order to accommodate the molecules and maximize molecule–surface and lateral intermolecular interactions; this is the origin of the significant decrease in the f_co values for the C atoms, in particular. This effect is found using both the vdW^surf and the MBD methods. Notice, however, that no systematic global search for the most stable overlayer structure was conducted due to the computational cost associated with the large HC2 unit cell.

As already discussed in the context of the experimental results, the NIXSW data clearly indicate that there must be two different adsorption geometries involved, and the simplest model is to assume equal occupation of the “up” and “down” orientations. Figure 8 shows a quantitative comparison of the experimental NIXSW coherent fractions, f_co, and positions, p, shown as vectors in an Argand diagram (f_coexp(−i2πp)) with the predicted values obtained from the DFT calculations assuming a 1:1 mix of the two different molecular orientations. A complete tabulation of the individual parameters is shown in Table S2. Figure 8 shows clearly that values calculated by the vdW^surf method, shown as dashed lines, provide less satisfactory agreement with the experimental results than the values calculated using the MBD method (full lines). Moreover, the best agreement is for the LC and HC1 models. In particular, the high f_co value for V and the low f_co value for O, which characterize the experimental results, are only reproduced in the PBE+MBD calculations for the LC and HC1 models. Indeed, even better agreement with theory and experiment would result from a mixture of these two models, a scenario that may well reflect the extent of intermolecular interactions in the disordered layer investigated experimentally. Notice that the parameter showing the worst agreement is the coherent position for the O atoms. However, with such a low measured value of the coherent fraction, the uncertainty in the associated coherent position value is high (at least ±0.1 and possibly significantly larger).

Figure 8.

Comparison of the experimental NIXSW coherent fractions and coherent positions, shown as vectors in an Argand diagram, for each of the elements within the VOPc molecule compared with the results of the DFT calculations for different unit meshes and computational methods, assuming equal occupation of the “up” and “down” orientations.

Overall, therefore, the DFT results provide clear quantitative support for the model implied by a simple qualitative evaluation of the NIXSW experimental results, namely, that this low-coverage preparation of VOPc on Cu(111) leads to a mixture of “up”- and “down”-oriented molecules of approximately equal occupancy. Substantially different occupancies would lead to a much higher coherent fraction for the O atoms, inconsistent with the experimental data. Of course, the adsorption energy associated with each orientation should provide a means to provide a quantitative estimate of their likely relative (equilibrium) occupancy. In this regard, however, the DFT results reveal significant variations in the adsorption energies for different models. For the lower-coverage structures, the adsorption energy of the “up” orientation is favored over the “down” orientation by amounts ranging from 0.21 eV in the PBE+vdW^surf calculations for the HC1 structure to 0.53 eV in the PBE+MBD calculations for the LC structure. Assuming a simple Boltzmann distribution, such large energy differences would be expected to lead to an almost 100% occupation of the “up” geometry if in equilibrium at room temperature. However, in calculations for higher-coverage models, in which “up” and “down” orientation molecules coexist, the adsorption energy is only slightly less favorable than for molecules that are only in the “up” orientation. In particular, in the HC2 unit mesh calculated using the PBE+MBD method, the adsorption energy of the mixed orientation model, in which the unit mesh contains one “up” molecule and one “down” molecule, is only 50 meV per molecule less favorable than the model with all molecules in the “up” orientation. This effect is likely to significantly influence the NIXSW experimental results taken at a coverage of ∼50% of a saturated single layer, in which most molecules must have other nearest-neighbor molecules. Indeed, it is notable that in the STM image of the ordered layer (Figure 3), molecules with one type of image generally have one or more neighbors of the other type (orientation). At the lowest coverage (Figure 2), there also appears to be a dominance of a single orientation in the isolated molecules that lack near-neighbors, an effect also particularly clear in the STM image of Figure S3. We note that, especially for the “down”-oriented molecules, we expect that the self-interaction error inherent to both dispersion-corrected functionals will lead to a misrepresentation of Pauli repulsion effects. This could potentially affect the relative energetics. Unfortunately, long-range-corrected hybrid functionals that would provide a partial remedy to this issue, such as HSE06+MBD, are currently computationally intractable for systems of this size.²⁸

While the NIXSW experiments were deliberately conducted at the lowest coverage compatible with acceptable data quality, it was noted above that at room temperature, second layer growth was found to occur before the first layer was complete. One might then speculate that some second layer growth could occur already at even lower coverages. One possible explanation of the qualitative NIXSW results is therefore that the presence of two molecular orientations could be a result of the double-layer islands on the surface. In particular, the structure of both bulk crystalline VOPc, but also thin epitaxial films of VOPc, involve double layers with a head-to-head orientational relationship. To explore this possibility, further DFT calculations were performed using the preferred PBE+MBD method on two double-layer structures that differ in their relative registry. The results for the energetically more favorable registry (which proves to be similar to the registry in bulk VOPc) are included in Table S2. Clearly, this structure does not lead to structural parameter values compatible with the experimental NIXSW data. In particular, a low coherent fraction is found for V, whereas a high coherent fraction is found for O, the opposite to the measured behavior.

3.5. Density-Functional Theory STM Simulations

In view of the many papers, described in the Introduction, that have attempted to use the appearance of STM images to determine the orientation of VOPc and similar adsorbed molecules (notably TiOPc), it is of interest to extract from the DFT calculations reported here some simple simulations of the images that would be expected. The standard approach to this, which we have used here, is that of Tersoff and Hamann.⁴⁰ Although this approach is widely used, it is important to recognize that it takes no explicit account of the nature of the scanning tip and is based only on the electronic structure of the surface being investigated. The results of simulations corresponding to two different sample bias potentials are shown for the LC phase in Figure 9.

Figure 9.

Results of DFT simulations of STM images of the LC VOPc “up” and “down” orientation models at two different sample bias potentials, together with the top views of schematic representations of the structures.

As might have been expected and has been widely (but not universally) assumed, the simulated images (at both bias voltages) show a bright central protrusion for VOPc in the “up” orientation, i.e., such that the V=O bond points out of the surface. However, the simulated images for the “down”-oriented molecule also have a bright central part of the molecular images. In detail, the simulated images for the two orientations do differ. What is less clear, though, is the extent to which this level of detail would be readily detected, bearing in mind the limited resolution achievable in most STM instruments. In practice, STM images of VOPc on Cu(111) show some molecules with bright centers, some without; however, the simulations predict that both molecular orientations should image with a bright center, albeit with the contrast between the center and perimeter of the molecule being weaker in the “down” orientation. Based on these simulations, it seems likely that the images showing the brightest centers probably do correspond to VOPc molecules in an “up” orientation. On this basis, the fact that STM results in a surface in which all molecules are isolated on the surface (Figure S3), showing almost only this type of bright-centered molecular image, suggests that these are all in the “up” orientations, consistent with the DFT energetics. Of course, the exact appearance of these images is likely to be dependent on the nature of the underlying substrate and the tip being employed for imaging. As a consequence, this conclusion cannot be generalized to all studies of adsorbed VOPc or, indeed, extended to studies of adsorbed TiOPc.

4. Conclusions

Previous investigations of VOPc adsorption on Cu(111), and other surfaces, have attempted to determine the molecular orientation by indirect means. Here we have presented the results of a structural investigation, using two quantitative experimental techniques, NIXSW and PhD. The limited range of the O 1s PhD data, recorded only at normal emission, has proved to be inconclusive. The strong scattering of the Cu substrate atoms has meant that the limited data range that proved effective in the study of VOPc on Au(111) [12] led to ambiguity in which “up”, “down”, and mixed “up” and “down” orientations all gave theory–experiment agreement within the acceptable range defined by the associated variance. By contrast, NIXSW results obtained from surfaces with VOPc coverages of ∼50% of a single saturated molecular layer are clearly incompatible with all adsorbed VOPc molecules being in the same orientation, with qualitative evaluation clearly favoring co-occupation of both orientations. A more quantitative evaluation of these results is afforded by the outcome of detailed density-functional theory calculations that clearly identify not only the optimum structural solution but also the best dispersion correction to obtain this experiment–theory agreement, namely, the many body dispersion on top of the PBE-GGA functional (PBE+MBD). Interestingly, these DFT results indicate that, at the lowest coverages, the “up” orientation of the molecules is strongly energetically favored. Indeed, ordered domains of pure “up” orientation are clearly favored over ordered domains of only “down” molecules at all coverages. However, mixed “up”-and-“down” domains at increased coverage have total energies very similar to those of pure “up” domains. This finding is in qualitative agreement with STM measurements at the lowest coverage, in which a higher rate of occurrence is observed of geometries that are typically associated with “up”-oriented molecules. However, our DFT-based Tersoff–Hamann simulations of the STM images expected from these molecular orientations cast some doubt on the ability to use STM images for a unique assignment of molecular orientations. This further underscores the importance of quantitative experimental structural information as provided by NIXSW and PhD.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.8b07530.

• LEED pattern and STM image of high-coverage ordered phase at room temperature; low-temperature STM at low coverage; experimental photoemission-monitored NIXSW absorption profiles and fits; tables of DFT structural parameter values and implied NIXSW parameters for single-orientation and double-orientation structural models (PDF)

The authors declare no competing financial interest.