Abstract
Amorphous molybdenum sulfide (MoSx) is a potent catalyst for the hydrogen evolution reaction (HER). Since mechanistic investigations on amorphous solids are particularly difficult, we use a bottom-up approach and study the [Mo3S13]2– nanocluster and its protonated forms. The mass selected pure [Mo3S13]2– as well as singly and triply protonated [HMo3S13]− and [H3Mo3S13]+ ions, respectively, were investigated by a combination of collision induced dissociation (CID) experiments and quantum chemical calculations. A rich variety of HxSy elimination channels was observed, giving insight into the structural flexibility of the clusters. In particular, it was calculated that the observed clusters tend to keep the Mo3 ring structure found in the bulk and that protons adsorb primarily on terminal disulfide units of the cluster. Mo–H bonds are formed only for quasi-linear species with Mo centers featuring empty coordination sites. Protonation leads to increased cluster stability against CID. The rich variety of CID dissociation products for the triply protonated [H3Mo3S13]+ ion, however, suggests that it has a large degree of structural flexibility, with roaming H/SH moieties, which could be a key feature of MoSx to facilitate HER catalysis via a Volmer−Heyrovsky mechanism.
Introduction
Molybdenum sulfide (MoS2) based catalysts have the potential to replace platinum as a hydrogen evolution catalyst in electrochemical water splitting.1 The material is also discussed as a catalyst for methanol synthesis from carbon dioxide and hydrogen.2 A comparison of a number of state-of-the-art molybdenum sulfide catalysts in their performance on electrochemical hydrogen evolution reaction (HER) shows that the total electrochemical activity is primarily determined by the number of active sites per geometric electrode area.3 Briefly, the HER is a multistep electrochemical process, which takes places either via the Volmer–Heyrovsky or via the Volmer–Tafel reaction mechanism.3,4 For both mechanisms, hydrogen adsorption and desorption are key reaction steps.4 The physicochemical quantity associated with this process is the change of free energy for hydrogen adsorption on the catalyst (ΔGH) that, according to the Sabatier principle, should ideally be ΔGH = 0.3−5
Amorphous MoSx shows HER activity comparable to noble metals, yet mechanistic investigations of this catalyst are particularly difficult. The actual mechanism of H2 formation is therefore still a matter of debate.6−8 The bottom-up approach, i.e. investigations on thiomolybdates clusters, e.g. [Mo3S13]2– and [Mo2S12]2– as key building blocks of MoSx, may lead to a better understanding of HER catalysis on MoSx.6 Additionally, [Mo3S13]2– and [Mo2S12]2– have been reported as scalable, very stable HER electrocatalysts with extremely high activity, which can be deposited onto any support by drop-casting.9,10 Electrochemical water splitting in acidic electrolytes and photoelectrochemical (PEC) cells have been described as possible applications of such cathodes.3,11
Lee et al. suggest that bridging S atoms are the active HER sites in the case of thiomolybdate clusters.12 Recently, homogeneous photocatalytic HER activity of thiomolybdate [Mo3S13]2– was reported.13 In a subsequent study, it was shown that under catalytic conditions, terminal disulfide ligands exchange with solvent (H2O) over time and influence the catalytic activity.14 In particular, partial exchange of terminal disulfides (S22–) with aqua ligands leads to [Mo3S(13-x)(H2O)x](x-2)+ (x = 2, 4) which could be identified as the most active catalytic species in solution.14 Small charged and neutral molybdenum sulfide clusters have also been studied both experimentally15−17 and theoretically18−23 to understand their catalytic properties. Further insight can also be gained by investigating the surface chemistry of molybdenum sulfide24 and chemically similar systems, e.g., molybdenum oxides25−29 or molybdenum-doped clusters.30−32 A series of [MoO(S2)2L2] complexes have been developed by Wu and co-workers as tunable molecular MoS2 edge-site mimics for electrocatalytic hydrogen production.33−35
Since thiomolybdate nanoclusters undergo structural changes during HER catalysis,14 investigations on the structural flexibility and chemical properties of the different sulfur moieties of the cluster are crucial in order to understand the catalytic activity of [Mo3S13]2–. Furthermore, a better fundamental understanding of the reaction mechanisms could facilitate targeted optimization of the catalysts. Therefore, we investigate here individual reaction steps with the help of precisely defined gas-phase models, namely the isotopically pure [92Mo3S13]2– nanocluster as well as its singly and triply protonated forms, [H92Mo3S13]− and [H392Mo3S13]+. We use Fourier transform ion cyclotron resonance mass spectrometry (FT-ICR MS) as an excellent tool for the investigation of ion–molecule reactions,36−39 including catalytic cycles,40−45 as well as for characterization of nanoclusters in the gas phase.46−49 Additionally, the results of the experiments are interpreted with the help of quantum chemical calculations.
Experimental Methods
Experiments were performed in ultrahigh vacuum (p ≈ 10–9 mbar) on a Bruker Apex Qe FT-ICR MS equipped with a combined electrospray ionization (ESI), matrix assisted laser desorption ionization (MALDI) Apollo II Dual ESI/MALDI Source ion source and a 9.4 T superconducting magnet as described previously.47 The ions are guided through a hexapole trap and a quadrupole mass filter to a hexapole collision cell where they are kinetically accelerated and undergo collision induced dissociation (CID) with the buffer gas. For high-resolution mass analysis, the ions are electrostatically transferred to the ICR cell. Electrospray ionization (ESI) of a 0.13 mM solution of isotopically enriched (NH4)2[92Mo3S13] in water–methanol (1:1) results in the transfer of the cluster ions to the gas phase.
After accumulation in the first hexapole, the ions of interest are preselected via the quadrupole mass filter and transferred to the second hexapole trap, which serves as a collision cell. The cell is filled with argon (99.999%) at a pressure in the range of 10–3 mbar, trapping time is 1 s. The collision cell hexapole bias voltage Vc correlates with the center-of-mass collision energy of the trapped ions with the background gas. When Vc is sufficiently high, the trapped ions start to fragment due to CID. The fragments are then cooled and trapped by subsequent collisions with argon and finally transferred to the ICR cell where their mass spectrum is acquired. Recording mass spectra at different collision voltages Vc yields the breakdown curves of the ion of interest with respect to Vc.
Isotopically pure (NH4)2[92Mo3S13] was prepared following a procedure of Müller et al. for the non-92Mo-enriched compound.50 In order to obtain the (NH4)6[92Mo7O24]·4H2O precursor, 50 mg of 92MoO3 (STB Isotope Germany) were dissolved in 0.25 mL of concentrated ammonia (25%, VWR chemicals) in a sealable GC-vial (21 mL) and left to dry overnight under air. The resulting colorless crystals (57.0 mg) were dissolved in 0.28 mL of demineralized water and 3.6 mL of ammonium polysulfide solution (>6%, Fisher Scientific UK) was added. The closed vial was kept at 90 °C for 5 days with slow stirring and then cooled to room temperature. The reaction mixture was centrifuged (2 min at 4100 rpm) and the supernatant discarded. The crude product was successively washed with ice-cold water (3 × 20 mL), ethanol (2 × 15 mL), carbon disulfide (10 mL) and tert-butyl methyl ether (2 × 10 mL). The identity of the product was confirmed by X-ray powder-diffraction and Raman spectroscopy.
Computational Methods
To analyze the properties of the observed ions, we used density functional theory (DFT). Structures were optimized at the B3LYP/def2TZVP level, the ωB97XD functional51 with the same basis set was then used to calculate single-point energies in the optimized structures as this functional was shown to provide more reliable results for second-row transition metals than B3LYP.52 Then, we reoptimized the 80 most important structures (as discussed further in the text) using the ωB97XD functional. Both structure and relative energies were only mildly influenced by the reoptimization, with an average difference in absolute isomer energies of 0.02 eV and only one energy difference exceeding 0.05 eV, see Table S2 in the Supporting Information. The zero-point energy correction is included in all reported energies. The Gaussian program was used for all calculations.53
The size of the investigated systems and their complicated electronic structure prohibit us from using more elaborate approaches for structure optimization, e.g. genetic algorithms.54 Also, not only the most stable structures are of interest here. Therefore, we investigated a large variety of bonding patterns using chemical intuition, with more than 600 different structures for 30 ions, in order to document the most important patterns in molybdenum sulfide cluster chemistry. In particular, we included structures with both cyclic and open (quasilinear) Mo3 moieties with various configurations of sulfur bridges and terminal groups (S or S2). For fragment structures, we considered both configurations with symmetrically distributed sulfur atoms among Mo atoms as well as structures created through a direct removal of, e.g., a S2 unit from the respective larger ion. Structures with hydrogen atoms were generated from the respective non-hydrogenated structures by adding hydrogen atoms on various sulfur atoms (terminal, bridging, apical). Finally, the formation of Mo–H bonds was also considered. Only selected ions are shown in the manuscript, all calculated structures are included in the Supporting Information.
The two lowest spin multiplicities were considered for each structure (i.e., singlet/triplet or doublet/quartet); for several structures, also higher spin multiplicities were tested to confirm that the corresponding states are less stable (see Supporting Information). The stability of the wave function was tested for all calculations with both B3LYP and ωB97XD functionals. Vibrational frequencies were calculated to verify that all calculated structures are local minima. Bond analysis was performed within the natural bond orbital (NBO) scheme55 as implemented in the Gaussian program, charges were calculated with the charges from electrostatic potentials using a grid-based method (CHELPG),56 with the atomic radius of Mo chosen to be 2.45 Å.
Results and Discussion
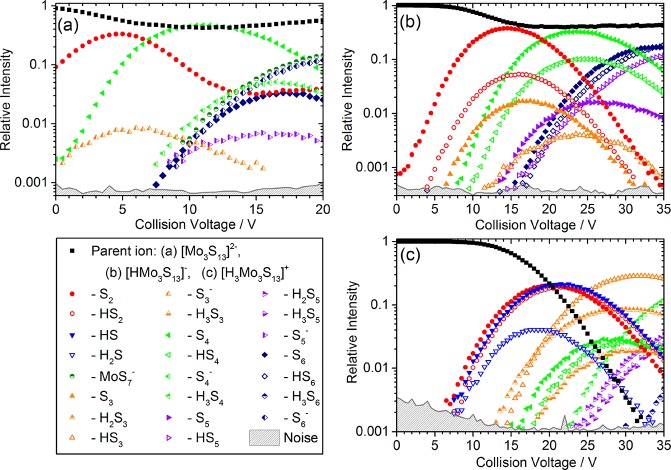
In the following, we discuss the fragmentation patterns of the three investigated species [Mo3S13]2–, [HMo3S13]−, and [H3Mo3S13]+. The analysis of the experimental results is accompanied by quantum chemical calculations of ion structure and dissociation energies. The breakdown curves of all three clusters are collected in Figure 1. The CID experiments yielded a variety of HxSy eliminations. In addition, HpOq addition is observed, especially in the case of [H3Mo3S13]+, due to traces of air in the collision cell. All observed product ions are listed in Table S1 in the Supporting Information.
Figure 1.
CID breakdown curves of the (a) thiomolybdate [Mo3S13]2–, (b) protonated thiomolybdate [HMo3S13]−, and (c) triply protonated thiomolybdate [H3Mo3S13]+ cluster. Elimination of one S2 is for all species the first fragmentation channel and also one of the most prominent.
Dissociation Patterns in [Mo3S13]2–
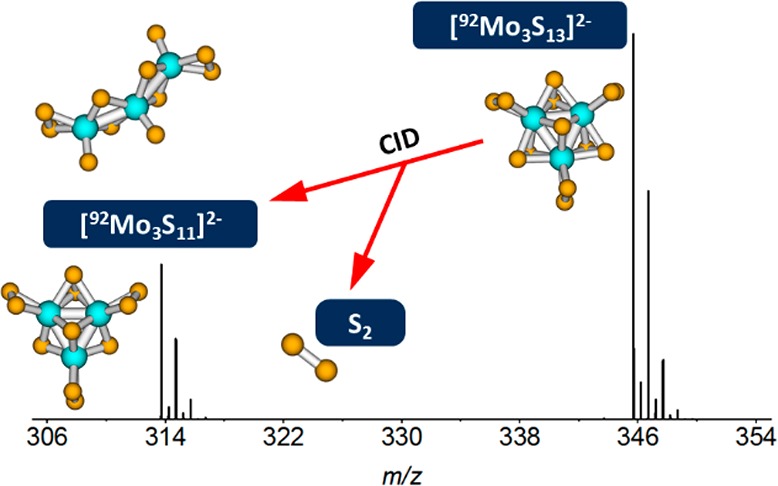
The breakdown curves of [Mo3S13]2– are shown in Figure 1a. Fragments can be split up into two groups, according to their appearance energy. In the low energy regime, elimination of one and two S2 units are pronounced fragmentation channels, observed even at Vc = 0 V. This indicates that disulfide ligands are present in the cluster and that these S2 ligands are relatively weakly bound. Traces of the [S3]− dissociation channel are also recorded for low voltages. In the high-energy regime, elimination of [S6] as well as [Sx]−, x = 3–6, producing singly charged ions, is observed. Finally, only one fragmentation channel with Mo elimination is recorded in the high-voltage regime, producing [Mo2S6]−. It would be expected that singly charged product ions show up in pairs, though here only the heavier counterparts were detected. A possible explanation is that due to the Coulomb explosion following charge separation,57 the lighter fragments obtain sufficient kinetic energies to leave the hexapole collision cell. To account for the loss of the light fragments from the collision cell, the measured ICR signal of singly charged fragments was multiplied by two in Figure 1a. The fragmentation of [Mo3S13]2– reaches a maximum at Vc = 11 V, where some 60% of the ions are fragmented. This is probably an artifact caused by the loss of some heavy fragment ions following Coulomb explosion. Even at the highest collision voltages, a significant fraction of the parent ions stays intact, which we attribute to space charge effects due to a large number of trapped ions in the collision cell.
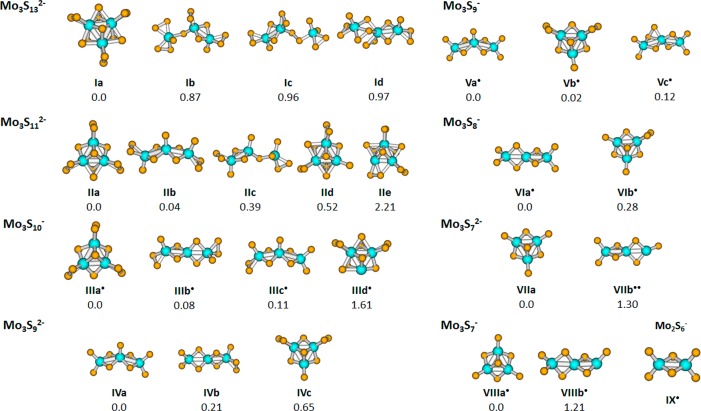
The most stable calculated structure of [Mo3S13]2– (Ia, see Figure 2) resembles the one that has been determined for this species by X-ray diffraction in the solid state,9,58 with a Mo3 ring and three distinct sulfur groups–three terminal S2, three bridging S2 and one apical S. The Mo–Mo interaction, with a bond length of 2.71 Å (compared to ∼2.7 Å encountered in bulk6), has a bonding character, as analyzed within the NBO scheme. CHELPG charge analysis shows that Mo centers are positively charged (+0.69 |e|) while terminal S2 groups are the most negatively charged ones (−0.83 |e|/S2), followed by the apical S (−0.38 |e|) and bridging S2 (−0.39 |e|/S2) units.
Figure 2.
Selected structures of the [Mo3S13]2– complex and of fragments formed during its dissociation along with their relative energies (in eV); calculated at the ωB97XD/def2TZVP level of theory. All structures have the lowest spin multiplicity, i.e., singlet or doublet, unless shown otherwise.
In higher lying local minima, the central Mo3 ring is open. Either a quasi-linear Mo–Mo–Mo motif (Id) or two clearly separated Mo2 and Mo units (Ib,c) can be formed. These structures are, however, less stable by about 1 eV (see Figure 2 and Supporting Information). According to the NBO analysis, a bonding interaction is only present within one Mo–Mo pair for isomers Ib–Id. These isomers have also the tendency to form S2 units, charge distribution is however more even compared to isomer Ia, with charges of +0.25–0.45 |e| on Mo, −(0.35–0.65) |e| on S2 units and −(0.15–0.40) |e| on individual S ligands.
The calculated dissociation energies of [Mo3S13]2– are summarized in Table 1 for the most relevant dissociation channels, as obtained for the most stable products at infinite separation. For neutral loss channels, this represents the lower limit for the activation barrier. For charge separation channels, where two singly charged ions are formed, the reverse Coulomb barrier must be added. As a rough estimate, we can take the interaction energy of two elementary charges at the cluster radius of 3.5 Å, which amounts to 4.1 eV. However, interaction with a positive charge center, in particular in a salt-bridge arrangement,59 may lower the Coulomb barrier. With and without charge separation, the reorganization energy between the structures present immediately after dissociation and the lowest-energy product structures may significantly increase the barrier for dissociation, as discussed in detail below.
Table 1. Dissociation Energy E (in eV) of Fragmentation Channels Observed in the Experiment, along with Dissociated Molecules and Ions Used To Calculate the Dissociation Energya.
| fragmentation channel | dissociated molecules | [Mo3S13]2– | [HMo3S13]− | [H3Mo3S13]+ |
|---|---|---|---|---|
| [S2] | S2 | 1.48 | 1.47 | 1.66 |
| [S3] | S2 + S | – | 4.32 | – |
| S3 | – | 1.98 | – | |
| [S3]− | S2– + S | 3.52 | – | – |
| S3– | 0.12 | – | – | |
| [S4] | 2S2 | 2.39 | 2.80 | 3.49 |
| [S4]− | S2– + S2 | 2.10 | – | – |
| [S5]− | S2– + S2 + S | 5.00 | – | – |
| S3– + S2 | 1.60 | – | – | |
| [S5] | 2S2 + S | – | 5.96 | – |
| [S6] | 3S2 | 5.25 | 4.87 | – |
| [S6]− | S2– + 2S2 | 3.96 | – | – |
| S3– + S3 | 2.74 | – | – | |
| [MoS7]− | MoS5– + S2 | 1.54 | – | – |
| MoS3– + 2S2 | 3.24 | – | – | |
| [HS] | HS | – | – | 2.19 |
| [HS2] | HS2 | – | 1.84 | 2.14 |
| [HS3] | HS + S2 | – | 3.50 | 3.74 |
| [HS4] | HS2 + S2 | – | 3.30 | 3.98 |
| [HS5] | HS + 2S2 | – | 4.98 | – |
| [HS6] | HS2 + 2S2 | – | 5.16 | – |
| [H2S] | H2S | – | – | 1.19 |
| [H2S3] | H2S + S2 | – | – | 2.81 |
| [H2S5] | H2S + 2 S2 | – | – | 5.77 |
| [H3S3] | H2S + HS2 | – | – | 3.30 |
| [H3S4] | HS + S2 + H2S | – | – | 5.98 |
| [H3S5] | HS2 + S2 + H2S | – | – | 6.43 |
| [H3S6] | 3HS2 | – | – | 7.94 |
For S2 evaporation, our calculations predict a relatively low dissociation energy of ∼1.5 eV. This energy is reached when the resulting [Mo3S11]2– cluster is allowed to relax to the most stable structure found, isomer IIa, with two bridging S units (instead of S2 bridging groups in Ia) and regenerated terminal S2 units. Immediately after dissociation, structures of higher energy might be expected (e.g., IId,e). The structure with a quasi-linear Mo–Mo–Mo motif (IIb) is calculated to be almost isoenergetic with respect to the one with a Mo3 ring (within ∼0.1 eV) due to the favorable bond arrangement with five Mo–S bonds formed per Mo atom. Isomer IIb is also more stable than the structure with a Mo3 ring before a considerable cluster reconstruction takes place (see isomers IId,e and the Supporting Information). Thus, it is possible that the cluster opens during the dissociation process. Note also that the quasi-linear isomer IIb can be created by opening isomer IIa, without considerable bond rearrangement.
The second prominent channel, [S4] evaporation, can be expected to proceed in a two-step S2 dissociation process. The most stable isomer IVa of the resulting [Mo3S9]2– fragment has a quasi-linear Mo–Mo–Mo conformation. A ring structure with three S bridges among Mo–Mo bonds IVc (instead of S2 bridging units in isomer Ia) lies higher in energy (∼0.7 eV). A similar picture is obtained for [S4]− dissociation producing [Mo3S9]−. Here, the closed structure Vb with a Mo3 ring is however close in energy to quasi-linear ones Va,c, as already discussed elsewhere.21
As can be seen in Table 1, the calculated asymptote for [S4]− dissociation lies about 0.3 eV below [S4] dissociation. However, [S4]− dissociation is observed at much higher voltages in the CID experiment, consistent with a reverse Coulomb barrier in the range of several electronvolts. In view of this, it is surprising that the minor [S3]− dissociation channel is observed at very low voltages in the experiment. Since S3– loss has a very low-lying asymptote of only 0.12 eV, it is more plausible than sequential loss of S2– + S. Formation of the low-energy product species is expected to demand significant reorganization, and the low overall activation barrier requires a specific arrangement of partial charges preceding Coulomb explosion. Both processes require the passage of tight transition states, which explains the small branching ratio of the [S3]− loss channel observed in the experiment. Immediately after S3– dissociation, isomer IIId might be formed. For the [Mo3S10]− product ion, closed (IIIa) and open (IIIb,c) structures have almost the same energy.
Further dissociation channels ([S5]−, [S6], [S6]−) appear in the CID experiment only at higher voltage and are also calculated to have high dissociation energies (Table 1). With respect to the ionic products, a competition between closed and open structures is observed in calculations for [Mo3S8]−. However, for [Mo3S7]2−/−, the quasi-linear structure is forced to dissociate a terminal sulfur atom that exposes a Mo atom (VIIb, VIIIb), increasing the energy of the conformation. Then, isomers with a Mo3 ring (VIIa, VIIIa) with a compact structure become the most stable ones again, with a difference between both conformations of ∼1.2–1.3 eV.
Finally, the [MoS7]− dissociation channel that produces [Mo2S6]− might lie as low in energy as 1.5 eV, depending on the product composition (Table 1). Judging from the late appearance of the fragment in the CID measurement, it can be expected that it proceeds over several steps, possibly through subsequent dissociation of [Mo3S9]2–. [Mo2S6]− is predicted to have a linear structure IX with four Mo–S bonds per Mo atom and without considerable binding interaction between Mo atoms (as analyzed within the NBO scheme). Note that this structure can be formed directly from the quasi-linear structure, e.g. IVa, without extensive bond rearrangement.
Dissociation Patterns in [HMo3S13]−
The detected fragmentation of [HMo3S13]− is shown in Figure 1b. All combinations of HxSy elimination (with x = 0,1 and y = 2–6) are observed, with the [S2] and [S4] dissociation channels being the most efficient ones. According to their appearance energies, the fragments can be split up into three groups, in each of which the fragment intensities increase in a parallel manner. Thio-oxo-species appear only at high collision voltages (Vc > 30 V) and their relative intensity stays below 0.2% (see Figure S1). Again, about 40% of the parent ion remains intact.
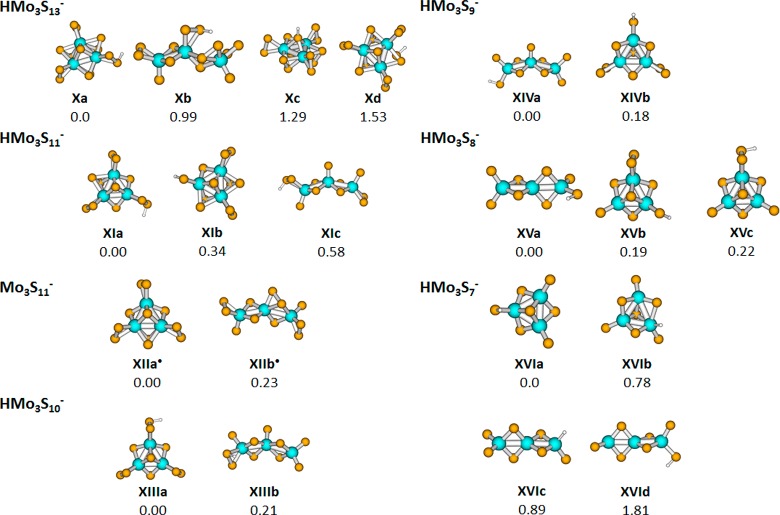
As could be expected from the charge analysis of isomer Ia discussed above, our calculations predict that the [Mo3S13]2– ion preferentially binds a proton on a terminal S2 group, forming isomer Xa (Figure 3). The difference between protonation of the first and the second S atom of the terminal S2 group is ∼0.1 eV (see Supporting Information). If H+ is bound to the apical S (Xc) or bridging S2 (Xd) units, the resulting species lie more than 1.2 eV higher in energy, reflecting the lower negative charge calculated for these groups. Two remaining terminal S2 units in isomer Xa are still the most negatively charged ones, with about −0.6 |e| (calculated using the CHELPG scheme), being thus most probably the next ones to react with further protons (see below).
Figure 3.
Selected structures of the [HMo3S13]− complex and of fragments formed during its dissociation along with their relative energies (in eV); calculated at the ωB97XD/def2TZVP level of theory. All structures have the lowest spin multiplicity, i.e., singlet or doublet.
The most stable structure of [HMo3S13]− with an open Mo3 ring Xb lies ∼1 eV higher in energy, reproducing the difference between the unprotonated structures Ia and Ib. Here, the proton is also preferentially adsorbed on a terminal S2 unit.
In agreement with the experiment, inspection of isomer Xa suggests that the most feasible channels should be S2 and HS2 dissociation. The S2 dissociation channel has quantitatively the same energy as S2 dissociation from [Mo3S13]2–, ∼ 1.5 eV; HS2 dissociation lies slightly higher in energy with ∼1.8 eV (in the case of full relaxation of the resulting ion). For S2 dissociation, structures XIa,b with a Mo3 ring are preferred after dissociation while for HS2, closed XIIa and open XIIb structures lie close in energy. The calculated structures are analogous to the ones observed in the [Mo3S13]2– dissociation series discussed above.
For the further three dissociation channels observed in the experiment ([S3], [S4], [HS4]), a small energy difference between closed and open structure is predicted for the resulting fragments. Several cyclic structures of the respective singly charged ions were already reported elsewhere.20 For the [S3] channel, we might observe dissociation of the whole S3 unit as this channel is calculated to be energetically preferred (2.0 eV when disregarding the reorganization energy), [S4] and [HS4] dissociation requires about 3 eV.
Our calculations predict that the dissociation channels appearing later in the CID measurements ([HS3], [S5], [S6], [HS5], and [HS6]) lie high in energy (>3.5 eV) and, as described above, the closed structure becomes again the most stable one for the [HMo3S7]− ion (XVIa) because of an exposed Mo atom in the quasi-linear structure (XVId). This ion is also a suitable candidate to investigate the probability of proton adsorption on a Mo atom. As can be seen in Figure 3, a structure with a Mo–H bond on a Mo3 ring (XVIb) lies ∼0.8 eV higher in energy than the analogous one with a S–H bond (XVIa). For the linear structure with an unsaturated Mo atom, the proton adsorbs preferentially on the Mo atom (XVIc), with an energy difference of 0.9 eV with respect to the structure with an S–H bond (XVId). The Mo–H bond is thus, as expected, preferred only for an unsaturated Mo atom.
Dissociation Patterns in [H3Mo3S13]+
For [H3Mo3S13]+, three fragmentation groups can be distinguished, in each of which the fragment intensities increase in a parallel manner. In Figure 1c, the breakdown curves yielding pure thiomolybdates [HxMo3Sy]+ are shown. A complete representation of the fragmentation curves, including the reaction channels producing thio-oxo-molybdates [HxMo3SyOz]+, is provided in Figure S2 in the Supporting Information. In Figure 4, the sum intensities of all pure thiomolybdate [HxMo3Sy]+ and thio-oxo-molybdate [HxMo3SyOz]+ species are shown. Considerable reactivity toward water is observed, especially for high collision energies (Vc > 22 V), indicating a relatively high reaction barrier with H2O. The maximum thiomolybdate fragmentation ratio approaches 80% at Vc ≈ 24 V. At Vc = 35 V, only 60% of the fragment ions are pure thiomolybdate and the remaining 40% are thio-oxo-molybdate species, produced by reactive collisions with water.
Figure 4.
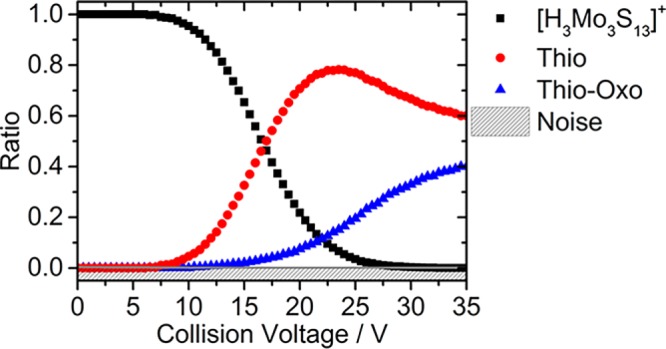
CID breakdown curves of [H3Mo3S13]+ showing the sum-intensities of thiomolybdate [HxMo3Sy]+ and thio-oxo-molybdate [HxMo3SyOz]+ clusters, denoted as Thio and Thio-Oxo respectively. Increased reactivity toward water is observed at high collision energies (Vc > 22 V), indicating a high activation barrier. Reactions with water are assigned to residual humidity inside the collision gas inlet.
As described above for the unprotonated and singly protonated clusters, the elimination of one S2 is the first fragmentation channel to open in the experiment. The most prominent channels are the elimination of [S2], [HS], [HS2], and [H2S]. The parent ion is fragmented away efficiently and, in comparison to the fragmentation patterns of the other two clusters, the breakdown curves are shifted toward higher collision energies. The additional protons seem to stabilize the [Mo3S13]2– cluster within the CID process.
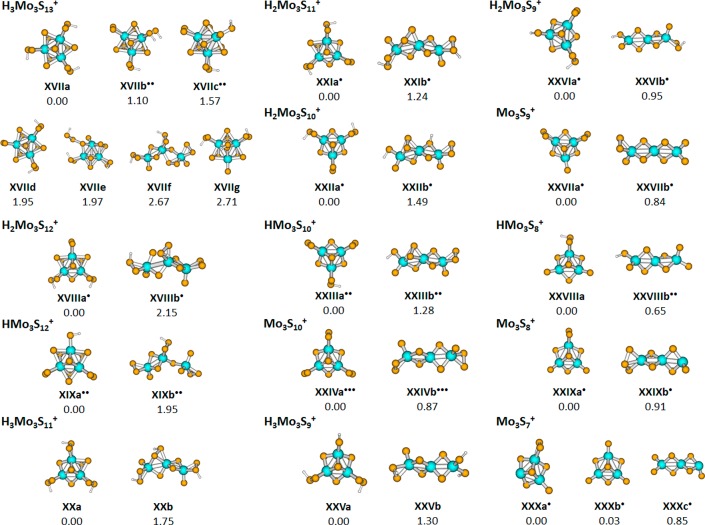
Representative calculated structures for the cationic dissociation series are shown in Figure 5. For the [H3Mo3S13]+ cation, the ring structure with one proton on each S2 terminal group (XVIIa) was predicted to be the most stable one. An open structure with three protons, XVIIf, also tends to distribute the three H+ among S2 groups, lies however ∼2.7 eV higher in energy.
Figure 5.
Selected structures of the [H3Mo3S13]+ complex and of fragments formed during its dissociation along with their relative energies (in eV); calculated at the ωB97XD/def2TZVP level of theory. All structures have the lowest spin multiplicity, i.e., singlet or doublet, unless shown otherwise.
The predicted structure of isomer XVIIa indicates that [HS2] and [HS] should be the only low-lying dissociation channels. However, the [S2] and [H2S] dissociation channels are also seen in the experiment. Calculated structures with a proton transferred to another S or S2 units (e.g., XVIIb-d) lie however higher in energy and cannot be expected to be formed in a considerable amount in the experiment before voltage is applied. Therefore, we conclude that terminal S2 and H2S moieties are formed on the cluster during the CID process. When energy is provided to the cluster, its structural flexibility is enhanced, and a proton might roam along the cluster (forming e.g. isomers XVIIb-d), making both S2 and H2S dissociation possible. The energy of these structures lies below the HS2 dissociation energy of ∼2.1 eV (see Figure 5 and Table 1). Alternatively, an SH group might move along the cluster, reaching e.g. structures XVIIe,g. Then, SH and H might recombine and form a considerably stable H2S molecule.
The calculated dissociation energies collected in Table 1 match the order in which groups of fragments appear in the experiment. Slightly higher dissociation energies with respect to [Mo3S13]2– and [HMo3S13]− ions are observed, in agreement with the later appearance of the ions in the CID breakdown curves. However, due to the high flexibility of the [H3Mo3S13]+ ion and its fragments expected from the calculations (and documented by the variety of dissociating molecules), total reaction energies must be taken with caution and a full (multistep) potential energy surface would be required to map the actual reaction pathways, including the activation energy of H/SH roaming on the cluster.
The most stable calculated fragment structures possess a Mo3 ring and follow the patterns already seen above. Namely, sulfur atoms are preferentially removed from the bridging S2 groups if cluster reorganization takes place. In contrast to [Mo3S13]2– and [HMo3S13]− anions, positively charged quasi-linear Mo–Mo–Mo structures are less stable than ones with a Mo3 ring by at least 0.6 eV for all ions studied. An increasing number of protons bound to the clusters generally increases the calculated energy gap between cyclic and quasi-linear structures, as can be seen, e.g., in the [H3Mo3S9]+/[H2Mo3S9]+/[Mo3S9]+ series (with the exception of [HMo3S8]+/[Mo3S8]+).
Compared to the previously discussed systems, there are several ions with a remarkable electronic structure. [HMo3S12]+ and [HMo3S10]+ have biradical and [Mo3S10]+ even triradical character. This is caused by electron depletion and can be intuitively understood in the case of the ring structures. Starting with a closed [Mo3S10]2– isomer IIIa, three electrons are removed from the most negatively charged units, i.e., the terminal S2 groups, producing the [Mo3S10]+ triradical XXIVa. Similarly to the situation in a substituted benzene,60 the central Mo3 unit separates three terminal S2 units of radical character, with the unpaired electron localized in p orbitals of sulfur atoms. The electronic structure of biradical cyclic compounds may be understood on the same grounds. In the case of quasi-linear structures, unpaired electrons are localized on both S2 groups and Mo atoms.
Implications for HER Catalysis
Recent thermal decomposition studies of [Mo3S13]2– clusters deposited on carbon nanotubes were interpreted in terms of preferential loss of the apical S atom, followed by bridging disulfide units.12 This is at odds with our present results. We never observe the loss of a single S atom in our experiments, ruling out loss of the apical S atom. In addition, the suggested lowest-energy pathway for [S3] loss, observed for [HMo3S13]−, does not involve the apical S atom. The question whether terminal or bridging S2 units are preferentially lost, however, is more complex. As discussed above, the initial loss of a terminal S2 is probably followed by significant reorganization, with a bridging S2 unit replacing the original terminal one in, e.g., structure IIe. This structure may relax further to IId, which contains a terminal as well as a bridging S ligand. Further rearrangement is required to reach the lowest energy configuration IIa of [Mo3S11]2–, which features two bridging S atoms.
More important, however, may be the result that the ring-opened structures Ib, Ic, and Id lie within 1 eV of the lowest energy structure and well below all dissociation channels. In catalysis studies involving [Mo3S13]2–, dissociation of sulfur is frequently discussed,12,14 but opening of the Mo3 ring is not considered. In particular, in interaction with an electrode surface, significant reconstruction of the [Mo3S13]2– structure together with an opening of the Mo3 ring, should be considered.
Finally, we would like to note that our results on protonated clusters favor the formation of S–H moieties over metal hydride type Mo–H species. Concerning the currently still unresolved dispute whether HER catalysis by [Mo3S13]2– or MoSx takes place via “metal-centered“ or “sulfur-centered” reaction pathways,6 the results presented in this study thus favor the sulfur-centered route. However, we are aware of the fact that the species investigated here only address the point of protonation of [Mo3S13]2– while HER also involves the transfer of electrons to the cluster. Whether reduced Mo3 species also preferentially bind H+ to terminal disulfide ligands is thus an important question, which deserves further attention.
Conclusions
We investigated the [Mo3S13]2–, [HMo3S13]−, and [H3Mo3S13]+ ions in the gas phase by a combination of collision induced dissociation (CID) experiments and theoretical calculations. We conclude that all ions have similar structure as the corresponding species in bulk, forming a Mo3 ring and three types of sulfur units (terminal S2, bridging S2 and apical S). However, the central Mo3 ring might open after dissociation of, e.g., an S2 group. It is questionable whether this could happen also on a molybdenum sulfide (MoSx) surface as the Mo3 ring might be supported in bulk due to additional interactions with the Mo–S-network.
The CID breakdown curves show a variety of dissociating species, with [S2], [HS], [HS2], and [H2S] dissociation channels being the first ones to open. Interestingly, no dissociation of single sulfur atoms was recorded. Protonation of the [Mo3S13]2– ion increases its stability within the CID process and protons are calculated to adsorb preferentially on terminal S2 groups, being the most negatively charged moieties of the [Mo3S13]2– ion. We also conclude that a Mo–H bond is preferred only for undercoordinated Mo centers so that our results overall support the model of a “sulfur-centered” mechanism of HER catalysis by [Mo3S13]2– or MoSx. Finally, a rich variety of CID dissociation products suggests that the triply protonated [H3Mo3S13]+ ion has a large degree of structural flexibility, with roaming H/SH moieties. This flexibility might be generally an important property of molybdenum sulfides to explain their good performance in HER catalysis.
Acknowledgments
This project is supported by the Klima- und Energiefonds, administered by the FFG under Project No. 853639, and put into effect in the framework of the programme “ENERGIE DER ZUKUNFT”. M.O. acknowledges support through the Lise Meitner Programme of the Austrian Science Fund (FWF), Project No. M2001-NBL. The computational results presented have been achieved using the HPC infrastructure LEO of the University of Innsbruck.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.8b08324.
Overview of all measured fragment ions; qualitative breakdown curves of protonated ions; structures, energies and coordinates of all calculated ions (PDF)
The authors declare no competing financial interest.
Dedication
Dedicated to Professor Hans-Joachim Freund and Professor Joachim Sauer for their seminal contributions to the understanding of elementary steps in catalysis.
Supplementary Material
References
- Karunadasa H. I.; Montalvo E.; Sun Y.; Majda M.; Long J. R.; Chang C. J. A Molecular MoS2 Edge Site Mimic for Catalytic Hydrogen Generation. Science 2012, 335, 698–702. 10.1126/science.1215868. [DOI] [PubMed] [Google Scholar]
- Liu C.; Liu P. Mechanistic Study of Methanol Synthesis from CO2 and H2 on a Modified Model Mo6S8 Cluster. ACS Catal. 2015, 5, 1004–1012. 10.1021/cs501354b. [DOI] [Google Scholar]
- Benck J. D.; Hellstern T. R.; Kibsgaard J.; Chakthranont P.; Jaramillo T. F. Catalyzing the Hydrogen Evolution Reaction (HER) with Molybdenum Sulfide Nanomaterials. ACS Catal. 2014, 4, 3957–3971. 10.1021/cs500923c. [DOI] [Google Scholar]
- Zheng Y.; Jiao Y.; Jaroniec M.; Qiao S. Z. Advancing the Electrochemistry of the Hydrogen-evolution Reaction Through Combining Experiment and Theory. Angew. Chem., Int. Ed. 2015, 54, 52–65. 10.1002/anie.201407031. [DOI] [PubMed] [Google Scholar]
- Parsons R. The Rate of Electrolytic Hydrogen Evolution and the Heat of Adsorption of Hydrogen. Trans. Faraday Soc. 1958, 54, 1053. 10.1039/tf9585401053. [DOI] [Google Scholar]
- Grutza M.-L.; Rajagopal A.; Streb C.; Kurz P. Hydrogen Evolution Catalysis by Molybdenum Sulfides (MoSx): Are Thiomolybdate Clusters like [Mo3S13]2- Suitable Active Site Models?. Sustainable Energy Fuels 2018, 2, 1893. 10.1039/C8SE00155C. [DOI] [Google Scholar]
- Lassalle-Kaiser B.; Merki D.; Vrubel H.; Gul S.; Yachandra V. K.; Hu X.; Yano J. Evidence from in Situ X-ray Absorption Spectroscopy for the Involvement of Terminal Disulfide in the Reduction of Protons by an Amorphous Molybdenum Sulfide Electrocatalyst. J. Am. Chem. Soc. 2015, 137, 314–321. 10.1021/ja510328m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran P. D.; Tran T. V.; Orio M.; Torelli S.; Truong Q. D.; Nayuki K.; Sasaki Y.; Chiam S. Y.; Yi R.; Honma I.; et al. Coordination Polymer Structure and Revisited Hydrogen Evolution Catalytic Mechanism for Amorphous Molybdenum Sulfide. Nat. Mater. 2016, 15, 640–646. 10.1038/nmat4588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kibsgaard J.; Jaramillo T. F.; Besenbacher F. Building an Appropriate Active-Site Motif into a Hydrogen-Evolution Catalyst with Thiomolybdate [Mo3S13]2- clusters. Nat. Chem. 2014, 6, 248–253. 10.1038/nchem.1853. [DOI] [PubMed] [Google Scholar]
- Huang Z.; Luo W.; Ma L.; Yu M.; Ren X.; He M.; Polen S.; Click K.; Garrett B.; Lu J.; et al. Dimeric [Mo2S12]2- Cluster: A Molecular Analogue of MoS2 Edges for Superior Hydrogen-Evolution Electrocatalysis. Angew. Chem., Int. Ed. 2015, 54, 15181–15185. 10.1002/anie.201507529. [DOI] [PubMed] [Google Scholar]
- Kan M.; Jia J.; Zhao Y. High Performance Nanoporous Silicon Photoelectrodes Co-catalyzed with an Earth Abundant [Mo3S13]2- Nanocluster via Drop Coating. RSC Adv. 2016, 6, 15610–15614. 10.1039/C6RA01109H. [DOI] [Google Scholar]
- Lee C.-H.; Lee S.; Lee Y.-K.; Jung Y. C.; Ko Y.-I.; Lee D. C.; Joh H.-I. Understanding the Origin of Formation and Active Sites for Thiomolybdate [Mo3S13]2- Clusters as Hydrogen Evolution Catalyst through the Selective Control of Sulfur Atoms. ACS Catal. 2018, 8, 5221–5227. 10.1021/acscatal.8b01034. [DOI] [Google Scholar]
- Lei Y.; Yang M.; Hou J.; Wang F.; Cui E.; Kong C.; Min S. Thiomolybdate [Mo3S13]2- Nanocluster: a Molecular Mimic of MoS2 Active Sites for Highly Efficient Photocatalytic Hydrogen Evolution. Chem. Commun. 2018, 54, 603–606. 10.1039/C7CC08178B. [DOI] [PubMed] [Google Scholar]
- Dave M.; Rajagopal A.; Damm-Ruttensperger M.; Schwarz B.; Nägele F.; Daccache L.; Fantauzzi D.; Jacob T.; Streb C. Understanding Homogeneous Hydrogen Evolution Reactivity and Deactivation Pathways of Molecular Molybdenum Sulfide Catalysts. Sustainable Energy Fuels 2018, 2, 1020–1026. 10.1039/C7SE00599G. [DOI] [Google Scholar]
- Gemming S.; Tamuliene J.; Seifert G.; Bertram N.; Kim Y. D.; Ganteför G. Electronic and Geometric Structures of MoxSy and WxSy (x = 1, 2, 4; y = 1–12) Clusters. Appl. Phys. A: Mater. Sci. Process. 2006, 82, 161–166. 10.1007/s00339-005-3345-7. [DOI] [Google Scholar]
- Kretzschmar I.; Fiedler A.; Harvey J. N.; Schröder D.; Schwarz H. Effects of Sequential Ligation of Molybdenum Cation by Chalcogenides on Electronic Structure and Gas-Phase Reactivity. J. Phys. Chem. A 1997, 101, 6252–6264. 10.1021/jp971941+. [DOI] [Google Scholar]
- Kretzschmar I.; Schröder D.; Schwarz H.; Armentrout P. B. Structure, Thermochemistry, and Reactivity of MSn+ Cations (M = V, Mo; n = 1–3) in the Gas Phase. Int. J. Mass Spectrom. 2003, 228, 439–456. 10.1016/S1387-3806(03)00137-4. [DOI] [Google Scholar]
- Wang Y.-Y.; Deng J.-J.; Wang X.; Che J.-T.; Ding X.-L. Small Stoichiometric (MoS2)n Clusters with the 1T Phase. Phys. Chem. Chem. Phys. 2018, 20, 6365–6373. 10.1039/C7CP07914A. [DOI] [PubMed] [Google Scholar]
- Wang B.; Wu N.; Zhang X.-B.; Huang X.; Zhang Y.-F.; Chen W.-K.; Ding K.-N. Probing the Smallest Molecular Model of MoS2 catalyst: S2 Units in the MoSn–/0 (n = 1–5) Clusters. J. Phys. Chem. A 2013, 117, 5632–5641. 10.1021/jp309163c. [DOI] [PubMed] [Google Scholar]
- Gemming S.; Seifert G.; Götz M.; Fischer T.; Ganteför G. Transition Metal Sulfide Clusters Below the Cluster-Platelet Transition: Theory and Experiment. Phys. Status Solidi B 2010, 247, 1069–1076. 10.1002/pssb.200945480. [DOI] [Google Scholar]
- Mayhall N. J.; Becher E. L. III; Chowdhury A.; Raghavachari K. Molybdenum Oxides Versus Molybdenum Sulfides: Geometric and Electronic Structures of Mo3Xy– (X = O, S and y = 6, 9) Clusters. J. Phys. Chem. A 2011, 115, 2291–2296. 10.1021/jp108344k. [DOI] [PubMed] [Google Scholar]
- Saha A.; Raghavachari K. Hydrogen Evolution from Water Through Metal Sulfide Reactions. J. Chem. Phys. 2013, 139, 204301. 10.1063/1.4830096. [DOI] [PubMed] [Google Scholar]
- Murugan P.; Kumar V.; Kawazoe Y.; Ota N. Ab Initio Study of Structural Stability of Mo-S Clusters and Size Specific Stoichiometries of Magic Clusters. J. Phys. Chem. A 2007, 111, 2778–2782. 10.1021/jp065646d. [DOI] [PubMed] [Google Scholar]
- Wen X.-D.; Zeng T.; Li Y.-W.; Wang J.; Jiao H. Surface Structure and Stability of MoSx Model Clusters. J. Phys. Chem. B 2005, 109, 18491–18499. 10.1021/jp051540r. [DOI] [PubMed] [Google Scholar]
- Kaya S.; Weissenrieder J.; Stacchiola D.; Todorova T. K.; Sierka M.; Sauer J.; Shaikhutdinov S.; Freund H.-J. Formation of One-dimensional Molybdenum Oxide on Mo(112). Surf. Sci. 2008, 602, 3338–3342. 10.1016/j.susc.2008.09.010. [DOI] [Google Scholar]
- Gregoriades L. J.; Döbler J.; Sauer J. Oxidation of Methanol to Formaldehyde on Silica-Supported Molybdena: Density Functional Theory Study on Models of Mononuclear Sites. J. Phys. Chem. C 2010, 114, 2967–2979. 10.1021/jp908609s. [DOI] [Google Scholar]
- Guo C. S.; Hermann K.; Hävecker M.; Thielemann J. P.; Kube P.; Gregoriades L. J.; Trunschke A.; Sauer J.; Schlögl R. Structural Analysis of Silica-Supported Molybdena Based on X-ray Spectroscopy: Quantum Theory and Experiment. J. Phys. Chem. C 2011, 115, 15449–15458. 10.1021/jp2034642. [DOI] [Google Scholar]
- Sievers M. R.; Armentrout P. B. Reactions of CO and CO2 with Gas-Phase Mo+, MoO+, and MoO2+. J. Phys. Chem. A 1998, 102, 10754–10762. 10.1021/jp983694v. [DOI] [Google Scholar]
- Waters T.; O’Hair R. A. J.; Wedd A. G. Gas-Phase Reactivity of Heterobinuclear Oxometalate Anions CrMoO6(OR)−, CrWO6(OR)−, and MoWO6(OR)− (R = H, nBu). Inorg. Chem. 2005, 44, 3356–3366. 10.1021/ic050288z. [DOI] [PubMed] [Google Scholar]
- Fielicke A.; Rademann K. Molybdenum Doped Bismuth Oxide Clusters and Their Reactivity Towards Ethene: Comparison with Pure Bismuth Oxide Clusters. Chem. Phys. Lett. 2002, 359, 360–366. 10.1016/S0009-2614(02)00639-5. [DOI] [Google Scholar]
- Ferrari P.; Vanbuel J.; Tam N. M.; Nguyen M. T.; Gewinner S.; Schöllkopf W.; Fielicke A.; Janssens E. Effects of Charge Transfer on the Adsorption of CO on Small Molybdenum-Doped Platinum Clusters. Chem. - Eur. J. 2017, 23, 4120–4127. 10.1002/chem.201604894. [DOI] [PubMed] [Google Scholar]
- Khairallah G. N.; Waters T.; Wedd A. G.; O’Hair R. A. C-F. Bond Activation of Trifluoroethanol and Trifluoroacetic Acid Catalysed by the Dimolybdate Anion, [Mo2O6(F)]−. Eur. J. Mass Spectrom. 2018, 24, 43–48. 10.1177/1469066717729250. [DOI] [PubMed] [Google Scholar]
- Garrett B. R.; Polen S. M.; Click K. A.; He M.; Huang Z.; Hadad C. M.; Wu Y. Tunable Molecular MoS2 Edge-Site Mimics for Catalytic Hydrogen Production. Inorg. Chem. 2016, 55, 3960–3966. 10.1021/acs.inorgchem.6b00206. [DOI] [PubMed] [Google Scholar]
- Garrett B. R.; Click K. A.; Durr C. B.; Hadad C. M.; Wu Y. [MoO(S2)2L]1- (L = picolinate or pyrimidine-2-carboxylate) Complexes as MoSx Inspired Electrocatalysts for Hydrogen Production in Aqueous Solution. J. Am. Chem. Soc. 2016, 138, 13726–13731. 10.1021/jacs.6b08652. [DOI] [PubMed] [Google Scholar]
- Garrett B. R.; Polen S. M.; Pimplikar M.; Hadad C. M.; Wu Y. Anion-Redox Mechanism of MoO(S2)2(2,2’-bipyridine) for Electrocatalytic Hydrogen Production. J. Am. Chem. Soc. 2017, 139, 4342–4345. 10.1021/jacs.7b01350. [DOI] [PubMed] [Google Scholar]
- Baloglou A.; Ončák M.; van der Linde C.; Beyer M. K. Gas-Phase Reactivity Studies of Small Molybdenum Cluster Ions with Dimethyl Disulfide. Top. Catal. 2018, 61, 20–27. 10.1007/s11244-017-0864-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lengyel J.; Med J.; Slavíček P.; Beyer M. K. Communication: Charge Transfer Dominates Over Proton Transfer in the Reaction of Nitric Acid with Gas-Phase Hydrated Electrons. J. Chem. Phys. 2017, 147, 101101. 10.1063/1.4999392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gernert I.; Beyer M. K. Evidence for Electron Transfer in the Reactions of Hydrated Monovalent First-Row Transition-Metal Ions M(H2O)n+, M = V, Cr, Mn, Fe, Co, Ni, Cu, and Zn, n < 40, toward 1-Iodopropane. J. Phys. Chem. A 2017, 121, 9557–9566. 10.1021/acs.jpca.7b08385. [DOI] [PubMed] [Google Scholar]
- Schwarz H. Chemistry with Methane: Concepts Rather Than Recipes. Angew. Chem., Int. Ed. 2011, 50, 10096–10115. 10.1002/anie.201006424. [DOI] [PubMed] [Google Scholar]
- van der Linde C.; Tang W. K.; Siu C.-K.; Beyer M. K. Electrons Mediate the Gas-Phase Oxidation of Formic Acid with Ozone. Chem. - Eur. J. 2016, 22, 12684–12687. 10.1002/chem.201603080. [DOI] [PubMed] [Google Scholar]
- Balaj O. P.; Balteanu I.; Roßteuscher T. T. J.; Beyer M. K.; Bondybey V. E. Catalytic Oxidation of CO with N2O on Gas-Phase Platinum Clusters. Angew. Chem., Int. Ed. 2004, 43, 6519–6522. 10.1002/anie.200461215. [DOI] [PubMed] [Google Scholar]
- Siu C.-K.; Reitmeier S. J.; Balteanu I.; Bondybey V. E.; Beyer M. K. Catalyst Poisoning in the Conversion of CO and N2O to CO2 and N2 on Pt4– in the Gas Phase. Eur. Phys. J. D 2007, 43, 189–192. 10.1140/epjd/e2007-00062-4. [DOI] [Google Scholar]
- Kappes M. M.; Staley R. H. Gas-Phase Oxidation Catalysis by Transition-Metal Cations. J. Am. Chem. Soc. 1981, 103, 1286–1287. 10.1021/ja00395a080. [DOI] [Google Scholar]
- Brönstrup M.; Schröder D.; Kretzschmar I.; Schwarz H.; Harvey J. N. Platinum Dioxide Cation: Easy To Generate Experimentally But Difficult To Describe Theoretically. J. Am. Chem. Soc. 2001, 123, 142–147. 10.1021/ja003138q. [DOI] [PubMed] [Google Scholar]
- Schnabel P.; Weil K. G.; Irion M. P. Proof of the Catalytic Activity of a Naked Metal Cluster in the Gas-Phase. Angew. Chem., Int. Ed. Engl. 1992, 31, 636–638. 10.1002/anie.199206361. [DOI] [Google Scholar]
- Bersenkowitsch N. K.; Ončák M.; van der Linde C.; Herburger A.; Beyer M. K. Photochemistry of Glyoxylate Embedded in Sodium Chloride Clusters, a Laboratory Model for Tropospheric Sea-Salt Aerosols. Phys. Chem. Chem. Phys. 2018, 20, 8143–8151. 10.1039/C8CP00399H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herburger A.; van der Linde C.; Beyer M. K. Photodissociation Spectroscopy of Protonated Leucine Enkephalin. Phys. Chem. Chem. Phys. 2017, 19, 10786–10795. 10.1039/C6CP08436B. [DOI] [PubMed] [Google Scholar]
- Lengyel J.; Ončák M.; Herburger A.; van der Linde C.; Beyer M. K. Infrared Spectroscopy of O•– and OH– in Water Clusters: Evidence for Fast Interconversion between O•– and OH•OH–. Phys. Chem. Chem. Phys. 2017, 19, 25346–25351. 10.1039/C7CP04577H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bondybey V. E.; Beyer M. K. Temperature Effects in Transition Metal Ion and Cluster Ion Reactions. J. Phys. Chem. A 2001, 105, 951–960. 10.1021/jp002746p. [DOI] [Google Scholar]
- Inorganic syntheses; Ginsberg A. P., Ed.; Wiley: New York, 1990; Vol. 27. [Google Scholar]
- Chai J.-D.; Head-Gordon M. Long-range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- Laury M. L.; Wilson A. K. Performance of Density Functional Theory for Second Row (4d) Transition Metal Thermochemistry. J. Chem. Theory Comput. 2013, 9, 3939–3946. 10.1021/ct400379z. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A., et al. Gaussian 09, Revision D.01; Gaussian Inc.: Wallingford, CT, 2013.
- Włodarczyk R.; Sierka M.; Kwapień K.; Sauer J.; Carrasco E.; Aumer A.; Gomes J. F.; Sterrer M.; Freund H.-J. Structures of the Ordered Water Monolayer on MgO(001). J. Phys. Chem. C 2011, 115, 6764–6774. 10.1021/jp200112c. [DOI] [Google Scholar]
- Foster J. P.; Weinhold F. Natural Hybrid Orbitals. J. Am. Chem. Soc. 1980, 102, 7211–7218. 10.1021/ja00544a007. [DOI] [Google Scholar]
- Breneman C. M.; Wiberg K. B. Determining Atom-Centered Monopoles from Molecular Electrostatic Potentials. the Need for High Sampling Density in Formamide Conformational Analysis. J. Comput. Chem. 1990, 11, 361–373. 10.1002/jcc.540110311. [DOI] [Google Scholar]
- Schröder D.; Schwarz H. Generation, Stability, and Reactivity of Small, Multiply Charged Ions in the Gas Phase. J. Phys. Chem. A 1999, 103, 7385–7394. 10.1021/jp991332x. [DOI] [Google Scholar]
- Müller A.; Wittneben V.; Krickemeyer E.; Bögge H.; Lemke M. Studies on the Triangular Cluster [Mo3S13]2-: Electronic Structure (Xα Calculations, XPS), Crystal Structure of (Ph4As)2[Mo3S13].2CH3CN and a Refinement of the Crystal Structure of (NH4)2[Mo3S13]H2O. Z. Anorg. Allg. Chem. 1991, 605, 175–188. 10.1002/zaac.19916050121. [DOI] [Google Scholar]
- Beyer M.; Williams E. R.; Bondybey V. E. Unimolecular Reactions of Dihydrated Alkaline Earth Metal Dications M2+(H2O)2, M = Be, Mg, Ca, Sr, and Ba: Salt-Bridge Mechanism in the Proton-Transfer Reaction M2+(H2O)2 -> MOH+ + H3O+. J. Am. Chem. Soc. 1999, 121, 1565–1573. 10.1021/ja982653+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler M.; Sander W. Triradicals. Acc. Chem. Res. 2014, 47, 31–44. 10.1021/ar4000218. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.