Assessing the validity of pressure-measuring insoles in quantifying gait variables

Abstract

Introduction

Pressure-measuring insoles can provide a portable alternative to existing gait analysis tools. However, there is disagreement among researchers on their accuracy and the appropriate calibration methods. The purposes of this study were to (1) determine the validity of pressure-measuring insoles for calculating stance time and support-phase impulse during walking using two calibration procedures, and (2) examine the effect of insole size on the results.

Methods

Data were collected from 39 participants (23.5 ± 3.24 yrs, 66.7 ± 17.5 kg, 1.64 ± 0.09 m), each wearing appropriately sized insoles as they walked over two consecutive force platforms. Two calibration methods were evaluated: (1) manufacturer’s recommendation, and (2) a participant weight-based approach. Qualitative and quantitative evaluations were conducted.

Results

The results indicated that the insoles measured longer stance times than the force platform (differences are less than 10%). Both calibration methods resulted in inaccurate impulse values (differences are 30 and 50% for the two calibration methods, respectively). The results showed that when using the first calibration method, impulse values depended on insole size. The second calibration consistently underestimated the impulse.

Conclusions

It was concluded that while the insoles provide acceptable qualitative representation of the gait, the two studied calibration methods may lead to a misleading quantitative assessment.

Introduction

Gait analysis can enhance the understanding of the kinematic and kinetic functions of an individual during walking. Accurate measurements of stance time and support-phase impulse are important components of this analysis. There are several tools available to measure ground reaction force (and thus impulse) dynamically, including force platforms and force instrumented treadmills. While force platforms are the gold standard in this area, they are not portable and generally cannot be used to evaluate multiple consecutive steps.^1–3 Alternatively, instrumented treadmills allow the measurement of multiple steps. However, treadmills can produce belt speed variations and may cause changes in the foot position during gait, which may make them unrepresentative of normal over-ground walking.^4,5

Nontethered, pressure-measuring insoles have been used as an alternative tool for gait analysis. These insoles are portable and can be used in various environments to measure multiple steps. Several pressure-measuring insole designs have been developed. For example, Lincoln et al.⁶ used insoles with five sensors that used a light emitter and receiver that sensed the proximity of a reflective material to measure three-dimensional ground reaction force. The reported results on a single participant proved promising, achieving errors below 13% when compared to the force platform for the three ground reaction force components. Crea et al.⁷ developed a pressure-measuring insole with 64 sensors outfitted with LEDs and light sensors. In this study, two participants were asked to walk over a force platform while wearing these insoles inside shoes. It was found that the force platform measured greater values, with a normalized root mean square error (NRMSE) of 80%. However, the two instruments had the same qualitative pattern of the force–time curves. Jacobs and Ferris⁸ instrumented their custom insole with eight pneumatic bladders, each outfitted with a single sensor. The insoles were placed into shoes and six participants wore them while walking over a force platform. The results showed NRMSE values below 10%, leading to the conclusions that the insoles were capable of accurately measuring ground reaction force. Motha et al.⁹ created a pressure-measuring insole that was based on the change of capacitance as a function of applied compression. They constructed an insole that was divided into three areas (hindfoot, midfoot, and forefoot) with one sensor in each area. Results indicated that this insole design was able to successfully measure applied pressure to determine force concentrations associated with changes in posture. These studies along with reviews of earlier research^10,11 have shown that pressure-measuring insoles, with few sensors are incapable of accurately measuring the total ground reaction force or center of pressure across the entire foot. Additionally, the results of these studies were limited by the custom construction of the insoles in many cases, which may limit generalizability and threaten external validity.

An alternative approach is to use commercial pressure-measuring insoles, which have a relatively large number of sensors, covering the entire plantar surface of the foot. The following is a brief review of relevant research in this area. Some researchers examined the mechanical characteristics of these insoles. Woodburn and Helliwell¹² examined small groups of four sensors on the F-Scan® insoles. This examination included the analysis of creep, hysteresis, and variability. The results showed errors in creep at 19% and hysteresis at 21%. At several instances, more than 10% variability between sensor groups was observed. Another examination of the F-Scan® insoles by Luo et al.¹³ confirmed the results of Woodburn and Helliwell¹² showing that variation existed between sensors. The study also showed that variability increased as surface hardness and temperature increased, and as loading rate decreased.¹³ To test the F-Scan® insoles, Nicolopoulos et al.¹⁴ examined several calibration methods to determine if a certain calibration could improve the measurement accuracy. It was found that the accuracy of the F-Scan® system was highly dependent on calibration, hysteresis, preconditioning, bending, and shear loading which might limit their clinical applicability. Hsiao et al.¹⁵ conducted a thorough investigation of the responses of the Pedar® and F-Scan® insole systems to multiple loading experiments using a bladder system that applied a wide range of pressure. Results showed that each insole performed best within a prescribed range of pressures, but when attempting to measure pressures outside this range, the error increased reaching up to 33.9%. A similar study by Giacomozzi¹⁶ compared several insoles including AM Cube®, Medilogic®, Novel EMED®, and Tekscan Matscan®. These insoles, which used different sensor technologies, also exhibited different error magnitudes with Novel EMED® showing the smallest error. These conclusions were consistent when examining error due to hysteresis and creep. Price et al.¹⁷ tested and compared the F-Scan®, Medilogic®, and Pedar® insoles using a pressure bladder. It was found that the Pedar® system displayed the lowest error. These reviewed experiments showed that the insoles experience hysteresis and drift. Additionally, calibration methods significantly affect the results of these insoles.

Researchers have also validated the insoles during walking. Chen and Bates¹⁸ examined the F-scan® insole by having 30 male participants wear them inside a standardized laboratory shoe while walking over a force platform. The authors compared the magnitude and temporal value of the vertical component first peak force, minimum force, and the second peak force for both instruments. It was found that the force values between the two instruments were not significantly different. There was, however, a significant delay in the temporal values of the variables. Barnett et al.¹⁹ tested the Pedar® pressure-measuring insoles, both inside shoes and taped to the foot to represent a barefoot condition. Both shod and barefoot conditions were tested with five participants who walked over a force platform. The results showed minimal differences in stance time but the insoles measured force values significantly lesser than the force platform results. Morin et al.²⁰ working with the F-Scan® insoles showed that the insoles underreported the vertical ground reaction force by an average of 30.15% when compared to a force platform. A similar experiment using Tekscan F-Scan® insoles in a barefoot condition was conducted by Ong and Wong.²¹ This work showed a high correlation between the ground reaction forces and stance time measured by the force platform and insoles after applying extended calibration, which was designed to correct for the dynamic pressure distribution during the actual test by using the subject’s weight to adjust the static calibration. To address the problem of insole calibration, Forner-Cordero et al.²² used Pedar® insoles, force platforms, and a multiple camera system to estimate the force measured by the insoles using an inverse dynamics calculation. Using five participants, the calibration resulted in highly correlated results. Fong et al.²³ used Pedar® insoles with 10 participants who walked over a force platform. Data from five of the participants were used to calibrate the insoles using linear regressions. These regression results were then used to calculate the insole ground reaction force for the other participants. Results showed that ground reaction force can be estimated with an error of approximately 5% in the vertical direction. A shod experiment was conducted using Zebris® insoles where participants were asked to walk on an instrumented treadmill.²⁴ The results of this experiment showed no significant difference in the ground reaction force or stance time measured between the two instruments. Koch et al.²⁵ developed a custom calibration method by loading and unloading the insoles with weights in steps of 5 kg up to 80 kg. Each loading or unloading step lasted a total of 25 s. The results of this calibration process showed each insole responded with a different time-dependent creeping pattern and hysteresis. A regression equation was used to calculate the forces measured by the insoles worn inside the shoes of 15 healthy participants as they walked over a force platform. The results from the gait analysis showed that the insoles could measure vertical ground reaction forces and stance times, within the bounds of approximately 18% error.

These studies show that researchers have not agreed upon the ability of the insoles to accurately measure gait variables. However, these differences could be due to a difference among brands/sensor technologies or inconsistent calibration methods. It was shown that some of the tested insoles were affected by hysteresis and measurement drift. Many of these studies were conducted while the insoles were placed inside shoes, which could have decreased the measured ground reaction forces in comparison to similar barefoot measurements.²⁶ Elevated temperature and humidity within the shoe might have contributed to insole measurement errors.^13,27 The effect of the number of sensors on the accuracy of measurements was not considered in much of the previous research.

The focus of this work was to assess the ability of the Medilogic® insoles to accurately measure gait variables in comparison to the force platform measurements. These insoles (Medilogic®) were selected since they have a large number of sensors. The purposes of this study were to (1) determine the validity of pressure-measuring insoles for measuring stance time and impulse during walking using two calibration procedures, and (2) examine the effect of insole size on the observed results. Experiments were conducted while the participants walked barefoot. Two calibration processes were examined: the manufacturer’s recommended calibration and a participant weight-based calibration.

Pressure-measuring insoles

Medilogic® pressure-measuring insoles (Schönefeld, Germany) were used for all experiments. As shown in Figure 1, each insole has a grid of sensors. The number of sensors ranges between 93 and 162 sensors as shown in Table 1. The sensors, which are 0.75 cm × 1.5 cm rectangles, measure the change in electrical resistance, which is proportional to the pressure applied to these sensors.²⁸ Each sensor outputs the pressures in the normal direction to the contact surface in the form of a 0–255 digital scale. The manufacturer stated that 255 bits are equal to 64 N/cm². It is recommended to use linear interpolation to convert the bit output to pressure based on these values.

Figure 1.

A Medilogic® left insole, size 43–44 (a) and its corresponding sensor map where each rectangle represents a single sensor (b).

Table 1.

Number of sensors per insole.

Insole size	Number of sensors
35–36	93
37–38	107
39–40	116
41–42	130
43–44	151
45–46	162

Methods

The objective of the experiment was to assess the ability of the Medilogic® pressure-measuring insoles to accurately measure temporal and kinetic variables during walking. More specifically, stance time and stance-phase impulse based on measuring the vertical component of the ground reaction force were examined. These dependent variables were measured over the entire support phase of gait. Since the force platform is the gold standard in force measurement, it was used as the reference measure.

Participants

A sample of 39 healthy, ambulatory adults (14 men, 25 women, 23.5 ± 3.24 yrs, 66.7 ± 17.5 kg, 1.64 ± 0.09 m) gave the institutionally approved written consent to participate (Protocol Number: 724468-4). The participant demographics are provided in Table 2. After the age, height, and mass data were obtained, the participants were fitted with pairs of Medilogic® pressure-measuring insoles that best matched their foot sizes. If the participant’s foot was between insole sizes, the larger size was chosen to ensure full coverage of the entire plantar surface. The insoles were placed inside thin socks provided by the researchers, next to the skin to simulate a barefoot walking scenario.

Table 2.

Participant demographics by insole size.

Insole size	Gender	Number of participants	Age (years) (Average ± std. dev.)	Mass (kg) (Average ± std. dev.)	Height (m) (Average ± std. dev.)
35–36	M	0	–	–	–
	F	4	23.0 ± 3.1	55.5 ± 7.8	1.53 ± 0.03
37–38	M	0	–	–	–
	F	14	23.1 ± 1.3	54.8 ± 7.5	1.58 ± 0.03
39–40	M	1	22.3	73.0	1.58
	F	5	21.9 ± 1.9	60.0 ± 6.8	1.70 ± 0.03
41–42	M	4	22.0 ± 1.4	69.8 ± 7.1	1.63 ± 0.06
	F	2	21.9 ± 0.3	74.0 ± 11.0	1.69 ± 0.01
43–44	M	6	27.4 ± 5.4	85.3 ± 10.3	1.71 ± 0.09
	F	0	–	–	–
45–46	M	3	24.5 ± 2.8	100.0 ± 21.3	1.77 ± 0.03
	F	0	–	–	–

Experimental protocol

After being fitted with insoles, the participants were asked to perform the following tasks:

1. Sit on a chair and lift feet off the floor (3–5 cm) for 5 s, which allowed for the identification of a noise level generated by contact with the socks.

2. Stand and remain stationary for 15 s.

3. Sit again and lift feet off the floor (3–5 cm) for another 5 s.

4. Stand and walk 5 m over two consecutively mounted force platforms (Kistler; Winterthur, Switzerland) using a nominally defined preferred speed (1.09 ± 0.17 m/s). The participants were asked to place only one foot on each platform to allow a direct comparison between the insole and the force platform measurements during each specific step (Figure 2).

Figure 2.

Exemplar participant stepping on each individual force platform while wearing the pressure-measuring insoles.

Each participant practiced these tasks at least twice until they felt comfortable. Since the participants wore the insoles for few minutes, it was deemed that the effects of the temperature and humidity on the insoles were negligible.

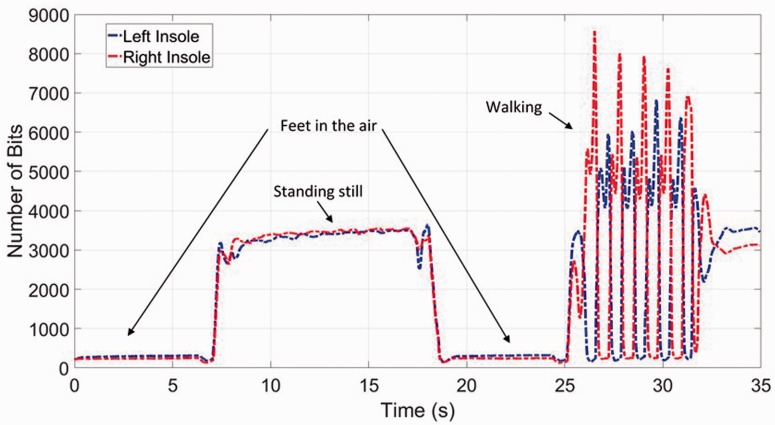
A successful trial was defined as the completion of all of the tasks listed (1–4) and having the entirety of each foot placed on the corresponding force platform. The above tasks were repeated until three successful trials were achieved for each participant. All insole sensor data were collected at 60 Hz (the maximum sampling frequency) while the force platform data were collected at 1000 Hz. This experimental procedure resulted in obtaining 117 data sets for each limb across all participants, for a total of 234 data sets. An exemplar time history of raw data (measured in bits) is given in Figure 3.

Figure 3.

A typical set of raw output data of the insoles versus time.

Data processing

Both insole and force platform data were filtered using a low-pass Butterworth filter with a cutoff frequency of 1/8 of the sampling frequency of each instrument. This resulted in a cutoff frequency of 7.5 Hz for the insoles and 125 Hz for the force platform. The use of separate cutoff frequencies prevented overattenuation of the time–force data. The filtered insole data were normalized to baseline (zeroed) based on the average bit measurement of the insole during the first “feet in the air” task (Task 1 in the experimental protocol). Then, it was determined how many time instances, or the number of data points for each instrument, there were for each limb and trial. This allowed for calculations to be made for each time point.

Two calibration methods were applied to the sensor data. The first method was according to the manufacturer’s suggested scaling factor of 255 bits equals 64 N/cm². The digital readings of each sensor were transformed into forces and summed as follows

$$F_{M,p,q,l,j}=\frac{64}{255}(\sum _{i=1}^n{O}_{i,j})a$$

where F_M,p,q,l,j is the ground reaction force using the manufacture calibration in Newtons, p is the participant number, q is the trial number, l is the limb (left or right), j is the time instant number, n is the number of sensors on the insoles used by participant p; O_i,j is the digital output of sensor i at instant j; and a is the area of the sensor.

The second calibration method was based on the digital output of the sensors while the participant was standing still during the second task of the experimental protocol and relating the digital output to the weight of the participant. This weight-based calibration had the potential of making the calibration factor adaptive for each participant. The weight-based calibration was performed using the following equation

$${\mathit{CF}}_{p,q,l}=\frac{W_p}{\frac{\sum _{j=K}^M((\sum _{i=1}^n{O}_{i,j})a)}{M-K+1}}$$

where CF_p,q,l is the calibration factor based on the participant’s weight, W_p is the weight of participant p, K is the first data instance of the standing still task, and M is the last data instance of the standing still task.

This weight-based calibration factor was combined with the output of the sensors to obtain the vertical component of the ground reaction force, F_W,p,q,l,j, during gait

$$F_{W,p,q,l,j}={\mathit{CF}}_{p,q,l}(\sum _{i=1}^n{O}_{i,j})a$$

The insole forces, based on the two calibration methods, were compared to the vertical component of the force platform ground reaction force, $F_{\mathit{FPp},q,l}$ since the insole sensors only measure pressure that is perpendicular to their surfaces. The insole and force platform force signals were normalized by dividing each by the weight of the participant.

To assess if the linear summation used was viable, a variability analysis was conducted. It was found that the variability of the sensor readings and thus, a linear summation of the sensors would produce little error. The results are included in Appendix 1.

Data analysis

Two dependent variables were calculated based on the force–time histories: stance time and the support-phase impulse. Stance time represents the temporal characteristics of the gait while impulse was selected as it is a representative of the entire ground reaction force–time history.

An onset threshold of 15 N was applied to the force platform and insole force signals to determine the beginning and end of the stance phase.²⁹ Support-phase impulse was defined as the integral of the force signal over stance time. In this work, support-phase impulse was calculated using the trapezoidal rule.

Following Herzog et al.,³⁰ the two variables were normalized to percent differences as follows

$${\mathit{STN}}_{p,q,l}=100(\frac{{\mathit{ST}}_{{\mathit{IN}}_{p,q,l}}-{\mathit{ST}}_{{\mathit{FP}}_{p,q,l}}}{\frac{1}{2}({\mathit{ST}}_{{\mathit{FP}}_{p,q,l}}+{\mathit{ST}}_{{\mathit{IN}}_{p,q,l}})})$$

$$\begin{array}{c}\multicolumn{1}{c}{{\mathit{IMN}}_{C,p,q,l}}\\ \multicolumn{1}{c}{=100(\frac{{\int }_0^{{\mathit{ST}}_{{\mathit{IN}}_{p,q,l}}}(\frac{F_{C,p,q,l}}{W_p})\mathit{dt}-{\int }_0^{{\mathit{ST}}_{{\mathit{FP}}_{p,q,l}}}(\frac{F_{\mathit{FPp},q,l}}{W_p})\mathit{dt}}{\frac{1}{2}({\int }_0^{{\mathit{ST}}_{{\mathit{FP}}_{p,q,l}}}(\frac{F_{\mathit{FPp},q,l}}{W_p})\mathit{dt}+{\int }_0^{{\mathit{ST}}_{{\mathit{IN}}_{p,q,l}}}(\frac{F_{C,p,q,l}}{W_p})\mathit{dt})})}\end{array}$$

where STN and IMN are the normalized stance time and gait impulse, respectively, and C is the calibration method used (manufacturer’s recommendation or weight-based calibration). In these two equations, a negative result indicates that the insole value was smaller than the force platform and a positive value indicates the opposite.

Results

Normalized stance time and support-phase impulse values were calculated for all 234 data sets. These dependent variables were compared qualitatively and quantitatively based on insole sizes. In order to address the question of whether participant weight influenced insole calibration, a correlation study was conducted with the dependent variables and calibration methods.

Qualitative assessment

It was noted that the shapes of the insole force–time histories, based on either insole calibration methods, were qualitatively similar to the corresponding force platform curves in all cases. Figure 4 shows comparison of ground reaction force–time histories for force platforms and insoles with both calibration methods. In most cases, the stance time of the insoles was observed to be greater than that of the force platform (Table 3).

Figure 4.

Typical force–time history measured by the force platform (solid black), the insole calibrated with the manufacturer’s setting (dashed red), and the insole calibrated by the participant’s weight (dotted blue). Three cases were observed when comparing the peaks of the curves based on the insole calibration method: (a) consistently overestimating, (b) consistently underestimating, or (c) mixed results.

Table 3.

Comparison of the stance time of the insoles with respect to the corresponding force platform values. Listed is the frequency of each behavior (N = 234).

Insole sizes	Overestimating	Underestimating	Accurate
35–36	24	0	0
37–38	81	2	1
39–40	31	4	1
41–42	36	0	0
43–44	36	0	0
45–46	17	1	0

The insoles responded in a variety of ways to loading. Using the peak values of the force platform (rearfoot impact and forefoot contact) curves as reference, the insole curves were classified with respect to the force platform curves as consistently overestimating, consistently underestimating, or mixed results (one peak higher and one peak lower). These categorical results are given in Table 4 and shown using exemplar cases in Figure 4.

Table 4.

Comparison of the force values of the ground reaction–time histories of the two calibration methods of the insoles with respect to the corresponding force platform data. Listed is the observed frequency of each behavior (N = 234).

Calibration method	Insole size	Consistent overestimating	Consistent underestimation	Mixed
Manufacturer	35–36	0	19	5
	37–38	0	74	10
	39–40	32	2	2
	41–42	33	0	3
	43–44	33	0	3
	45–46	10	1	7
Weight based	35–36	0	24	0
	37–38	0	82	2
	39–40	0	34	2
	41–42	0	36	0
	43–44	0	36	0
	45–46	0	17	1

Quantitative assessment

To achieve a better understanding of the effects of the calibration method on the output of the insoles, a quantitative analysis was conducted. We calculated the average and standard deviation of the normalized stance time and impulse values for each insole size. The results are summarized in Tables 5 and 6 for stance time and support-phase impulse, respectively.

Table 5.

The average and standard deviation values of the normalized difference of stance time (STN) between the instruments by insole size.

Insole size	Number of total participants	STN (average ± std. dev.)
35–36	4	8.80 ± 4.93
37–38	14	5.88 ± 3.30
39–40	6	3.34 ± 3.54
41–42	6	4.62 ± 2.05
43–44	6	4.47 ± 1.78
45–46	3	7.23 ± 3.63
All insoles	39	5.48 ± 3.59

Table 6.

The average and standard deviation values of the normalized difference of impulse (IMN) between the two calibration methods of the insoles and the force platforms by insole size.

Insole size	Number of total participants	IMN (average ± std. dev.)
		Manufacturer’s calibration	Weight-based calibration
35–36	4	−13.61 ± 8.34	−33.96 ± 5.94
37–38	14	−26.23 ± 11.91	−32.14 ± 8.41
39–40	6	21.67 ± 15.55	−48.01 ± 14.61
41–42	6	22.39 ± 11.11	−39.36 ± 11.23
43–44	6	14.98 ± 7.57	−30.29 ± 6.85
45–46	3	7.05 ± 9.48	−32.45 ± 9.34
All insoles	39	−1.19 ± 24.13	−35.62 ± 11.43

Pearson correlations were conducted between participant weight and each of the normalized dependent variables at the level of insole size. The results are summarized in Table 7. The strength of the correlation was interpreted using the following definitions³¹:

• coefficient values less than ± 0.3: negligible correlations;

• values between ± 0.3 and ± 0.5: weak correlations;

• values between ± 0.5 and ± 0.8: moderate correlations;

• values between ± 0.8 and ± 1.0 were deemed to be strong correlations.

Table 7.

Pearson correlation results for the dependent variables, STN and IMN participant weight for each insole size.

Insole size	STN	IMN
		Manufacturer’s calibration	Weight-based calibration
35–36	−0.10	−0.60	0.04
37–38	−0.12	0	0.31
39–40	0.12	−0.21	0.08
41–42	−0.04	0.41	−0.10
43–44	−0.18	−0.16	−0.29
45–46	0.56	0.56	0.38
All insoles	−0.10	0.40	0.13

Discussion

The purposes of this study were to (1) determine the validity of pressure-measuring insoles for measuring stance time and impulse during walking using two calibration procedures, and (2) examine the effect of insole size on the observed results. In all cases, both calibration methods used on the insoles resulted in force–time histories that were qualitatively similar to the corresponding force platform curves, which confirmed the results of Ong and Wong.²¹ The manufacturer’s calibration underestimated the peaks of the time–ground reaction curves for the two smallest insole sizes while overestimated these peaks for the other insole sizes. The insole size 37 was on the boundary of the change between underestimation and overestimation, which most probably led to the high number of cases in the mixed category. The weight-based calibration consistently underestimated these peaks.

It was observed that the insoles estimated stance time with reasonable accuracy, defined as less than 10% deviation (Table 5). The higher stance time average and standard deviation for the smallest and largest insole sizes may be due to the limited number of participants with these sizes who participated in the study. These differences were consistent with the observation of Ong and Wong,²¹ Braun et al.,²⁴ and Koch et al.²⁵

It can be seen that the support-phase impulse values, based on either insole calibration method, were different from those calculated using the force platform (Table 6). Consistent with the qualitative analysis, the results for the manufacturer’s calibration were not consistent, with the smaller insoles overestimating the impulse. The weight-based calibration consistently underestimated the impulse. Table 6 shows that the manufacturer’s calibration was consistently more accurate than the weight-based calibration for every insole size. Table 6 also shows that the standard deviations for both calibration methods were of the same order of magnitude. Thus, it is apparent that analyzing the data based on insole size may help explain the contrasting results of several studies, where Chen and Bates,¹⁸ Ong and Wong,²¹ and Braun et al.²⁴ reported matches between the force platform and insole data while Crea et al.,⁷ Barnett et al.,¹⁹ and Morin et al.²⁰ showed significant differences. These studies did not document the insole sizes. Correlations between dependent variables and participant weight showed negligible to weak correlations for individual insole sizes and combining all of the insole sizes, suggesting no effect of participant weight on outcome measures.

Other factors could have contributed to the insole measurement errors including the possible slippage of the insole within the participant’s socks.⁷ Also, the effects of velocity were not examined within this study. Future studies may consider examining these factors in addition to the effect of hysteresis, creep, and other mechanical properties that may influence the response and output of the insoles. These mechanical properties could be implemented with dynamic calibration processes, such as system identification modeling or utilizing an individualized weight mapping to determine a calibration factor, to create a more accurate insole result. Finally, further studies should compare the insoles and the force platform at similar sampling frequencies to allow a more direct comparison.

Conclusion

This study aimed to (1) determine the validity of Medilogic® pressure-measuring insoles in measuring stance time and support-phase impulse during barefoot walking using two different calibration methods and, (2) examine the effects of insole size on these two variables.

Comparison of the ground reaction force temporal curves measured by insoles to the corresponding force platform curves shows that the insoles can be used for qualitative assessment of gait. It was observed that when the manufacturer’s calibration method was used, the smaller sizes overestimated the ground reaction force while the larger sizes underestimated the forces. However, weight-based calibration consistently underestimated the forces. Correlation results determined for the individual insole sizes and for a combination of the sizes suggested that participant weight was not a factor that influenced either the stance time or support-phase impulse.

The results indicate that the insoles measure slightly longer stance times but within 10% error. The support-phase impulse values exhibited larger error. The impulse results exhibited both size and calibration method dependencies.

It was therefore concluded that the two presented calibration methods of the Medilogic® insoles were not suitable for measurement of the support-phase impact. Future work should focus on identifying an appropriate calibration method that incorporates other factors including the material properties of the insoles.

Appendix 1

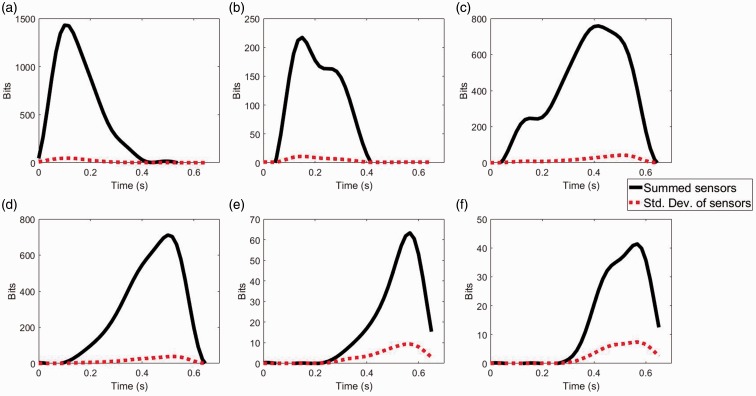
The exemplar figures of variability analysis. The variability of the active sensors summed over an exemplar step is shown in Figure 5. It can be seen that the variability is small. Figure 6 displays the variability analysis for the specific regions of the foot (an example of these regions is shown in Figure 7). The region-specific exemplar curves of Figure 6 show the bits summed over a single step and the variability of those sensor values. The variability is small for each region.

Figure 5.

An exemplar curve of the sensors summed over a step and the corresponding standard deviation of those sensor bit values. This image shows that the variability in active sensors is small.

Figure 6.

A set of exemplar curves of the sensors summed over a step and the standard deviation of those sensor bit values. The sensors were divided into anatomical regions based on the sensor location on the insole. This image shows that the variability in active sensors is small for all regions, with the toes showing the largest standard deviation values. (a) Heel sensors, (b) midfoot sensors, (c) metatarsals 3–5 sensors, (d) metatarsals 1–2 sensors, (e) toes 3–5 sensors, and (f) toes 1–2 sensors.

Figure 7.

An example of an insole (size 37 EUR) with the sensors coded to each anatomical region. These regions were used to produce region-specific variability analyses.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research has been supported by the University of Nevada, Las Vegas (Faculty Opportunity Award #2220-272-76TP) and the Mountain West Clinical Translational Research Infrastructure Network (Mini-Grant Award #2364-254-910 F).

Guarantor

JDB.

Contributorship

JDB developed the protocol under the supervision of MBT and JSD. JDB and DEL recruited participants and collected the data. The data was analyzed by JDB. The first draft of the manuscript was written by JDB and all authors reviewed and edited the manuscript. The final version of the manuscript has been approved by all authors. MBT and JSD were responsible for securing funding for the project.